Model-Free Power Control for Low-Voltage AC Dispatchable Microgrids with Multiple Points of Connection †
Abstract
:1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contributions and Paper Organization
- •
- An improved version of the PBC (i.e., MPBC) that treats the arbitrary inverter connections (i.e., line-to-line and line-to-neutral) in a proper and individual manner to increase the degree of freedom of the control strategy. Thus, the objective is to make each DER process only the power terms that fit into its type of connection (i.e., line-to-line and line-to-neutral). To do so, different scalar coefficients are defined for single-phase line-to-line and line-to-neutral DERs, which doubles the degree of freedom of the PBC algorithm in relation to its previous versions. Hence, accurate power sharing among the DERs and unbalance current compensation are achieved if line-to-line DERs and line-to-neutral DERs share balanced power components, while unbalanced and homopolar power components are steered to line-to-neutral DERs. Also, MPBC results in faster dynamic response and lower grid power losses than the conventional PBC and it is self-adjusted to different grid topologies.
- •
- In addition, a power flow control strategy is presented for meshed µGs with multiple PCCs. This scenario has not yet been explored in the literature with the use of PBC, and it is analyzed in this paper as a case study of the MPBC application to control one PCC of the meshed µG at a time, according to the references defined by the DSO.
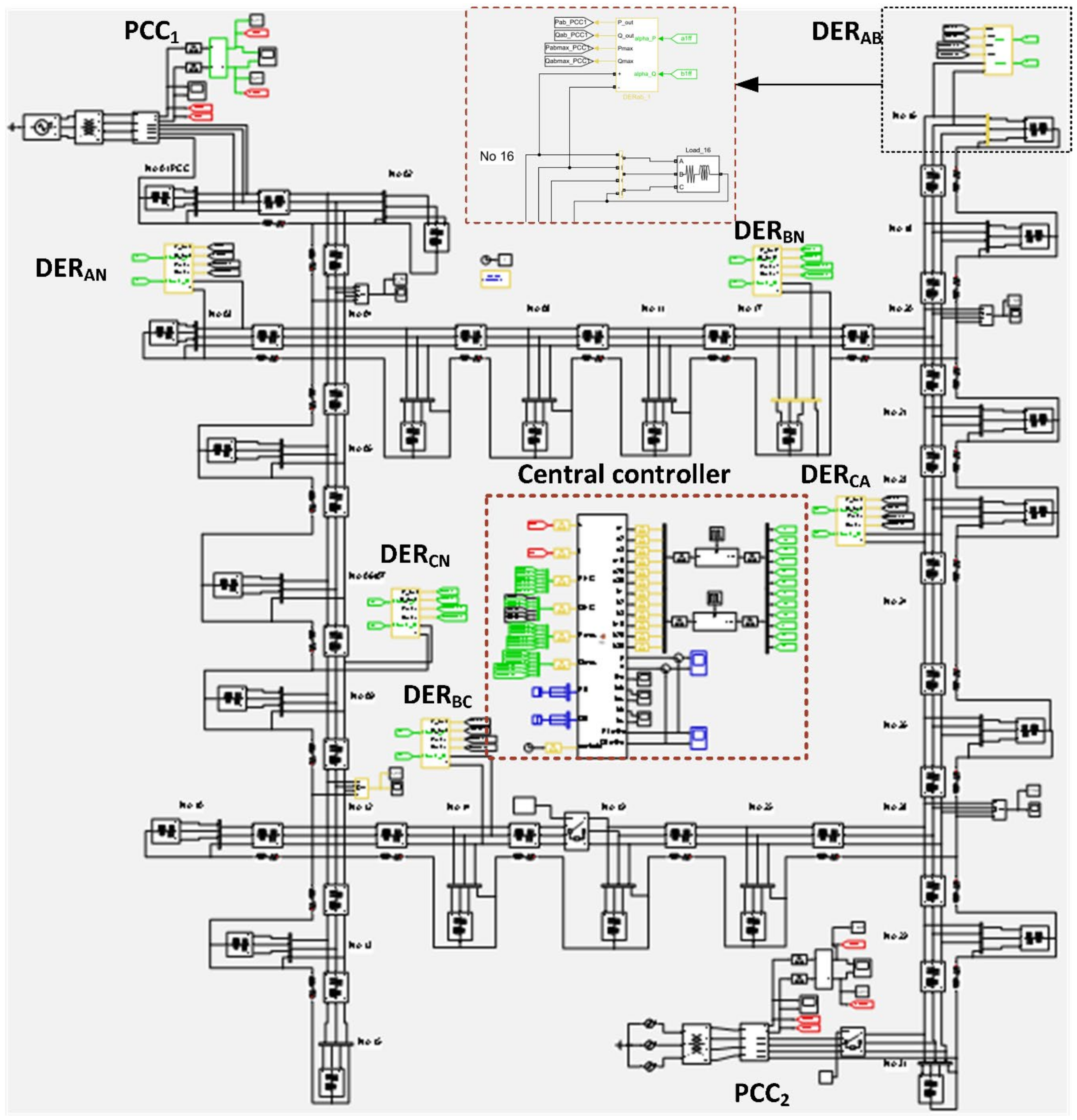
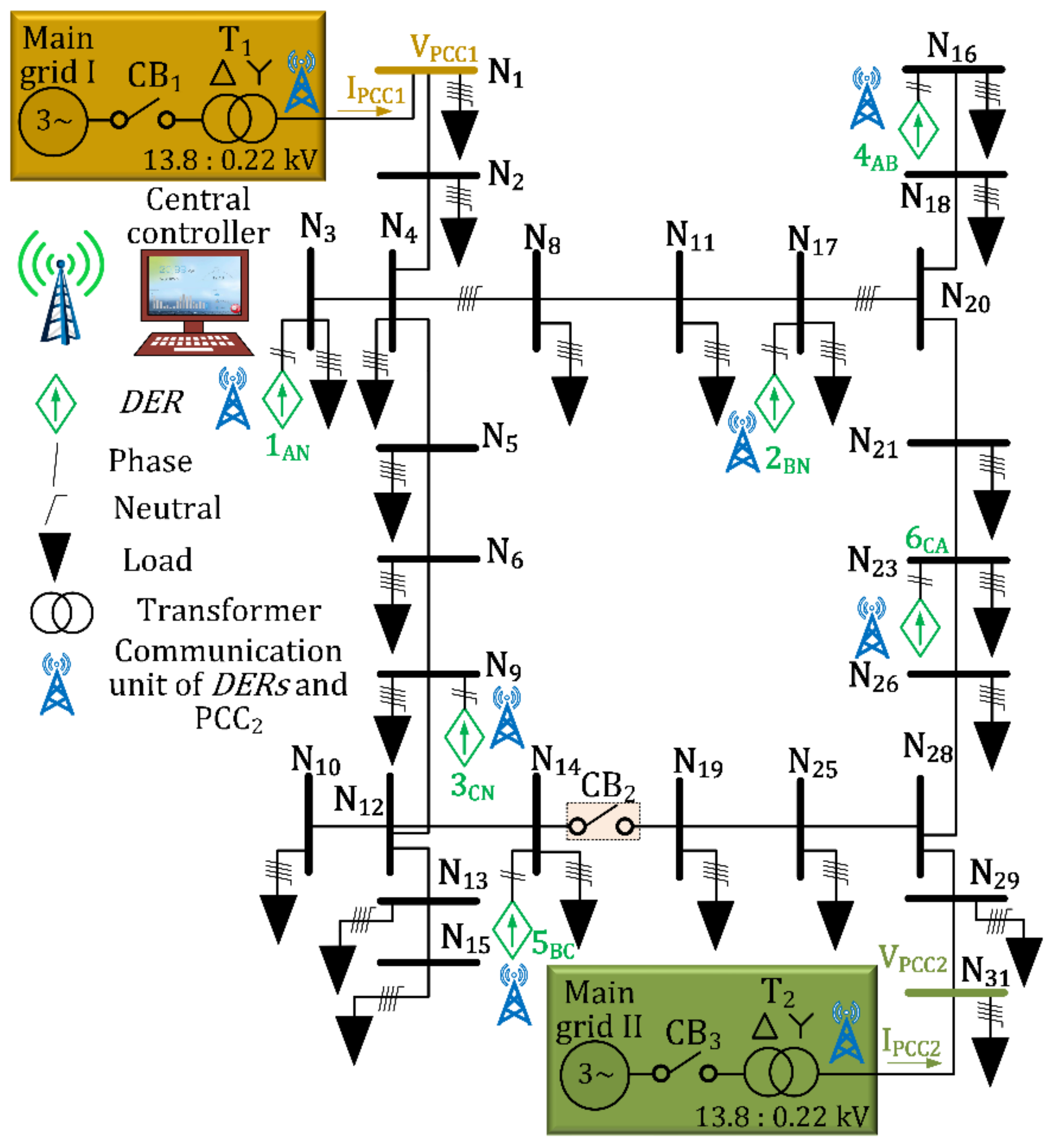
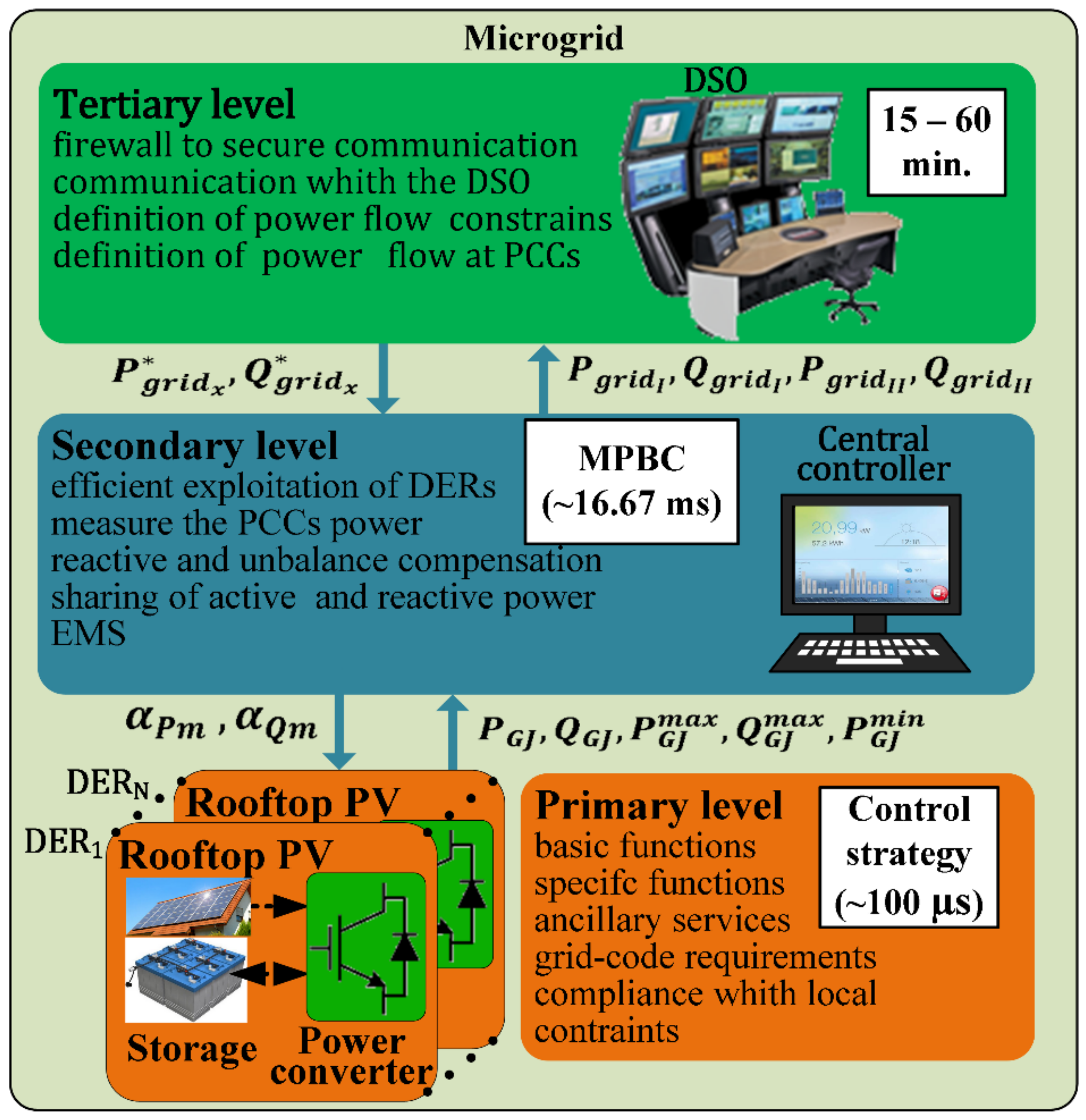
2. Structure, Topology and Control Approach of the Microgrid Testbench
3. Modified Power-Based Control (MPBC)
3.1. Power Quantities at the µG Points of Common Coupling (PCCs)
- •
- Homopolar power ( and ): the power components of these vectors are calculated for each PCC phase considering only the homopolar components of the currents, which are extracted by using .An inherent characteristic of the homopolar power is that . Also, it is possible to calculate the vectors of non-homopolar power at the PCC phases as: and .
- •
- Balanced power ( and ): these vectors represent a three-phase balanced load-equivalent power consumption, and their elements are calculated for each phase in function of the rms values of the PCC line-to-neutral voltages as:
3.2. Power Transformation Matrices
3.3. Data Packet of the MPBC Distributed Energy Resources (DERs)
- •
- Active and reactive power injected into the µG: ;
- •
- Maximum active and reactive power it can inject into the µG: varies according to the available energy resources of each DER at the cycle , while depends on and the nominal power of the DER;
- •
- Maximum active power that it can absorb from the µG: .
3.4. MPBC Algorithm
- •
- If there are only line-to-line connected DERs in the µG, their power references are calculated by:Equations (12) and (13) address balanced active power and reactive power to the line-to-line DERs and neglect the homopolar power, which cannot be injected by line-to-line connected DERs. In this case, the reactive power injected by the line-to-line DERs compensates unbalance power consumption caused by non-homopolar currents.
- •
- If there are only line-to-neutral connected DERs in the µG, no power decomposition is necessary since the line-to-neutral connection allows a complete phase-decoupled power injection. Thus, the power references are computed as:
- •
- If both line-to-line and line-to-neutral DERs are connected to the µG, these two types of DERs can share the PCC power demands. To do so, let and be the maximum power capacities obtained from and using (6) and (7). Then, the vectors of demand-sharing coefficients are defined as:and the power shared are calculated as:in which is the identity matrix. Hence, the power references for the line-to-neutral DERs are:and for the line-to-line DERs:
- •
- For the line-to-line connected DERs:
- •
- For the line-to-neutral DERs:
3.5. Power References in Each DER
- •
- On the DER connected between phases and :
- •
- On the DER connected between phase and the neutral conductor:
4. Simulation Results
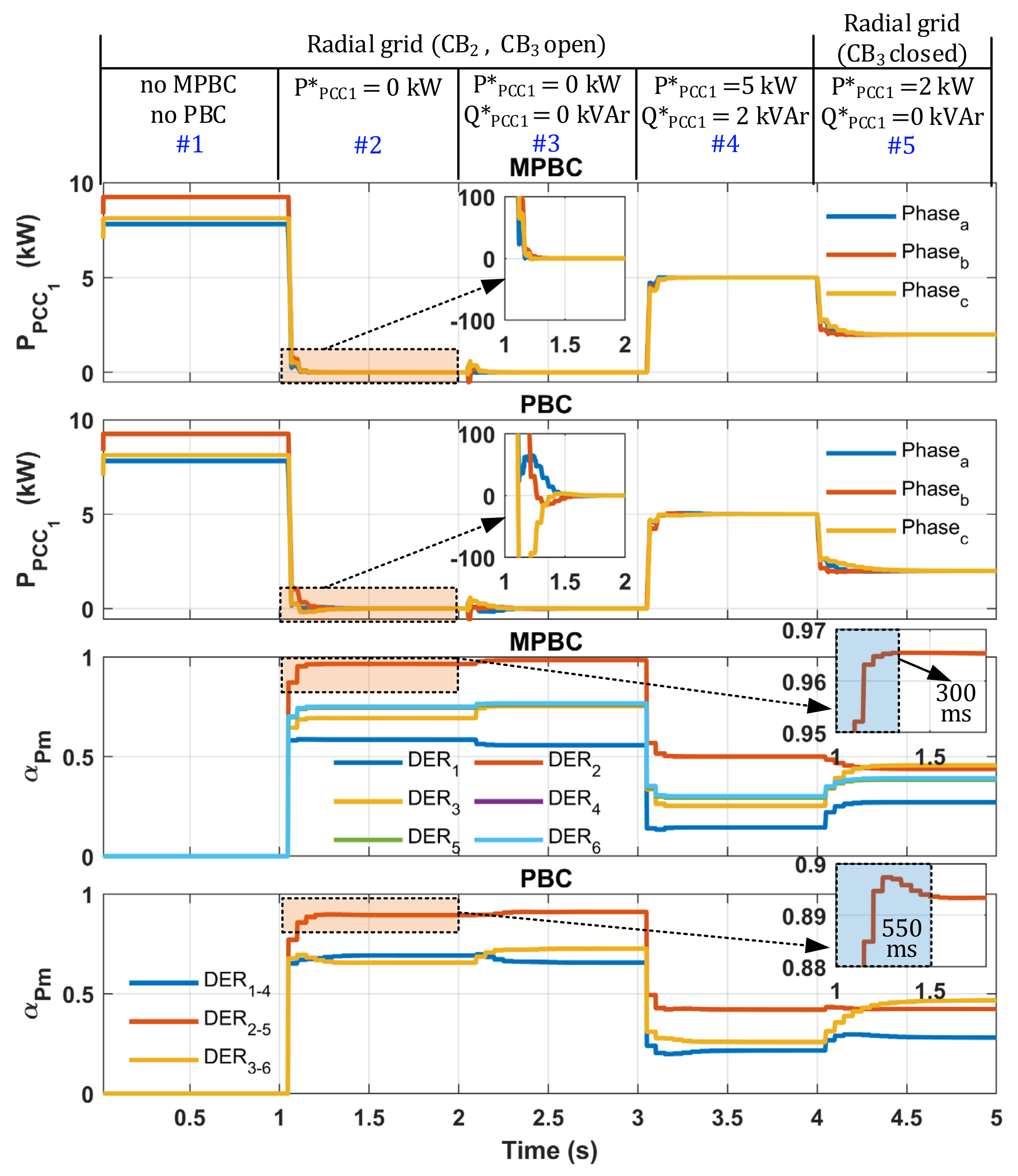
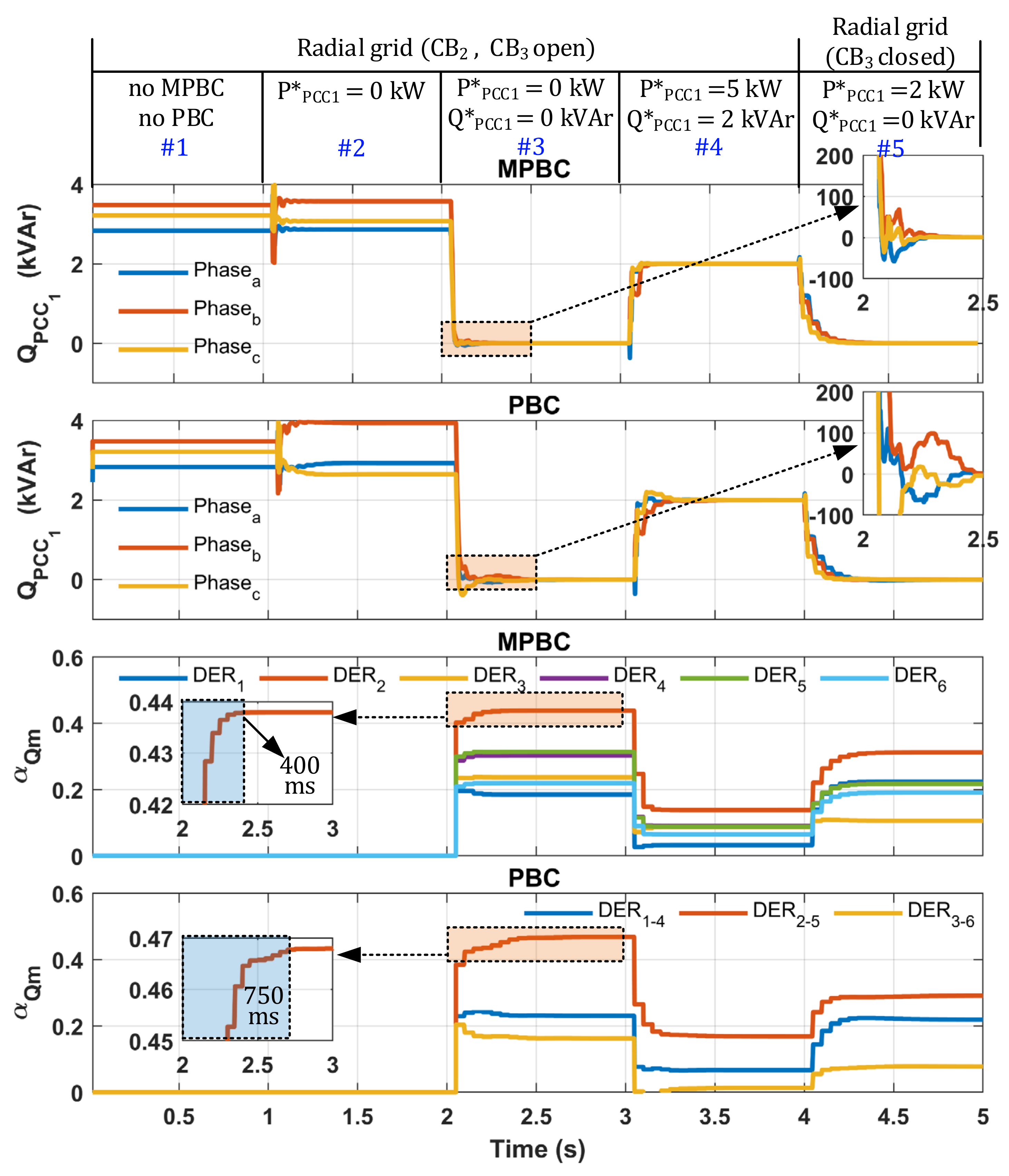
4.1. Comparison between MPBC and PBC
- •
- Interval #1, the DERs are disabled, and the load demand is fully supplied by the mains itself through PCC1.
- •
- At instant 1 s (interval #2), the algorithm is enabled and starts to control only active power through the PCC1 considering .
- •
- At instant 2 s (interval #3), active and reactive power references in PCC1 are: , .
- •
- At instant 3 s (interval #4), active and reactive power references in PCC1 are: , .
- •
- Finally, at instant 4 s (interval #5), CB3 is closed, and the µG starts to operate with two PCCs. The power references in PCC1 are: , .
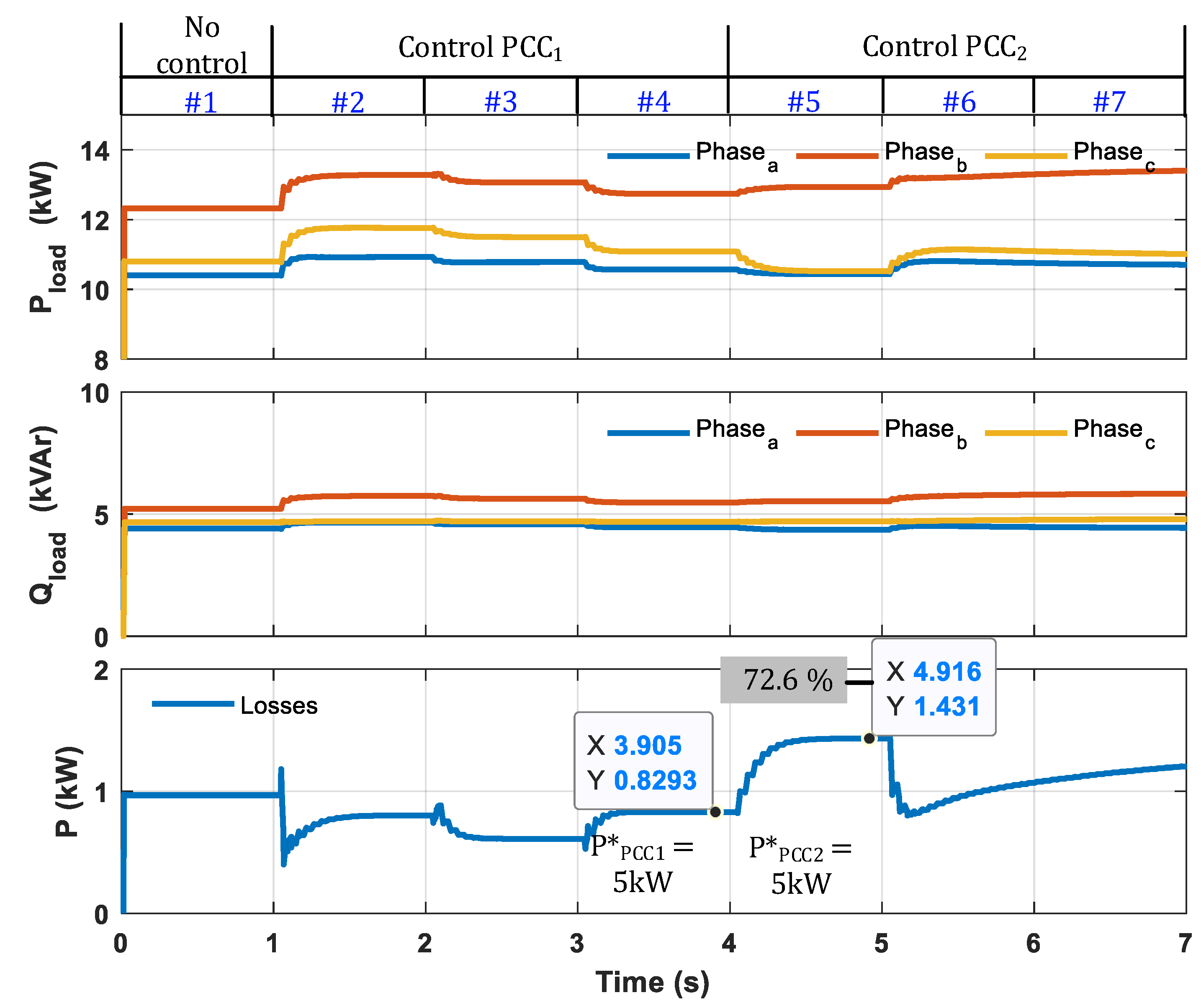
4.2. MPBC Applied to Meshed µG with Multiple PCCs
- •
- Interval #1: DERs are disabled, and the load demand is fully supplied by the mains itself through PCC1 and PCC2.
- •
- At instant 1 s (interval #2), the algorithm is enabled with power control on PCC1 with the following references: , .
- •
- At instant 2 s (interval #3), power references to PCC1 are defined as: , .
- •
- At instant 3 s (interval #4), power references to PCC1 are defined as: , .
- •
- At instant 4 s (interval #5), the DSO changes the power references for PCC2, thus , .
- •
- At instant 5 s (interval #6), power references to PCC2 are defined as: , . Being kept in this condition until the end of (interval #7).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CC | Central Controller |
| CCM | Current-Controlled Mode |
| DERs | Distributed Energy Resources |
| DSO | Distribution System Operator |
| EMS | Energy Management Systems |
| ESSs | Energy Storage Systems |
| ICT | Information and Communication Technology |
| µG | Microgrid |
| µGCs | Microgrid Clusters |
| MPBC | Modified Power-Based Control |
| PBC | Power-Based Control |
| PCCs | Points of Common Coupling |
| PQ | Power Quality |
| VCM | Voltage-Controlled Mode |
Appendix A
References
- IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. In IEEE Std 1547-2018; (Revision IEEE Std 1547-2003); IEEE: New York, NY, USA, 2018; pp. 1–138.
- Younesi, A.; Shayeghi, H.; Siano, P.; Safari, A.; Alhelou, H.H. Enhancing the Resilience of Operational Microgrids through a Two-Stage Scheduling Strategy Considering the Impact of Uncertainties. IEEE Access 2021, 9, 18454–18464. [Google Scholar] [CrossRef]
- Abessi, A.; Jadid, S.; Salama, M.M.A. A New Model for a Resilient Distribution System after Natural Disasters Using Microgrid Formation and Considering ICE Cars. IEEE Access 2021, 9, 4616–4629. [Google Scholar] [CrossRef]
- Cheng, Z.; Duan, J.; Chow, M.Y. To Centralize or to Distribute: That Is the Question: A Comparison of Advanced Microgrid Management Systems. IEEE Ind. Electron. Mag. 2018, 12, 6–24. [Google Scholar] [CrossRef]
- Ismael, S.M.; Abdel Aleem, S.H.E.; Abdelaziz, A.Y.; Zobaa, A.F. State-of-the-art of hosting capacity in modern power systems with distributed generation. Renew. Energy 2019, 130, 1002–1020. [Google Scholar] [CrossRef]
- Alam, M.N.; Chakrabarti, S.; Ghosh, A. Networked Microgrids: State-of-the-Art and future perspectives. IEEE Trans. Ind. Inform. 2019, 15, 1238–1250. [Google Scholar] [CrossRef]
- Shoeb, M.A.; Shafiullah, G.M.; Shahnia, F. Coupling Adjacent Microgrids and Cluster Formation under a Look-Ahead Approach Reassuring Optimal Operation and Satisfactory Voltage and Frequency. IEEE Access 2021, 9, 78083–78097. [Google Scholar] [CrossRef]
- Zhou, Q.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Flexible Division and Unification Control Strategies for Resilience Enhancement in Networked Microgrids. IEEE Trans. Power Syst. 2020, 35, 474–486. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Wang, H.; Zhang, H.; Yang, W.; Cao, R. Research on bi-level optimized operation strategy of microgrid cluster based on iabc algorithm. IEEE Access 2021, 9, 15520–15529. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Chen, C. Networked microgrids for self-healing power systems. IEEE Trans. Smart Grid 2016, 7, 310–319. [Google Scholar] [CrossRef]
- Zhou, B.; Zou, J.; Chung, C.Y.; Wang, H.; Liu, N.; Voropai, N.; Xu, D. Multi-microgrid Energy Management Systems: Architecture, Communication, and Scheduling Strategies. J. Mod. Power Syst. Clean Energy 2021, 9, 463–476. [Google Scholar] [CrossRef]
- Rosado, S.P.; Khadem, S.K. Development of Community Grid: Review of Technical Issues and Challenges. IEEE Trans. Ind. Appl. 2019, 55, 1171–1179. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, P.; Wang, Y.; Xu, Z.; Guerrero, J.M. Dynamic Characteristics Analysis and Stabilization of PV-Based Multiple Microgrid Clusters. IEEE Trans. Smart Grid 2019, 10, 805–818. [Google Scholar] [CrossRef] [Green Version]
- Bandeiras, F.; Pinheiro, E.; Gomes, M.; Coelho, P.; Fernandes, J. Review of the cooperation and operation of microgrid clusters. Renew. Sustain. Energy Rev. 2020, 133, 110311. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Begovic, M.M.; Chen, C. Coordinated energy management of networked microgrids in distribution systems. IEEE Trans. Smart Grid 2015, 6, 45–53. [Google Scholar] [CrossRef]
- Fathi, M.; Bevrani, H. Statistical cooperative power dispatching in interconnected microgrids. IEEE Trans. Sustain. Energy 2013, 4, 586–593. [Google Scholar] [CrossRef]
- Marzband, M.; Parhizi, N.; Savaghebi, M.; Guerrero, J.M. Distributed Smart Decision-Making for a Multimicrogrid System Based on a Hierarchical Interactive Architecture. IEEE Trans. Energy Convers. 2016, 31, 637–648. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.X.; Xu, Y.; Wu, X.X.; He, J.; Guerrero, J.M.; Liu, C.-C.; Schneider, K.P.; Ton, D.T. A Two-Layer Distributed Cooperative Control Method for Islanded Networked Microgrid Systems. IEEE Trans. Smart Grid 2020, 11, 942–957. [Google Scholar] [CrossRef]
- Mazidi, M.; Rezaei, N.; Ardakani, F.J.; Mohiti, M.; Guerrero, J.M. A hierarchical energy management system for islanded multi-microgrid clusters considering frequency security constraints. Int. J. Electr. Power Energy Syst. 2020, 121, 106134. [Google Scholar] [CrossRef]
- Lu, X.; Lai, J.; Yu, X. A Novel Secondary Power Management Strategy for Multiple AC Microgrids with Cluster-Oriented Two-Layer Cooperative Framework. IEEE Trans. Ind. Inform. 2021, 17, 1483–1495. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Z.; Shahidehpour, M.; Lai, L.L.; Wang, Z.; Zhu, Q. Reconfigurable Distribution Network for Managing Transactive Energy in a Multi-Microgrid System. IEEE Trans. Smart Grid 2020, 11, 1286–1295. [Google Scholar] [CrossRef]
- Fu, L.; Liu, B.; Meng, K.; Dong, Z.Y. Optimal Restoration of an Unbalanced Distribution System into Multiple Microgrids Considering Three-Phase Demand-Side Management. IEEE Trans. Power Syst. 2021, 36, 1350–1361. [Google Scholar] [CrossRef]
- Tenti, P.; Caldognetto, T. Optimal control of Local Area Energy Networks (E-LAN). Sustain. Energy Grids Netw. 2018, 14, 12–24. [Google Scholar] [CrossRef]
- Caldognetto, T.; Buso, S.; Tenti, P.; Brandao, D.I. Power-Based Control of Low-Voltage Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1056–1066. [Google Scholar] [CrossRef]
- Brandao, D.I.; Caldognetto, T.; Marafão, F.P.; Simões, M.G.; Pomilio, J.A.; Tenti, P. Centralized Control of Distributed Single-Phase Inverters Arbitrarily Connected to Three-Phase Four-Wire Microgrids. IEEE Trans. Smart Grid 2017, 8, 437–446. [Google Scholar] [CrossRef] [Green Version]
- Brandao, D.I.; Araujo, L.S.; Alonso, A.M.S.; dos Reis, G.L.; Liberado, E.V.; Marafao, F.P. Coordinated Control of Distributed Three-and Single-phase Inverters Connected to Three-Phase Three-Wire Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 3861–3877. [Google Scholar] [CrossRef] [Green Version]
- Brandão, D.; Pomilio, J.; Marafão, F.; Alonso, A. Experimental Validation of a Fully-Dispatchable Microgrid With Central Controller. Braz. J. Power Electron. 2018, 23, 281–291. [Google Scholar] [CrossRef]
- Serban, I.; Cespedes, S.; Marinescu, C.; Azurdia-Meza, C.A.; Gomez, J.S.; Hueichapan, D.S. Communication requirements in microgrids: A practical survey. IEEE Access 2020, 8, 47694–47712. [Google Scholar] [CrossRef]
- Schneider Electric Efficient Green Power for Islandable Microgrids. Available online: https://download.schneider-electric.com/files?p_enDocType=Technical+leaflet&p_File_Name=AU+Schneider+Electric+EcoStruxure+Microgrid+Operation+brochure_WEB.pdf&p_Doc_Ref=998-20651229_AU-GB (accessed on 20 October 2020).
- General Electric GridNode: Microgrid Solution. Available online: https://www.gegridsolutions.com/products/brochures/services/microgrid-solutions-flyer-33153-en-202005-ltr-r005-lr.pdf (accessed on 20 October 2020).
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the art in research on microgrids: A review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Liu, Q.; Caldognetto, T.; Buso, S. Review and Comparison of Grid-Tied Inverter Controllers in Microgrids. IEEE Trans. Power Electron. 2020, 35, 7624–7639. [Google Scholar] [CrossRef]
- Brandao, D.I.; de Araújo, L.S.; Caldognetto, T.; Pomilio, J.A. Coordinated control of three- and single-phase inverters coexisting in low-voltage microgrids. Appl. Energy 2018, 228, 2050–2060. [Google Scholar] [CrossRef]




| PBC Generation. | Features | Topology/Number of PCCs |
|---|---|---|
| PBC-I [24] | Proposed to single-phase µG. Proportional power sharing among DERs by two scalar coefficients (αP, αQ). If extended for three-phase grids, it does not compensate current unbalance. All DERs are considered current-controlled modes (CCM), and the µG shows just one PCC. | Radial (1Φ) 4 Nodes 1 PCC |
| PBC-II [25] | Proposed to three-phase four-wire µG. It proportionally shares power among DERs that are connected at the same m-phase and provides current unbalance compensation at the PCC using six scalar phase coefficients αPm and αQm, on which m represents phases a, b and c. The three-phase DERs operate unbalanced. All DERs are considered CCM, and the µG shows just one PCC. | Radial (3Φ+N) 13 Nodes 1 PCC |
| PBC-III [26] | Proposed for three-phase three-wire µG. It proportionally shares the power among the DERs connected in the same phase and provides current unbalance compensation at the PCC using eight scalar phase coefficients αPm, αQm, αP3Φ and αQ3Φ. Three-phase DERs can operate balanced. DERs are of CCM and voltage-controlled modes (VCM), and the µG shows just one PCC. | Radial (3Φ) 13 Nodes 1 PCC |
| MPBC Herein | Proposed for three-phase four-wire µG. Line-to-line and line-to-neutral DERs share balanced power quantities, while unbalanced and homopolar power are steered only to line-to-neutral DERs. The DERs are CCM, and the µG shows multi-PCC. | Meshed (3Φ+N) 29 Nodes 2 PCC |
| Topology | Circuit Breakers Status | Power Supply |
|---|---|---|
| radial | (CB1 – CB3) closed e (CB2) open | PCC1 e PCC2 |
| radial | (CB1) closed e (CB2 – CB3) open | PCC1 |
| radial | (CB3) closed e (CB1, CB2) open | PCC2 |
| meshed | (CB1, CB2 e CB3) closed | PCC1 e PCC2 |
| meshed | (CB1 – CB2) closed e (CB3) open | PCC1 |
| Parameter | DERj (N3, N17, N9, N16, N14, N26) |
|---|---|
| Connection in phase | (a, b, c, ab, bc, ca) |
| Power rating [kVA] | (6.0, 6.0, 6.0, 8.0, 8.0, 8.0) |
| Power capacity [kW] | (5.0, 5.0, 5.0, 7.0, 7.0, 7.0) |
| Max. power capacity [kW] | (5.0, 5.0, 5.0, 7.0, 7.0, 7.0) |
| Min. power capacity [kW] | −(5.0, 5.0, 5.0, 7.0, 7.0, 7.0) |
| t = 1 s | t = 1.5 s | t = 3 s | t = 3.5 s | Eq. | |
|---|---|---|---|---|---|
| [7815, 9244, 8124] | [0, 0, 0] | [0, 0, 0] | [5000, 5000, 5000] | ||
| [2831, 3474, 3212] | [2861, 3569, 3066] | [0, 0, 0] | [2000, 2000, 2000] | ||
| [−372, 316, 56] | [−146, −53, 199] | [0, 0, 0] | [5, −3, −2] | ||
| [150, 247, −397] | [−145, 199, −54] | [0, 0, 0] | [0, −5, 5] | ||
| [8187, 8928, 8068] | [146, 53, −199] | [0, 0, 0] | [4995, 5003, 5002] | ||
| [2681, 3228, 3610] | [3005, 3370, 3122] | [0, 0, 0] | [2000, 2005, 1995] | ||
| [8408, 8379, 8396] | [0, 0, 0] | [0, 0, 0] | [4998, 5004, 4998] | (1) | |
| [3178, 3167, 3173] | [3163, 3160, 3174] | [0, 0, 0] | [1999, 2002, 1999] | (1) | |
| [−221, 549, −328] | [146, 53, −199] | [0, 0, 0] | [−4, −1, 5] | (2) | |
| [−497, 61, 436] | [−158, 210, −52] | [0, 0, 0] | [1, 3, −4] | (2) | |
| [126, 126, 126] | [127, 127, 127] | [127, 127, 127] | [127, 127, 127] | ||
| [126, 126, 126] | [127, 127, 127] | [127, 127, 127] | [127, 127, 127] | ||
| (4) | |||||
| (5) | |||||
| [0, 0, 0] | [2927, 4827, 3464] | [2790, 4919, 3768] | [722, 2498, 1269] | (8) | |
| [0, 0, 0] | [5220, 5229, 5252] | [5331, 5339, 5369] | [2063, 2062, 2109] | (9) | |
| [0, 0, 0] | [0, 0, 0] | [1071, 1554, 1248] | [193, 809, 519] | (8) | |
| [0, 0, 0] | [0, 0, 0] | [2083, 2159, 1506] | [716, 702, 513] | (9) | |
| [5000, 5000, 5000] | [5000, 5000, 5000] | [5000, 5000, 5000] | [5000, 5000, 5000] | (10) | |
| [7000, 7000, 7000] | [7000, 7000, 7000] | [7000, 7000, 7000] | [7000, 7000, 7000] | (11) | |
| [6000, 6000, 6000] | [5750, 3779, 5499] | [5795, 3547, 5285] | [5999, 5869, 5991] | (10) | |
| [8000, 8000, 8000] | [6989, 6982, 6962] | [6894, 6886, 6858] | [7977, 7977, 7975] | (11) | |
| [0.416, 0.417, 0.417] | [0.417, 0.417, 0.416] | [0.417, 0.416, 0.417] | [0.417, 0.417, 0.417] | (16) | |
| [0.428, 0.429, 0.429] | [0.452, 0.351, 0.441] | [0.457, 0.340, 0.435] | [0.429, 0.424, 0.429] | (17) | |
| [3502, 3493, 3498] | [0, 0, 0] | [−2084, −2082, −2084] | [−1, 2, −1] | (18) | |
| [1361, 1358, 1360] | [1429, 1110, 1398] | [-915, −679, −870] | [0, 1, 0] | (19) | |
| [4906, 4886, 4898] | [0, 0, 0] | [−2916, −2918, −2916] | [−1, 2, −1] | (20) | |
| [1816, 1809, 1813] | [1733, 2050, 1775] | [-1085, −1320, −1130] | [0, 1, 0] | (21) | |
| [2908, 4358, 3226] | [2927, 4827, 3464] | [702, 2842, 1683] | [722, 2498, 1269] | (22) | |
| [1014, 1665, 1399] | [1127, 1519, 1291] | [155, 877, 378] | [193, 809, 519] | (23) | |
| [4895, 4886, 4909] | [5220, 5229, 5252] | [2411, 2417, 2460] | [2063, 2062, 2109] | (24) | |
| [1812, 1809, 1818] | [2013, 2091, 1455] | [807, 792, 614] | [716, 702, 513] | (25) | |
| [0.699, 0.698, 0.701] | [0.746, 0.747, 0.750] | [0.344, 0.345, 0.351] | [0.295, 0.295, 0.301] | (26) | |
| [0, 0, 0] | [0, 0, 0] | [0.117, 0.115, 0.089] | [0.090, 0.088, 0.064] | (27) | |
| [0.582, 0.872, 0.645] | [0.585, 0.965, 0.693] | [0.140, 0.568, 0.337] | [0.144, 0.500, 0.254] | (28) | |
| [0, 0, 0] | [0, 0, 0] | [0.027, 0.247, 0.071] | [0.032, 0.138, 0.087] | (29) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
dos Reis, G.; Liberado, E.; Marafão, F.; Sousa, C.; Silva, W.; Brandao, D. Model-Free Power Control for Low-Voltage AC Dispatchable Microgrids with Multiple Points of Connection. Energies 2021, 14, 6390. https://doi.org/10.3390/en14196390
dos Reis G, Liberado E, Marafão F, Sousa C, Silva W, Brandao D. Model-Free Power Control for Low-Voltage AC Dispatchable Microgrids with Multiple Points of Connection. Energies. 2021; 14(19):6390. https://doi.org/10.3390/en14196390
Chicago/Turabian Styledos Reis, Geovane, Eduardo Liberado, Fernando Marafão, Clodualdo Sousa, Waner Silva, and Danilo Brandao. 2021. "Model-Free Power Control for Low-Voltage AC Dispatchable Microgrids with Multiple Points of Connection" Energies 14, no. 19: 6390. https://doi.org/10.3390/en14196390








