Calculation Method of Allowable Continuous Current for Direct Burial Laying HVDC Underground Cable
Abstract
:1. Introduction
2. The Method for Calculating Allowable Current of HVDC Underground Cable
2.1. AC Cable Allowable Current Formula
2.2. HVDC Cable Allowable Current
2.2.1. Maximum Resistance of DC Conductor (R)
- Resistivity (ρ) and temperature correction factor (α) of conductor.
- Cross-sectional area (copper, aluminum).
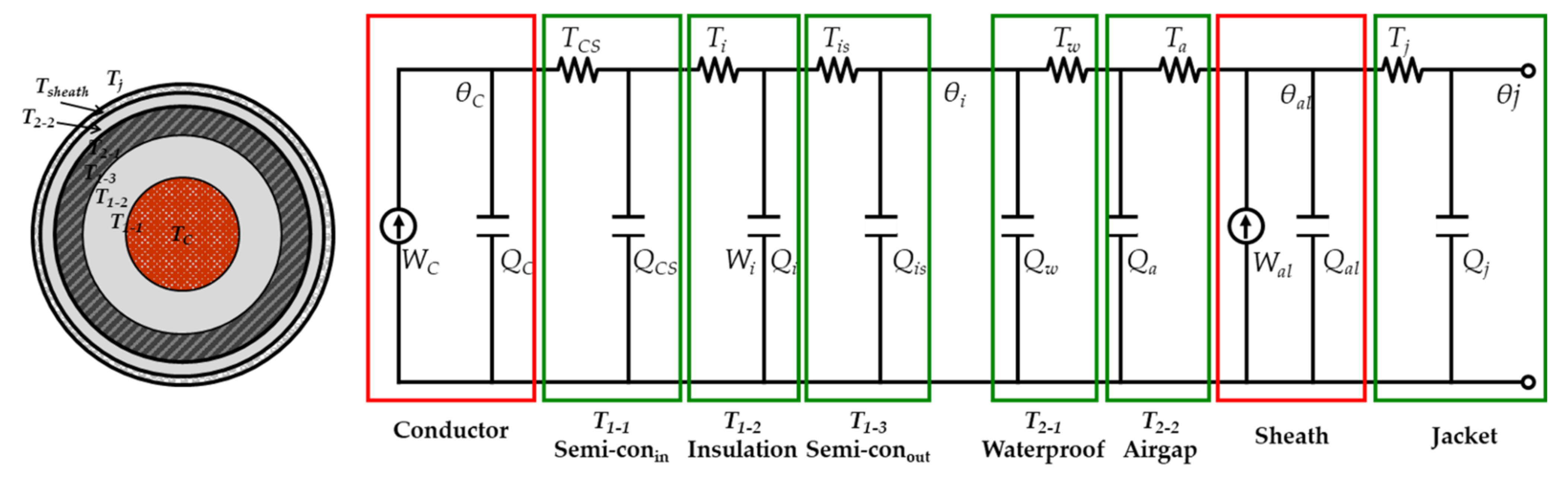
2.2.2. Thermal Resistance According to the Thermal Gradient
- Thermal resistance of the insulator (T1).
- The case of specific thermal resistance is the same (Ex. XLPE cable).
- 2.
- The case of thermal resistance is not the same (Ex. MI-PPLP cable).
- Thermal resistance of waterproof tape and air gap (T2).
- Thermal resistance of the metal sheath (T3).
- Types of metal sheath.
- 2.
- Structural features.
- Thermal resistance of surrounding environment (T4).
- Thermal resistance according to soil depth when installing single cables.
- 2.
- Thermal resistance according to soil depth when installing multiple cables.
- 3.
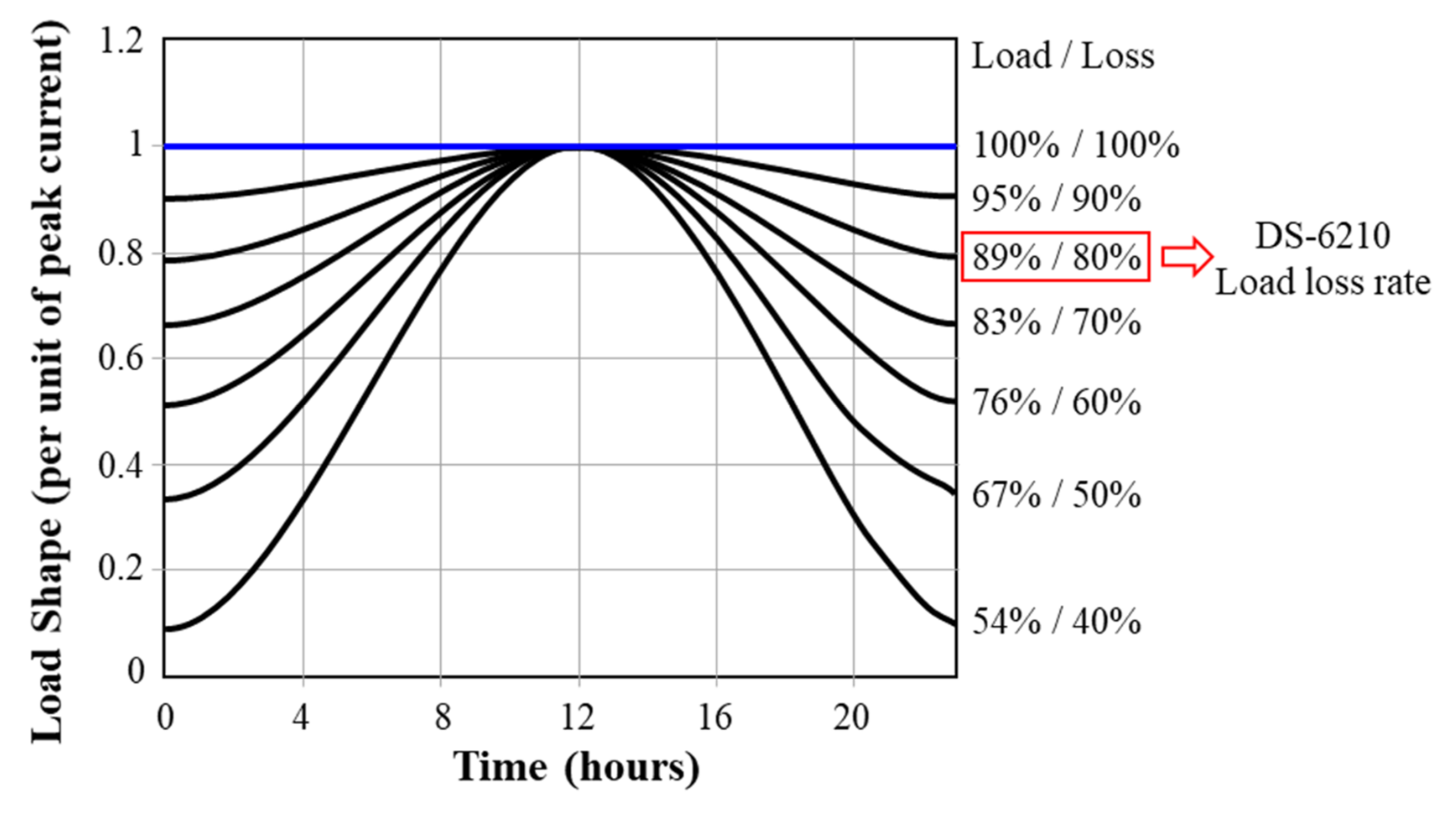
- Thermal resistance according to load change conditions.
- 4.
- Calculation of thermal resistance in direct burial laying.
3. HVDC Cable Continuous Allowable Current Simulation Conditions
3.1. Cable System Modeling and Soil Temperature Conditions
3.1.1. Cable Specifications and Soil Conditions
- Soil thermal resistance.
3.1.2. Cable Arrangement Conditions
3.1.3. Calculation Tool for Applying Continuous Allowable Current for HVDC Underground Transmission Cable
4. Comparative Analysis of Continuous Allowable Current of HVDC Underground Transmission Cable
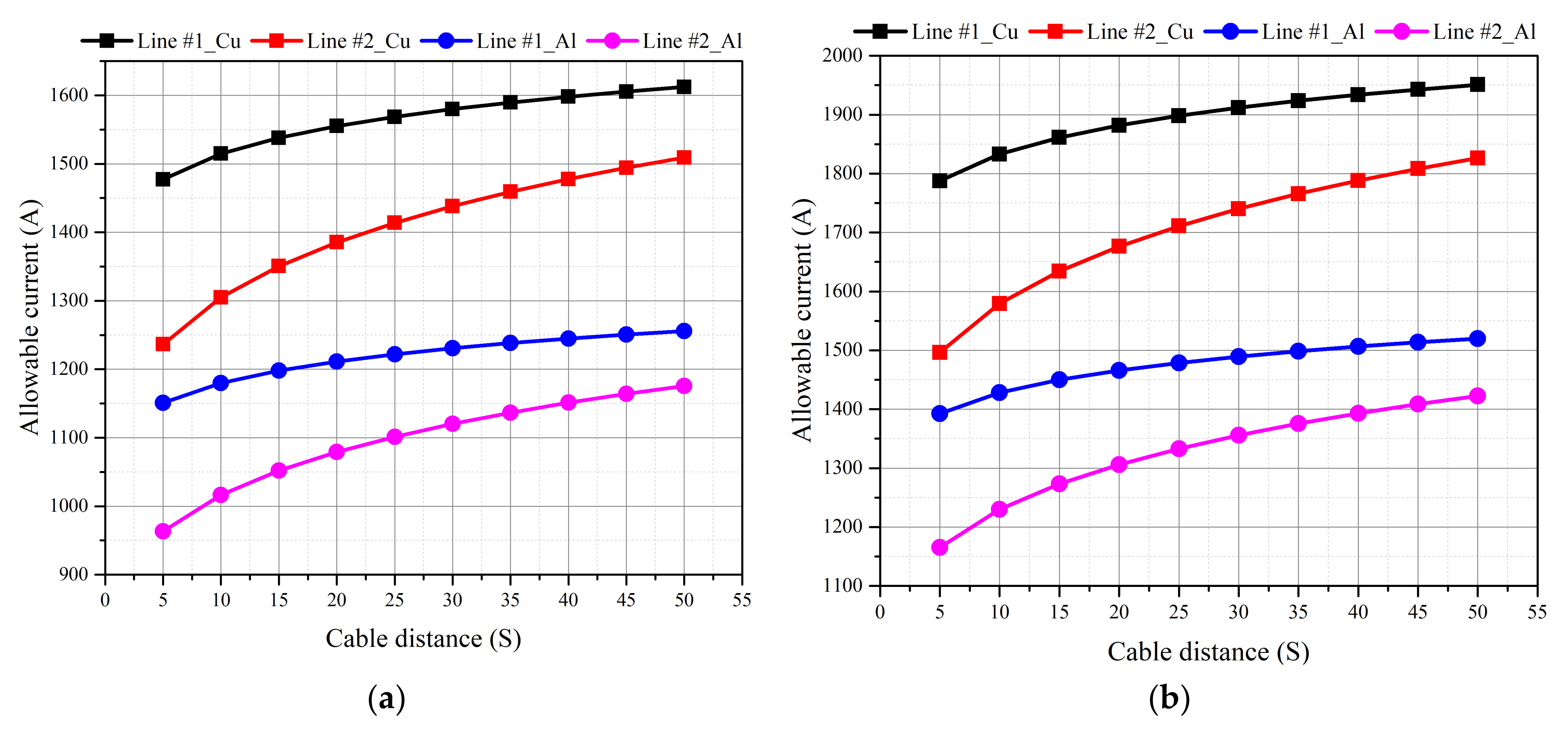
4.1. Calculation of Continuous Allowable Current Considering Major Factor
Calculation of Allowable Current for Direct Burial Laying
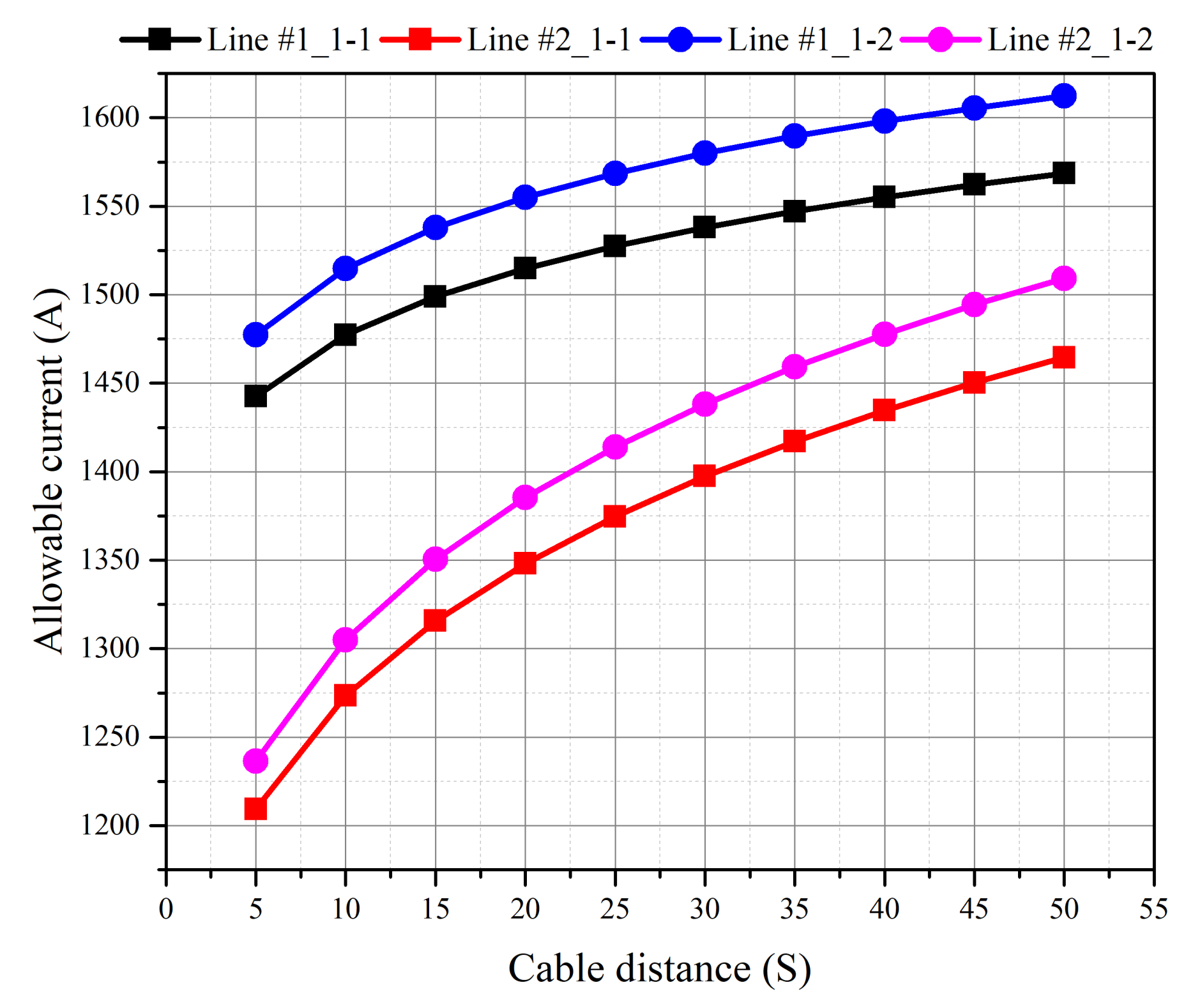
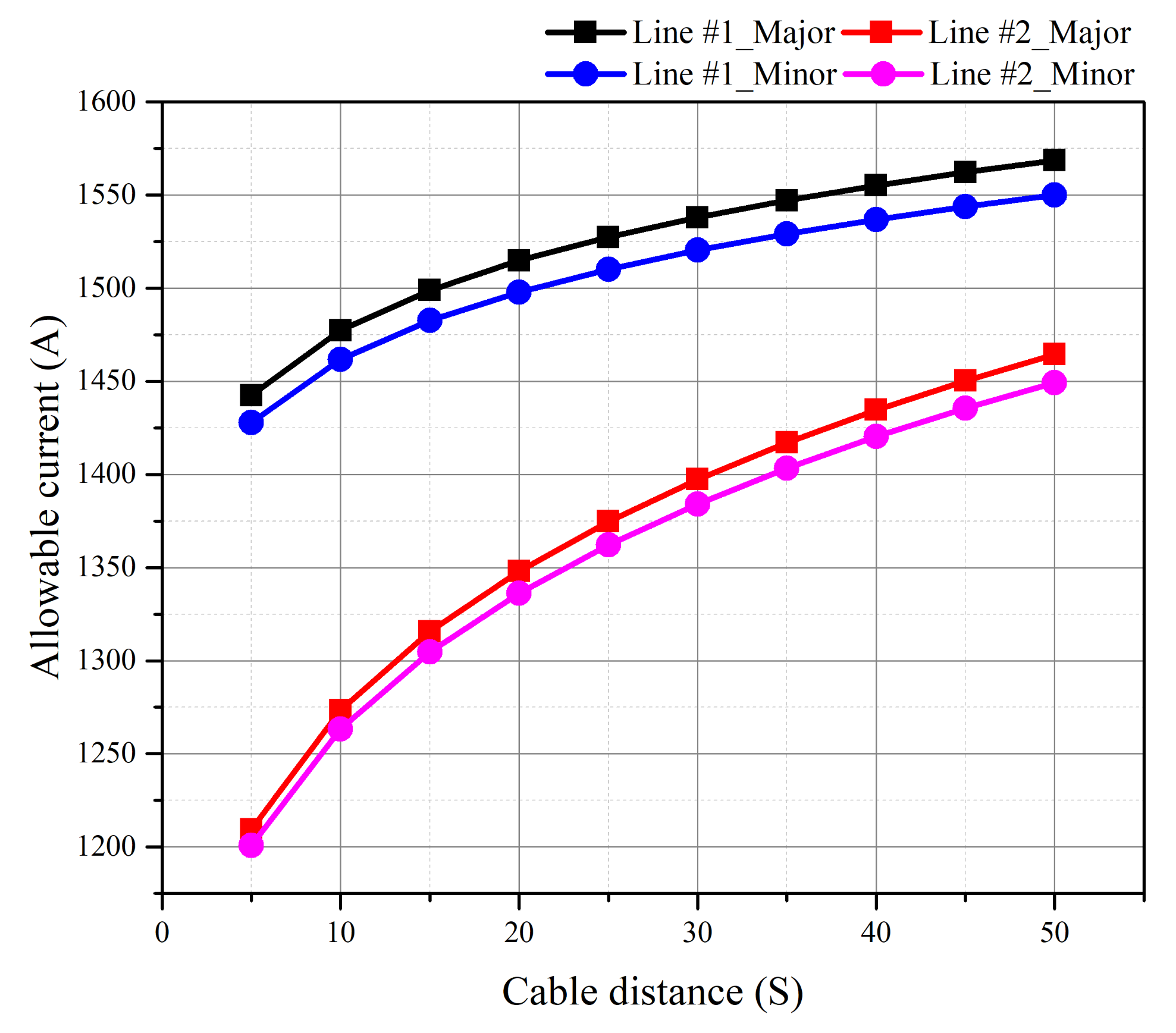
4.2. Continuous Allowable Current Calculation Considering Minor and Major Factor
Comparison of Allowable Current Results
5. Conclusions
- (1)
- Core factors affecting the continuous allowable current value of direct burial laying HVDC underground cables can be divided into internal factors (cable specifications (conductor thermal resistance, T1, T2, T3)) and external factors (T4). It was confirmed that the cable conductor-specific thermal resistance has the greatest influence among internal factors due to the nature of direct current without an alternating magnetic field, and the surrounding environmental condition (T4) in which the cable is buried is an important key factor.
- (2)
- A simulation was performed to calculate the allowable current of the direct burial laying HVDC underground cable by season and laying condition, and it was confirmed that the allowable current in summer and winter differed greatly, and that the DC cable was greatly affected by the surrounding environment. In addition, in order to find the optimal laying arrangement of HVDC underground cables, various arrangement conditions were assumed, and a comparative analysis was conducted, and it was confirmed that a difference in allowable current value of up to 3% occurred depending on the laying method of the same cable in the direct laying method.
- (3)
- To compare the effects of internal factors on the allowable current of HVDC underground cables, referring to the technical documentation, the allowable current calculation simulation was conducted by dividing the allowable current into major and minor factors. When only the major factor was considered, the allowable current value was 1.2% further increased. Therefore, the effect of waterproof tape and airgaps included in the minor factor is not large, and occasionally, the continuous allowable current can be calculated by considering only the major factor.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, F.; Wang, Y.; Zhao, L.; Liang, L.; Tao, W. Study on thermal load capacity of transmission line based on IEEE standard. J. Inf. Process. Syst. 2019, 15, 464–477. [Google Scholar]
- Dubitsky, S.; Greshnyakov, G.; Korovkin, N. Comparison of finite element analysis to IEC-60287 for predicting underground cable ampacity. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016. [Google Scholar]
- Slegers, J. Transmission Line Loading: Sag Calculations and High-Temperature Conductor Technologies; Iowa State University: Ames, IA, USA, 2011; pp. 1–24. [Google Scholar]
- Dong, X.; Wang, C.; Liang, J.; Han, X.; Zhang, F.; Sun, H.; Wang, M.; Ren, J. Calculation of power transfer limit considering electro-thermal coupling of overhead transmission line. IEEE Trans. Power Syst. 2014, 29, 1503–1511. [Google Scholar] [CrossRef]
- Beryozkina, S.; Sauhats, A.; Vanzovichs, E. Climate conditions impact on the permissible load current of the transmission line. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 13–23 June 2011. [Google Scholar]
- Kim, D.-M.; Kim, J.-O. Prediction of transmission-line rating based on thermal overload probability using weather models. Eur. Trans. Electr. Power 2010, 20, 534–544. [Google Scholar] [CrossRef]
- Salata, F.; Nardecchia, F.; Vollaro, A.D.L.; Gugliermetti, F. Underground electric cables a correct evaluation of the soil thermal resistance. Appl. Therm. Eng. 2015, 78, 268–277. [Google Scholar] [CrossRef]
- Xu, X.; Yuan, Q.; Sun, X.; Hu, D.; Wang, J. Simulation analysis of carrying capacity of tunnel cable in different laying ways. Int. J. Heat Mass Transf. 2019, 130, 455–459. [Google Scholar] [CrossRef]
- Brakelmann, H.; Anders, G.J. Current rating considerations in designing HVDC cable installations. IEEE Trans. Power Deliv. 2018, 33, 2315–2323. [Google Scholar] [CrossRef]
- Mardiana, R. Parameters affecting the ampacity of HVDC submarine power cables. In Proceedings of the 2011 2nd International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 15–17 November 2011. [Google Scholar]
- IEC 60287-2-1 Ed.2. Electrical Cables—Calculation of the Current Rating—Part 2-1 Thermal Resistance—Calculation of Thermal Resistance; IEC: Geneva, Switzerland, 2015. [Google Scholar]
- Yang, L.; Qiu, W.; Huang, J.; Hao, Y.; Fu, M.; Hou, S.; Li, L. Comparison of Conductor-Temperature Calculations Based on Different Radial-Position-Temperature Detections for High-Voltage Power Cable. Energies 2018, 11, 117. [Google Scholar] [CrossRef] [Green Version]
- IEC 60287-1-1 Ed.2.1. Electrical Cables—Calculation of the Current Rating—Part 1-1 Current Rating Equations (100% Load Factor) and Calculation of Losses—General; IEC: Geneva, Switzerland, 2014. [Google Scholar]
- Almallah, M.R. Ampacity of HV Multi-Insulation Cables at Different Cooling Methods: HVAC and HVDC Power Cables; Scholars’ Press: Atlanta, GA, USA, 2016. [Google Scholar]
- Anders, G.J.; Institute of Electrical and Electronics Engineers. Rating of Electric Power Cables in Unfavorable Thermal Environment; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Graneau, P. Underground Power Transmission; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1979.
- IEC 60228 Ed.3. Conductors of Insulated Cables; IEC: Geneva, Switzerland, 2004. [Google Scholar]
- IEC 60287-2-3 Ed.1. Electric Cables—Calculation of the Current Rating—Part 2-3: Thermal Resistance—Cables Installed in Ventilated Tunnels; IEC: Geneva, Switzerland, 2017. [Google Scholar]
- Worzyk, T. Submarine Power Cables: Design, Installation, Repair, Environmental Aspects; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]






| Conductor Materials | Resistivity (ρ20) at 20 °C (Ω∙m) | Temperature Correction Factor (α20) at 20 °C (1/K) |
|---|---|---|
| Copper | 1.7241 × 10−8 | 3.93 × 10−3 |
| Aluminum | 2.8264 × 10−8 | 4.03 × 10−3 |
| Cross-Sectional Area (mm2) | Copper (Ω/km) | Aluminum (Ω/km) | ||
|---|---|---|---|---|
| Equation (1) | Equation (2) | Equation (1) | Equation (2) | |
| 2000 | 8.621 × 10−3 | 8.793 × 10−3 | 1.413 × 10−2 | 1.441 × 10−2 |
| 2100 | 8.210 × 10−3 | 8.374 × 10−3 | 1.346 × 10−2 | 1.373 × 10−2 |
| 2200 | 7.837 × 10−3 | 7.994 × 10−3 | 1.285 × 10−2 | 1.310 × 10−2 |
| 2300 | 7.496 × 10−3 | 7.646 × 10−3 | 1.229 × 10−2 | 1.253 × 10−2 |
| 2400 | 7.184 × 10−3 | 7.327 × 10−3 | 1.178 × 10−2 | 1.201 × 10−2 |
| 2500 | 6.896 × 10−3 | 7.034 × 10−3 | 1.131 × 10−2 | 1.153 × 10−2 |
| Moisture Content | Weathered Soil A (W/(m·K)) | Weathered Soil A + Sand (W/(m·K)) | Weathered Soil B (W/(m·K)) |
|---|---|---|---|
| 5% | 0.97 | 0.94 | 1.09 |
| 10% | 0.58 | 0.58 | 0.55 |
| 15% | 0.52 | 0.46 | 0.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, K.-h.; Kwon, I.; Lee, B.-w. Calculation Method of Allowable Continuous Current for Direct Burial Laying HVDC Underground Cable. Energies 2021, 14, 6431. https://doi.org/10.3390/en14196431
Park K-h, Kwon I, Lee B-w. Calculation Method of Allowable Continuous Current for Direct Burial Laying HVDC Underground Cable. Energies. 2021; 14(19):6431. https://doi.org/10.3390/en14196431
Chicago/Turabian StylePark, Kyu-hoon, Il Kwon, and Bang-wook Lee. 2021. "Calculation Method of Allowable Continuous Current for Direct Burial Laying HVDC Underground Cable" Energies 14, no. 19: 6431. https://doi.org/10.3390/en14196431
APA StylePark, K.-h., Kwon, I., & Lee, B.-w. (2021). Calculation Method of Allowable Continuous Current for Direct Burial Laying HVDC Underground Cable. Energies, 14(19), 6431. https://doi.org/10.3390/en14196431






