New Equation for Optimal Insulation Dependency on the Climate for Office Buildings
Abstract
1. Introduction
2. Methods
- Step 1:
- A reference office building was simulated with input values from the EN 16798-1:2018 standard (Table 1) and test reference year (TRY) weather file of the corresponding climate.
- Step 2:
- Two continuous variables, namely windows’ thermal transmittance and thermal resistance of external wall insulation, and three discrete variables, namely window-wall-ratio (WWR), the solar heat gain coefficient of windows (g value), and the unit cost of energy, were considered.
- Step 3:
- Cost functions of window (Equation (2)) and wall insulation (Equation (3)) as well as cost-optimal Equations (Equation (6)) were constructed.
- Step 4:
- Cost-optimal solution for each climate were found, including energy needs for heating and cooling, thermal transmittance of windows and external walls.
- Step 5:
- Degree days were calculated with actual, variable base temperature by using Equation (7).
- Step 6:
- The same steps 1–5 were followed in four climates. The reference climate could be any of these, but in this case, it was Tallinn TRY.
- Step 7:
- Equation (9) was applied to obtain the power function.
2.1. Building Description
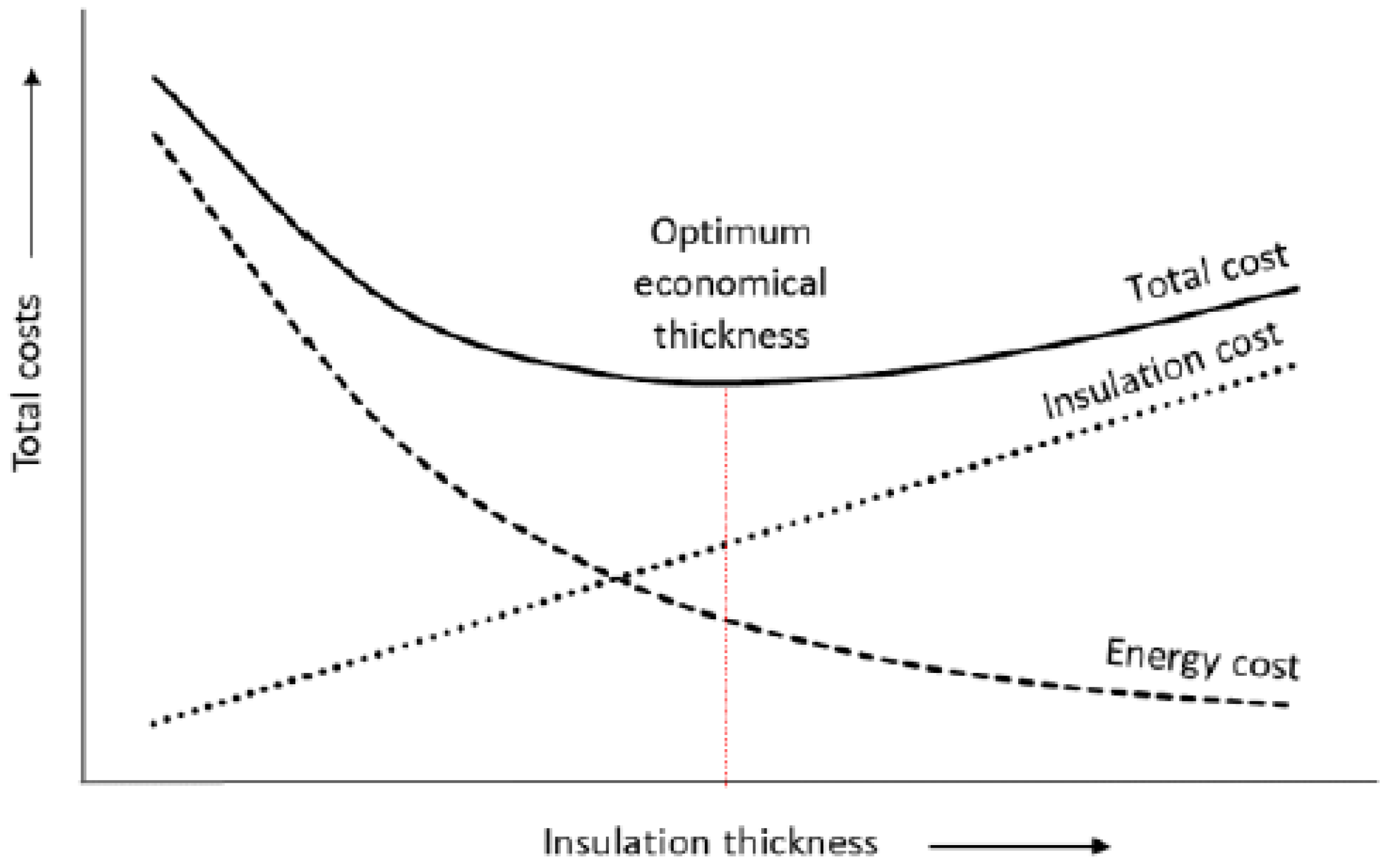
2.2. Continuous Variables, Cost Functions, and Cost Optimality
2.3. Sensitivity Analysis
3. Results
3.1. Degree Days and Climate Normalization Equation
3.2. Base Temperature for Heating and Cooling
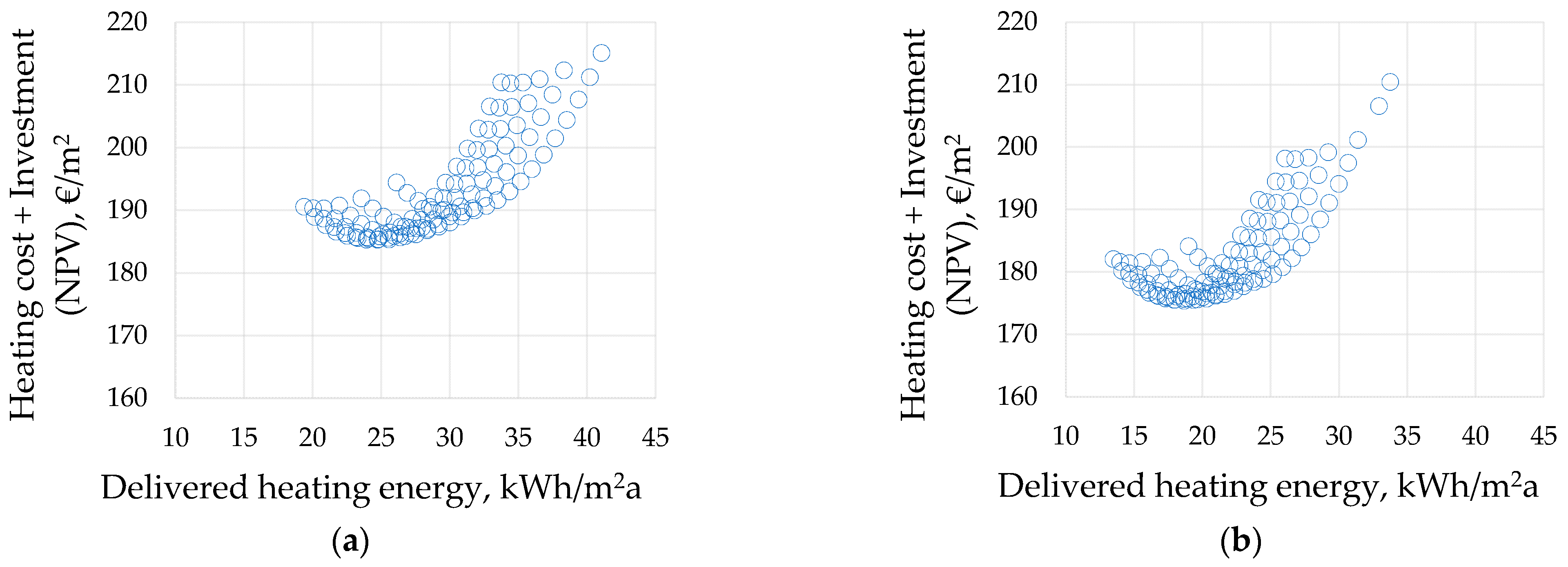
3.3. Cost Optimal Solution Based on Investment and Heating Energy Cost
3.4. Sensitivity Analysis Based on Investment and Heating Energy Cost
3.5. Cost Optimal Solution based on Investment and Total Energy Cost
3.6. Sensitivity Analysis Based on Investment and Total Energy Cost
3.7. Application of the Method on a Monthly Basis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| Cooling energy price, €/kWh | |
| Total energy price with considering the present value factor, € | |
| The lowest cost (investment and operational cost), € | |
| Cost of a ground floor, € | |
| Cost of a roof, € | |
| Cost of a total external wall, € | |
| Cost of total windows, € | |
| Heating or cooling degree days, °Cd | |
| Escalation, % | |
| Energy need, kWh/m2a | |
| Cooling energy use, kWh | |
| Heating energy use, kWh | |
| Energy need for space heating in a respective climate, kWh/m2a | |
| Energy need for space heating in a reference climate, kWh/m2a | |
| EER | Energy efficiency ratio, - |
| Present value factor, - | |
| Thermal conductance of a respective building, W/K | |
| Thermal conductance of building for a respective climate, W/K | |
| Thermal conductance of building for a reference climate, W/K | |
| Heating energy price, €/kWh | |
| Heating degree days of building for a respective climate, °Cd | |
| Heating degree days of building for a reference climate, °Cd | |
| Number of years, year | |
| Real interest rate, % | |
| Area weighted average thermal transmittance for a reference climate, W/m2K | |
| Optimal thermal transmittance of respective building for a reference climate, W/m2K | |
| Area weighted average thermal transmittance for a respective climate, W/m2K | |
| Optimal thermal transmittance of building for a respective climate, W/m2K | |
| Thermal transmittance of a window, W/m2K | |
| Thermal resistance of a wall, m2K/W | |
| Unit cost of a window, €/m2 | |
| Unit cost of a wall, €/m2 |
References
- Building Performance Institute Europe (BPIE). Europe’s Building under the Microscope. A Country-by-Country Review of the Energy Performance of Buildings; Buildings Performance Institute Europe BPIE: Brussels, Belgium, 2011. [Google Scholar]
- EURAC. D2.1a—Survey on the Energy Needs and Architectural Features of the EU Building Stock iNSPiRE Project—Development of Systemic Packages for Deep Energy Enovation of Residential and Tertiary Buildings including Envelope and Systems; BSRIA: Bracknell, UK, 2014; pp. 33–46. [Google Scholar]
- Commission Recommendation (EU). 2016/1318 of 29 July 2016 on Guidelines for the Promotion of Nearly Zero-Energy Buildings and Best Practices to Ensure That, by 2020, All New Buildings Are Nearly Zero-Energy Buildings; Commission Recommendation (EU), European Commission: Brussels, Belgium, 2016. [Google Scholar]
- Eisenhower, B.; O’Neill, Z.; Fonoberov, V.A.; Mezić, I. Uncertainty and sensitivity decomposition of building energy models. J. Build. Perform. Simul. 2012, 5, 171–184. [Google Scholar] [CrossRef]
- Bucking, S.; Zmeureanu, R.; Athienitis, A. A methodology for identifying the influence of design variations on building energy performanc. J. Build. Perform. Simul. 2014, 7, 411–426. [Google Scholar] [CrossRef]
- Sun, Y.; Heo, Y.; Tan, M.; Xie, H.; Wu, C.F.J.; Augenbroe, G. Uncertainty quantification of microclimate variables in building energy models. J. Build. Perform. Simul. 2014, 7, 17–32. [Google Scholar] [CrossRef]
- Kaynakli, O. A review of the economical and optimum thermal insulation thickness for building applications. Renew. Sustain. Energy Rev. 2012, 16, 415–425. [Google Scholar] [CrossRef]
- European Commission. Commission Delegated Regulation (EU) No 244/2012 of 16 January 2012 supplementing Directive 2010/31/EU of the European Parliament and of the Council on the Energy Performance of Buildings by Establishing a Comparative Methodology Framework for Calculating Cost-Optimal Levels of Minimum Energy; European Commission: Brussels, Belgium, 2012. [Google Scholar]
- Ibrahim, M.; Ghaddar, N.; Ghali, K. Optimal location and thickness of insulation layers for minimizing building energy consumption. J. Build. Perform. Simul. 2012, 5, 384–398. [Google Scholar] [CrossRef]
- Rosti, B.; Omidvar, A.; Monghasemi, N. Optimal insulation thickness of common classic and modern exterior walls in different climate zones of Iran. J. Build. Eng. 2020, 27, 100954. [Google Scholar] [CrossRef]
- Bolattürk, A. Determination of optimum insulation thickness for building walls with respect to various fuels and climate zones in Turkey. Appl. Therm. Eng. 2006, 26, 1301–1309. [Google Scholar] [CrossRef]
- D’Agostino, D.; Rossi, F.d.; Marigliano, M.; Marino, C.; Minichiello, F. Evaluation of the optimal thermal insulation thickness for an office building in different climates by means of the basic and modified “cost-optimal” methodology. J. Build. Eng. 2019, 24, 100743. [Google Scholar] [CrossRef]
- Ucar, A.; Balo, F. Determination of the energy savings and the optimum insulation thickness in the four different insulated exterior walls. Renew. Energy 2010, 35, 88–94. [Google Scholar] [CrossRef]
- Ozel, M. Determination of optimum insulation thickness based on cooling transmission load for building walls in a hot climate. Energy Convers. Manag. 2013, 66, 106–114. [Google Scholar] [CrossRef]
- Dylewski, R.; Adamczyk, J. Economic and environmental benefits of thermal insulation of building external walls. Build. Environ. 2011, 46, 2615–2623. [Google Scholar] [CrossRef]
- Jaber, S.; Ajib, S. Thermal and economic windows design for different climate zones. Energy Build. 2011, 43, 3208–3215. [Google Scholar] [CrossRef]
- Kontoleon, K.J.; Zenginis, D.G. Analysing Heat Flows Through Building Zones in Aspect of their Orientation and Glazing Proportion, under Varying Conditions. Procedia Environ. Sci. 2017, 38, 348–355. [Google Scholar] [CrossRef]
- Thalfeldt, M.; Ergo, P.; Kurnitski, J.; Hendrik, V. Facade design principles for nearly zero energy buildings in a cold climate. Energy Build. 2013, 67, 309–321. [Google Scholar] [CrossRef]
- Pikas, E.; Thalfeldt, M.; Kurnitski, J. Cost optimal and nearly zero energy building solutions for office buildings. Energy Build. 2014, 74, 30–42. [Google Scholar] [CrossRef]
- Yu, J.; Yang, C.; Tian, L.; Liao, D. A study on optimum insulation thicknesses of external walls in hot summer and cold winter zone of China. Appl. Energy 2009, 86, 2520–2529. [Google Scholar] [CrossRef]
- Karlsson, J.; Roos, A.; Karlsson, B. Building and climate influence on the balance temperature of buildings. Build. Environ. 2003, 38, 75–81. [Google Scholar] [CrossRef]
- Harvey, L.D.D. Using modified multiple heating-degree-day (HDD) and cooling-degree-day (CDD) indices to estimate building heating and cooling loads. Energy Build. 2020, 229, 110475. [Google Scholar] [CrossRef]
- Calise, F.; D’Accadia, D.M.; Barletta, C.; Battaglia, V.; Pfeifer, A.; Duic, N. Detailed modelling of the deep decarbonisation scenarios with demand response technologies in the heating and cooling sector: A case study for Italy. Energies 2017, 10, 1535. [Google Scholar] [CrossRef]
- Granja, A.D.; Labaki, L.C. Influence of External Surface Colour on the Periodic Heat Flow through a Flat Solid Roof with Variable Thermal Resistance; John Wiley Sons Ltd: Hoboken, NJ, USA, 2003; pp. 771–779. [Google Scholar]
- Daouas, N.; Hassen, Z.; Aissia, H.B. Analytical periodic solution for the study of thermal performance and optimum insulation thickness of building walls in Tunisia. Appl. Therm. Eng. 2010, 30, 319–326. [Google Scholar] [CrossRef]
- Ahmed, K.; Carlier, M.; Feldmann, C.; Kurnitski, J. A new method for contrasting energy performance and near-zero energy building requirements in different climates and countries. Energies 2018, 11, 1334. [Google Scholar] [CrossRef]
- Ahmed, K.; Yoon, G.; Ukai, M.; Kurnitski, J. How to compare energy performance requirements of Japanese and European office buildings. In Proceedings of the E3S Web of Conference 111, Clima, Bucharest, Romania, 26–29 May 2019. [Google Scholar]
- Seppänen, O. Rakennusten Lämmitys, 2nd ed.; Gummerus Oy: Jyväskylä, Finnish, 2001. [Google Scholar]
- IDA Indoor Climate and Energy, Equa Simulations AB. Available online: http://www.equa.se/en/ida-ice/ (accessed on 24 December 2015).
- Sahlin, P. Modeling and Simulation Methods for Modular Continuous System in Buildings; Doctoral Dissertation KTH: Stockholm, Sweden, 1996. [Google Scholar]
- EN ISO 13791. Thermal Performance of Buildings. Calculation of Internal of a Room in Summer without Mecahanical Cooling. General Criteria and Validation Procedures; CEN European Committee for Standardization: Brussels, Belgium, 2004.
- Travesi, J.; Maxwell, G.; Klaassen, C.; Holtz, M. Empirical Validation of IOWA Energy Resource Station Building Energy Analysis Simulation Models, Report of Task 22, Subtask Building Energy Analysis Tools; International Energy Agency—Solar heating and Cooling Programme: Paris, France, 2001. [Google Scholar]
- Simson, R.; Arumägi, E.; Kuusk, K.; Kurnitski, J. Redefining cost-optimal nZEB levels for new residential buildings. In Proceedings of the E3S Web of Conferences 111, 03035, CLIMA, Bucharest, Romania, 26–29 May 2019. [Google Scholar]
- Ahmed, K.; Akhondzada, A.; Kurnitski, J.; Olesen, B. Occupancy schedules for energy simulation in New prEN16798-1 and ISO/FDIS 17772-1 standards. Sustain. Cit. Soc. 2017, 35, 134–144. [Google Scholar] [CrossRef]
- Ahmed, K.; Kurnitski, J.; Olesen, B. Data for occupancy internal heat gain calculation in main building categories. Data Brief 2017, 15, 1030–1034. [Google Scholar] [CrossRef] [PubMed]
- Alfano, F.R.A.; Olesen, B.W.; Palella, I.B.; Riccio, G. Thermal comfort: Design and assessment for energy saving. Energy Build. 2014, 81, 326–336. [Google Scholar] [CrossRef]
















| Input Parameters | Data |
|---|---|
| Occupant, m2/person | 17 |
| Appliances, W/m2 | 12 |
| Lighting, W/m2 | 6 |
| Operational hour of appliances and lighting | 7:00–18:00 |
| All usage factor | 0.55 |
| Usages of domestic hot water, L/(m2 a) | 100 |
| Operation hour of fan | 6:00–19:00 |
| Ventilation rate, L/(s·m2) | 1.4 |
| Heating setpoint, °C | 21 |
| Cooling setpoint, °C | 25 |
| Efficiency of district heating | 0.97 |
| 1 EER for cooling | 3.5 |
| Input Data | Tallinn | Sapporo | Paris | Brussels |
|---|---|---|---|---|
| Range of insulation thickness, m | 0.1–0.25 | 0.1–0.25 | 0.05–0.23 | 0.05–0.23 |
| Step for thickness, m | 0.03 | 0.03 | 0.03 | 0.03 |
| Range of thermal transmittance, W/m2K | 0.6–1.5 | 0.6–1.5 | 0.8–1.7 | 0.8–1.7 |
| Step for transmittance, W/m2K | 0.05 | 0.05 | 0.05 | 0.05 |
| Total combination | 114 | 114 | 133 | 133 |
| WWR % | g Value | WWR × g |
|---|---|---|
| 30 | 0.22 | 0.066 |
| 40 | 0.22 | 0.088 |
| 50 | 0.22 | 0.110 |
| 30 | 0.35 | 0.105 |
| 40 | 0.35 | 0.140 |
| 50 | 0.35 | 0.175 |
| Cost Optimal Parameters | Tallinn | Sapporo | Paris | Brussels |
|---|---|---|---|---|
| Cost optimal solution for a single floor model | ||||
| Lowest cost optimal unit cost, €/m2 | 117.8 | 109.5 | 101.5 | 103.3 |
| 1 Window U-value, W/m2K | 0.85 | 0.90 | 0.95 | 0.95 |
| 1 External wall insulation thickness, m | 0.22 | 0.19 | 0.17 | 0.17 |
| 1 External wall U-value, W/m2K | 0.1487 | 0.1712 | 0.1904 | 0.1904 |
| 1,2 Total conductance, W/K | 164.77 | 177.31 | 188.88 | 188.88 |
| 1 Total heating energy use, kWh/m2a | 21.95 | 17.77 | 13.30 | 14.56 |
| 1 Total heating energy use, kWh/a | 18,373 | 14,876 | 11,131 | 12,188 |
| 1,3 Total degree days, °C | 4646 | 3496 | 2455 | 2689 |
| Area weighted average U-value of building envelope, W/m2K | 0.425 | 0.458 | 0.490 | 0.490 |
| 1 Normalized average U-value (n = 0.5), W/m2K | 0.425 | 0.490 | 0.585 | 0.559 |
| 1 Normalized average U-value (n = 0.2), W/m2K | 0.425 | 0.450 | 0.483 | 0.474 |
| Cost optimal solution for a whole building model | ||||
| Lowest cost optimal unit cost, €/m2 | 185.3 | 175.4 | 168.4 | 170.4 |
| 1 Window U-value, W/m2K | 0.90 | 0.90 | 0.95 | 0.95 |
| 1 External wall insulation thickness, m | 0.22 | 0.19 | 0.17 | 0.17 |
| 1 External wall U-value, W/m2K | 0.1487 | 0.1712 | 0.1904 | 0.1904 |
| 1,2 Total conductance, W/K | 1119.3 | 1156.0 | 1221.4 | 1221.42 |
| 1 Total heating energy use, kWh/m2a | 132.43 | 99.97 | 80.03 | 87.67 |
| 1 Total heating energy use, kWh/a | 110,848 | 83,672 | 66,988 | 73,383 |
| 1,3 Total degree days, °C | 4126 | 3016 | 2285 | 2503 |
| Area weighted average U-value of building envelope, W/m2K | 0.373 | 0.389 | 0.417 | 0.417 |
| 1 Normalized average U-value (n = 0.5), W/m2K | 0.373 | 0.436 | 0.501 | 0.479 |
| 1 Normalized average U-value (n = 0.2), W/m2K | 0.373 | 0.397 | 0.420 | 0.412 |
| Cost Optimal Parameters | Tallinn | Sapporo | Paris | Brussels |
|---|---|---|---|---|
| Cost optimal solution for a whole building model (a whole building model) | ||||
| Lowest cost optimal unit cost, €/m2 | 189.2 | 187.7 | 176.9 | 176.1 |
| 1 Window U-value, W/m2K | 0.900 | 0.900 | 0.950 | 0.950 |
| 1 External wall insulation thickness, m | 0.22 | 0.19 | 0.17 | 0.17 |
| 1 External wall U-value, W/m2K | 0.1487 | 0.171 | 0.190 | 0.190 |
| 1,2 Total conductance, W/K | 1119.28 | 1156.0 | 1221.4 | 1221.4 |
| 1 Total heating energy use, kWh/m2a | 24.74 | 18.68 | 14.95 | 16.38 |
| 1 Total cooling energy use, kWh/m2a | 6.89 | 21.63 | 14.93 | 9.99 |
| 1 Total energy use, kWh/m2a | 31.64 | 40.30 | 29.88 | 26.37 |
| 1 Total energy use, kWh/a | 141,732 | 180,556 | 133,877 | 118,141 |
| 1,3 Total degree days, °C | 5276 | 6508 | 4567 | 4030 |
| Area weighted average U-value of building envelope, W/m2K | 0.373 | 0.389 | 0.417 | 0.417 |
| 1 Normalized average U-value (n = 0.5), W/m2K | 0.373 | 0.336 | 0.401 | 0.427 |
| Difference of average U-value vs. normalized U-value, n = 0.5 | 0.0% | −13.6% | −3.9% | 2.3% |
| 1 Normalized average U-value (n = 0.2), W/m2K | 0.373 | 0.358 | 0.384 | 0.394 |
| Difference of average U-value vs. normalized U-value, n = 0.2 | 0.0% | −8.0% | −8.0% | −5.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, K.; Kurnitski, J. New Equation for Optimal Insulation Dependency on the Climate for Office Buildings. Energies 2021, 14, 321. https://doi.org/10.3390/en14020321
Ahmed K, Kurnitski J. New Equation for Optimal Insulation Dependency on the Climate for Office Buildings. Energies. 2021; 14(2):321. https://doi.org/10.3390/en14020321
Chicago/Turabian StyleAhmed, Kaiser, and Jarek Kurnitski. 2021. "New Equation for Optimal Insulation Dependency on the Climate for Office Buildings" Energies 14, no. 2: 321. https://doi.org/10.3390/en14020321
APA StyleAhmed, K., & Kurnitski, J. (2021). New Equation for Optimal Insulation Dependency on the Climate for Office Buildings. Energies, 14(2), 321. https://doi.org/10.3390/en14020321






