Adaptive Control for Energy Exchange with Probabilistic Interval Predictors in Isolated Microgrids
Abstract
:1. Introduction
1.1. Background
1.2. Related Work
1.3. Contributions
- An adaptive probabilistic energy management method based on the MPC framework and two-stage control is proposed to improve the utilization of the interval predictions and the dispatch performances in isolated microgrids with high penetrations of RES;
- An adaptive reserve strategy is adopted to further exploit the information provided by the interval predictions and prepare for the possible variations in the future so that the system stability could be maintained in an adaptive manner;
- The aggressive-conservative level of system is also introduced to guarantee certain system capacity and adjust the reserve strategy, where the system state and the future trends are evaluated to affect the system propensity on making decisions;
- Simulation results show that the proposed method achieves good performances in terms of both system stability and economic efficiency, and it is capable of maintaining good performance even when the situation is extremely hostile.
1.4. Outline
2. System Model
2.1. Interval Predictions
2.2. Dispatchable Generators
2.3. Energy Storage Units
2.4. Energy Balance
3. The Adaptive Reserve Strategy
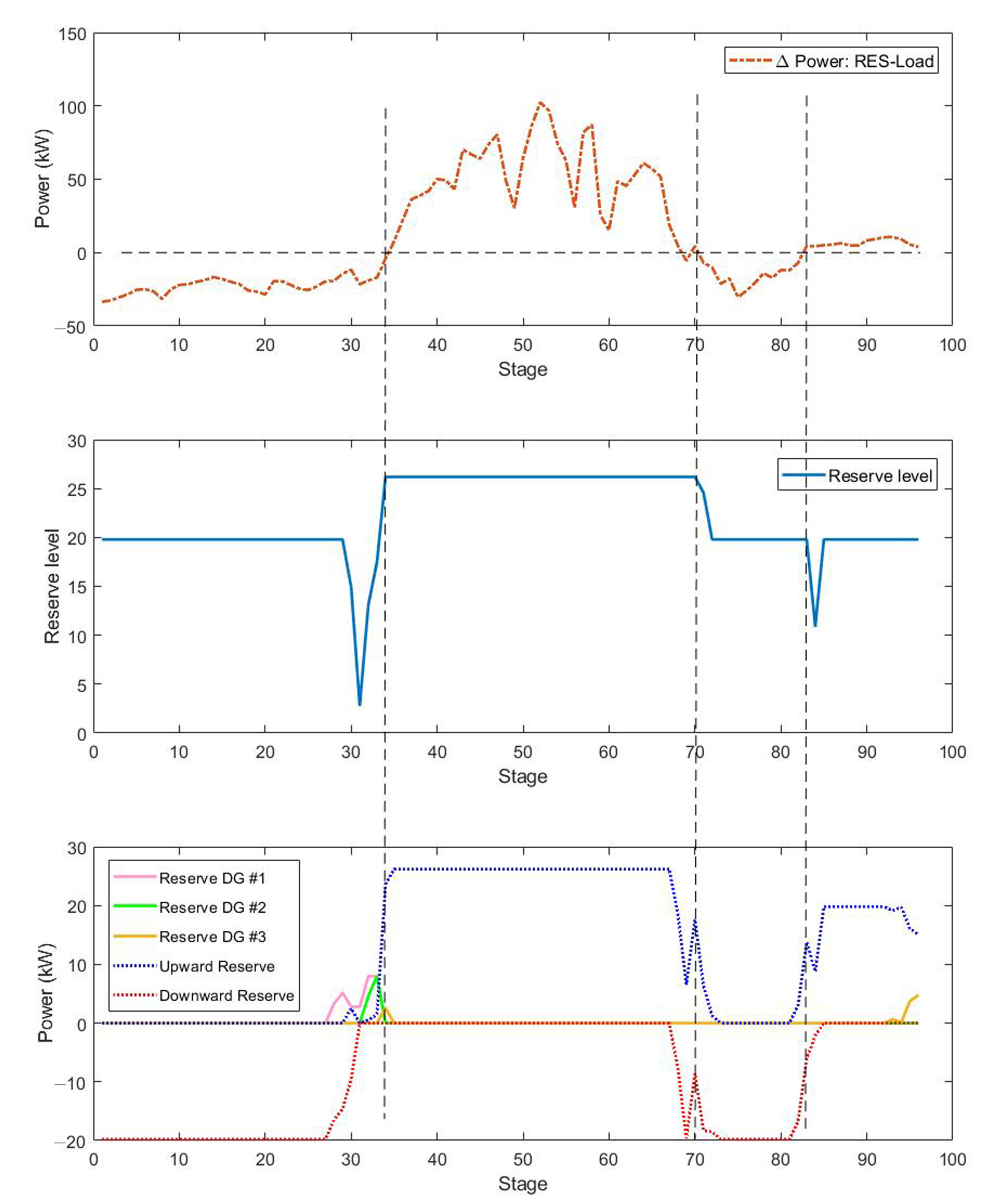
3.1. The Adaptive Reserves
3.2. The Adaptive Reserve Strategy
4. Optimization and Control Method
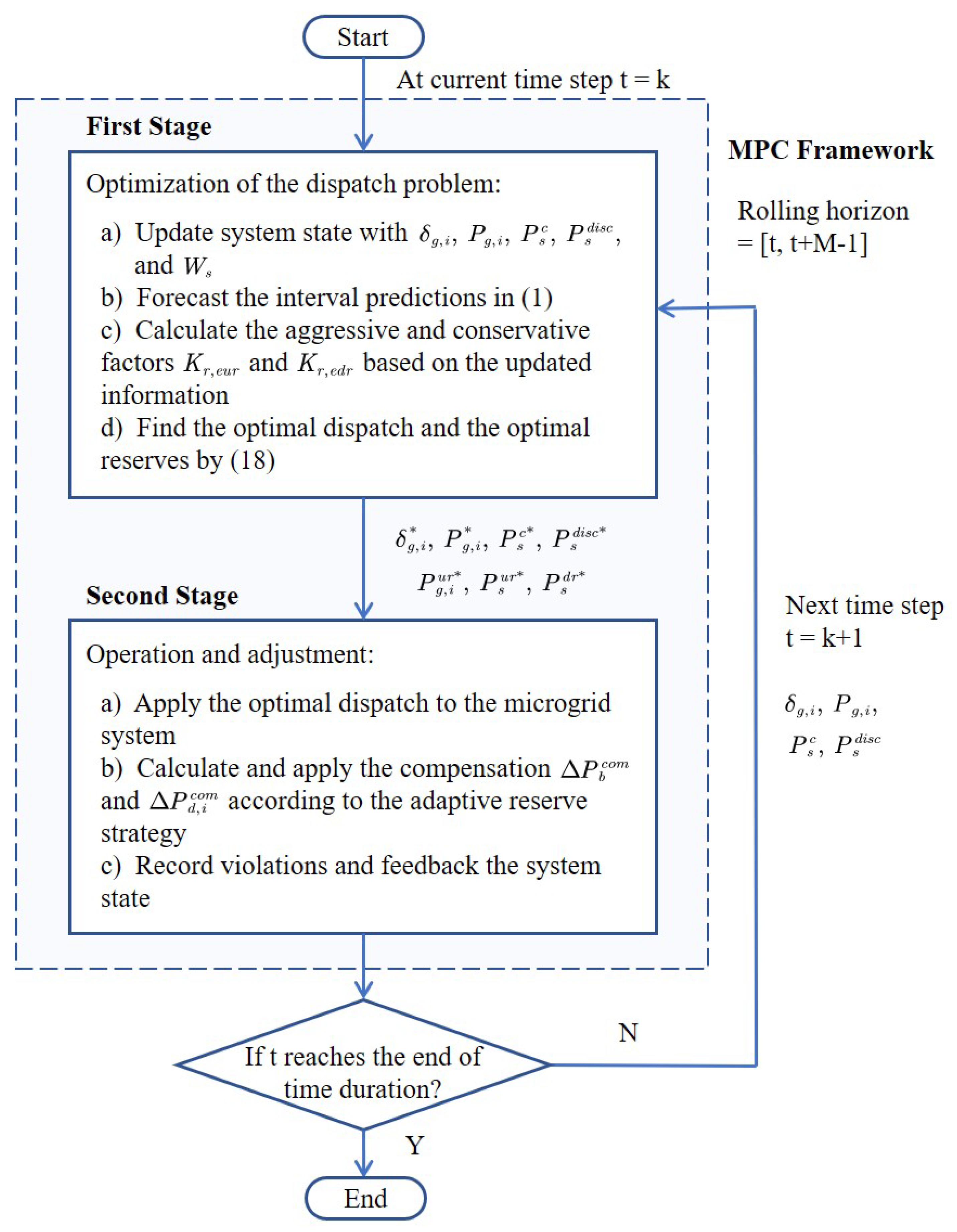
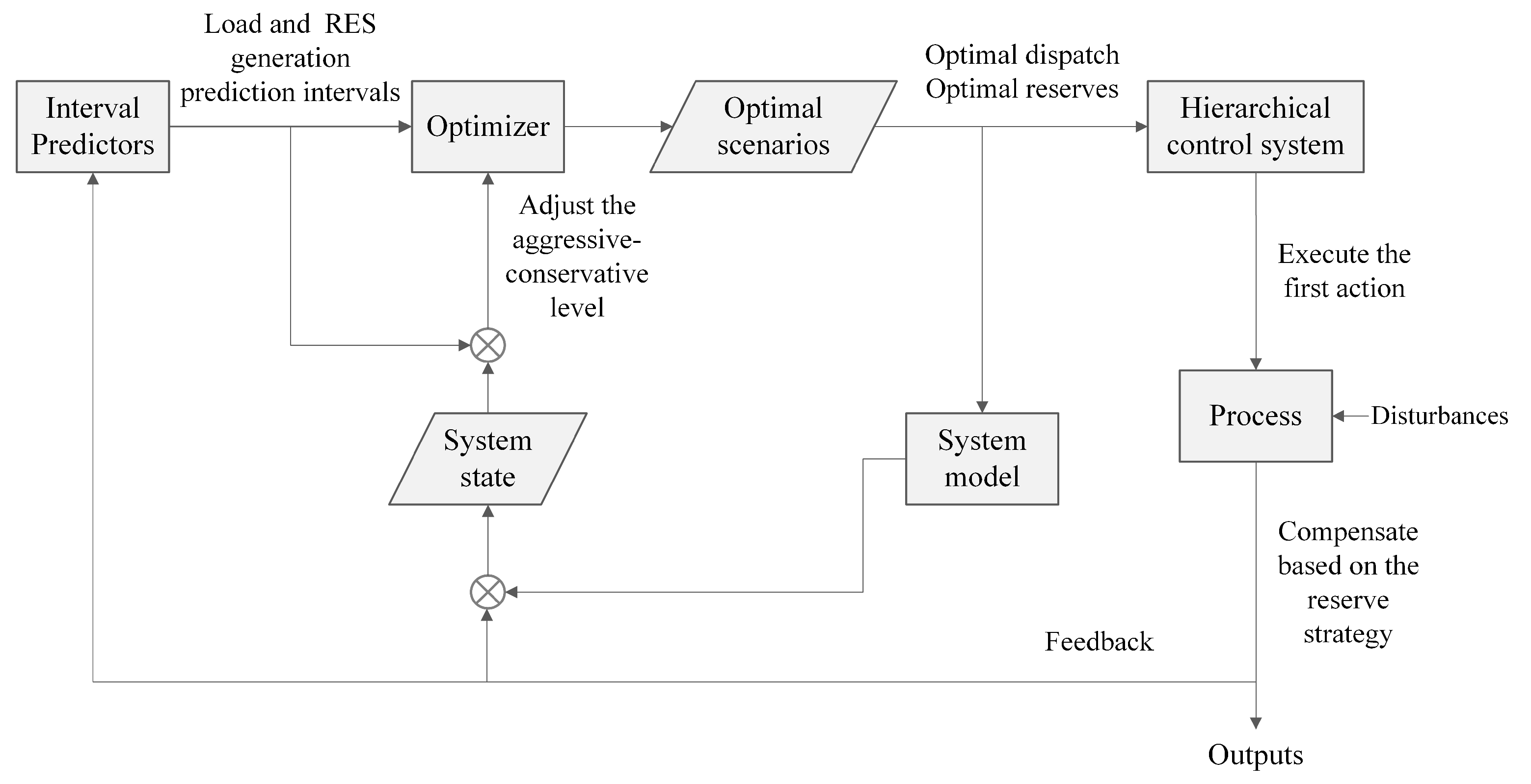
4.1. The MPC Framework
4.2. The MPC-Based Optimization Problem
4.3. Two-Stage Control Model
4.4. The Energy Management Strategy
5. Simulations
5.1. Performance Metrics
- (1)
- Isolated Loss of Load Probability (ILOLP). This metric indicates the stability performance in terms of running time. It is the fraction of time duration that the load demand is not satisfied in isolated microgrids with:where is the number of violations, is the time interval of each step, and T is the total operation duration;
- (2)
- Isolated Load Loss Rate (ILLR). This metric describes the severity of the violations during the whole operation in isolated microgrids compared with the average load demand, which is formulated as:where N is the total operation steps and denotes the actual load demand power. IALL is a common metric called Isolated Average Load Loss presenting the unsatisfied load demand each time the violation occurs, and it is given by:with denoting the violated load power.
5.2. Case Study
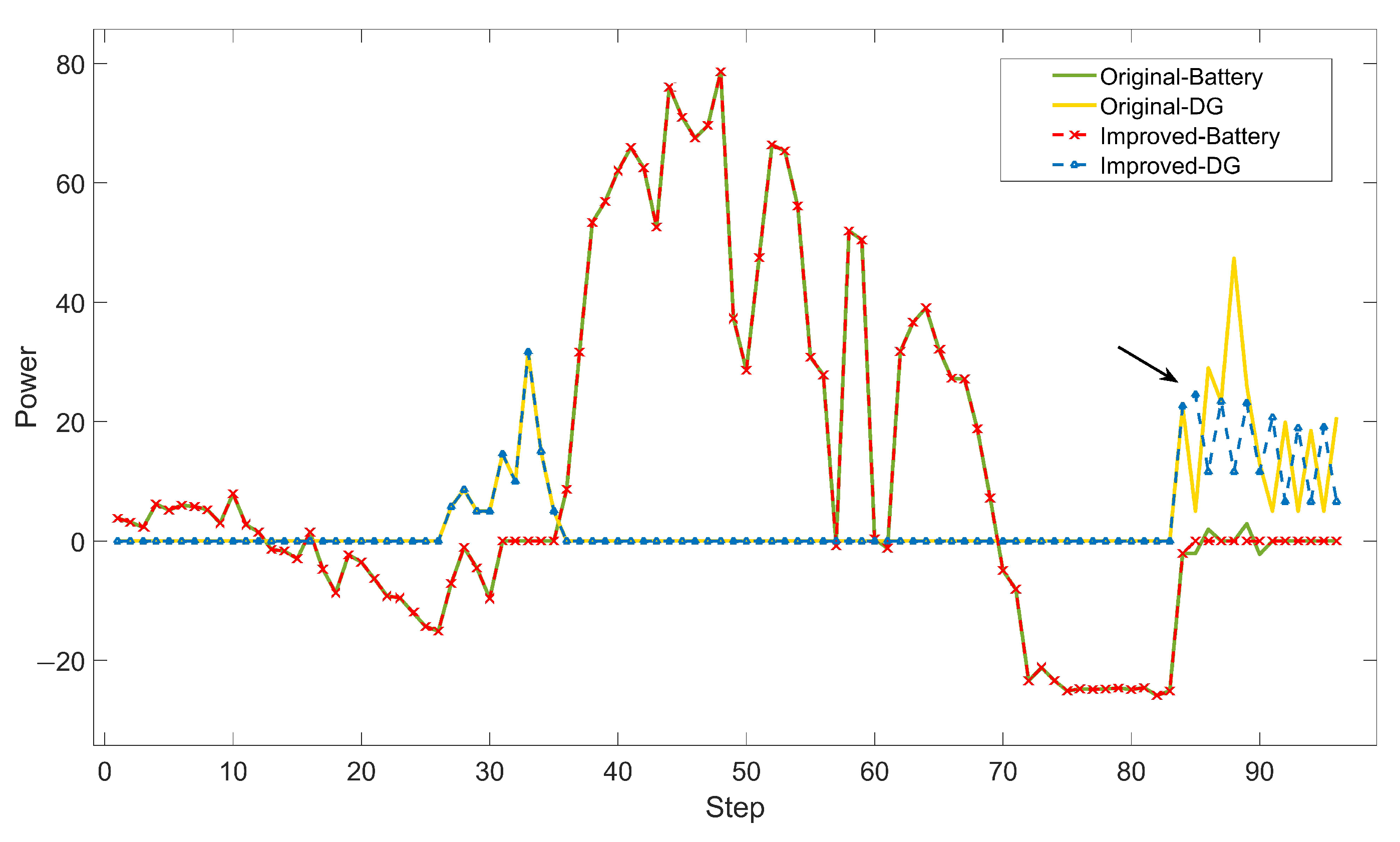
5.3. Performance Analysis
5.4. The Extreme Case Study
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al-Turjman, F.; Abujubbeh, M. IoT-enabled smart grid via SM: An overview. Future Gener. Comput. Syst. 2019, 96, 579–590. [Google Scholar] [CrossRef]
- Dragičević, T.; Siano, P.; Prabaharan, S. Future generation 5G wireless networks for smart grid: A comprehensive review. Energies 2019, 12, 2140. [Google Scholar]
- Hui, H.; Ding, Y.; Shi, Q.; Li, F.; Song, Y.; Yan, J. 5G network-based Internet of Things for demand response in smart grid: A survey on application potential. Appl. Energy 2020, 257, 113972. [Google Scholar] [CrossRef]
- Lasseter, R.H.; Paigi, P. Microgrid: A conceptual solution. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 6, pp. 4285–4290. [Google Scholar]
- Kazerani, M.; Tehrani, K. Grid of Hybrid AC/DC Microgrids: A New Paradigm for Smart City of Tomorrow. In Proceedings of the 2020 IEEE 15th International Conference of System of Systems Engineering (SoSE), Budapest, Hungary, 2–4 June 2020; pp. 175–180. [Google Scholar]
- Badal, F.R.; Das, P.; Sarker, S.K.; Das, S.K. A survey on control issues in renewable energy integration and microgrid. Prot. Control Mod. Power Syst. 2019, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Pedrasa, M.A.; Spooner, T. A survey of techniques used to control microgrid generation and storage during island operation. In Proceedings of the 2006 Australasian Universities Power Engineering Conference (AUPEC’06), Melbourne, Australia, 10–13 December 2006; pp. 1–6. [Google Scholar]
- Olivares, D.E.; Cañizares, C.A.; Kazerani, M. A Centralized Energy Management System for Isolated Microgrids. IEEE Trans. Smart Grid 2014, 5, 1864–1875. [Google Scholar] [CrossRef]
- Kayalvizhi, S.; Vinod Kumar, D.M. Load Frequency Control of an Isolated Micro Grid Using Fuzzy Adaptive Model Predictive Control. IEEE Access 2017, 5, 16241–16251. [Google Scholar] [CrossRef]
- Sobu, A.; Wu, G. Optimal operation planning method for isolated micro grid considering uncertainties of renewable power generations and load demand. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Washington, DC, USA, 16–20 January 2012; pp. 1–6. [Google Scholar]
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z.; Lin, J.; Hu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2015, 1, 38–46. [Google Scholar] [CrossRef]
- Soares, J.; Pinto, T.; Lezama, F.; Morais, H. Survey on complex optimization and simulation for the new power systems paradigm. Complexity 2018, 2018, 2340628. [Google Scholar] [CrossRef] [Green Version]
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Sortomme, E.; El-Sharkawi, M.A. Optimal Power Flow for a System of Microgrids with Controllable Loads and Battery Storage. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–5. [Google Scholar]
- Sachs, J.; Sawodny, O. A Two-Stage Model Predictive Control Strategy for Economic Diesel-PV-Battery Island Microgrid Operation in Rural Areas. IEEE Trans. Sustain. Energy 2016, 7, 903–913. [Google Scholar] [CrossRef]
- Luna, A.C.; Diaz, N.L.; Graells, M.; Vasquez, J.C.; Guerrero, J.M. Mixed-Integer-Linear-Programming-Based Energy Management System for Hybrid PV-Wind-Battery Microgrids: Modeling, Design, and Experimental Verification. IEEE Trans. Power Electron. 2017, 32, 2769–2783. [Google Scholar] [CrossRef] [Green Version]
- Parisio, A.; Rikos, E.; Glielmo, L. A Model Predictive Control Approach to Microgrid Operation Optimization. IEEE Trans. Control. Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Xia, X. Optimal dispatch for a microgrid incorporating renewables and demand response. Renew. Energy 2017, 101, 16–28. [Google Scholar] [CrossRef]
- Chaudhary, P.; Rizwan, M. Energy management supporting high penetration of solar photovoltaic generation for smart grid using solar forecasts and pumped hydro storage system. Renew. Energy 2018, 118, 928–946. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Holguín, E.; Garces, A.; Grisales-Noreña, L.F. Economic dispatch of energy storage systems in dc microgrids employing a semidefinite programming model. J. Energy Storage 2019, 21, 1–8. [Google Scholar] [CrossRef]
- Nasr, M.A.; Nikkhah, S.; Gharehpetian, G.B.; Nasr-Azadani, E.; Hosseinian, S.H. A multi-objective voltage stability constrained energy management system for isolated microgrids. Int. J. Electr. Power Energy Syst. 2020, 117, 105646. [Google Scholar] [CrossRef]
- Pinson, P.; Kariniotakis, G. Conditional Prediction Intervals of Wind Power Generation. IEEE Trans. Power Syst. 2010, 25, 1845–1856. [Google Scholar] [CrossRef] [Green Version]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Verrilli, F.; Parisio, A.; Glielmo, L. Stochastic model predictive control for optimal energy management of district heating power plants. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 807–812. [Google Scholar]
- Olivares, D.E.; Lara, J.D.; Cañizares, C.A.; Kazerani, M. Stochastic-Predictive Energy Management System for Isolated Microgrids. IEEE Trans. Smart Grid 2015, 6, 2681–2693. [Google Scholar] [CrossRef]
- Rastegar, M.; Fotuhi-Firuzabad, M.; Zareipour, H.; Moeini-Aghtaieh, M. A Probabilistic Energy Management Scheme for Renewable-Based Residential Energy Hubs. IEEE Trans. Smart Grid 2017, 8, 2217–2227. [Google Scholar] [CrossRef]
- Ma, X.; Dong, J.; Djouadi, S.M.; Nutaro, J.J.; Kuruganti, T. Stochastic control of energy efficient buildings: A semidefinite programming approach. In Proceedings of the 2015 IEEE International Conference on Smart Grid Communications (SmartGridComm), Miami, FL, USA, 2–5 November 2015; pp. 780–785. [Google Scholar]
- Kou, P.; Liang, D.; Gao, L.; Gao, F. Stochastic Coordination of Plug-In Electric Vehicles and Wind Turbines in Microgrid: A Model Predictive Control Approach. IEEE Trans. Smart Grid 2016, 7, 1537–1551. [Google Scholar] [CrossRef]
- Sáez, D.; Ávila, F.; Olivares, D.; Cañizares, C.; Marín, L. Fuzzy Prediction Interval Models for Forecasting Renewable Resources and Loads in Microgrids. IEEE Trans. Smart Grid 2015, 6, 548–556. [Google Scholar] [CrossRef] [Green Version]
- Pekaslan, D.; Wagner, C.; Garibaldi, J.M.; Marin, L.G.; Sáez, D. Uncertainty-Aware Forecasting of Renewable Energy Sources. In Proceedings of the 2020 IEEE International Conference on Big Data and Smart Computing (BigComp), Busan, Korea, 19–22 February 2020; pp. 240–246. [Google Scholar]
- Marín, L.G.; Cruz, N.; Sáez, D.; Sumner, M.; Núñez, A. Prediction interval methodology based on fuzzy numbers and its extension to fuzzy systems and neural networks. Expert Syst. Appl. 2019, 119, 128–141. [Google Scholar] [CrossRef] [Green Version]
- Valencia, F.; Sáez, D.; Collado, J.; Ávila, F.; Marquez, A.; Espinosa, J.J. Robust Energy Management System Based on Interval Fuzzy Models. IEEE Trans. Control Syst. Technol. 2016, 24, 140–157. [Google Scholar] [CrossRef]
- Cartagena, O.; Muñoz-Carpintero, D.; Sáez, D. A Robust Predictive Control Strategy for Building HVAC Systems Based on Interval Fuzzy Models. In Proceedings of the 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Mohan, V.; Suresh, R.; Singh, J.G.; Ongsakul, W.; Madhu, N. Microgrid Energy Management Combining Sensitivities, Interval and Probabilistic Uncertainties of Renewable Generation and Loads. IEEE J. Emerg. Sel. Top. Circuits Syst. 2017, 7, 262–270. [Google Scholar] [CrossRef]
- Cheng, J.; Duan, D.; Cheng, X.; Yang, L.; Cui, S. Probabilistic Microgrid Energy Management with Interval Predictions. Energies 2020, 13, 3116. [Google Scholar] [CrossRef]
- Vandoorn, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Optimality and stability. Automatica 2000, 36, 789–814. [Google Scholar]
- Palma-Behnke, R.; Benavides, C.; Lanas, F.; Severino, B.; Reyes, L.; Llanos, J.; Sáez, D. A Microgrid Energy Management System Based on the Rolling Horizon Strategy. IEEE Trans. Smart Grid 2013, 4, 996–1006. [Google Scholar] [CrossRef] [Green Version]
- Bertsekas, D.P. Dynamic Programming and Optimal Control; Athena Scientific: Nashua, NH, USA, 1995; pp. 402–445. [Google Scholar]
- Venayagamoorthy, G.K.; Sharma, R.K.; Gautam, P.K.; Ahmadi, A. Dynamic Energy Management System for a Smart Microgrid. IEEE Trans. Neural Netw. Learn. Syst. 2016, 1, 1643–1656. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A. Hierarchical Structure of Microgrids Control System. IEEE Trans. Smart Grid 2012, 3, 1963–1976. [Google Scholar] [CrossRef]
- Zhang, Y.; Gatsis, N.; Giannakis, G.B. Robust Energy Management for Microgrids with High-Penetration Renewables. IEEE Trans. Sustain. Energy 2013, 4, 944–953. [Google Scholar] [CrossRef] [Green Version]
- Leonori, S.; Paschero, M.; Mascioli, F.M.F.; Rizzi, A. Optimization strategies for Microgrid energy management systems by Genetic Algorithms. Appl. Soft Comput. 2020, 86, 105903. [Google Scholar] [CrossRef]
- Tehrani, K.; Member, I. A Smart Cyber Physical Multi-Source Energy System for an Electric Vehicle Prototype. J. Syst. Archit. 2020, 111, 101804. [Google Scholar] [CrossRef]
- Griva, I.; Nash, S.G.; Sofer, A. Linear and Nonlinear Optimization; SIAM: Philadelphia, PA, USA, 2009; pp. 149–162. [Google Scholar]
- Tsikalakis, A.G.; Hatziargyriou, N.D. Centralized control for optimizing microgrids operation. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Paul, T.G.; Hossain, S.J.; Ghosh, S.; Mandal, P.; Kamalasadan, S. A Quadratic Programming Based Optimal Power and Battery Dispatch for Grid-Connected Microgrid. IEEE Trans. Ind. Appl. 2018, 54, 1793–1805. [Google Scholar] [CrossRef]
- An, L.N.; Quoc-Tuan, T. Optimal energy management for grid connected microgrid by using dynamic programming method. In Proceedings of the 2015 IEEE Power Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Kanchev, H.; Lu, D.; Colas, F.; Lazarov, V.; Francois, B. Energy Management and Operational Planning of a Microgrid with a PV-Based Active Generator for Smart Grid Applications. IEEE Trans. Ind. Electron. 2011, 58, 4583–4592. [Google Scholar] [CrossRef] [Green Version]
- Elsied, M.; Oukaour, A.; Youssef, T.; Gualous, H.; Mohammed, O. An advanced real time energy management system for microgrids. Energy 2016, 114, 742–752. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Abdou, A.F. Modified PSO algorithm for real-time energy management in grid-connected microgrids. Renew. Energy 2019, 136, 746–757. [Google Scholar] [CrossRef]
- Ghorbani, S.; Rahmani, R.; Unland, R. Multi-agent autonomous decision making in smart micro-grids’ energy management: A decentralized approach. In Proceedings of the German Conference on Multiagent System Technologies, Leipzig, Germany, 23–26 August 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 223–237. [Google Scholar]
- Su, W.; Wang, J.; Roh, J. Stochastic energy scheduling in microgrids with intermittent renewable energy resources. IEEE Trans. Smart grid 2013, 5, 1876–1883. [Google Scholar] [CrossRef]
- Xiang, Y.; Liu, J.; Liu, Y. Robust energy management of microgrid with uncertain renewable generation and load. IEEE Trans. Smart Grid 2015, 7, 1034–1043. [Google Scholar] [CrossRef]
- Mondal, A.; Misra, S.; Patel, L.S.; Pal, S.K.; Obaidat, M.S. DEMANDS: Distributed energy management using noncooperative scheduling in smart grid. IEEE Syst. J. 2017, 12, 2645–2653. [Google Scholar] [CrossRef]
- Kuznetsova, E.; Li, Y.F.; Ruiz, C.; Zio, E.; Ault, G.; Bell, K. Reinforcement learning for microgrid energy management. Energy 2013, 59, 133–146. [Google Scholar] [CrossRef]
- Moehle, N.; Busseti, E.; Boyd, S.; Wytock, M. Dynamic energy management. arXiv 2019, arXiv:1903.06230. [Google Scholar]
- Leonori, S.; Martino, A.; Mascioli, F.M.F.; Rizzi, A. Microgrid Energy Management Systems Design by Computational Intelligence Techniques. Appl. Energy 2020, 277, 115524. [Google Scholar] [CrossRef]
- Richards, A.; How, J. Mixed-integer programming for control. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 4, pp. 2676–2683. [Google Scholar]
- Padberg, M.; Rinaldi, G. A branch-and-cut algorithm for the resolution of large-scale symmetric traveling salesman problems. SIAM Rev. 1991, 33, 60–100. [Google Scholar] [CrossRef]
- Chen, Y.; Casto, A.; Wang, F.; Wang, Q.; Wang, X.; Wan, J. Improving Large Scale Day-Ahead Security Constrained Unit Commitment Performance. IEEE Trans. Power Syst. 2016, 31, 4732–4743. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Control Strategies for Microgrids with Distributed Energy Storage Systems: An Overview. IEEE Trans. Smart Grid 2018, 9, 3652–3666. [Google Scholar] [CrossRef] [Green Version]
- Löfberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 284–289. [Google Scholar]
- Gurobi Optimization Inc. Gurobi Optimizer Reference Manual. 2014. Available online: http://www.gurobi.com (accessed on 22 December 2020).
- Gu, W.; Wang, Z.; Wu, Z.; Luo, Z.; Tang, Y.; Wang, J. An Online Optimal Dispatch Schedule for CCHP Microgrids Based on Model Predictive Control. IEEE Trans. Smart Grid 2017, 8, 2332–2342. [Google Scholar] [CrossRef]
- Raimondi Cominesi, S.; Farina, M.; Giulioni, L.; Picasso, B.; Scattolini, R. A Two-Layer Stochastic Model Predictive Control Scheme for Microgrids. IEEE Trans. Control Syst. Technol. 2018, 26, 1–13. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Wu, L.; Shahidehpour, M.; Li, Z. New Metrics for Assessing the Reliability and Economics of Microgrids in Distribution System. IEEE Trans. Power Syst. 2013, 28, 2852–2861. [Google Scholar] [CrossRef]
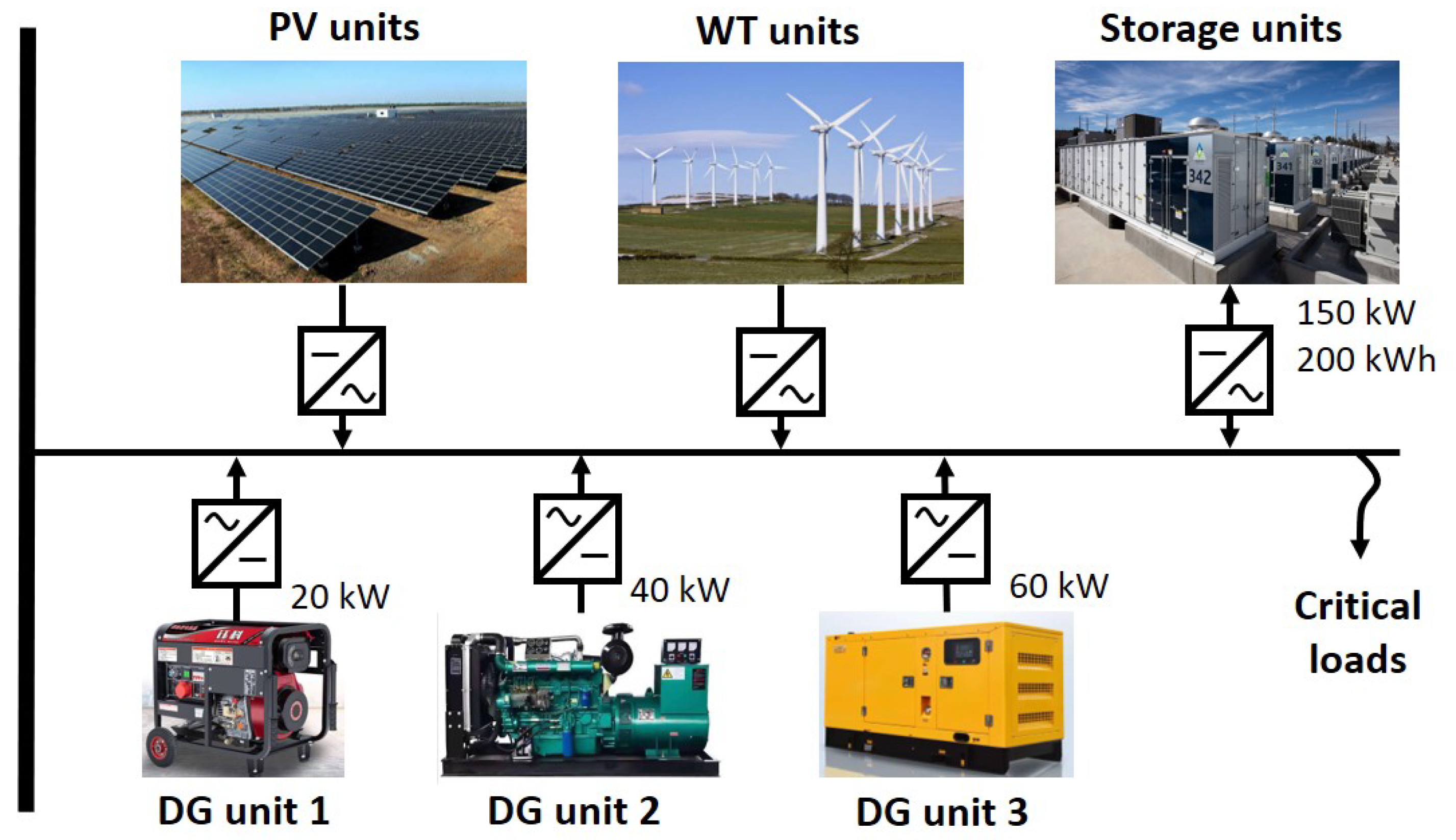


| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 200 kWh | 3 | ||
| 10 kWh | 20/40/60 kW | ||
| 150 kW | 5/10/15 | ||
| 0 | 8 kW | ||
| 0.9 | 0 | ||
| 0.05 | 0.8 |
| Method | Number of Violations | Violated Power (kW) | Operation Cost ($) |
|---|---|---|---|
| Our proposed method | 0 | 0 | 1220.3 |
| Our previous method | 2 | 28.76 | 1392.2 |
| Existing robust method | 1 | 23.21 | 1513.0 |
| Method | ILOLP (%) | IALL (kW) | ILLR (%) | Operation Cost ($) |
|---|---|---|---|---|
| Our proposed method | 0.52 | 13.86 | 23.96 | 1316.5 |
| Our previous method | 1.98 | 18.15 | 31.37 | 1400.9 |
| Existing robust method | 0.52 | 20.98 | 36.27 | 1434.0 |
| Method | ILOLP (%) | IALL (kW) | ILLR (%) | Operation Cost ($) |
|---|---|---|---|---|
| Our method with no prediction inputs | 2.08 | 24.07 | 41.61 | 1578.05 |
| Only hierarchical control with no prediction inputs | 53.13 | 39.21 | 67.78 | 10109.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Duan, D.; Cheng, X.; Yang, L.; Cui, S. Adaptive Control for Energy Exchange with Probabilistic Interval Predictors in Isolated Microgrids. Energies 2021, 14, 375. https://doi.org/10.3390/en14020375
Cheng J, Duan D, Cheng X, Yang L, Cui S. Adaptive Control for Energy Exchange with Probabilistic Interval Predictors in Isolated Microgrids. Energies. 2021; 14(2):375. https://doi.org/10.3390/en14020375
Chicago/Turabian StyleCheng, Jiayu, Dongliang Duan, Xiang Cheng, Liuqing Yang, and Shuguang Cui. 2021. "Adaptive Control for Energy Exchange with Probabilistic Interval Predictors in Isolated Microgrids" Energies 14, no. 2: 375. https://doi.org/10.3390/en14020375
APA StyleCheng, J., Duan, D., Cheng, X., Yang, L., & Cui, S. (2021). Adaptive Control for Energy Exchange with Probabilistic Interval Predictors in Isolated Microgrids. Energies, 14(2), 375. https://doi.org/10.3390/en14020375





