Efficient Multi-Objective CFD-Based Optimization Method for a Scroll Distributor
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Model
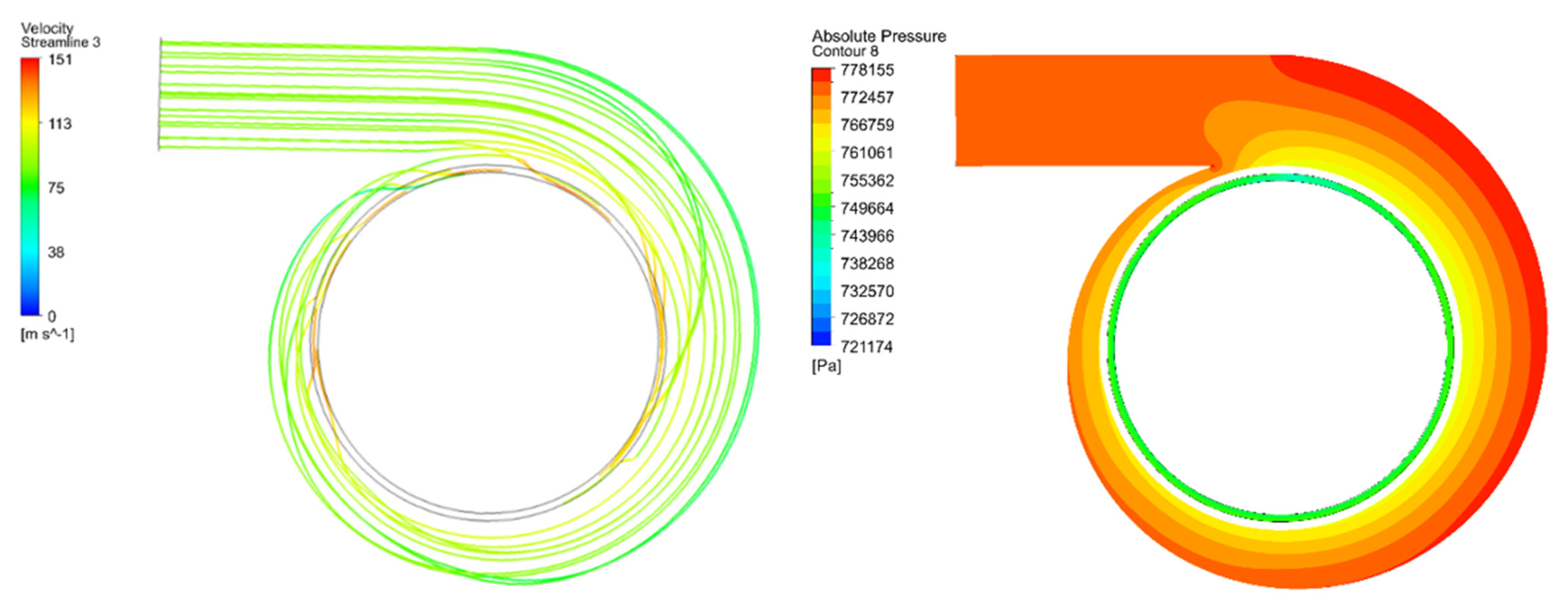
2.2. Investigation of the Initial Distributor Configuration
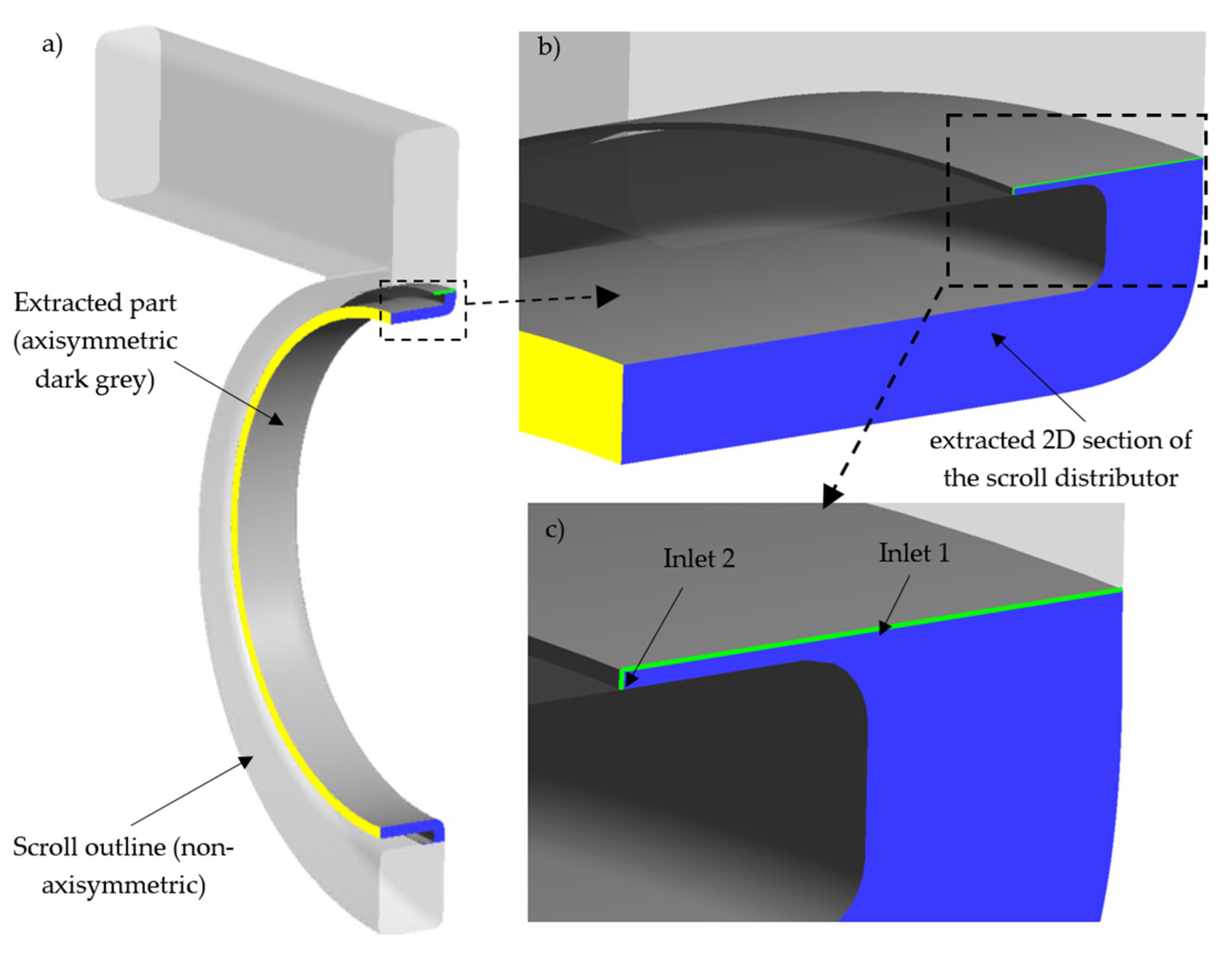
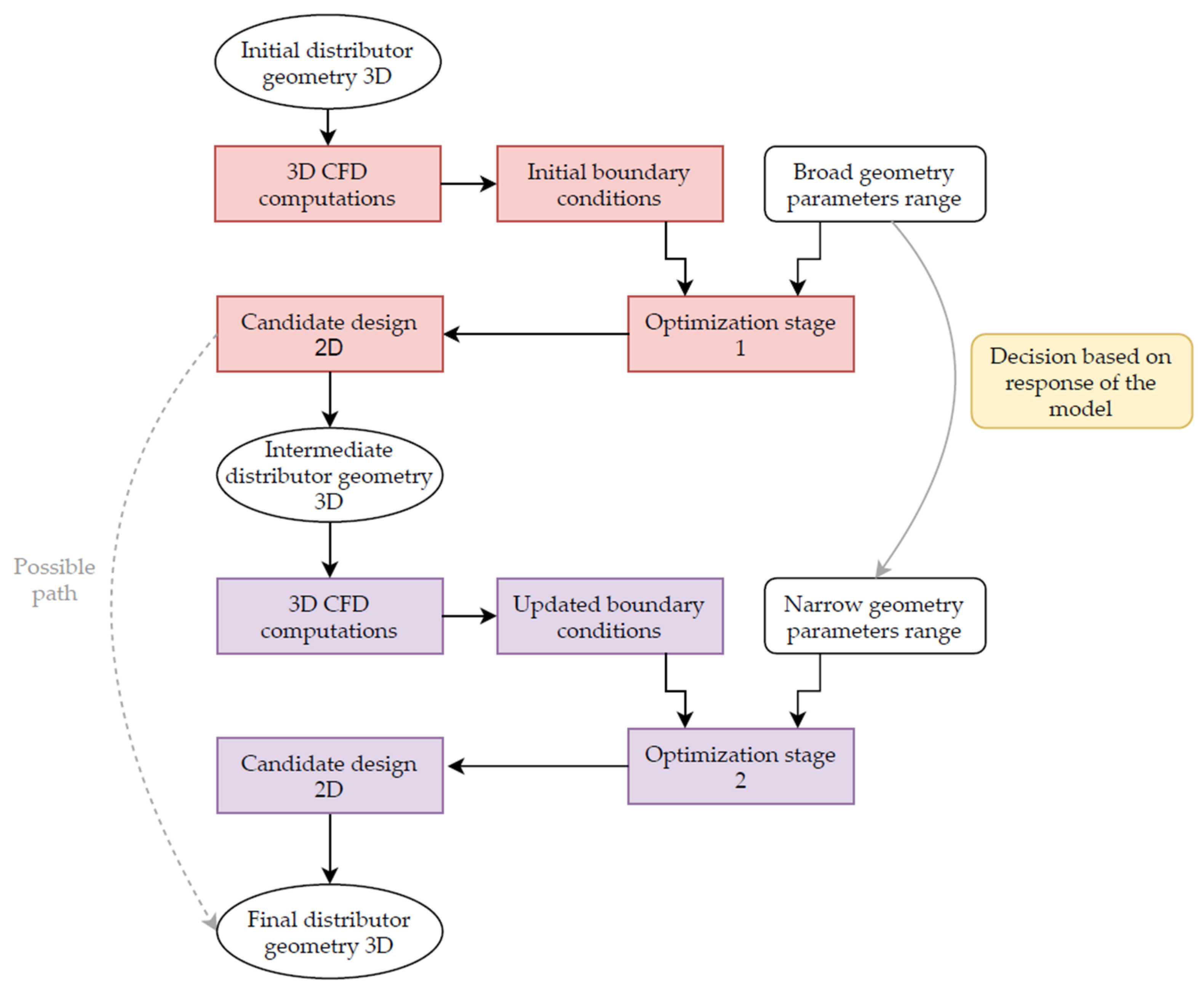
2.3. Problem Downsizing Method
2.4. Two-Dimensional Simulation
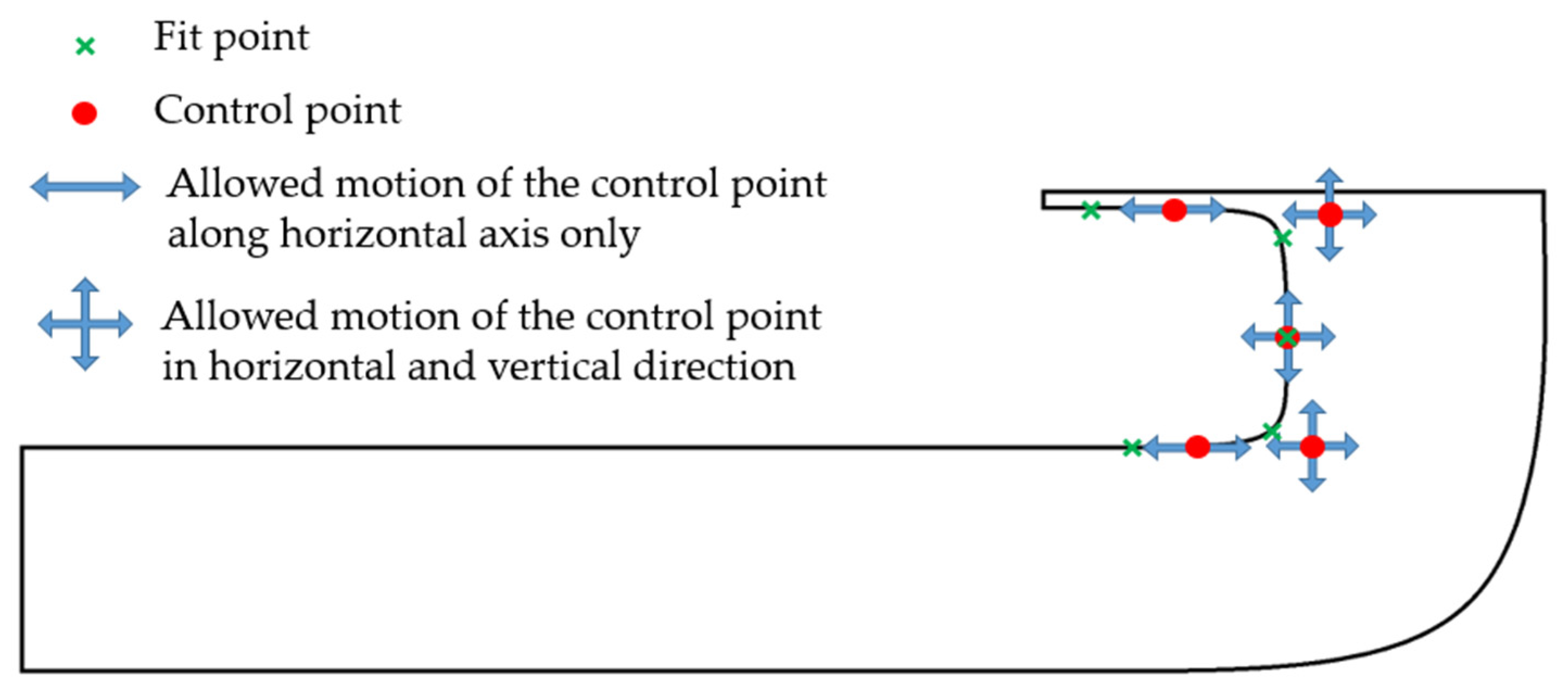
2.5. Model Geometry Parameterization
2.6. Optimization Procedure
3. Optimization Criteria
4. Results and Discussion
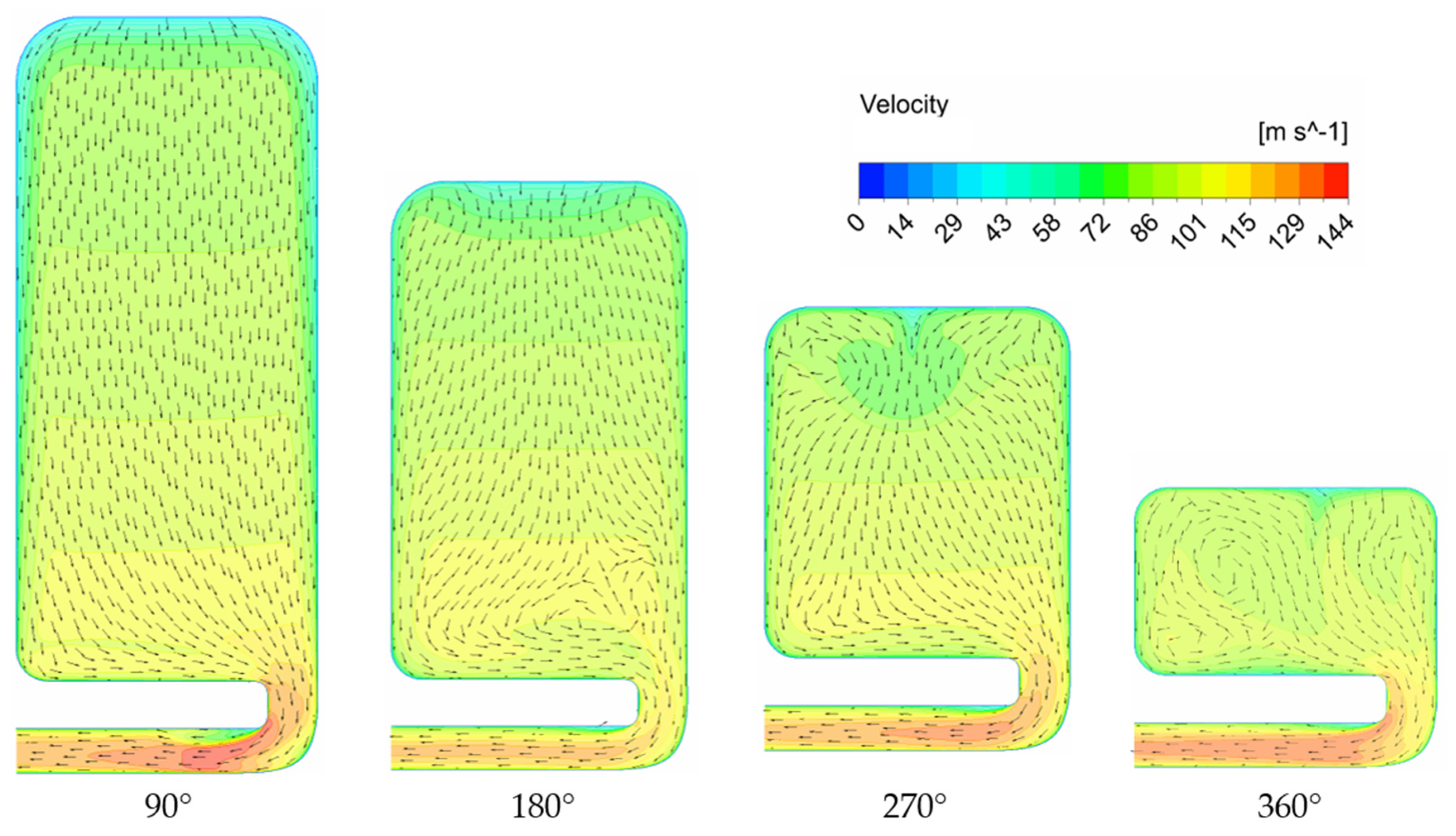
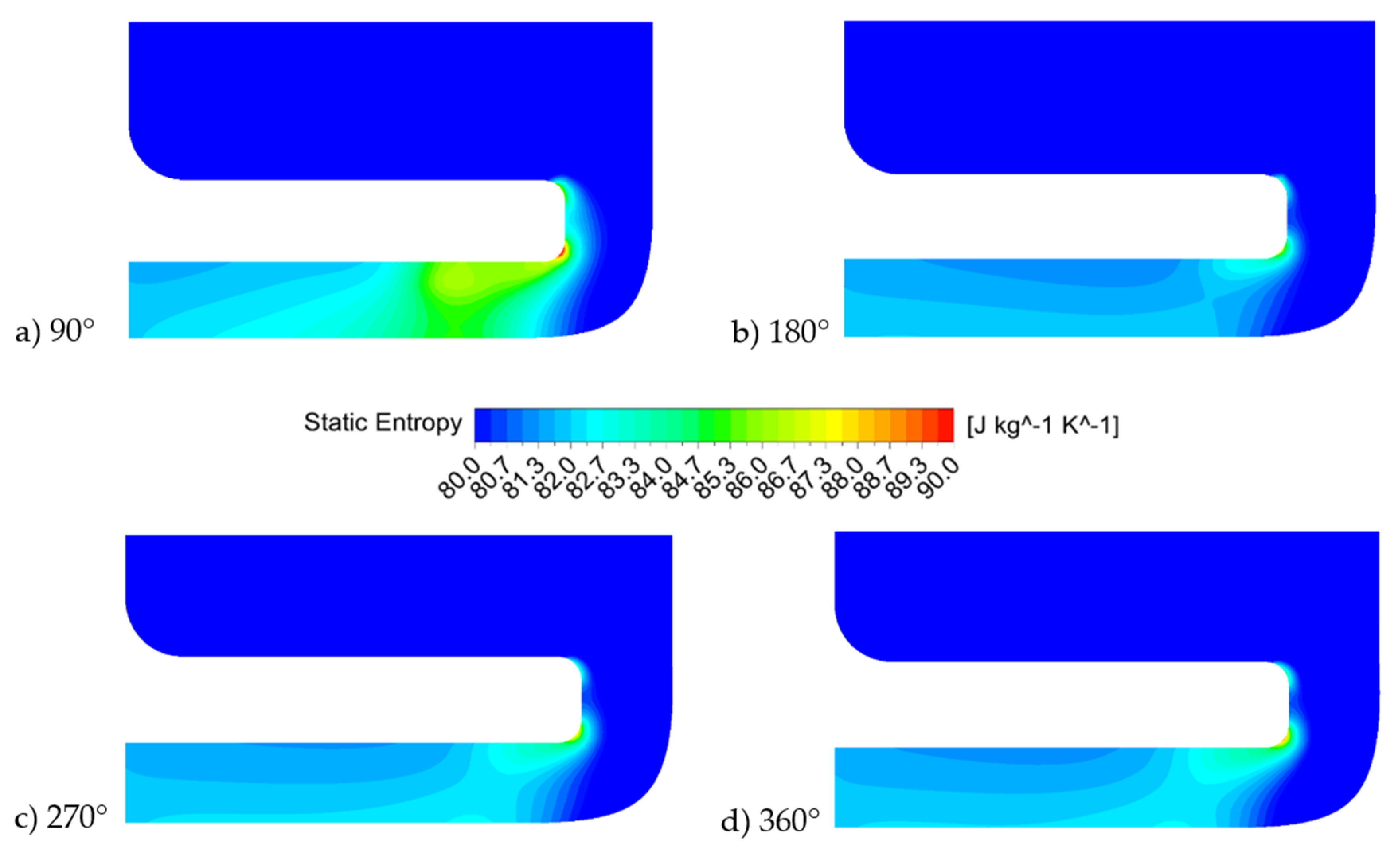
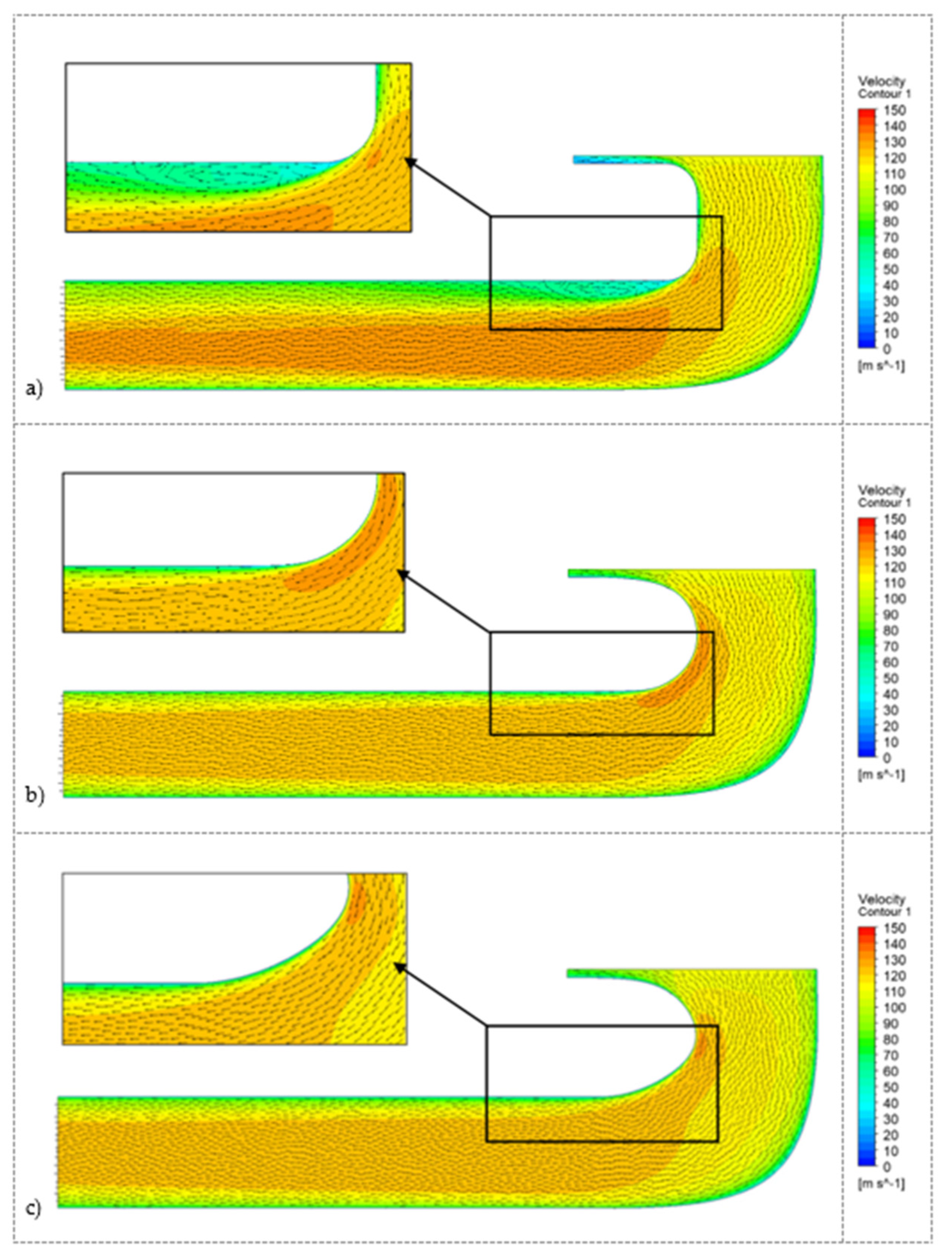
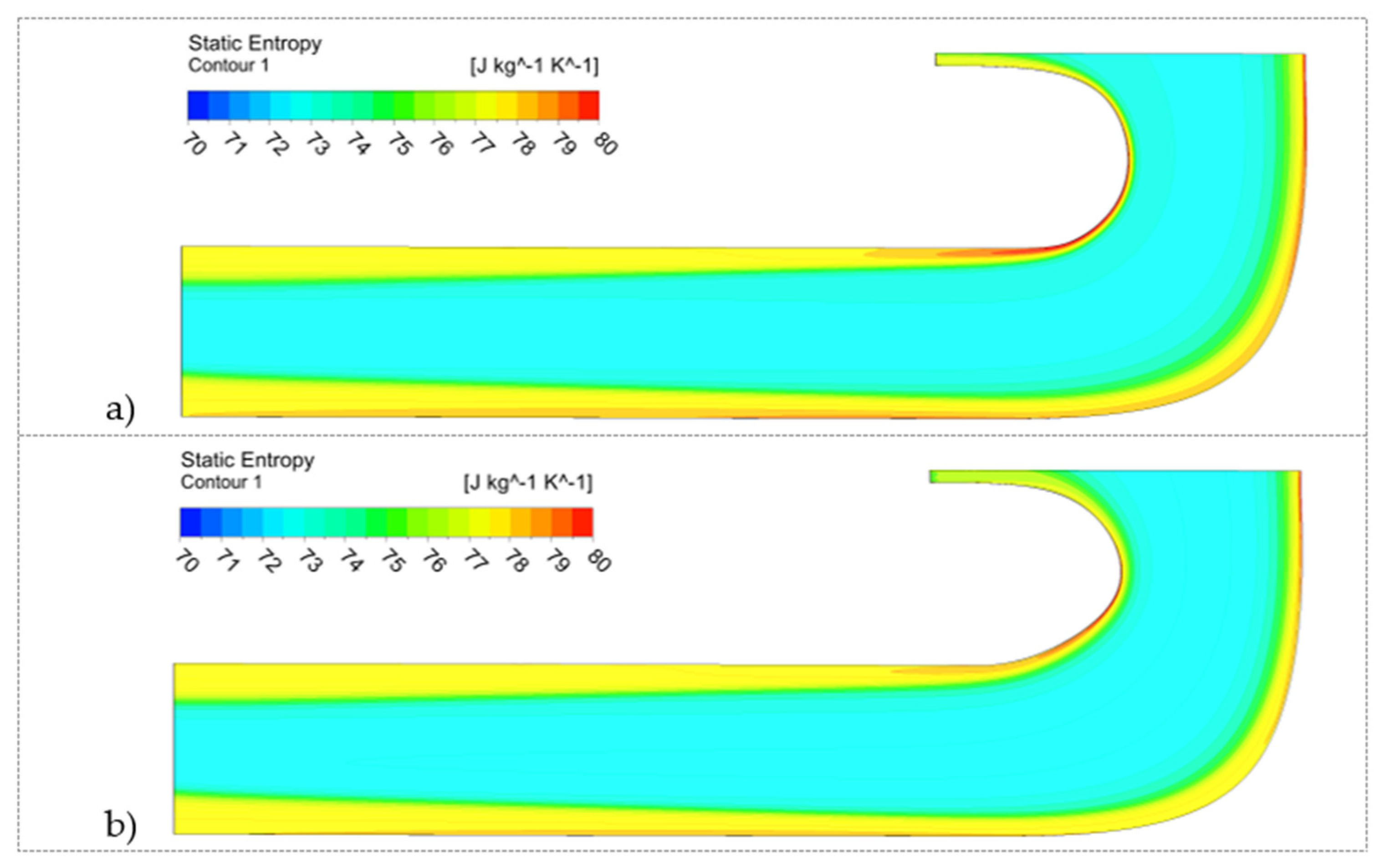
4.1. Downsized Solution Analysis
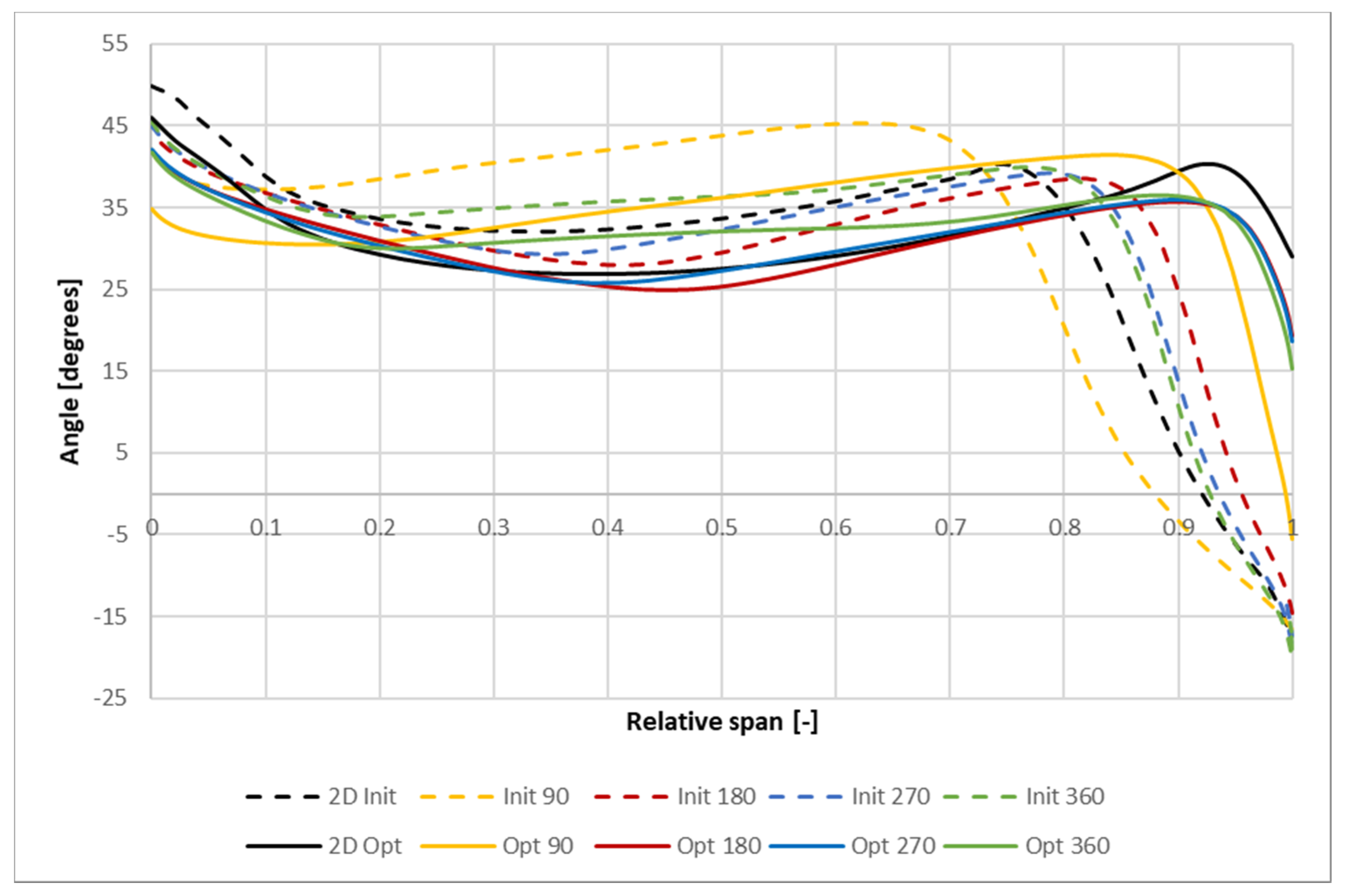
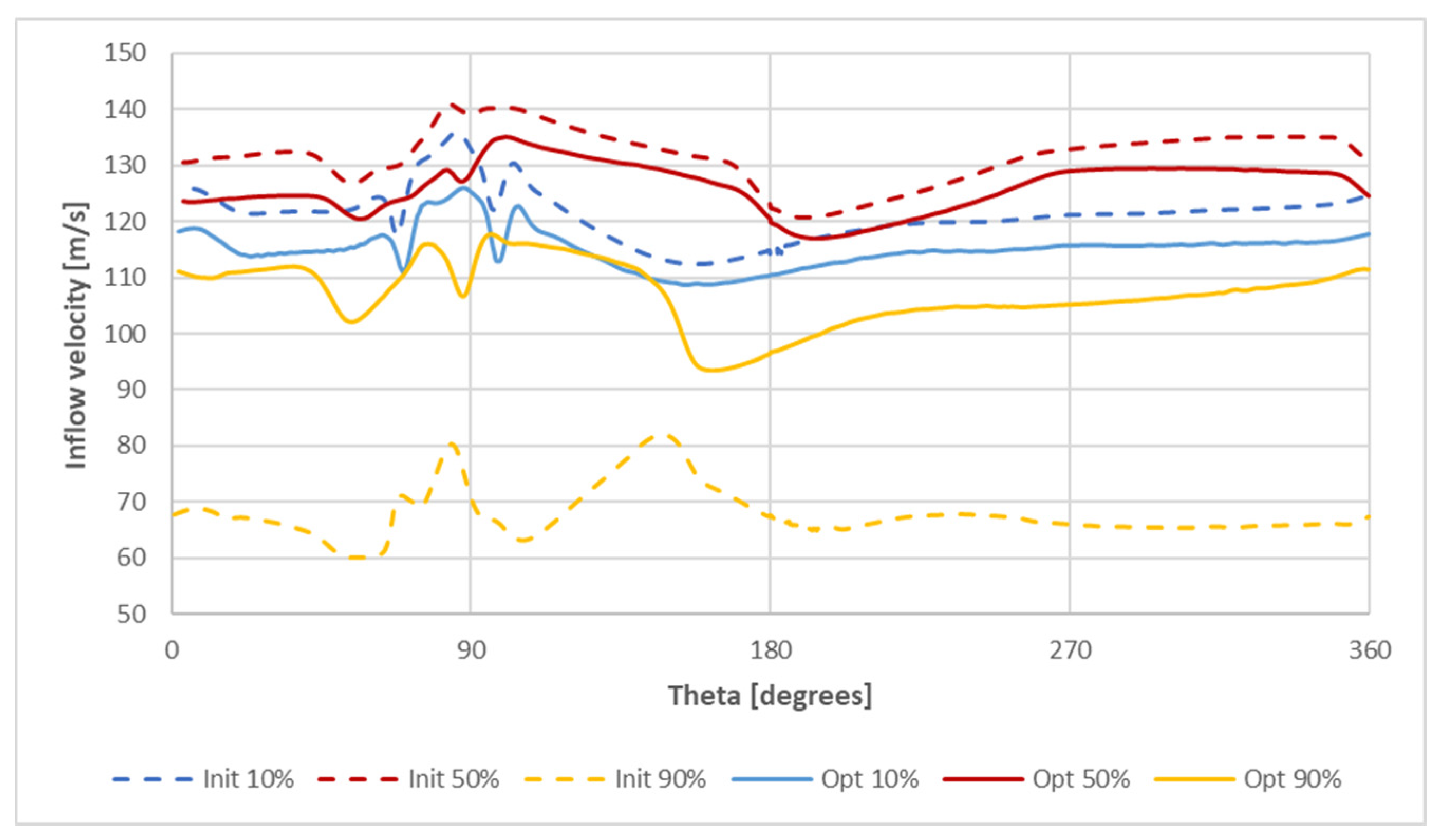
4.2. Verification of the Optimized Solution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thevenin, D.; Janiga, G. Optimizaion and Computational Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; ISBN 9783540721529. [Google Scholar]
- Xu, C.; Müller, M. Development and Design of a Centrifugal Compressor Volute. Int. J. Rotating Mach. 2005, 190–196. [Google Scholar] [CrossRef] [Green Version]
- Pan, D.; Whitfield, A.; Wilson, M. Design considerations for the volutes of centrifugal fans and compressors measured. Proc. Inst. Mech. Eng. 2015, 213, 401–410. [Google Scholar]
- Lu, F.A.; Qi, D.T.; Wang, X.J.; Zhou, Z.; Zhou, H.H. A numerical optimization on the vibroacoustics of a centrifugal fan volute. J. Sound Vib. 2012, 331, 2365–2385. [Google Scholar] [CrossRef]
- Kim, J.H.; Oh, K.T.; Pyun, K.B.; Kim, C.K.; Choi, Y.S.; Yoon, J.Y. Design optimization of a centrifugal pump impeller and volute using computational fluid dynamics. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 032025. [Google Scholar] [CrossRef]
- Lipian, M.; Kulak, M.; Stepien, M. Fast track integration of computational methods with experiments in smallwind turbine development. Energies 2019, 12, 1625. [Google Scholar] [CrossRef] [Green Version]
- Oka, N.; Furukawa, M.; Yamada, K.; Itou, S.; Ibaraki, S.; Iwakiri, K.; Hayashi, Y. Optimum aerodynamic design of centrifugal compressor impeller using an inverse method based on meridional viscous flow analysis. Proc. ASME Turbo Expo 2017, 2017, 1–10. [Google Scholar]
- Tüchler, S.; Chen, Z.; Copeland, C.D. Multipoint shape optimisation of an automotive radial compressor using a coupled computational fluid dynamics and genetic algorithm approach. Energy 2018, 165, 543–561. [Google Scholar] [CrossRef]
- Olivero, M.; Pasquale, D.; Ghidoni, A.; Rebay, S. Three-dimensional turbulent optimization of vaned diffusers for centrifugal compressors based on metamodel-assisted genetic algorithms. Optim. Eng. 2014, 15, 973–992. [Google Scholar] [CrossRef]
- Baloni, B.D.; Pathak, Y.; Channiwala, S.A. Centrifugal blower volute optimization based on Taguchi method. Comput. Fluids 2015, 112, 72–78. [Google Scholar] [CrossRef]
- Kim, S.; Choi, Y.-S.; Lee, K.-Y.; Yoon, J.-Y. Design Optimization of Centrifugal Pump Impellers in a Fixed Meridional Geometry using DOE. Int. J. Fluid Mach. Syst. 2009, 2, 172–178. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Zhang, C.L. Evaluation of elliptical finned-tube heat exchanger performance using CFD and response surface methodology. Int. J. Therm. Sci. 2014, 75, 45–53. [Google Scholar] [CrossRef]
- Lian, Y.; Liou, M.S. Multiobjective optimization using coupled response surface model and evolutionary algorithm. AIAA J. 2005, 43, 1316–1325. [Google Scholar] [CrossRef]
- Samad, A.; Kim, K.Y. Shape optimization of an axial compressor blade by multi-objective genetic algorithm. Proc. Inst. Mech. Eng. Part A J. Power Energy 2008, 222, 599–611. [Google Scholar] [CrossRef]
- Hartwig, L.; Bestle, D. Compressor blade design for stationary gas turbines using dimension reduced surrogate modeling. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017; pp. 1595–1602. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; Zhang, Y.; Zhu, S.P. Structural reliability analysis and uncertainties-based collaborative design and optimization of turbine blades using surrogate model. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1219–1227. [Google Scholar] [CrossRef]
- Verstraete, T.; Alsalihi, Z.; Van den Braembussche, R.A. Multidisciplinary Optimization of a Radial Compressor for Microgas Turbine Applications. J. Turbomach. 2010, 132, 031004. [Google Scholar] [CrossRef]
- Stajuda, M.; Obidowski, D.; Karczewski, M.; Józwik, K. Modified virtual blade method for propeller modelling. Mech. Mech. Eng. 2018, 22, 603–617. [Google Scholar] [CrossRef]
- Lipian, M.; Karczewski, M.; Jozwik, K. Analysis and comparison of numerical methods for design and development of small Diffuser-Augmented Wind Turbine (DAWT). In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 5525–5531. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Q.; Xiang, X.; Zhao, W.; Zhou, X. A hybrid viscous body force model for low-speed centrifugal compressors. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 1–16. [Google Scholar] [CrossRef]
- Neverov, V.V.; Kozhukhov, Y.V.; Yablokov, A.M.; Lebedev, A.A. Optimization of a centrifugal compressor impeller using CFD: The choice of simulation model parameters. In Proceedings of the IOP Conference Series: Materials Science and Engineering, London, UK, 11–13 September 2017; Volume 232. [Google Scholar] [CrossRef]
- Jóźwik, K.; Papierski, A.; Sobczak, K.; Obidowski, D.; Kryłłowicz, W.; Marciniak, E.; Wróbel, G.; Marciniak, A.; Wróblewski, P.; Kobierska, A.; et al. Radial fan controlled with impeller movable blades—CFD investigations. Trans. Inst. Fluid-Flow Mach. 2016, 131, 17–40. [Google Scholar]
- Japikse, D. Centrifugal Compressor Design and Performance; Concepts ETI: White River Junction, VT, USA, 1996; ISBN 9780933283039. [Google Scholar]
- Ansys Inc. ANSYS CFX-Solver Theory Guide 19.2; Ansys Inc.: Canonsburg, PA, USA, 2009. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transf. 2003, 1, 625–632. [Google Scholar] [CrossRef]
- Sobczak, K.; Obidowski, D.; Reorowicz, P.; Marchewka, E. Numerical investigations of the savonius turbine with deformable blades. Energies 2020, 13, 3717. [Google Scholar] [CrossRef]
- Obidowski, D.; Reorowicz, P.; Witkowski, D.; Sobczak, K.; Jóźwik, K. Methods for determination of stagnation in pneumatic ventricular assist devices. Int. J. Artif. Organs 2018, 41, 653–663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stajuda, M.; Karczewski, M.; Obidowski, D.; Jóźwik, K. Development of a CFD model for propeller simulation. Mech. Mech. Eng. 2016, 20, 579–593. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130, 0780011–0780014. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]






| Parameter | Value |
|---|---|
| Simulation type | Steady state, RANS |
| Turbulence model | Shear Stress Transport (SST) |
| Medium | Air, compressible |
| Discretization scheme | Second order |
| Inlet boundary condition | Mass flow rate, 2 kg/s |
| Static temperature, 500 K | |
| Turbulence intensity, 5% | |
| Turbulent to molecular viscosity ratio, 10 | |
| Outlet boundary condition | Static pressure, 7.5 bar |
| Walls boundary condition | Smooth, adiabatic |
| Parameter | Value |
|---|---|
| Simulation type | Steady state, RANS |
| Turbulence model | Shear Stress Transport (SST) |
| Medium | Air, compressible |
| Discretization scheme | Second order |
| Inlet boundary condition | Velocity vector, from 3D solution |
| Static temperature, from 3D solution | |
| Turbulence kinetic energy (TKE), from 3D solution | |
| Dissipation of turbulence kinetic energy, from 3D solution | |
| Outlet boundary condition | Static pressure, 7.5 bar |
| Walls boundary condition | Smooth, adiabatic |
| Sides of quasi-2D section | Periodic interface |
| Parameter | Value | ||
|---|---|---|---|
| N—number of control volumes | Mesh 1: 65,000, Mesh 2: 150,000; Mesh 3: 350,000 | ||
| —mesh size ratio | 1.220 | ||
| —mesh size ratio | 1.326 | ||
| = Total pressure difference [Pa] | = Flow angle [degrees] | = Averaged velocity at the leading edge location [m/s] | |
| 20,150 | 31.50 | 120.28 | |
| 19,835 | 31.24 | 119.95 | |
| 19,650 | 31.10 | 119.67 | |
| 1.73% | 0.17% | 1.39% | |
| 2.9% | 0.34% | 1.70% | |
| Criterion | Target |
|---|---|
| VCC | Minimize |
| VAC | Minimize |
| Static entropy difference | Minimize |
| Reversed flow area | Minimize |
| Kinetic energy correction factor | Minimize |
| Geometry | Improvement from Initial | |
|---|---|---|
| Optimized | 0.5060 | 16.29% |
| Intermediate | 0.5101 | 15.61% |
| Initial | 0.6045 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obidowski, D.; Stajuda, M.; Sobczak, K. Efficient Multi-Objective CFD-Based Optimization Method for a Scroll Distributor. Energies 2021, 14, 377. https://doi.org/10.3390/en14020377
Obidowski D, Stajuda M, Sobczak K. Efficient Multi-Objective CFD-Based Optimization Method for a Scroll Distributor. Energies. 2021; 14(2):377. https://doi.org/10.3390/en14020377
Chicago/Turabian StyleObidowski, Damian, Mateusz Stajuda, and Krzysztof Sobczak. 2021. "Efficient Multi-Objective CFD-Based Optimization Method for a Scroll Distributor" Energies 14, no. 2: 377. https://doi.org/10.3390/en14020377
APA StyleObidowski, D., Stajuda, M., & Sobczak, K. (2021). Efficient Multi-Objective CFD-Based Optimization Method for a Scroll Distributor. Energies, 14(2), 377. https://doi.org/10.3390/en14020377





