Interturn Short-Circuit Fault Detection of a Five-Phase Permanent Magnet Synchronous Motor
Abstract
:1. Introduction
2. Model Analysis
2.1. Five-Phase PMSM Healthy Model
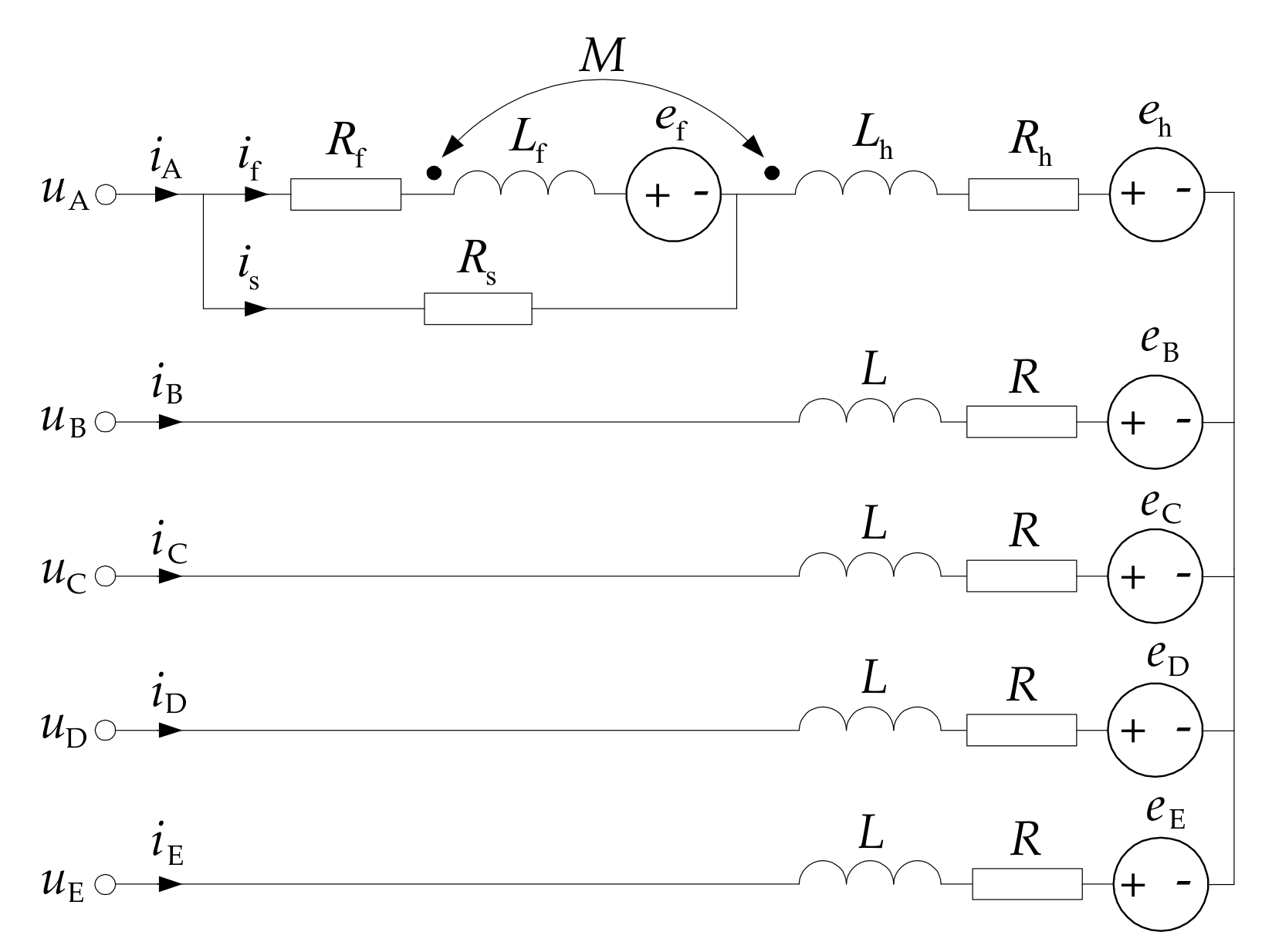
2.2. Five-Phase PMSM Faulty Model
3. Single-Phase Generalized Instantaneous Reactive Power Theory Based on Hilbert Transform
3.1. Principles and Properties of Hilbert Transformation
3.2. Principles and Properties of Single-Phase Generalized Instantaneous Reactive Power Theory
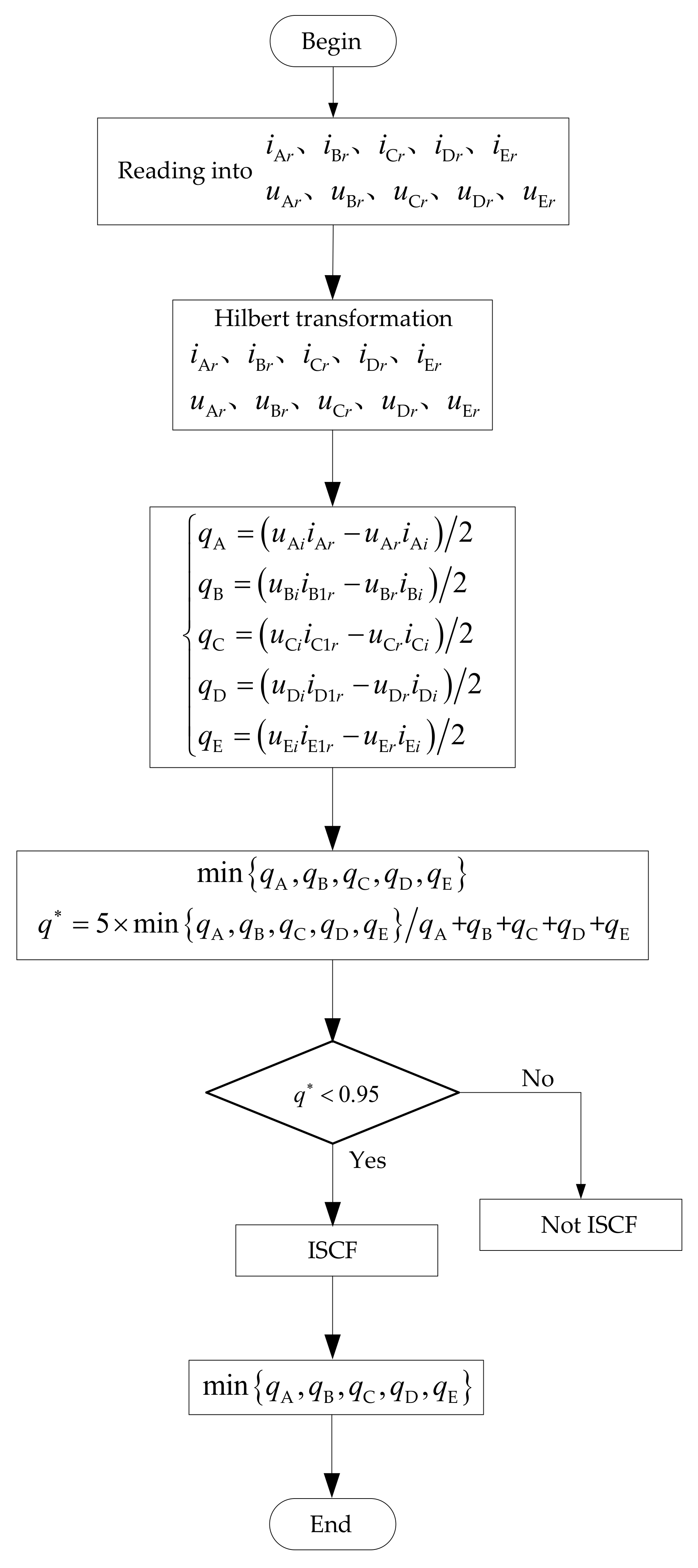
4. Analysis of the Method for Detecting the ISCF
4.1. The Theoretical Analysis
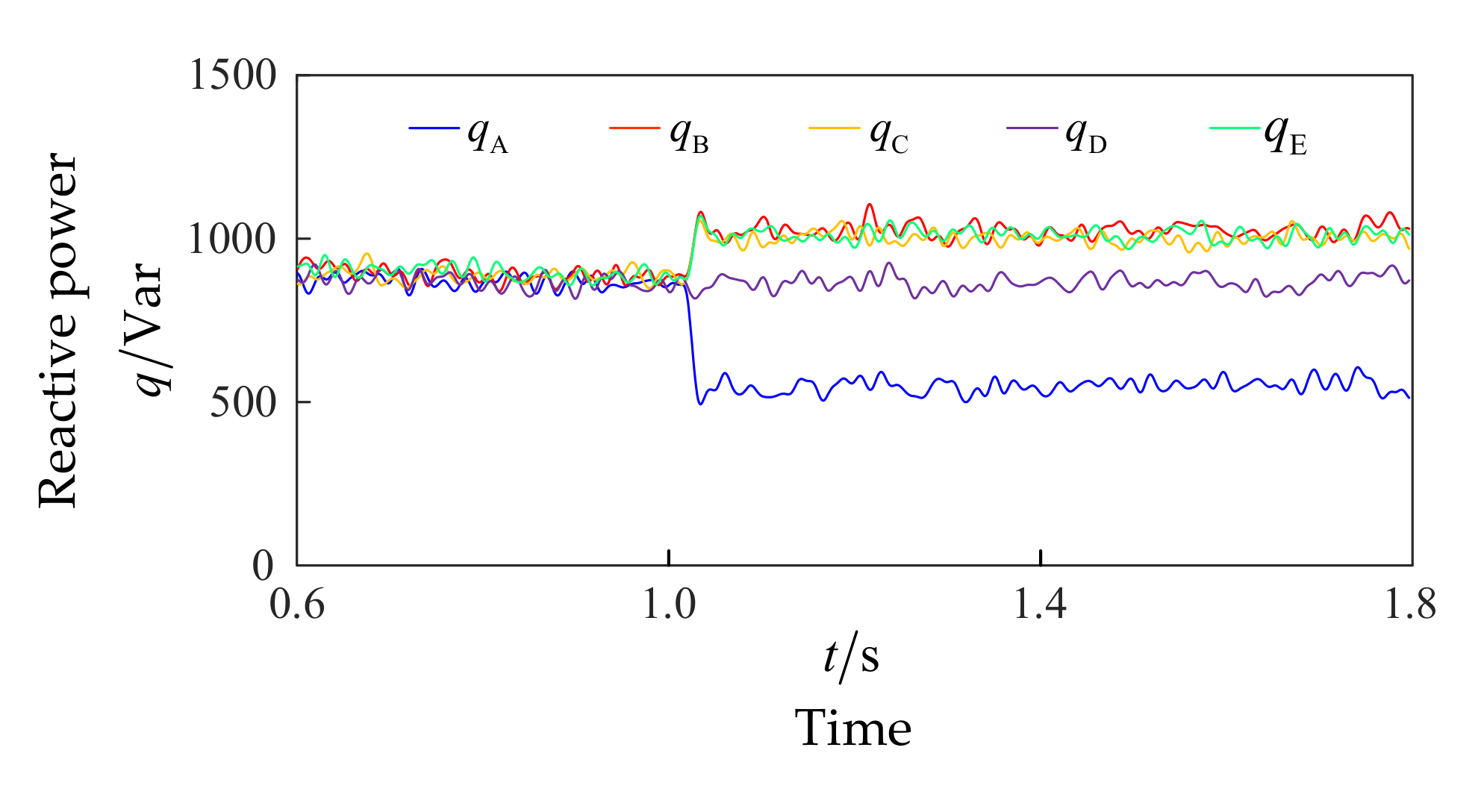
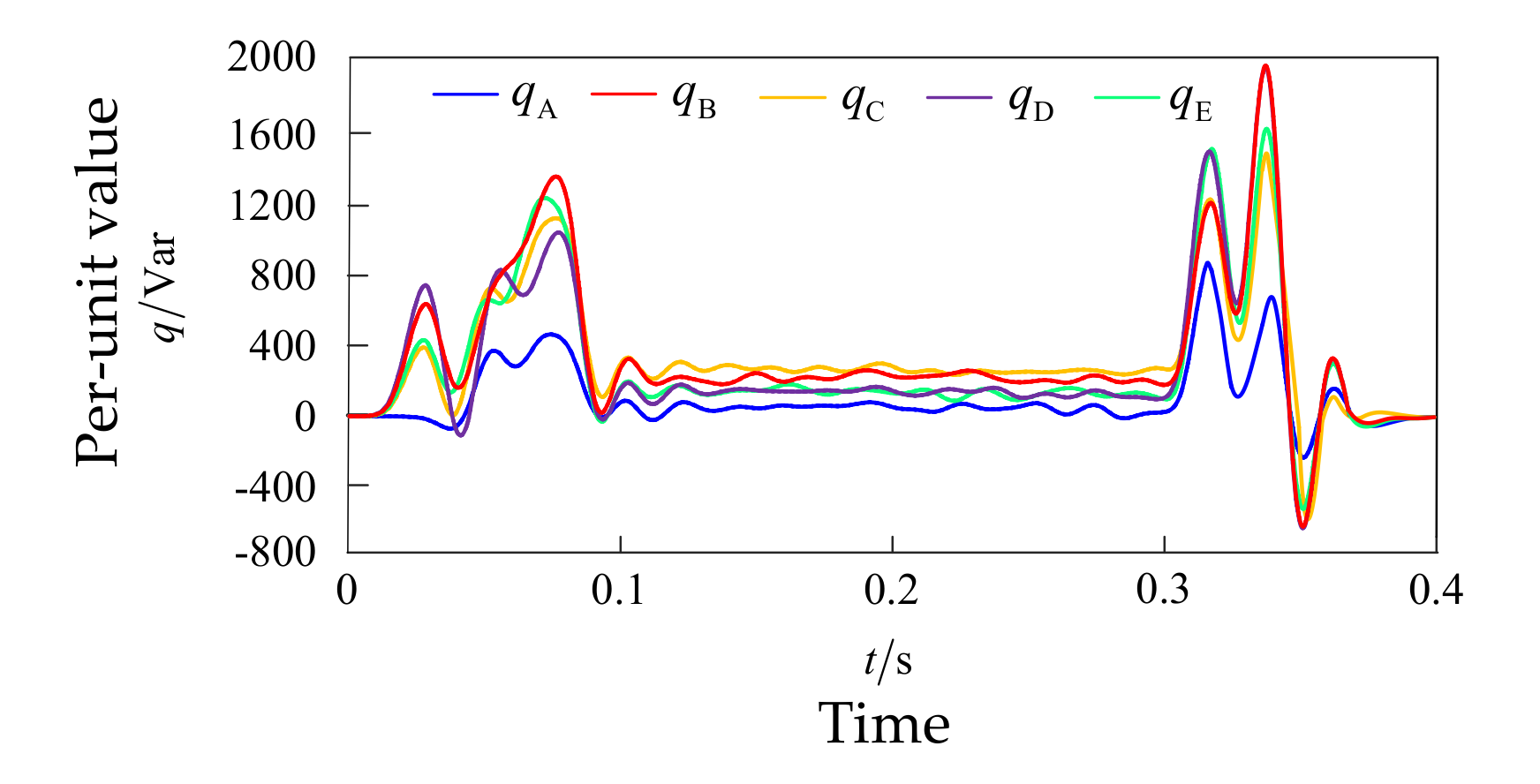
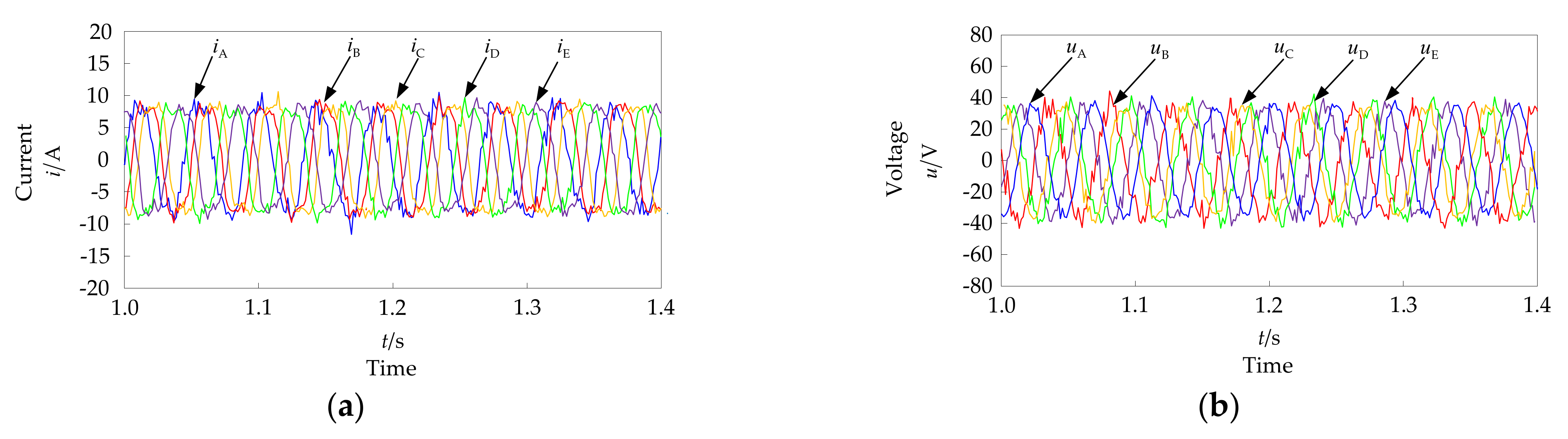
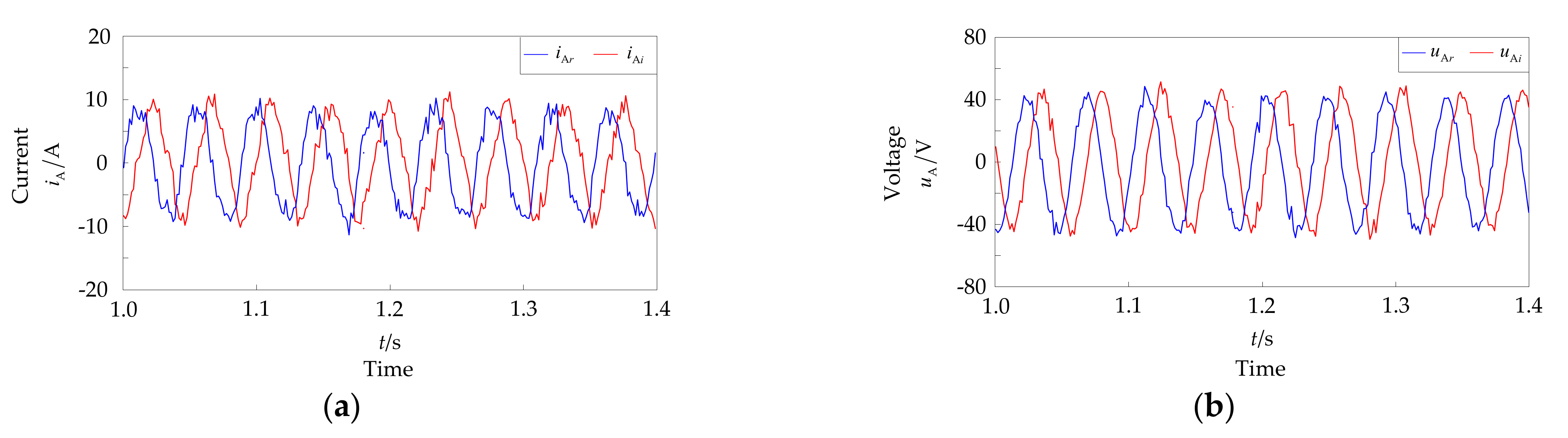
4.2. Simulation Analysis of ISCF Detection under Steady-State Operation
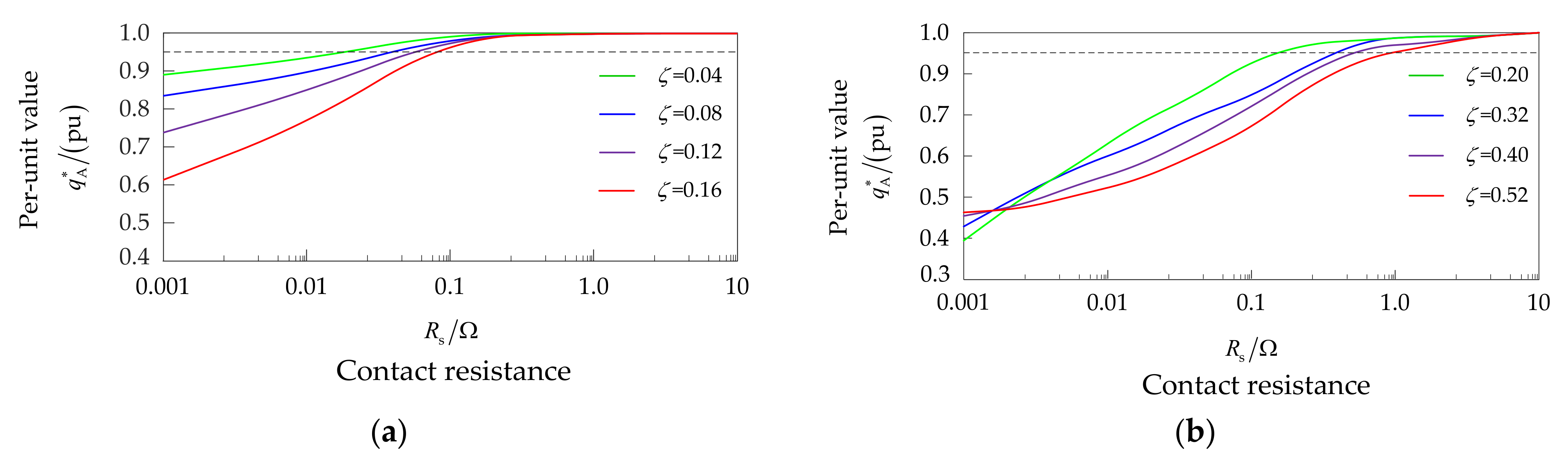
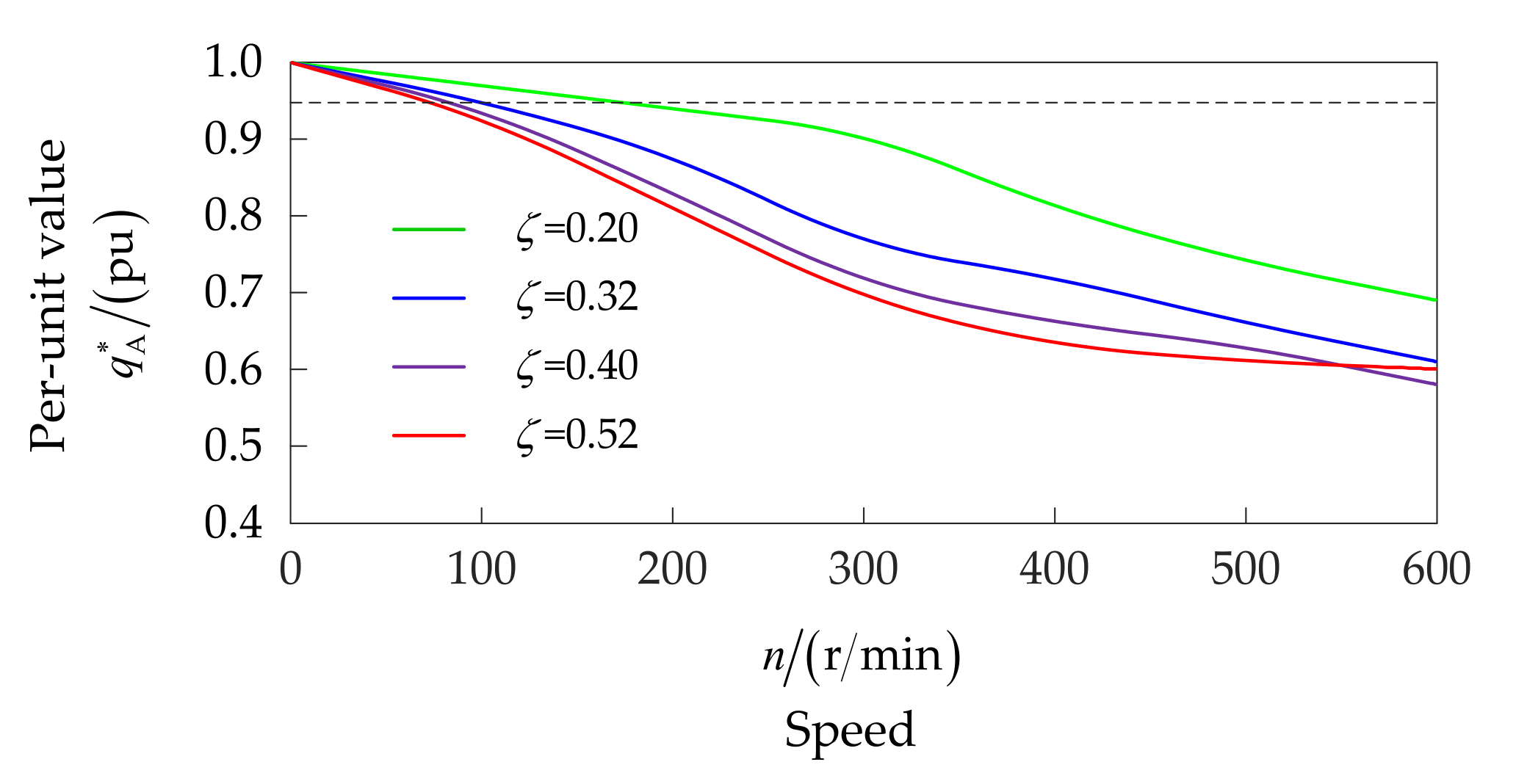
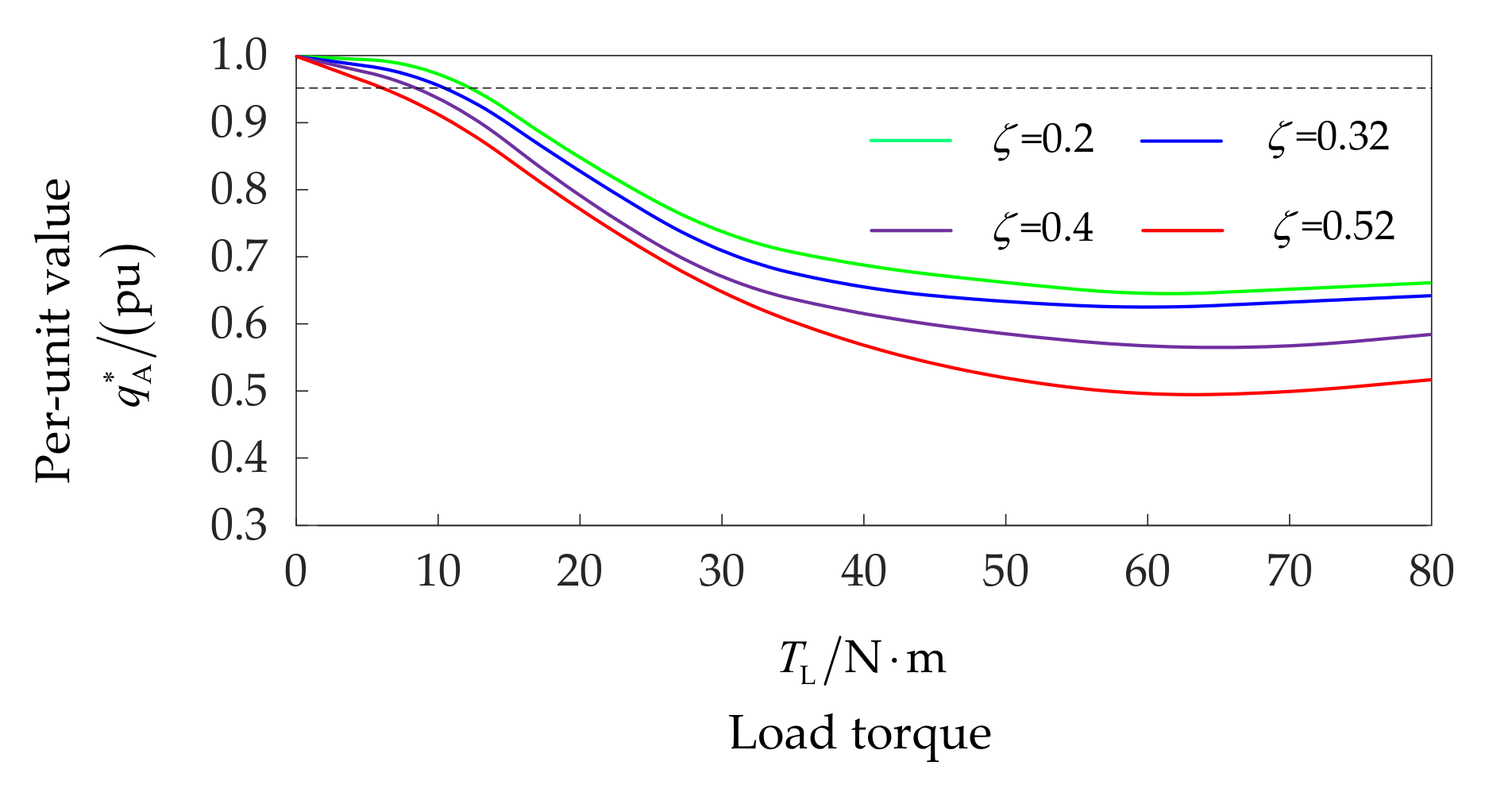
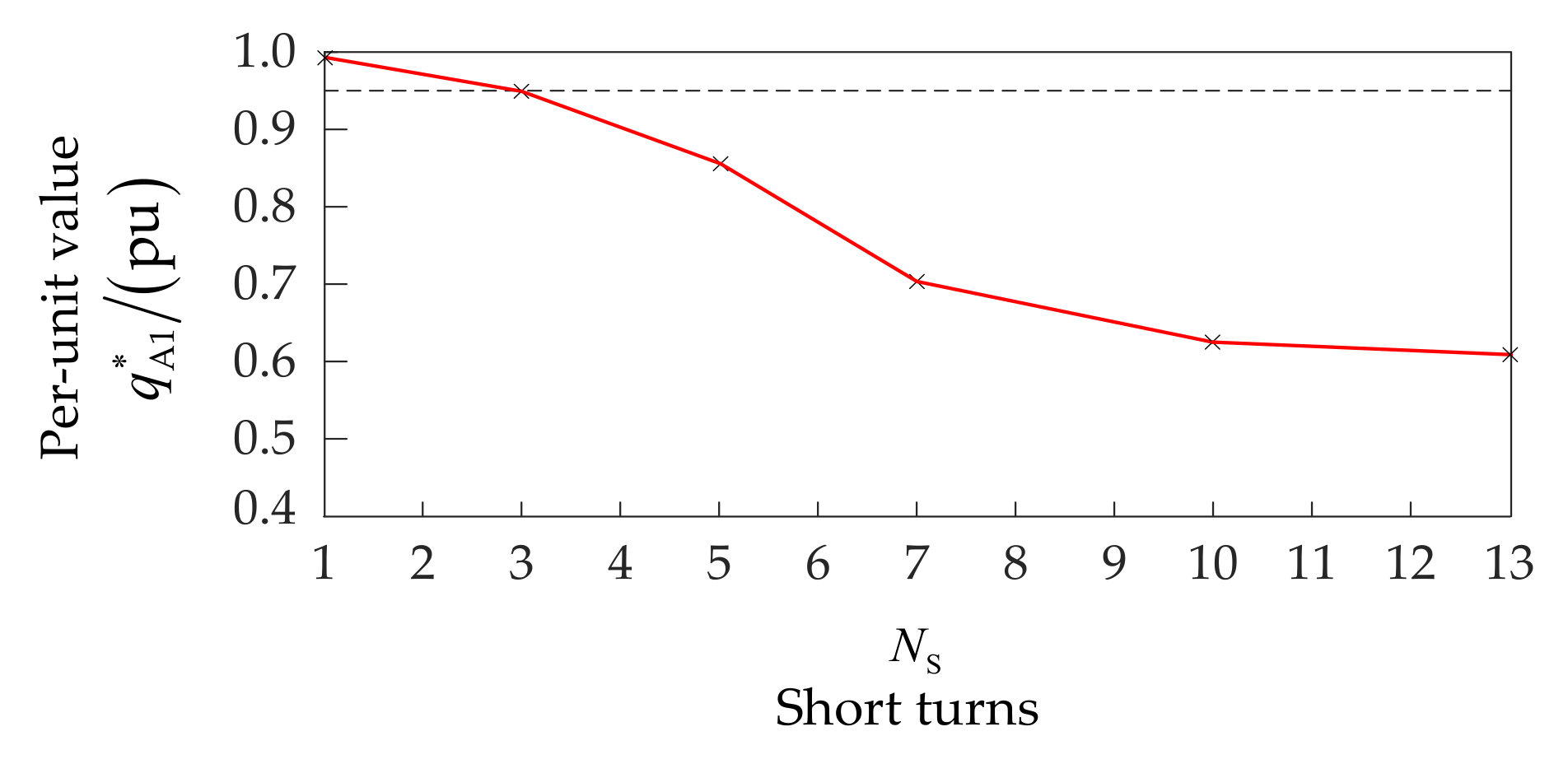
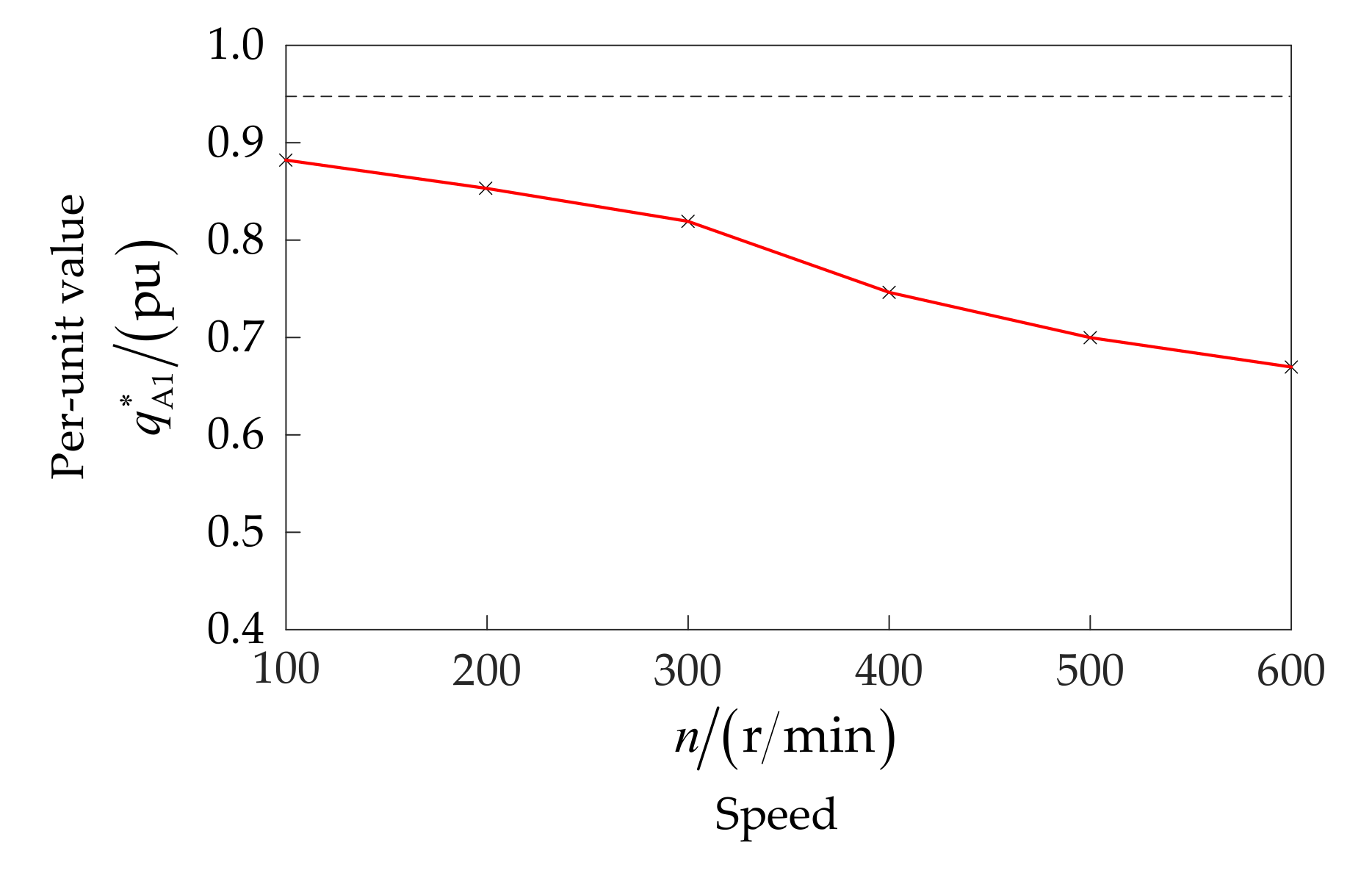
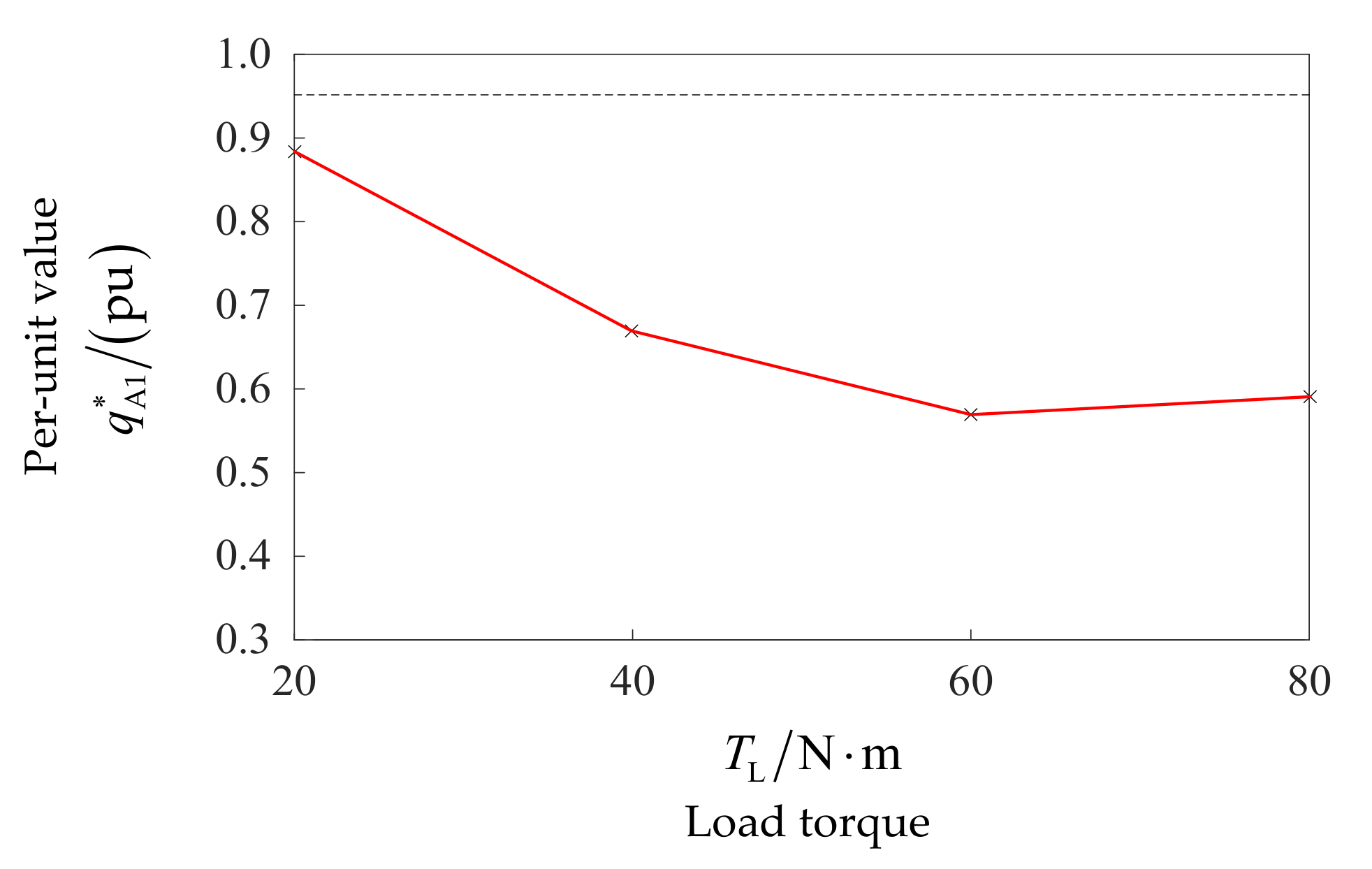
4.3. Analysis of the Influence Factors on the ISCF Detection of a Motor under Steady-State Operation
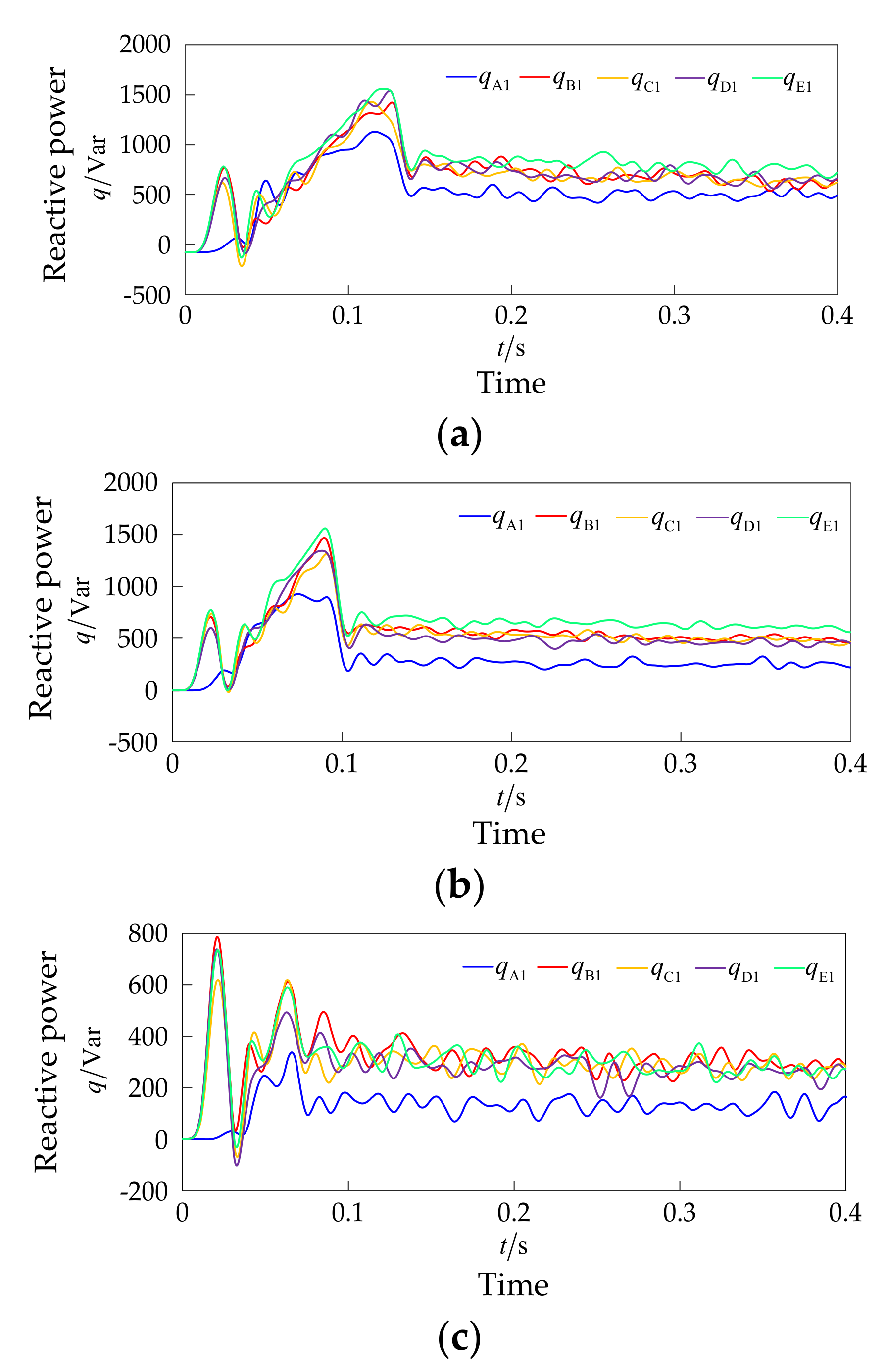
5. Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ehsani, M.; Gao, Y.; Miller, J.M. Hybrid electric vehicles: Architecture and motor drives. IEEE Proc. 2007, 95, 719–728. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, M.; Zhang, B.; Zhu, Y.; Ding, S. A fault-tolerant permanent-magnet traction module for subway application. IEEE Trans. Power Electron. 2014, 29, 1646–1658. [Google Scholar] [CrossRef]
- Jeong, H.; Moon, S.; Kim, S.W. An Early Stage Interturn Fault Diagnosis of PMSMs by Using Negative-Sequence Components. IEEE Trans. Ind. Electron. 2017, 64, 5701–5708. [Google Scholar] [CrossRef]
- Yang, S.; Hsu, Y.; Chou, P.; Liu, C.; Chen, G.; Li, K. Fault Detection and Tolerant Capability of Parallel-Connected Permanent Magnet Machines Under Stator Turn Fault. IEEE Trans. Ind. Appl. 2018, 54, 4447–4456. [Google Scholar] [CrossRef]
- Qi, Y.; Zafarani, M.; Gurusamy, V.; Akin, B. Advanced Severity Monitoring of Interturn Short Circuit Faults in PMSMs. IEEE Trans. Transp. Electrif. 2019, 5, 395–404. [Google Scholar] [CrossRef]
- Qi, Y.; Bostanci, E.; Zafarani, M.; Akin, B. Severity Estimation of Interturn Short Circuit Fault for PMSM. IEEE Trans. Ind. Electron. 2019, 66, 7260–7269. [Google Scholar] [CrossRef]
- Ge, Y.; Song, B.; Pei, Y.; Mollet, Y.A.B.; Gyselinck, J.J.C. Analytical Expressions of Isolation Indicators for Permanent-Magnet Synchronous Machines Under Stator Short-Circuit Faults. IEEE Trans. Energy Convers. 2019, 34, 984–992. [Google Scholar] [CrossRef]
- Haddad, R.Z.; Lopez, C.A.; Foster, S.N.; Strangas, E.G. A Voltage-Based Approach for Fault Detection and Separation in Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Appl. 2017, 53, 5305–5314. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Pourhossein, K.; Mohammadi-Ivatloo, B.; Mohammadi, F. Locating Inter-Turn Faults in Transformer Windings Using Isometric Feature Mapping of Frequency Response Traces. IEEE Trans. Ind. Inform. 2020. [Google Scholar] [CrossRef]
- Kim, K. Simple Online Fault Detecting Scheme for Short-Circuited Turn in a PMSM Through Current Harmonic Monitoring. IEEE Trans. Ind. Electron. 2011, 58, 2565–2568. [Google Scholar] [CrossRef]
- Eftekhari, M.; Moallem, M.; Sadri, S.; Hsieh, M. Online Detection of Induction Motor’s Stator Winding Short-Circuit Faults. IEEE Syst. J. 2014, 8, 1272–1282. [Google Scholar] [CrossRef]
- Zhao, J.; Guan, X.; Li, C.; Mou, Q.; Chen, Z. Comprehensive Evaluation of Inter-Turn Short Circuit Faults in PMSM Used for Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 1–11. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, W.; Głowacz, Z. Fault Diagnosis of Three Phase Induction Motor Using Current Signal, MSAF-Ratio15 and Selected Classifiers. Arch. Metall. Mater. 2017, 62, 2413–2419. [Google Scholar] [CrossRef]
- Qi, Y.; Bostanci, E.; Gurusamy, V.; Akin, B. A Comprehensive Analysis of Short-Circuit Current Behavior in PMSM Interturn Short-Circuit Faults. IEEE Trans. Power Electron. 2018, 33, 10784–10793. [Google Scholar] [CrossRef]
- Cui, R.; Fan, Y.; Li, C. On-Line Inter-Turn Short-Circuit Fault Diagnosis and Torque Ripple Minimization Control Strategy Based on OW Five-Phase BFTHE-IPM. IEEE Trans. Energy Convers. 2018, 33, 2200–2209. [Google Scholar] [CrossRef]
- Wu, F.; EL-Refaie, A.M.; Zheng, P. Diagnosis and Remediation of Single-Turn Short Circuit in a Multiphase FSCW PM Machine Based on T-type Equivalent Circuit. IEEE Trans. Ind. Appl. 2020, 56, 158–169. [Google Scholar] [CrossRef]
- Wu, F.; Tong, C.; Sui, Y. Influence of third harmonic back EMF on modeling and remediation of winding short circuit in a multiphase PM machine with FSCWs. IEEE Trans. Ind. Electron. 2016, 63, 6031–6041. [Google Scholar] [CrossRef]
- Shichuan, D.; Qingming, W.; Jun, H. Inter-turn fault diagnosis of permanent magnet synchronous machine considering model predictive control. Chin. Soc. Electr. Eng. 2019, 39, 3697–3708. [Google Scholar] [CrossRef]
- Saitou, M.; Shimizu, T. Generalized theory of instanta-neous active and reactive powers in single-phase circuits based on Hilbert transform. In Proceedings of the 2002 IEEE 33rd Annual IEEE Power Electronics Specialists Conference, Cairns, QLD, Australia, 23–27 June 2002; pp. 1419–1424. [Google Scholar]
- Lv, K.; Gao, C.; Si, J. Fault coil location of inter-turn short-circuit for direct-drive permanent magnet synchronous motor using knowledge graph. IET Electr. Power Appl. 2020, 14, 1712–1721. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Sun, Z. Electromagnetic-thermal coupled modelling and analysis of inter-turn short-circuit faults of a permanent magnet alternator. J. Eng. 2019, 2019, 4426–4431. [Google Scholar] [CrossRef]
- Berzoy, A.; Mohammed, O.A.; Restrepo, J. Analysis of the Impact of Stator Interturn Short-Circuit Faults on Induction Machines Driven by Direct Torque Control. IEEE Trans. Energy Convers. 2018, 33. [Google Scholar] [CrossRef]
- Sadeghi, R.; Samet, H.; Ghanbari, T. Detection of Stator Short-Circuit Faults in Induction Motors Using the Concept of Instantaneous Frequency. IEEE Trans. Industr. Inform. 2019, 15, 4506–4515. [Google Scholar] [CrossRef]
- Zhang, J.; Zhan, W.; Ehsani, M. Fault-Tolerant Control of PMSM with Inter-Turn Short-Circuit Fault. IEEE Trans. Energy Convers. 2019, 34, 2267–2275. [Google Scholar] [CrossRef]
- Sarikhani, A.; Mohammed, O.A. Inter-Turn Fault Detection in PM Synchronous Machines by Physics-Based Back Electromotive Force Estimation. IEEE Trans. Ind. Electron. 2013, 60, 3472–3484. [Google Scholar] [CrossRef]
- Moon, S.; Jeong, H.; Lee, H.; Kim, S.W. Interturn Short Fault Diagnosis in a PMSM by Voltage and Current Residual Analysis with the Faulty Winding Model. IEEE Trans. Energy Convers. 2018, 33, 190–198. [Google Scholar] [CrossRef]
- Yiguang, C.; Yuling, P.; Xin, H. Magnetomotive force in permanent magnet synchronous machine with concentrated fractional-slot winding. Trans. China Eletrotech. Soc. 2010, 25, 30–36. [Google Scholar] [CrossRef]
- Sarkhanloo, M.S.; Ghalledar, D.; Azizian, M.R. Diagnosis of stator winding turn to turn fault of induction motor using space vector pattern based on neural network. In Proceedings of the The 3rd Conference on Thermal Power Plants, Tehran, Iran, 18–19 October 2011; pp. 1–6. [Google Scholar]
- Yucheng, G.; Wei, Z.; Songling, H. Reactive power definition single-phase circuits based on instantaneous reactive power theory. Electr. Meas. Instrum. 2016, 53, 1–8. [Google Scholar]
- Akagi, H.; Kanazawa, Y.; Nabae, A. Instantaneous reactive power compensators comprising switching devices without energy storage components. IEEE Trans. Ind. Appl. 2008, 20, 625–630. [Google Scholar] [CrossRef]














| Parameter | Value |
|---|---|
| Rated power | 6.3 kW |
| Rated speed | 600 rpm |
| Rated current | 22 A |
| Stator resistance R | 0.1638 Ω |
| Stator inductance L | 3.5 mH |
| 1st PM flux linkage | 0.121 Wb |
| 3rd PM flux linkage | 0.0051 Wb |
| The number of turns per coil | 25 |
| Pole pair | 11 |
| Half of small teeth κ | π/180 rad |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Chen, Y. Interturn Short-Circuit Fault Detection of a Five-Phase Permanent Magnet Synchronous Motor. Energies 2021, 14, 434. https://doi.org/10.3390/en14020434
Yang Z, Chen Y. Interturn Short-Circuit Fault Detection of a Five-Phase Permanent Magnet Synchronous Motor. Energies. 2021; 14(2):434. https://doi.org/10.3390/en14020434
Chicago/Turabian StyleYang, Zhongyi, and Yiguang Chen. 2021. "Interturn Short-Circuit Fault Detection of a Five-Phase Permanent Magnet Synchronous Motor" Energies 14, no. 2: 434. https://doi.org/10.3390/en14020434




