Finite Element Analysis on Shear Behavior of High-Strength Bolted Connectors under Inverse Push-Off Loading
Abstract
:1. Introduction
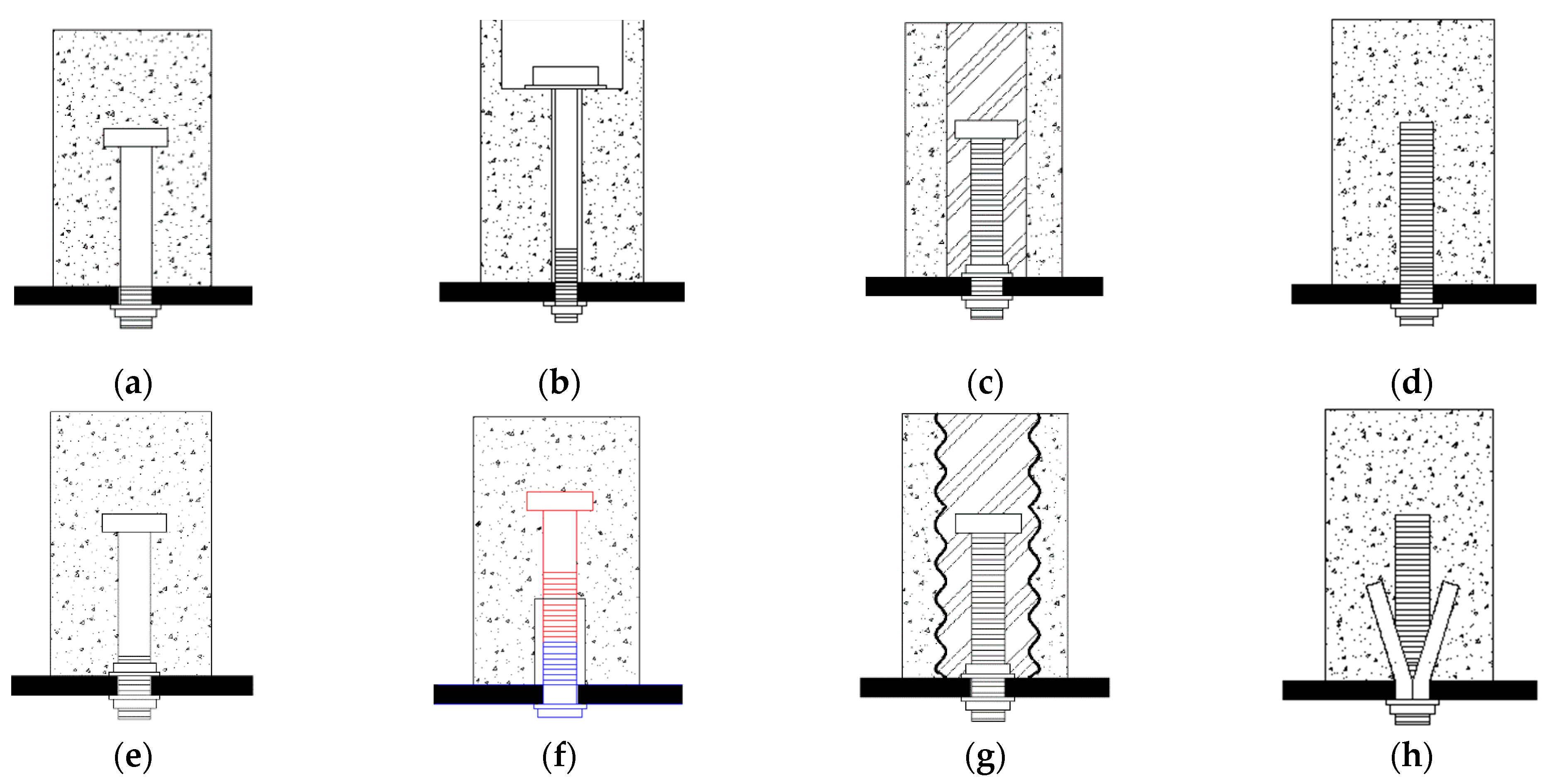
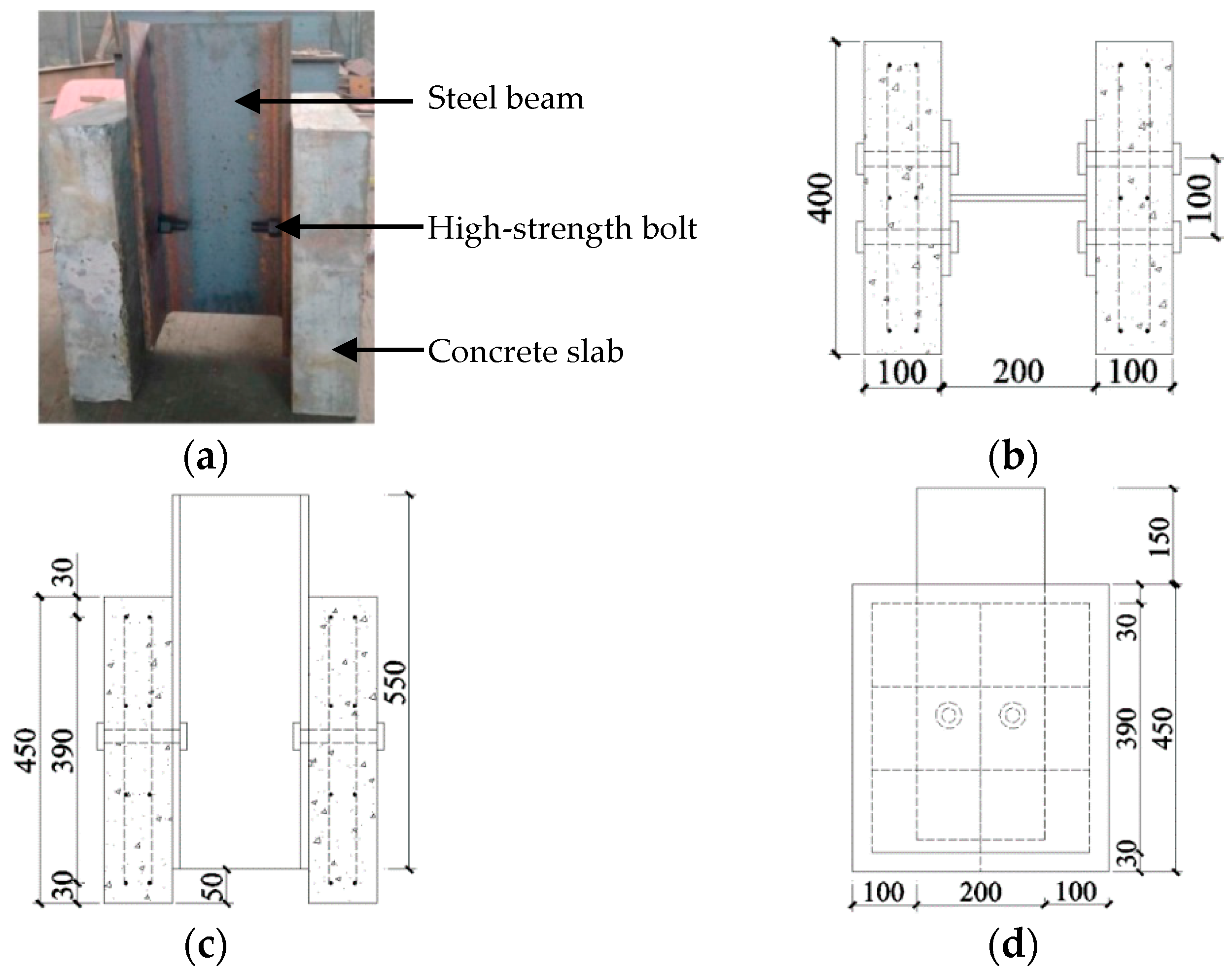
2. Finite Element Model
2.1. Model Geometry
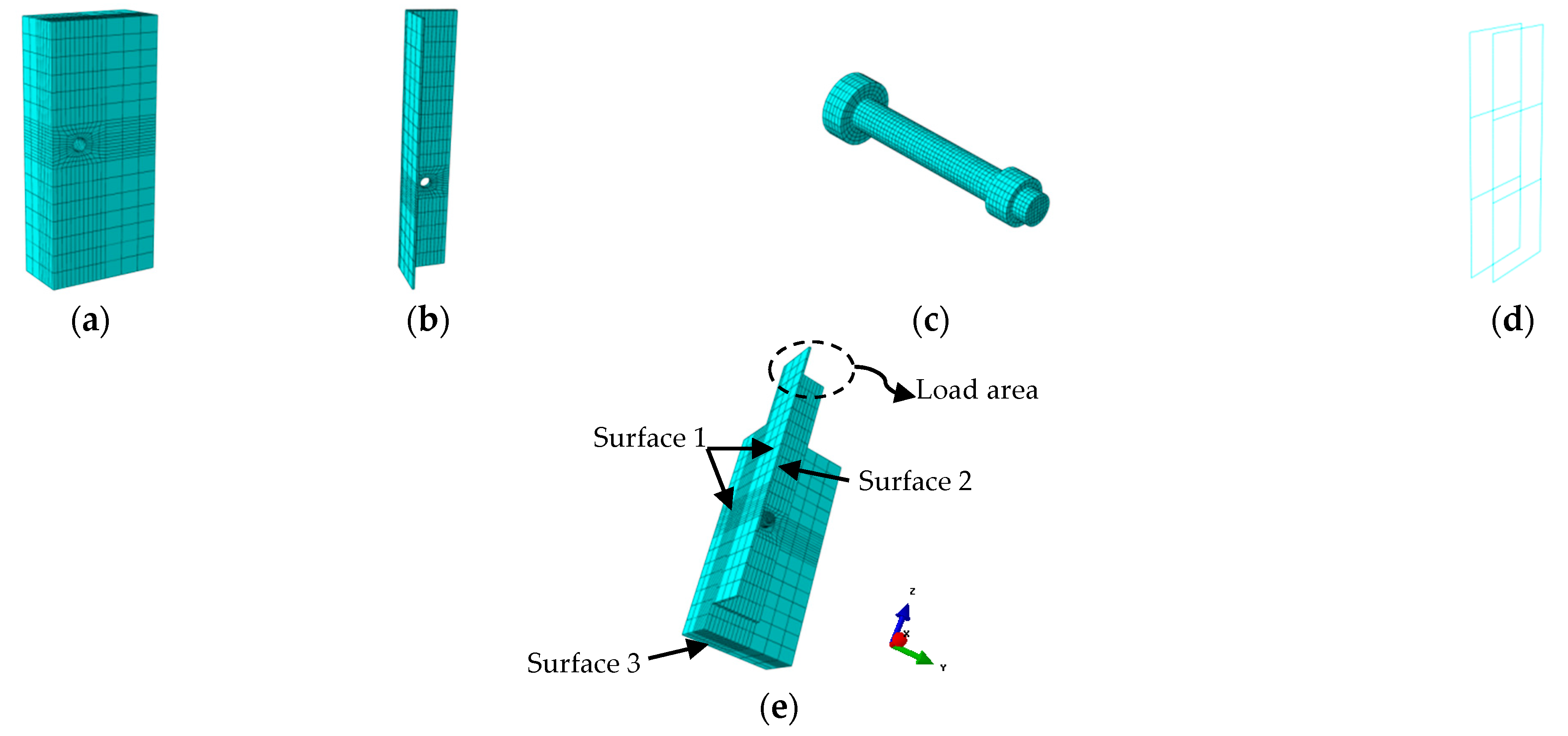
2.2. Finite Element Mesh
2.3. Material Modeling
2.4. Boundary Conditions
2.5. Interaction and Constraint Conditions
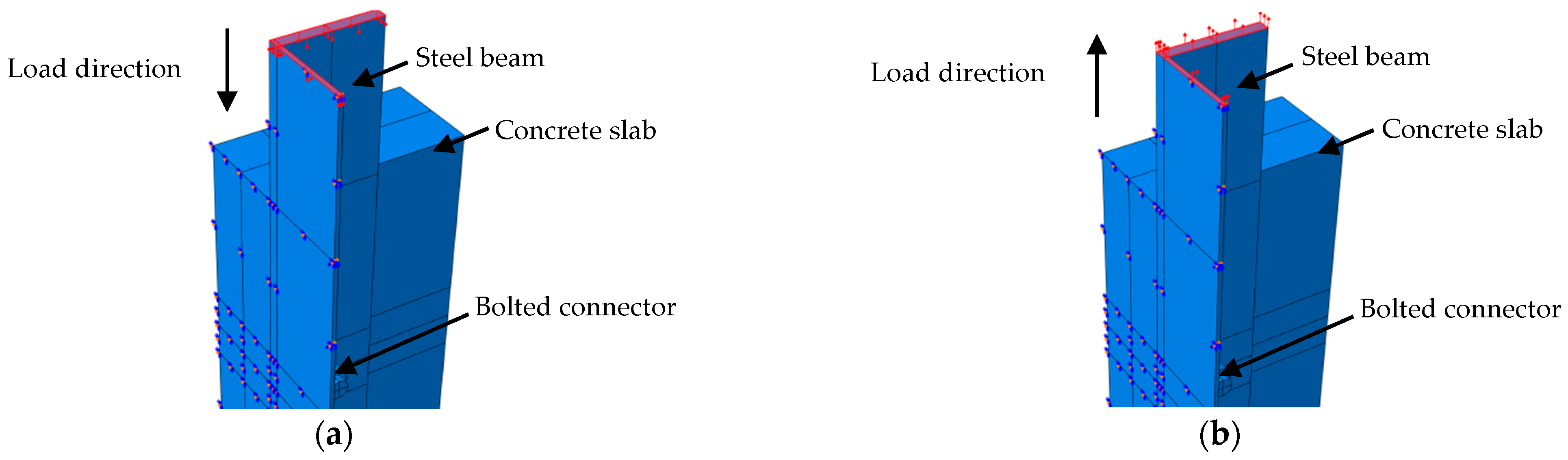
2.6. Load Application and Analysis Steps
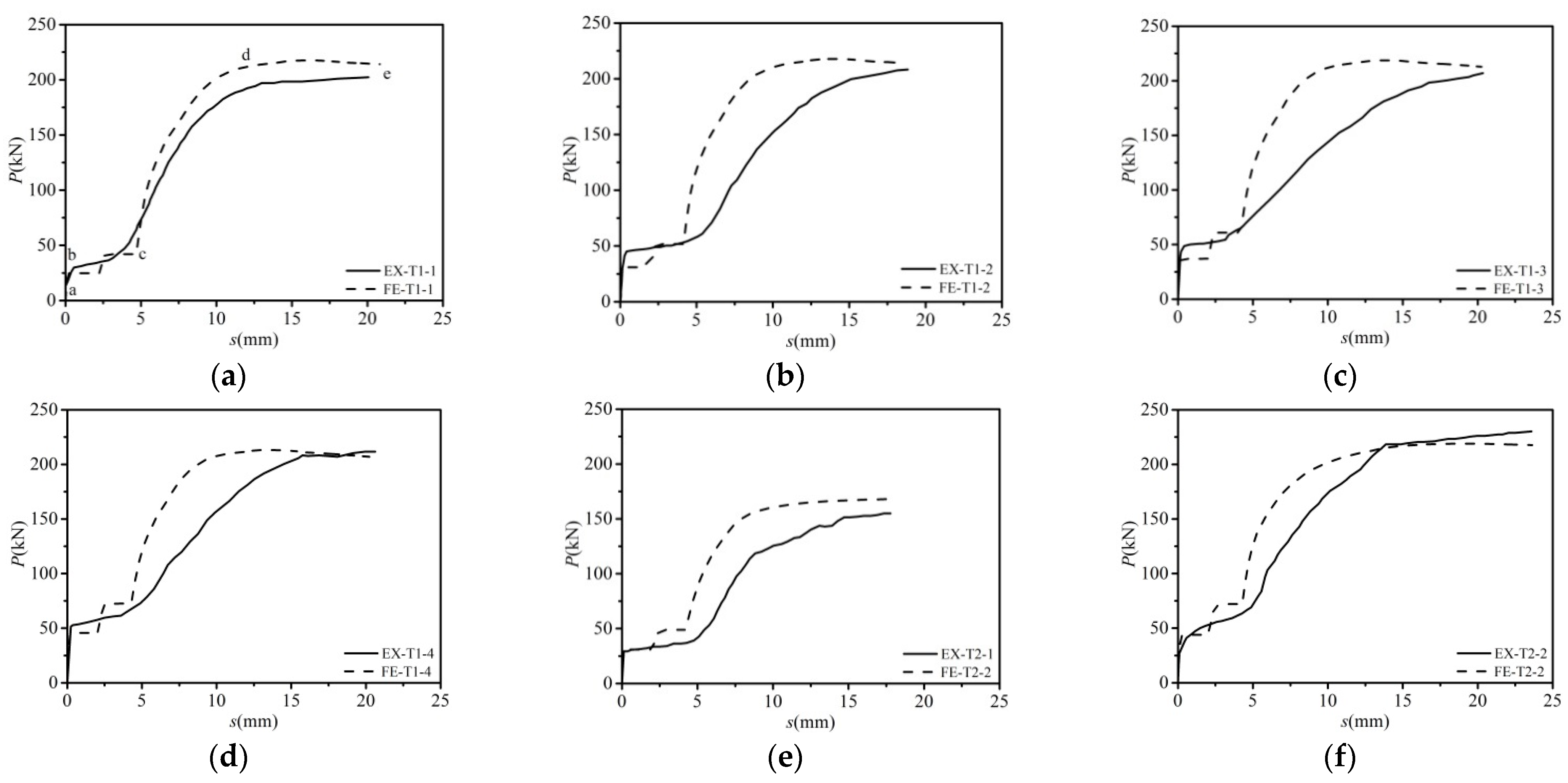
2.7. Validation of FEMs
3. Prediction of Shear Behavior under Inverse Push-Off Loading
3.1. FEM
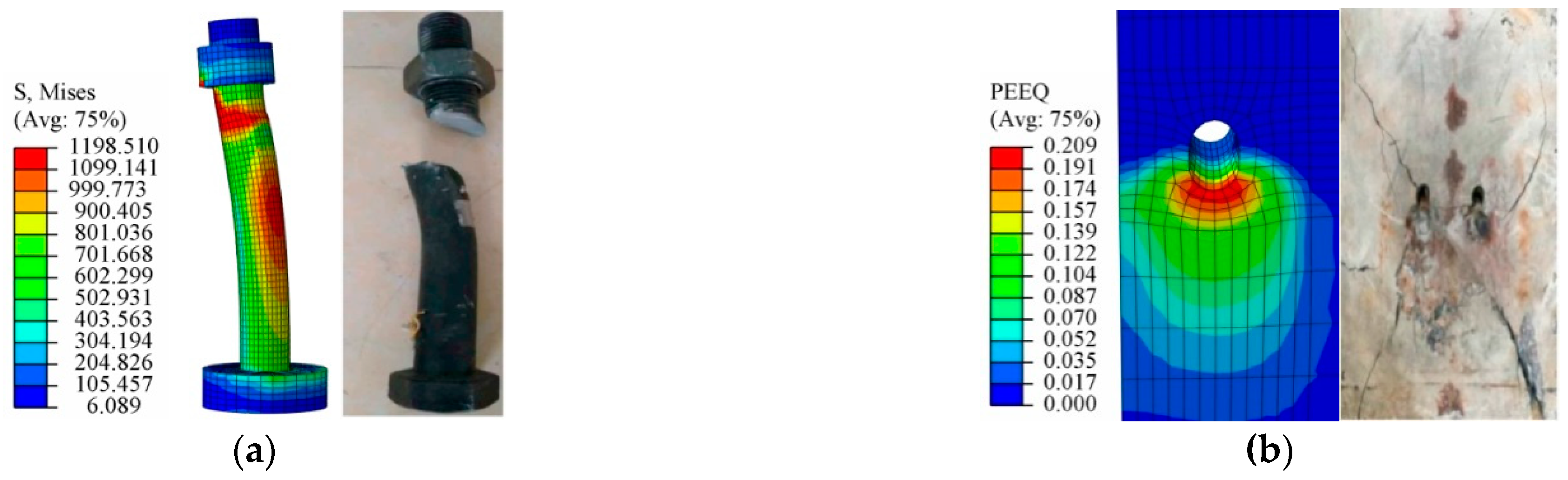
3.2. Results and Discussion
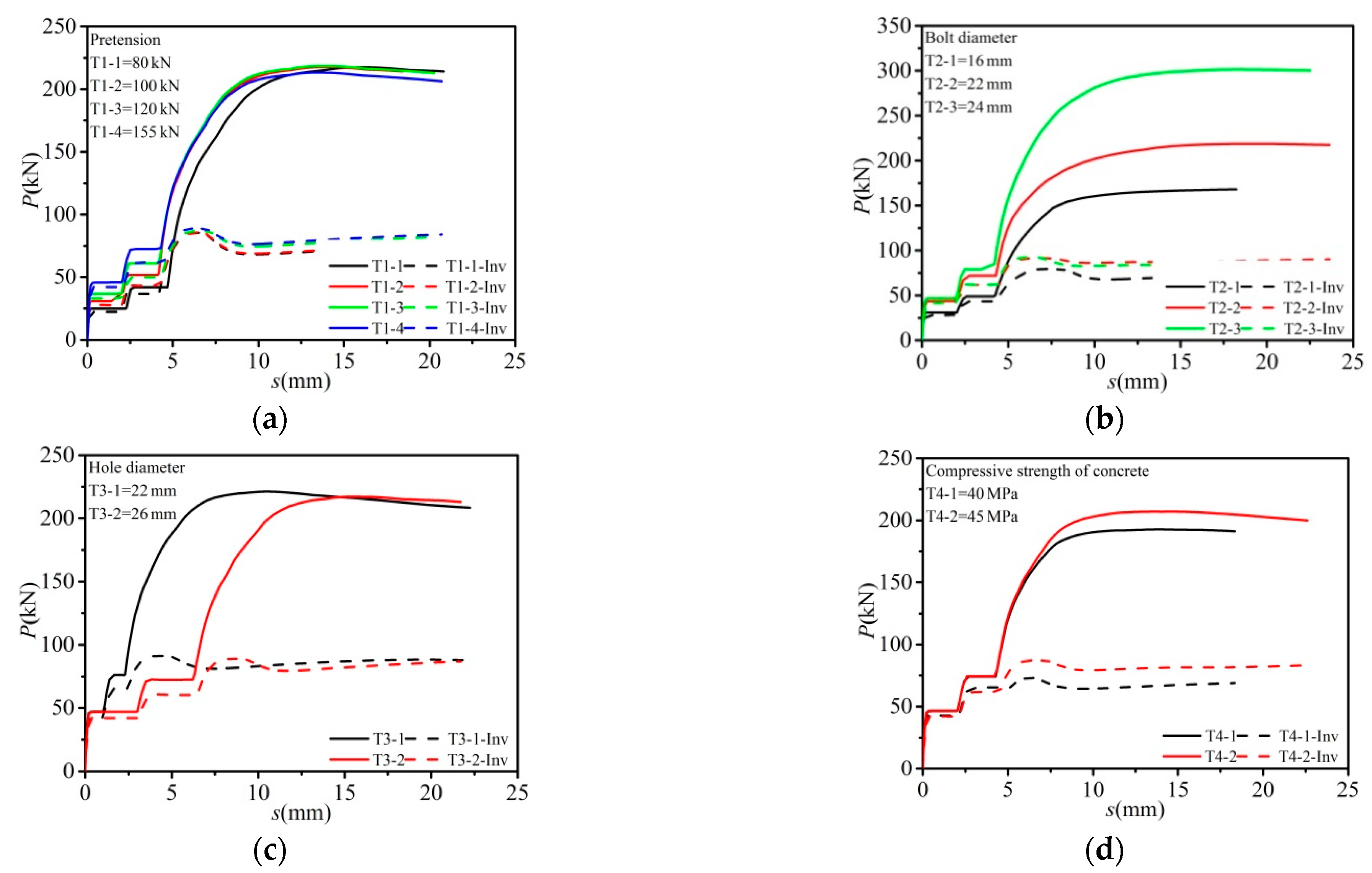
3.3. Parametric Study
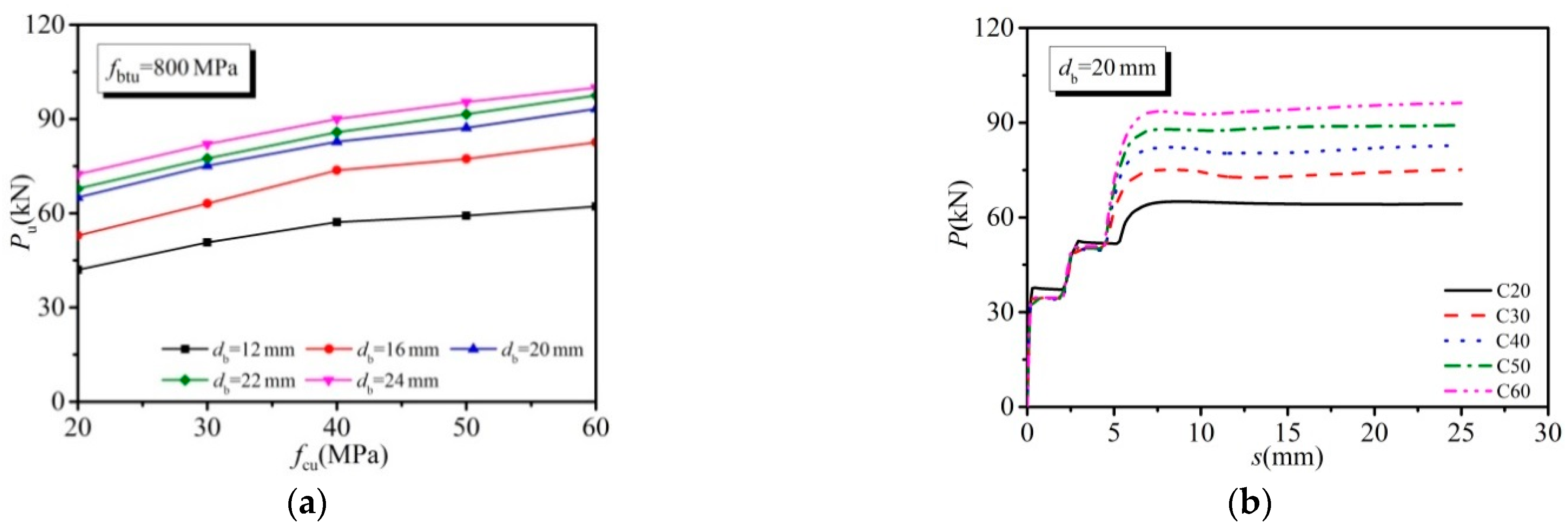
3.3.1. Effect of Concrete Strength
3.3.2. Effect of Bolt Diameter
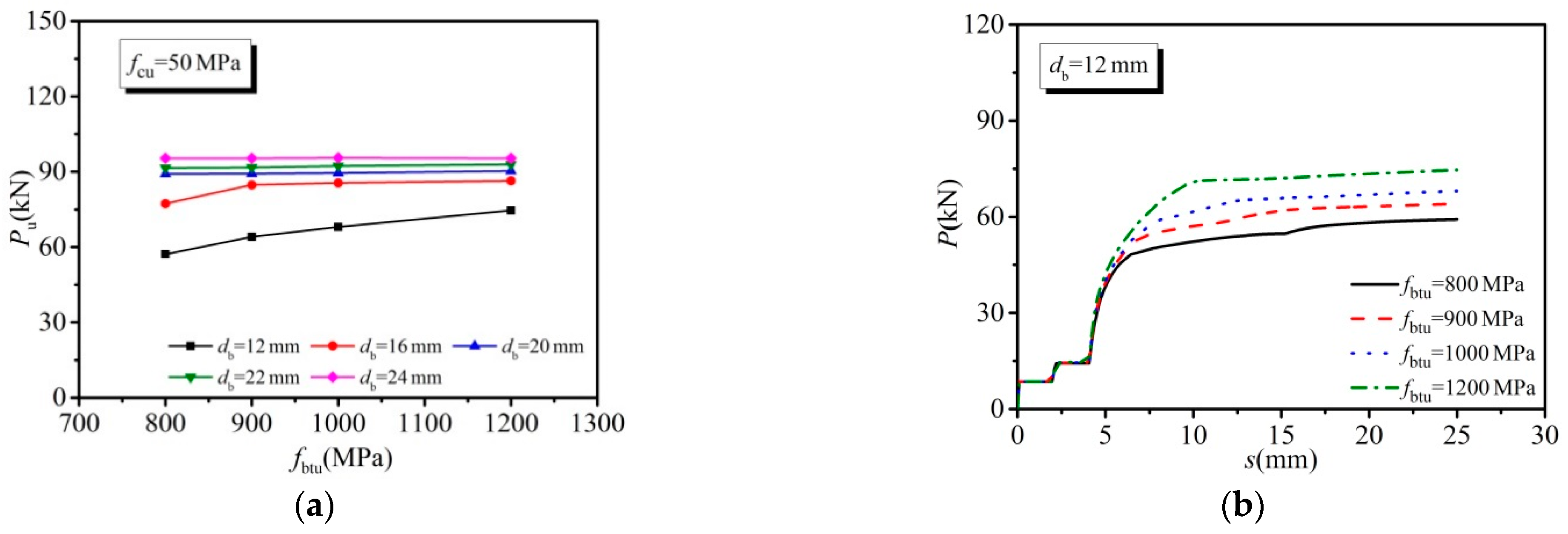
3.3.3. Effect of Bolt Tensile Strength
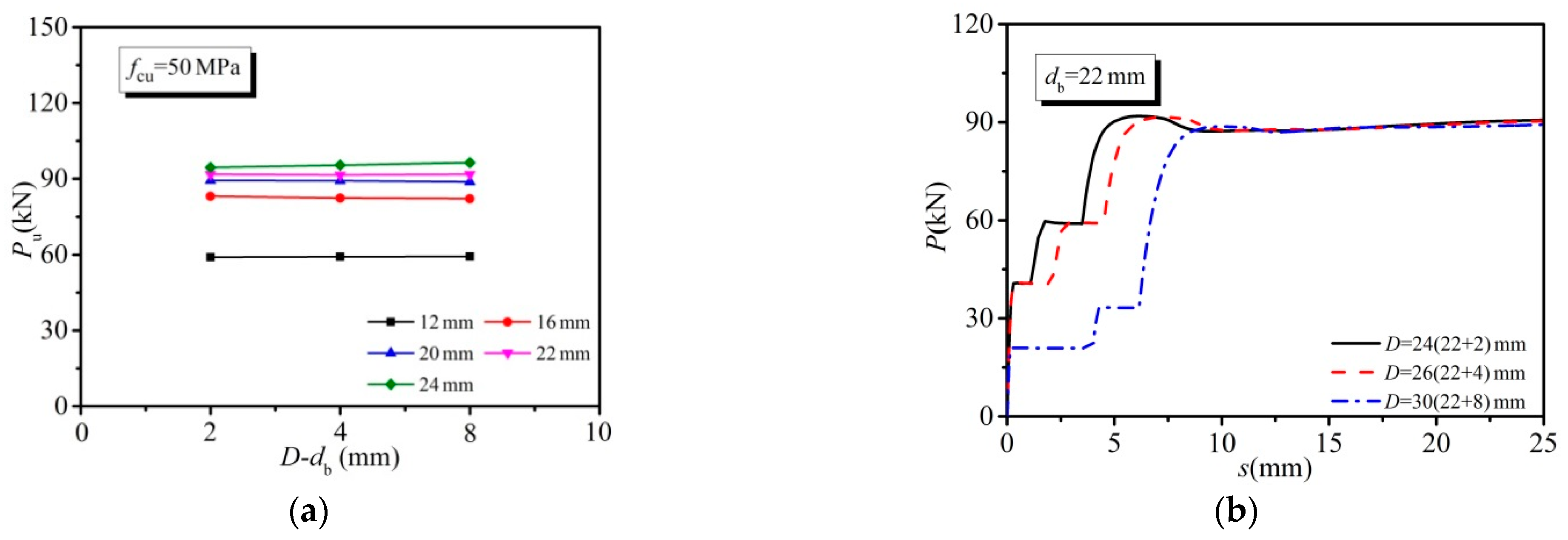
3.3.4. Effect of Concrete Slab Hole Diameter
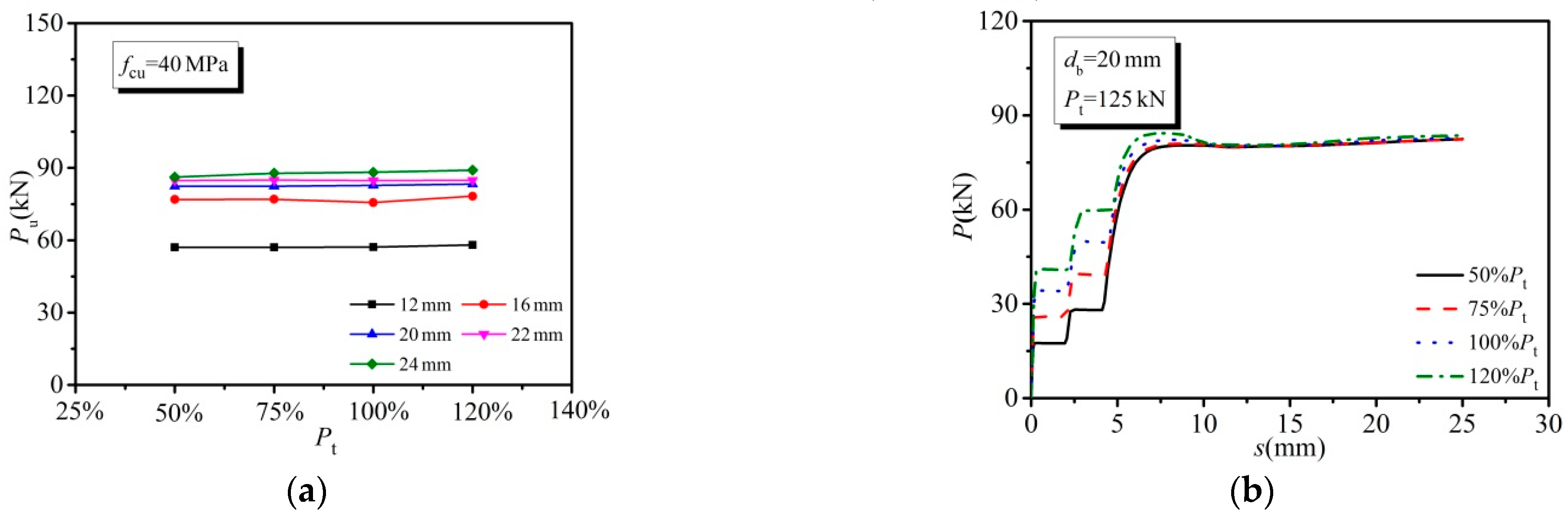
3.3.5. Effect of Bolt Pretension
4. Design Recommendations
5. Conclusions
- The 3D nonlinear numerical model was capable of accurately and reasonably predicting the fundamental behavior of the HSBSCs in push-off tests on the shear capacity and the load–slip response.
- The tendency of the load–slip curves of HSBSCs under inverse push-off loading was similar to that of push-off tests and could be divided into four stages. The shear bearing resistance of HSBSCs of the inverse models was lower that of those in the inverse push-off FEMs, and concrete failure was the main failure mode.
- The shear capacity of HSBSCs subjected to inverse push-off loading was primarily dependent upon the concrete strength and the bolt diameter, and when the bolt diameter was smaller than 20 mm, the bolt tensile strength exhibited some influence. The clearances between concrete slab holes and bolts as well as the bolt pretension had a slight effect on the shear capacity of the HSBSCs.
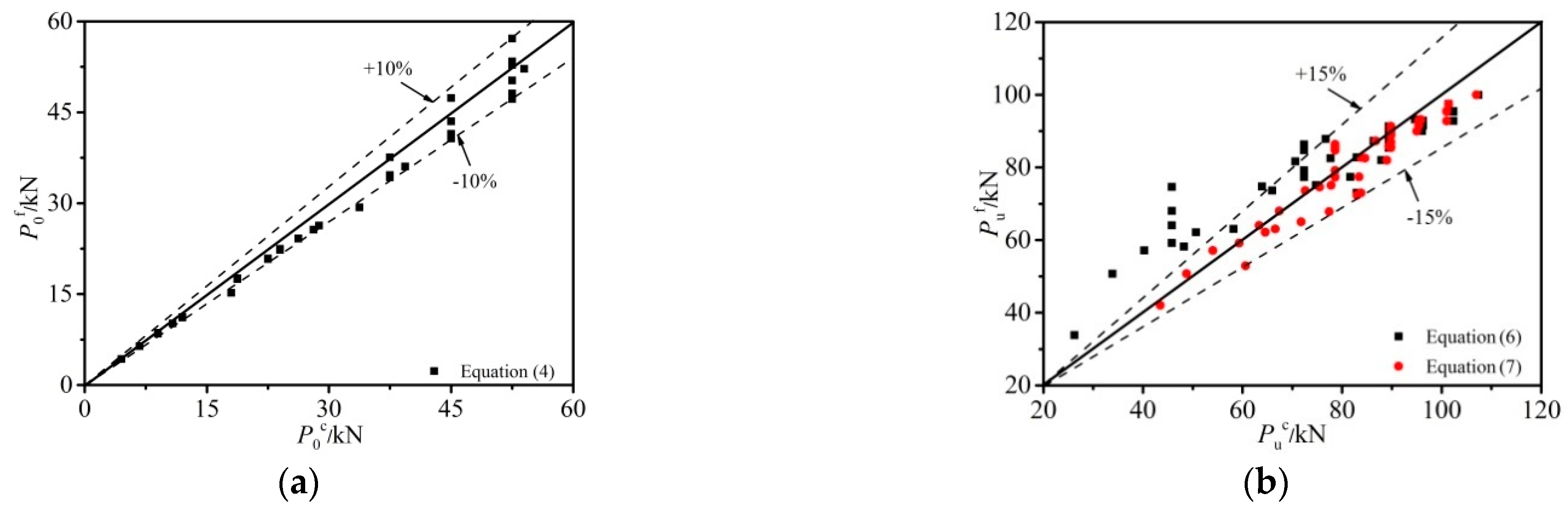
- Based on the comprehensive parametric studies, the shear load of HSBSCs at the friction-transferring force stage can be estimated by the formula proposed by Liu et al. A practical design formula for predicting the shear capacity of HSBSCs under inverse push-off loading was proposed, and the predicted results agreed reasonably well with the FE analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | Concrete slab hole diameter | Es | Elastic modules of steel |
| db | High-strength bolt diameter | Ebs | Elastic modules of high-strength bolt |
| Pb | Bolt pretension | P0 | Shear load at the first slip |
| fcu | Compressive cube strength of concrete | P0f | Shear load at the first slip of FE result |
| fc | Compressive strength of concrete | Pu | Ultimate load |
| fc’ | Compressive cylinder strength of concrete | Puf | Ultimate load of FE result |
| fy | Yield strength of steel | PuL | Ultimate load in inverse push-off test |
| fu | Ultimate strength of steel | Puc | Ultimate shear strength of calculate result |
| fbtu | Ultimate strength of high-strength bolt | Pu(6) | Ultimate shear strength of the bolt according to Equation (6) |
References
- Ollgaard, J.; Slutter, R.; Fisher, J. Shear strength of stud connectors in lightweight and normal-weight concrete. AISC Eng. J. 1971, 8, 55–64. [Google Scholar]
- Shim, C.; Lee, P.; Yoon, T. Static behavior of large stud shear connectors. Eng. Struct. 2004, 26, 1853–1860. [Google Scholar] [CrossRef]
- Lam, D.; Ellobody, E. Behavior of headed stud shear connectors in composite beam. J. Struct. Eng. 2005, 1, 96–107. [Google Scholar] [CrossRef]
- Lam, D. Capacities of headed stud shear connectors in composite steel beams with precast hollowcore slabs. J. Constr. Steel Res. 2007, 63, 1160–1174. [Google Scholar] [CrossRef]
- Nguyen, H.; Kim, S. Finite element modelling of push-out tests for large stud shear connectors. J. Constr. Steel Res. 2009, 65, 1909–1920. [Google Scholar] [CrossRef]
- Manik, M.; Bhowmick, A. A finite element based approach for fatigue life prediction of headed shear studs. Structures 2019, 19, 161–172. [Google Scholar]
- Vigneri, V.; Odenbreit, C.; Braun, M. Numerical evaluation of the plastic hinges developed in headed stud shear connectors in composite beams with profiled steel sheeting. Structures 2019, 21, 103–110. [Google Scholar] [CrossRef] [Green Version]
- Dallam, L. High strength bolt shear connectors-push out tests. J. Proc. 1968, 65, 767–769. [Google Scholar]
- Marshall, W.; Nelson, H.; Banerjee, H. An experimental study of the use of high-strength friction-grip bolts as shear connectors in composite beams. Struct. Eng. 1971, 49, 171–178. [Google Scholar]
- Dedic, D.; Klaiber, W. High-strength bolts as shear connectors in rehabilitation work. Concr. Int. 1984, 6, 41–46. [Google Scholar]
- Kwon, G.; Engelhardt, M.; Klingner, R. Behavior of post-installed shear connectors under static and fatigue loading. J. Constr. Steel Res. 2010, 66, 532–541. [Google Scholar]
- Kwon, G.; Engelhardt, M.; Klingner, R. Experimental behavior of bridge beams retrofitted with postinstalled shear connectors. J. Bridge Eng. 2011, 16, 536–545. [Google Scholar]
- Dai, X.; Lam, D.; Saveri, E. Effect of concrete strength and stud collar size to shear capacity of demountable shear connectors. J. Struct. Eng. 2015, 141, 04015025–1-10. [Google Scholar]
- Rehman, N.; Lam, D.; Dai, X.; Ashour, A. Experimental study on demountable shear connectors in composite slabs with profiled decking. J. Struct. Eng. 2016, 122, 178–189. [Google Scholar]
- Yang, F.; Liu, Y.; Jiang, Z.; Xin, H. Shear performance of a novel demountable steel-concrete bolted connector under static push-out tests. Eng. Struct. 2018, 160, 133–146. [Google Scholar]
- Moynihan, M.; Allwood, J. Viability and performance of demountable composite connectors. J. Constr. Steel Res. 2014, 99, 47–56. [Google Scholar]
- Chen, J.; Wang, W.; Ding, F.; Xiang, P.; Yu, Y.; Liu, X.; Xu, F.; Yang, C.; Long, S. Behavior of an advanced bolted shear connector in prefabricated steel-concrete composite beams. Materials 2019, 12, 2958. [Google Scholar]
- Pavlović, M.; Marković, Z.; Veljković, M.; Budevac, D. Bolted shear connectors vs. headed studs behaviour in push-out tests. J. Struct. Eng. 2013, 88, 134–149. [Google Scholar]
- Zhang, Y.; Chen, B.; Liu, A.; Pi, Y.; Zhang, J.; Wang, Y.; Zhong, L. Experimental study on shear behavior of high strength bolt connection in prefabricated steel-concrete composite beam. Compos. Part B 2019, 159, 481–489. [Google Scholar]
- Liu, X.; Bradford, M.; Michael, S. Behavior of high-strength friction-grip bolted shear connectors in sustainable composite beams. J. Struct. Eng. 2015, 141, 1–12. [Google Scholar]
- Liu, X.; Bradford, M.; Chen, Q.; Ban, H. Finite element modelling of steel-concrete composite beams with high-strength friction-grip bolt shear connectors. Finite Elem. Anal. Des. 2016, 108, 54–65. [Google Scholar] [CrossRef]
- Liu, X.; Bradford, M.; Ataei, A. Flexural performance of innovative sustainable composite steel-concrete beams. Eng. Struct. 2017, 130, 282–296. [Google Scholar] [CrossRef]
- Ataei, A.; Bradford, M.; Liu, X. Experimental study of composite beams having a precast geopolymer concrete slab and deconstructable bolted shear connectors. Eng. Struct. 2016, 114, 1–13. [Google Scholar] [CrossRef]
- Ataei, A.; Zeynalian, M.; Yazdi, Y. Cyclic behaviour of bolted shear connectors in steel-concrete composite beams. Eng. Struct. 2019, 198, 109455. [Google Scholar] [CrossRef]
- Tan, E.; Varsani, H.; Liao, F. Experimental study on demountable steel-concrete connectors subjected to combined shear and tension. Eng. Struct. 2019, 183, 110–123. [Google Scholar] [CrossRef]
- Ding, F.; Yin, G.; Wang, H.; Wang, L.; Guo, Q. Static behavior of stud connectors in bi-direction push-off tests. Thin-Walled Struct. 2017, 120, 307–318. [Google Scholar] [CrossRef]
- Yin, G.; Ding, F.; Wang, H.; Wang, L.; Guo, Q. Behavior of headed shear stud connectors subjected to cyclic loading. Steel Compos. Struct. 2017, 25, 705–716. [Google Scholar]
- Abaqus. Computer Software, Version 6.14; SIMULIA: Providence, RI, USA, 2014.
- Ding, F.; Ying, X.; Zhou, L.; Yu, Z. Unified calculation method and its application in determining the uniaxial mechanical properties of concrete. Front. Archit. Civ. Eng. China 2011, 5, 381–393. [Google Scholar] [CrossRef]
- Ding, F.; Yu, Z. Strength criterion for plain concrete under multiaxial stress based on damage Poisson’s ratio. Acta Mech. Solida Sin. 2006, 19, 307–316. [Google Scholar] [CrossRef]
- Loh, H.; Uy, B.; Bradford, M. The effects of partial shear connection in composite flush end plate joints Part II-Analytical study and design appraisal. J. Constr. Steel Res. 2006, 62, 391–412. [Google Scholar] [CrossRef]
- GB 50017-2017. Standard for Design of Steel Structures; China Architecture and Building Press: Beijing, China, 2017. [Google Scholar]




| Dilation Angle (ψ) | Flow Potential Eccentricity (e) | Biaxial/Uniaxial Compressive Strength Ratio (fb0/fc0) | Ratio (K) |
|---|---|---|---|
| 40° | 0.1 | 1.225 | 2/3 |
| Specimen | Pretension (kN) | Hole Diameter (mm) | Bolt Diameter (mm) | Concrete Strength (MPa) | P0 (kN) | Pu (kN) | P0f (kN) | Puf (kN) | P0/P0f | P/Puf |
|---|---|---|---|---|---|---|---|---|---|---|
| T1-1 | 80 | 24 | 20 | 50 | 22.5 | 207.0 | 24.7 | 217.5 | 0.911 | 0.95 |
| T1-2 | 100 | 24 | 20 | 50 | 30.0 | 207.5 | 30.5 | 217.8 | 0.984 | 0.95 |
| T1-3 | 120 | 24 | 20 | 50 | 37.5 | 207.5 | 36.2 | 218.6 | 1.036 | 0.95 |
| T1-4 | 155 | 24 | 20 | 50 | 53.5 | 212.5 | 45.4 | 213.2 | 1.178 | 1.00 |
| T2-1 | 155 | 20 | 16 | 50 | 23.5 | 156.3 | 30.6 | 168.2 | 0.768 | 0.93 |
| T2-2 | 155 | 26 | 22 | 50 | 53.0 | 231.3 | 43.5 | 218.9 | 1.218 | 1.06 |
| T2-3 | 155 | 28 | 24 | 50 | 54.5 | 266.8 | 44.1 | 301.4 | 1.236 | 0.89 |
| T3-1 | 155 | 22 | 20 | 50 | 53.0 | 209.2 | 47.1 | 221.1 | 1.125 | 0.95 |
| T3-2 | 155 | 26 | 20 | 50 | 32.5 | 172.5 | 46.6 | 217.1 | 0.697 | 0.79 |
| T4-1 | 155 | 24 | 20 | 40 | 37.5 | 169.8 | 46.4 | 192.7 | 0.808 | 0.88 |
| T4-2 | 155 | 24 | 20 | 45 | 35.5 | 172.8 | 46.6 | 207.0 | 0.762 | 0.83 |
| Mean | 0.975 | 0.925 | ||||||||
| Coefficient of variation | 0.194 | 0.082 | ||||||||
| Variable | Range of Variable |
|---|---|
| Concrete strength | fcu = 20, 30, 40, 50, 60 MPa |
| Bolt diameter | db = 12, 16, 20, 22, 24 mm |
| Bolt tensile strength | fbtu = 800, 900, 1000, 1200 MPa |
| Clearance between the concrete slab hole and the bolt | (D–db) = 2, 4, 8 mm |
| Bolt pretension | Pb = 0.2Pt, 0.5Pt, 1.0Pt, 1.2Pt |
| P0f/Pu(4) | Puf/Pu(6) | Puf/Pu(7) | |
|---|---|---|---|
| Mean (µ) | 0.934 | 1.065 | 0.973 |
| Coefficient of variation (η) | 0.039 | 0.169 | 0.049 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhang, X.-d.; Ding, F.-x.; Zhou, X.-l. Finite Element Analysis on Shear Behavior of High-Strength Bolted Connectors under Inverse Push-Off Loading. Energies 2021, 14, 479. https://doi.org/10.3390/en14020479
Wang W, Zhang X-d, Ding F-x, Zhou X-l. Finite Element Analysis on Shear Behavior of High-Strength Bolted Connectors under Inverse Push-Off Loading. Energies. 2021; 14(2):479. https://doi.org/10.3390/en14020479
Chicago/Turabian StyleWang, Wei, Xie-dong Zhang, Fa-xing Ding, and Xi-long Zhou. 2021. "Finite Element Analysis on Shear Behavior of High-Strength Bolted Connectors under Inverse Push-Off Loading" Energies 14, no. 2: 479. https://doi.org/10.3390/en14020479
APA StyleWang, W., Zhang, X.-d., Ding, F.-x., & Zhou, X.-l. (2021). Finite Element Analysis on Shear Behavior of High-Strength Bolted Connectors under Inverse Push-Off Loading. Energies, 14(2), 479. https://doi.org/10.3390/en14020479







