Designing of Dynamic Spectrum Shifting in Terms of Non-Local Space-Fractional Mechanics

Abstract

In this paper, the applicability of the space-fractional non-local formulation (sFCM) to design 1D material bodies with a specific dynamic eigenvalue spectrum is discussed. Such a formulated problem is based on the proper spatial distribution of material length scale, which maps the information about the underlying microstructure (it is important that the material length scale is one of two additional material parameters of sFCM compared to the classical local continuum mechanics—the second one, the order of fractional continua—is treated herein as a scaling parameter only). Technically, the design process for finding adequate length scale distribution is not trivial and requires the use of an inverse optimization procedure. In the analysis, the objective function considers a subset of eigenvalues reduced to a single value based on Kreisselmeier–Steinhauser formula. It is crucial that the total number of eigenvalues considered must be smaller than the limit which comes from the ratio of the sFCM length scale to the length of the material body.

1. Introduction

It is now well understood that behaviour of solid bodies strongly depends on the ratio of its size to underlying microstructure [1,2,3] and it can be superior (in the sense of mechanical, chemical and electronic properties) when bodies dimensions become comparable to characteristic dimensions of microstructure [4]. This attribute of each body, known as scale effect (SE), and the designers are taking advantage of this phenomena when developing new devices, e.g., sensors and actuators for nanotechnological applications [5,6,7], micro-thruster of nano-satellites [8], torsional accelerometers [9], nano-motors, micro/nano-resonators [10] and many others cf. the review paper [11]. One should note that the abovementioned elaboration of new designing concepts is mainly due to utilising mathematical modelling; thus, it must include SE mapping also.

There are a variety of available mechanical models which allow to include SE, i.e., paridynamics [12,13], integral-type concepts [14], general non-local theories [15,16], strain-gradient theories [17,18,19,20], micropolar theories [21,22,23], theories of material surfaces/surface elasticity theory [24], cf. the review paper [25]. However, in this paper, we follow the space-fractional non-local formulation (sFCM) proposed in [26], where SE is introduced through the application of fractional calculus (FC) [27,28,29]. Herein, it is important, because the designing procedure to obtain the specific dynamic properties of the analysed material body is the crux of presented considerations, that the applicability of sFCM was proved based on validation with rigorous experiments [30,31]. Furthermore, as presented in [32] the answer to the question: Is there a discrete structure that is homogenized by sFCM? This is positive and moreover, such an answer is true in terms of the static and dynamic answer—in the last case, both in terms of eigenvalues and eigenvectors; such results have been never presented before for competitive theories.

This paper extends the results presented in [32] to show the applicability of sFCM to design 1D material bodies with a specific dynamic eigenvalue spectrum. Such a formulated problem is based on the proper spatial distribution of material length scale which maps the information about the underlying microstructure (it is important that the material length scale is one of two additional material parameters of sFCM compared to the classical local continuum mechanics—the second one, the order of fractional continua—is treated herein as a scaling parameter only). Technically, the design process for finding adequate length scale distribution is not trivial and requires the use of an inverse optimization procedure. The objective function considers a subset of eigenvalues reduced to a single value based on the Kreisselmeier–Steinhauser formula [33]. It is also crucial that, as in [32], the total number of eigenvalues considered must be smaller than the limit which comes from the ratio of the sFCM length scale to the length of the material body.

The paper is structured as follows: Section 2 deals with the fundamentals of sFCM theory. Section 3 defines the inverse optimization procedure for finding length scale distribution to control the dynamic eigenvalue spectrum. Section 4 describes the selected optimisation results. Finally, Section 5 concludes the paper.

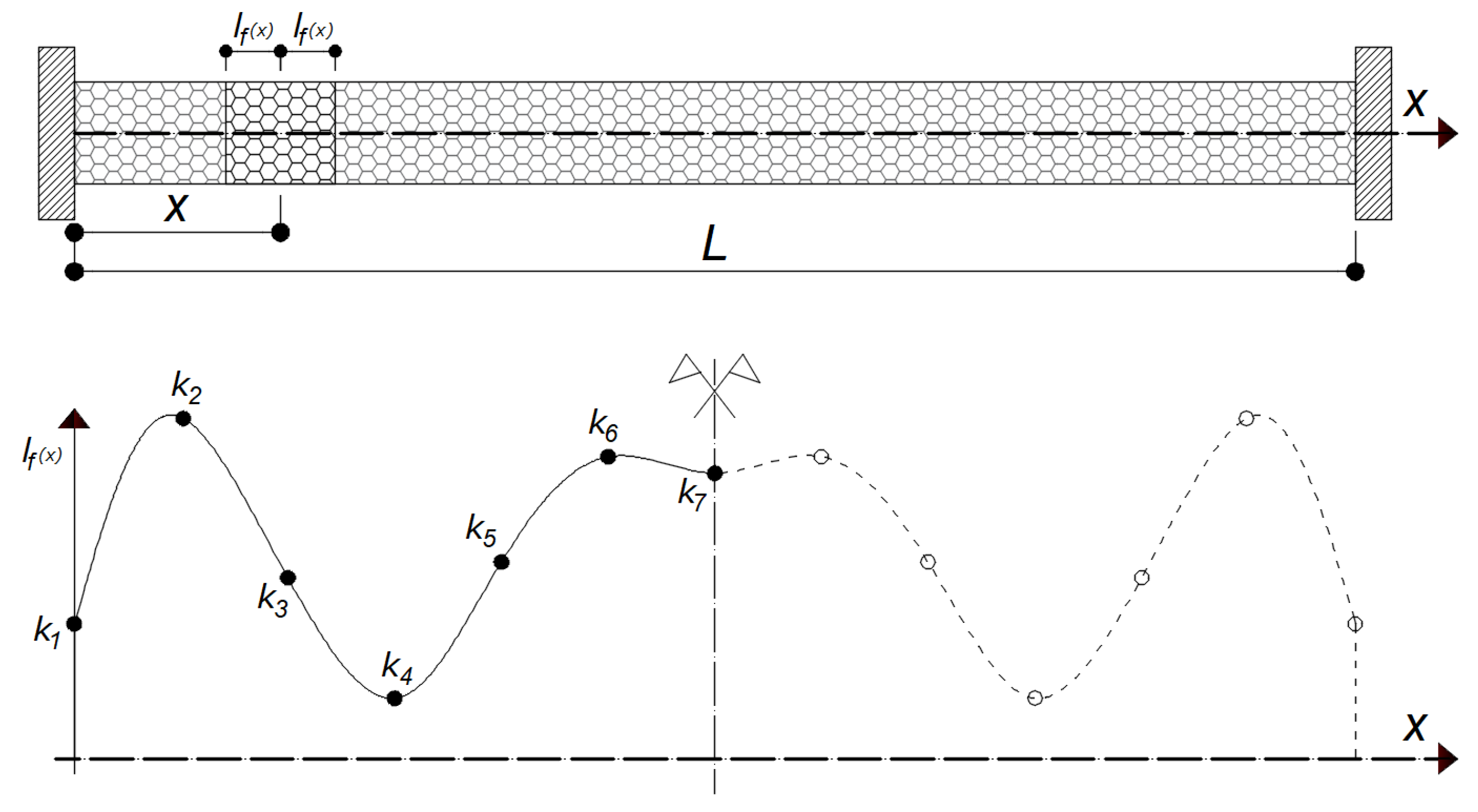
2. Dynamic Equilibrium for 1d Sfcm Body Including Spatially Variable Length Scale

The foundations for dynamic equilibrium for 1D sFCM body were formulated for a constant length scale in [34,35]. Subsequently, after introducing variable length scale concept to sFCM in [36], an extension of [34,35] was proposed in [32]. Herein, the governing equations obtained in [32] are summarised shortly for a clear interpretation of results presented in the next sections.

2.1. Governing Equation

The dynamic equilibrium of 1D sFCM body can be expressed as follows [35]

$$\begin{array}{c}\hfill \frac{\Gamma (2-\alpha )}{2\Gamma \left(2\right)}\frac{\partial }{\partial x}\left[E{\ell }_f{\left(x\right)}^{\alpha -1}\left({}_{x-{\ell }_f}^C{D}_x^{\alpha }U(x,t){-}_x^C{D}_{x+{\ell }_f}^{\alpha }U(x,t)\right)\right]+b(x,t)=\rho \ddot{U}(x,t),\end{array}$$

(1)

where $\Gamma$ is the Euler gamma function, $\alpha \in (0,1]$ (where for $\alpha =1$ classical local solution is recovered), x denotes the spatial variable, E is the Young modulus, ${\ell }_f={\ell }_f\left(x\right)$ is the length scale (herein a known function), U is the axial displacement, b is the axial body force, $\rho$ is density, and $\ddot{(·)}$ denote the second time derivative. In the following sections, the spatial distribution of the ${\ell }_f$ parameter plays the fundamental role in controlling/designing of course of dynamic eigenvalue spectrum [36,37,38]. Furthermore, in Equation (1), ${}^C{D}^{\alpha }$ denotes the left- and right-sided Caputo derivatives:

$$\begin{array}{c}\hfill {}_a^C{D}_t^{\alpha }f\left(t\right)=\frac{1}{\Gamma (n-\alpha )}{\int }_a^t\frac{f^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{\alpha -n+1}}d\tau ,\mathrm{for}t>a,\end{array}$$

(2)

and

$$\begin{array}{c}\hfill {}_t^C{D}_b^{\alpha }f\left(t\right)=\frac{{(-1)}^n}{\Gamma (n-\alpha )}{\int }_t^b\frac{f^{\left(n\right)}\left(\tau \right)}{{(\tau -t)}^{\alpha -n+1}}d\tau ,\mathrm{for}t<b,\end{array}$$

(3)

respectively. Finally, the configuration for both ends (i.e., $x=x_0$ and $x=x_r$) clamped is considered, i.e.,

$$U(x_0,t)=U_L,U(x_r,t)=U_R,$$

(4)

where $x_0$ and $x_r$ denote points on the boundary.

2.2. Approximation

The trapezoidal rule for the Caputo operators, under the assumption of uniformly distributed discretization points $x_i$, is used [39].

The left sided Caputo derivative is approximated according to the following rule:

$${}_{x-{\ell }_f}^C{D}_x^{\alpha }U\left(x\right){|}_{x=x_i}{=}_{x_{i-m}}^C{D}_x^{\alpha }U\left(x\right){|}_{x=x_i}\cong \sum _{k=i-m}^{i}U{}_k^{\prime }{r}_{i,k}^{\left(\alpha \right)},$$

(5)

whereas for the right-sided Caputo derivative, we have

$${}_x^C{D}_{x+{\ell }_f}^{\alpha }U\left(x\right){|}_{x=x_i}{=}_x^C{D}_{x_{i+m}}^{\alpha }U\left(x\right){|}_{x=x_i}\cong \sum _{k=i}^{i+m}U{}_k^{\prime }{s}_{i,k}^{\left(\alpha \right)},$$

(6)

where

$$r_{i,k}^{\left(\alpha \right)}=\frac{{\left(\Delta x\right)}^{1-\alpha }}{\Gamma \left(3-\alpha \right)}\left\{\begin{array}{cc}{\left(m-1\right)}^{2-\alpha }+\left(2-\alpha -m\right)m^{1-\alpha }& \mathrm{for}k=i-m,\\ {\left(i-k+1\right)}^{2-\alpha }-2{\left(i-k\right)}^{2-\alpha }+{\left(i-k-1\right)}^{2-\alpha }& \mathrm{for}k=i-m+1,\dots ,i-1,\\ 1& \mathrm{for}k=i,\end{array}\right.$$

(7)

and

$$s_{i,k}^{\left(\alpha \right)}=\frac{-{\left(\Delta x\right)}^{1-\alpha }}{\Gamma \left(3-\alpha \right)}\left\{\begin{array}{cc}{\left(m-1\right)}^{2-\alpha }+\left(2-\alpha -m\right)m^{1-\alpha }& \mathrm{for}k=i+m,\\ {\left(k-i+1\right)}^{2-\alpha }-2{\left(k-i\right)}^{2-\alpha }+{\left(k-i-1\right)}^{2-\alpha }& \mathrm{for}k=i+1,\dots ,i+m-1,\\ 1& \mathrm{for}k=i.\end{array}\right.$$

(8)

2.3. Eigenvalue Problem

As in [32], we assume in Equation (1) that $b(x,t)=0$ and that the separation of the variables holds

$$U\left(x,t\right)=U\left(x\right)e^{i\omega t}.$$

(9)

The assumption made in Equation (9), utilising approximations Equations (5) and (6), together with boundary conditions Equation (4), allows us to rewrite Equation (1) to the equivalent matrix form

$$(\mathbf{K}+{\lambda }_f^2\mathbf{I}){\mathbf{U}}_0=\mathbf{0},$$

(10)

with the solution

$$det(\mathbf{K}+{\lambda }_f^2\mathbf{I})=\mathbf{0},$$

(11)

where $\mathbf{K}$ is the fractional stiffness matrix, ${\lambda }_f^2={\omega }^2\rho$ and $\omega =\omega (\alpha ,{\ell }_f)$ denotes the natural frequency for the sFCM, and $\mathbf{I}$ denotes the identity matrix. Furthermore, boundary conditions are included as presented in [36].

3. Eigenvalue Spectrum Shifting—Identification of Length Scale Distribution

The general goal of the presented inverse problem is to find length scale distribution which modifies the dynamic response (Equation (11)) according to the cumulative value of eigenvalues computed using Kreisselmeier–Steinhauser function.

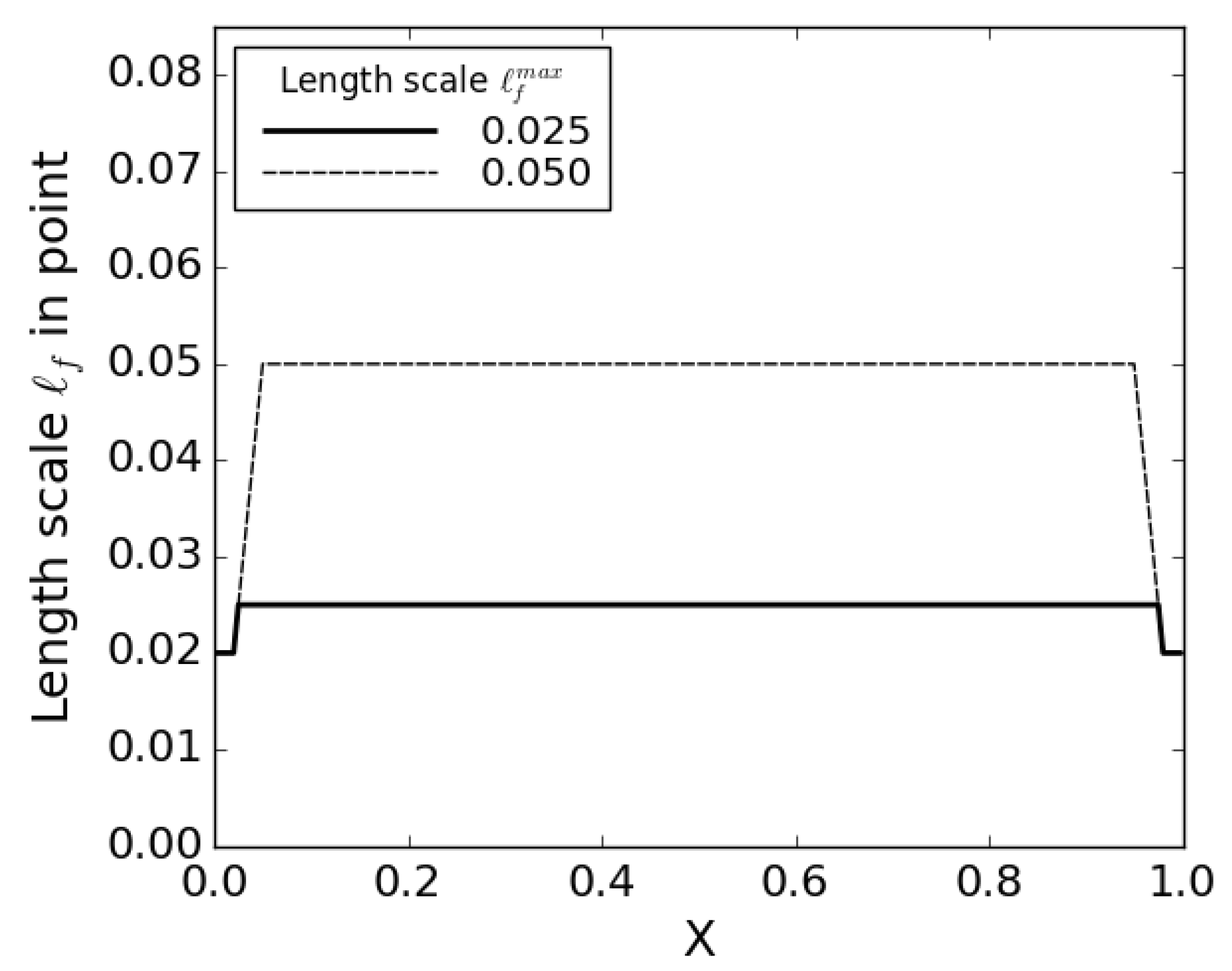
3.1. Model

Aa mentioned 1D sFCM body fixed at both ends is analyzed (Figure 1). For the sake of simplicity, the non-dimensional case is considered, so L = 1 and for the fractional model $E=1$, $\rho =1$. Herein, as the maximum value of the length scale parameters in non-local theories are usually not larger than 10–20% of the macroscopic characteristic dimension of the structure; therefore, ${\ell }_f\le 0.2$.

There are six control (“knot”) points, $\mathbf{k}$ (cf. Figure 1), defining the length scale (${\ell }_f$) distribution along the axis x, namely

$$\mathbf{k}=k_{i}i=1,2,\dots ,6.$$

(12)

For further analysis, we assume that vector ${\mathbf{k}}_v$ denotes vector $\mathbf{k}$ with components of value v. Next, the values between the knot points k are interpolated using cubic Hermite interpolator. Denoting the interpolator as $\Omega$, the length scale at point x can be expressed as follows:

$${\ell }_{f,\mathbf{k}}\left(x\right)=\left\{\begin{array}{c}\Omega (\mathbf{k},x)x\le L/2,\hfill \\ \Omega (\mathbf{k},L-x)x>L/2.\hfill \end{array}\right.$$

(13)

According to the results obtained in [36], near to the ends of the structure, the length scale is linearly reduced from ${\ell }_f^{max}$ to $2\Delta x$. As a consequence, in the framework of the applied approximation, no information on displacements outside the body is required.

In the optimization procedure, the reduction of ${\ell }_f$ is carried out by application of the non-dimensional correction functional $\Psi$ in a form

$$\Psi \left(g\right)=\left\{\begin{array}{cc}max(x,2\Delta x)\hfill & g\left(x\right)>x,\hfill \\ max(L-x,2\Delta x)\hfill & g\left(x\right)>(L-x),\hfill \\ g\left(x\right)\hfill & otherwise,\hfill \end{array}\right.$$

(14)

where $g\left(x\right)$ is any function of class $C_0$. As a result, the final function describing the length scale distribution can be defined in the following form

$${\overline{\ell }}_{f,\mathbf{k}}=\Psi \left({\ell }_{f,\mathbf{k}}\right).$$

(15)

The graphical representation of function ${\overline{\ell }}_{f,\mathbf{k}}$ for the extreme case, i.e., $k_i={\ell }_f^{max}$ is presented in Figure 2.

It is important, that model discretization depends on maximal length scale, namely for ${\ell }_f^{max}=0.05\to \Delta x=0.005$ and for ${\ell }_f^{max}=0.025\to \Delta x=0.0025$.

To solve the formulated optimization problem a dedicated procedure was developed in Python to build the global system of equations (Equation (11)). Due to the varied length scale, the governing equation for the particular points was built dynamically (cf. github.com/szajek) and the system of equations was solved using the LU decomposition [40] with partial pivoting and row interchanges.

3.2. Dynamic Response Evaluation

The dynamic response of the presented 1-D sFCM body is measured as a weighted sum of eigenvalues using Kreisselmeier–Steinhauser formula [33] in the form (the value of $KS({\ell }_f^{max},\alpha ,\mathbf{k})$ increases along with eigenvalues)

$$KS({\ell }_f^{max},\alpha ,\mathbf{k})=\frac{1}{{\rho }_{KS}}·{log}_e\left(\sum _i^{n_f\left({\ell }_f^{max}\right)}{e}^{{\rho }_{KS}f(\alpha ,\mathbf{k},i)}\right)$$

(16)

where ${\rho }_{KS}=0.1$ and

$$f(\alpha ,\mathbf{k},i)=\frac{{\omega }_i\left({\overline{\ell }}_{f,\mathbf{k}}\right)}{{\omega }_1\left({\overline{\ell }}_{f,\mathbf{k}}\right)}.$$

(17)

The complexity of mode shape is limited by the size of underlying microstructure described by ${\ell }_f$ in the model. Moreover, as mentioned in the introduction, the wavelength limit is estimated by analogy to the spring-mass (discrete) structure [32]. Additionally, taking into account the inaccuracy due to the boundary condition application, the number of eigenvalues considered is limited based on the maximal length scale as follows:

$$n_f\left({\ell }_f^{max}\right)=\left\{\begin{array}{cc}16\hfill & {\ell }_f^{max}=0.05,\hfill \\ 32\hfill & {\ell }_f^{max}=0.025.\hfill \end{array}\right.$$

(18)

The reference values of cumulative eigenvalues can be computed according to the equation

$$K{S}_{ref}(v,\alpha )=KS(v,\alpha ,{\mathbf{k}}_v).$$

(19)

It should be noted that the values for a classical (local) model (when $\alpha \to 1$) equal $K{S}_{ref}(0.05,1)=405.4$ and $K{S}_{ref}(0.025,1)=1098.5$.

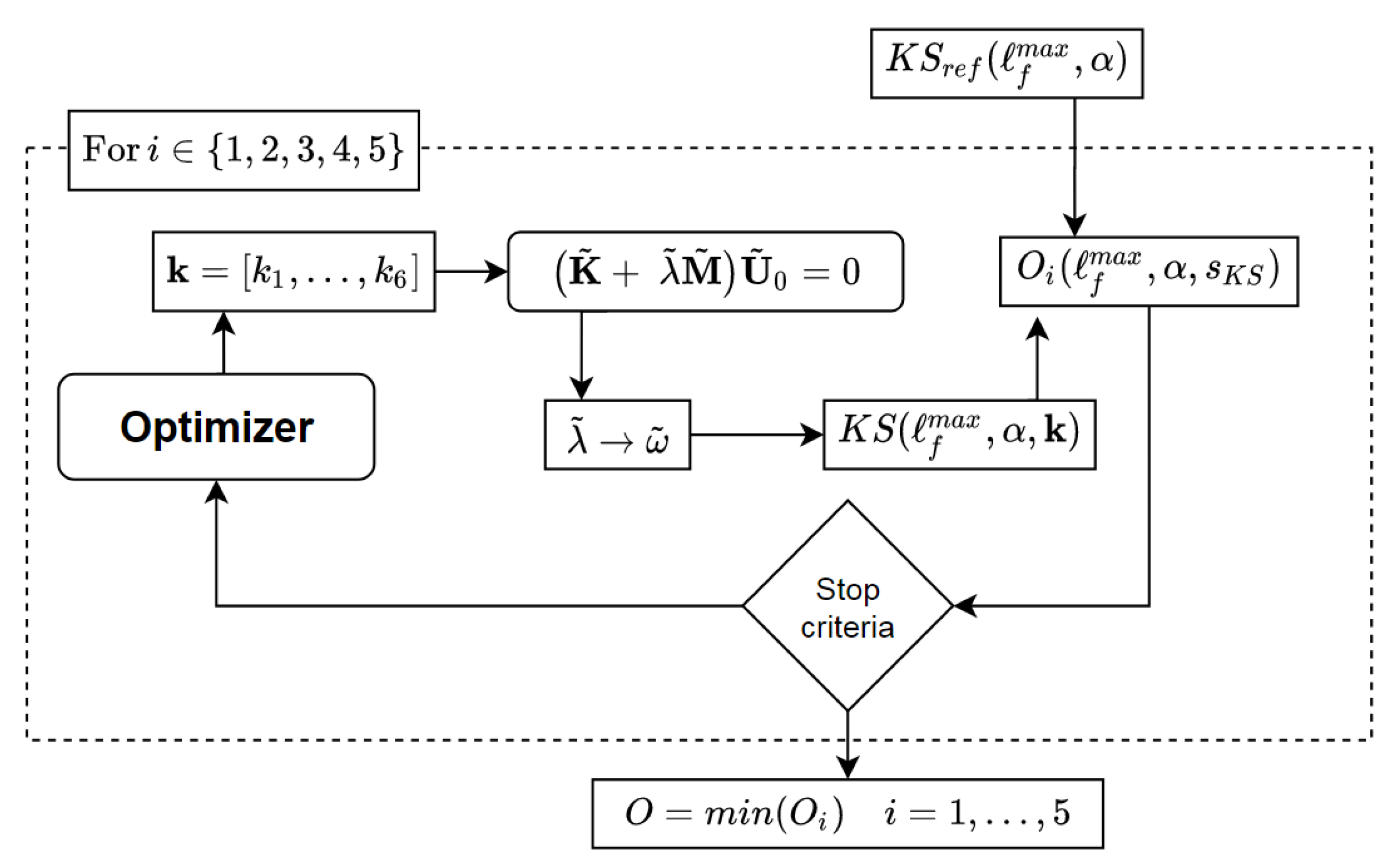
3.3. Optimization Problem

The following optimization problem was formulated for each configuration of ${\ell }_f^{max}$ and $\alpha$:

$$\begin{array}{cc}\hfill & \underset{\mathbf{k}}{min}O({\ell }_f^{max},\alpha ,s_{KS})=\left|KS({\ell }_f^{max},\alpha ,\mathbf{k})-s_{KS}·K{S}_{ref}({\ell }_f^{max},\alpha )\right|,\hfill \\ \hfill & \mathrm{subject}\mathrm{to}:\hfill \\ \hfill & \Delta x\left({\ell }_f^{max}\right)\le k_i\le {\ell }_f^{max}.\hfill \end{array}$$

(20)

where $s_{KS}$ denotes the scaling parameter $\ge 1$. The set of scale factors ($s_{KS}$) for each configuration of (${\ell }_f^{max}$, $\alpha$) was chosen from 1 to $s_{KS,max}$ computed as follows:

$$s_{KS,max}({\ell }_f^{max},\alpha )=\frac{K{S}_{ref}(\Delta x\left({\ell }_f^{max}\right),\alpha )}{K{S}_{ref}({\ell }_f^{max},\alpha )}.$$

(21)

3.4. Algorithm

The problem described by Equation (20) was solved by coupling the computational model with an optimizer. The general overview of the procedure is presented in Figure 3. For a given ${\ell }_f^{max}$ and $\alpha$, the reference value of the weighted sum of eigenvalues is computed according to the Kreisselmeier–Steinhauser formula, $K{S}_{ref}({\ell }_f^{max},\alpha )$. Next, the optimizer starts and iteratively propose vectors of values in control points, $\mathbf{k}$, which are a basis for model rebuilding—setting a length scale value for particular points along the body. The exact value of the length scale at point is calculated using Equations (13)–(15). Next, the eigenproblem is solved and the obtained eigenvalues are used to compute $KS({\ell }_f^{max},\alpha ,\mathbf{k})$ for the current length scale distribution. The difference between expected dynamic response (considering $s_{KS}$) and the obtained one is computed according the objective function in Equation (20). For each configuration of ${\ell }_f^{max}$ and $\alpha$, the problem is solved five times and the solution characterized by the smallest value of the objective function is chosen.

The hybrid algorithm joining two optimization strategies was used, namely, a local search algorithm and an evolutionary algorithm. As a local search optimizer, the Limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm [41,42] implemented in the SciPy package was chosen. The evolutionary algorithm started with the initial population of 70 propositions (individuals—random values of $\Delta x\left({\ell }_f^{max}\right)\le k_i\le {\ell }_f^{max}$) and improved them by application of genetic operators. After seven iterations (generations) the best solution was set as a starting point for a local search procedure. The evolutionary strategy configuration was as follows: two-point crossover with a probability of 0.5, tournament selection with a group of three individuals, the Gaussian mutation of mean $0.0$ with a standard deviation of $1.0$ and probability $0.02$. The mutation was applied for each parameter independently. The most important settings for local procedure are minimal relative change of an objective function—taken as $2.22\times {10}^{-9}$(default value in the SciPy package), maximum number of iterations—taken as 15,000 and the step size for the numerical approximation of the Jacobian—taken as ${10}^{-3}$.

4. Results

The reference value of $K{S}_{ref}$ was computed according to Equation (19) for four values of ${\ell }_f^{max}\in \{0.0025,0.005,0.025,0.05\}$ and three values of $\alpha \in \{0.6,0.8,0.9\}$. The results are collected in

Table 1. Reference value of $K{S}_{ref}$ and $s_{KS,max}$ for various combination of maximal length scale ${\ell }_f^{max}$ and material order $\alpha$.

${\mathit{KS}}_{\mathit{ref}}$		${\mathit{\ell }}_{\mathit{f}}^{\mathit{max}}$				${\mathit{s}}_{\mathit{KS},\mathit{max}}$		${\mathit{\ell }}_{\mathit{f}}^{\mathit{max}}$
		0.05	0.025	0.005	0.0025			0.05	0.025
$\mathbf{\alpha }$	0.9	390.5	994.6	405.1	1096.2	$\mathbf{\alpha }$	0.9	1.04	1.10
	0.8	378.2	907.3	404.8	1094.3		0.8	1.07	1.21
	0.6	358.9	772.1	404.4	1091.4		0.6	1.13	1.41

. The lowest values of ${\ell }_f^{max}$ are an effect of used discretization, namely, $\Delta x=0.005$ and for $\Delta x=0.0025$ for ${\ell }_f^{max}=0.05$ and ${\ell }_f^{max}=0.025$, respectively (cf. Section 3.1). Based on $K{S}_{ref}$ maximal values of scale factor was established according to Equation (21).

The optimization problem formulated in Equation (20) was solved for two values of ${\ell }_f^{max}\in \{0.025,0.05\}$, three values of $\alpha \in \{0.6,0.8,0.9\}$ and set of a scale factor $s_{KS}\in (1,s_{KS,max})$. The optimization problem for each configuration of (${\ell }_f^{max}$, $\alpha$, $s_{KS}$) was solved five times and the solution with the lowest objective function value was chosen. The best solutions—an objective value and parameters—are presented in

Table 2. Objective value and parameters for the best solutions: length scale ${\ell }_f^{max}=0.025$ and $\alpha \in \{0.6,0.8,0.9\}$.

${\mathit{\ell }}_{\mathit{f}}^{\mathit{max}}$	$\mathit{\alpha }$	${\mathit{s}}_{\mathit{KS}}$	O	Parameters k
0.025	0.6	1	5.95 $\times {10}^{-10}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$
		1.05	8.97 $\times {10}^{-9}$	2.41 $\times {10}^{-2}$	2.22 $\times {10}^{-2}$	2.00 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.22 $\times {10}^{-2}$	2.29 $\times {10}^{-2}$
		1.1	1.74 $\times {10}^{-2}$	2.50 $\times {10}^{-3}$	2.27 $\times {10}^{-2}$	2.43 $\times {10}^{-2}$	1.78 $\times {10}^{-2}$	7.84 $\times {10}^{-3}$	2.23 $\times {10}^{-2}$
		1.15	7.88 $\times {10}^{-5}$	6.50 $\times {10}^{-3}$	1.97 $\times {10}^{-2}$	3.14 $\times {10}^{-3}$	1.63 $\times {10}^{-2}$	2.48 $\times {10}^{-2}$	9.95 $\times {10}^{-3}$
		1.2	1.00 $\times {10}^{-3}$	1.54 $\times {10}^{-2}$	1.81 $\times {10}^{-2}$	8.08 $\times {10}^{-3}$	1.85 $\times {10}^{-2}$	7.54 $\times {10}^{-3}$	1.76 $\times {10}^{-2}$
		1.25	2.01 $\times {10}^{-2}$	2.25 $\times {10}^{-2}$	1.29 $\times {10}^{-2}$	1.41 $\times {10}^{-2}$	1.51 $\times {10}^{-2}$	1.35 $\times {10}^{-2}$	1.40 $\times {10}^{-2}$
		1.3	3.17 $\times {10}^{-4}$	9.60 $\times {10}^{-3}$	7.29 $\times {10}^{-3}$	8.83 $\times {10}^{-3}$	1.62 $\times {10}^{-2}$	1.46 $\times {10}^{-2}$	7.67 $\times {10}^{-3}$
		1.4	1.19 $\times {10}^{-3}$	3.23 $\times {10}^{-3}$	6.64 $\times {10}^{-3}$	2.59 $\times {10}^{-3}$	5.78 $\times {10}^{-3}$	2.74 $\times {10}^{-3}$	2.50 $\times {10}^{-3}$
	0.8	1	2.47 $\times {10}^{-9}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$
		1.05	2.01 $\times {10}^{-5}$	1.41 $\times {10}^{-2}$	2.35 $\times {10}^{-2}$	1.23 $\times {10}^{-2}$	1.87 $\times {10}^{-2}$	2.29 $\times {10}^{-2}$	2.36 $\times {10}^{-2}$
		1.1	1.28 $\times {10}^{-3}$	4.76 $\times {10}^{-3}$	1.01 $\times {10}^{-2}$	1.03 $\times {10}^{-2}$	1.93 $\times {10}^{-2}$	2.26 $\times {10}^{-2}$	1.86 $\times {10}^{-2}$
		1.15	1.95 $\times {10}^{-4}$	2.37 $\times {10}^{-2}$	6.52 $\times {10}^{-3}$	2.50 $\times {10}^{-3}$	8.64 $\times {10}^{-3}$	1.87 $\times {10}^{-2}$	1.30 $\times {10}^{-2}$
		1.2	3.14 $\times {10}^{-4}$	2.50 $\times {10}^{-3}$	3.04 $\times {10}^{-3}$	4.77 $\times {10}^{-3}$	4.80 $\times {10}^{-3}$	6.29 $\times {10}^{-3}$	4.14 $\times {10}^{-3}$
	0.9	1	3.23 $\times {10}^{-9}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$
		1.01	8.94 $\times {10}^{-4}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	2.50 $\times {10}^{-2}$	1.99 $\times {10}^{-2}$	2.39 $\times {10}^{-2}$	2.35 $\times {10}^{-2}$
		1.02	1.60 $\times {10}^{-3}$	1.36 $\times {10}^{-2}$	2.10 $\times {10}^{-2}$	2.16 $\times {10}^{-2}$	2.02 $\times {10}^{-2}$	2.39 $\times {10}^{-2}$	2.39 $\times {10}^{-2}$
		1.03	2.44 $\times {10}^{-3}$	7.54 $\times {10}^{-3}$	2.44 $\times {10}^{-2}$	2.07 $\times {10}^{-2}$	1.37 $\times {10}^{-2}$	2.47 $\times {10}^{-2}$	1.80 $\times {10}^{-2}$
		1.05	5.18 $\times {10}^{-4}$	9.02 $\times {10}^{-3}$	6.43 $\times {10}^{-3}$	1.97 $\times {10}^{-2}$	2.43 $\times {10}^{-2}$	2.17 $\times {10}^{-2}$	5.65 $\times {10}^{-3}$
		1.06	2.21 $\times {10}^{-5}$	1.54 $\times {10}^{-2}$	1.75 $\times {10}^{-2}$	5.14 $\times {10}^{-3}$	2.37 $\times {10}^{-2}$	2.50 $\times {10}^{-3}$	1.24 $\times {10}^{-2}$

and

Table 3. Objective value and parameters for the best solutions: length scale ${\ell }_f^{max}=0.05$ and $\alpha \in \{0.6,0.8,0.9\}$.

${\mathit{\ell }}_{\mathit{f}}^{\mathit{max}}$	$\mathit{\alpha }$	${\mathit{s}}_{\mathit{KS}}$	O	Parameters k
0.05	0.6	1	1.47 $\times {10}^{-10}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$
		1.0125	1.21 $\times {10}^{-3}$	1.61 $\times {10}^{-2}$	4.96 $\times {10}^{-2}$	3.94 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	4.28 $\times {10}^{-2}$	4.97 $\times {10}^{-2}$
		1.025	6.82 $\times {10}^{-5}$	3.53 $\times {10}^{-2}$	3.90 $\times {10}^{-2}$	3.87 $\times {10}^{-2}$	4.53 $\times {10}^{-2}$	4.29 $\times {10}^{-2}$	4.75 $\times {10}^{-2}$
		1.0375	1.39 $\times {10}^{-7}$	4.46 $\times {10}^{-2}$	3.70 $\times {10}^{-2}$	4.28 $\times {10}^{-2}$	4.84 $\times {10}^{-2}$	1.55 $\times {10}^{-2}$	3.85 $\times {10}^{-2}$
		1.05	4.99 $\times {10}^{-3}$	3.06 $\times {10}^{-2}$	4.21 $\times {10}^{-2}$	6.63 $\times {10}^{-3}$	4.35 $\times {10}^{-2}$	3.99 $\times {10}^{-2}$	1.40 $\times {10}^{-2}$
		1.075	1.67 $\times {10}^{-4}$	1.71 $\times {10}^{-2}$	3.42 $\times {10}^{-2}$	1.97 $\times {10}^{-2}$	3.59 $\times {10}^{-2}$	2.25 $\times {10}^{-2}$	2.52 $\times {10}^{-2}$
		1.0875	2.57 $\times {10}^{-6}$	5.01 $\times {10}^{-3}$	6.01 $\times {10}^{-3}$	3.57 $\times {10}^{-2}$	1.93 $\times {10}^{-2}$	3.40 $\times {10}^{-2}$	1.46 $\times {10}^{-2}$
		1.1	2.79 $\times {10}^{-7}$	2.67 $\times {10}^{-2}$	1.64 $\times {10}^{-2}$	3.37 $\times {10}^{-2}$	1.56 $\times {10}^{-2}$	1.88 $\times {10}^{-2}$	6.54 $\times {10}^{-3}$
	0.8	1	1.63 $\times {10}^{-11}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$
		1.01	1.99 $\times {10}^{-3}$	2.87 $\times {10}^{-2}$	4.76 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	3.14 $\times {10}^{-2}$	4.91 $\times {10}^{-2}$	4.98 $\times {10}^{-2}$
		1.02	2.63 $\times {10}^{-7}$	1.92 $\times {10}^{-2}$	4.25 $\times {10}^{-2}$	2.56 $\times {10}^{-2}$	3.91 $\times {10}^{-2}$	4.81 $\times {10}^{-2}$	4.27 $\times {10}^{-2}$
		1.03	2.34 $\times {10}^{-10}$	2.66 $\times {10}^{-2}$	3.94 $\times {10}^{-2}$	3.67 $\times {10}^{-2}$	7.17 $\times {10}^{-3}$	3.02 $\times {10}^{-2}$	4.95 $\times {10}^{-2}$
		1.04	1.58 $\times {10}^{-3}$	5.00 $\times {10}^{-2}$	3.17 $\times {10}^{-2}$	2.62 $\times {10}^{-2}$	3.91 $\times {10}^{-2}$	3.32 $\times {10}^{-2}$	1.00 $\times {10}^{-2}$
		1.05	2.38 $\times {10}^{-4}$	5.00 $\times {10}^{-2}$	1.78 $\times {10}^{-2}$	3.94 $\times {10}^{-2}$	1.48 $\times {10}^{-2}$	3.20 $\times {10}^{-2}$	5.00 $\times {10}^{-3}$
		1.06	1.46 $\times {10}^{-2}$	2.33 $\times {10}^{-2}$	1.70 $\times {10}^{-2}$	2.57 $\times {10}^{-2}$	1.05 $\times {10}^{-2}$	1.98 $\times {10}^{-2}$	1.35 $\times {10}^{-2}$
	0.9	1	1.08 $\times {10}^{-10}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$	5.00 $\times {10}^{-2}$
		1.02	6.99 $\times {10}^{-8}$	4.29 $\times {10}^{-2}$	1.55 $\times {10}^{-2}$	2.57 $\times {10}^{-2}$	4.39 $\times {10}^{-2}$	4.26 $\times {10}^{-2}$	2.34 $\times {10}^{-2}$
		1.025	1.19 $\times {10}^{-5}$	3.69 $\times {10}^{-2}$	1.38 $\times {10}^{-2}$	1.09 $\times {10}^{-2}$	3.60 $\times {10}^{-2}$	2.60 $\times {10}^{-2}$	3.54 $\times {10}^{-2}$
		1.03	1.08 $\times {10}^{-4}$	9.70 $\times {10}^{-3}$	2.50 $\times {10}^{-2}$	1.38 $\times {10}^{-2}$	1.80 $\times {10}^{-2}$	1.21 $\times {10}^{-2}$	2.89 $\times {10}^{-2}$

. All obtained solutions are characterized by $O<0.02$, which means that the expected dynamic behaviour was obtained with a high accuracy; the maximal error of 0.00385% was for ${\ell }_f^{max}=0.05$, $\alpha =0.8$ and $s_{KS}=1.06$. The total number of solved optimization problems equal ca. 200 with more than 130,000 single analyses (the calculations took several days—Intel Core i7-67000HQ, 16GB RAM). The results—eigenvalues spectra—are presented in Figure 4 and Figure 5.

Analysing the values $K{S}_{ref}$ and $s_{KS,max}$ from Table 1, a few important observations can be made. First and foremost, the potential for modifying dynamic response by changing a length scale, measured as $s_{KS,max}$, depends on both: material order $\alpha$ and the maximal permitted value of the length scale, ${\ell }_f^{max}$. However, the role of ${\ell }_f^{max}$ due to a different number of considered eigenvalues $n_f$ is difficult to evaluate. Secondly, the value of $s_{KS,max}$, as it should be, tends to zero for the classical continuum model as $\alpha \to 1$. Finally, for all cases, as ${\ell }_f^{max}\to 0$ (dimensions of the body become considerably larger than the characteristic length scale), the solutions for a classical model are obtained independently on material order $\alpha$.

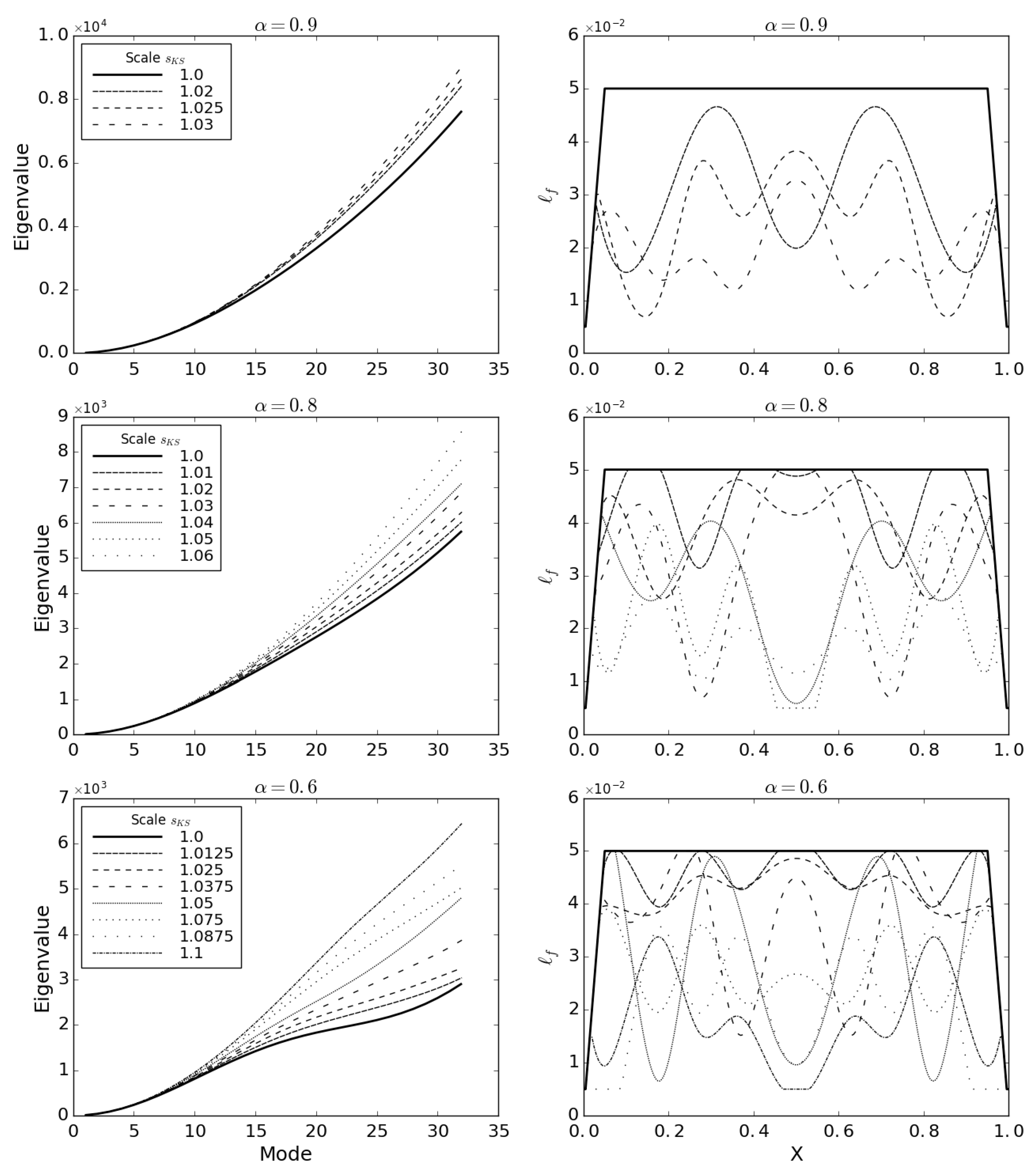
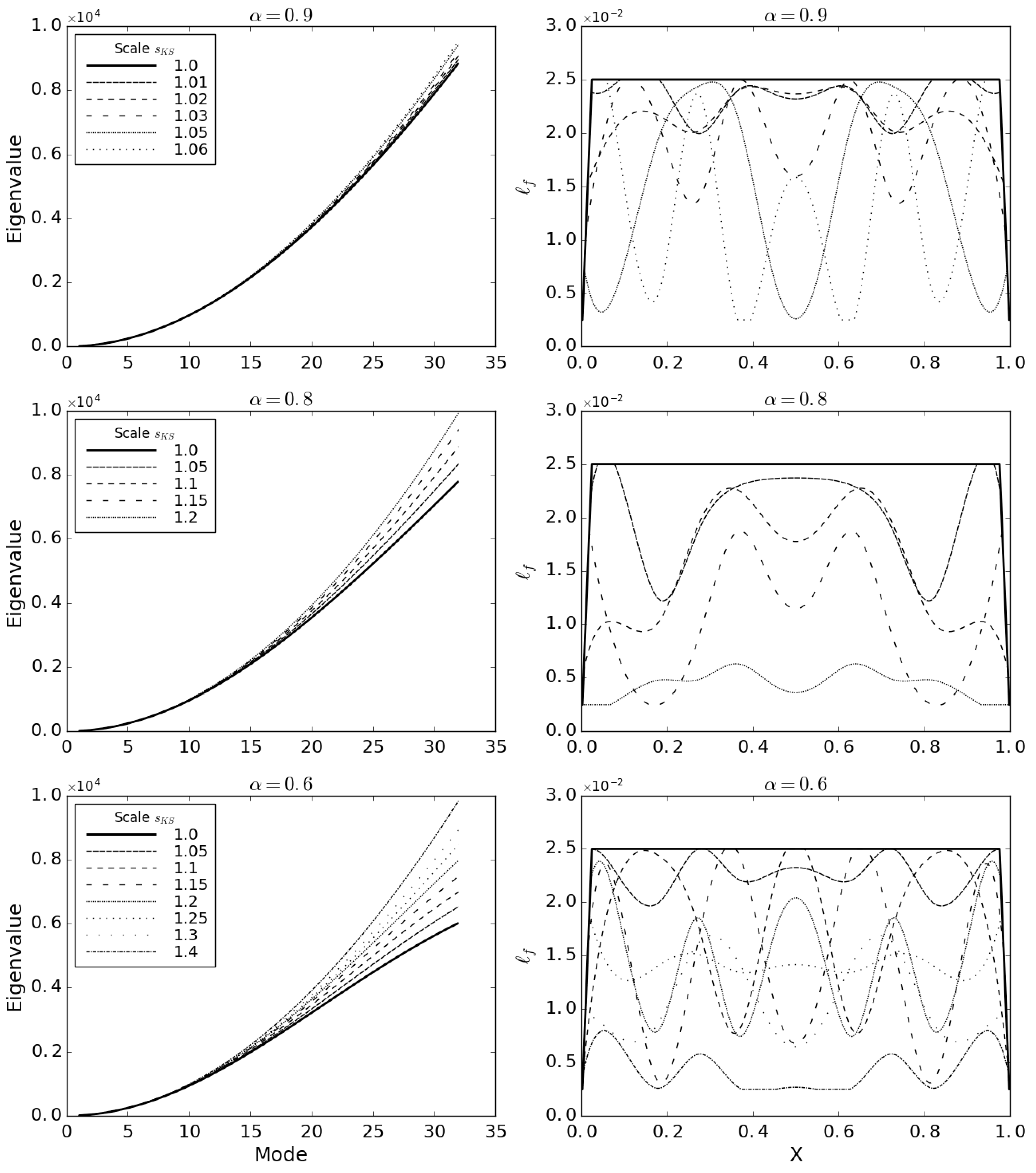
Figure 4 and Figure 5 confirms the previous observations in the context of the potential of a dynamic response change. The biggest differences in eigenvalue spectra can be seen for $\alpha =0.6$. For each case, however, the “design” of length scale leads to unique spectra between the extreme ones.

5. Conclusions

In this paper, the applicability of sFCM to design the material bodies with demanded dynamic eigenvalue spectrum is presented. The considered subject is meaningful both from the theoretical and practical points of view, especially when dealing with the design of sensors and actuators for nanotechnological applications, e.g., micro-thrusters of nano-satellites, torsional accelerometers, nano-motors or micro/nano-resonators. The problem is stated as a non-trivial inverse optimization task. As shown, different spectra are produced from different underlying microstructure distributions, which is described by the variable-length scale in the model. The obtained outcomes confirmed the correctness of our methodology, the optimization procedure and its implementation.

This in-depth study allows us to formulate the following conclusions:

• Designing the demanding dynamic response of a structure emphasising the scale effect by modifying length scale in the space-Fractional Continuum Mechanical model is possible;
• The potential for modifying dynamic response—measured as a weighted sum of eigenvalues—by changing a length scale is the biggest when the order of material continua $\alpha \to 0$ and tends to zero for $\alpha \to 1$ (the classical local model);
• The demanding dynamic response can be obtained by solving the inverse problem utilising hybridized optimization procedure joining the genetic and the limited-memory BFGS algorithms.