Thermodynamic Analysis of the Effect of Green Hydrogen Addition to a Fuel Mixture on the Steam Methane Reforming Process
Abstract
:1. Introduction
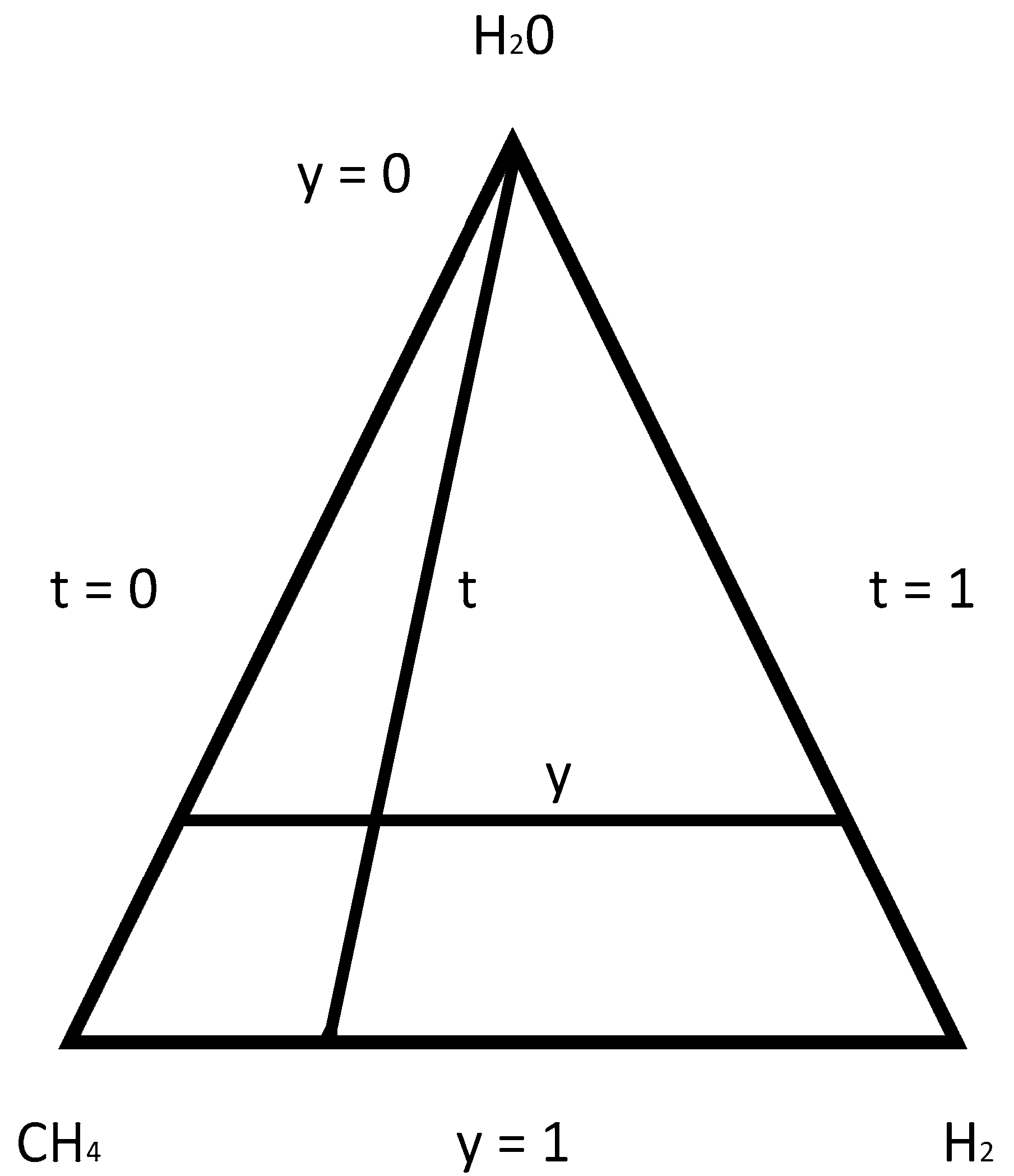
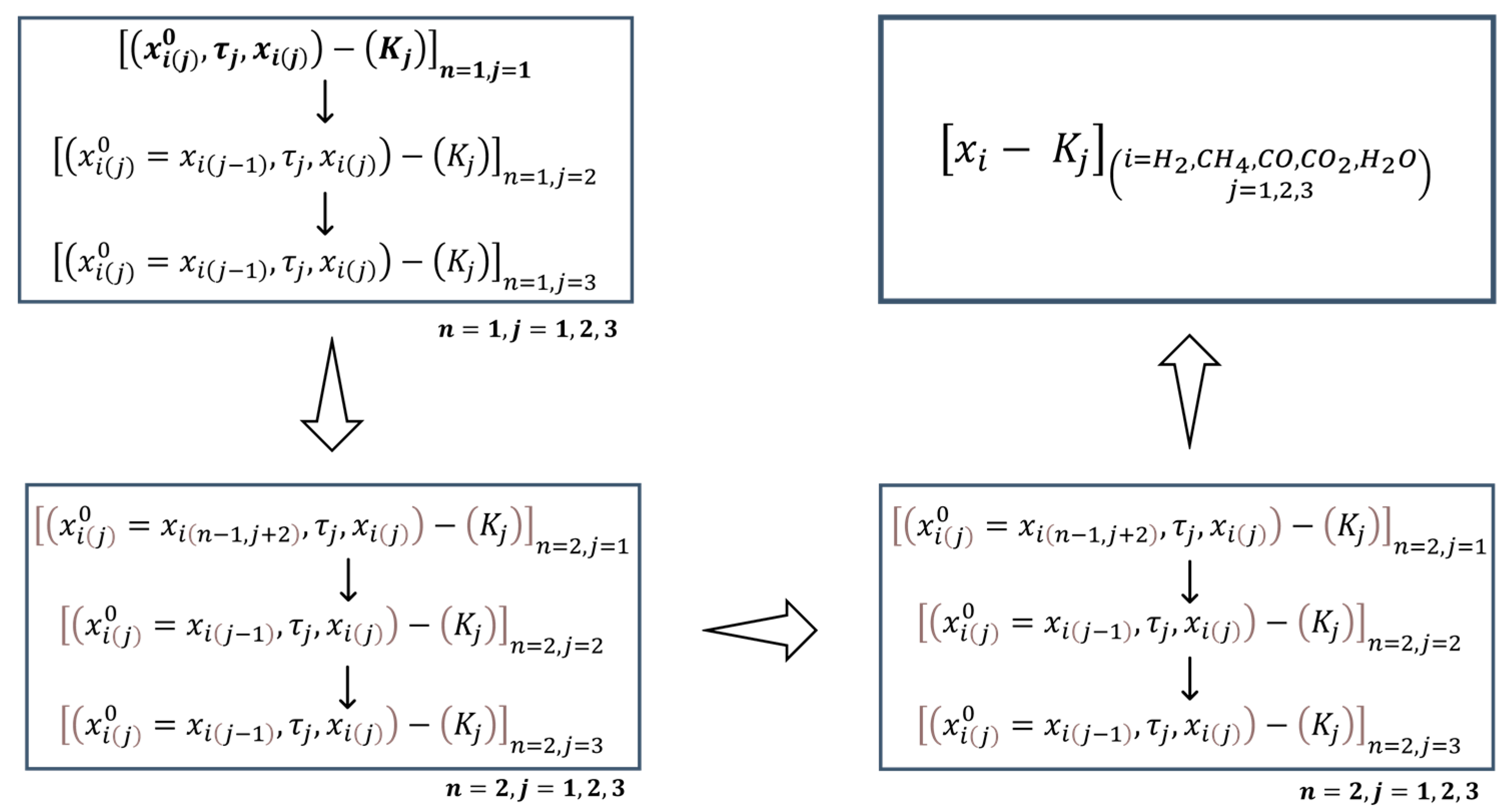
2. Thermodynamic Analysis
3. Analysis and Interpretation of Model Calculations
4. Summary
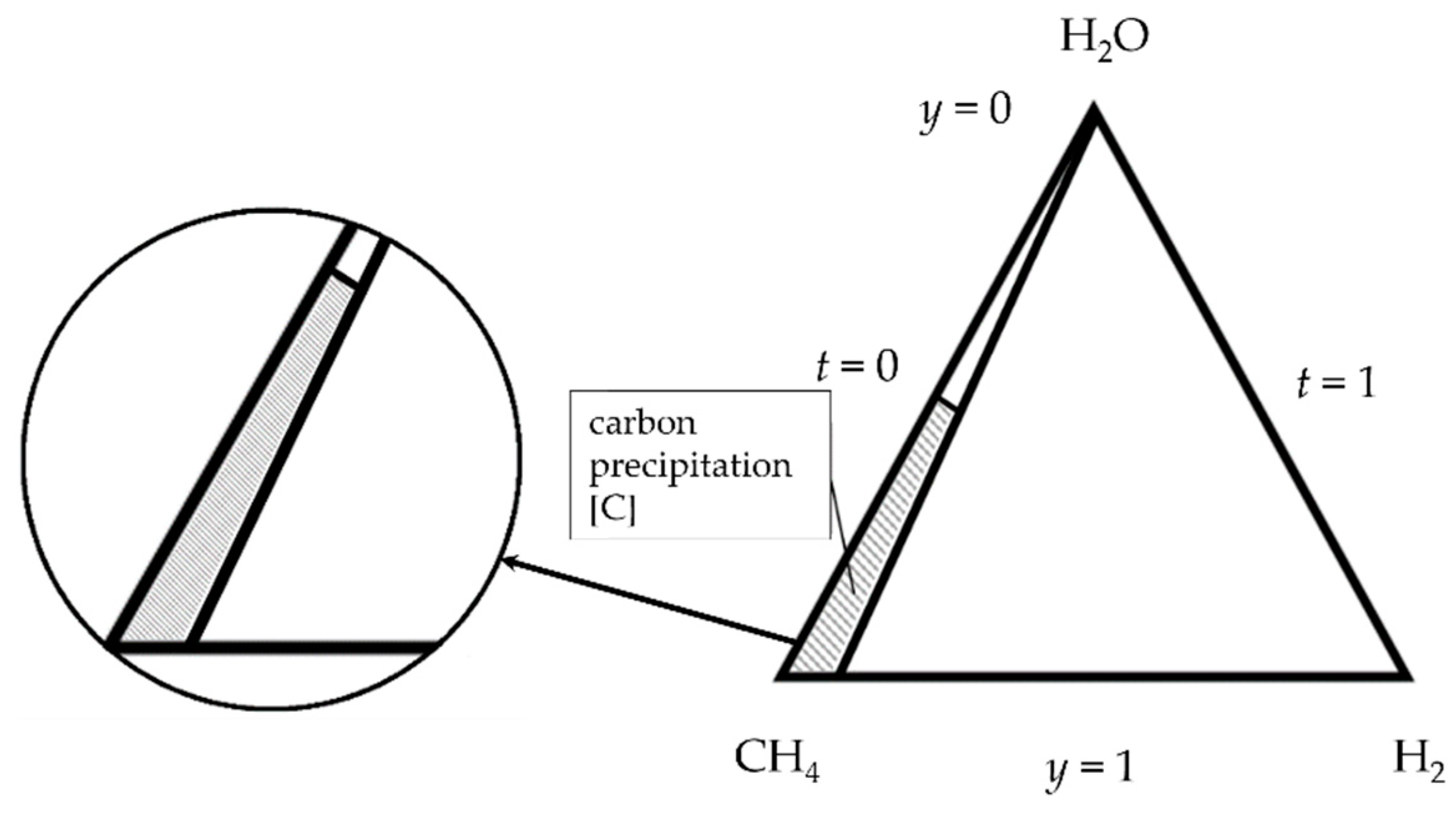
- Adding hydrogen, in a mixture with methane (t = 0–0.2) to system (CH4/H2)–H2O limits the range within which carbon deposits form, which promotes conversion of methane by the possibility of decreasing initial steam pressure .
- Therefore, it is possible to simplify the determination of carbon deposition range in the process of steam reforming of gaseous mixture (CH4/H2) with an approach based on the familiarity with this phenomenon in binary two-component systems (H2O–CH4, H2O–H2, CH4–H2), according to Toop’s model assumptions.
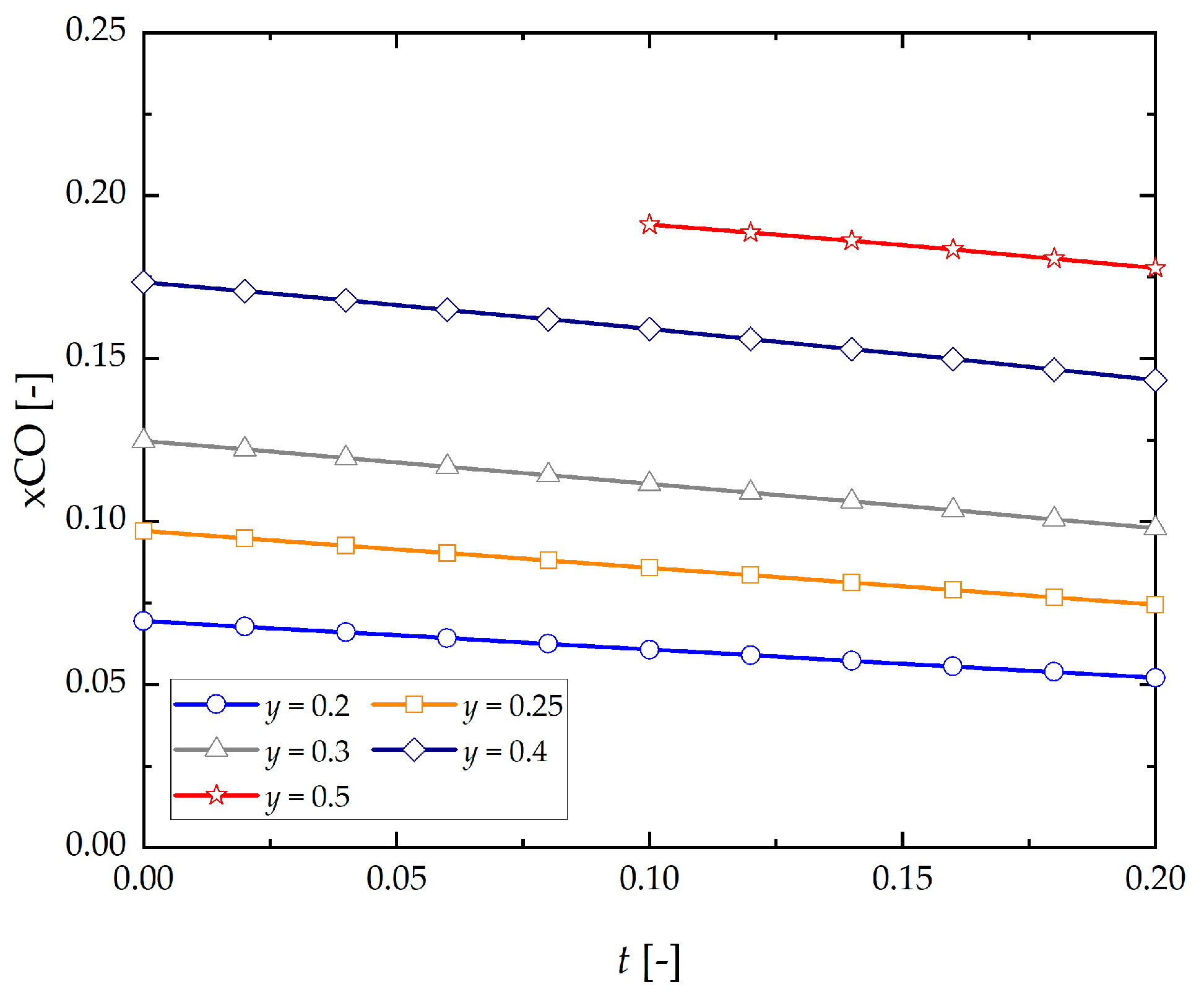
- As steam content added to the system in an area free from carbon deposition for a range of initial concentrations (t = 0–0.2; y = 0.2–y[C]) increases, there occurs a monotonic decrease in equilibrium concentrations of H2, CO, CH4 and an increase of CO2, H2O in the process being analyzed.
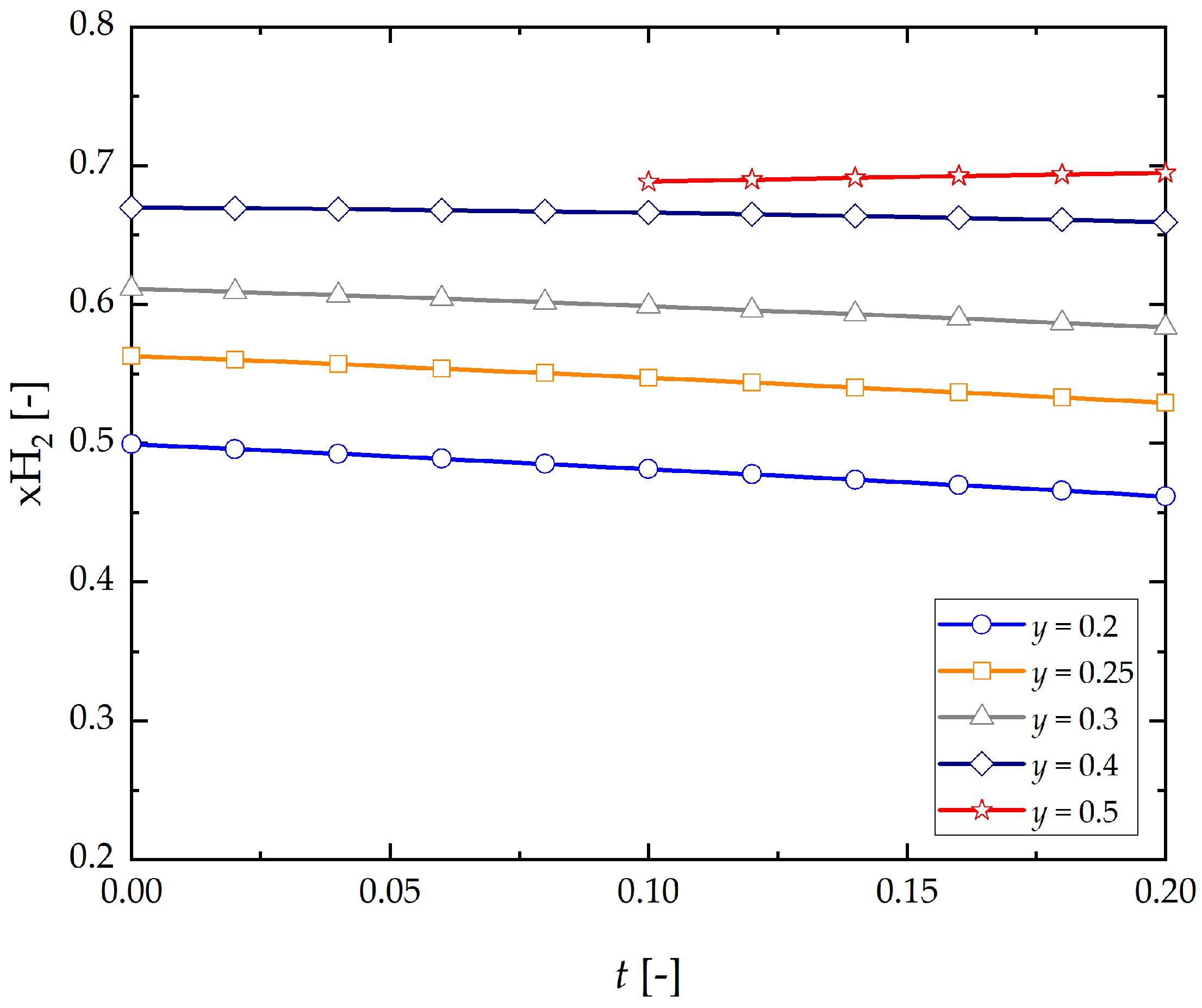
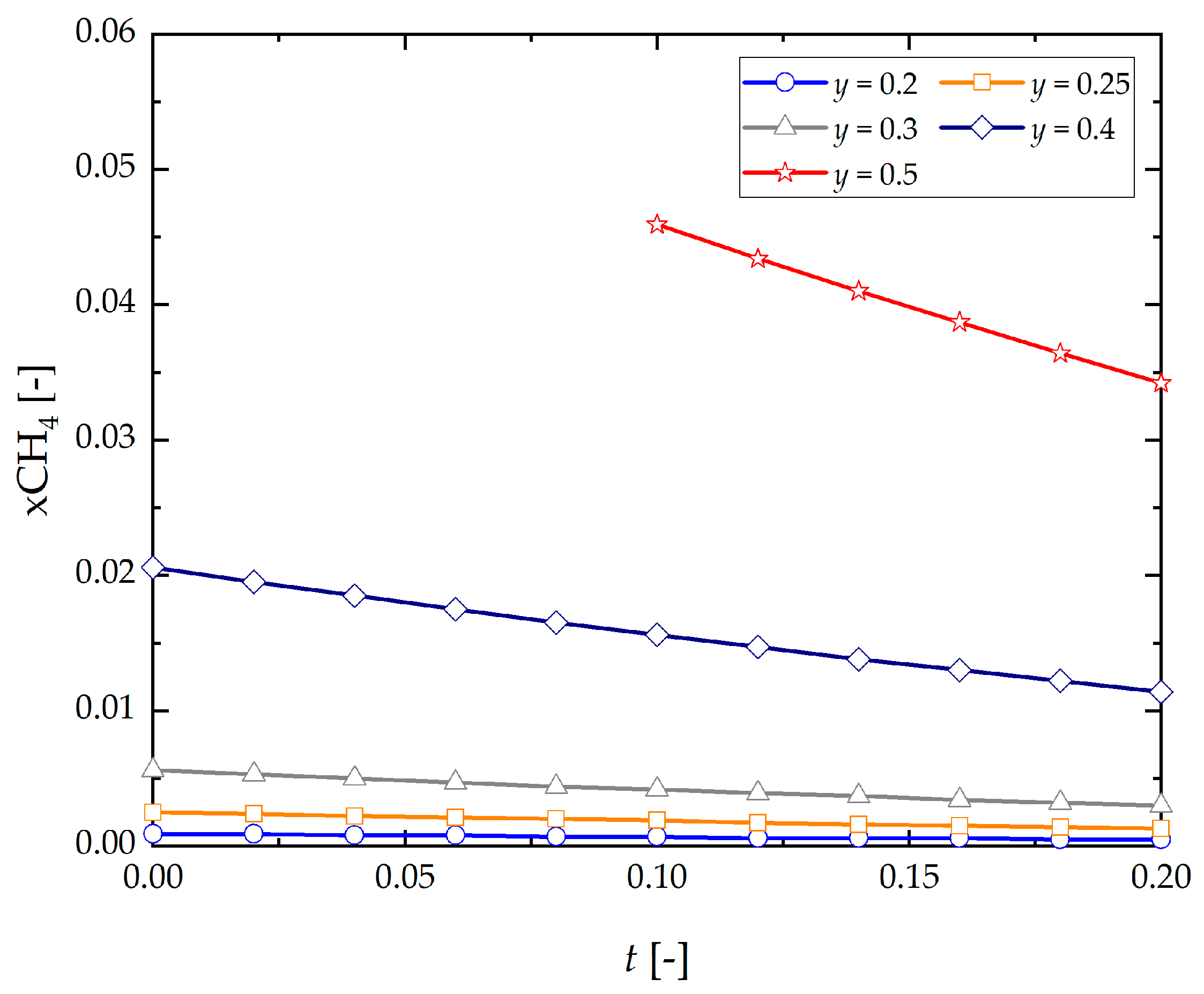
- The generation of hydrogen in reforming gaseous phase (CH4/H2)–H2O slightly decreases as this component increases in the initial composition , within the range y = 0.25–0.4, and an increase promotes this phenomenon.
- Equilibrium concentration of CO decreases as t increases, and steam intensifies this phenomenon.
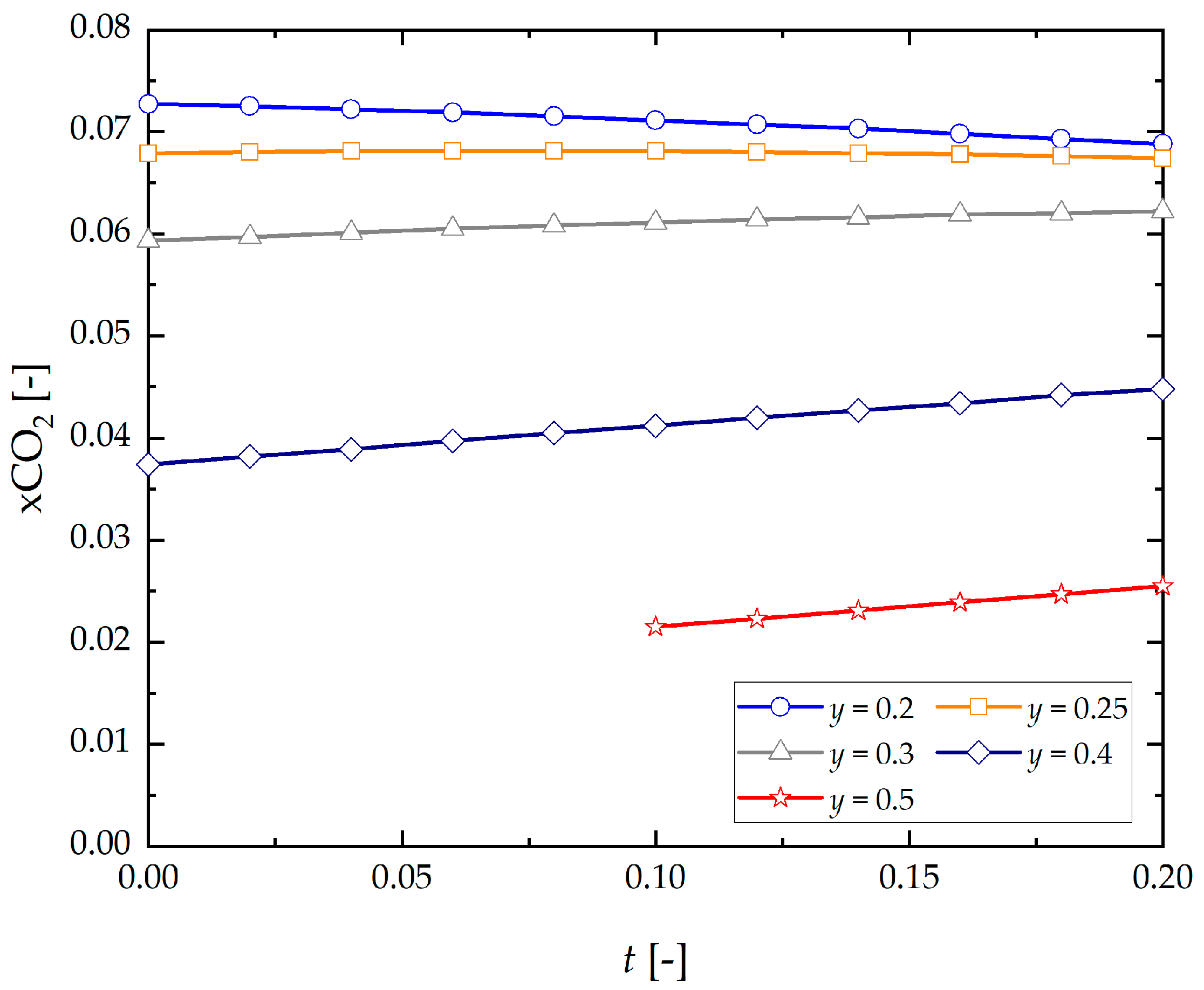
- An increase in initial concentration of hydrogen in methane, and steam ) in turn promotes generation of CO2 in process gases, it being understood that at high concentrations ) corresponding to y = 0.25 steam neutralizes effect on rising tendency of CO2 in the process products.
- Concentrations of H2O in the gaseous phase in thermodynamic equilibrium of the process increase in proportion to the initial composition of hydrogen and steam of the gaseous mixture being supplied into the system.
- CH4 content in the products decreases with initial concentration of hydrogen and steam ).
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gahleitner, G. Hydrogen from renewable electricity: An international review of power-to-gas pilot plants for stationary applications. Int. J. Hydrogen Energy 2013, 3, 2039–2061. [Google Scholar] [CrossRef]
- Grond, L.; Schulze, P.; Holstein, J. Systems Analyses Power to Gas: A Technology Review; DNV KEMA Energy & Sustainability; KEMA: Groningen, The Netherlands, 2013. [Google Scholar]
- Altfeld, K.; Pinchbeck, D. Admissible Hydrogen Concentrations in Natural Gas Systems; Gas For Energy; DIV Deutscher Industrieverlag: Munchen, Germany, 2013; Available online: https://www.gerg.eu/wp-content/uploads/2019/10/HIPS_Final-Report.pdf (accessed on 11 October 2021).
- Müller-Syring, G.; Henel, M.; Köppel, W.; Mlaker, H.; Sterner, M.; Höcher, T. Entwicklung von Modularen Konzepten zur Erzeugung, Speicherung und Einspeisung von Wasserstoff und Methan ins Erdgasnetz; DVGW-Projekt G1-07-10; DNV KEMA: Arnhem, The Netherlands, 2013; Available online: https://www.dvgw.de/medien/dvgw/forschung/berichte/g1_07_10.pdf (accessed on 11 October 2021).
- Melaina, M.W.; Antonia, O.; Penev, M. Blending Hydrogen into Natural Gas Pipeline Networks: A Review of Key Issues Technical; Report NREL/TP-5600-51995; National Renewable Energy Laboratory: Denver, CO, USA, 2013. Available online: https://www.nrel.gov/docs/fy13osti/51995.pdf (accessed on 11 October 2021).
- van der Zwaan, B.; Schoots, K.; Rivera-Tinoco, R.; Verbong, G. The cost of pipelining climate change mitigation: An overview of the economics of CH4, CO2 and H2 transportation. Appl. Energy 2011, 88, 3821–3831. [Google Scholar] [CrossRef] [Green Version]
- Dodds, P.E.; Demoullin, S. Conversion of the UK gas system to transport hydrogen. Int. J. Hydrogen Energy 2013, 38, 7189–7200. [Google Scholar] [CrossRef] [Green Version]
- Durbin, D.J.; Malardier-Jugroot, C. Review of hydrogen storage techniques for on board vehicle applications. Int. J. Hydrogen Energy 2013, 38, 14595–14617. [Google Scholar] [CrossRef]
- Messaoudani, Z.L.; Rigas, F.; Hamid, B.D.M.; Hassan, C.R.C. Hazards, safety and knowledge gaps on hydrogen transmission via natural gas grid: A critical review. Int. J. Hydrogen Energy 2016, 41, 17511–17525. [Google Scholar] [CrossRef]
- Gondal, I.A. Hydrogen integration in power-to-gas networks. Int. J. Hydrogen Energy 2018, 44, 1803–1815. [Google Scholar] [CrossRef]
- Meng, B.; Gu, C.; Zhang, L.; Zhou, C.; Li, X.; Zhao, Y.; Zheng, J.; Chen, X.; Han, Y. Hydrogen effects on X80 pipeline steel in high-pressure natural gas/hydrogen mixtures. Int. J. Hydrogen Energy 2016, 42, 7404–7412. [Google Scholar] [CrossRef]
- Kaczmarczyk, R.; Gurgul, S. A thermodynamic analysis of heavy hydrocarbons reforming for solid oxide fuel cell application as a part of hybrid energy systems. Energies 2021, 14, 337. [Google Scholar] [CrossRef]
- Chalusiak, M.; Wrobel, M.; Mozdzierz, M.; Berent, K.; Szmyd, J.S.; Kimijima, S.; Brus, G. A numerical analysis of unsteady transport phenomena in a Direct Internal Reforming Solid Oxide Fuel Cell. Int. J. Heat Mass Transf. 2019, 131, 1032–1051. [Google Scholar] [CrossRef]
- Tomiczek, M.; Kaczmarczyk, R.; Mozdzierz, M.; Brus, G. A numerical analysis of heat and mass transfer during the steam reforming process of ethane. Heat Mass Transf. 2017, 54, 2305–2314. [Google Scholar] [CrossRef]
- Liu, C.; Ye, J.; Jiang, J.; Pan, Y. Progresses in the preparation of coke resistant Ni-based catalyst for steam and CO2 reforming of methane. ChemCatChem 2011, 3, 529–541. [Google Scholar] [CrossRef]
- Tang, S.B.; Qiu, F.L.; Lu, S.J. Effect of supports on the carbon deposition of nickel catalysts for methane reforming with CO2. Catal. Today 1995, 24, 253–255. [Google Scholar] [CrossRef]
- Tomishige, K.; Himeno, Y.; Matsuo, Y.; Yoshinaga, Y.; Fujimoto, K. Catalytic performance and carbon deposition behavior of a NiO-MgO solid solution in methane reforming with carbon dioxide under pressurized conditions. Ind. Eng. Chem. Res. 2000, 39, 1891–1897. [Google Scholar] [CrossRef]
- Das, S.; Ashok, J.; Bian, Z.; Dewangan, N.; Wai, M.H.; Du, Y.; Borgna, A.; Hidajat, K.; Kawi, S. Silica—Ceria sandwiched Ni core—Shell catalyst for low temperature dry reforming of biogas: Coke resistance and mechanistic insights. Appl. Catal. B Environ. 2018, 230, 220–236. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, L.; Wang, Y.; Wang, S.; Zhao, Q.; Mao, D.; Hu, C. Low-temperature catalytic CO2 Dry reforming of methane on Ni-Si/ZrO2 catalyst. ACS Catal. 2018, 8, 6495–6506. [Google Scholar] [CrossRef]
- Shen, J.; Reule, A.A.C.; Semagina, N. Ni/MgAl2O4 catalyst for low-temperature oxidative dry methane reforming with CO2. Int. J. Hydrogen Energy 2019, 44, 4616–4629. [Google Scholar] [CrossRef]
- Agrafiotis, C.; Von Storch, H.; Roeb, M.; Sattler, C. Solar thermal reforming of methane feedstocks for hydrogen and syngas production—A review. Renew. Sustain. Energy Rev. 2014, 29, 656–682. [Google Scholar] [CrossRef]
- Gokon, N.; Yamawaki, Y.; Nakazawa, D.; Kodama, T. Ni/MgO-Al2O3 and Ni-Mg-O catalyzed SiC foam absorbers for high temperature solar reforming of methane. Int. J. Hydrogen Energy 2010, 35, 7441–7453. [Google Scholar] [CrossRef]
- Tan, S.S.; Zou, L.; Hu, E. Photocatalytic reduction of carbon dioxide into gaseous hydrocarbon using TiO2 pellets. Catal. Today 2006, 115, 269–273. [Google Scholar] [CrossRef]
- Ohno, T.; Sarukawa, K.; Tokieda, K.; Matsumura, M. Morphology of a TiO2 photocatalyst (Degussa, P-25) consisting of anatase and rutile crystalline phases. J. Catal. 2001, 203, 82–86. [Google Scholar] [CrossRef]
- Park, H.; Park, Y.; Kim, W.; Choi, W. Surface modification of TiO2 photocatalyst for environmental applications. J. Photochem. Photobiol. C Photochem. Rev. 2013, 15, 1–20. [Google Scholar] [CrossRef]
- Yoshida, H.; Hirao, K.; Nishimoto, J.; Shimura, K.; Kato, S.; Itoh, H.; Hattori, T. Hydrogen production from methane and water on platinum loaded titanium oxide photocatalysts. J. Phys. Chem. C 2008, 112, 5542–5551. [Google Scholar] [CrossRef]
- Shimura, K.; Kato, S.; Yoshida, T.; Itoh, H.; Hattori, T.; Yoshida, H. Photocatalytic steam reforming of methane over sodium tantalate. J. Phys. Chem. C 2010, 114, 3493–3503. [Google Scholar] [CrossRef]
- Balázs, L.; Baán, K.; Varga, E.; Oszkó, A.; Erdőhelyi, A.; Kónya, Z.; Kiss, J. Photo-induced reactions in the CO2-methane system on titanate nanotubes modified with Au and Rh nanoparticles. Appl. Catal. B Environ. 2016, 199, 473–484. [Google Scholar]
- Cho, Y.; Yamaguchi, A.; Miyauchi, M. Photocatalytic methane reforming: Recent advances. Catalysts 2021, 11, 18. [Google Scholar] [CrossRef]
- Susmozas, A.; Iribarren, D.; Dufour, J. Life-cycle performance of indirect biomass gasification as a green alternative to steam methane reforming for hydrogen production. Int. J. Hydrogen Energy 2013, 38, 9961–9972. [Google Scholar] [CrossRef]
- Di Marcoberardino, G.; Vitali, D.; Spinelli, F.; Binotti, M.; Manzolini, G. Green hydrogen production from raw biogas: A Techno-economic investigation of conventional processes using pressure swing adsorption unit. Processes 2018, 6, 19. [Google Scholar] [CrossRef] [Green Version]
- Minutillo, M.; Perna, A.; Sorce, A. Green hydrogen production plants via biogas steam and autothermal reforming processes energy and exergy analyses. Appl. Energy 2020, 277, 115452. [Google Scholar] [CrossRef]
- Tuna, C.E.; Silveira, J.L.; da Silva, M.E.; Boloy, R.M.; Braga, L.B.; Pérez, N.P. Biogas steam reformer for hydrogen production: Evaluation of the reformer prototype and catalysts. Int. J. Hydrogen Energy 2018, 43, 2108–2120. [Google Scholar] [CrossRef] [Green Version]
- Prodromidis, G.N.; Coutelieris, F.A. The effect of biogas origin on the electricity production by solid oxide fuel cells. Appl. Sci. 2021, 11, 3112. [Google Scholar] [CrossRef]
- Pajak, M.; Brus, G.; Szmyd, J.S. Catalyst distribution optimization scheme for effective green hydrogen production from biogas reforming. Energies 2021, 14, 5558. [Google Scholar] [CrossRef]
- Ptak, W.; Sukiennik, M. Changes in the composition of the gaseous phase of a system resulting from the process of a chemical reaction. Bull. Acad. Pol. Sci. 1969, 17, 21–25. [Google Scholar]
- Ptak, W.; Sukiennik, M. The kinetics characteristic of complex systems. Arch. Metall. 1973, 18, 275–289. [Google Scholar]
- Ptak, W.; Sukiennik, M.; Olesinski, R.; Kaczmarczyk, R. Deformation of a properties resulting from a chemical reaction stoichiometry. Arch. Metall. 1987, 32, 355–362. [Google Scholar]
- Kaczmarczyk, R.; Gurgul, S. Model approach of carbon deposition phenomenon in mixed H2O/CO2 methane reforming process. Arch. Metall. Mater. 2014, 59, 1379–1383. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarczyk, R.; Gurgul, S. Model approach of carbon deposition phenomenon in steam and dry methane reforming process. Arch. Metall. Mater. 2014, 59, 145–148. [Google Scholar] [CrossRef] [Green Version]
- Brus, G. Experimental and numerical studies on chemically reacting gas flow in the porous structure of a solid oxide fuel cells internal fuel reformer. Int. J. Hydrogen Energy 2012, 37, 17225–17234. [Google Scholar] [CrossRef]
- Sciazko, A.; Komatsu, Y.; Brus, G.; Kimijima, S. A novel approach to improve the mathematical modelling of the internal reforming process for solid oxide fuel cells using the orthogonal least squares method. Int. J. Hydrogen Energy 2014, 39, 16372–16389. [Google Scholar] [CrossRef]
- Sciazko, A.; Komatsu, Y.; Brus, G.; Kimijima, S.; Szmyd, J.S. A novel approach to the experimental study on methane/steam reforming kinetics using the Orthogonal Least Squares method. J. Power Sources 2014, 262, 245–254. [Google Scholar] [CrossRef]
- Pajak, M.; Mozdzierz, M.; Chalusiak, M.; Kimijima, S.; Szmyd, J.S.; Brus, G. A numerical analysis of heat and mass transfer processes in a macro-patterned methane/steam reforming reactor. Int. J. Hydrogen Energy 2018, 43, 20474–20487. [Google Scholar] [CrossRef]
- Delgado, K.H.; Maier, L.; Tischer, S.; Zellner, A.; Stotz, H. Surface reaction kinetics of steam-and CO2-reforming as well as oxidation of methane over nickel-based catalysts. Catalysts 2015, 5, 871–904. [Google Scholar] [CrossRef] [Green Version]
- York, A.P.E.; Xiao, T.C.; Green, M.L.H.; Claridge, J.B. Methane oxyforming for synthesis gas production. Catal. Rev. 2007, 49, 511–560. [Google Scholar] [CrossRef]
- Knacke, O.; Kubaschewski, O.; Hesselmann, K. Thermochemical Properties of Inorganic Substaces; Springer: Berlin, Germany, 1991. [Google Scholar]
- Toop, G.W. Predicting ternary activities using binary data. Trans. Metall. Soc. AIME 1965, 233, 850–855. [Google Scholar]
- Kohler, F. Estimation of the thermodynamic data for a ternary system from the corresponding binary systems. Monatsh. Chem. 1960, 91, 738–740. [Google Scholar] [CrossRef]
- Muggianu, Y.M.; Gambino, M.; Bros, J.P. Enthalpies de formation des alliages liquides bismuth-étain-gallium à 723 K. Choix d’une représentation analytique des grandeurs d’excès intégrales et partielles de mélange. J. Chim. Phys. 1975, 72, 83–88. [Google Scholar] [CrossRef]
- Hillert, M. Empirical methods of predicting and representing thermodynamic properties of ternary solution phases. Calphad 1980, 4, 1–12. [Google Scholar] [CrossRef]
- Pelton, A.D.; Blander, M. Thermodynamic analysis of ordered liquid solutions by a modified quasichemical approach—Application to silicate slags. Metall. Mater. Trans. B 1986, 17, 805–815. [Google Scholar] [CrossRef]
- Chartrand, P.; Pelton, A.D. On the choice of “geometric” thermodynamic models. J. Phase Equilibria 2000, 21, 141–147. [Google Scholar] [CrossRef]
- Pelton, A.D. A general “geometric” thermodynamic model for multicomponent solutions. Calphad 2001, 25, 319–328. [Google Scholar] [CrossRef]


| j | Reaction | |
|---|---|---|
| 1 | CH4(g) + H2O(g) ↔ CO(g) + 3H2(g) | 2 |
| 2 | CO(g) + H2O(g)↔ CO2(g) + H2(g) | 0 |
| 3 | CH4(g) + CO2(g) ↔ 2CO(g) + 2H2(g) | 2 |
| i = 1,…,5 | j = 1 | j = 2 | j = 3 |
| H2 | |||
| CO | |||
| H2O | |||
| CO2 | |||
| CH4 | |||
| j | Reaction | |||
|---|---|---|---|---|
| 5 | ||||
| 6 | ||||
| [J/mol], R = 8.314 [J/mol K] | ||||
| t | y[C] | y[C] (22) | y[C] Toop (20) | ||||
|---|---|---|---|---|---|---|---|
| 0.00 | 0.450 | 0.550 | 0.4500 | 0.0000 | 1.222 | 0.4505 | 0.4500 |
| 0.02 | 0.465 | 0.535 | 0.4557 | 0.0093 | 1.174 | 0.4615 | 0.4610 |
| 0.05 | 0.480 | 0.520 | 0.4560 | 0.0240 | 1.140 | 0.4780 | 0.4775 |
| 0.10 | 0.505 | 0.495 | 0.4545 | 0.0505 | 1.089 | 0.5054 | 0.5050 |
| 0.20 | 0.555 | 0.445 | 0.4440 | 0.1110 | 1.002 | 0.5604 | 0.5600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaczmarczyk, R. Thermodynamic Analysis of the Effect of Green Hydrogen Addition to a Fuel Mixture on the Steam Methane Reforming Process. Energies 2021, 14, 6564. https://doi.org/10.3390/en14206564
Kaczmarczyk R. Thermodynamic Analysis of the Effect of Green Hydrogen Addition to a Fuel Mixture on the Steam Methane Reforming Process. Energies. 2021; 14(20):6564. https://doi.org/10.3390/en14206564
Chicago/Turabian StyleKaczmarczyk, Robert. 2021. "Thermodynamic Analysis of the Effect of Green Hydrogen Addition to a Fuel Mixture on the Steam Methane Reforming Process" Energies 14, no. 20: 6564. https://doi.org/10.3390/en14206564
APA StyleKaczmarczyk, R. (2021). Thermodynamic Analysis of the Effect of Green Hydrogen Addition to a Fuel Mixture on the Steam Methane Reforming Process. Energies, 14(20), 6564. https://doi.org/10.3390/en14206564







