The Corona Phenomenon in Overhead Lines: Critical Overview of Most Common and Reliable Available Models
Abstract
:1. Introduction
2. Main Corona Effects
2.1. Luminosity
2.2. Audible Noise
2.3. Radio Interference
3. Corona Inception and Development
3.1. Microscopic Level
DC, AC, Impulse Corona
- Negative DC corona: when a negative polarity voltage close to the inception value is applied, negative corona starts in the form of current pulses, known as “Trichel pulses”; the pulses’ frequency increases with the increasing value of the applied voltage. The intermittent nature of these localised discharges is related to the space charge, which contribute to weaken the electric field in the electrode proximity (holding back the pulses) and to subsequent space charge removal. Further increase in the voltage leads to a pulseless glow, which may turn into negative streamers of growing length if the voltage reaches values close to the insulation breakdown [13].
- Positive DC corona: from experimental data [29], the inception voltage for positive DC corona is slightly lower, compared to negative DC corona. According to [28], this is reasonably due to the electrons being accelerated in the direction of the increasing electric field, i.e., towards the anode, facilitating ionization processes. Mixed opinions may be found in the literature on this subject; for instance, in [13], corona discharge due to negative polarity applied voltages is stated to occur at lower field values, with respect to positive polarity (the difference being enhanced when sharp-shaped electrodes are considered). This is in accordance with experimental values found in [30], and with values for the critical corona onset gradient in [31]. However, it is shared opinion that experimental activities aimed at assessing the corona onset field are strongly dependent on atmospherical conditions, humidity, configuration and available free charges in the vicinity of the conductor under test. Fundamental steps in the study of positive DC corona are found in [32]. It first develops in the form of burst pulses; depending on the electrode radius, gap length and magnitude of the applied voltage, some onset streamers may be produced as well, reaching larger radial distances from the electrode and being choked off by negative ions in the gap. Increasing voltage and higher densities of negative space charge suppress the onset streamers in favor of a diffused glow in the proximity of the anode (Hermstein’s glow); streamers finally causing the insulation breakdown are observed at higher voltages, developing from the glow region [28].
- AC corona: when a sinusoidal voltage source triggers corona, combined modes typical of positive and negative DC corona may be observed. In particular, a critical distance can be introduced, depending on the voltage peak value and frequency, accounting for the path covered by the charge particles during the quarters of periods from the voltage peaks to zero crossings; if the critical distance is such that no residual space charge is left by the end of the half period (i.e., suitable time has passed for the ions to migrate toward the electrode of opposite polarity and being neutralized), corona modes in the positive and negative half cycles are expected to be equal to the DC modes with corresponding polarity. Otherwise, the residual space charge will influence the development of the corona modes during the subsequent half-cycle with opposite polarity [28].
- Impulse corona: with fast front voltages, corona mainly develops in the streamer mode, being the role played by the space charge limited by its slower dynamics [33].
3.2. Macroscopic Level
3.3. Inception Criterion
3.3.1. Inception Field by Peek
3.3.2. Inception Field by Olsen and Yamazaki
3.3.3. Inception Field by Mikropoulos and Zagkanas
3.4. Role of the Irregularity Factor: Stranded Conductors and Bundles
3.4.1. Stranded Conductors
3.4.2. Bundles
4. Models for Corona Simulation
4.1. FEM Models
4.2. Physics-Based Models
4.2.1. Correia de Barros’ Model
4.2.2. Malik’s Model
4.2.3. Cooray’s Model
4.3. Empirical Models
4.3.1. Inoue’s Model
4.3.2. Gary’s Model
4.3.3. Podporkin and Sivaev’s Model
4.3.4. Suliciu’s Model
4.3.5. CIGRÉ Model
4.4. Circuit-Based Models
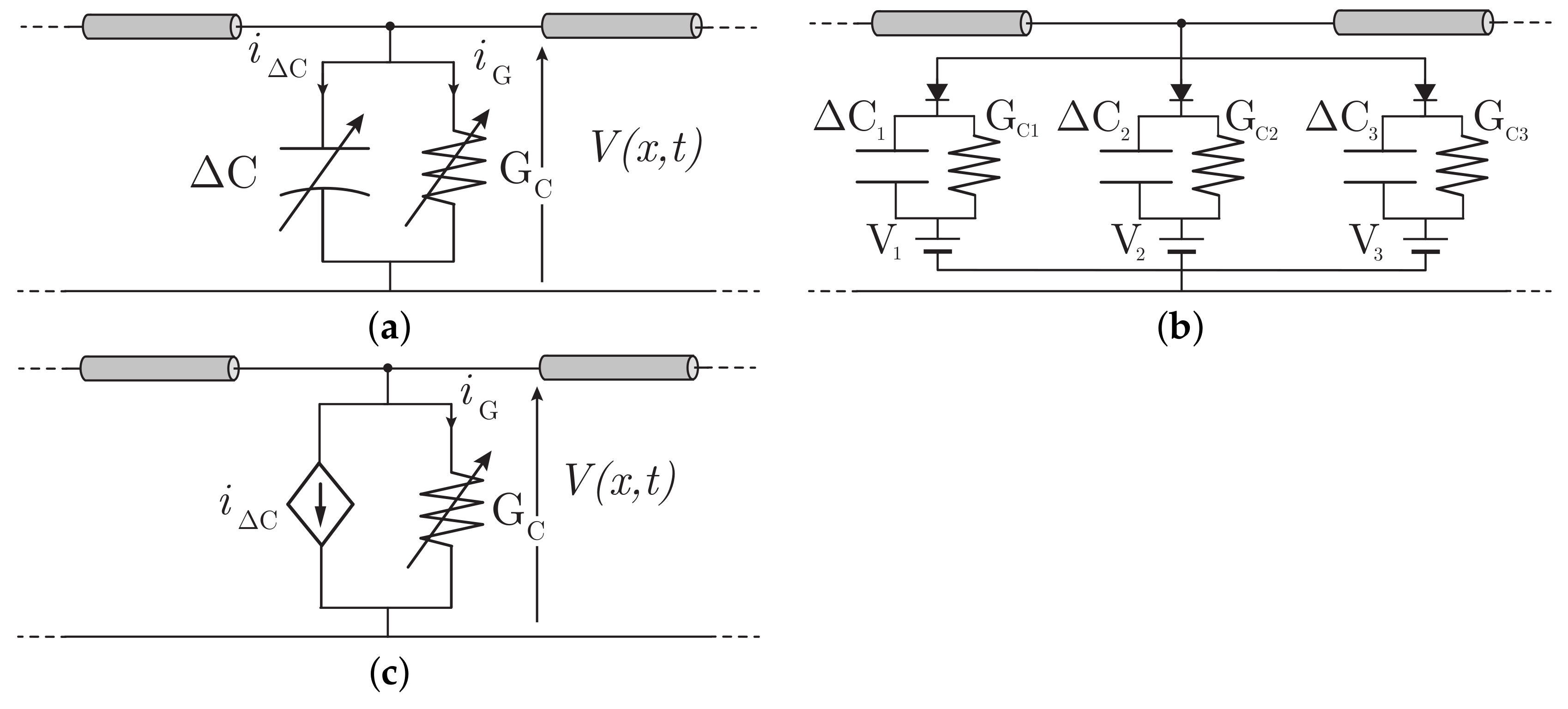
4.4.1. Hara and Umoto’s Model
4.4.2. Motoyama and Ametani’s Model
4.4.3. Maccioni-Araneo et al. Model
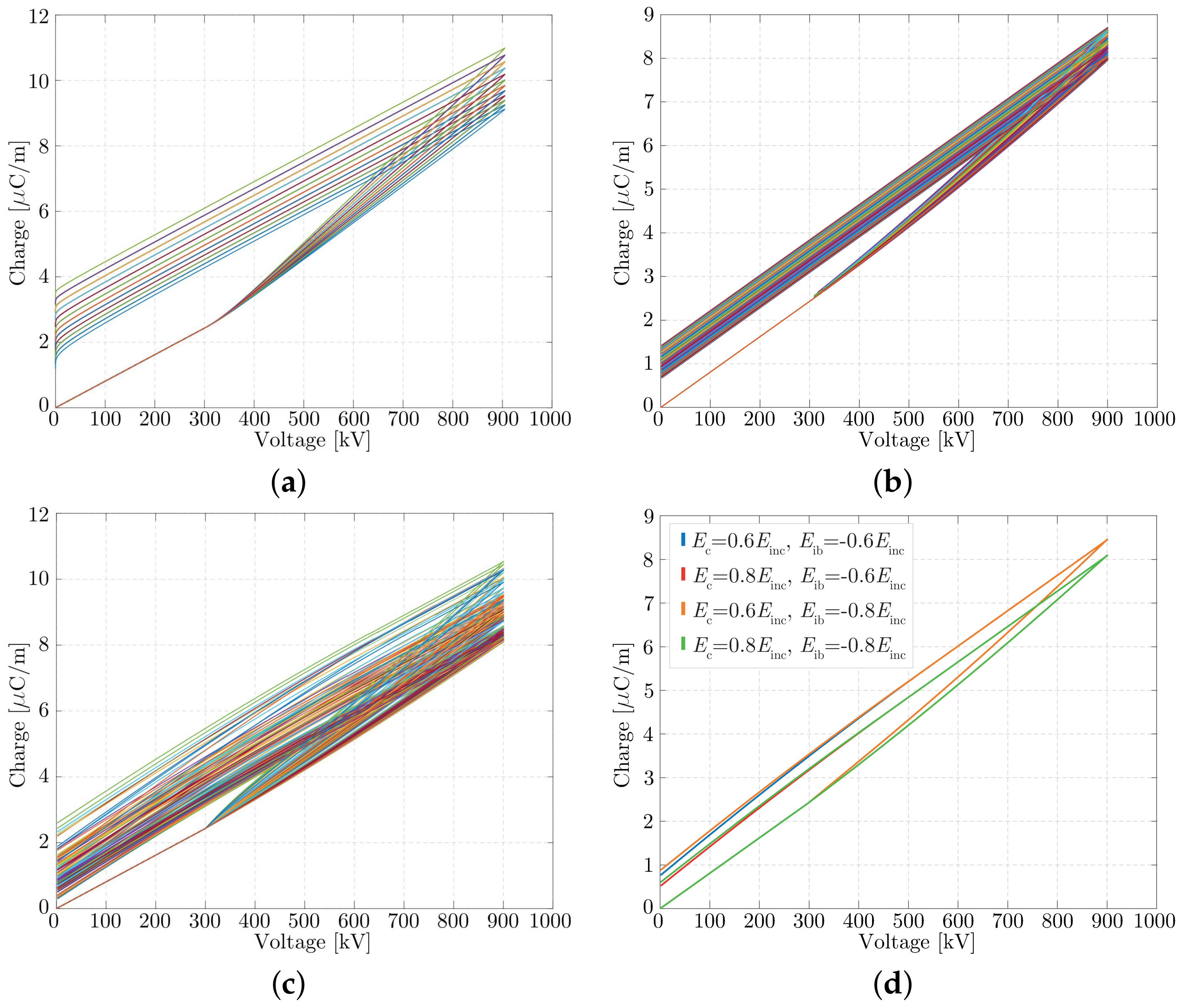
5. Results: Comparison of the Models Responses to the Variability of Input Parameters
5.1. Sensitivity Curves for Physics-Based Models
5.2. Sensitivity Curves for Empirical Models
5.3. Sensitivity Curves for Circuit-Based Models
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Laplante, P.A. Electrical Engineering Dictionary; CRC Press LLC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Gallimberti, I. The mechanism of the long spark formation. J. Phys. Colloq. 1979, 40, C7-193. [Google Scholar]
- Faraday, M. VIII. Experimental Researches in Electricity—Thirteenth Series; Philosophical Transactions of the Royal Society of London: London, UK, 1838; pp. 125–168. [Google Scholar]
- Peek, F.W. The law of corona and the dielectric strength of air. Proc. Am. Inst. Electr. Eng. 1911, 30, 1485–1561. [Google Scholar]
- Peek, F.W. The law of corona and dielectric strength of air—II. Proc. Am. Inst. Electr. Eng. 1912, 31, 1085–1126. [Google Scholar] [CrossRef]
- Peek, F.W. Dielectric Phenomena in High Voltage Engineering; McGraw-Hill Book Company, Incorporated: London, UK, 1920. [Google Scholar]
- Rizk, F.A.; Trinh, G.N. High Voltage Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Goldman, M.; Goldman, A.; Sigmond, R. The corona discharge, its properties and specific uses. Pure Appl. Chem. 1985, 57, 1353–1362. [Google Scholar] [CrossRef] [Green Version]
- Gary, C.; Moreau, M. L’Effet de Couronne en Tension Alternative; Collection de la Direction des Etudes et Recherches d’Electricité de France: Paris, France, 1976. [Google Scholar]
- Riba, J.R.; Larzelere, W.; Rickmann, J. Voltage correction factors for air-insulated transmission lines operating in high-altitude regions to limit corona activity: A review. Energies 2018, 11, 1908. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, K.; Olsen, R.G. Application of a corona onset criterion to calculation of corona onset voltage of stranded conductors. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 674–680. [Google Scholar]
- Bousiou, E.I.; Mikropoulos, P.N.; Zagkanas, V.N. Experimental Investigation of the Overvoltage Steepness Effects on Corona Inception Characteristics. In The International Symposium on High Voltage Engineering; Springer: Cham, Switzerland, 2019; pp. 1413–1422. [Google Scholar]
- Lings, R. EPRI AC Transmission Line Reference Book: 200 KV and Above, 3rd ed.; Electric Power Research Institute: Palo Alto, CA, USA, 2005. [Google Scholar]
- Wagner, C.F.; Lloyd, B.L. Effects of corona on traveling waves. Electr. Eng. 1955, 74, 1071. [Google Scholar] [CrossRef]
- Krzewiński, S.; Frącz, P.; Urbaniec, I.; Turba, T. Comparative analysis of optical signals emitted by corona on a laboratory model of transmission lines made of various materials. J. Spectrosc. 2017, 2017, 8423797. [Google Scholar]
- Tyler, N.J.; Stokkan, K.A.; Hogg, C.R.; Nellemann, C.; Vistnes, A.I. Cryptic impact: Visual detection of corona light and avoidance of power lines by reindeer. Wildl. Soc. Bull. 2016, 40, 50–58. [Google Scholar] [CrossRef] [Green Version]
- Engel, Z.; Wszołek, T. Audible noise of transmission lines caused by the corona effect: Analysis, modelling, prediction. Appl. Acoust. 1996, 47, 149–163. [Google Scholar] [CrossRef]
- IEEE Std 430-2017. IEEE Standard Procedures for the Measurement of Radio Noise from Overhead Power Lines and Substations; Revision of IEEE Std 430-1986; IEEE Standards Association: Piscataway, NJ, USA, 2017; pp. 1–34. [Google Scholar]
- IEC. CISPR TR 18-1 Radio Interference Characteristics of Overhead Power Lines and High-Voltage Equipment—Part 1: Description of Phenomena; IEC: Geneva, Switzerland, 2017. [Google Scholar]
- CIGRE. Guide for Measurement of Radio Frequency Interference from HV and MV Substations; CIGRE Technical Brochure 391; CIGRE: Paris, France, 2009. [Google Scholar]
- Liu, Z. Ultra-High Voltage AC/DC Grids; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Donini, A.; Spezie, R.; Cortina, R.; Piana, E.A.; Turri, R. Accurate prediction of the corona noise produced by overhead transmission lines. In Proceedings of the AEIT International Annual Conference, Capri, Italy, 5–7 October 2016; pp. 1–6. [Google Scholar]
- Adamiak, K.; Atrazhev, V.; Atten, P. Corona discharge in the hyperbolic point-plane configuration: Direct ionization criterion versus an approximate formulations. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 1015–1024. [Google Scholar] [CrossRef]
- Townsend, J.S. Electricity in gases; Clarendon Press: New York, NY, USA, 1915. [Google Scholar]
- Georghiou, G.E.; Papadakis, A.; Morrow, R.; Metaxas, A. Numerical modelling of atmospheric pressure gas discharges leading to plasma production. J. Phys. Appl. Phys. 2005, 38, R303. [Google Scholar] [CrossRef]
- Wadhwa, C. High Voltage Engineering; New Age International: New Delhi, India, 2006. [Google Scholar]
- Raizer, Y.P.; Allen, J.E. Gas Discharge Physics; Springer: Berlin, Germany, 1997; Volume 2. [Google Scholar]
- Giao, T.N.; Jordan, J.B. Modes of corona discharges in air. IEEE Trans. Power App. Syst. 1968, 5, 1207–1215. [Google Scholar] [CrossRef]
- Bousiou, E.I.; Mikropoulos, P.N.; Zagkanas, V.N. Experimental investigation of negative DC corona on conductor bundles: A comparison with positive corona. In Proceedings of the 2017 52nd International Universities Power Engineering Conference (UPEC), Heraklion, Greece, 28–31 August 2017; pp. 1–5. [Google Scholar]
- Mikropoulos, P.; Zagkanas, V.; Koustoulidis, T. Experimental investigation of DC corona on stranded conductors under variable air density. In Proceedings of the 2012 47th International Universities Power Engineering Conference (UPEC), Uxbridge, UK, 4–7 September 2012; pp. 1–6. [Google Scholar]
- CIGRE. Addendum to Doc. 20: Interferences Produced by Corona Effect of Electric Systems; CIGRE: Paris, France, 1966. [Google Scholar]
- Loeb, L.B. Electrical Coronas, Their Basic Physical Mechanisms; University of California Press: Berkeley, CA, USA, 1965. [Google Scholar]
- Abdel-Salam, M. High-Voltage Engineering: Theory and Practice, Revised and Expanded; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Baldo, G.; Gallimberti, I.; Garcia, H.; Hutzler, B.; Jouaire, J.; Simon, M. Breakdown phenomena of long gaps under switching impulse conditions influence of distance and voltage level. IEEE Trans. Power App. Syst. 1975, 94, 1131–1140. [Google Scholar] [CrossRef]
- Correia de Barros, M.T. Efeito Coroa em Linhas de Transporte de Energia. Ph.D. Thesis, IST-Tecnical University of Lisbon, Lisbon, Portugal, 1985. [Google Scholar]
- Maruvada, P.S.; Menemenlis, H.; Malewski, R. Corona characteristics of conductor bundles under impulse voltages. IEEE Trans. Power App. Syst. 1977, 96, 102–115. [Google Scholar] [CrossRef]
- Mikropoulos, P.N.; Zagkanas, V.N. Impulse corona inception in the coaxial cylindrical electrode arrangement in air: Effects of the steepness of the applied voltage. In Proceedings of the 18th International Symposium on High Voltage Engineering, Seoul, Korea, 25–30 August 2013. [Google Scholar]
- Bousiou, E.I.; Mikropoulos, P.N.; Zagkanas, V.N. Corona inception field of typical overhead line conductors under variable atmospheric conditions. Electr. Power Syst. Res. 2020, 178, 106032. [Google Scholar] [CrossRef]
- Mikropoulos, P.N.; Zagkanas, V.N. Threshold inception conditions for positive DC corona in the coaxial cylindrical electrode arrangement under variable atmospheric conditions. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 278–286. [Google Scholar] [CrossRef]
- Maruvada, P.S.; Janischewskyj, W. DC corona on smooth conductors in air. Steady-state analysis of the ionisation layer. Proc. Inst. Electr. Eng. 1969, 116, 161–166. [Google Scholar]
- Baker, A.; Comber, M.; Ottosen, K. Investigation of the corona performance of conductor bundles for 800-kV transmission. IEEE Trans. Power App. Syst. 1975, 94, 1117–1130. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y. Experimental investigation and modeling of corona characteristics under lightning impulses. J. Electrost. 2017, 90, 85–90. [Google Scholar] [CrossRef]
- Stone, L.N. EHV single and twin bundle conductors-influence of conductor diameter and strand diameter on radio influence voltage and corona initiation voltage. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1959, 78, 1434–1438. [Google Scholar] [CrossRef]
- El-Bahy, M.M.; Abouelsaad, M.; Abdel-Gawad, N.; Badawi, M.; El-Bahy, M.M.; Abouelsaad, M.; Abdel-Gawad, N.; Badawi, M. Onset voltage of negative corona on stranded conductors. J. Phys. D Appl. Phys. 2007, 40, 3094. [Google Scholar] [CrossRef]
- Abou-Seada, M.S. Digital Computer Calculation of Corona Thresholds in Nonuniform Fields. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 1970. [Google Scholar]
- Bousiou, E.I.; Mikropoulos, P.N.; Zagkanas, V.N. Experimental investigation of positive DC corona on conductor bundles. In Proceedings of the 2016 51st International Universities Power Engineering Conference (UPEC), Coimbra, Portugal, 6–9 September 2016; pp. 1–5. [Google Scholar]
- Maruvada, P.S. A survey of methods for calculating transmission line conductor surface voltage gradients. IEEE Trans. Power App. Syst. 1979, 6, 1996–2014. [Google Scholar]
- Alessandrini, V.; Fanchiotti, H.; Canal, C.G.; Vucetich, H. Exact solution of electrostatic problem for a system of parallel cylindrical conductors. J. Appl. Phys. 1974, 45, 3649–3661. [Google Scholar] [CrossRef]
- Durbin, P.A.; Turyn, L. Analysis of the positive DC corona between coaxial cylinders. J. Phys. Appl. Phys. 1987, 20, 1490–1495. [Google Scholar] [CrossRef]
- Monrolin, N.; Praud, O.; Plouraboué, F. Revisiting the positive DC corona discharge theory: Beyond Peek’s and Townsend’s law. Phys. Plasmas 2018, 25, 063503. [Google Scholar] [CrossRef] [Green Version]
- Stracqualursi, E.; Araneo, R.; Andreotti, A. The Impact of Different Corona Models on FD Algorithms for the Solution of Multiconductor Transmission Lines Equations. High Volt. 2021, 1–14. [Google Scholar] [CrossRef]
- Correia de Barros, M.T. Identification of the capacitance coefficients of multiphase transmission lines exhibiting corona under transient conditions. IEEE Trans. Power Del. 1995, 10, 1642–1648. [Google Scholar] [CrossRef]
- De Jesus, C.; Correia de Barros, M.T. Modelling of corona dynamics for surge propagation studies. IEEE Trans. Power Del. 1994, 9, 1564–1569. [Google Scholar] [CrossRef]
- Correia de Barros, M.T.; De Jesus, C. Wide bandwidth modeling of corona on high voltage transmission lines. Annu. Rep. Conf. Electr. Insul. Dielectr. Phenom. 1993, 1, 846. [Google Scholar]
- Huang, K.; Zhang, X.; Xiao, X. Modelling of the corona characteristics under damped oscillation impulses. IET Gener. Transm. Distrib. 2016, 10, 1648–1653. [Google Scholar] [CrossRef]
- Li, X.R.; Malik, O.P.; Zhao, Z.D. A Practical Mathematical Model of Corona for Calculation of Transients on Transmission Lines. IEEE Power Eng. Rev. 1989, 9, 75. [Google Scholar] [CrossRef]
- Ganesan, L.; Thomas, M.J. Studies on the influence of corona on overvoltage surges. Electr. Power Syst. Res. 2000, 53, 97–103. [Google Scholar] [CrossRef]
- Anane, Z.; Bayadi, A.; Huang, K. Distortion phenomena on transmission lines using corona modeling ATP/EMTP. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 383–389. [Google Scholar] [CrossRef]
- Cooray, V. Charge and voltage characteristics of corona discharges in a coaxial geometry. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 734–743. [Google Scholar] [CrossRef]
- Evans, J.L.; Thomas, D.W.; Greedy, S. Modeling the influence of corona discharge on High-Voltage surges propagating along Transmission-Lines using TLM. In Proceedings of the 2015 IEEE International Symposium on Electromagnetic Compatibility (EMC), Dresden, Germany, 16–22 August 2015; pp. 981–986. [Google Scholar]
- Inoue, A. Propagation analysis of overvoltage surges with corona based upon charge versus voltage curve. IEEE Trans. Power App. Syst. 1985, 3, 655–662. [Google Scholar] [CrossRef]
- Gary, C.; Dragan, G.; Langu, I. Impulse corona discharge energy around the conductors. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Seattle, WA, USA, 7–12 October 1990; Volume 1, pp. 922–924. [Google Scholar]
- Podporkin, G.V.; Sivaev, A.D. Lightning impulse corona characteristics of conductors and bundles. IEEE Trans. Power Del. 1997, 12, 1842–1847. [Google Scholar] [CrossRef]
- Mihailescu-Suliciu, M.; Suliciu, I. A Rate Type Constitutive Equation for the Description of the Corona Effect. IEEE Trans. Power App. Syst. 1981, PAS-100, 3681–3685. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, X.; Tao, S. Electromagnetic Transient Analysis of Overhead Lines Including Corona and Frequency-Dependence Effects Under Damped Oscillation Surges. IEEE Trans. Power Del. 2018, 33, 2198–2206. [Google Scholar] [CrossRef]
- CIGRE. Guide to Procedures for Estimating the Lightning Performance of Transmission Lines; CIGRE SC33. 10; CIGRE: Paris, France, 1991. [Google Scholar]
- Imece, A.F.; Durbak, D.W.; Elahi, H. Modeling guidelines for fast front transients. IEEE Trans. Power Del. 1996, 11, 493–506. [Google Scholar]
- Umoto, J.; Hara, T. Numerical analysis of surge propagation on single-conductor systems considering corona losses. Electr. Eng. Japan 1969, 89, 21–728. [Google Scholar]
- Lee, K.C. Non-Linear Corona Models in an Electromagnetic Transients Program (EMTP). IEEE Trans. Power App. Syst. 1983, PAS-102, 2936–2942. [Google Scholar] [CrossRef]
- Motoyama, H.; Ametani, A. Development of a linear model for corona wave deformation and its effects on lightning surges. Electr. Eng. Japan 1987, 107, 98–106. [Google Scholar] [CrossRef]
- Araneo, R.; Maccioni, M.; Lauria, S.; Geri, A.; Gatta, F.M.; Celozzi, S. Comparison of corona models for computing the surge propagation in multiconductor power lines. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar]
- Guan, Y.; Vaddi, R.S.; Aliseda, A.; Novosselov, I. Analytical model of electro-hydrodynamic flow in corona discharge. Phys. Plasmas 2018, 25, 083507. [Google Scholar] [CrossRef]
- Janischewskyj, W.; Gela, G. Finite element solution for electric fields of coronating DC transmission lines. IEEE Trans. Power App. Syst. 1979, 3, 1000–1012. [Google Scholar] [CrossRef]
- Jin, J.M. The Finite Element Method in Electromagnetics; Wiley-IEEE Press: Hoboken, NJ, USA, 2014. [Google Scholar]
- Lu, T.; Feng, H.; Cui, X.; Zhao, Z.; Li, L. Analysis of the ionized field under HVDC transmission lines in the presence of wind based on upstream finite element method. IEEE Trans. Magn. 2010, 46, 2939–2942. [Google Scholar] [CrossRef]
- Johnson, T.; Jakobsson, S.; Wettervik, B.; Andersson, B.; Mark, A.; Edelvik, F. A finite volume method for electrostatic three species negative corona discharge simulations with application to externally charged powder bells. J. Electrost. 2015, 74, 27–36. [Google Scholar] [CrossRef]
- Liu, L. Physics of Electrical Discharge Transitions in Air. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2017. [Google Scholar]
- Zhao, L.; Adamiak, K. EHD flow produced by electric corona discharge in gases: From fundamental studies to applications (a review). Part. Sci. Technol. 2016, 34, 63–71. [Google Scholar] [CrossRef]
- Kaptzov, N.A. Elektrische Vorgänge in Gasen und im Vakuum, 2nd ed.; Hochschulbucher für Physik, Deutscher Verl. der Wissenschaften: Berlin, Germany, 1955. [Google Scholar]
- Riba, J.R.; Morosini, A.; Capelli, F. Comparative study of AC and positive and negative DC visual corona for sphere-plane gaps in atmospheric air. Energies 2018, 11, 2671. [Google Scholar] [CrossRef] [Green Version]
- Sattari, P.; Castle, G.S.P.; Adamiak, K. FEM-FCT-Based Dynamic Simulation of Corona Discharge in Point-Plane Configuration. IEEE Trans. Ind. Appl. 2010, 46, 1699–1706. [Google Scholar] [CrossRef]
- Xiao, F.; Zhang, B. Transient Overvoltage on HVDC Overhead Transmission Lines With Background DC Space Charges and Impulse Corona. IEEE Trans. Power Del. 2021, 36, 2921–2928. [Google Scholar] [CrossRef]
- Adamiak, K. Adaptive approach to finite element modelling of corona fields. IEEE Trans. Ind. Appl. 1994, 30, 387–393. [Google Scholar] [CrossRef]
- Waters, R.; Jones, R. The impulse breakdown voltage and time-lag characteristics of long gaps in air I. The positive discharge. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1964, 256, 185–212. [Google Scholar]
- Nijdam, S.; Teunissen, J.; Ebert, U. The physics of streamer discharge phenomena. Plasma Sources Sci. Technol. 2020, 29, 103001. [Google Scholar] [CrossRef]
- Smythe, W.R. Static and Dynamic Electricity; McGraw-Hill: New York, NY, USA, 1950. [Google Scholar]
- Morrow, R. The theory of positive glow corona. J. Phys. Appl. Phys. 1997, 30, 3099–3114. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Q. Effects of geometrical parameters of two height-unequal adjacent objects on corona discharges from their tips during a thunderstorm. Atmos. Res. 2017, 190, 113–120. [Google Scholar] [CrossRef]
- Gallagher, T.J.; Dudurych, I.M. Model of corona for an EMTP study of surge propagation along HV transmission lines. IEE Proc. C 2004, 151, 61–66. [Google Scholar] [CrossRef]
- Chen, L.; MacAlpine, J.M.K.; Bian, X.; Wang, L.; Guan, Z. Comparison of methods for determining corona inception voltages of transmission line conductors. J. Electrost. 2013, 71, 269–275. [Google Scholar] [CrossRef]
- Carsimamovic, A.; Mujezinovic, A.; Carsimamovic, S.; Bajramovic, Z.; Kosarac, M.; Stankovic, K. Analyzing of AC Corona Discharge Parameters of Atmospheric Air. Procedia Comput. Sci. 2016, 83, 766–773. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Tan, Z.; Li, K. Modified Peek formula for calculating positive DC Corona inception electric field under variable humidity. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1377–1382. [Google Scholar] [CrossRef]
- Leman, J.T.; Olsen, R.G. Bulk FDTD Simulation of Distributed Corona Effects and Overvoltage Profiles for HSIL Transmission Line Design. Energies 2020, 13, 2474. [Google Scholar] [CrossRef]
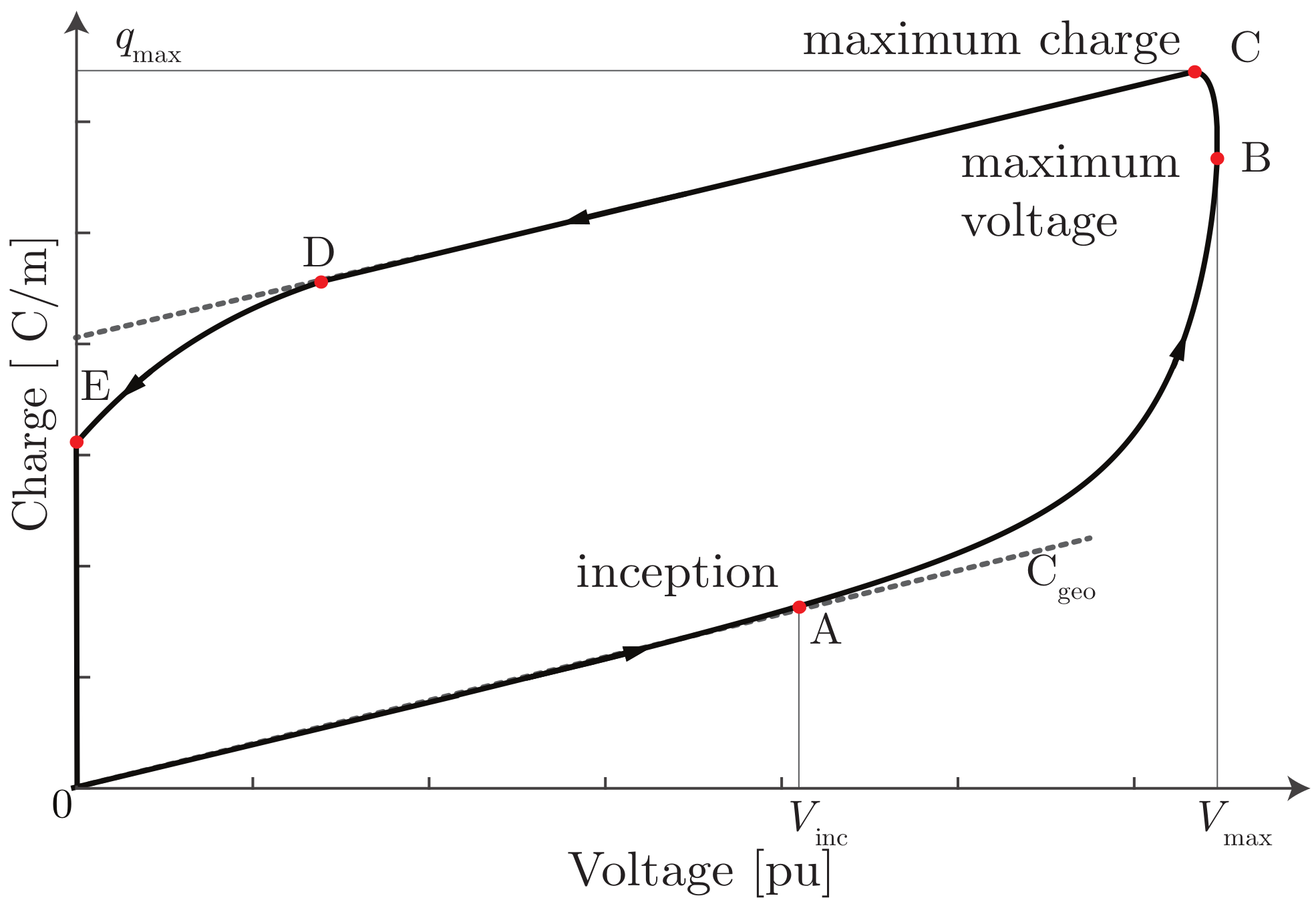
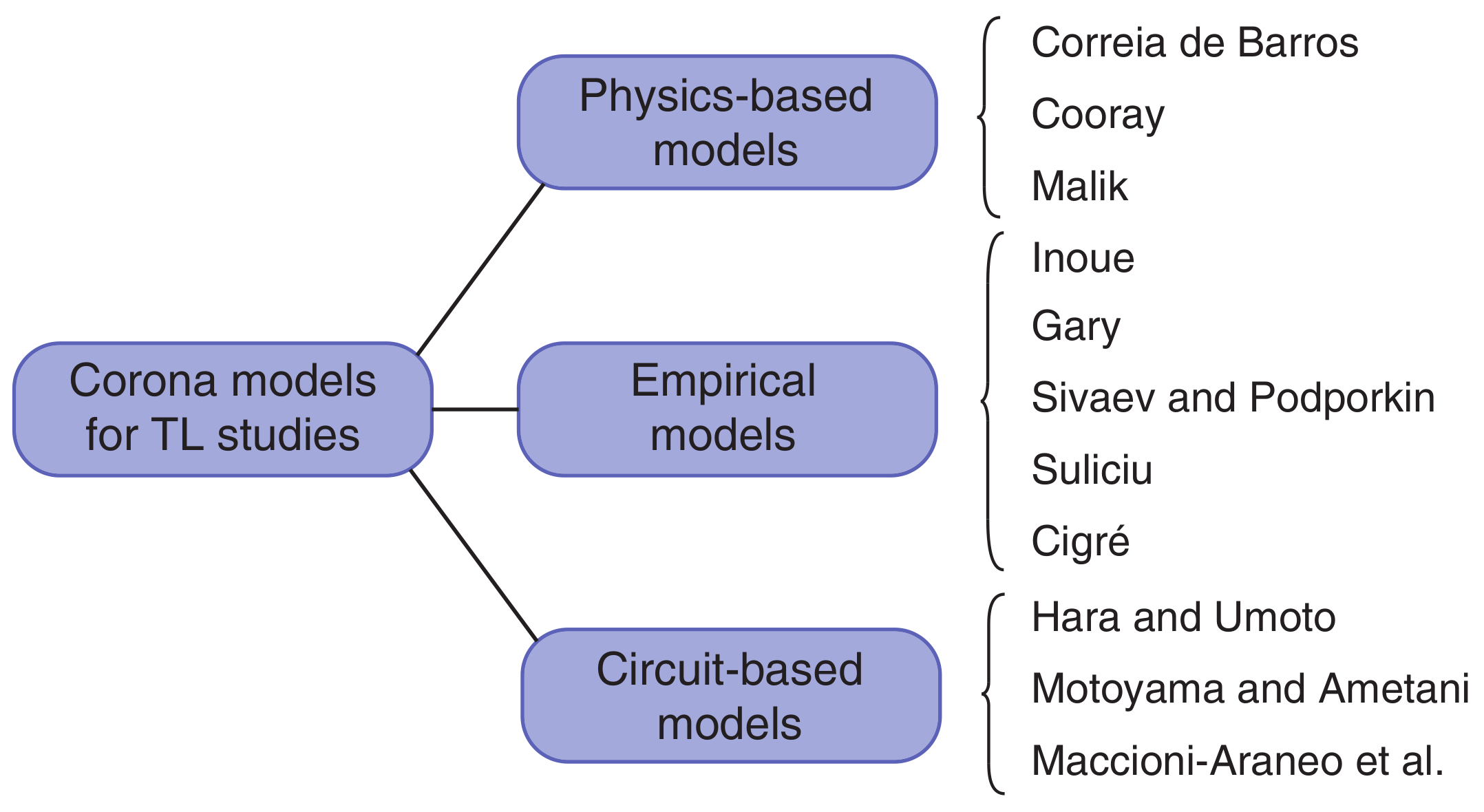
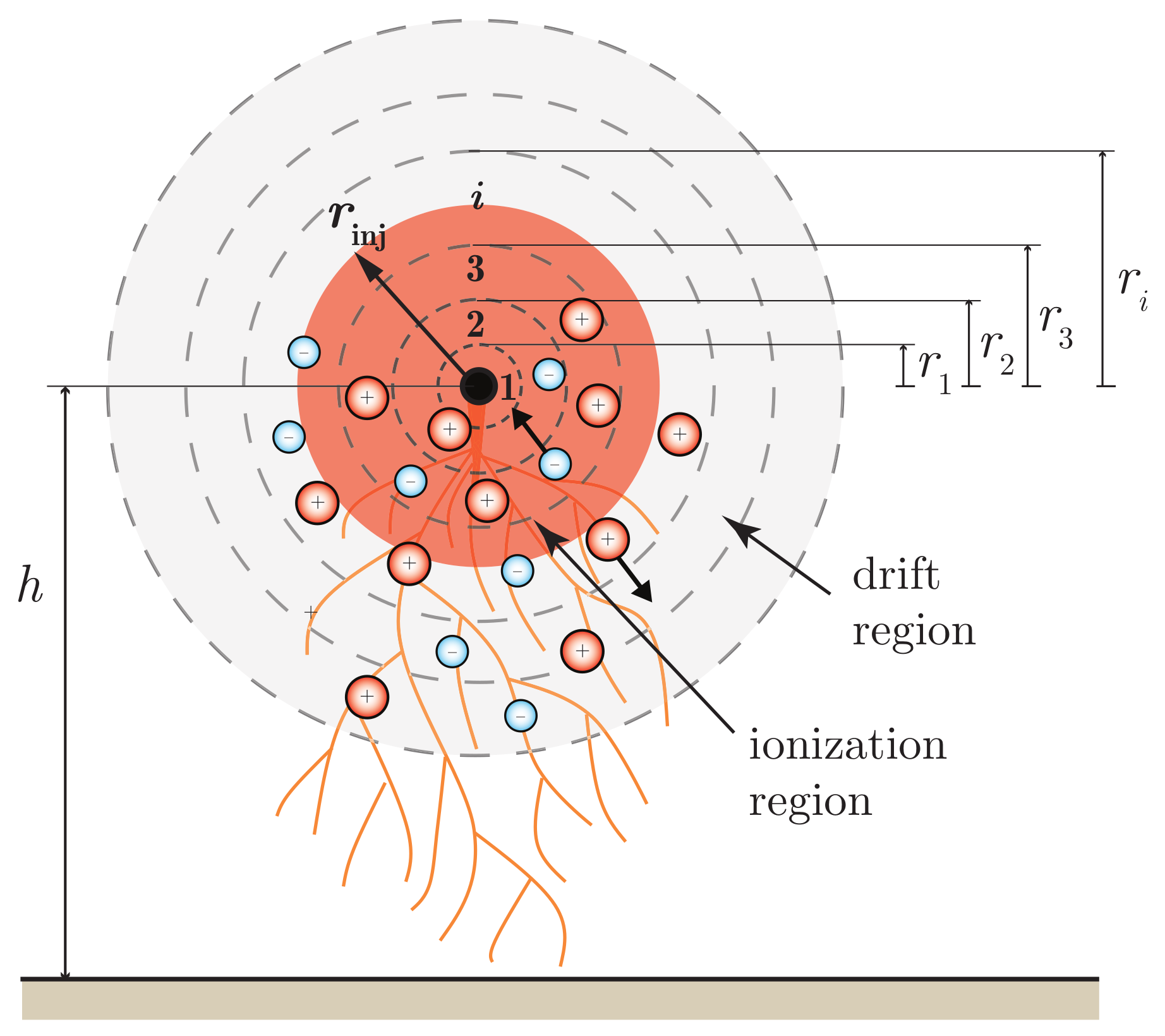
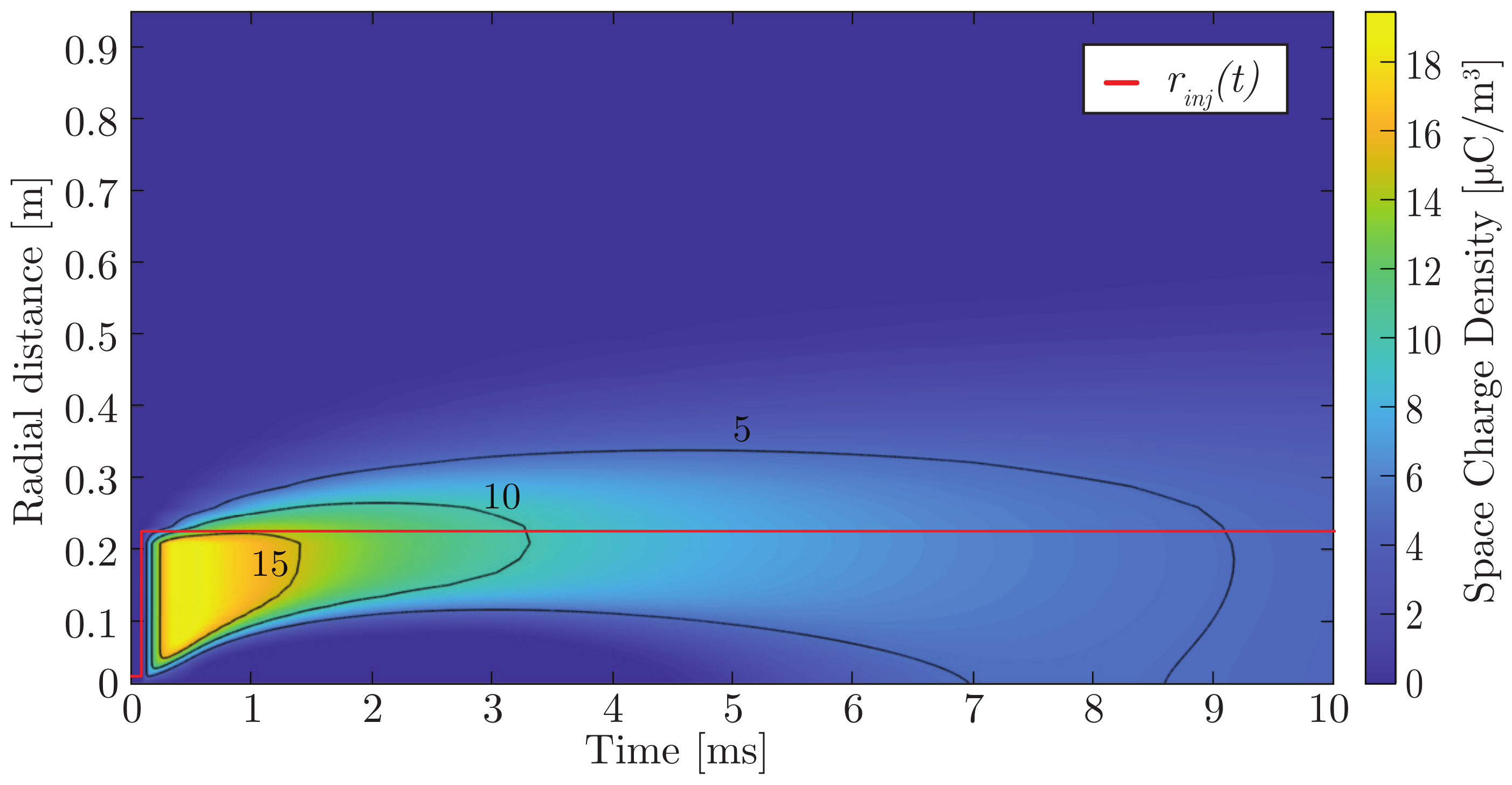


| Model | Ref. | Model Features | Related | |
|---|---|---|---|---|
| Physics-based models | Correia de Barros | [35,52,53,54] | Multi-layer space discretization, solution of drift equations | [55] |
| Malik et al. | [56] | One-layer model with time dependent radius | [57,58] | |
| Cooray | [59] | One-layer model with time dependent radius | [60] | |
| Empirical models | Inoue | [61] | Expression of the corona capacitance | - |
| Gary et al. | [62] | Expression of the total charge | - | |
| Podporkin and Sivaev | [63] | Expression of the total charge | - | |
| Suliciu et al. | [64] | Expression of the corona over-current | [65] | |
| CIGRÉ | [66] | Expression of the corona dynamic capacitance | [67] | |
| Circuit models | Hara and Umoto | [68] | Voltage-dependent shunt capacitor and resistor | [69] |
| Motoyama and Ametani | [70] | Shunt capacitor and resistor, piece-wise constant functions of the voltage | - | |
| Maccioni, Araneo et al. | [71] | Voltage-dependent current generator and shunt resistor | - |
| Parameter | Value |
|---|---|
| R |
| Parameter | Value |
|---|---|
| Parameter | Value |
|---|---|
| < | |
| − |
| Number of Input Parameters | Input Parameters | Applied Voltage Waveform | |
|---|---|---|---|
| Correia de Barros | 4 | , , , | Impulse and AC steady-state voltage |
| Malik et al. | 2 | , | Impulse voltage |
| Cooray et al. | 3 | , , | Impulse voltage |
| Inoue | 2 | , | Impulse voltage |
| Gary et al. | 1 | B | Impulse voltage |
| Podporkin and Sivaev | 3 | , , a | Impulse voltage |
| Suliciu et al. | 4 | , , , | Impulse voltage |
| CIGRÉ | 2 | K, | Impulse voltage |
| Hara and Umoto | 2 | , | Impulse voltage |
| Motoyama and Ametani | 2 | , | Impulse voltage |
| Maccioni, Araneo et al. | 1 | Impulse voltage |
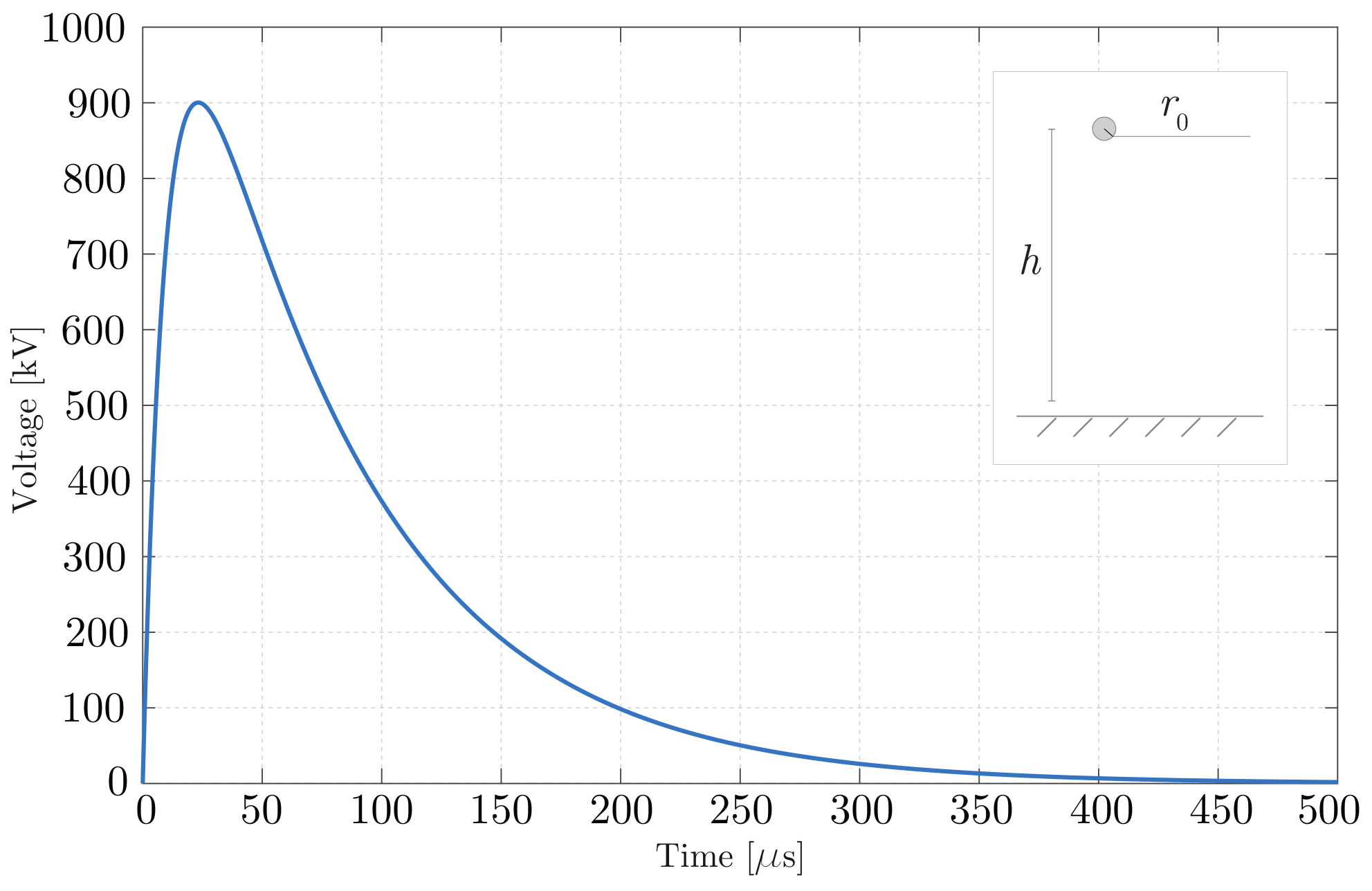
| h | 7.5 m |
| 1.57 cm | |
| 300 kV |
| Advantages | Disadvantages | |
|---|---|---|
| Correia de Barros |
|
|
| Malik |
|
|
| Cooray |
|
|
| Inoue |
|
|
| Gary et al. |
|
|
| Podporkin and Sivaev |
|
|
| Suliciu |
|
|
| CIGRÉ |
|
|
| Hara and Umoto |
|
|
| Motoyama and Ametani |
|
|
| Maccioni, Araneo et al. |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stracqualursi, E.; Araneo, R.; Celozzi, S. The Corona Phenomenon in Overhead Lines: Critical Overview of Most Common and Reliable Available Models. Energies 2021, 14, 6612. https://doi.org/10.3390/en14206612
Stracqualursi E, Araneo R, Celozzi S. The Corona Phenomenon in Overhead Lines: Critical Overview of Most Common and Reliable Available Models. Energies. 2021; 14(20):6612. https://doi.org/10.3390/en14206612
Chicago/Turabian StyleStracqualursi, Erika, Rodolfo Araneo, and Salvatore Celozzi. 2021. "The Corona Phenomenon in Overhead Lines: Critical Overview of Most Common and Reliable Available Models" Energies 14, no. 20: 6612. https://doi.org/10.3390/en14206612








