Parametric Study of a Supercritical CO2 Power Cycle for Waste Heat Recovery with Variation in Cold Temperature and Heat Source Temperature †
Abstract
:1. Introduction
2. System Analysis
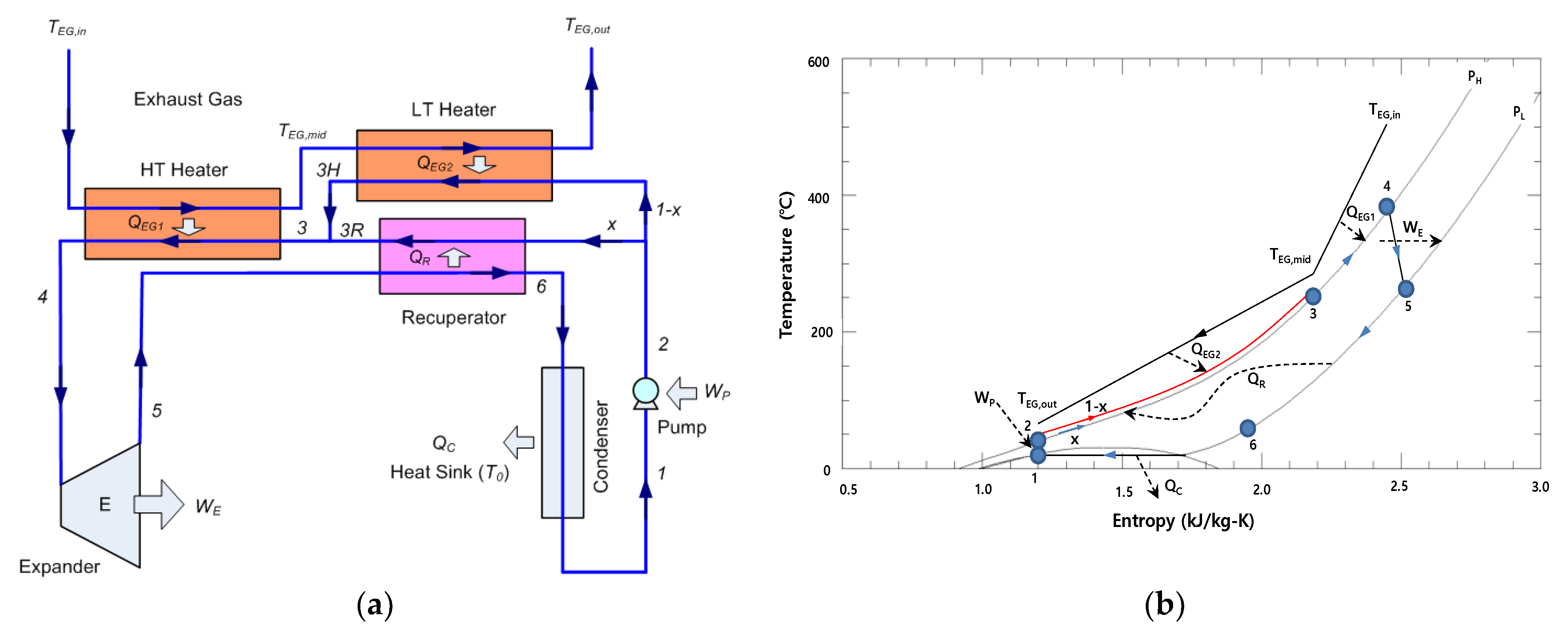
2.1. System Considered in Investigation
2.2. Energy Analysis
3. Split Supercritical CO2 Rankine Cycle for Waste Heat Recovery
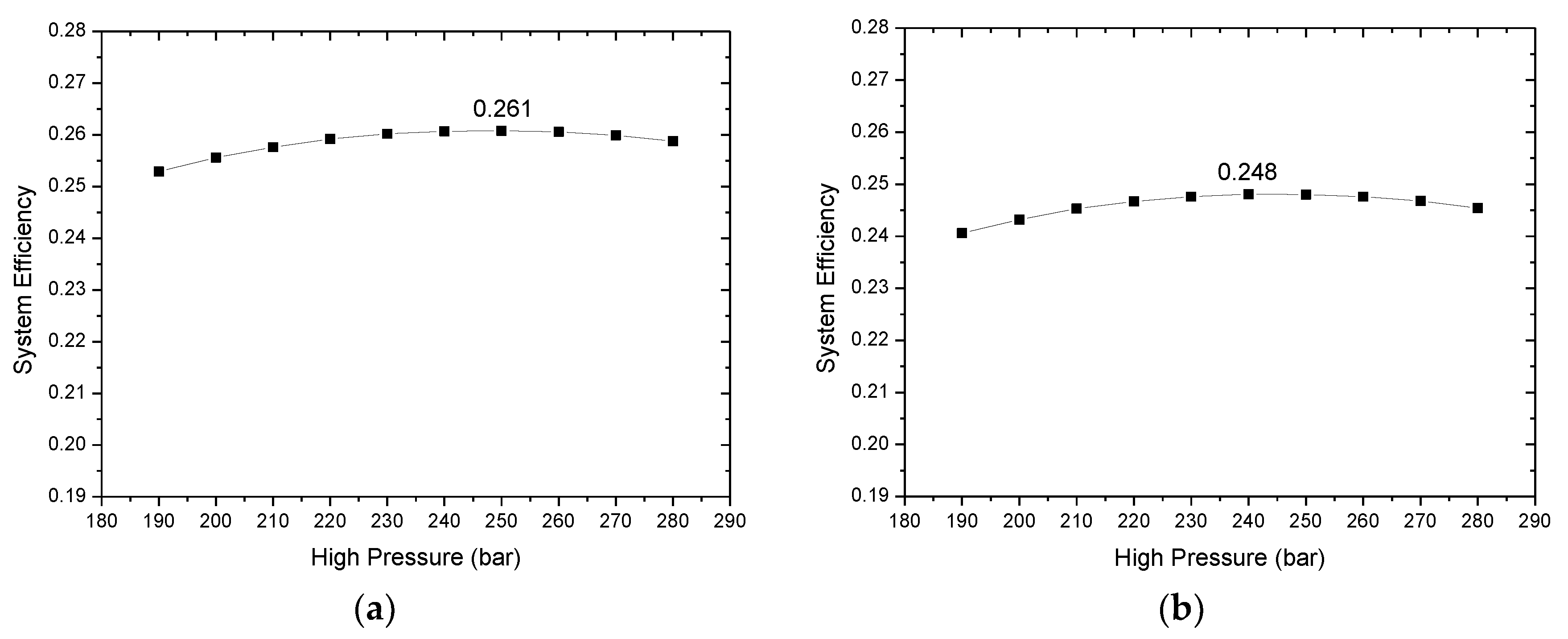
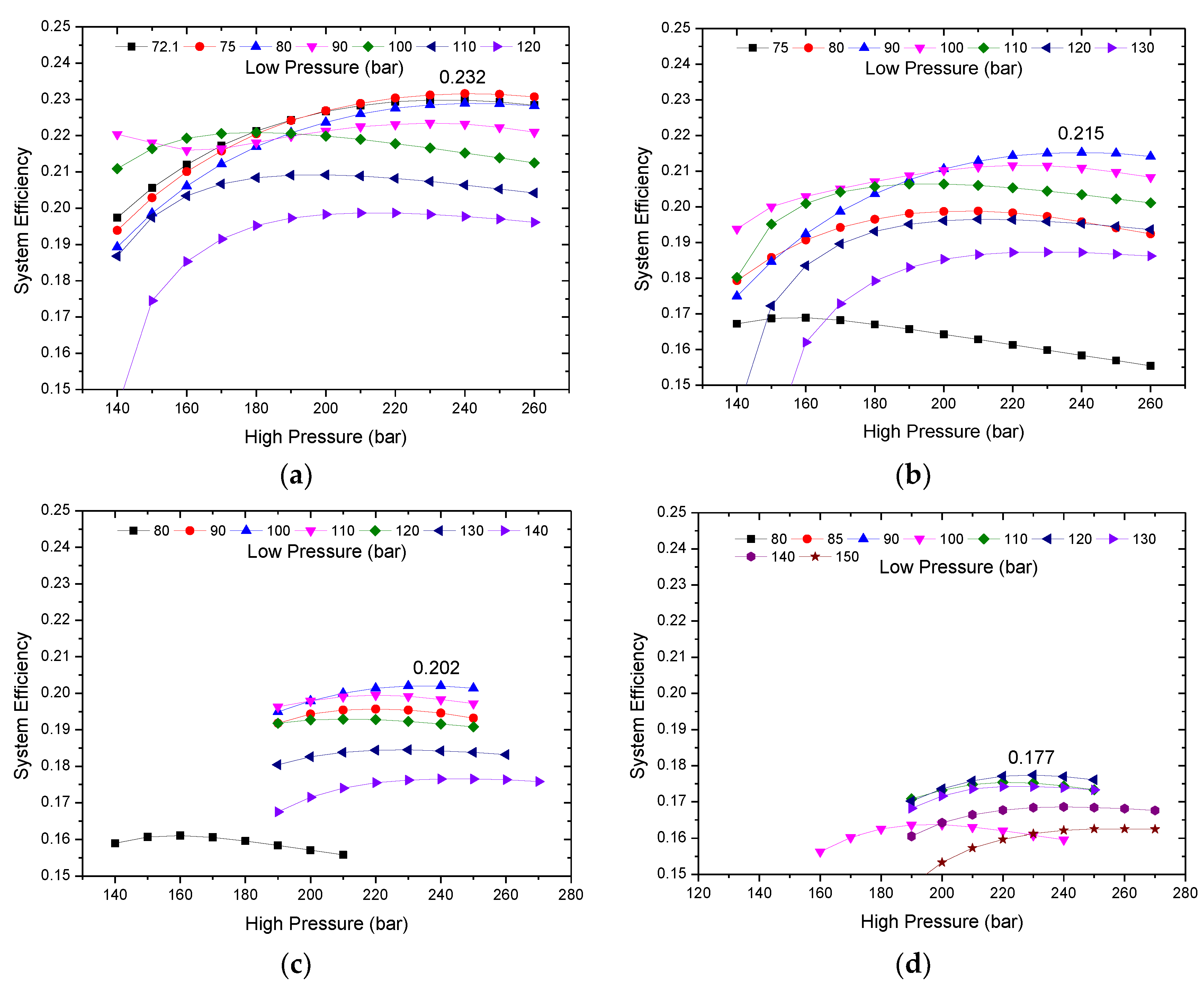
3.1. Parametric Study of Cycle
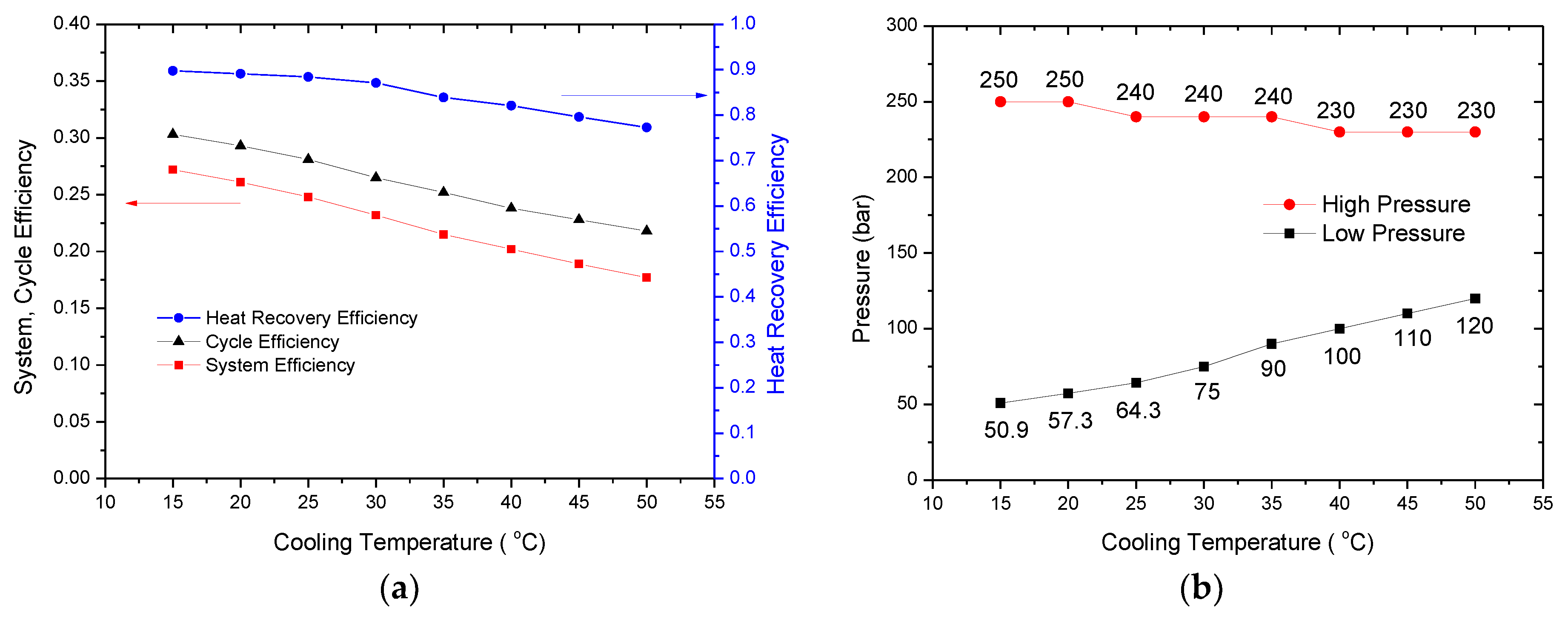
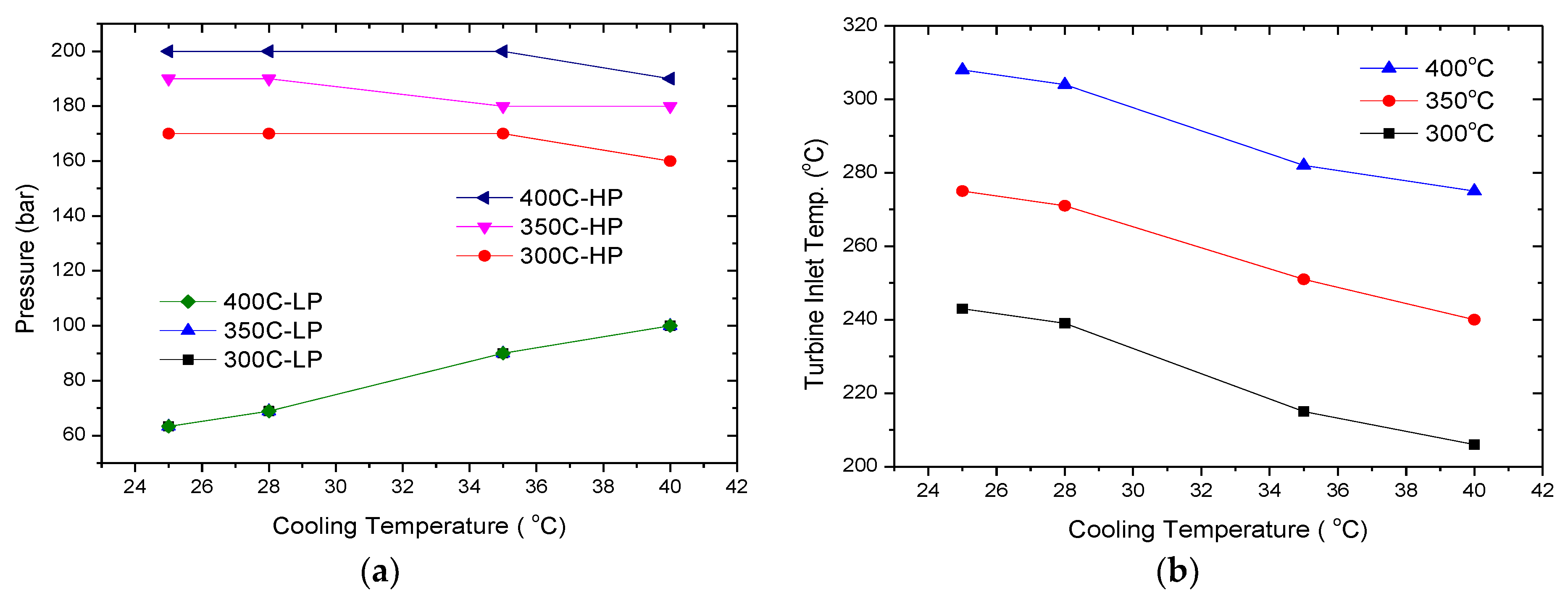
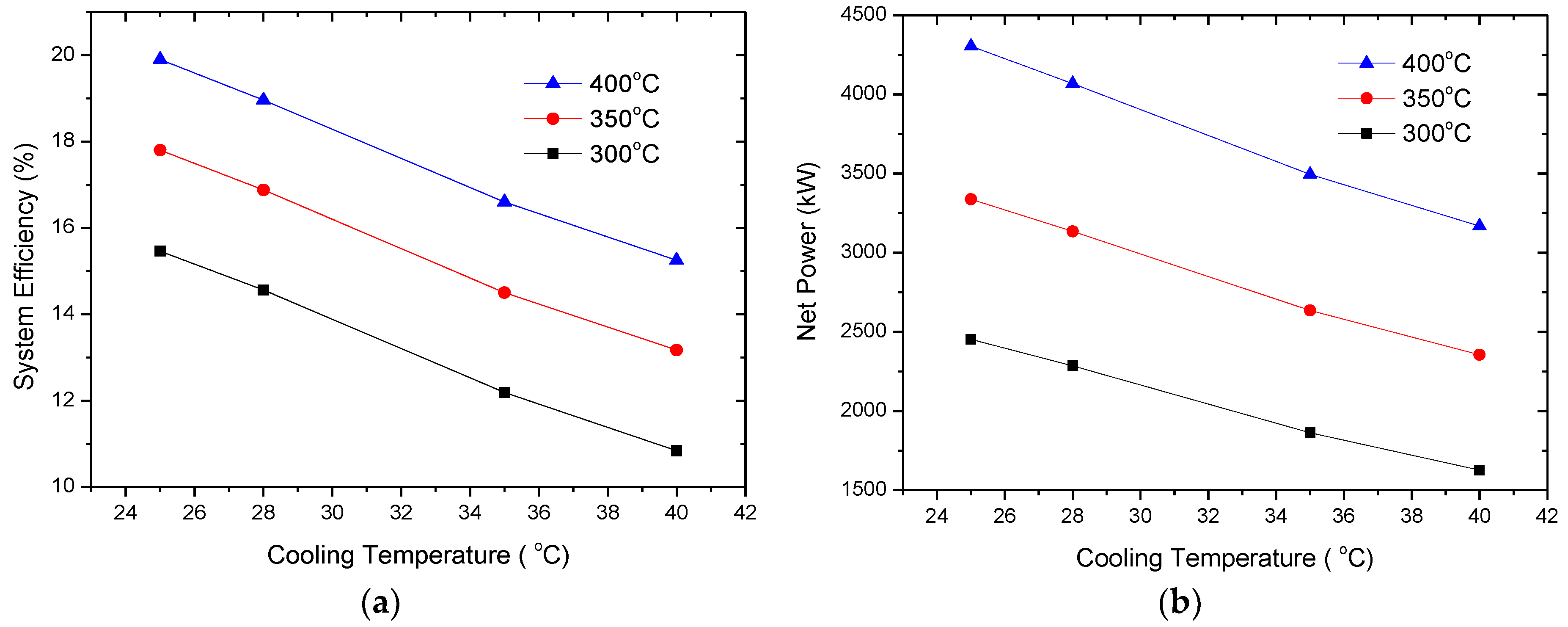
3.2. Effects of Cooling Temperature
3.3. Effects of Heat Source Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Isobaric specific heat, kJ/kg·K | |
| h | Specific enthalpy, kJ/kg |
| Mass flow rate, kg/s | |
| P | Pressure, kPa |
| Rate of heat, kW | |
| T | Temperature, °C |
| Rate of work, kW | |
| Special characters | |
| Heat exchanger effectiveness | |
| η | Efficiency |
| Subscripts and superscripts | |
| 0 | Atmospheric (environmental) state |
| C | Condenser |
| cyc | Cycle |
| e | Expander |
| EG | Exhaust gas |
| H | Heater |
| HR | Heat recovery |
| i | State point |
| in | inlet |
| max | Maximum |
| net | Net output |
| out | Outlet |
| P | Pump |
| R | Recuperator |
| s | Isentropic process |
| sys | System |
| T | Turbine |
| + | Input |
| − | Output |
References
- Ahn, Y.; Bae, S.J.; Kim, M.; Cho, S.K.; Baik, S.; Lee, J.I.; Cha, J.E. Review of Supercritical CO2 Power Cycle Technology and Current Status of Research and Development. Nucl. Eng. Technol. 2015, 47, 647–661. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Cho, Y.; Kim, M.S.; Kim, M. Characteristics and Optimization of Supercritical CO2 Recompression Power Cycle and the Influence of Pinch Point Temperature Difference of Recuperators. Energy. 2018, 147, 1216–1226. [Google Scholar] [CrossRef]
- Marchionni, M.; Bianchi, G.; Tassou, S.A. Review of Supercritical Carbon Dioxide (sCO2) Technologies for High-Grade Waste Heat to Power Conversion. SN Appl. Sci. 2020, 2, 611. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Yang, Q.; Cui, G. Supercritical Carbon Dioxide(s-CO2) Power Cycle for Waste Heat Recovery: A Review from Thermodynamic Perspective. Processes 2020, 8, 1461. [Google Scholar] [CrossRef]
- Wu, C.; Yan, X.-J.; Wang, S.-S.; Bai, K.-L.; Di, J.; Cheng, S.-F.; Li, J. System Optimisation and Performance Analysis of CO2 Transcritical Power Cycle for Waste Heat Recovery. Energy 2016, 100, 391–400. [Google Scholar] [CrossRef]
- Huck, P.; Freund, S.; Lehar, M.; Peter, M. Performance Comparison of Supercritical CO2 Versus Steam Bottoming Cycles for Gas Turbine Combined Cycle Applications. In Proceedings of the 5th International Symposium—Supercritical CO2 Power Cycles, San Antonio, TX, USA, 28–31 March 2016. [Google Scholar]
- Held, T.J. Supercritical CO2 cycles for gas turbine combined cycle power plants. In Proceedings of the Power Gen International, Las Vegas, NV, USA, 8–10 December 2015. [Google Scholar]
- Manjunath, K.; Sharma, O.P.; Tyagi, S.K.; Kaushik, S.C. Thermodynamic Analysis of a Supercritical/Transcritical CO2—Based Waste Heat Recovery Cycle for Shipboard Power and Cooling Applications. Energy Convers. Manag. 2018, 155, 262–275. [Google Scholar] [CrossRef]
- Kim, Y.M.; Shin, D.G.; Kim, C.G.; Cho, G.B. Single-Loop Organic Rankine Cycles for Engine Waste Heat Recovery Using Both Low- and High-Temperature Heat Sources. Energy 2016, 96, 482–494. [Google Scholar] [CrossRef]
- Kim, Y.M.; Sohn, J.L.; Yoon, E.S. Supercritical CO2 Rankine Cycles for Waste Heat Recovery from Gas Turbine. Energy 2017, 118, 893–905. [Google Scholar] [CrossRef]
- Moroz, L.; Burlaka, M.; Rudenko, O.; Joly, C. Evaluation of Gas Turbine Exhaust Heat Recovery Utilizing Composite Supercritical CO2 Cycle. In Proceedings of the International Gas Turbine Congress, Tokyo, Japan, 15–20 November 2015. [Google Scholar]
- Cho, S.K.; Kim, M.; Baik, S.; Ahn, Y.; Ik Lee, J. Investigation of the Bottoming Cycle for High Efficiency Combined Cycle Gas Turbine System with Supercritical Carbon Dioxide Power Cycle. In Proceedings of the ASME Turbo Expo: Turbine Technical Conference and Exposition GT, Montréal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Zhang, Q.; Ogren, R.M.; Kong, S. Thermo-Economic Analysis and Multi-Objective Optimization of a Novel Waste Heat Recovery System with a Transcritical CO2 Cycle for Offshore Gas Turbine Application. Energy Convers. Manag. 2018, 172, 212–227. [Google Scholar] [CrossRef]
- Sánchez Villafana, E.D.; Vargas Machuca Bueno, J.P. Thermoeconomic and Environmental Analysis and Optimization of the Supercritical CO2 Cycle Integration in a Simple Cycle Power Plant. Appl. Therm. Eng. 2019, 152, 1–12. [Google Scholar] [CrossRef]
- Wright, S.; Davidson, C.; Scammell, W. Thermo-Economic Analysis of Four sCO2 Waste Heat Recovery Power Systems. In Proceedings of the 5th International Symposium on Supercritical CO2 Power Cycles, San Antonio, TX, USA, 28–31 March 2016. [Google Scholar]
- Cao, Y.; Ren, J.; Sang, Y.; Dai, Y. Thermodynamic Analysis and Optimization of a Gas Turbine and Cascade CO2 Combined Cycle. Energy Convers. Manag. 2017, 144, 193–204. [Google Scholar] [CrossRef]
- Manente, G.; Fortuna, F.M. Supercritical CO2 Power Cycles for Waste Heat Recovery: A Systematic Comparison Between Traditional and Novel Layouts with Dual Expansion. Energy Convers. Manag. 2019, 197, 111777. [Google Scholar] [CrossRef]
- Heo, J.Y.; Ahn, Y.; Lee, J.I. A Study of S-CO2 Power Cycle for Waste Heat Recovery Using Isothermal Compressor. In Proceedings of the ASME Turbo Expo: Turbomach, Technical Conference and Exposition GT, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Wright, S.A.; Davidson, C.S.; Scammell, W.O. Bulk Energy Storage Using a Supercritical CO2 Waste Heat Recovery Power Plant. In Proceedings of the 4th International Symposium—Supercritical CO2 Power Cycles, Pittsburg, PA, USA, 9–10 September 2014. [Google Scholar]
- Weiland, N.T.; White, C.W.; O’Connell, A.C. Effects of Cold Temperature and Main Compression Intercooling on Recuperator and Recompression Cycle Performance. In Proceedings of the 2nd European sCO2 Conference, Essen, Germany, 30–31 August 2018; Volume 2018. [Google Scholar]
- Hossain, M.J.; Chowdhury, J.I.; Balta-Ozkan, N.; Asfand, F.; Saadon, S.; Imran, M. Design optimization of supercritical carbon-dioxide (s-CO2) cycles for waste heat recovery from marine engines. J. Energy Resour. Technol. 2021, 143, 120901. [Google Scholar] [CrossRef]
- Held, T.J. Initial test results of a megawatt-class supercritical CO2 heat engine. In Proceedings of the 4th International Symposium—Supercritical CO2 Power Cycles, Pittsburg, PA, USA, 9–10 September 2014. [Google Scholar]
- F-Chart Software, Engineering Equation Solver (EES). 2019. Available online: http://www.fchart.com/ees (accessed on 1 August 2021).
- Lemmon, E.W.; Mclinden, M.O.; Huber, M.L. NIST Standard Reference Database 23, Version 10.0, Reference Fluid Thermodynamic and Transport Properties-REFPROP; National Institute of Standards and Technology (NIST): Boulder, CO, USA, 2018; Volume 23.



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.-M.; Lee, Y.-D.; Ahn, K.-Y. Parametric Study of a Supercritical CO2 Power Cycle for Waste Heat Recovery with Variation in Cold Temperature and Heat Source Temperature. Energies 2021, 14, 6648. https://doi.org/10.3390/en14206648
Kim Y-M, Lee Y-D, Ahn K-Y. Parametric Study of a Supercritical CO2 Power Cycle for Waste Heat Recovery with Variation in Cold Temperature and Heat Source Temperature. Energies. 2021; 14(20):6648. https://doi.org/10.3390/en14206648
Chicago/Turabian StyleKim, Young-Min, Young-Duk Lee, and Kook-Young Ahn. 2021. "Parametric Study of a Supercritical CO2 Power Cycle for Waste Heat Recovery with Variation in Cold Temperature and Heat Source Temperature" Energies 14, no. 20: 6648. https://doi.org/10.3390/en14206648
APA StyleKim, Y.-M., Lee, Y.-D., & Ahn, K.-Y. (2021). Parametric Study of a Supercritical CO2 Power Cycle for Waste Heat Recovery with Variation in Cold Temperature and Heat Source Temperature. Energies, 14(20), 6648. https://doi.org/10.3390/en14206648






