A Comparative Study of High-Temperature Latent Heat Storage Systems
Abstract
:1. Introduction
2. System Description
3. Numerical Methodology
- (i).
- The energy equations for both solid and liquid phases are a single set of equation;
- (ii).
- Stefan’s boundary condition need not be explicitly fulfilled at the interface;
- (iii).
- The method considers the phase change to take place in a temperature interval which creates a mushy zone;
- (iv).
- The explicit reference to the moving interface is eliminated.
4. Governing Equations and Assumptions
- Thermo-physical properties are treated as uniform and isotropic in both phases of PCM;
- Motion in molten PCM is treated as incompressible and laminar;
- Volume change of PCM is ignored during melting and solidification;
- Energy dissipation due to viscosity is neglected;
- The Boussinessq assumption is invoked to model the density variation;
- It is perfectly insulated with no-slip and no-penetration boundary.
5. Results and Discussion
5.1. Model Verification and Validation
5.2. Thermal Performance of Silicon-Based LHS System
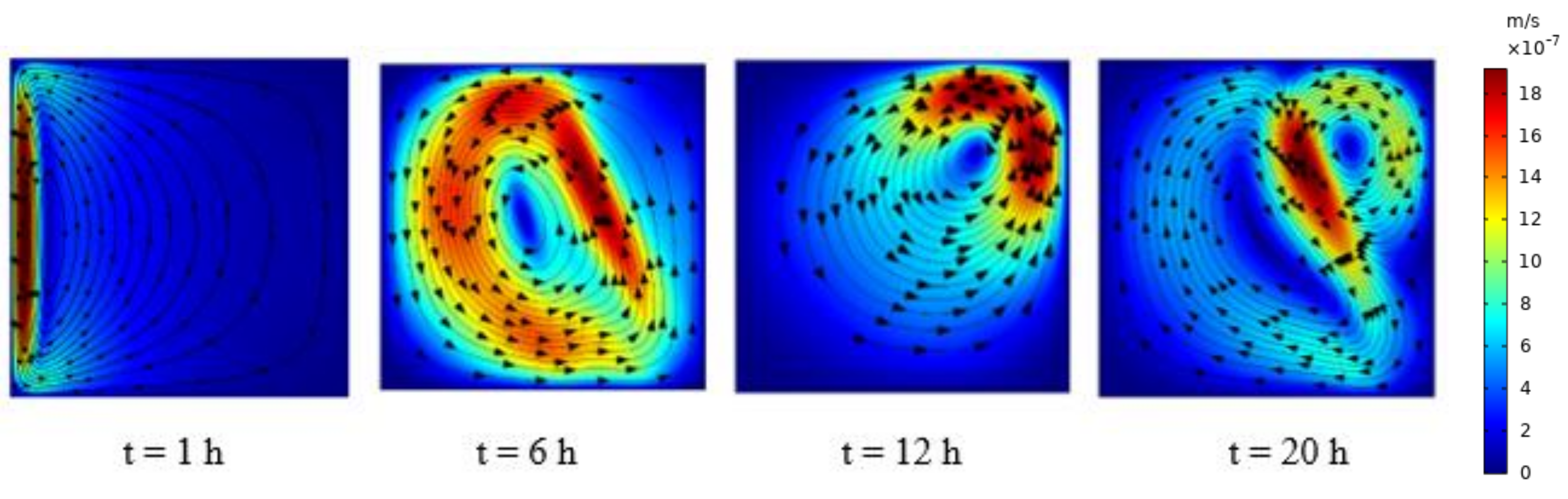
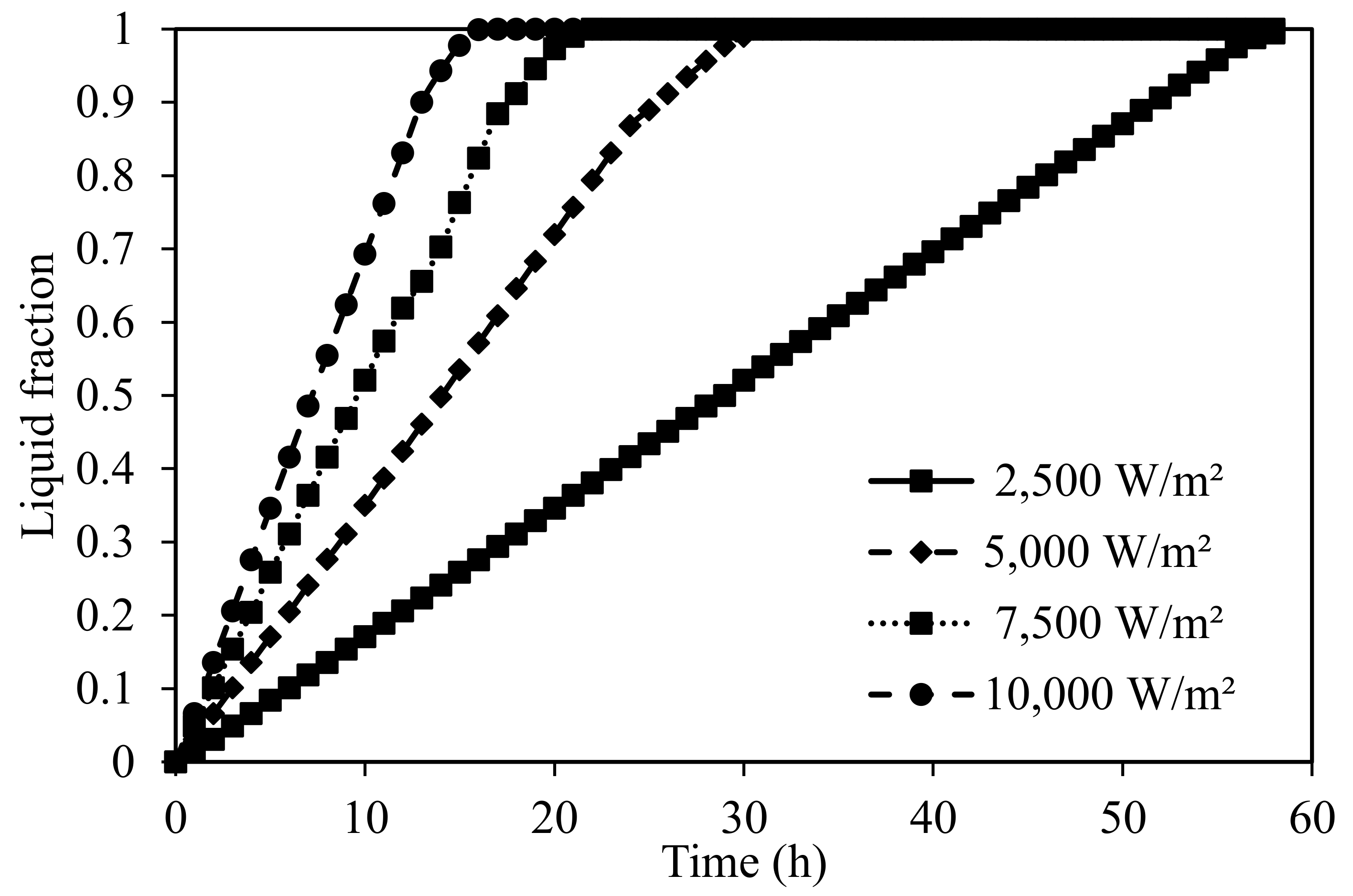
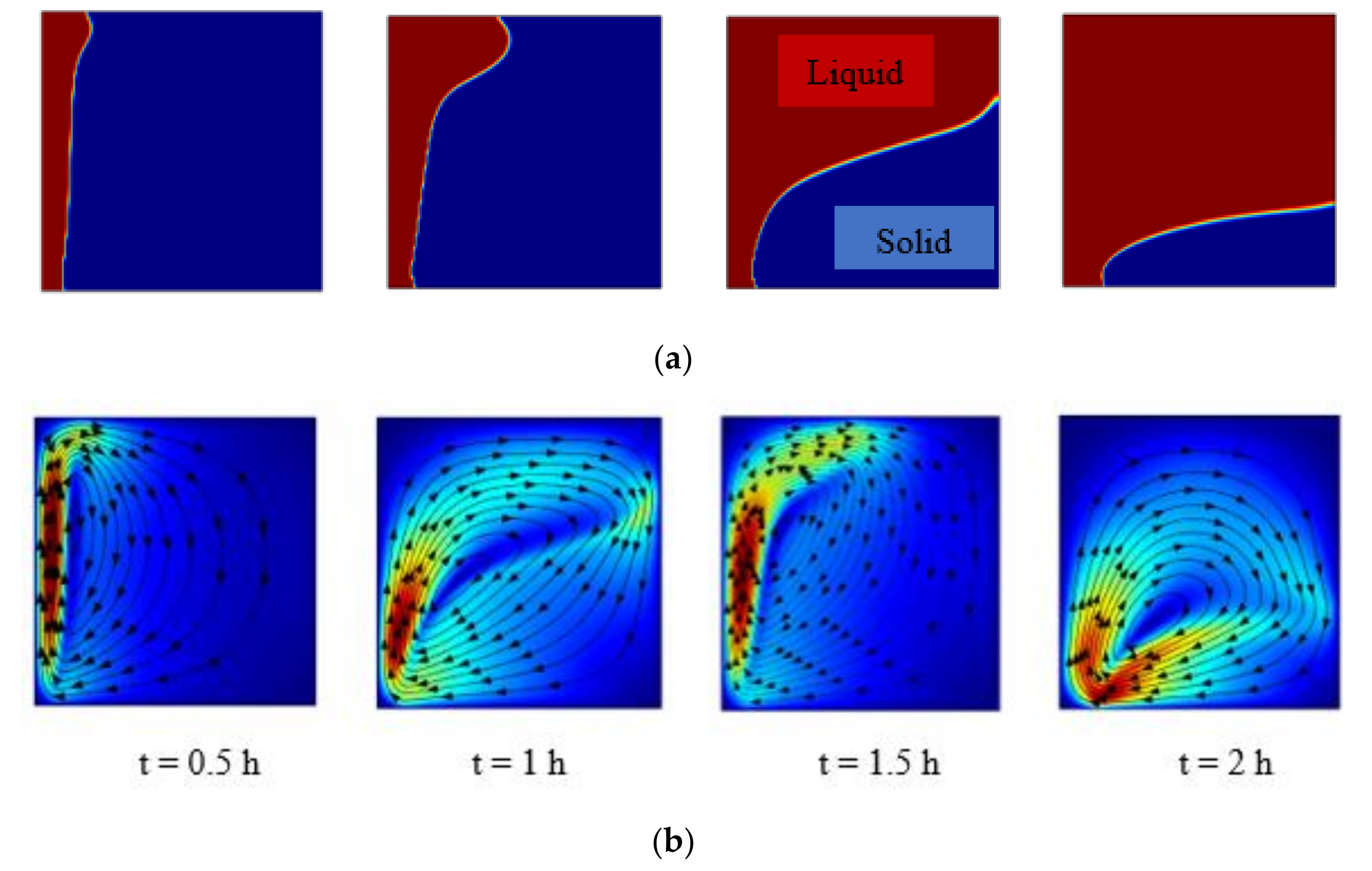
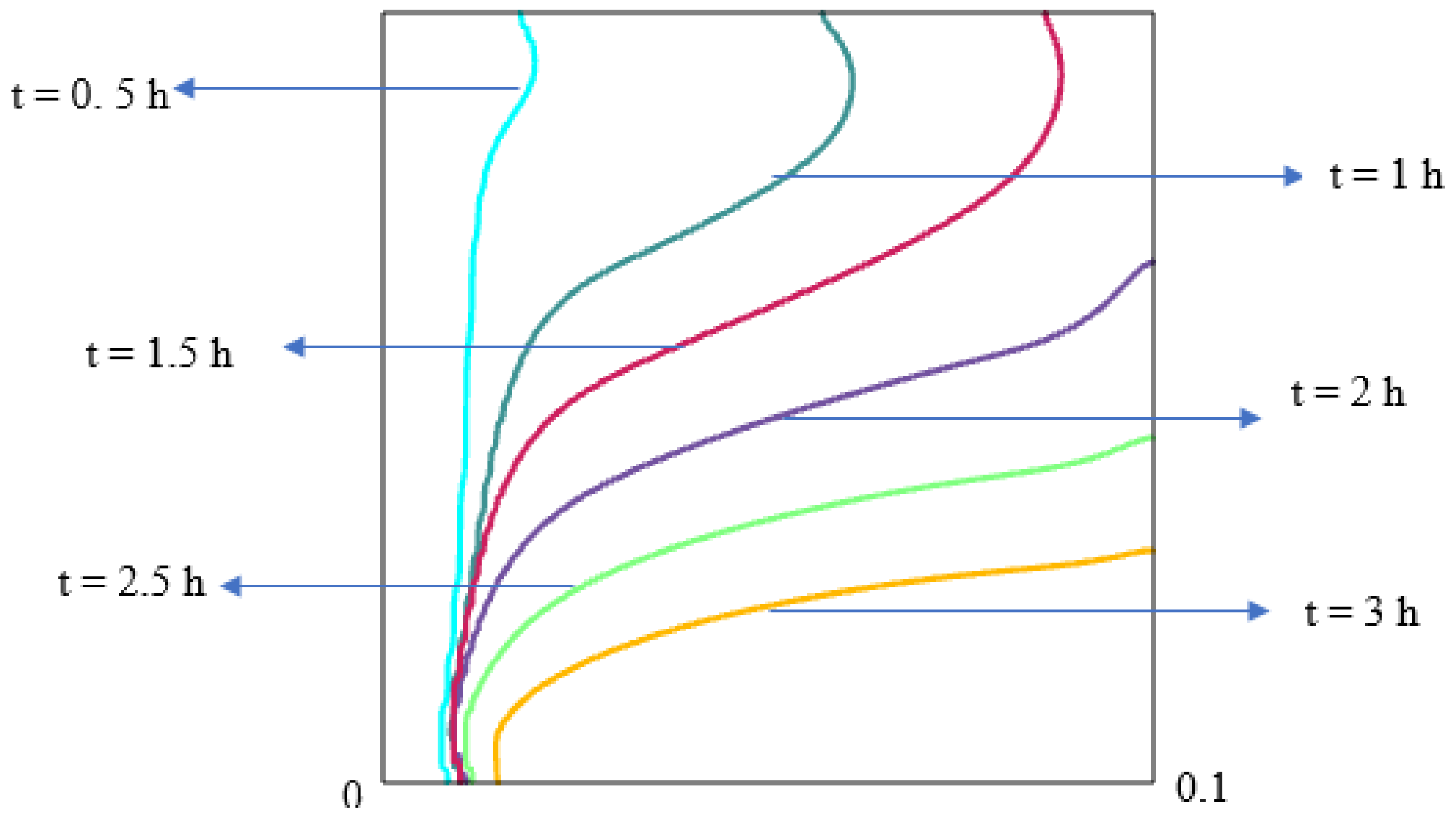
5.2.1. Charging of Silicon Domain
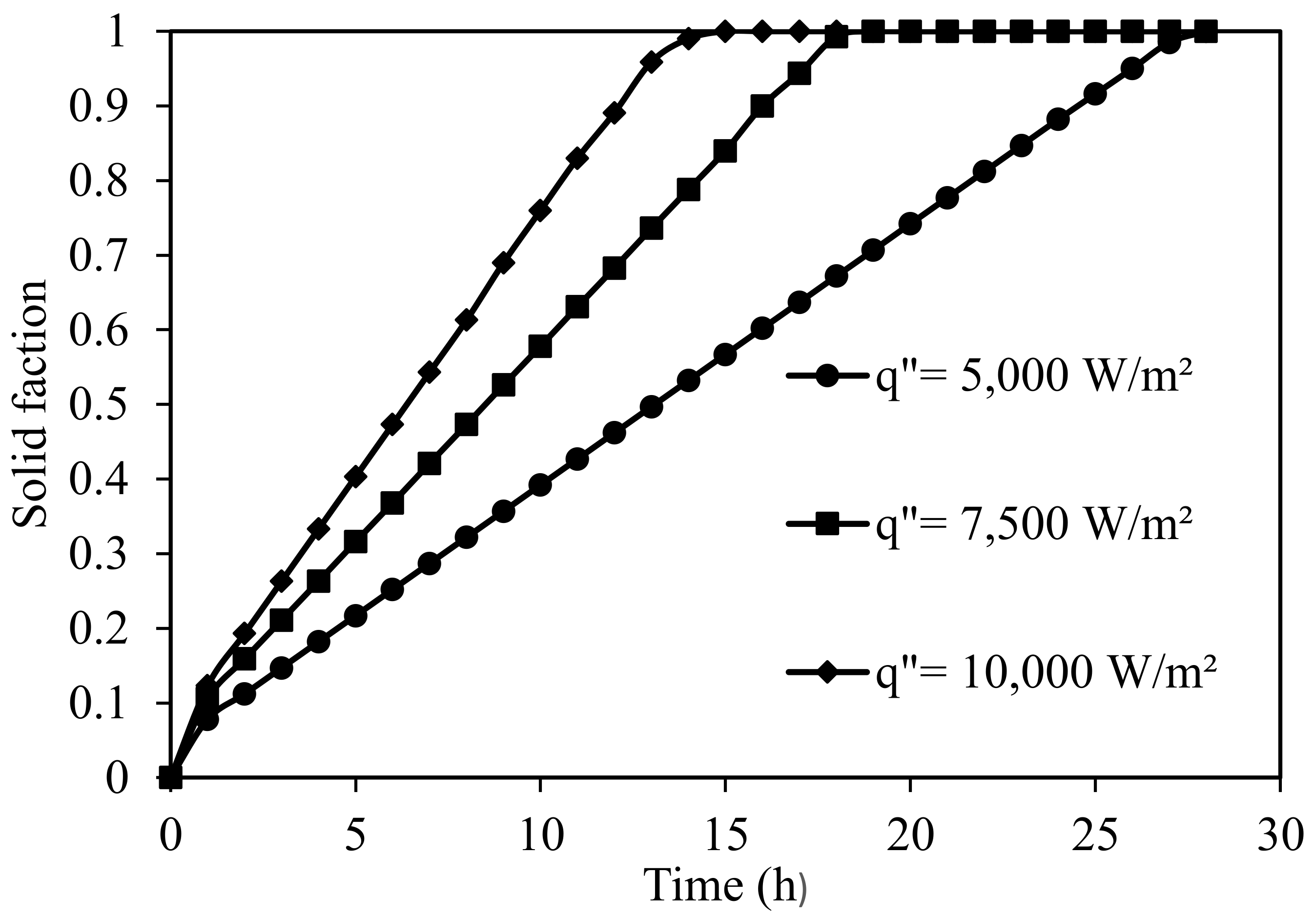
5.2.2. Discharge of Silicon Domain
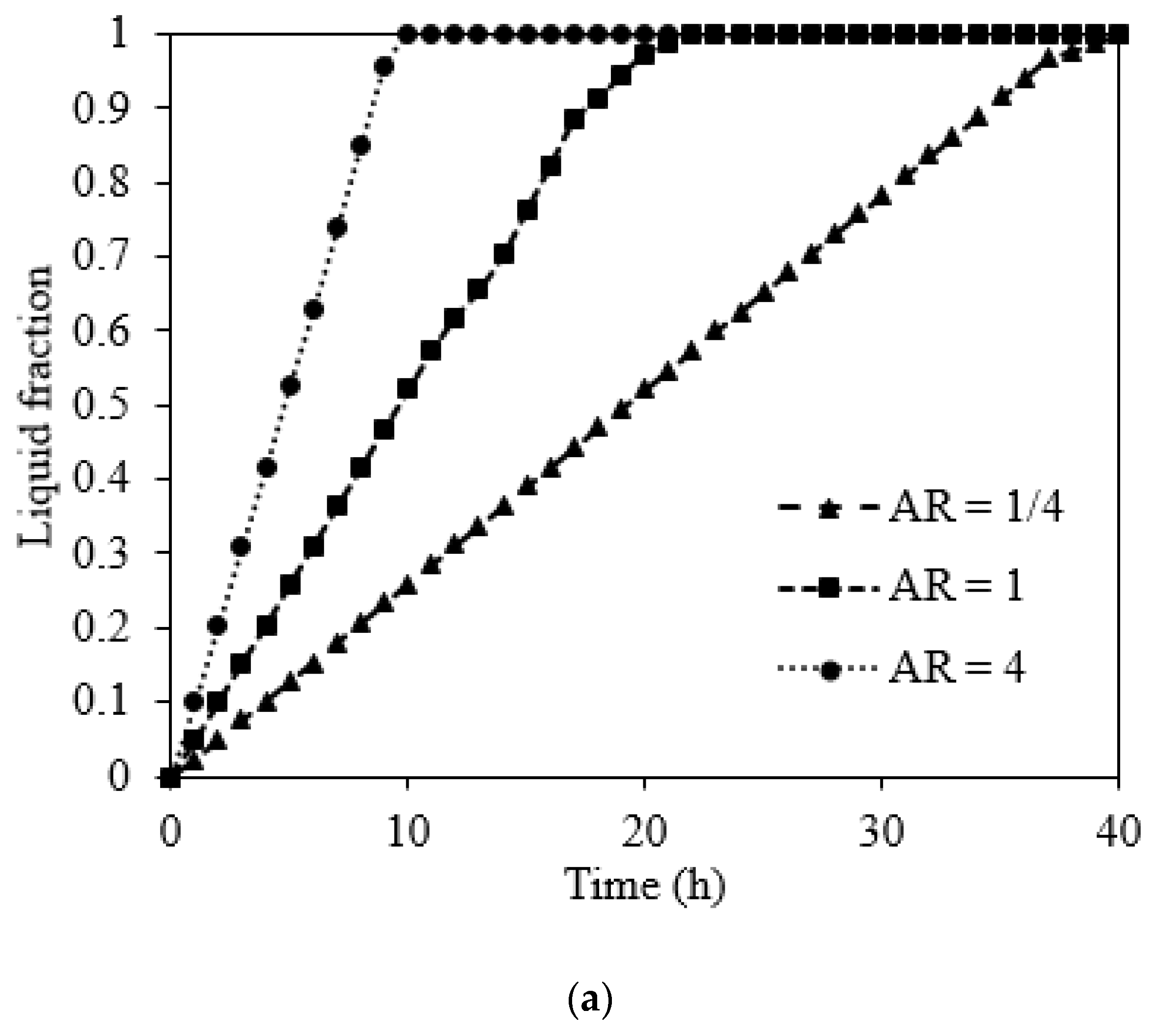
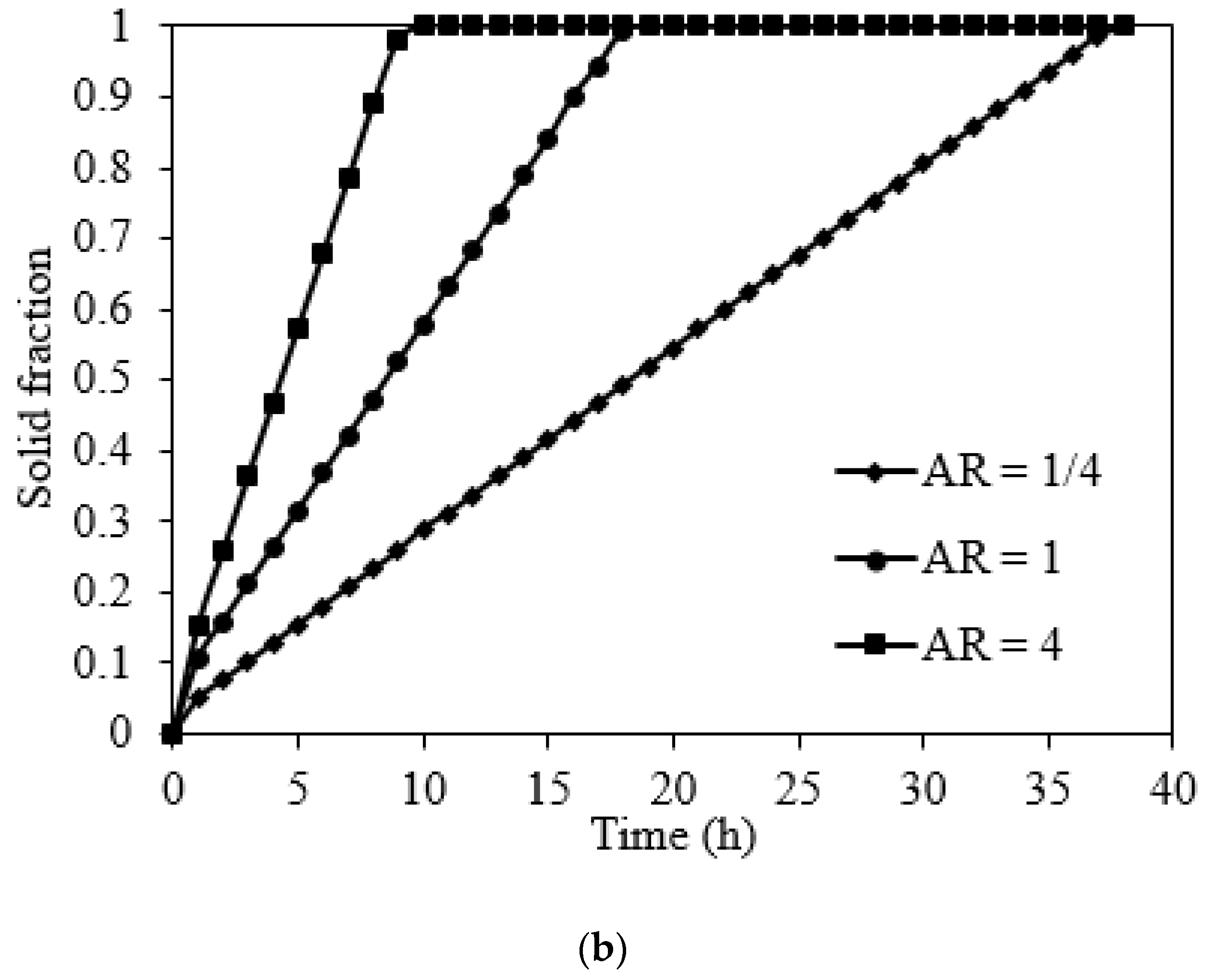
5.2.3. Effect of the Orientation of Domain on Charging and Discharge Performance
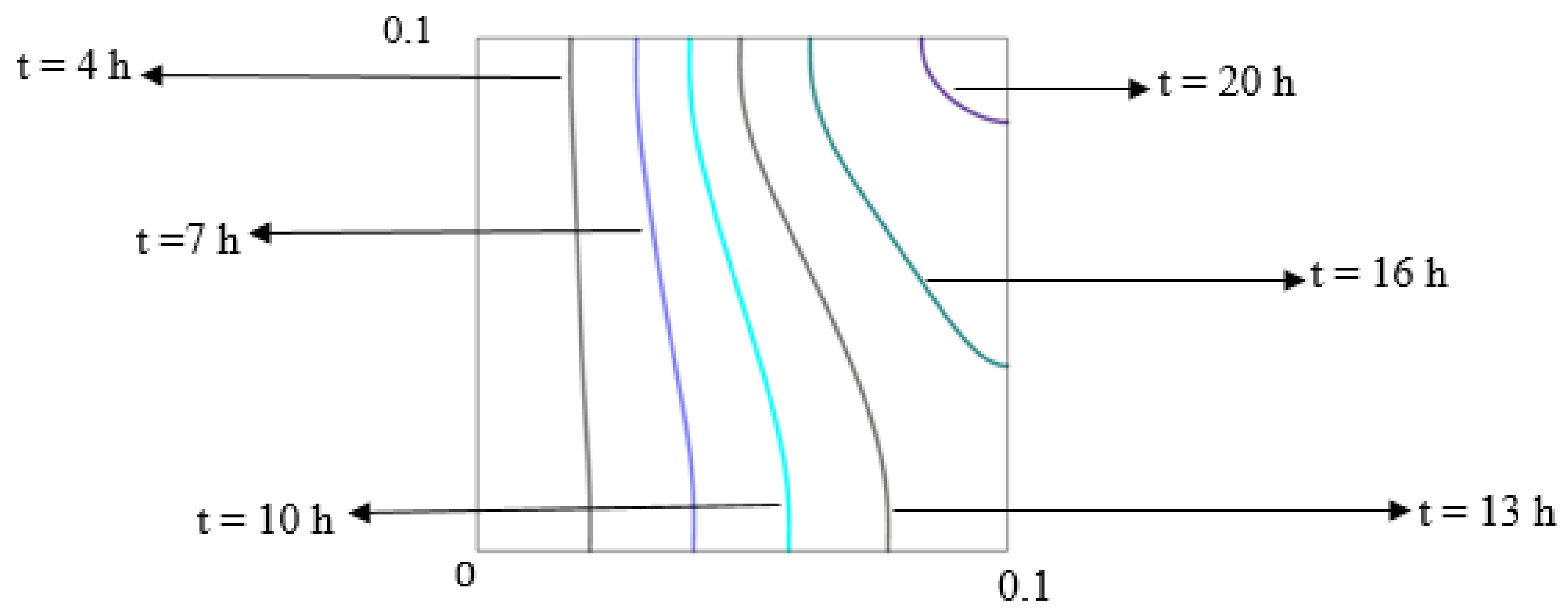
5.3. Charging Performance of NaNO3 Domain
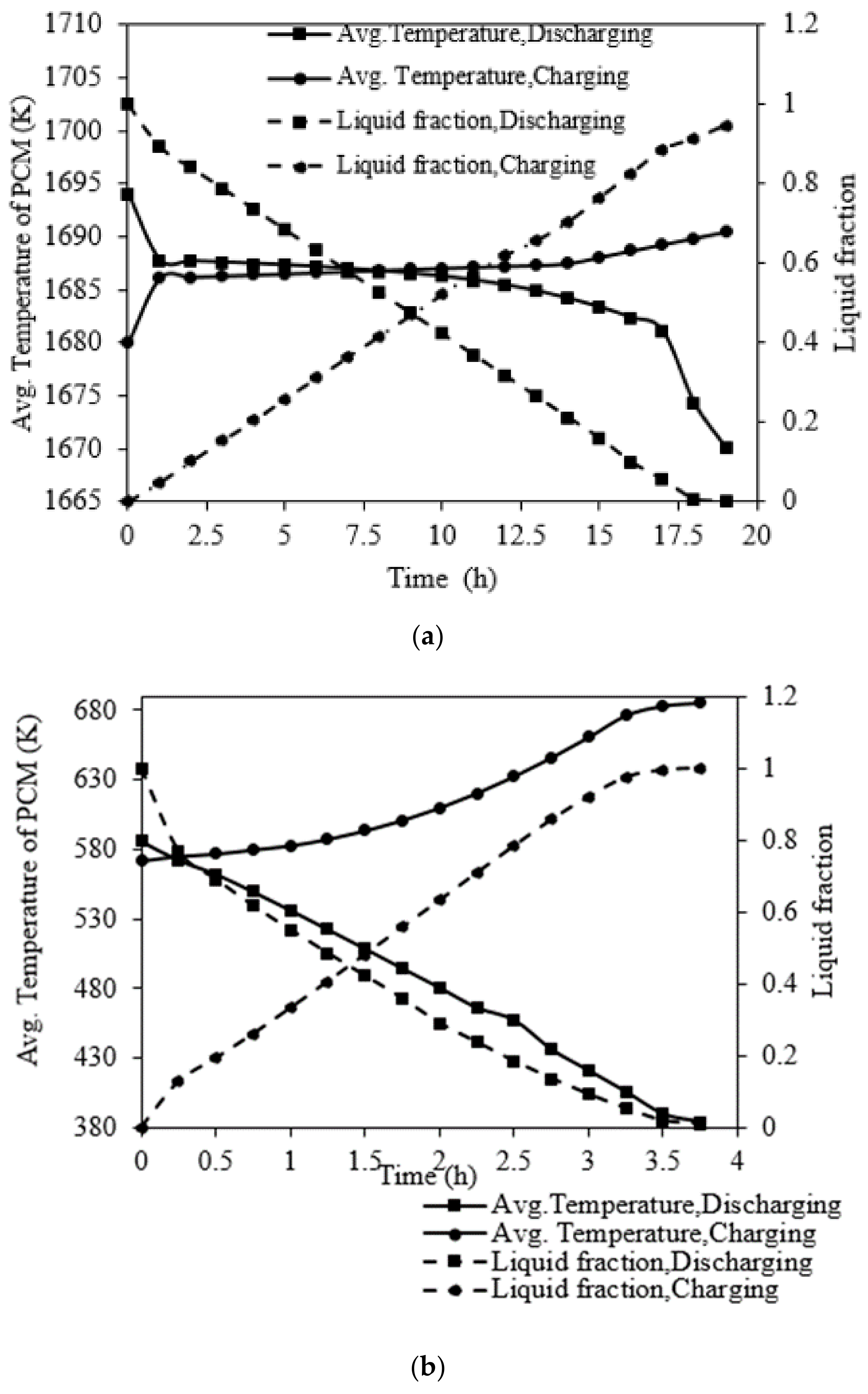
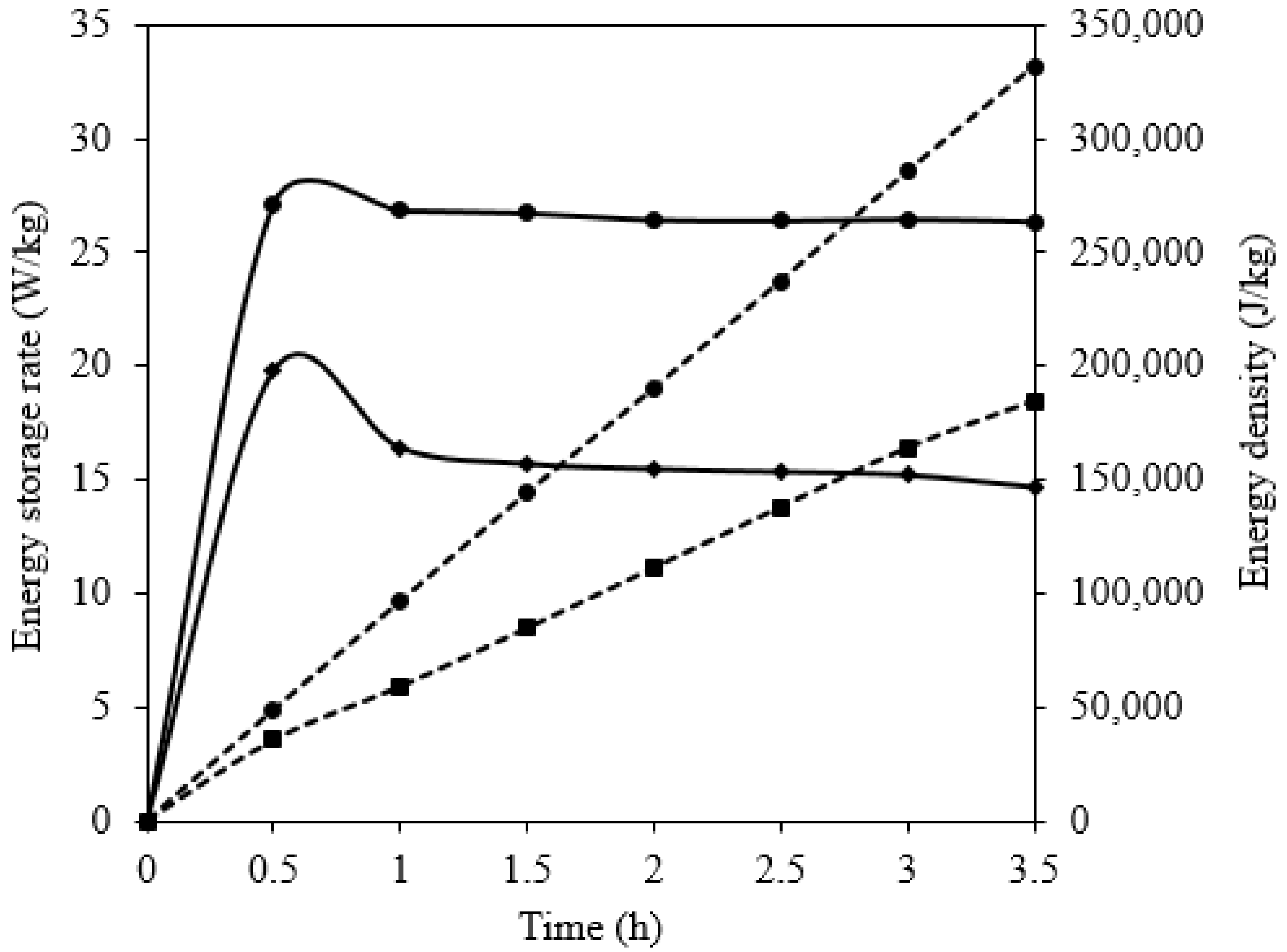
5.4. Comparison of Charging and Discharge Performance between the Silicon and NaNO3 Domains
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AR | Aspect ratio |
| CSP | Concentrated solar power |
| FEM | Finite element method |
| Gen | Generation |
| LCoE | Levelized cost of energy |
| TCHS | Thermochemical heat storage |
| LHS | Latent heat storage |
| LF | Liquid fraction |
| PCM | Phase change medium |
| SF | Solid fraction |
| SHS | Sensible heat storage |
| Greek Symbols: | |
| β | Liquid fraction |
| ε | Constant in karman-Cosney equation |
| μ | Dynamic viscosity (Pa·s) |
| ρ | Density (kg/m3) |
| Symbols: | |
| Amush | Mushy zone constant |
| CP | Specific heat capacity (J/kgK) |
| Fb | Bouyancy force (N) |
| S(T) | Porosity function |
| hsl | Latent heat (J/kg) |
| kT | Volumetric expansion coefficient (1/K) |
| Edis | Dissipative energy (J/m3) |
| L | Height of domain (m) |
| q″ | Heat flux (W/m2) |
| T | Temperature (K) |
| u,v | Velocity components (m/s) |
| W | Width of domain (m) |
| Subscripts: | |
| Sol (s) | Solid |
| Liq (l) | Liquid |
| Mod | Modified |
| o | Reference |
References
- Steiger, J. II—Renewable Energy Resources. In Renewable Energy Resources in ASEAN; ISEAS Publishing: Heng Mui Keng Terrace, Singapore, 2018. [Google Scholar] [CrossRef]
- Zablocki, A. Energy Storage: Fact. Sheet (2019); EESI: Washington, DC, USA, 2019; Volume 2040, pp. 1–8. [Google Scholar]
- Sarbu, I.; Sebarchievici, C. A comprehensive review of thermal energy storage. Sustainability 2018, 10, 191. [Google Scholar] [CrossRef] [Green Version]
- Alva, G.; Lin, Y.; Liu, L.; Fang, G. Synthesis, characterization and applications of microencapsulated phase change materials in thermal energy storage: A review. Energy Build. 2017, 144, 276–294. [Google Scholar] [CrossRef]
- Pelay, U.; Luo, L.; Fan, Y.; Stitou, D.; Rood, M. Technical data for concentrated solar power plants in operation, under construction and in project. Data Br. 2017, 13, 597–599. [Google Scholar] [CrossRef] [PubMed]
- Dincer, I.; Rosen, M.A. Thermal Energy Storage Systems and Applications, 2nd ed.; Wiley: Chichester, UK, 2011. [Google Scholar]
- Mehos, M.; Turchi, C.; Vidal, J.; Wagner, M.; Ma, Z.; Ho, C.; Kolb, W.; Andraka, C.; Kruzienga, A. Concentrating Solar Power Gen3 Demonstration Roadmap; Technical Report; National Renewable Energy Lab (NREL): Golden, CO, USA, 2017. [Google Scholar] [CrossRef] [Green Version]
- Luft, W. High-temperature solar thermal energy storage. Int. J. Sol. Energy 1985, 3, 25–40. [Google Scholar] [CrossRef]
- Zhang, H.; Baeyens, J.; Cáceres, G.; Degrève, J.; Lv, Y. Thermal energy storage: Recent developments and practical aspects. Prog. Energy Combust. Sci. 2016, 53, 1–40. [Google Scholar] [CrossRef]
- Nazir, H.; Batool, M.; Bolivar Osorio, F.J.; Isaza-Ruiz, M.; Xu, X.; Vignarooban, K.; Phelan, P.; Inamuddin; Kanna, A.M. Recent developments in phase change materials for energy storage applications: A review. Int. J. Heat Mass Transf. 2019, 129, 491–523. [Google Scholar] [CrossRef]
- De Gracia, A.; Cabeza, L.F. Phase change materials and thermal energy storage for buildings. Energy Build. 2015, 103, 414–419. [Google Scholar] [CrossRef] [Green Version]
- Jegadheeswaran, S.; Pohekar, S.D. Performance enhancement in latent heat thermal storage system: A review. Renew. Sustain. Energy Rev. 2009, 13, 2225–2244. [Google Scholar] [CrossRef]
- Lin, Y.; Jia, Y.; Alva, G.; Fang, G. Review on thermal conductivity enhancement, thermal properties and applications of phase change materials in thermal energy storage. Renew. Sustain. Energy Rev. 2018, 82, 2730–2742. [Google Scholar] [CrossRef]
- Bauer, T.; Steinmann, W.-D.; Laing, D.; Tamme, R. Thermal Energy Storage Materials and Systems. Annu. Rev. Heat Transf. 2012, 15, 131–177. [Google Scholar] [CrossRef]
- Kotzé, J.P. Thermal Energy Storage in Metallic Phase Change Materials. Ph.D. Thesis, Stellenbosh University, Stellenbosh, South Africa, 2014. [Google Scholar]
- Birchenall, C.E.; Telkes, M. Thermal storage in metals. In Sharing the Sun: Solar Technology in the Seventies, Proceedings of the Joint Conference, Winnipeg, MB, Canada, 15–20 August 1976; International Solar Energy Society: Freiburg im Breisgau, Germany, 1976; pp. 138–154. [Google Scholar]
- He, Q.; Zhang, W. A study on latent heat storange exchangers with the high-temperature phase-change material. Int. J. Energy Res. 2001, 25, 331–341. [Google Scholar] [CrossRef]
- Kotzé, J.P.; Von Backström, T.W.; Erens, P.J. Simulation and testing of a latent heat thermal energy storage unit with metallic phase change material. Energy Procedia 2014, 49, 860–869. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wang, H.; Li, X.; Wang, D.; Zhang, Q.; Chen, G.; Zhifeng, R. Aluminum and silicon-based phase change materials for high capacity thermal energy storage. Appl. Therm. Eng. 2015, 89, 204–208. [Google Scholar] [CrossRef]
- Robinson, A. Ultra-high temperature thermal energy storage. Part 1: Concepts. J. Energy Storage 2017, 13, 277–286. [Google Scholar] [CrossRef] [Green Version]
- Choi, K.J.; Hong, J.S. Experimental studies of melting phenomena from a constant heat flux vertical plate. Exp. Heat Transf. 1990, 3, 49–63. [Google Scholar] [CrossRef]
- Marušić, A.; Lončar, D. Experimental validation of high-temperature latent heat storage model using melting front propagation data. Appl. Therm. Eng. 2020, 164, 114520. [Google Scholar] [CrossRef]
- Khare, S.; Dell’Amicom, M.; Knight, C.; McGarry, S. Selection of materials for high temperature latent heat energy storage. Sol. Energy Mater. Sol. Cells 2012, 107, 20–27. [Google Scholar] [CrossRef]
- Yadav, A.; Samir, S. Experimental and numerical investigation of spatiotemporal characteristics of thermal energy storage system in a rectangular enclosure. J. Energy Storage 2019, 21, 405–417. [Google Scholar] [CrossRef]
- Kheirabadi, A.C.; Groulx, D. The Effect of the Mushy-Zone Constant on Simulated Phase Change Heat Transfer. In Proceedings of the CHT-15, 6th International Symposium on Advances in Computational Heat Transfer, New Brunswick, NJ, USA, 25–29 May 2015; Begel House Inc.: Danbury, CT, USA, 2015; Volume 22, pp. 528–549. [Google Scholar] [CrossRef] [Green Version]
- Assis, E.; Katsman, L.; Ziskind, G.; Letan, R. Numerical and experimental study of melting in a spherical shell. Int. J. Heat Mass Transf. 2007, 50, 1790–1804. [Google Scholar] [CrossRef]
- Srinivasan, M.; Nagarajan, S.G.; Ramasamy, P. Computational Study of Heat Transfer on Molten Silicon during Directional Solidification for Solar Cell Applications. Procedia Eng. 2015, 127, 1250–1255. [Google Scholar] [CrossRef] [Green Version]
- Veeraragavan, A.; Montgomery, L.; Datas, A. Night time performance of a storage integrated solar thermophotovoltaic (SISTPV) system. Sol. Energy 2014, 108, 377–389. [Google Scholar] [CrossRef] [Green Version]
- Zeneli, M.; Malgarinos, I.; Nikolopoulos, A.; Nikolopoulos, N.; Grammelis, P.; Karellas, S.; Kakaras, E. Numerical simulation of a silicon-based latent heat thermal energy storage system operating at ultra-high temperatures. Appl. Energy 2019, 242, 837–853. [Google Scholar] [CrossRef]
- Ray, A.K.; Rakshit, D.; Ravi Kumar, K.; Gurgenci, H. Silicon as high-temperature phase change medium for latent heat storage: A thermo-hydraulic study. Sustain. Energy Technol. Assess. 2021, 46, 101249. [Google Scholar] [CrossRef]
- Ogoh, W.; Groulx, D. Effects of the heat transfer fluid velocity on the storage characteristics of a cylindrical latent heat energy storage system: A numerical study. Heat Mass Transf. 2012, 48, 439–449. [Google Scholar] [CrossRef]
- Groulx, D.; Biwole, P.H. Solar PV Passive Temperature Control Using Phase Change Materials. In Proceedings of the International Heat Transfer Conference 15, Kyoto, Japan, 10–14 August 2014. [Google Scholar] [CrossRef]
- COMSOL Multiphysics Reference Manual; Version 5.4; COMSOL: Burlington, MA, USA, 2018.
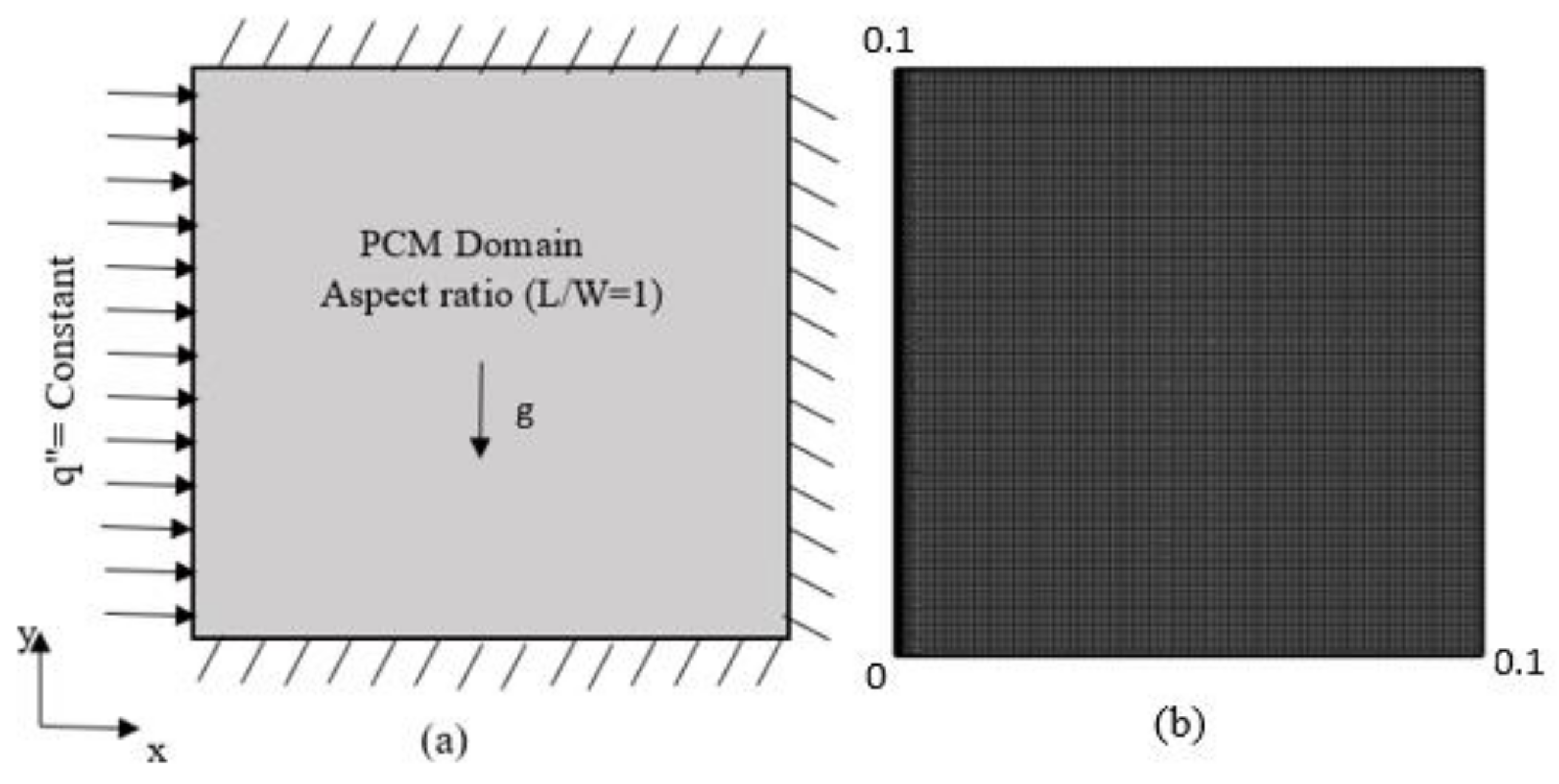
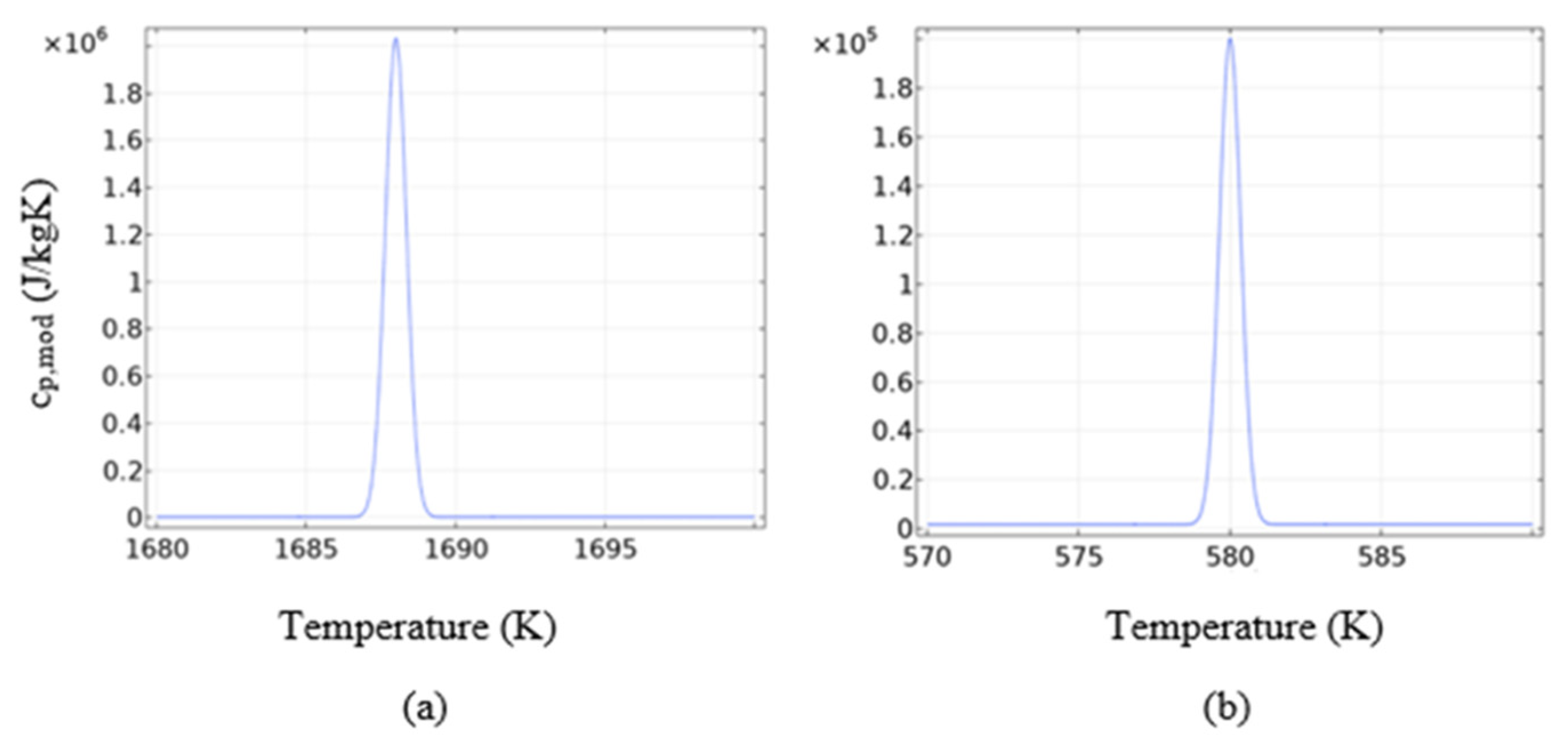
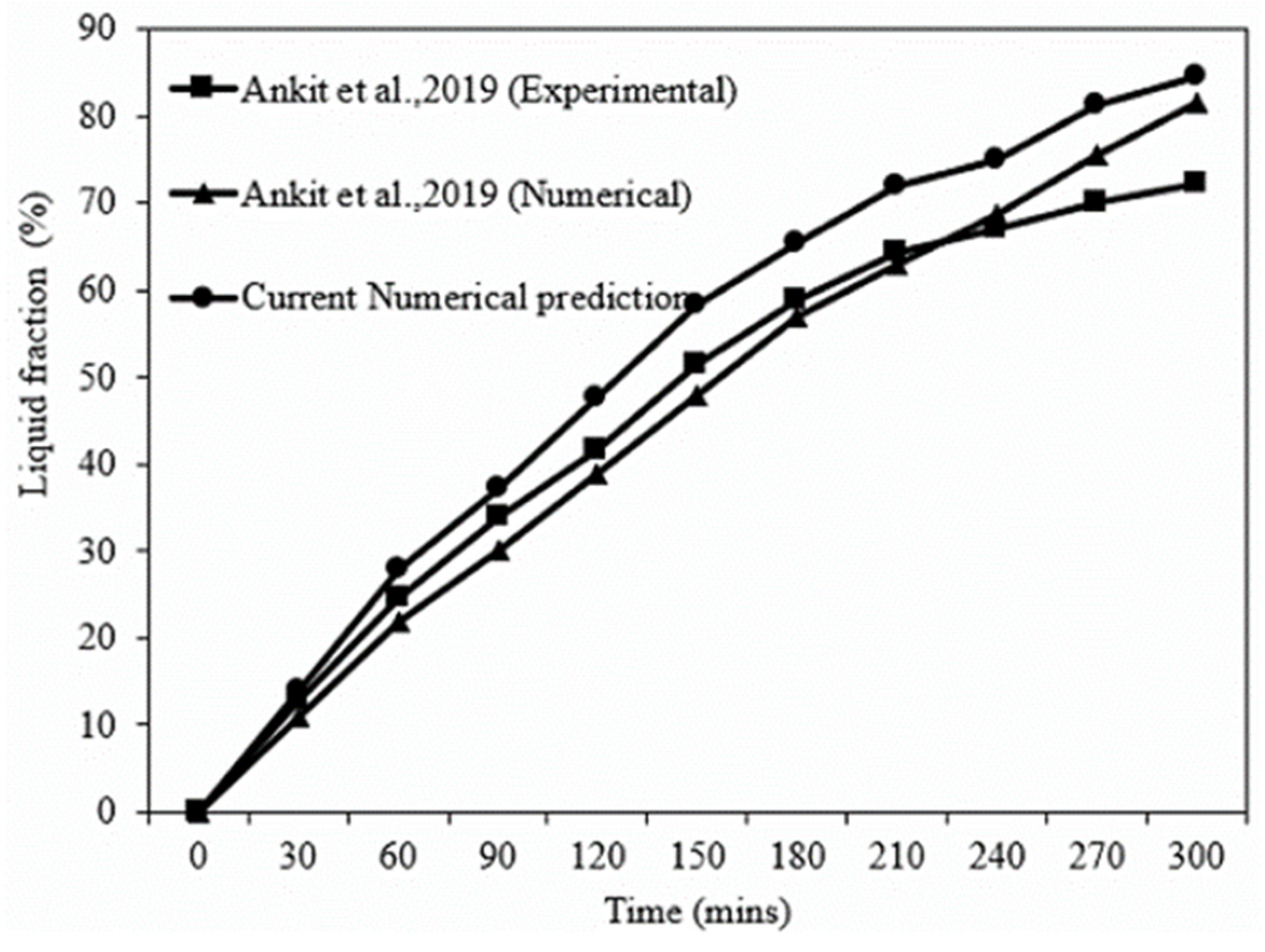

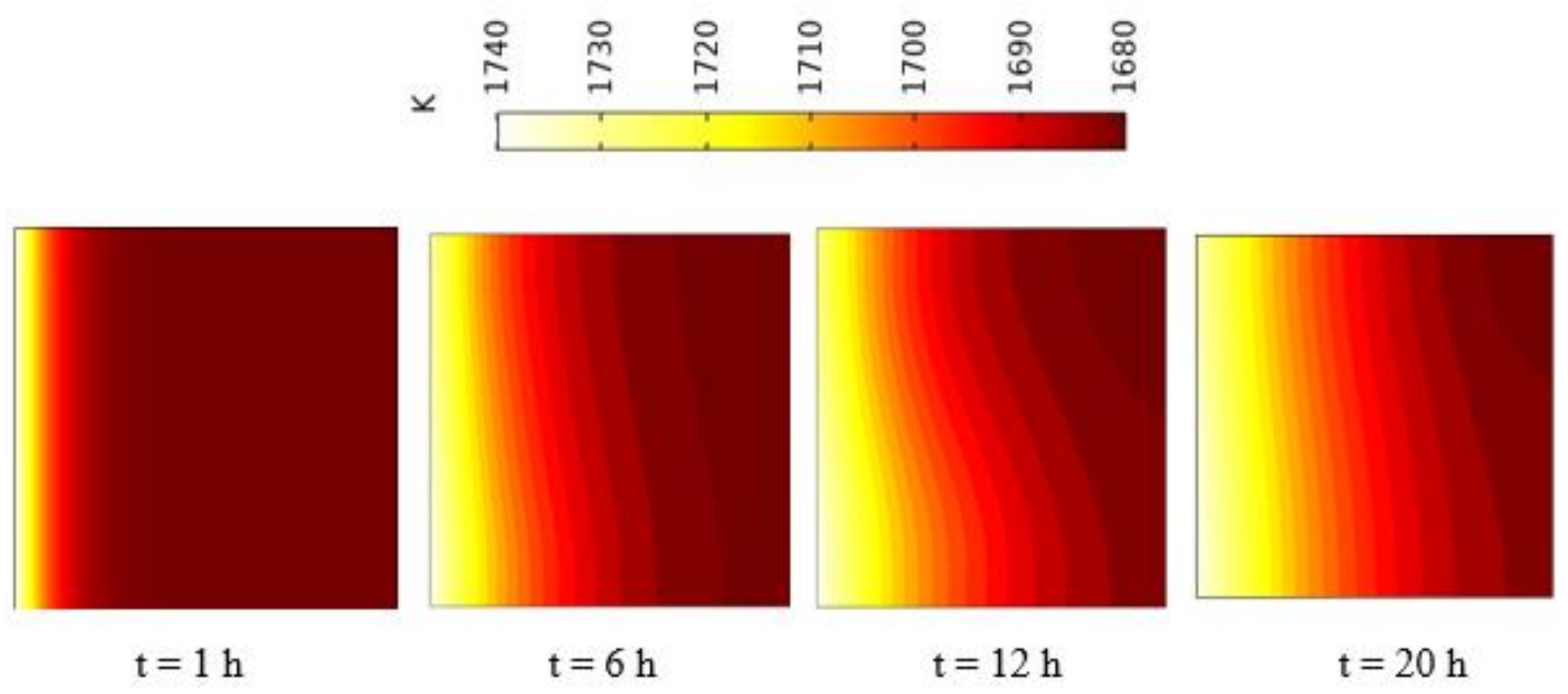




| Thermo-Physical Properties | Melting Temperature (K) | Latent Heat of Fusion (J/kg) | Density (kg/m3) | Specific Heat (J/kg K) | Thermal Conductivity (W/m K) | Dynamic Viscosity (Pa·s) |
|---|---|---|---|---|---|---|
| NaNO3 | Tsol = 578 Tliq = 580 | 176,000 | ρsol = 2180 ρliq = 1908 | cp,sol = 1600 cp,liq = 1655 | ksol = 0.8 kliq = 0.6 | µ = 0.00269 |
| Silicon | Tsol = 1686 Tliq = 1688 | 1,800,000 | ρsol = 2330 ρliq = 2570 | cp,sol = cp,liq = 1040 | ksol = 25 kliq = 50 | µ = 0.0008 |
| Charging | Discharging | ||||
|---|---|---|---|---|---|
| Parameters | Silicon | NaNO3 | Parameters | Silicon | NaNO3 |
| Subcooling | 8 K | Supercooling | 8 K | ||
| Aspect ratio | 1 (0.1 m × 0.1 m) | Aspect ratio | 1 (0.1 m × 0.1 m) | ||
| Heat flux (x = 0, y) | 2500,5000,7500 (W/m2) | Heat flux (x = 0, y) | −7500 W/m2 | ||
| Velocity | u,v (x = 0,L and y = 0,H) = 0 | Velocity | u,v (x = 0,L and y = 0,H) = 0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ray, A.K.; Rakshit, D.; Ravi Kumar, K.; Gurgenci, H. A Comparative Study of High-Temperature Latent Heat Storage Systems. Energies 2021, 14, 6886. https://doi.org/10.3390/en14216886
Ray AK, Rakshit D, Ravi Kumar K, Gurgenci H. A Comparative Study of High-Temperature Latent Heat Storage Systems. Energies. 2021; 14(21):6886. https://doi.org/10.3390/en14216886
Chicago/Turabian StyleRay, Alok Kumar, Dibakar Rakshit, K. Ravi Kumar, and Hal Gurgenci. 2021. "A Comparative Study of High-Temperature Latent Heat Storage Systems" Energies 14, no. 21: 6886. https://doi.org/10.3390/en14216886
APA StyleRay, A. K., Rakshit, D., Ravi Kumar, K., & Gurgenci, H. (2021). A Comparative Study of High-Temperature Latent Heat Storage Systems. Energies, 14(21), 6886. https://doi.org/10.3390/en14216886







