New Experimental Approach for the Determination of the Heat Generation in a Li-Ion Battery Cell

Abstract

With regard to safety, efficiency and lifetime of battery systems, the thermal behavior of battery cells is of great interest. The use of models describing the thermoelectric behavior of battery cells improves the understanding of heat generation mechanisms and enables the development of optimized thermal management systems. In this work, a novel experimental approach is presented to determine both the irreversible heat due to ohmic losses and the reversible heat due to entropy changes directly via heat flow measurements. No additional information about thermal properties of the battery cell, such as heat capacity or thermal conductivity, are required. Thus, the exothermic and endothermic nature of reversible heat generated in a complete charge/discharge cycle can be investigated. Moreover, the results of the proposed method can potentially be used to provide an additional constraint during the identification process of the equivalent circuit model parameters. The described method is applied to a 23 $\mathrm{A}$$\mathrm{h}$ lithium titanate cell and the corresponding results are presented.

1. Introduction

The phenomenological modeling approach using an equivalent circuit model (ECM) to describe the electrical behavior of Li-Ion cells is widely used in academia and industry. The standard ECM of a Li-Ion battery cell consists of an ideal voltage source whose voltage depends on the state of charge (SoC), an internal ohmic resistance $R_0$, and one or more parallel resistor-capacitor (RC) networks that approximate transient effects with various time constants. Additionally, a voltage hysteresis dependent on the current flow direction and a Warburg impedance can be added to increase the model accuracy. However, accurate determination of the internal resistance and RC components is essential because they significantly affect the terminal voltage of the cell. In most of the literature dealing with RC models such as [1,2,3] among others, the capacitor of the RC-network is assumed to be constant when formulating the differential equation, which leads to the well known form

$$\frac{d{V}_i}{dt}=\frac{I}{C_i}-\frac{V_i}{R_i·C_i},$$

(1)

where $V_i$ is the voltage drop across the ith RC-network and I is the total amount of current flowing through the battery cell. In order to study the difference between varying orders of RC models and other types of lumped parameter models comparative research can be found in the literature [4,5]. Thereby, the model quality is often compared based on the accuracy of the terminal voltage. Of course, this is very important when the ECM is used for electrical considerations, such as SoC estimation [6]. However, if the model is coupled with a thermal simulation, the correct estimation of the generated heat is also of great interest [7,8].

In general, the heat generation in Li-Ion batteries under charge or discharge is considered to include two main effects [9,10,11]. On the one hand, the over-potential due to ohmic losses, charge transfer at the interfaces and mass transfer limitations in combination with the current flowing from the anode to the cathode and vice versa, causes the generation of an irreversible heat flow according to

$${\dot{Q}}_{\mathrm{irr}}=\left(V-V_{\mathrm{OCV}}\right)I,$$

(2)

where V is the terminal voltage, $V_{\mathrm{OCV}}$ the open circuit voltage (OCV) and I the current flowing through the cell. The irreversible heat is always exothermic, which is defined to be positive. Therefore, the discharge current must have a negative sign for Equation (2) to be consistent. In terms of the equivalent circuit model the over-potential and hence the irreversible heat can be expressed as

$${\dot{Q}}_{\mathrm{irr}}=\left(V_0+\sum _{i=1}^N{V}_i\right)I,$$

(3)

which is the sum of the voltage drops across the individual resistors times the total current I flowing through the battery cell. Thereby, $V_0$ is the voltage drop across the internal resistance, $V_i$ is the voltage drop across the ith of the N RC-networks employed in the ECM. In addition, according to the literature [12,13] an entropic heat flow is expected to appear due to charge and discharge reactions at the electrodes, which can be expressed as

$${\dot{Q}}_{\mathrm{rev}}=T\frac{\Delta S}{n·F}I=T\frac{\partial V_{\mathrm{OCV}}}{\partial T}I,$$

(4)

where T is the cell temperature, $\Delta S$ the entropy change, n the charge number pertaining to the reaction ($n=1$ for Li-Ion batteries), F the Faraday constant, and I the charge/discharge current. The reversible heat can be both exothermic or endothermic depending on the state of charge and the direction of current flow. The two parts from Equations (2) and (4) contribute to the total amount of heat flow ${\dot{Q}}_{\mathrm{tot}}$ generated by the cell. When combining dozens or hundreds of cells to form a large scale battery system, the thermal behavior of a single cell and hence its heat generation is of great interest. As concluded by Zhao et al. [14] the reversible heat should not be neglected in heat generation models. Especially, if the simulation of the thermoelectric behavior is used for the design of an appropriate thermal management system, which allows the battery system to be operated under the best possible conditions. In order to come up with such a model, experimental efforts are required to identify the relevant model parameters.

In many studies the reversible heat is determined by measuring the change in open circuit voltage as a function of the cell temperature at various SoC levels [15,16]. This so-called potentiometric method leads to the entropic heat coefficient $\Delta S/\left(n·F\right)$ and therefore the reversible heat can be calculated according to Equation (4). This method has widely been used to study the influence of various parameters on the entropic coefficient [17]. Greifes et al. [18] has successfully combined the potentiometric method with the pulse relaxation method to safe time and effort. A detailed study of the potentiometric method by Zilberman et al. [19] even shows nonlinear behavior and hysteresis effects in the relationship between voltage and temperature and suggests to minimize the temperature pulse amplitude.

Another approach in the literature is based on accelerated-rate calorimetry (ARC), in which the generated heat and the corresponding increase in cell temperature are measured directly [20]. Under the assumption of a homogeneous cell temperature the total heat is calculated using the measured heat flow and the thermal properties of the cell according to

$${\dot{Q}}_{\mathrm{tot}}=m·c_p\frac{\mathrm{d}{T}_{\mathrm{m}}}{\mathrm{d}t}+{\dot{Q}}_{\mathrm{m}},$$

(5)

which essentially means that the total heat flow ${\dot{Q}}_{\mathrm{tot}}$ generated is equal to the measured heat flow ${\dot{Q}}_{\mathrm{m}}$ at the surface of the cell (i.e., the amount of heat exchanged with the environment per unit of time) plus the derivative of the measured cell temperature $T_{\mathrm{m}}$ with respect to time (i.e., the sensible heat stored in the thermal mass of the cell). This is necessary because the heat flow detected at the cell surface can be understood as the output of a first order delay element, whose input corresponds to the internally generated heat. A similar approach is reported in [21,22], where local heat flux and temperature measurements were used instead of an ARC. According to Sheng et al. [23] a similar approach with an improved calibration method was used to achieve results comparable to the one obtained from ARC measurements. The main benefit offered by the approaches described in [21,22,23] is the much lower cost of the required test equipment. In all these methods, which involve heat flow measurements, an increase in cell temperature is accepted during the course of an experiment. This implicates some difficulties, since most of the parameters depend on the cell temperature itself. In the method presented by Geng et al. [24], the cell is kept virtually in a thermal steady state during the determination of the entropic coefficient. This is achieved by a series of relatively short charge/discharge pulses that result in a moderate temperature change.

In all of the previously mentioned approaches, which aim to reduce the time required by the potentiometric method, thermal properties, such as the specific heat capacity and thermal conductivity, of the cell are needed. There are numerous methods to experimentally determine the specific heat capacity $c_{\mathrm{p}}$ of a battery cell. In contrast, the thermal conductivity k from the interior of the cell to its surface can be rather difficult to obtain.

This work describes a method to determine the entropic coefficient and the generated irreversible heat using localized heat flow measurements based on the pulse relaxation method. Thereby, the surface temperature of the cell is kept at a constant level, thus neither the specific heat capacity $c_{\mathrm{p}}$ nor the thermal conductivity k of the cell are required, which can be considered a significant advantage over existing approaches. To the authors’ knowledge this type of experimental approach has not been reported before.

In the following section, the experimental setup is described and an analytical solution for the expected thermal response is derived. Afterwards, the measurement results are presented and the agreement with the previously found analytical function is discussed. Furthermore, a reduced test procedure with minimal experimental effort is proposed. Finally, it is considered how this method could also improve the determination of RC parameters and where its limitations lie.

2. Materials and Methods

The method described in this paper was applied to a prismatic lithium titanate cell. The outer dimension of the cell is product-units=brackets-power (103 × 115 × 22) mm³ and it provides a nominal storage capacity of 23 $\mathrm{A}$$\mathrm{h}$. A specially developed test bench was used to measure the generated heat flow during charge/discharge cycles. The test bench consists of several temperature and heat flow sensors (THFS) arranged around the cell under test. The specially developed and calibrated THFS units comprise a type K thermocouple for measuring the surface temperature and a thermoelectric generator (Peltier-element) as a heat flow sensor. The calibration procedure used to achieve high accuracy heat flow measurements is described in [25]. The most important feature of the THFS units is the ability to actively control the surface temperature or the transmitted heat by means of a closed loop control system. At the same time, the heat flow emitted or absorbed by the battery cell is measured along with the surface temperature. A detailed description of the used test bench and its modes of operation is given in [26].

In this particular experiment with the cell mentioned above, a total of 44 sensors were used, each with an active measuring surface of (15 × 15) mm². The sensors thus cover approximately 30% of the cell surface, while the remaining area is covered with a thermal insulation foam. For this investigations, the THFS were operated in temperature controlled mode with a set point of 25 °C. In order to minimize the heat loss across the thermal insulation foam in between the active THFS units, the complete setup is placed inside an air-conditioned chamber (see Figure 1). The temperature inside the chamber is maintained at the same level as the surface temperature of the cell by means of a radiator with a fan to generate a forced air flow.

To charge and discharge the battery cell a NL-1V8C320 source/sink device from Höcherl & Hackl (H&H) is used in conjunction with a specifically designed LabView™ interface. The cell voltage is measured at the battery terminals using separate sensing probes. For accurate voltage measurements a four channel 24-bit analog digital converter (ADC) from the NI-cDAQ series is used (NI-9219). In order to determine the actual current flow, the voltage drop across a calibrated shunt with a resistance of (103.694 ± 0.092) μΩ is measured. In accordance to the manufacturers specifications the ADC exhibits a type B standard uncertainty of ±9.5 μV for voltage measurements up to 100 $\mathrm{mV}$. Using the law of error propagation the combined standard uncertainty of the current measurement can be calculated to be $\pm 0.1$ $\mathrm{A}$, which corresponds ±0.1% for current values up to 100 $\mathrm{A}$.

At the beginning of the experiment the cell is in thermal and electrical equilibrium at 90% SoC. The cell is then discharged to 10% SoC with a sequence of 10 constant current pulses. The exact same sequence of current pulses is then used to charge the cell in order to reach the initial SoC, thus completing a full discharge/charge cycle. The maximum SoC range, which can be covered by this type of experiment depends on the internal resistance of the cell and the utilized C-rate. Therefore, the headroom between the open circuit voltage and the end-of-charge voltage must be large enough to account for the voltage drop across the internal resistance caused by the highest current pulse amplitude. A relaxation phase of 1 $\mathrm{h}$ is introduced between two consecutive current pulses in order to allow the cell to approach the thermal equilibrium state. The experiment was repeated with five different current levels as given in

Table 1. Sequence of applied current pulse amplitude and duration for the five conducted experiments. The transferred electrical charge $q_{\mathrm{el}}$ and therefore the SoC levels are identical in all experiments.

SoC before	0.25C		0.5C		1C		1.5C		3C
Pulse	${\mathit{I}}_{\mathbf{p}}$	${\mathit{t}}_{\mathbf{p}}$	${\mathit{I}}_{\mathbf{p}}$	${\mathit{t}}_{\mathbf{p}}$	${\mathit{I}}_{\mathbf{p}}$	${\mathit{t}}_{\mathbf{p}}$	${\mathit{I}}_{\mathbf{p}}$	${\mathit{t}}_{\mathbf{p}}$	${\mathit{I}}_{\mathbf{p}}$	${\mathit{t}}_{\mathbf{p}}$
90.0%	$-5.8$$\mathrm{A}$	12 $\min$	$-11.5$$\mathrm{A}$	6 $\min$	$-23.1$$\mathrm{A}$	3 $\min$	$-34.5$$\mathrm{A}$	2 $\min$	$-69.1$$\mathrm{A}$	1 $\min$
85.0%	$-5.8$$\mathrm{A}$	12 $\min$	$-11.5$$\mathrm{A}$	6 $\min$	$-23.1$$\mathrm{A}$	3 $\min$	$-34.5$$\mathrm{A}$	2 $\min$	$-69.1$$\mathrm{A}$	1 $\min$
80.0%	$-5.8$$\mathrm{A}$	24 $\min$	$-11.5$$\mathrm{A}$	12 $\min$	$-23.1$$\mathrm{A}$	6 $\min$	$-34.5$$\mathrm{A}$	4 $\min$	$-69.2$$\mathrm{A}$	2 $\min$
69.9%	$-5.8$$\mathrm{A}$	24 $\min$	$-11.5$$\mathrm{A}$	12 $\min$	$-23.1$$\mathrm{A}$	6 $\min$	$-34.5$$\mathrm{A}$	4 $\min$	$-69.2$$\mathrm{A}$	2 $\min$
59.9%	$-5.8$$\mathrm{A}$	24 $\min$	$-11.5$$\mathrm{A}$	12 $\min$	$-23.1$$\mathrm{A}$	6 $\min$	$-34.6$$\mathrm{A}$	4 $\min$	$-69.2$$\mathrm{A}$	2 $\min$
49.8%	$-5.8$$\mathrm{A}$	24 $\min$	$-11.5$$\mathrm{A}$	12 $\min$	$-23.1$$\mathrm{A}$	6 $\min$	$-34.6$$\mathrm{A}$	4 $\min$	$-69.2$$\mathrm{A}$	2 $\min$
39.7%	$-5.8$$\mathrm{A}$	24 $\min$	$-11.5$$\mathrm{A}$	12 $\min$	$-23.1$$\mathrm{A}$	6 $\min$	$-34.5$$\mathrm{A}$	4 $\min$	$-69.2$$\mathrm{A}$	2 $\min$
29.7%	$-5.8$$\mathrm{A}$	24 $\min$	$-11.5$$\mathrm{A}$	12 $\min$	$-23.1$$\mathrm{A}$	6 $\min$	$-34.6$$\mathrm{A}$	4 $\min$	$-69.2$$\mathrm{A}$	2 $\min$
19.6%	$-5.8$$\mathrm{A}$	12 $\min$	$-11.5$$\mathrm{A}$	6 $\min$	$-23.1$$\mathrm{A}$	3 $\min$	$-34.5$$\mathrm{A}$	2 $\min$	$-69.2$$\mathrm{A}$	1 $\min$
14.6%	$-5.8$$\mathrm{A}$	12 $\min$	$-11.5$$\mathrm{A}$	6 $\min$	$-23.1$$\mathrm{A}$	3 $\min$	$-34.5$$\mathrm{A}$	2 $\min$	$-69.2$$\mathrm{A}$	1 $\min$
9.5%	$5.8$$\mathrm{A}$	12 $\min$	$11.5$$\mathrm{A}$	6 $\min$	$23.0$$\mathrm{A}$	3 $\min$	$34.5$$\mathrm{A}$	2 $\min$	$69.1$$\mathrm{A}$	1 $\min$
14.6%	$5.8$$\mathrm{A}$	12 $\min$	$11.5$$\mathrm{A}$	6 $\min$	$23.0$$\mathrm{A}$	3 $\min$	$34.5$$\mathrm{A}$	2 $\min$	$69.1$$\mathrm{A}$	1 $\min$
19.6%	$5.8$$\mathrm{A}$	24 $\min$	$11.5$$\mathrm{A}$	12 $\min$	$23.0$$\mathrm{A}$	6 $\min$	$34.5$$\mathrm{A}$	4 $\min$	$69.2$$\mathrm{A}$	2 $\min$
29.6%	$5.8$$\mathrm{A}$	24 $\min$	$11.5$$\mathrm{A}$	12 $\min$	$23.0$$\mathrm{A}$	6 $\min$	$34.5$$\mathrm{A}$	4 $\min$	$69.2$$\mathrm{A}$	2 $\min$
39.7%	$5.8$$\mathrm{A}$	24 $\min$	$11.5$$\mathrm{A}$	12 $\min$	$23.1$$\mathrm{A}$	6 $\min$	$34.5$$\mathrm{A}$	4 $\min$	$69.2$$\mathrm{A}$	2 $\min$
49.7%	$5.8$$\mathrm{A}$	24 $\min$	$11.5$$\mathrm{A}$	12 $\min$	$23.1$$\mathrm{A}$	6 $\min$	$34.5$$\mathrm{A}$	4 $\min$	$69.2$$\mathrm{A}$	2 $\min$
59.8%	$5.8$$\mathrm{A}$	24 $\min$	$11.5$$\mathrm{A}$	12 $\min$	$23.1$$\mathrm{A}$	6 $\min$	$34.5$$\mathrm{A}$	4 $\min$	$69.1$$\mathrm{A}$	2 $\min$
69.8%	$5.8$$\mathrm{A}$	24 $\min$	$11.5$$\mathrm{A}$	12 $\min$	$23.1$$\mathrm{A}$	6 $\min$	$34.5$$\mathrm{A}$	4 $\min$	$69.1$$\mathrm{A}$	2 $\min$
79.8%	$5.8$$\mathrm{A}$	12 $\min$	$11.5$$\mathrm{A}$	6 $\min$	$23.0$$\mathrm{A}$	3 $\min$	$34.4$$\mathrm{A}$	2 $\min$	$56.0$$\mathrm{A}$	1 $\min$
83.9%	$5.7$$\mathrm{A}$	12 $\min$	$11.5$$\mathrm{A}$	6 $\min$	$23.0$$\mathrm{A}$	3 $\min$	$33.9$$\mathrm{A}$	2 $\min$	$41.4$$\mathrm{A}$	1 $\min$

.

In the literature, many different methods are described to determine the internal resistance of the battery cell [27,28]. The aim of the approach presented in this paper was to capture the purely resistive component, thus any influence such as the change of OCV or transient phenomenon must be suppressed. For this purpose, a triggered high-speed voltage measurement with a pre-trigger buffer was employed. For each detected rising or falling edge in the current signal, the 2 $\mathrm{k}$$\mathrm{Hz}$ data acquisition system was activated for a few seconds. Since the DC power supply used can only realize a finite current slope, the data points captured during the ramp-up can be used to determine the internal resistance $R_0$. The results of such a hi-speed measurement is shown in Figure 2. At the beginning the cell exhibits an OCV of about $2.36$ $\mathrm{V}$. Then the DC power supply generates a current ramp to the desired discharge current of $-34.5$ $\mathrm{A}$, which is than held constant for the rest of the discharge pulse. Obviously, the terminal voltage of the cell drops further, due to the transient over-potential and SoC change, after the constant current has been reached. The ramp-up section of the curve, shown in red in Figure 2, lasts 100 $\mathrm{m}$$\mathrm{s}$ and is defined by a lower and upper current threshold. As can be seen, this section of the curve clearly exhibits a linear relationship between the terminal voltage of the cell and the applied current, indicating that purely resistive behavior is present. To quantify the slope and thus the ohmic resistance, a linear regression is used, which in this particular case yields a value of $0.6$ $\mathrm{m}$$\mathsf{\Omega }$.

Analytical Solution of the ECM Thermal Response

Consider a cell whose surface is actively cooled to maintain a temperature of lets say 25 °C. Furthermore, it is assumed that the cell was kept under these conditions long enough to reach a thermal equilibrium state before the experiment is started. If the cell is now charged or discharged using a constant current pulse with amplitude $I_{\mathrm{p}}$ for a certain duration $t_{\mathrm{p}}$, the generated heat leads to an internal temperature gradient and thus to a measurable heat flow at the surface of the cell. Consider the thermal state of the cell at time $t_{\mathrm{p}}$ (i.e., at the end of the charge or discharge pulse):

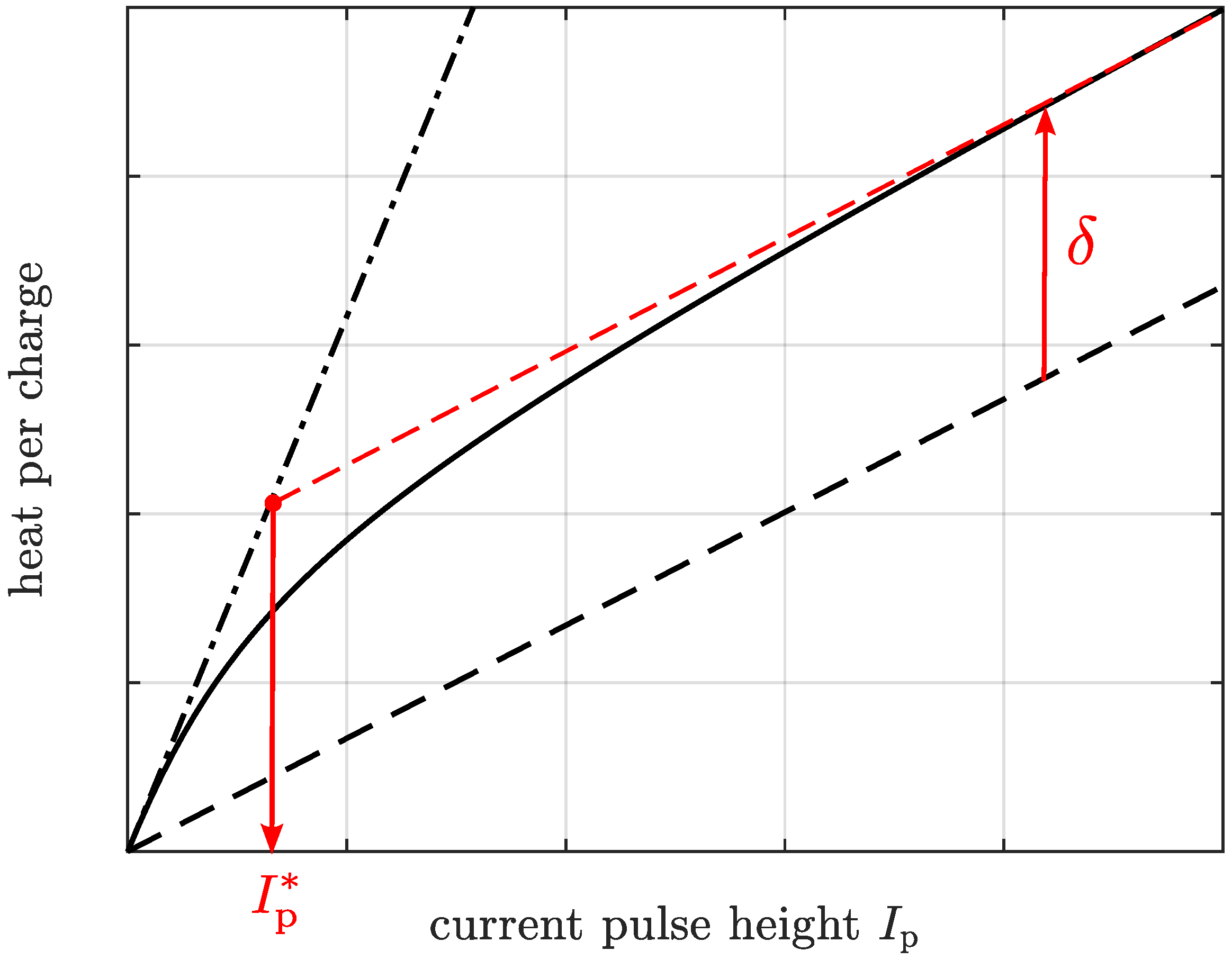
• A certain amount of heat $Q_{\mathrm{tot}}$ has been generated due to the current pulse.
• Some part of this heat has already been released into the environment due to the existing internal temperature gradient.
• The other part of the generated heat is still stored in the heat capacity of the battery cell.

Thereafter, the cell is kept in a thermal relaxation state, with no further charging or discharging taking place until the final time $t_{\mathrm{f}}$ is reached. Within this time, the stored thermal energy is released to the environment and the cell approaches the same thermal equilibrium state as before the current pulse was applied. Hence, it can be stated that the integral of the heat flow ${\dot{Q}}_{\mathrm{m}}$ measured at the surface is equal to the total amount of heat $Q_{\mathrm{tot}}$ generated by the charge or discharge pulse, as expressed by

$$Q_{\mathrm{tot}}={\int }_0^{t_{\mathrm{f}}}{\dot{Q}}_{\mathrm{m}}dt=Q_{\mathrm{irr}}+Q_{\mathrm{rev}}.$$

(6)

In the following, presupposing that the transferred charge $q_{\mathrm{el}}=I_{\mathrm{p}}·t_{\mathrm{p}}$ is constant (i.e., the pulse duration $t_{\mathrm{p}}$ is reduced by a factor of two, when the current pulse height $I_{\mathrm{p}}$ is doubled), analytical functions are derived to illustrate the dependency of the reversible and irreversible heat on the C-rate. Calculating the integral of Equation (4) over the current pulse duration $t_{\mathrm{p}}$ yields to

$$Q_{\mathrm{rev}}={\int }_0^{t_{\mathrm{p}}}T\frac{\Delta S}{n·F}{I}_{\mathrm{p}}dt=T\frac{\Delta S}{n·F}{I}_{\mathrm{p}}·t_{\mathrm{p}}=T\frac{\Delta S}{n·F}{q}_{\mathrm{el}},$$

(7)

which is a function of the electric charge $q_{\mathrm{el}}$, but independent of the C-rate itself. In the same way the irreversible heat can be calculated by integrating over the pulse duration $t_{\mathrm{p}}$ according to

$$Q_{\mathrm{irr}}={\int }_0^{t_{\mathrm{p}}}{I}_{\mathrm{p}}\left(V-V_{OCV}\right)dt=I_{\mathrm{p}}\left({\int }_0^{t_{\mathrm{p}}}{V}_{0}dt+{\int }_0^{t_{\mathrm{p}}}{V}_{1}dt\right).$$

(8)

Here the over potential $\left(V-V_{OCV}\right)$ is separated in two parts, where $V_0$ is the voltage drop across the internal resistance $R_0$ and $V_1$ is the voltage drop across the RC-network. For the sake of simplicity the analytical solution will be derived and discussed based on a single RC-network. However, the findings can be generalized for any number of RC-networks in an ECM.

The voltages $V_0$ and $V_1$ are given in Equations (9)–(12) together with the corresponding integrals used in Equation (8). Thereby, the input I of the differential equation given in Equation (1) is considered to be the heaviside function $I=I_{\mathrm{p}}·\sigma \left(t\right)$ with a constant current amplitude of $I_{\mathrm{p}}$. In addition, it is assumed that the initial voltage across the RC-network is $V_1\left(0\right)=0$, thus for $t\ge 0$ it follows that

$$\begin{array}{cc}\hfill V_0& =R_0·I_{\mathrm{p}},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\int }_0^{t_{\mathrm{p}}}{V}_{0}dt& =R_0·I_{\mathrm{p}}·t_{\mathrm{p}},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill V_1& =R_1·I_{\mathrm{p}}·\left(1-{\mathrm{e}}^{-t/\tau }\right),\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\int }_0^{t_{\mathrm{p}}}{V}_{1}dt& =R_1·I_{\mathrm{p}}·t_{\mathrm{p}}-R_1·I_{\mathrm{p}}·\tau ·\left(1-{\mathrm{e}}^{-t_{\mathrm{p}}/\tau }\right).\hfill \end{array}$$

(12)

Here, the irreversible heat generated during a current pulse can be normalized with the electrical charge, which leads to the following expression

$$\xi =\frac{Q_{\mathrm{irr}}}{q_{\mathrm{el}}}=R_0·I_{\mathrm{p}}+R_1·I_{\mathrm{p}}-\frac{R_1·I_{\mathrm{p}}·\tau }{t_{\mathrm{p}}}\left(1-{\mathrm{e}}^{-t_{\mathrm{p}}/\tau }\right).$$

(13)

In the above representation the current pulse amplitude $I_{\mathrm{p}}$ and the current pulse duration $t_{\mathrm{p}}$ are not independent from each other, but rather coupled through the constant electric charge transferred in each pulse. Therefore, Equation (13) can be expressed strictly as a function of either $I_{\mathrm{p}}$ or $t_{\mathrm{p}}$ leading to

$$\xi \left(I_{\mathrm{p}}\right)=R_0·I_{\mathrm{p}}+R_1·I_{\mathrm{p}}-\frac{R_1{\left(I_{\mathrm{p}}\right)}^2\tau }{q_{\mathrm{el}}}\left(1-{\mathrm{e}}^{-q_{\mathrm{el}}/\left(\tau ·I_{\mathrm{p}}\right)}\right)$$

(14)

and

$$\xi \left(t_{\mathrm{p}}\right)=\frac{(R_0+R1)q_{\mathrm{el}}}{t_{\mathrm{p}}}-\frac{R_1·q_{\mathrm{el}}·\tau }{{\left(t_{\mathrm{p}}\right)}^2}·\left(1-{\mathrm{e}}^{-t_{\mathrm{p}}/\tau }\right).$$

(15)

As can be seen in Figure 3, the analytical solution approaches a purely resistive behavior with $(R_0+R_1)·I_{\mathrm{p}}$ for small currents. This is reasonable, because a small current amplitude is equivalent to a long pulse duration, in which case the transient portion of $V_1$ becomes negligible if $t_{\mathrm{p}}\gg \tau$. To confirm this, the limit of the derivative of $\xi \left(I_{\mathrm{p}}\right)$ with respect to $I_{\mathrm{p}}$ must be calculated. In order to simplify this calculation, a change of variables is made using $\gamma =t_{\mathrm{p}}/\tau$ to represent the ratio between the pulse duration and the time constant of the RC-network in use, which leads to

$$\frac{d\xi \left(I_{\mathrm{p}}\right)}{d{I}_{\mathrm{p}}}{|}_{I_{\mathrm{p}}=\frac{q_{\mathrm{el}}}{\tau ·\gamma }}=R_0+R_1\left(1+{\mathrm{e}}^{-\gamma }\right)-\frac{2R_1\left(1-{\mathrm{e}}^{-\gamma }\right)}{\gamma }.$$

(16)

Therefore, the limit can be calculated as

$$\underset{I_{\mathrm{p}}\to 0}{lim}\frac{d\xi \left(I_{\mathrm{p}}\right)}{d{I}_{\mathrm{p}}}=\underset{\gamma \to \infty }{lim}{R}_0+R_1\left(1+{\mathrm{e}}^{-\gamma }\right)-\frac{2R_1\left(1-{\mathrm{e}}^{-\gamma }\right)}{\gamma }=R_0+R_1.$$

(17)

For large C-rates on the other hand, the generated heat per charge seams to approach a constant offset to the lower bound behavior $R_0·I_{\mathrm{p}}$. This offset can be calculated according to

$$\delta =\underset{I_{\mathrm{p}}\to \infty }{lim}\left(\xi \left(I_{\mathrm{p}}\right)-R_0·I_{\mathrm{p}}\right)=\underset{\gamma \to 0}{lim}\frac{R_1·q_{\mathrm{el}}}{\gamma ·\tau }-\frac{R_1·q_{\mathrm{el}}\left(1-{\mathrm{e}}^{-\gamma }\right)}{{\gamma }^2·\tau }=\frac{R_1·q_{\mathrm{el}}}{2·\tau },$$

(18)

when using the same change in variables introduced earlier. Between the two extreme cases $(I_{\mathrm{p}}\to 0)$ and $(I_{\mathrm{p}}\to \infty )$, a transition point can be defined using the intersection of the two asymptotes as defined by

$$(R_0+R_1)I_{\mathrm{p}}^{*}=R_0·I_{\mathrm{p}}^{*}+\delta .$$

(19)

The transition current $I_{\mathrm{p}}^{*}$ can be calculated from Equation (19) by a simple rearrangement of the terms, which leads to

$$I_{\mathrm{p}}^{*}=\frac{\delta }{R_1}=\frac{q_{\mathrm{el}}}{2·\tau }.$$

(20)

If the reversible heat $Q_{rev}$ in Equation (7) is normalized with the constant electric charge $q_{\mathrm{el}}$, it can be combined with the expression from Equation (14), which represents the normalized irreversible heat. This sum is equal to the integral of the measured heat flow ${\dot{Q}}_m$ divided by the integral of the measured current (i.e., the electric charge $q_{\mathrm{el}}$) according to

$$\frac{Q_{\mathrm{m}}}{q_{\mathrm{el}}}=\xi \left(I_{\mathrm{p}}\right)+\frac{\Delta S}{n·F}T.$$

(21)

The resulting relationship in Equation (21) can be used to perform a non-linear best fit on the experimental data. The constant term, i.e., the ordinate intercept, can than be divided by the absolute temperature T in order to calculate the entropic heat coefficient (EHC). Moreover, the above derived analytical solution is also valid for a sum of more than one RC-network. Indeed, the calculated limits in Equations (17) and (18) still hold, when replacing the single resistor value $R_1$ with the sum of all resistor values present $\left({\sum }_{i=1}^N{R}_i\right)$. Of course, the shape of the function in the transition region will change in this case, since it will be described by the superposition of N terms according to Equation (12). However, the effect on the constant term is negligible.

3. Results

The results of the measured heat flow will be discussed on the basis of an exemplary chosen data set, namely the 3C experiment between 60% to 70% SoC. For the comparison with the analytic function and the evaluation of the goodness of fit, all experiments at the above mentioned SoC interval are considered. In the last step, the results of different methods for determining the reversible heat over the whole SoC range are compared.

As an example, Figure 4 shows the result of a measurement carried out in accordance with the procedure described above. In order to achieve the desired 10% change in the SoC a 69 $\mathrm{A}$ (3C) current pulse with a duration of 2 $\min$ is applied. As can be seen, the total amount of heat generated during the discharge pulse is significantly higher than that during the charging phase. This already indicates the presence of reversible processes in this particular state of charge. Furthermore, it is noticeable that only a fraction of the generated heat is released during the first 2 $\min$ of the experiment (i.e., during the actual current pulse). The exact amount of heat released during each phase of the test are given in

Table 2. Total amount of heat generated during a 3C charge/discharge pulse, compared to the amount of heat released during the first 2 $\min$. Thereby, $t_{\mathrm{f}}=60\min$ is the total time of the experiment, while $t_{\mathrm{p}}=2\min$ is the current pulse duration.

Current Direction	Total Amount of Heat ${\int }_0^{{\mathit{t}}_{\mathbf{f}}}{\dot{\mathit{Q}}}_{\mathit{m}}d\mathit{t}$	Heat Released during Pulse ${\int }_0^{{\mathit{t}}_{\mathbf{p}}}{\dot{\mathit{Q}}}_{\mathit{m}}d\mathit{t}$	Percentage of Heat Released after ${\mathit{t}}_{\mathbf{p}}$
discharge	$2156.2$$\mathrm{J}$	$406.1$$\mathrm{J}$	81.2%
charge	$631.7$$\mathrm{J}$	$211.0$$\mathrm{J}$	66.6%

.

As shown in the close-up of Figure 4 the measured heat flow is still rising, even after the current has been switched off. This extreme case of the effect only takes place for very short current pulses and correspondingly high C-rates. Nevertheless, the percentage of heat released after the current pulse (i.e., for $t\ge t_{\mathrm{p}}$) is above 46% for all the measurements taken. Hence, it can be concluded that the thermal relaxation phase is an essential part of the test procedure to ensure that all heat generated during a charge or discharge pulse is captured by the heat flow measurements. The analysis of the measured heat flow as depicted in Figure 4 involves time integration over long time periods. Therefore, a high accuracy and in particular a low offset of the heat flow measurement is essential. A sensor offset as low as 1 $\mathrm{m}$$\mathrm{W}$ would add up to an error of $3.6$ $\mathrm{J}$ over one hour. Although this is less than 0.2% of the largest energy measured (i.e., $2156.2$ $\mathrm{J}$ during the 3C discharge pulse at 70% SoC), the error might be in the same order of magnitude as the measured value itself at another operating point. For instance, during the 1.5C charge pulse in Figure 5 the reversible and irreversible components cancel each other out, so that the total amount of heat measured is only $2.5$ $\mathrm{J}$.

In order to perform the nonlinear least square fit on the measured data, the analytic function given in Equation (21) should be used. However, since the measured behavior of the cell during charging and discharging is not always symmetrical, two different sets of coefficients were used for the fit. This leads to the final form

$$\left(I_{\mathrm{p}}<0\right)·{\xi }_{-}\left(I_{\mathrm{p}}\right)+\left(I_{\mathrm{p}}>0\right)·{\xi }_{+}\left(I_{\mathrm{p}}\right)+\frac{\Delta S}{n·F}T,$$

(22)

where ${\xi }_{-}\left(I_{\mathrm{p}}\right)$ and ${\xi }_{+}\left(I_{\mathrm{p}}\right)$ represent the irreversible heat according to Equation (14). Thereby, the internal ohmic resistance $R_0$ is determined based on current and voltage data as described earlier. Therefore, the remaining coefficients for the fit are $R_1$ and $\tau$, which represent an equivalent time constant and the total resistance of all transient phenomenon. In

Table 3. Fitted coefficients including the 95% confidence bound.

SoC Range	$\left(\mathbf{\Delta }\mathit{S}/\mathit{n}\mathit{·}\mathit{F}\right)\mathit{T}$	${\mathit{R}}_{1+}$	${\mathit{R}}_{1-}$	${\mathit{\tau }}_{+}$	${\mathit{\tau }}_{-}$
90% to 85%	$-5.4\left(31\right)$$\mathrm{m}$$\mathrm{V}$	$3.38\left(52\right)$$\mathrm{m}$$\mathsf{\Omega }$	$1.88\left(26\right)$$\mathrm{m}$$\mathsf{\Omega }$	$21\left(23\right)$$\mathrm{s}$	$41.7\left(95\right)$$\mathrm{s}$
85% to 80%	$-12.0\left(41\right)$$\mathrm{m}$$\mathrm{V}$	$2.93\left(57\right)$$\mathrm{m}$$\mathsf{\Omega }$	$1.90\left(32\right)$$\mathrm{m}$$\mathsf{\Omega }$	$27\left(18\right)$$\mathrm{s}$	$42.4\left(97\right)$$\mathrm{s}$
80% to 70%	$-26.2\left(43\right)$$\mathrm{m}$$\mathrm{V}$	$2.45\left(35\right)$$\mathrm{m}$$\mathsf{\Omega }$	$1.90\left(34\right)$$\mathrm{m}$$\mathsf{\Omega }$	$22\left(13\right)$$\mathrm{s}$	$45\left(12\right)$$\mathrm{s}$
70% to 60%	$-108.8\left(46\right)$$\mathrm{m}$$\mathrm{V}$	$3.13\left(43\right)$$\mathrm{m}$$\mathsf{\Omega }$	$2.40\left(37\right)$$\mathrm{m}$$\mathsf{\Omega }$	$48\left(14\right)$$\mathrm{s}$	$50\left(11\right)$$\mathrm{s}$
60% to 50%	$-16.6\left(36\right)$$\mathrm{m}$$\mathrm{V}$	$2.21\left(31\right)$$\mathrm{m}$$\mathsf{\Omega }$	$2.46\left(28\right)$$\mathrm{m}$$\mathsf{\Omega }$	$33\left(13\right)$$\mathrm{s}$	$48.4\left(77\right)$$\mathrm{s}$
50% to 40%	$1.7\left(26\right)$$\mathrm{m}$$\mathrm{V}$	$2.30\left(23\right)$$\mathrm{m}$$\mathsf{\Omega }$	$2.38\left(20\right)$$\mathrm{m}$$\mathsf{\Omega }$	$40.3\left(93\right)$$\mathrm{s}$	$45.5\left(61\right)$$\mathrm{s}$
40% to 30%	$-0.0\left(32\right)$$\mathrm{m}$$\mathrm{V}$	$2.27\left(28\right)$$\mathrm{m}$$\mathsf{\Omega }$	$2.47\left(25\right)$$\mathrm{m}$$\mathsf{\Omega }$	$44\left(12\right)$$\mathrm{s}$	$44.3\left(76\right)$$\mathrm{s}$
30% to 20%	$-3.7\left(29\right)$$\mathrm{m}$$\mathrm{V}$	$2.16\left(27\right)$$\mathrm{m}$$\mathsf{\Omega }$	$2.62\left(23\right)$$\mathrm{m}$$\mathsf{\Omega }$	$48\left(12\right)$$\mathrm{s}$	$43.3\left(68\right)$$\mathrm{s}$
20% to 15%	$-5.4\left(49\right)$$\mathrm{m}$$\mathrm{V}$	$2.36\left(60\right)$$\mathrm{m}$$\mathsf{\Omega }$	$3.15\left(44\right)$$\mathrm{m}$$\mathsf{\Omega }$	$50\left(18\right)$$\mathrm{s}$	$49\left(11\right)$$\mathrm{s}$
15% to 10%	$-6.2\left(48\right)$$\mathrm{m}$$\mathrm{V}$	$2.49\left(60\right)$$\mathrm{m}$$\mathsf{\Omega }$	$3.31\left(44\right)$$\mathrm{m}$$\mathsf{\Omega }$	$53\left(17\right)$$\mathrm{s}$	$48\left(11\right)$$\mathrm{s}$

the fitted coefficients for the data shown in Figure 5 are given together with their respective confidence bound.

4. Discussion

The fit shown in Figure 5 exhibits an adjusted coefficient of determination of ${\overline{R}}^2=0.9996$ and residuals below $2.5$ $\mathrm{m}$$\mathrm{J}$/$\mathrm{A}$$\mathrm{s}$, thus it can be stated that the observed data is well described by the model that has been utilized. Further, it is noticeable that the prediction bounds are small only for small currents around $I_{\mathrm{p}}=0 \mathrm{A}$. This means that the fit with the existing data set is incapable to extrapolate the behavior. The reason for this becomes clear, when the transition current is calculated according to Equation (20), which corresponds to $84.1$ $\mathrm{A}$ (3.7C). Hence, all available data points lie in the low current domain, where the dominant behavior is equal to

$$\frac{Q_{\mathrm{m}}}{q_{\mathrm{el}}}=\left(R_0+R_1\right)I_{\mathrm{p}}+\frac{\Delta S}{n·F}T.$$

(23)

Because the constant term depends only on the low current domain, it exhibits the lowest confidence bound of ±4.2% of the fitted value. The resistive coefficients $R_1$, which are fitted independently for both current directions, already show a slightly higher confidence bound of ±13.7% and ±15.4%, respectively. This can be explained due to the fact, that this coefficient also determines the behavior in the high current domain, where no experimental data is available. The effect becomes even more distinct for the time constants $\tau$, which according to Equation (18) only have an influence on the high current domain. As a consequence, the correspondingly high confidence intervals of ±22.0% and ±29.2% arise. If one seeks to improve the confidence bounds of these coefficients, experimental data describing the behavior in the high current domain is required. This can be accomplished in two different ways. First, the current amplitude $I_{\mathrm{p}}$ could be further increased. However, in doing so, the cell must be able to cope with the applied charge/discharge currents. In addition, the SoC range for experiments is reduced by the increasing voltage drop. Secondly, the electric charge $q_{\mathrm{el}}$ transferred in one current pulse could be reduced, since it is proportional to the transition point according to Equation (20). For instance, to achieve a transition point of $I_{\mathrm{p}}=23\mathrm{A}$ (1C), the electric charge must be reduced by a factor of 3.7, resulting in rather small SoC steps of only 2.7%. Despite the advantage of a higher resolution over the SoC range, the disadvantage of a significantly increased test duration might prevail. This is due to the fact that the thermal relaxation phase of 1 $\mathrm{h}$ is required after each of the nearly 40 current pulses.

However, if the main focus is on the determination of the EHC, the available data are conclusive. Under certain circumstances, the number of experiments required could be reduced. At low C-rates, the measured heat approaches the purely reversible component. Therefore, the mean value from the two experiments with the smallest positive and negative current could be used, respectively. Thereafter, the ordinate intersect, i.e., the entropic heat coefficient, can be calculated as

$$EHC=\frac{Q_{\mathrm{m}}\left(0.25C\right)+Q_{\mathrm{m}}(-0.25C)}{2·q_{\mathrm{el}}·T}.$$

(24)

When analyzing the deviation of the two methods shown in Figure 6 together with the fitted coefficients in Table 3, it can be stated that the deviation increases with increasingly asymmetrical behavior. This makes sense, since for perfectly symmetrical data any two points with the same current magnitude but opposite direction could be used for the averaging approach. However, as the asymmetric behavior increases, smaller and smaller current magnitudes would have to be used to obtain a good approximation for the constant term.

For verification purposes, the entropic heat coefficient at 65% SoC was also determined by means of the potentiometric method. To do so, the open circuit voltage was measured at 4 different temperatures in the range of 20 °C to 35 °C. The measured data in

Table 4. Open circuit voltage measured as a function of cell temperature at 65% SoC for verification purposes.

T	20 $°\mathrm{C}$	25 $°\mathrm{C}$	30 $°\mathrm{C}$	35 $°\mathrm{C}$
OCV	$2.338777$$\mathrm{V}$	$2.337033$$\mathrm{V}$	$2.335198$$\mathrm{V}$	$2.333188$$\mathrm{V}$

follows a quadratic behavior of the form

$$f\left(T\right)=-2.65\times {10}^{-6}{T}^2-2.26\times {10}^{-4}T+2.34.$$

(25)

After calculating the gradient of the second order polynomial describing the OCV, it can be evaluated at the relevant temperature of 25 $°\mathrm{C}$, which leads to

$$\frac{df\left(T\right)}{dT}=-5.30\times {10}^{-6}T-2.26\times {10}^{-4}{|}_{T=25°\mathrm{C}}=-358.5\mathsf{\mu }\mathrm{V}/\mathrm{K}.$$

(26)

This value is in good agreement with the values obtained from the fitted coefficient (i.e., $-365.0$ $\mathsf{\mu }$$\mathrm{V}$/$\mathrm{K}$) and averaging method (i.e., $-357.5$ $\mathsf{\mu }$$\mathrm{V}$/$\mathrm{K}$), respectively.

5. Conclusions and Outlook

The results presented in this paper show, that the described method is a viable approach to determine the entropic heat coefficient of a Li-Ion battery cell through heat flow measurements. A major difference to existing studies is the constant surface temperature of the battery cell throughout the experiment. Also, the approach might be advantageous because the used current pulse profile is identical to the one used for the parameter identification of the ECM. Hence, no additional experiments are needed to determine the entropic heat coefficient. In particular, it was demonstrated that the proposed method does not require the knowledge of the thermal properties of the cell, which are often difficult to obtain. It can be further concluded, that the presented method is not suitable to fit the parameters of more than one RC-network. Although, this would be possible in principal, many more measurements with various current amplitudes would be necessary. This requirement renders the approach unfeasible for this task.

However, further synergies of the test procedure can be utilized. For instance, the parameter $\tau$ could be identified based on the electrical relaxation data. This may reduce the high uncertainty of this parameter as shown in the results of this paper. Furthermore, the measured irreversible heat can potentially be used as an additional constraint in identifying the ECM parameters. Future work will therefore focus on combining the method presented here with the classical determination of the resistance and capacitance values of RC networks to provide an experimentally verified thermoelectric model. The reason for the dependency of the irreversible heat on the current direction, which has led to the observed asymmetric behavior, will also be investigated further. For this purpose, a next generation of the described test bench is being built to further increase the accuracy of the temperature and heat flow measurements.