Fractal Characterization of Pressure-Relief Gas Permeability Evolution in a Mining Fracture Network
Abstract
:1. Introduction
2. Fractal Model and Fractal Permeability Equation of Mining Fracture
2.1. Fractal Model of Mining Fracture
2.2. Seepage-Fractal Equation of Pressure-Relief Gas in Mining Fractures
2.2.1. The Basic Assumptions
- The gas flow in the goaf is regarded as seepage, obeys the generalized Darcy’s law, and is an incompressible fluid.
- The gas in the goaf flows at a mainly low-speed steady state.
- Gas migration in the goaf is an isothermal process.
2.2.2. Model Derivation
3. Methodology
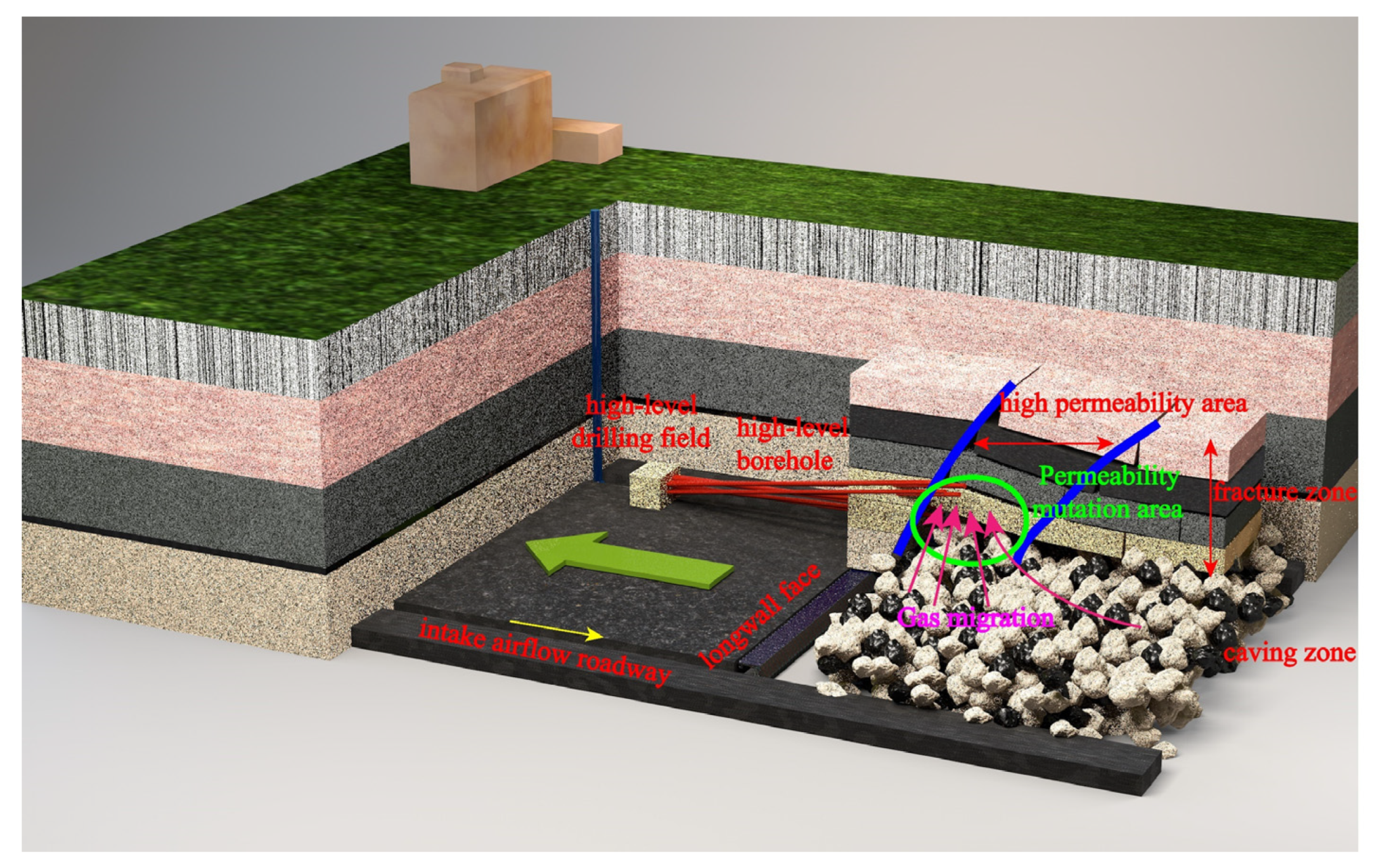
3.1. Engineering Background
3.2. Physical Similarity Simulation Experiment Design
3.2.1. The Experimental Equipment
3.2.2. The Similar Parameter Design of the Model
3.2.3. Model Building and Loading
3.2.4. The Extraction of the Model
3.3. Calculation Method of the Fractal Dimension
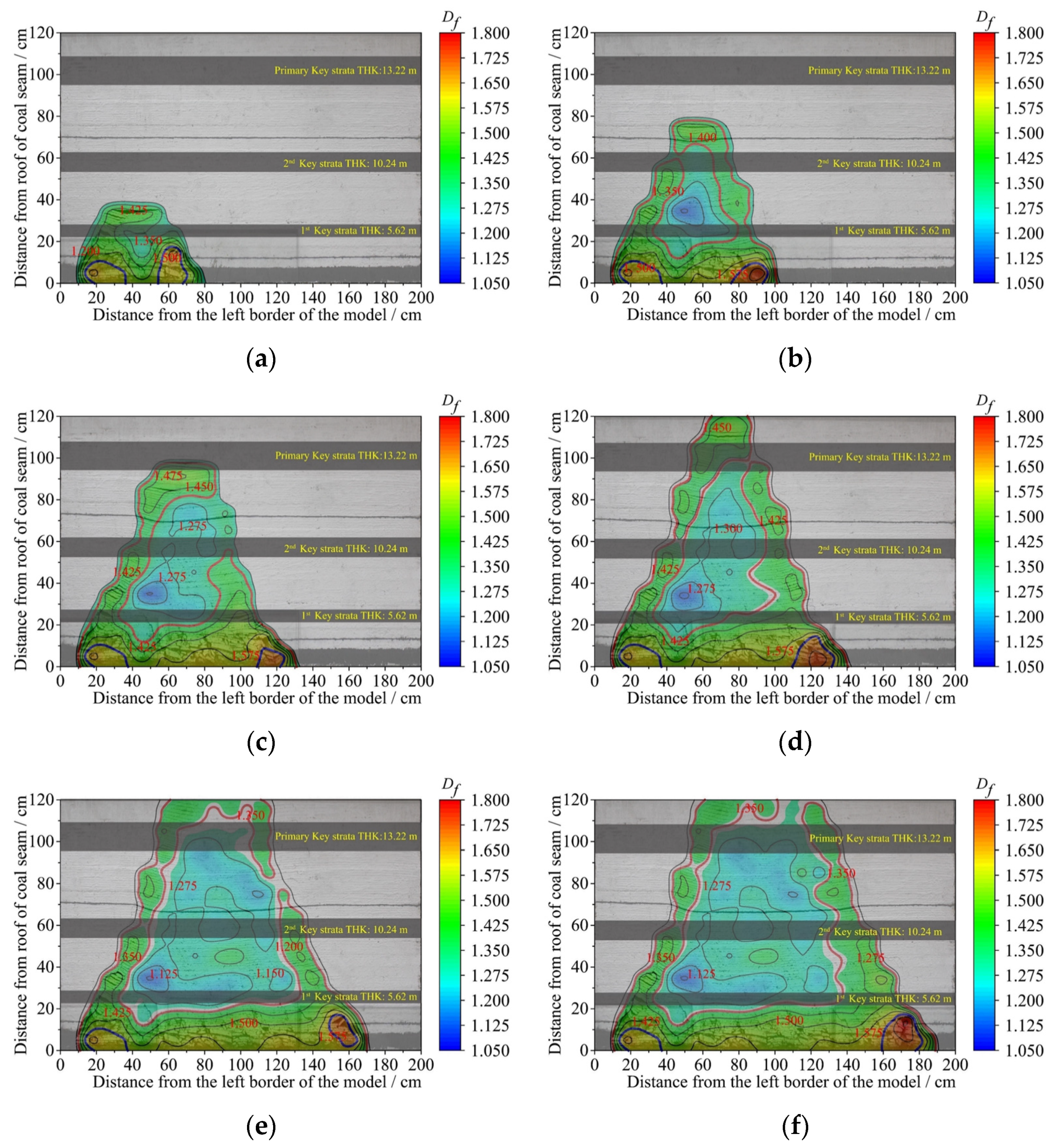
3.3.1. Calculation Method of the Fractal Dimension of the Fracture Aperture (Df)
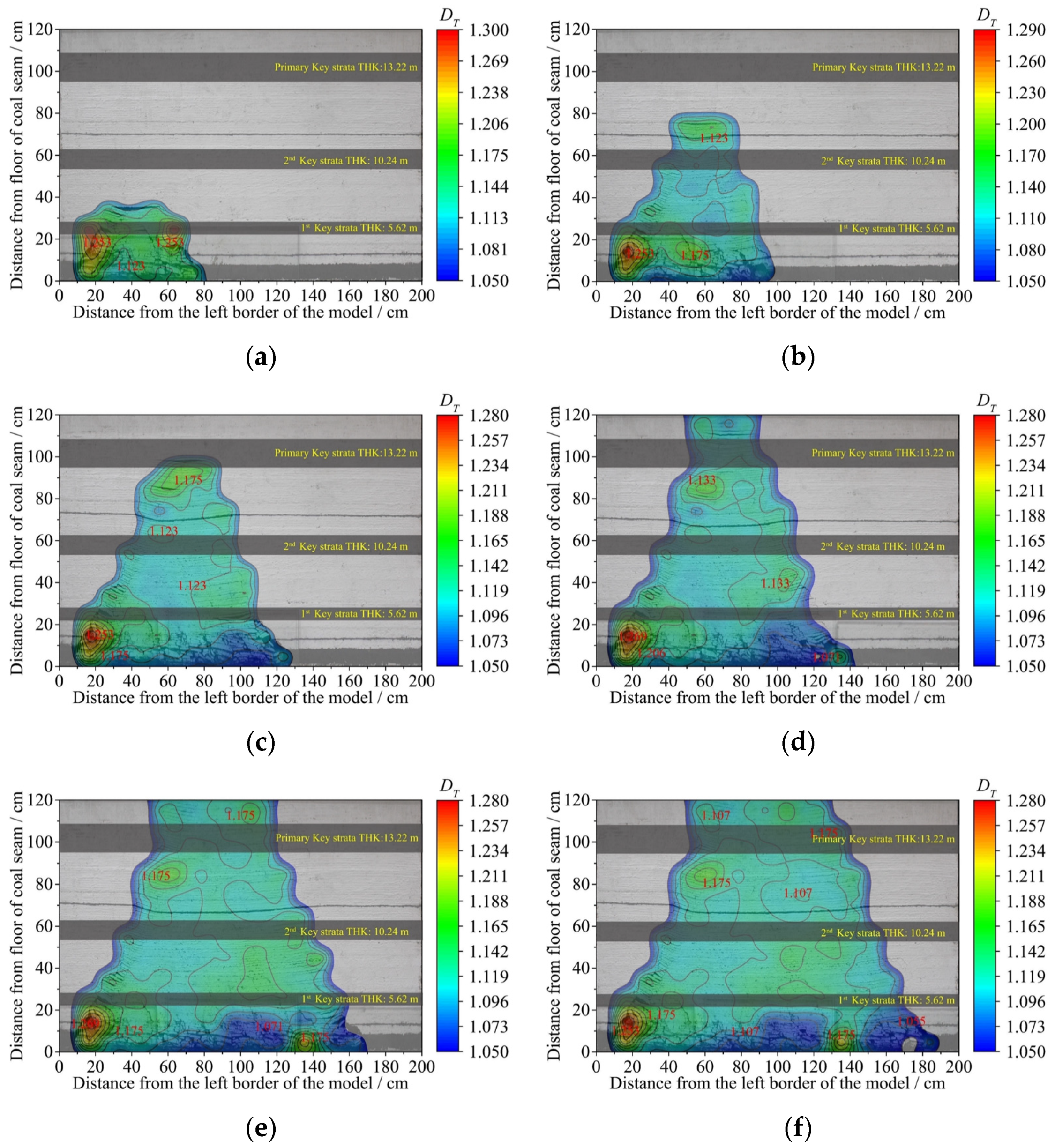
3.3.2. Calculation Method of the Fractal Dimension of the Fracture Tortuosity (DT)
4. Distribution Characteristics of the Fractal Dimension of the Fracture Network
4.1. Distribution Characteristics of the Fracture Opening Fractal Dimension
4.2. Distribution Law of the Tortuosity Fractal Dimension
4.3. Analysis of the Dynamic Evolution Process of the Fractal Dimension
5. Distribution Regulation of Pressure-Relief Gas Permeability and Its Engineering Verification
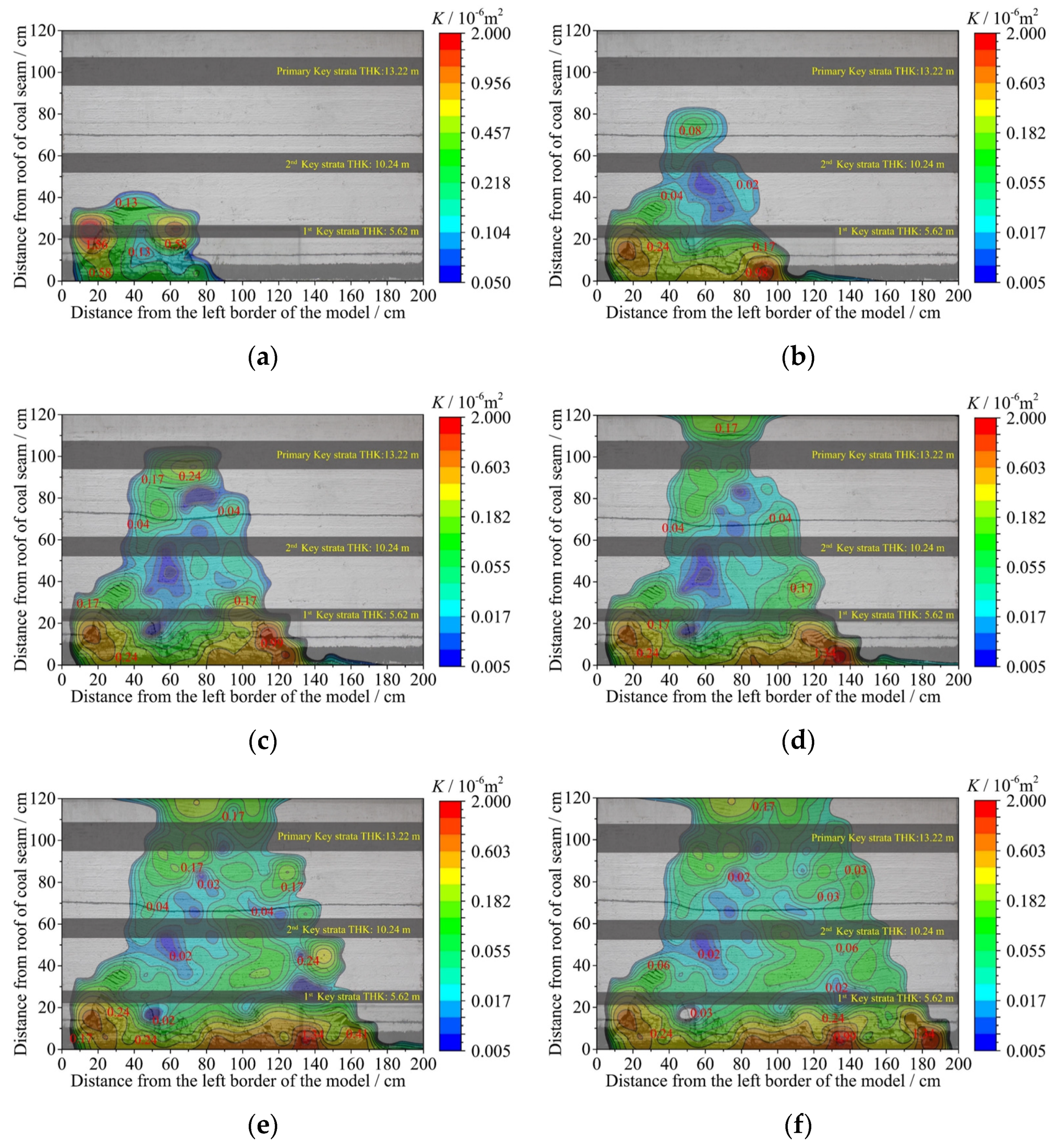
5.1. Distribution Regulation of Pressure-Relief Gas Permeability of Overburden Rock
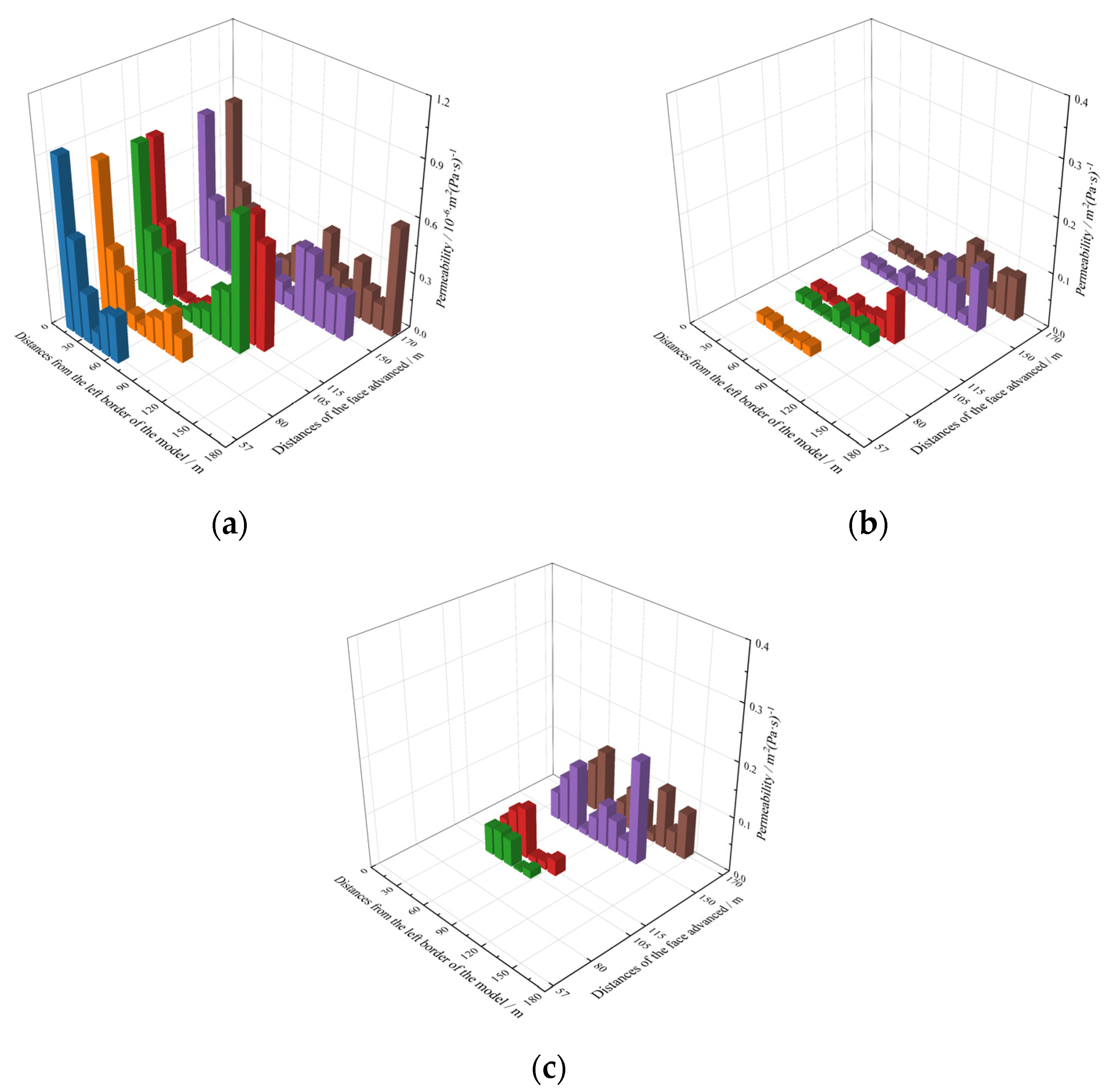
5.2. Analysis of the Evolution Process of the Pressure-Relief Gas Permeability
5.3. Inversion of the High Permeability Drilling Drainage Permeability
5.3.1. Permeability Measurement Method
- The permeability of pressure-relief gas in the goaf will not change due to extraction.
- The flow process of pressure-relief gas to the borehole is regarded as an isothermal process and conforms to Darcy’s law.
- The influence of the resistance along the way on the axial flow of gas in the borehole is ignored.
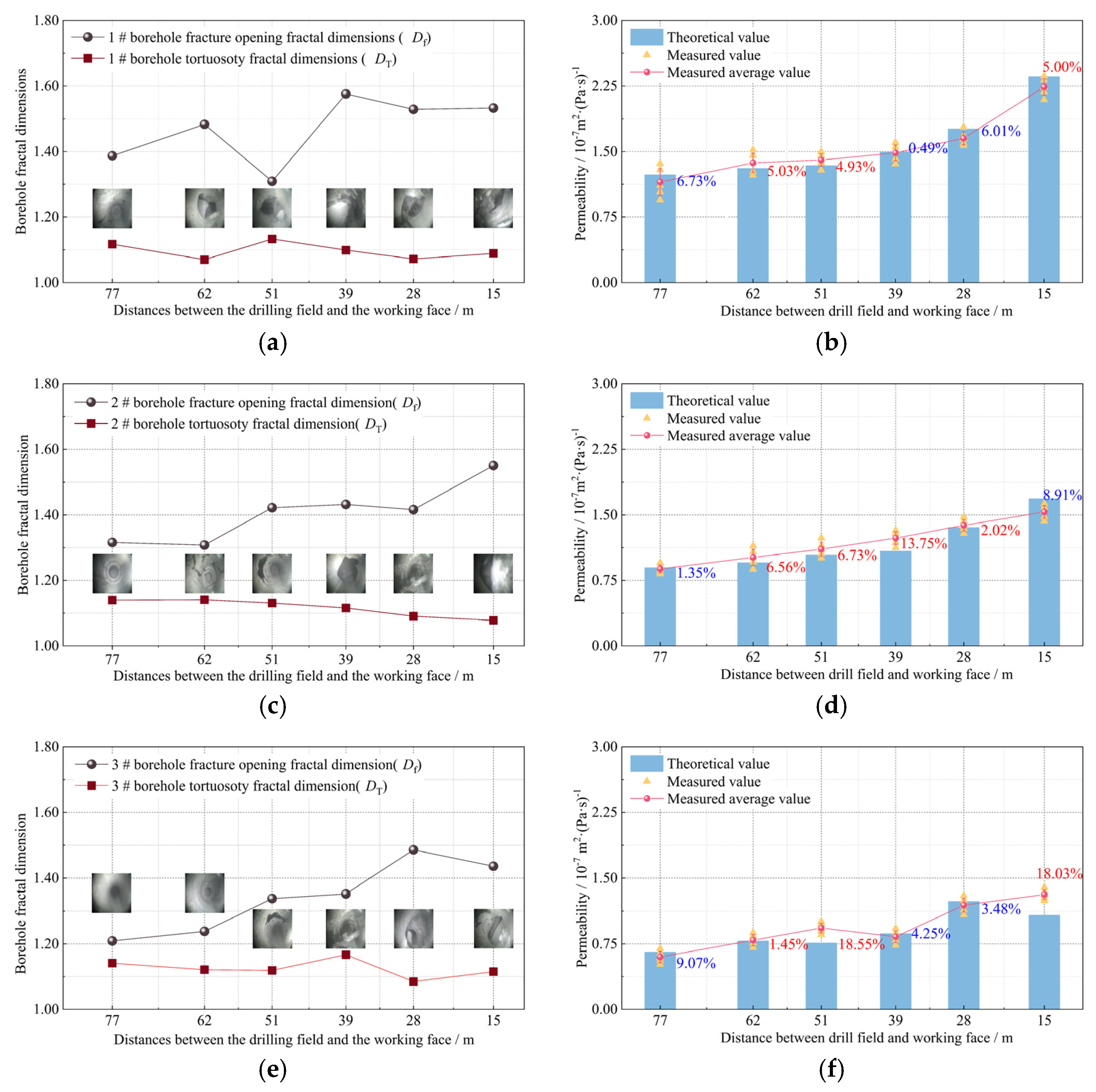
5.3.2. Permeability Inversion Results
6. Engineering Practice of Pressure-Relief Gas Drainage
6.1. Gas Drainage System Layout
6.1.1. Basis for the Layout of the Extraction System
6.1.2. Layout Parameters of the Extraction System
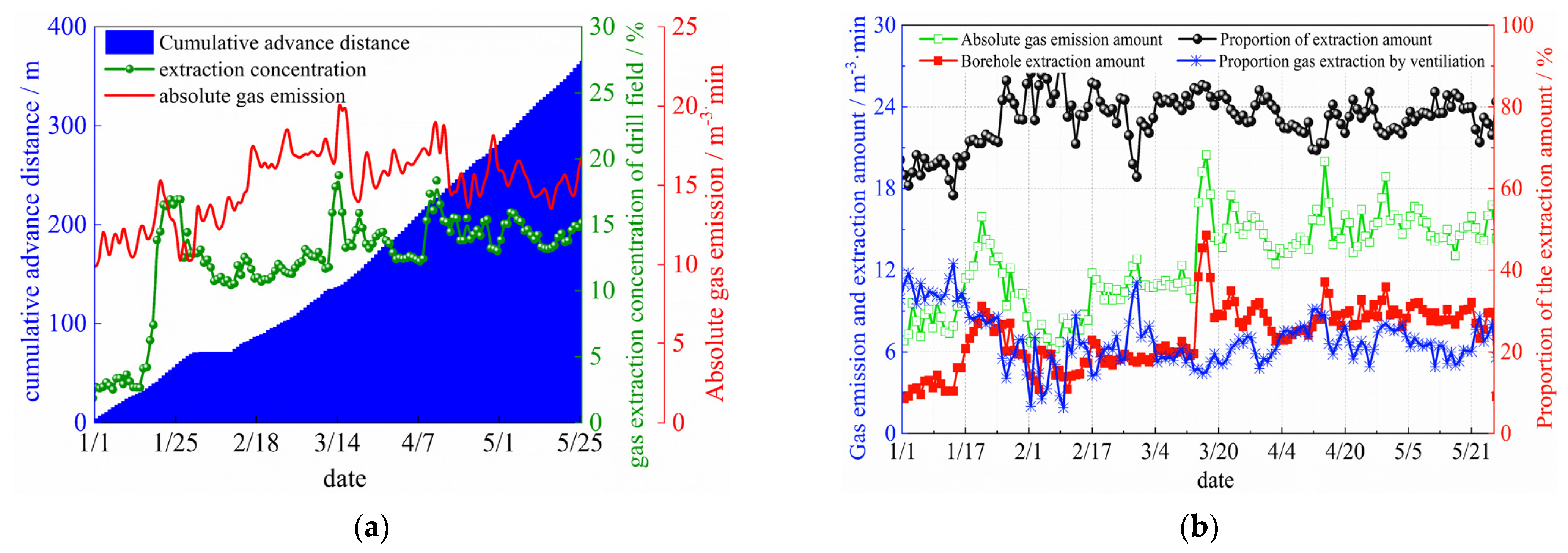
6.2. Analysis of the Gas Drainage Effect
7. Conclusions
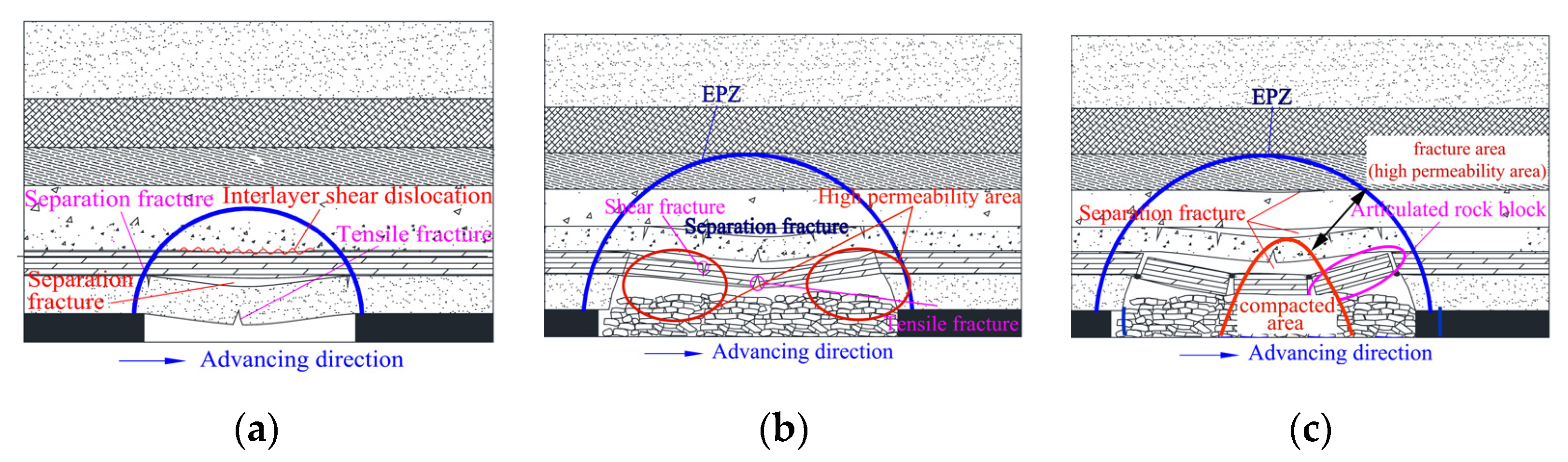
- The plane fracture network obtained by the physical simulation experiment is divided into small scales, and the fractal dimension of each module is calculated. This can clearly reflect the distribution and evolution of the fractal dimension and the tortuosity in different areas of overburden mining. The caving zone, the delamination zone at the top of the fracture network, and the fracture zones at both ends of the goaf are considered high fractal dimension regions where the fractal dimensions are above 1.425, and the maximum value can reach up to 1.70. The central compaction zone above the fall zone is considered a low fractal dimension region where the fractal dimensions are below 1.325. The fractal dimension of the step of a periodic pressure is found to be more than 20% higher than the surrounding area.
- The permeability control equation of the goaf fracture network represented by the fractal dimension does not contain any empirical parameters, and each parameter has a specific physical meaning, which can reveal the influence mechanism of the goaf fracture network permeability. The average error between the theoretical model and the actual value is only 8.11%, which is within the range of engineering accuracy. Meanwhile, it can guide how to use the fractal theory to study the pressure-relief gas flow model in the goaf.
- The high permeability area in the fracture network generally shows the shape of an elliptical paraboloid. Permeability evolution considers the main key layer contact gangue as the critical point that the panel advances to 115 m. Before approaching the main key layer contact gangue, the permeability increases with the advancing distance, and its maximum value is 2.0 × 10−7 m2. Once the key layer touches the gangue, the permeability gradually decreases.
- During the mining process, the pressure-relief gas drainage system is arranged in the abrupt permeability zone at the junction of the caving zone and the fracture zone, and the maximum pressure-relief gas extraction rate can reach 93.7%, which guarantees the safe and efficient recovery of the test longwall face.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| f(λ) | Probability density function of the fracture opening | v | Gas seepage velocity in borehole |
| Df | Fractal dimension of fractures opening | a | λmin/λmax |
| λ | Fracture opening | CL | Geometric similarity ratio |
| λmax | Maximum fracture opening | Cγ | Bulk density similarity ratio |
| λmin | Minimum fracture opening | Cσ | Stress similarity ratio |
| Lt(λ) | Actual seepage path length of gas in the fracture | Lp | Geometric parameters of the prototype |
| DT | Fractal dimension of fractures opening | Lm | Geometric parameters of the model |
| L0 | Straight line length of seepage in the fracture | γp | Severity parameter of the prototype |
| S | Flow area of pressure-relief gas in the fractured medium | γm | Severity parameter of the model |
| q(λ) | Gas flow rate per unit width | ε | Strain |
| q′(λ) | Gas flow per unit width after correction of tortuosity | α | Friction angle |
| ρ | Gas density | f | Friction coefficient |
| g | Acceleration of gravity | μ | Poisson’s ratio |
| µ | Kinematic viscosity coefficient of gas | Cε | Strain similarity ratio |
| ΔP | Gas pressure gradient | Cα | Friction angle similarity ratio |
| τ | Fissure tortuosity | Cf | Friction coefficient similarity ratio |
| Q | Total seepage flow in the fracture network | Cu | Poisson’s ratio similarity ratio |
| K | Permeability coefficient | CE | Elastic modulus similarity ratio |
| Kbh | Gas permeability around the borehole | Ct | Time similarity ratio |
| Qbh | Drainage flow rate of the borehole |
References
- Luo, Z.M.; Hao, Q.Q.; Wang, T.; Li, R.K.; Cheng, F.M.; Deng, J. Experimental study on the deflagration characteristics of methane-ethane mixtures in a closed duct. Fuel 2020, 259, 116295. [Google Scholar] [CrossRef]
- Sa, Z.; Liu, J.; Li, J.; Zhang, Y. Research on effect of gas pressure in the development process of gassy coal extrusion. Saf. Sci. 2019, 115, 28–35. [Google Scholar] [CrossRef]
- He, Z.; Wu, Q.; Wen, L.; Fu, G. A process mining approach to improve emergency rescue processes of fatal gas explosion accidents in Chinese coal mines. Saf. Sci. 2018, 111, 154–166. [Google Scholar] [CrossRef]
- Guo, X.; Li, Y.; Zhou, G.; He, Z.; Xu, Y. Stability Analysis and Reasonable Layout of Floor Drainage Roadway above Confined Water and under Mining Influence. Geofluids 2021, 2021, 5578717. [Google Scholar] [CrossRef]
- Zou, Q.; Liu, H.; Cheng, Z.; Zhang, T.; Lin, B. Effect of Slot Inclination Angle and Borehole-Slot Ratio on Mechanical Property of Pre-cracked Coal: Implications for ECBM Recovery Using Hydraulic Slotting. Nat. Resour. Res. 2020, 29, 1705–1729. [Google Scholar] [CrossRef]
- Zhao, P.; Zhuo, R.; Li, S.; Shu, C.-M.; Laiwang, B.; Jia, Y.; Shi, Y.; Suo, L. Analysis of advancing speed effect in gas safety extraction channels and pressure-relief gas extraction. Fuel 2020, 265, 116825. [Google Scholar] [CrossRef]
- Zhang, C.; Tu, S.H.; Zhao, Y.X. Compaction characteristics of the caving zone in a longwall goaf: A review. Environ. Earth Sci. 2019, 78, 27. [Google Scholar] [CrossRef]
- Zhou, F.B.; Xia, T.Q.; Wang, X.X.; Zhang, Y.F.; Sun, Y.N.; Liu, J.S. Recent developments in coal mine methane extraction and utilization in China: A review. J. Nat. Gas Sci. Eng. 2016, 31, 437–458. [Google Scholar] [CrossRef]
- Changbao, J.; Xiaodong, L.; Wensong, W.; Wenhui, W.; Minke, D. Three-dimensional visualization of the evolution of pores and fractures in reservoir rocks under triaxial stress. Powder Technol. 2021, 378, 585–592. [Google Scholar]
- Mark, C. Coal bursts that occur during development: A rock mechanics enigma. Int. J. Min. Ence Technol. 2017, 28, 35–42. [Google Scholar] [CrossRef]
- Warmuzinski, K. Harnessing methane emissions from coal mining. Process Saf. Environ. Prot. 2008, 86, 315–320. [Google Scholar] [CrossRef]
- Karacan, C.O.; Esterhuizen, G.S.; Schatzel, S.J.; Diamond, W.P. Reservoir simulation-based modeling for characterizing longwall methane emissions and gob gas venthole production. Int. J. Coal Geol. 2007, 71, 225–245. [Google Scholar] [CrossRef]
- Jun, L.; Changbao, J.; Zhuo, J.; Wensong, W.; Wanjun, Z.; Huan, Y. Three-dimensional physical model experiment of mining-induced deformation and failure characteristics of roof and floor in deep underground coal seams. Process Saf. Environ. Prot. 2021, 150, 400–415. [Google Scholar]
- Du, F.; Wang, K.; Zhang, X.; Xin, C.; Wang, G. Experimental Study of Coal-Gas Outburst: Insights from Coal-Rock Structure, Gas Pressure and Adsorptivity. Nat. Resour. Res. 2020, 29, 2481–2493. [Google Scholar] [CrossRef]
- Hu, G.; Xu, J.; Ren, T.; Gu, C.; Qin, W.; Wang, Z. Adjacent seam pressure-relief gas drainage technique based on ground movement for initial mining phase of longwall face. Int. J. Rock Mech. Min. Sci. 2015, 77, 237–245. [Google Scholar] [CrossRef]
- Guo, W.; Zhao, G.; Lou, G.; Wang, S. A New Method of Predicting the Height of the Fractured Water-Conducting Zone Due to High-Intensity Longwall Coal Mining in China. Rock Mech. Rock Eng. 2019, 52, 2789–2802. [Google Scholar] [CrossRef]
- Nazife, E. Microstructural investigation of subcritical crack propagation and Fracture Process Zone (FPZ) by the reduction of rock fracture toughness under cyclic loading. Eng. Geol. 2016, 208, 181–190. [Google Scholar]
- Wang, G.; Wu, M.M.; Wang, R.; Xu, H.; Song, X. Height of the mining-induced fractured zone above a coal face. Eng. Geol. 2017, 216, 140–152. [Google Scholar] [CrossRef]
- Wang, G.; Huang, W.; Sun, L.; Wu, M.; Zhang, X. High Drilling Methane Drainage in Fracturing Zones Formed by Water Injection into Boreholes. Arch. Min. Ences 2016, 61, 137–156. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Xu, J.; Xie, J. Effects of arch structure in unconsolidated layers on fracture and failure of overlying strata. Int. J. Rock Mech. Min. Sci. 2019, 114, 141–152. [Google Scholar] [CrossRef]
- Cyrul, T. Prediction of rock and gas outburst occurrence. Eng. Geol. 1993, 33, 241–250. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, Z.; Wei, W.; Guo, D.; Li, S.; Zhao, P. The critical factors for permeability-formation factor relation in reservoir rocks: Pore-throat ratio, tortuosity and connectivity. Energy 2019, 188, 116051. [Google Scholar] [CrossRef]
- Qian, M.; Xu, J. Study on the “O-shape” Circle distribution charateristics of mining-induced fractures in the overlying strata. J. China Coal Soc. 1998, 23, 466–469. [Google Scholar]
- Guo, H.; Yuan, L.; Shen, B.; Qu, Q.; Xue, J. Mining-induced strata stress changes, fractures and gas flow dynamics in multi-seam longwall mining. Int. J. Rock Mech. Min. Ences 2012, 54, 129–139. [Google Scholar] [CrossRef]
- Li, S.; Lin, H.; Zhao, P.; Xiao, P.; Pan, H. Dynamic evolution of mining fissure elliptic paraboloid zone and extraction coal and gas. J. China Coal Soc. 2014, 39, 1455–1462. [Google Scholar]
- Shu-gang, L.; Ping-wu, S.; Ming-gao, Q. Distribution features of Mining Fissure Elliptic Paraboloid Zone. Ground Press. Strat. Control 1999, 3, 44–46. [Google Scholar]
- Qu, Q.; Xu, J.; Wu, R.; Qin, W.; Hu, G. Three-zone characterisation of coupled strata and gas behaviour in multi-seam mining. Int. J. Rock Mech. Min. Sci. 2015, 78, 91–98. [Google Scholar] [CrossRef]
- Smith, J.; Ghabraie, B.; Ren, G.; Holden, L. Application of 3D laser scanner, optical transducers and digital image processing techniques in physical modelling of mining-related strata movement. Int. J. Rock Mech. Min. Sci. 2015, 100, 219–230. [Google Scholar]
- Guangming, Y.; Heping, X.; Jianfeng, Z.; Lun, Y. Fractal evolution of a crack network in overburden rock rtratum. Discret. Dyn. Nat. Soc. 2014, 5, 47–52. [Google Scholar]
- Wang, G.Y.; Yu, G.M.; Yu, Y.J.; Lu, S.B.; Kang, Y. Study on Cracks Fractal Evolution Laws of Mining Rock Mass. J. Min. Saf. Eng. 2012, 29, 859–863. [Google Scholar]
- Liu, R.; Li, B.; Jiang, Y.; Huang, N. Review: Mathematical expressions for estimating equivalent permeability of rock fracture networks. Hydrogeol. J. 2016, 24, 1623–1649. [Google Scholar] [CrossRef]
- Pointe, P.R.L. A method to characterize fracture density and connectivity through fractal geometry. Int. J. Rock Mech. Min. Ences Geomech. Abstr. 1988, 25, 421–429. [Google Scholar] [CrossRef]
- Pengxiang, Z.; Risheng, Z.; Shugang, L.; Chi-Min, S.; Yongyong, J.; Haifei, L.; Zechen, C.; Chun-Hsing, H.; Bin, L.; Peng, X. Fractal characteristics of methane migration channels in inclined coal seams. Energy 2021, 225, 120127. [Google Scholar]
- Zhao, P.X.; Zhuo, R.S.; Li, S.G.; Lin, H.F.; Shu, C.M.; Laiwang, B.; Jia, Y.Y.; Suo, L. Fractal characteristics of gas migration channels at different mining heights. Fuel 2020, 271, 117479. [Google Scholar] [CrossRef]
- Xue, D.J.; Zhou, H.W.; Wang, C.S.; Gao, H.L. Percolation model of mining-induced crack evolution of the overlying strata. J. China Univ. Min. Technol. 2013, 42, 917–922. [Google Scholar]
- Zhou, H.W.; Zhang, T.; Xue, D.J.; Xue, J.H. Evolution of mining-crack network in overburden strata of longwall face. J. China Coal Soc. 2011, 36, 1957–1962. [Google Scholar]
- Li, H.-Y.; Wang, W.-H.; Ji, Q.-X.; Zhang, L. Study on fissure development rule of overlying strata influenced by mining based on fractal theory. J. China Coal Soc. 2014, 39, 1023–1030. [Google Scholar]
- Xue, D.J.; Zhou, H.W.; Tang, X.L.; Zhao, Y.F. Evolution of mining induced enhancement and distribution of gas permeability in coal seam and surrounding rock. J. China Coal Soc. 2013, 38, 930–935. [Google Scholar]
- Yu, B. Analysis of flow in fractal porous media. Appl. Mech. Rev. 2008, 61, 050601. [Google Scholar] [CrossRef]
- Wheatcraft, S.W.; Tyler, S.W. An explanation of scale-dependent dispersivity in heterogeneous aquifers using concepts of fractal geometry. Water Resour. Res. 1988, 24, 566–578. [Google Scholar] [CrossRef]
- Si, G.; Jamnikar, S.; Lazar, J.; Shi, J.-Q.; Durucan, S.; Korre, A.; Zavšek, S. Monitoring and modelling of gas dynamics in multi-level longwall top coal caving of ultra-thick coal seams, part I: Borehole measurements and a conceptual model for gas emission zones. Int. J. Coal Geol. 2015, 144, 98–110. [Google Scholar] [CrossRef]
- Deng, J.; Liu, L.; Lei, C.; Wang, C.; Xiao, Y. Spatiotemporal distributions of the temperature and index gases during the dynamic evolution of coal spontaneous combustion. Combust. Sci. Technol. 2021, 193, 1679–1695. [Google Scholar] [CrossRef]
- Neuzil, C.; Tracy, J.V. Flow through fractures. Water Resour. Res. 1981, 17, 191–199. [Google Scholar] [CrossRef]
- Klimczak, C.; Schultz, R.A.; Parashar, R.; Reeves, D.M. Cubic law with aperture-length correlation: Implications for network scale fluid flow. Hydrogeol. J. 2010, 18, 851–862. [Google Scholar] [CrossRef]
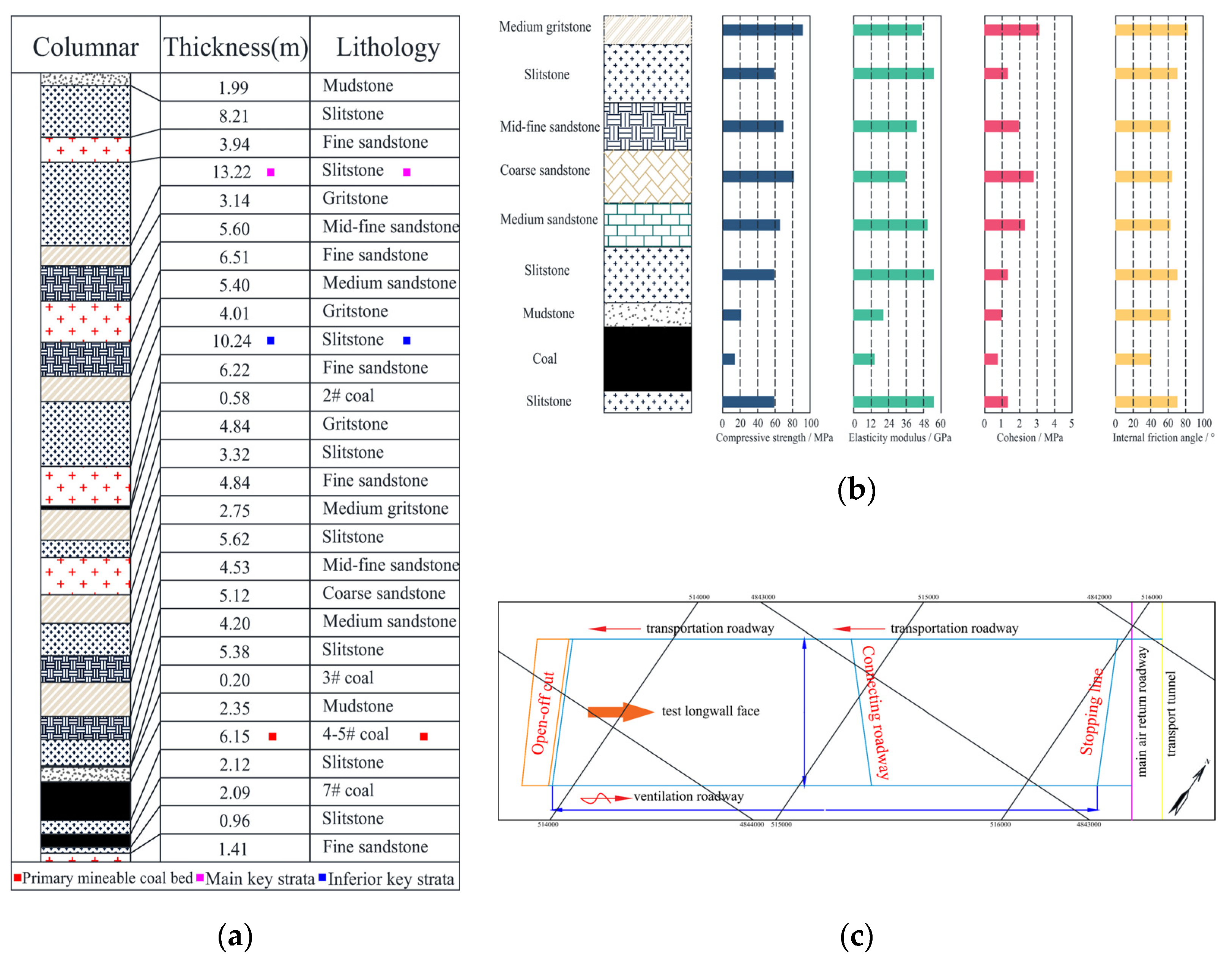
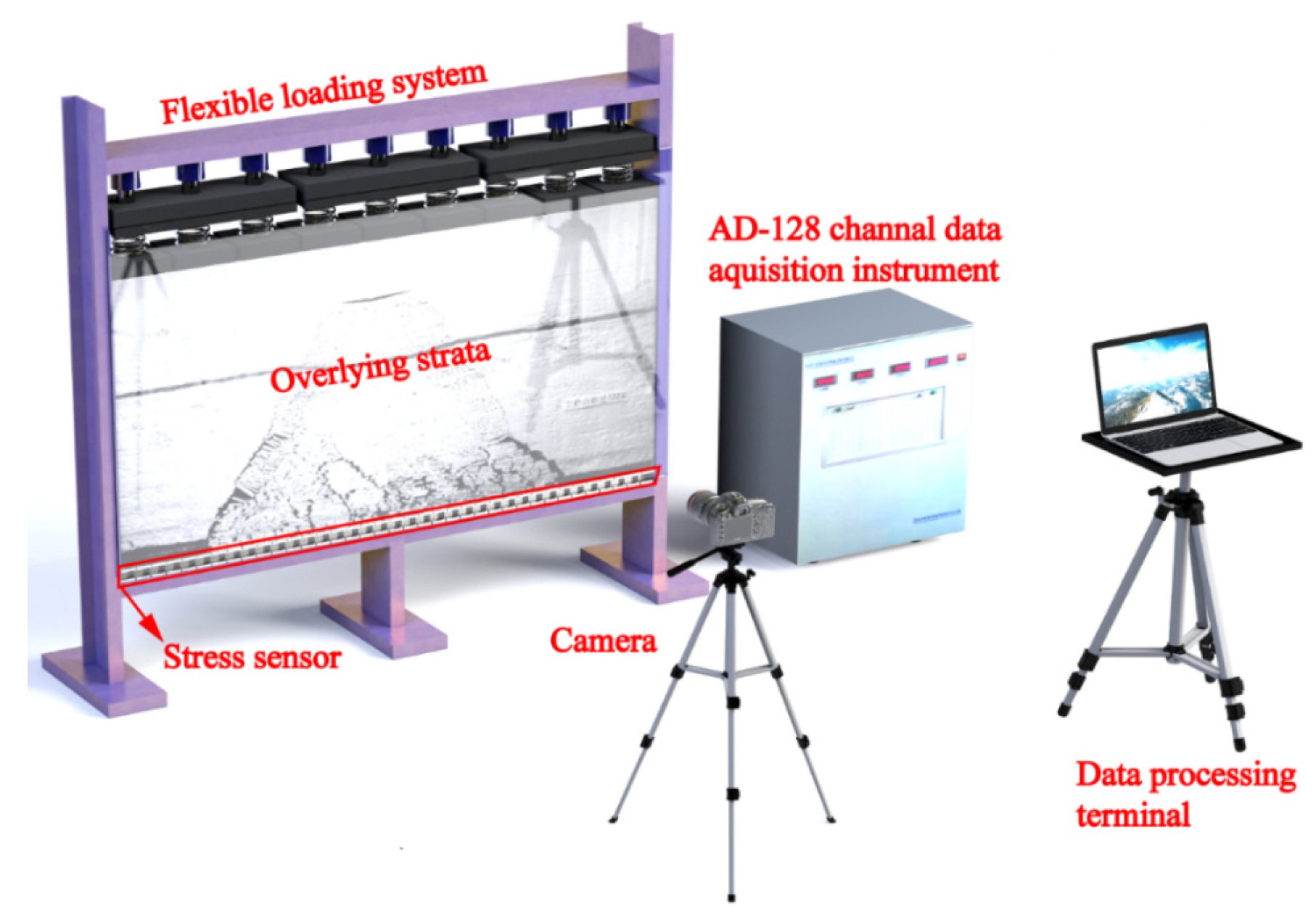
| Layer No. | Lithology | Thickness /cm | Layer No. | Lithology | Thickness /cm |
|---|---|---|---|---|---|
| 1 | Mudstone | 2.0 | 13 | Gritstone | 4.8 |
| 2 | Siltstone | 8.2 | 14 | Siltstone | 3.3 |
| 3 | Fine sandstone | 4.0 | 15 | Fine sandstone | 4.8 |
| 4 | Siltstone | 13.2 | 16 | Medium gritstone | 2.8 |
| 5 | Gritstone | 3.1 | 17 | Siltstone | 3.3 |
| 6 | Mid-fine sandstone | 5.6 | 18 | Mid-fine sandstone | 4.5 |
| 7 | Fine sandstone | 6.5 | 19 | Coarse sandstone | 5.1 |
| 8 | Medium sandstone | 5.4 | 20 | Medium sandstone | 4.2 |
| 9 | Gritstone | 4.0 | 21 | Siltstone | 5.4 |
| 10 | Siltstone | 10.2 | 22 | 3# coal seam | 0.2 |
| 11 | Fine sandstone | 6.2 | 23 | Mudstone | 2.4 |
| 12 | 2# coal seam | 0.6 | 24 | 4–5# coal seam | 6.2 |
| Lithology | Bulk Density /kN·m3 | Compressive Strength /MPa | Poisson’s Ratio | Ratio | |||
|---|---|---|---|---|---|---|---|
| Field | Model | Field | Model | Field | Model | ||
| Mudstone | 20.80 | 13.87 | 20.50 | 0.17 | 0.195 | 0.195 | 9:0.3:0.7 |
| Siltstone | 26.40 | 17.60 | 36.90 | 0.25 | 0.278 | 0.278 | 8:0.2:0.8 |
| Fine sandstone | 26.60 | 17.73 | 65.10 | 0.43 | 0.280 | 0.280 | 7:0.4:0.6 |
| Gritstone | 26.20 | 17.47 | 58.50 | 0.39 | 0.260 | 0.260 | 7:0.5:0.5 |
| Mid-fine sandstone | 26.00 | 17.33 | 48.80 | 0.33 | 0.253 | 0.253 | 8:0.4:0.6 |
| Medium sandstone | 26.50 | 17.67 | 46.20 | 0.31 | 0.230 | 0.230 | 8:0.3:0.7 |
| Coarse sandstone | 26.30 | 17.53 | 69.00 | 0.46 | 0.250 | 0.250 | 7:0.3:0.7 |
| Coal seam | 14.60 | 9.73 | 13.50 | 0.09 | 0.275 | 0.275 | 9:0.5:0.5 |
| Drilling Number | The Projected Length of the Borehole in the Advancing Direction (m) | End Position of Drilling | |
|---|---|---|---|
| Vertical Distance (m) | Horizontal Distance (m) | ||
| 1# | 100 | 3 | 5 |
| 2# | 100 | 18 | 12 |
| 3# | 100 | 30 | 20 |
| Drilling Number | Drilling Diameter (mm) | End Position of Drilling | |
|---|---|---|---|
| Vertical Distance (m) | Horizontal Distance (m) | ||
| 1–1# | 133 | 3 | 2 |
| 1–2# | 133 | 6 | 5 |
| 1–3# | 133 | 9 | 8 |
| 1–4# | 133 | 12 | 12 |
| 1–5# | 133 | 15 | 15 |
| 2–1# | 133 | 18 | 6 |
| 2–2# | 133 | 21 | 10 |
| 2–3# | 133 | 24 | 12 |
| 2–4# | 133 | 27 | 16 |
| 2–5# | 133 | 30 | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Li, S.; Lin, H.; Ding, Y.; Shuang, H.; Liu, S.; Tian, Y. Fractal Characterization of Pressure-Relief Gas Permeability Evolution in a Mining Fracture Network. Energies 2021, 14, 7031. https://doi.org/10.3390/en14217031
Xu P, Li S, Lin H, Ding Y, Shuang H, Liu S, Tian Y. Fractal Characterization of Pressure-Relief Gas Permeability Evolution in a Mining Fracture Network. Energies. 2021; 14(21):7031. https://doi.org/10.3390/en14217031
Chicago/Turabian StyleXu, Peiyun, Shugang Li, Haifei Lin, Yang Ding, Haiqing Shuang, Sibo Liu, and Yu Tian. 2021. "Fractal Characterization of Pressure-Relief Gas Permeability Evolution in a Mining Fracture Network" Energies 14, no. 21: 7031. https://doi.org/10.3390/en14217031
APA StyleXu, P., Li, S., Lin, H., Ding, Y., Shuang, H., Liu, S., & Tian, Y. (2021). Fractal Characterization of Pressure-Relief Gas Permeability Evolution in a Mining Fracture Network. Energies, 14(21), 7031. https://doi.org/10.3390/en14217031






