Effects of Damaged Rotor on Wake Dynamics of Vertical Axis Wind Turbines
Abstract
:1. Introduction
2. Numerical Modelling of the Vertical Axis Wind Turbine
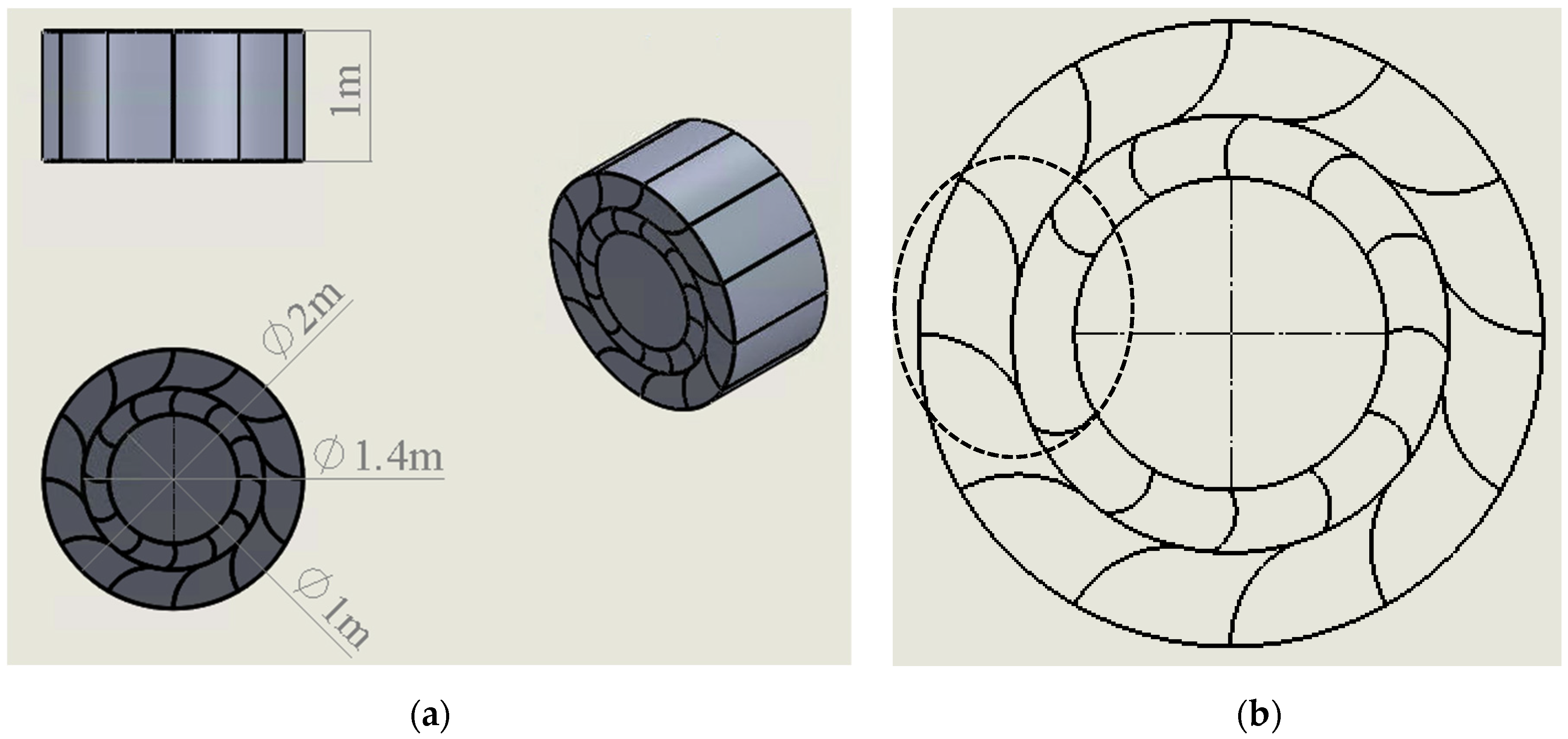
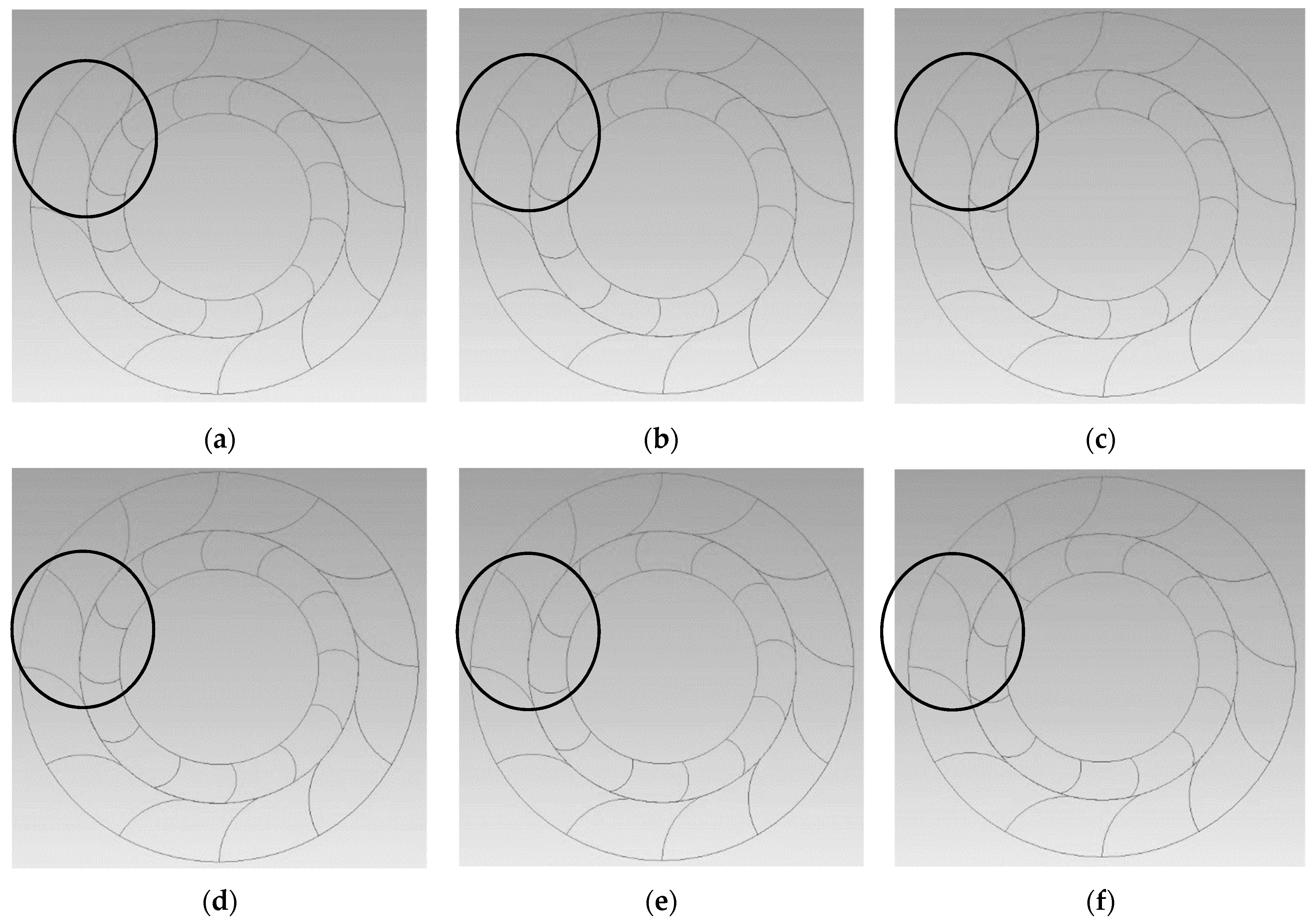
2.1. Geometry of the Vertical Axis Wind Turbine
2.2. Meshing of the Flow Domain
2.3. Boundary Conditions and Fluid Properties
2.4. Rotation of the Vertical Axis Wind Turbine
- P is the power generated by the VAWT; P = ωT, where ω is the rotational speed (in rad/s) and T is the torque (in Nm) generated by the rotor.
- A is the swept area of the VAWT (in m2); A = Dh, where D is the rotor’s outer diameter (=1.4 m) and h is the height of the VAWT (=1 m).
- R is the rotor radius (in m); R = D/2 = 0.7 m.
2.5. Turbulence Modelling
2.6. Temporal Discretisation
3. Results and Discussions
3.1. Torque Output Comparison between Healthy and Damaged VAWTs
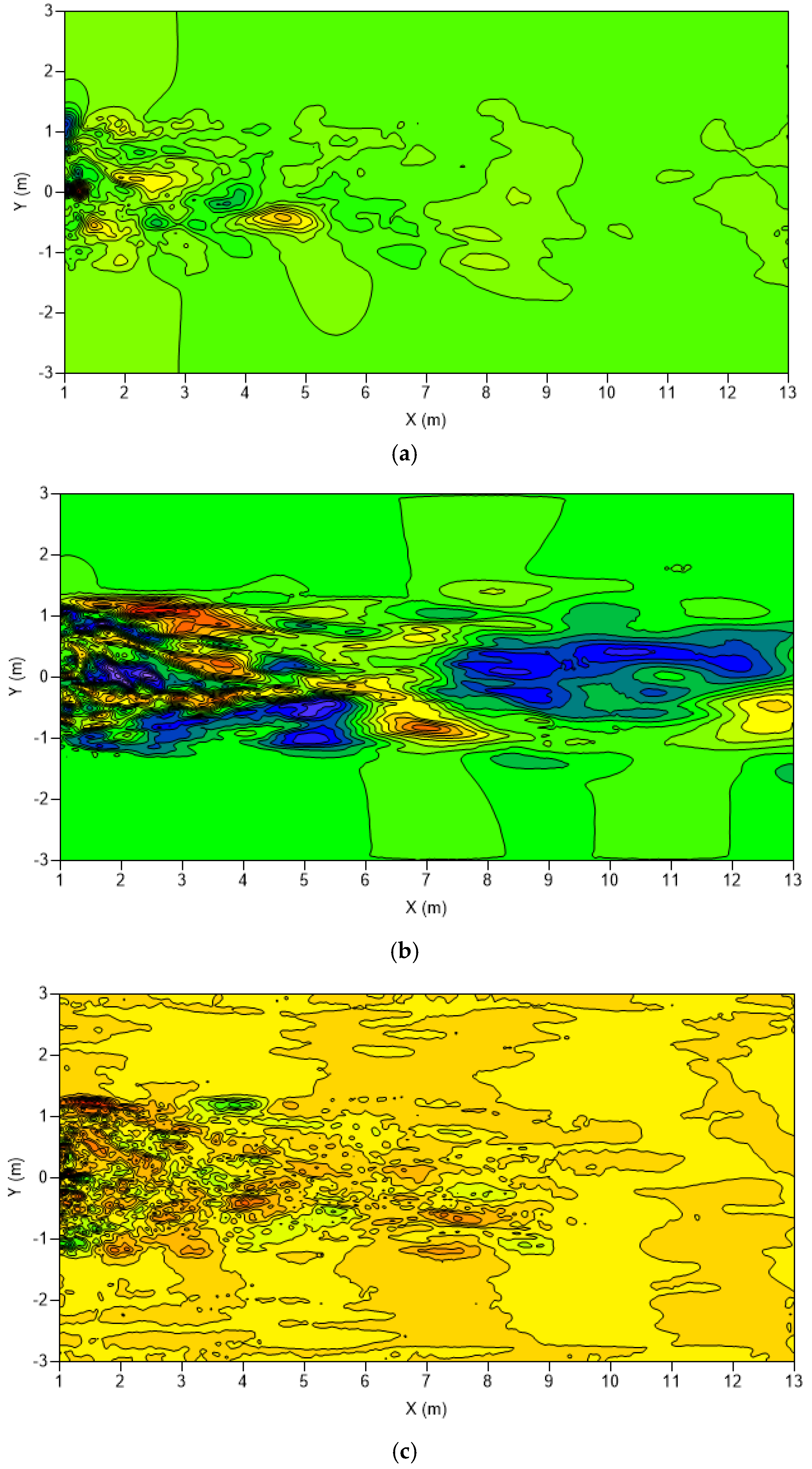
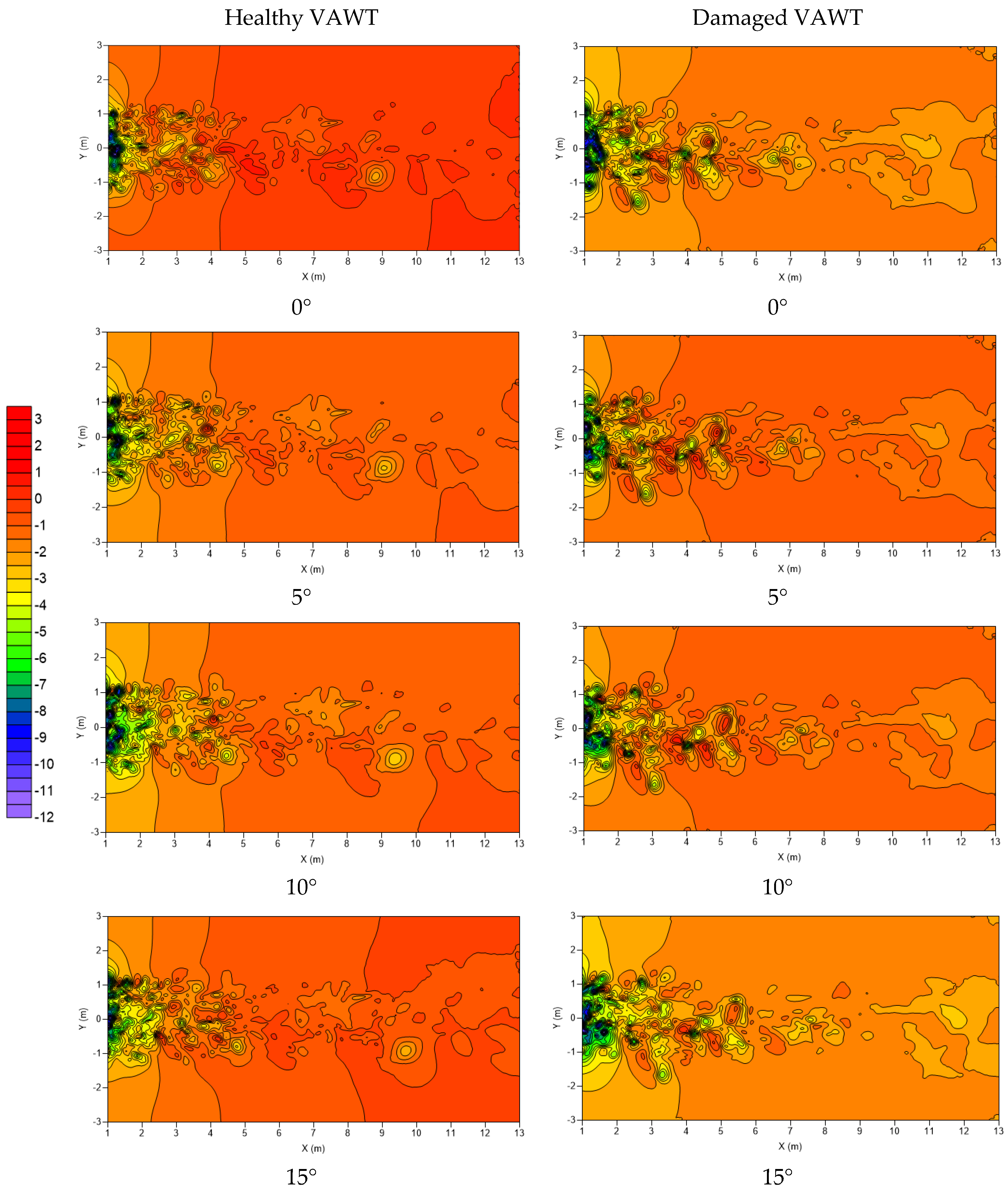
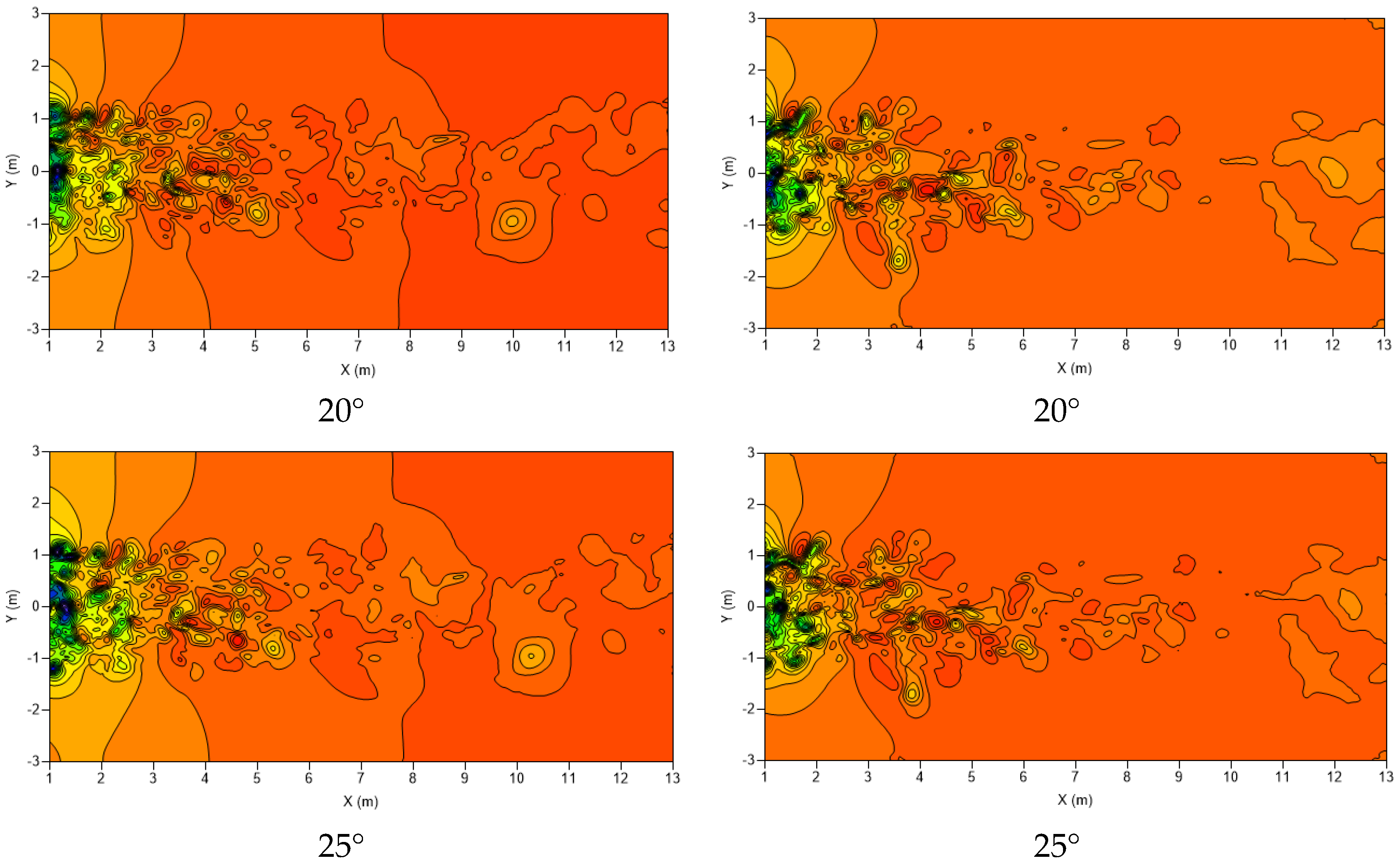
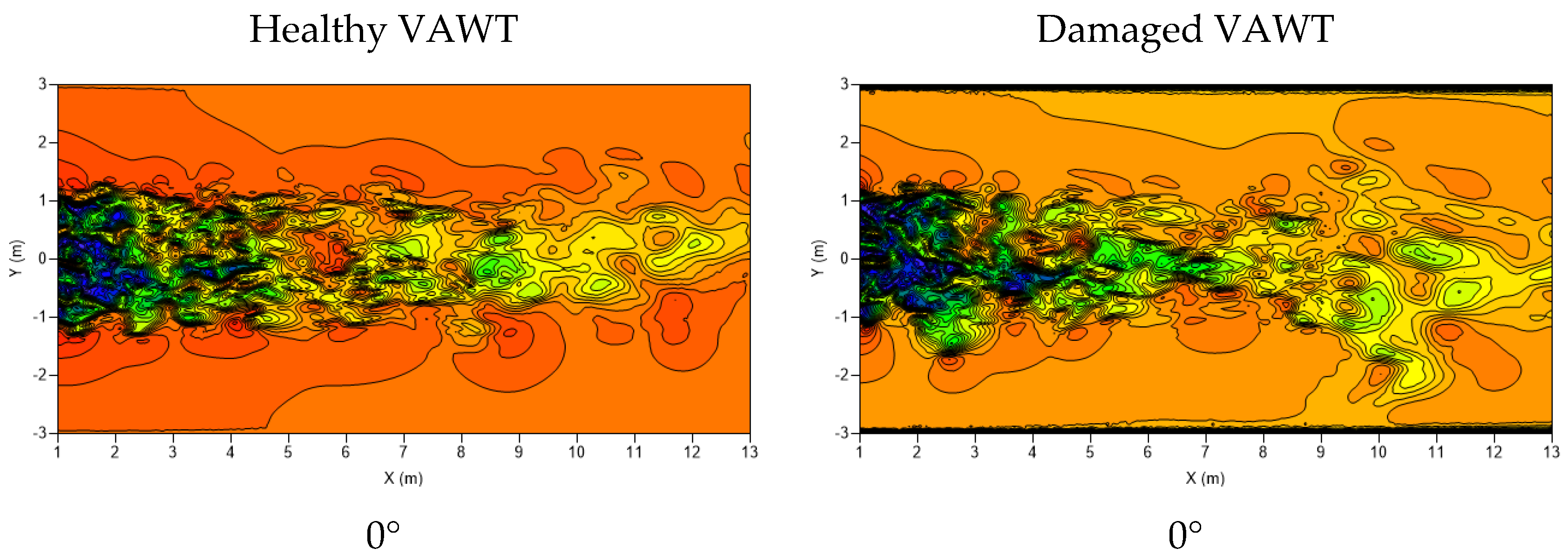
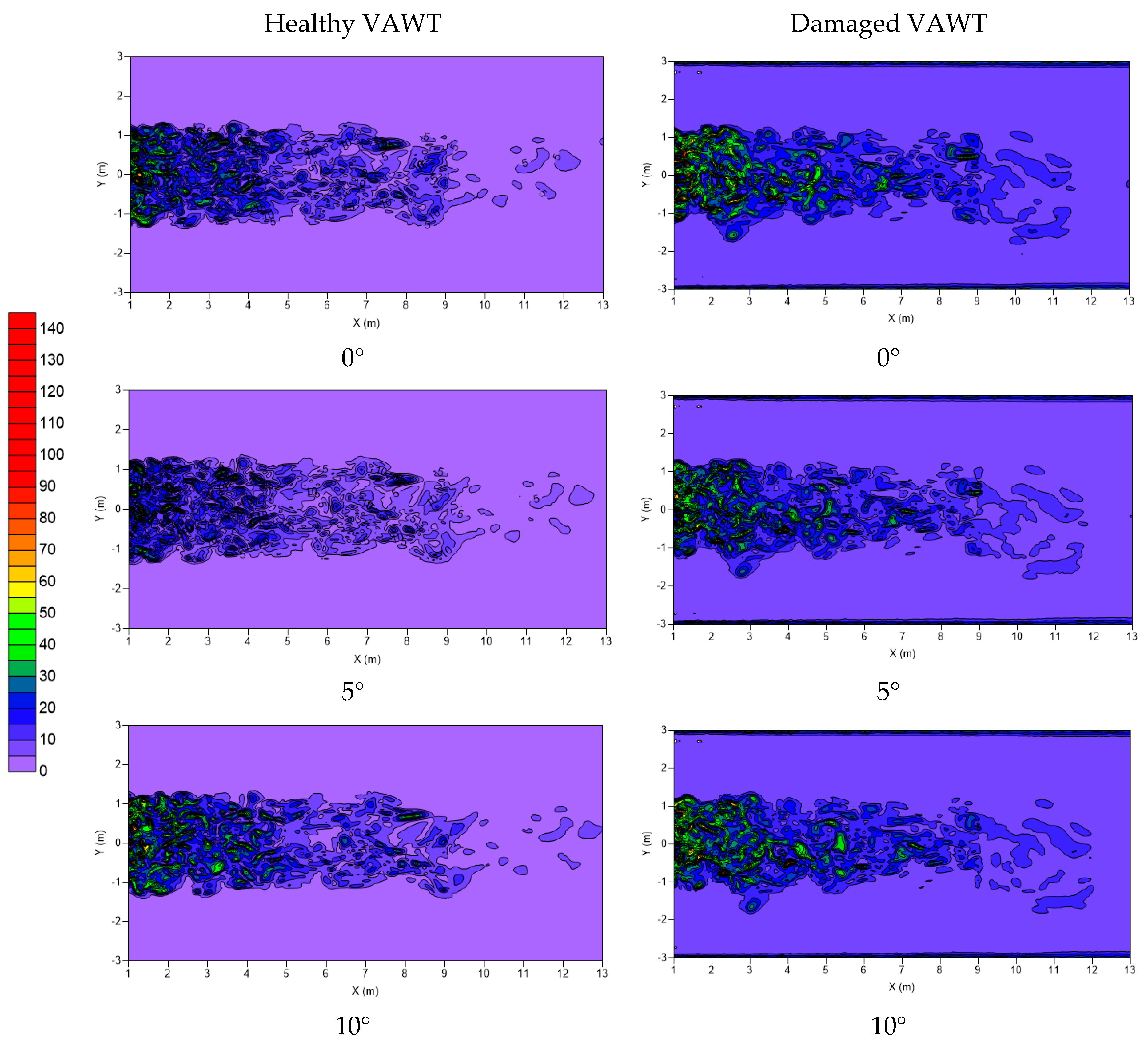
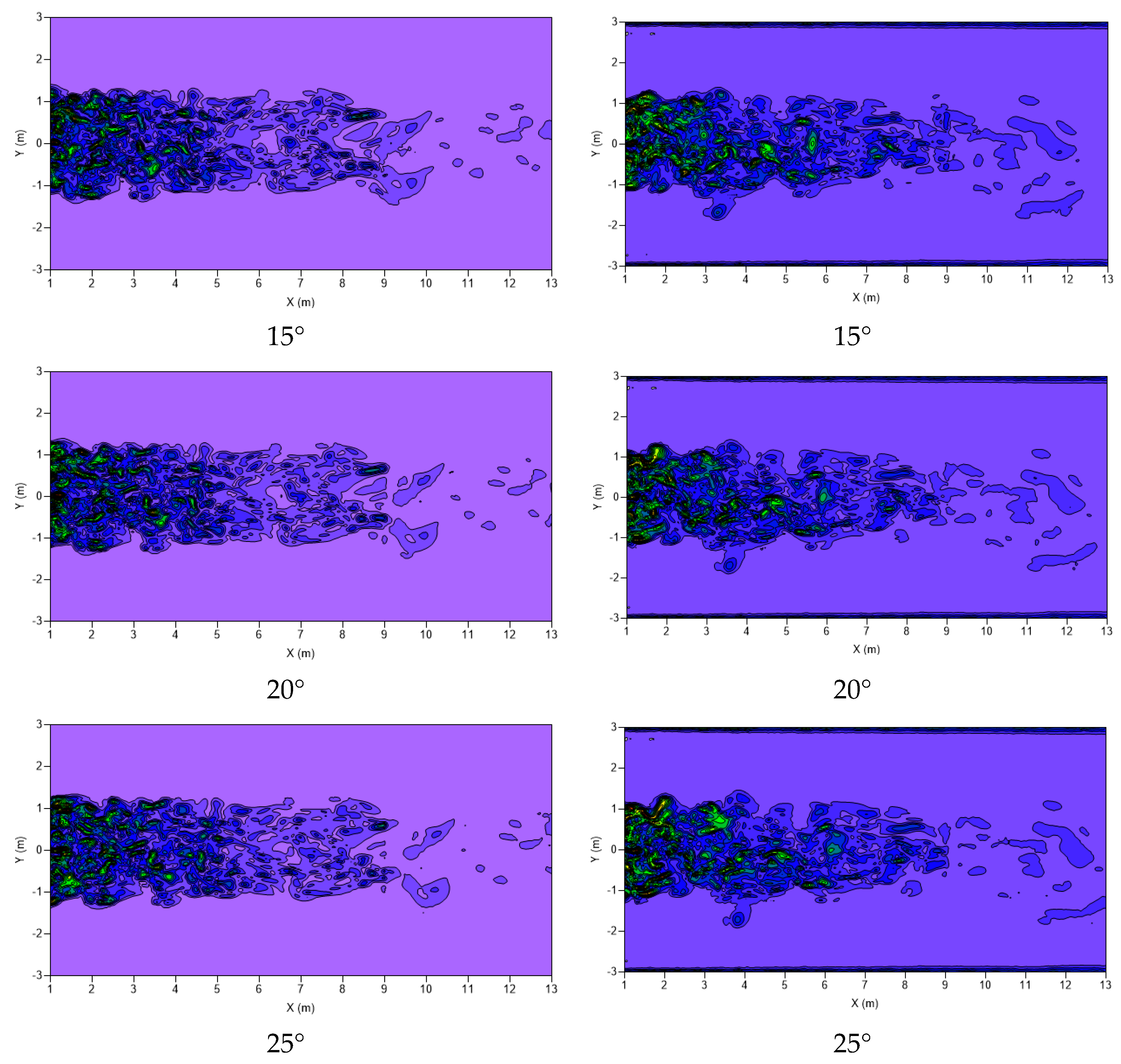
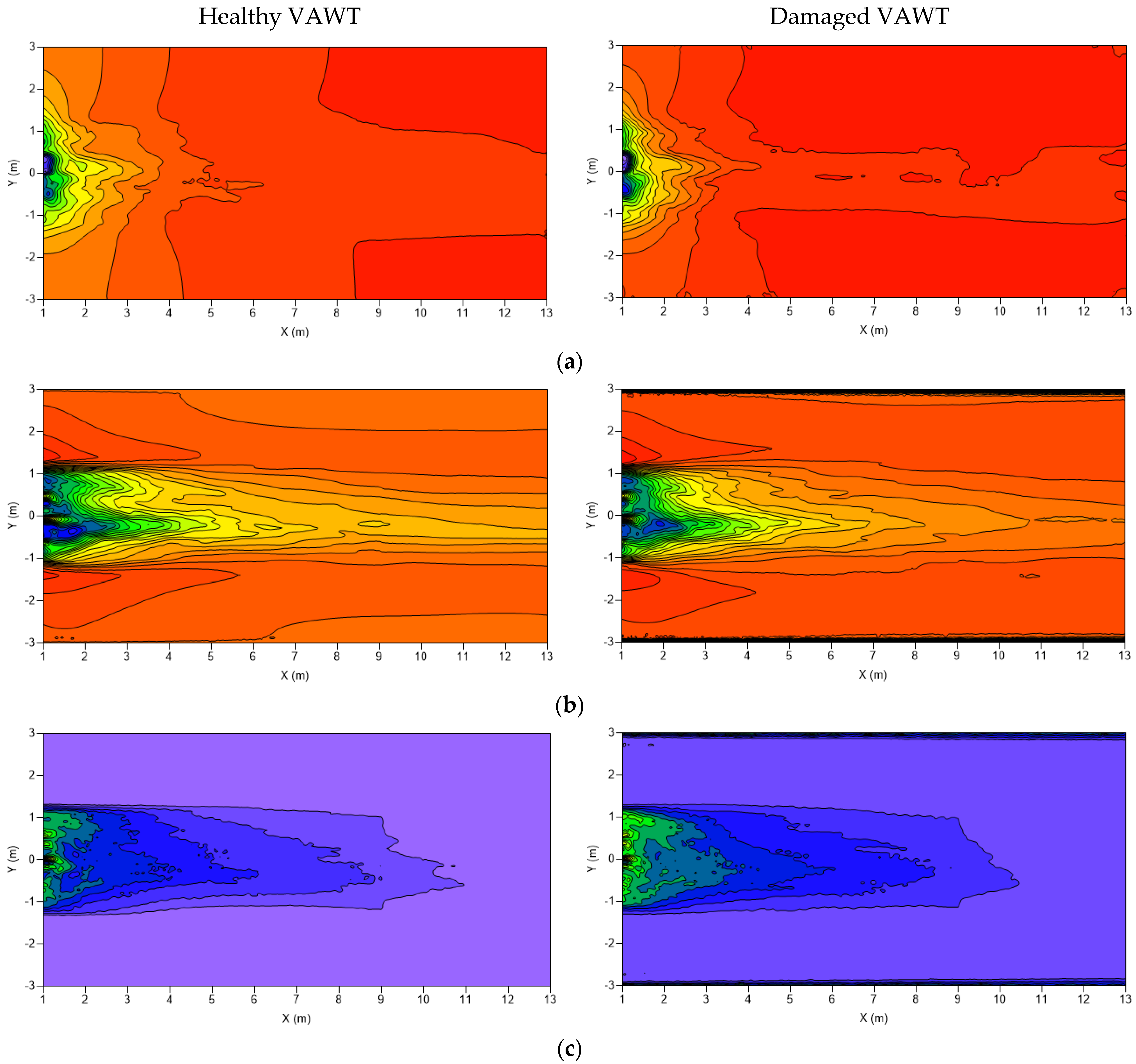
3.2. Flow Field Analysis of Healthy and Damaged VAWTs
- Pressure in the wake region is slightly higher, on average, than the pressure in the wake region of the healthy VAWT;
- The breakup of coherent structures is more complex/nonuniform and these structures are still present further downstream than the healthy VAWT.
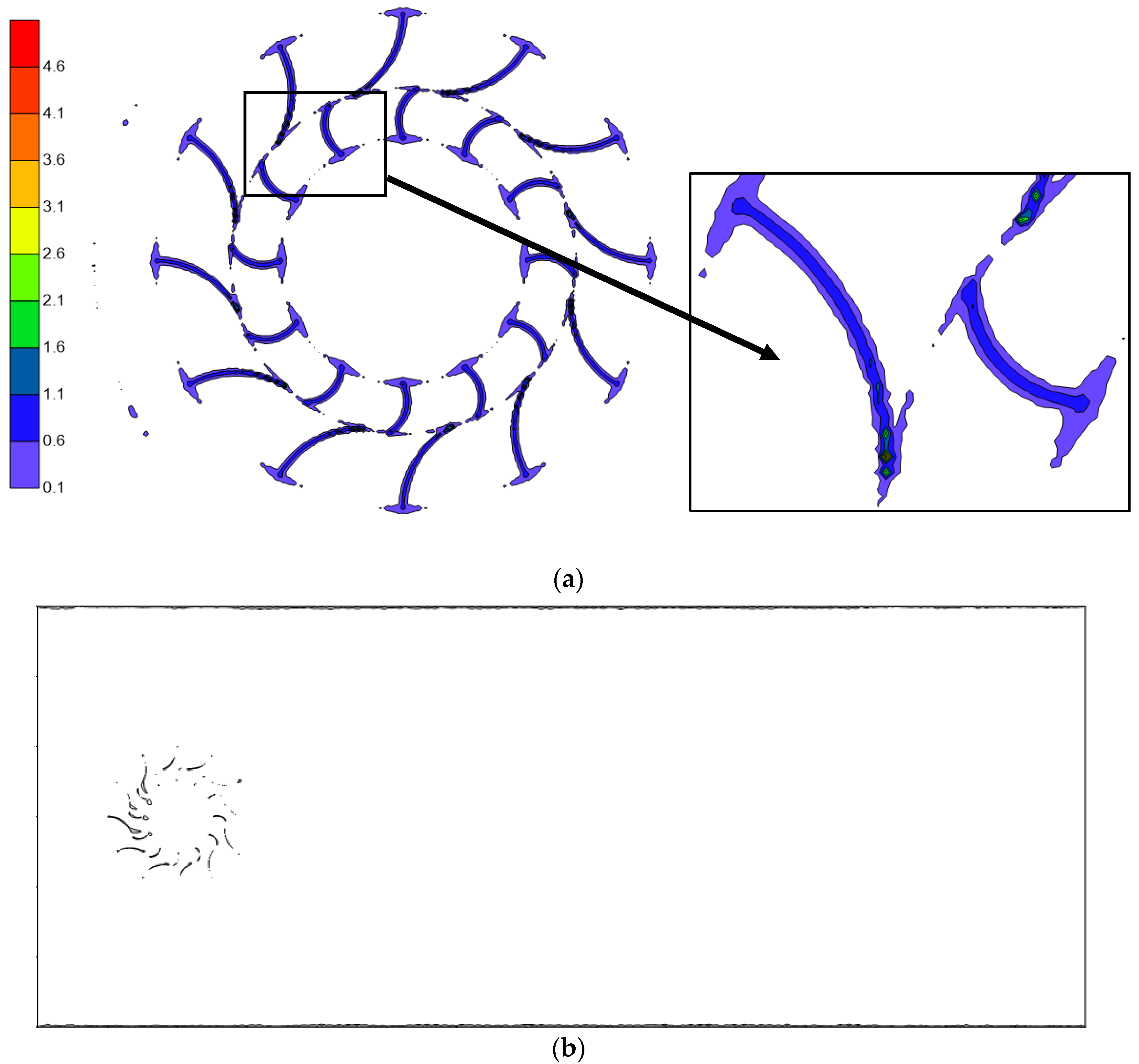
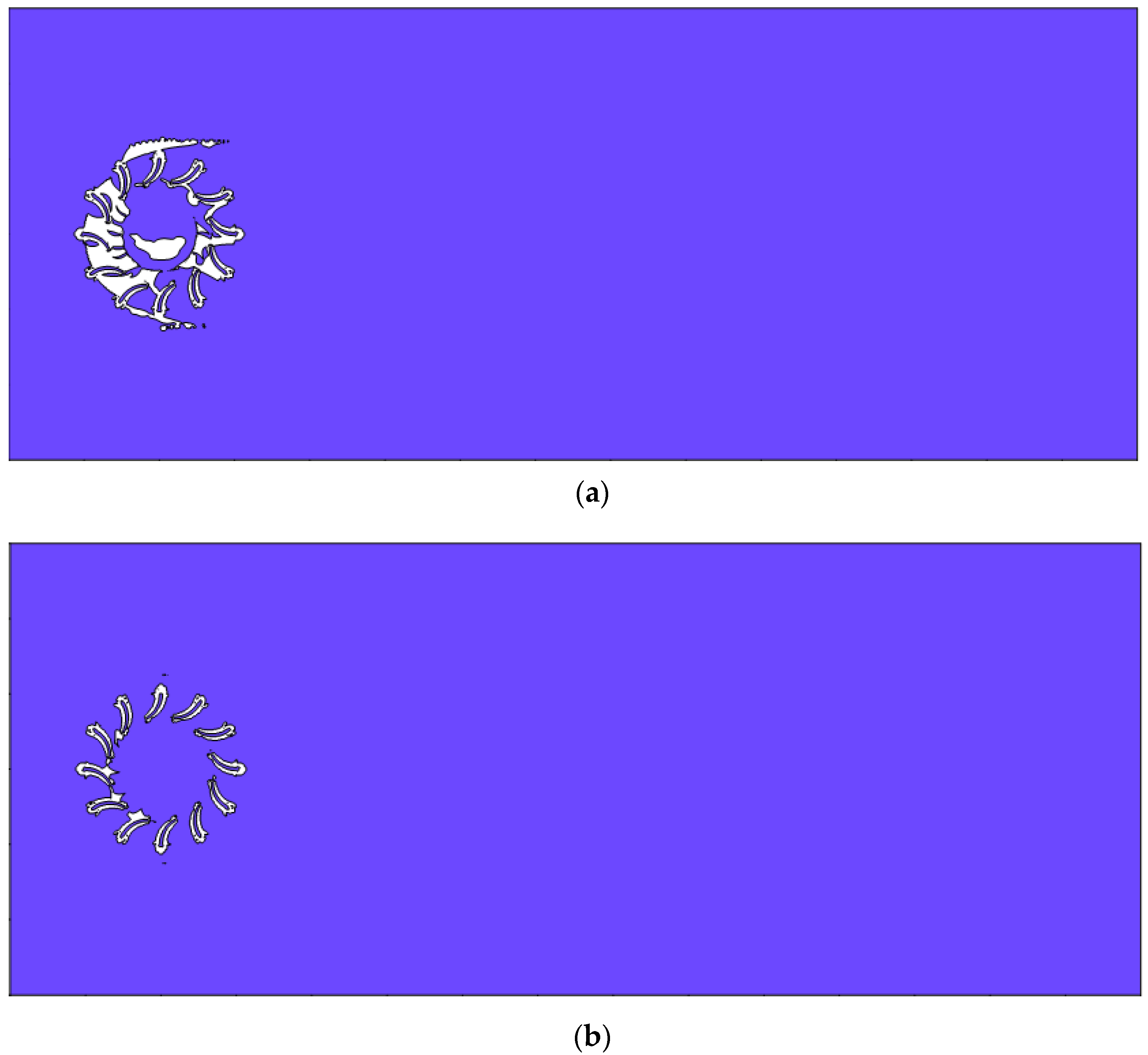
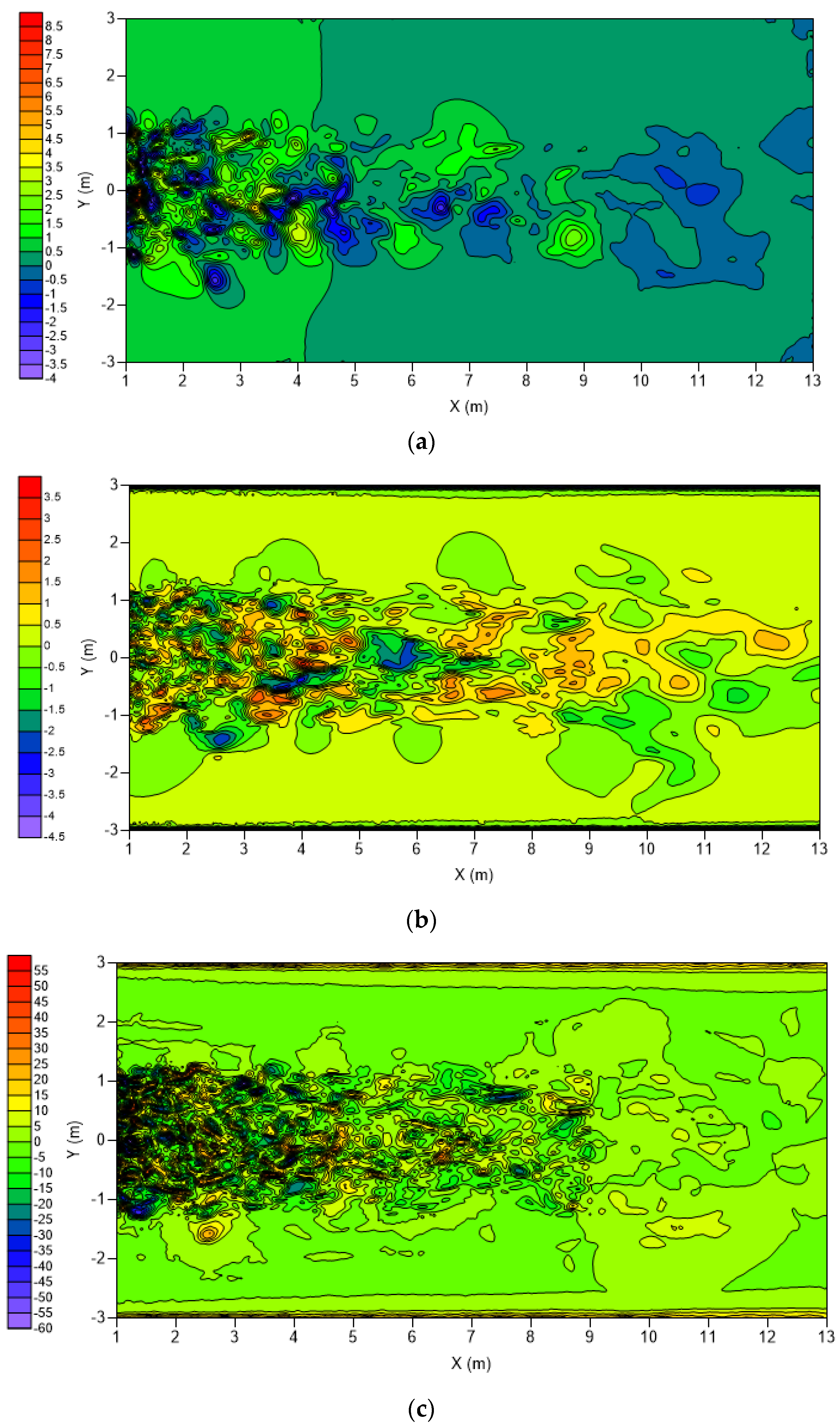
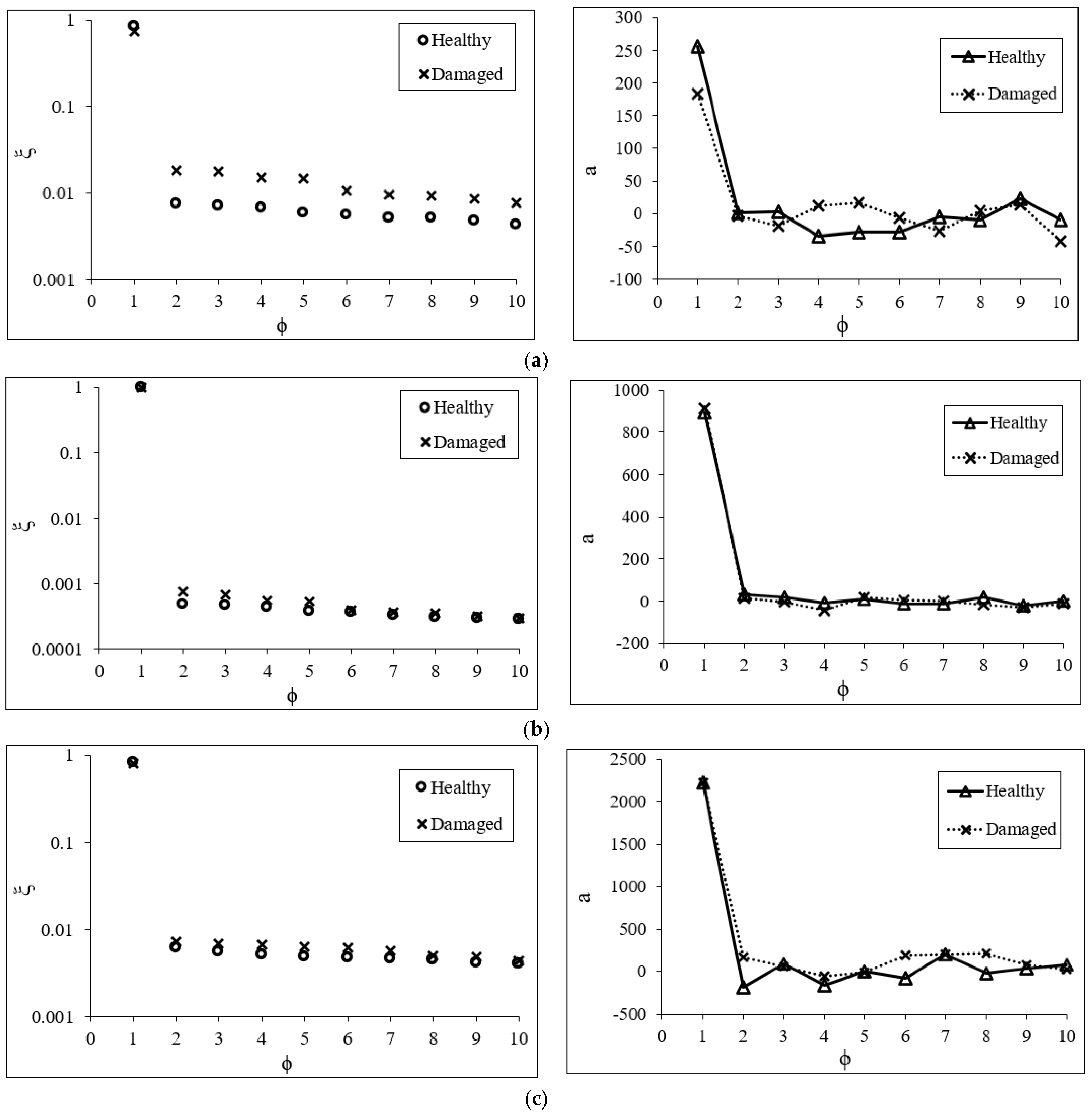
3.3. Proper Orthogonal Decomposition (POD)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A

Appendix B
References
- Chen, J.; Wang, X.; Li, H.; Jiang, C.; Bao, L. Design of the Blade under Low Flow Velocity for Horizontal Axis Tidal Current Turbine. J. Mar. Sci. Eng. 2020, 8, 989. [Google Scholar] [CrossRef]
- Barnes, A.; Cross, D.; Hughes, B. Towards a Standard Approach for Future Vertical Axis Wind Turbine Aerodynamics Research and Development. Renew. Sustain. Energy Rev. 2021, 148, 111221. [Google Scholar] [CrossRef]
- Peng, H.; Liu, H.; Yang, J. A Review on the Wake Aerodynamics of H-Rotor Vertical Axis Wind Turbines. Energy 2021, 232, 121003. [Google Scholar] [CrossRef]
- Posa, A. Influence of Tip Speed Ratio on Wake Features of a Vertical Axis Wind Turbine. J. Wind. Eng. Ind. Aerodynamics 2020, 197, 104076. [Google Scholar] [CrossRef]
- Scheurich, F.; Fletcher, T.; Brown, R. Simulating the Aerodynamic Performance and Wake Dynamics of a Vertical Axis Wind Turbine. Wind Energy 2011, 14, 159–177. [Google Scholar] [CrossRef] [Green Version]
- Hezaveh, S.; Zeid, E.; Lohry, M.; Martinelli, L. Simulation and Wake Analysis of a Single Vertical Axis Wind Turbine. Wind Energy 2017, 20, 713–730. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. On the Accuracy of Turbulence Models for CFD Simulations of Vertical Axis Wind Turbines. Energy 2019, 180, 838–857. [Google Scholar] [CrossRef]
- Du, B.; He, Y.; He, Y.; Zhang, C. Progress and Trends in Fault Diagnosis for Renewable and Sustainable Energy System based on Infrared Thermography: A Review. Infrared Phys. Technol. 2020, 109, 103383. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, D. A Survey on Wind Turbine Condition Monitoring and Fault Diagnosis—Part II: Signals and Signal Processing Methods. IEEE Trans. Ind. Electron. 2015, 62, 6546–6557. [Google Scholar] [CrossRef]
- Dhanraj, A.; Sugumaran, V. A Comparative Study of Bayes Classifiers for Blade Fault Diagnosis in Wind Turbines through Vibration Signals. Struct. Durab. Health Monit. 2017, 11, 69–90. [Google Scholar]
- Park, K.; Asim, T.; Mishra, R.; Pradhan, S. Condition Based Monitoring of Vertical Axis Wind Turbines using Computational Fluid Dynamics. In Proceedings of the 39th National Conference on Fluid Mechanics and Fluid Power, Surat, India, 13–15 December 2012. [Google Scholar]
- Park, K.; Asim, T.; Mishra, R. Simulation Based Approach to Predict Vertical Axis Wind Turbine Faults using Computational Fluid Dynamics. In Proceedings of the 1st International Conference on Through-Life Engineering Services, Bedfordshire, UK, 5–6 November 2012. [Google Scholar]
- Park, K.; Asim, T.; Mishra, R. Computational Fluid Dynamics based Fault Simulations of a Vertical Axis Wind Turbines. J. Phys. Conf. Ser. 2012, 364, 012138. [Google Scholar] [CrossRef] [Green Version]
- Park, K.; Asim, T.; Mishra, R. Effect of Blade Faults on the Performance Characteristics of a Vertical Axis Wind Turbine. In Proceedings of the 26th International Congress of Condition Monitoring and Diagnostic Engineering Management, Helsinki, Finland, 11–13 June 2013. [Google Scholar]
- Park, K.; Asim, T.; Mishra, R. Numerical Investigations on the Effect of Blade Angles of a Vertical Axis Wind Turbine on its Performance Output. Int. J. Cond. Monit. Diagn. Eng. Manag. 2015, 18, 3–10. [Google Scholar]
- Mohamed, F.; Park, K.; Pradhan, S.; Mishra, R.; Zala, K.; Asim, T.; Al-Obaidi, A. The Effect of Blade Angles of the Vertical Axis Wind Turbine on the Output Performance. In Proceedings of the 27th International Congress of Condition Monitoring and Diagnostic Engineering Management, Brisbane, Australia, 16–18 September 2014. [Google Scholar]
- Shahzad, A.; Asim, T.; Park, K.; Pradhan, S.; Mishra, R. Numerical Simulations of Effects of Faults in a Vertical Axis Wind Turbine’s Performance. In Proceedings of the 2nd International Workshop and Congress on eMaintenance, Lulea, Sweden, 13–14 December 2012. [Google Scholar]
- Asim, T.; Mishra, R. Numerical Investigations on the Performance Degradation of a Vertical Axis Wind Turbine Operating in Dusty Environment. In Proceedings of the FLUVISU, Pleumeur-Bodou/Lannion, France, 16–20 November 2015. [Google Scholar]
- Aboufares, G.; Zala, K.; Mishra, R.; Asim, T. Effects of Sand Particle Size on the Performance Characteristics of a Vertical Axis Wind Turbine. In Proceedings of the 6th International and 43rd National Conference on Fluid Mechanics and Fluid Power, Allahabad, India, 15–17 December 2016. [Google Scholar]
- Zahariev, M.; Asim, T.; Mishra, R.; Nsom, B. Effects of blade tapering on the performance of vertical axis wind turbines analysed through advanced visualization techniques. Int. J. Cond. Monit. Diagn. Eng. Manag. 2019, 22, 69–74. [Google Scholar]
- Shahzad, A.; Asim, T.; Mishra, R.; Paris, A. Performance of a Vertical Axis Wind Turbine under Accelerating and Decelerating flows. Procedia CIRP 2013, 11, 311–316. [Google Scholar] [CrossRef] [Green Version]
- Asim, T.; Mishra, R.; Ubbi, K.; Zala, K. Computational Fluid Dynamics based Optimal Design of Vertical Axis Marine Current Turbines. Procedia CIRP 2013, 11, 323–327. [Google Scholar] [CrossRef] [Green Version]
- Asim, T.; Mishra, R.; Kaysthagir, S.; Aboufares, G. Performance comparison of a Vertical Axis Wind Turbine using Commercial and Open-Source Computational Fluid Dynamics based codes. In Proceedings of the 5th International Conference on Jets, Wakes and Separated Flows, Stockholm, Sweden, 16–18 June 2016. [Google Scholar]
- Park, K.; Asim, T.; Mishra, R.; Marangwanda, G. Computational Fluid Dynamics based Performance Optimisation of Vertical Axis Marine Current Turbines. In Proceedings of the 2nd International Workshop and Congress on eMaintenance, Lulea, Sweden, 13–14 December 2012. [Google Scholar]
- Long, Z.; Ming, C.; An-An, X.; Fang, W. CFD Simulation Methods for Rotor based on N-S Equation. Mater. Sci. Eng. 2019, 685, 012031. [Google Scholar]
- Rane, S.; Kovacevic, A.; Stosic, N. Grid Generation for CFD Analysis and Design of a Variety of Twin-Screw Machines. Designs 2019, 3, 30. [Google Scholar] [CrossRef] [Green Version]
- Moghadam, Z.; Guibault, F.; Garon, A. On the Evaluation of Mesh Resolution for Large-Eddy Simulation of Internal Flows using OpenFoam. Fluids 2021, 6, 24. [Google Scholar] [CrossRef]
- Pujol, T.; Massaguer, A.; Massaguer, E.; Montoro, L.; Comamala, M. Net Power Coefficient of Vertical and Horizontal Wind Turbines with Crossflow Runners. Energies 2018, 11, 110. [Google Scholar] [CrossRef] [Green Version]
- Asim, T.; Mishra, R. Large Eddy Simulation based Analysis of Complex Flow Structures within the Volute of a Vaneless Centrifugal Pump. Sadhana 2017, 42, 505–516. [Google Scholar] [CrossRef] [Green Version]
- Muralidhar, S.; Podvin, B.; Mathelin, L.; Fraigneau, Y. Spatio-temporal Proper Orthogonal Decomposition of turbulent channel flow. J. Fluid Mech. 2019, 864, 614–639. [Google Scholar] [CrossRef] [Green Version]
- Gareth, C. Design, Operation and Diagnostics of a Vertical Axis Wind Turbine. Ph.D. Thesis, University of Huddersfield, Huddersfield, UK, 2012. [Google Scholar]
- Berkooz, G.; Holmes, P.; Lumley, J. The Proper Orthogonal Decomposition in the Analysis of Turbulent Flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Liu, J. Contributions to the understanding of Large-Scale Coherent Structures in Developing Free Turbulent Shear Flows. Adv. Appl. Mech. 1988, 26, 183–209. [Google Scholar]
- Sirovich, L. Turbulence and the Dynamics of Coherent Structures, Part 1: Coherent Structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Asim, T. Computational Fluid Dynamics based Diagnostics and Optimal Design of Hydraulic Capsule Pipelines. Ph.D. Thesis, University of Huddersfield, Huddersfield, UK, 2013. [Google Scholar]
- Singh, D.; Aliyu, A.; Charlton, M.; Mishra, R.; Asim, T.; Oliveira, A. Local Multiphase Flow Characteristics of a Severe-Service Control Valve. J. Pet. Sci. Eng. 2020, 195, 107557. [Google Scholar] [CrossRef]
- Ghori, M.; Nirwan, J.; Asim, T.; Chahid, Y.; Farhaj, S.; Khizer, Z.; Timmins, P.; Conway, B. MUCO-DIS: A new AFM-based Nanoscale Dissolution Technique. AAPS PharmSciTech 2020, 21, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Singh, D.; Charlton, M.; Asim, T.; Mishra, R.; Townsend, A.; Blunt, L. Quantification of Additive Manufacturing Induced Spatial distribution of the Global and Local Performance Characteristics of a Complex Multi-Stage Control Valve Trim. J. Pet. Sci. Eng. 2020, 190, 107053. [Google Scholar] [CrossRef]
- Lumley, J.L. The Structure of Inhomogeneous Turbulent Flows. In Atmospheric Turbulence and Radio Wave Propagation; Yaglom, A., Tatarski, V., Eds.; Nauka: Moscow, Russia, 1967; pp. 166–177. [Google Scholar]
- Fukunaga, K. Introduction to Statistical Pattern Recognition; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Loeve, M. Probability Theory; Springer: Berlin, Germany, 1977. [Google Scholar]
- Schmid, P. Dynamic Mode Decomposition of Numerical and Experimental Data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]





| Torque Characteristics | Healthy VAWT | Damaged VAWT | Difference w.r.t. Healthy VAWT |
|---|---|---|---|
| (Nm) | (Nm) | (%) | |
| Average | 5.8 | 5.6 | −2.52 |
| Maximum | 6.7 | 7.2 | +7.46 |
| Minimum | 5.0 | 4.4 | −12.39 |
| Amplitude | 1.7 | 2.8 | +66.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asim, T.; Islam, S.Z. Effects of Damaged Rotor on Wake Dynamics of Vertical Axis Wind Turbines. Energies 2021, 14, 7060. https://doi.org/10.3390/en14217060
Asim T, Islam SZ. Effects of Damaged Rotor on Wake Dynamics of Vertical Axis Wind Turbines. Energies. 2021; 14(21):7060. https://doi.org/10.3390/en14217060
Chicago/Turabian StyleAsim, Taimoor, and Sheikh Zahidul Islam. 2021. "Effects of Damaged Rotor on Wake Dynamics of Vertical Axis Wind Turbines" Energies 14, no. 21: 7060. https://doi.org/10.3390/en14217060
APA StyleAsim, T., & Islam, S. Z. (2021). Effects of Damaged Rotor on Wake Dynamics of Vertical Axis Wind Turbines. Energies, 14(21), 7060. https://doi.org/10.3390/en14217060








