Damping Formation Mechanism and Damping Injection of Virtual Synchronous Generator Based on Generalized Hamiltonian Theory

Abstract

Invertor as a virtual synchronous generator (VSG) to provide virtual inertia and damping can improve the stability of a microgrid, in which the damping is one of the fundamental problems in dynamics. From the view of the Hamiltonian dynamics, this paper researches the damping formation mechanism and damping injection control of VSG. First, based on the energy composition and dynamic characteristics of VSG, the differential equations system of VSG is established and is transformed into the generalized Hamiltonian system. Second, the effects of the three parameters of VSG, the damping coefficient D, active power droop coefficient, and time constant of excitation T_E on damping characteristics are researched from a dynamic perspective, and simulation research is carried out with an isolated microgrid. Lastly, the control design method of Hamiltonian structure corrections used to add the damping factor and design the equivalent control inject damping to improve the stability of the isolated microgrid. Research shows that the voltage and frequency stability of the isolated microgrid can be effectively improved by selecting three key parameters of VSG and damping injection control. The innovations of this paper are 1. The Hamiltonian model of the inverter is deduced and established by taking the inverter as a virtual generator. 2. Based on the Hamiltonian model, damping characteristics of inverter in the microgrid are studied. 3. Hamiltonian structure correction method is applied to the inverter, and equivalent damping injection is designed to improve the stability of the microgrid.

1. Introduction

It has become a standard configuration model that the DC storage unit and inverter are used to compensate for adjustment in a microgrid. The inverter unit is regarded as the virtual synchronous generator (VSG) to provide virtual inertia and virtual damping for the microgrid to improve control performance. After this idea is put forward, extensive attention is received. From 2008 up to now, several topologies are introduced for the VSG systems [1], such as the VSYNC project [2], the Institute of Electrical Power Eng. (IEPE) at Clausthal University of Technology in Germany [3], the VSG research team at Kawasaki Heavy Industries (KHIs) [4], and the ISE Laboratory in Osaka University in Japan [5].

Research has been focused on the virtual inertia and virtual damping provided by the VSG [6,7,8,9]. According to existing problems in the inverter, grid-connect to provide improved methods are the main research approach. A pre-synchronization control method is used to make the output the same as the reference value under the sudden change of frequency and voltage amplitude [10] and is used to eliminate the phase jump [11]. Considering a special operation condition to design a controller of VSG, for example, a comprehensive control strategy of VSG under unbalanced voltage conditions is proposed to solve the current unbalance and power oscillations [12]; oscillation damping and proper transient active power-sharing are achieved by adjusting the virtual stator reactance based on state-space analyses [13], control design of VSG during symmetrical voltage fault [14], a novel control strategy based on the virtual synchronous generator (VSG) for improving transient response of parallel power converters during large disturbance in the stand-alone microgrid [15], the algebraic-type VSG with a minimal number of parameters has an ability to suppress the system frequency and voltage deviations [16], a VSG based on superconducting magnetic energy storage technology to emulate the needed inertia power [17], the transient angle stability of a paralleled synchronous and virtual synchronous generators (SG-VSG) system is investigated by comparing it with that of the paralleled VSGs system. It is observed that the paralleled SG-VSG system is more prone to transient instability due to the differences between their speed governors [18]. Decoupling the active and reactive power can obtain a multi-loop control structure in the inverter [19,20]. The influence of VSG key parameters, e.g., virtual inertia, damping factor, and droop coefficient on system stability are investigated, and the corresponding mathematical calculation method of the unstable region is obtained [21]. The control performance of VSG can be further improved by combining it with the control theory, such as virtual synchronous generator control strategy in microgrid application for stand-alone sites [22], using the improved whale algorithm to improve the frequency control ability of virtual synchronous generator [23], an H_∞ robust control method for robust\optimal tuning of the virtual parameters [24], self-tuning algorithms to search for optimal parameters during the operation of the VSG to minimize the amplitude and rate of change of the frequency variation [25], and so on. In these studies, VSG is usually placed in a microgrid environment and studied by combining signal analysis and simulation, but few studies have been carried out from the perspective of system dynamics.

The key issue of VSG is the virtual inertia and damping which are essential problems of dynamics. Therefore, from the perspective of system dynamics to study operation and control of VSG, it is possible to obtain more inner dynamics characteristics and structure information of VGS. The generalized Hamiltonian control theory developed in recent years shows many excellent properties in revealing the dynamic mechanism of system operation control. Its structure matrix provides the connection information for the system parameters, while its damping matrix provides the damping characteristics on the port of system parameters [26,27,28]. Many achievements have been made in the application of generalized Hamiltonian theory to power and energy systems, including the Hamiltonian modeling and the stabilizing method [29,30], the energy-based robust Hamiltonian adaptive control [31] combined with power system robust control theory [32], energy shaping and damping inject, etc. Some exploratory work has been carried out on the generalized Hamiltonian modeling of the inverter and VSG in microgrid systems. The second-order Hamiltonian model is derived by simplifying the grid-connected VSG as an equivalent circuit form [33,34]. The Hamiltonian function of AC microgrid containing spinning machines, power electronic inverters, and energy storage devices are constructed to analyze the stability of microgrid [35]. A port-controlled Hamiltonian model of dual active bridge source-side converters in a microgrid is built [36].

Based on the typical inverter structure and the concept of VSG, this paper establishes the generalized Hamiltonian model of VSG, constructs the isolated micro-grid system for simulation, and studies the formation mechanism of VSG damping and the problem of controlling injection damping.

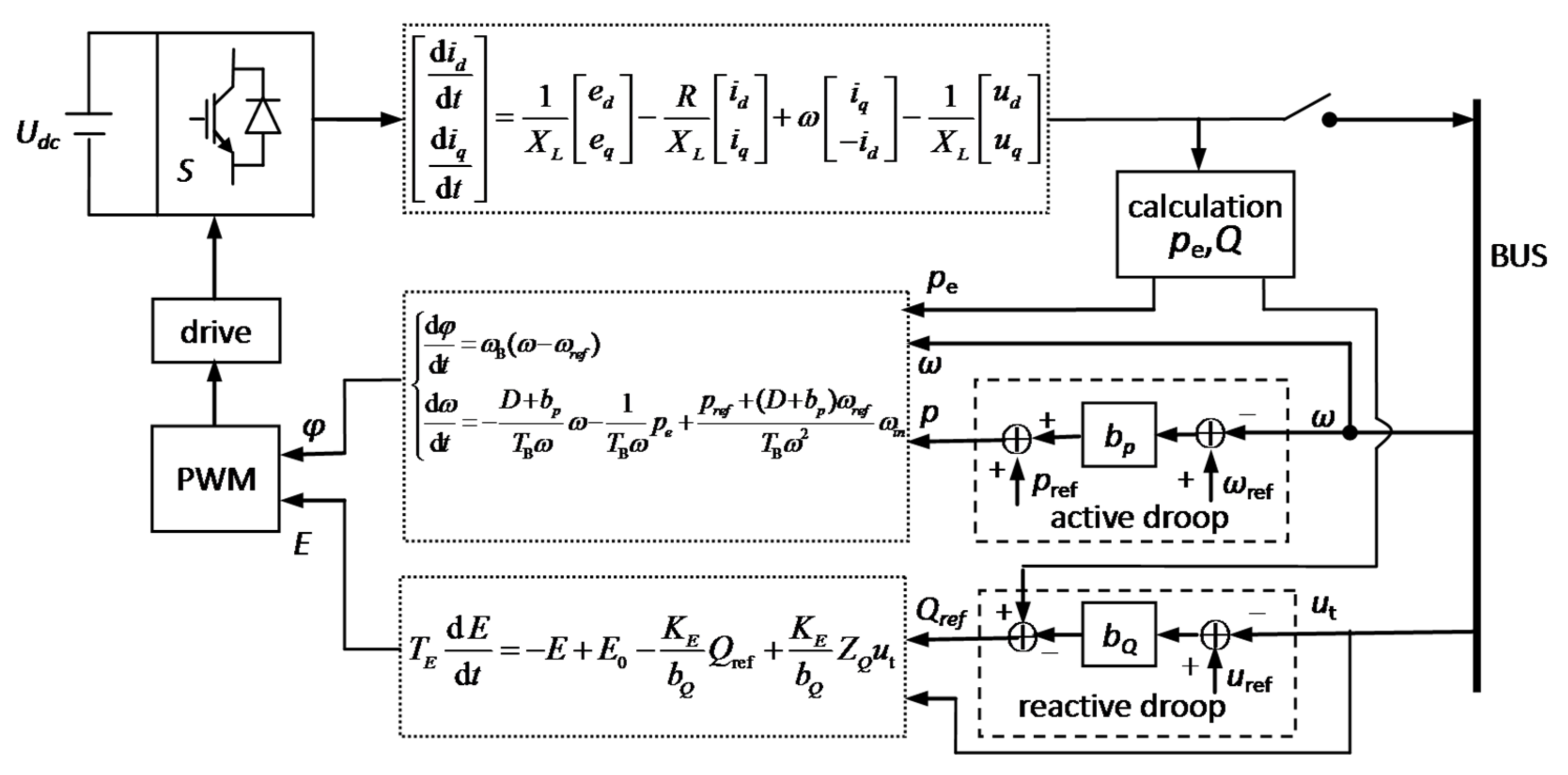
2. Virtual Synchronous Generator

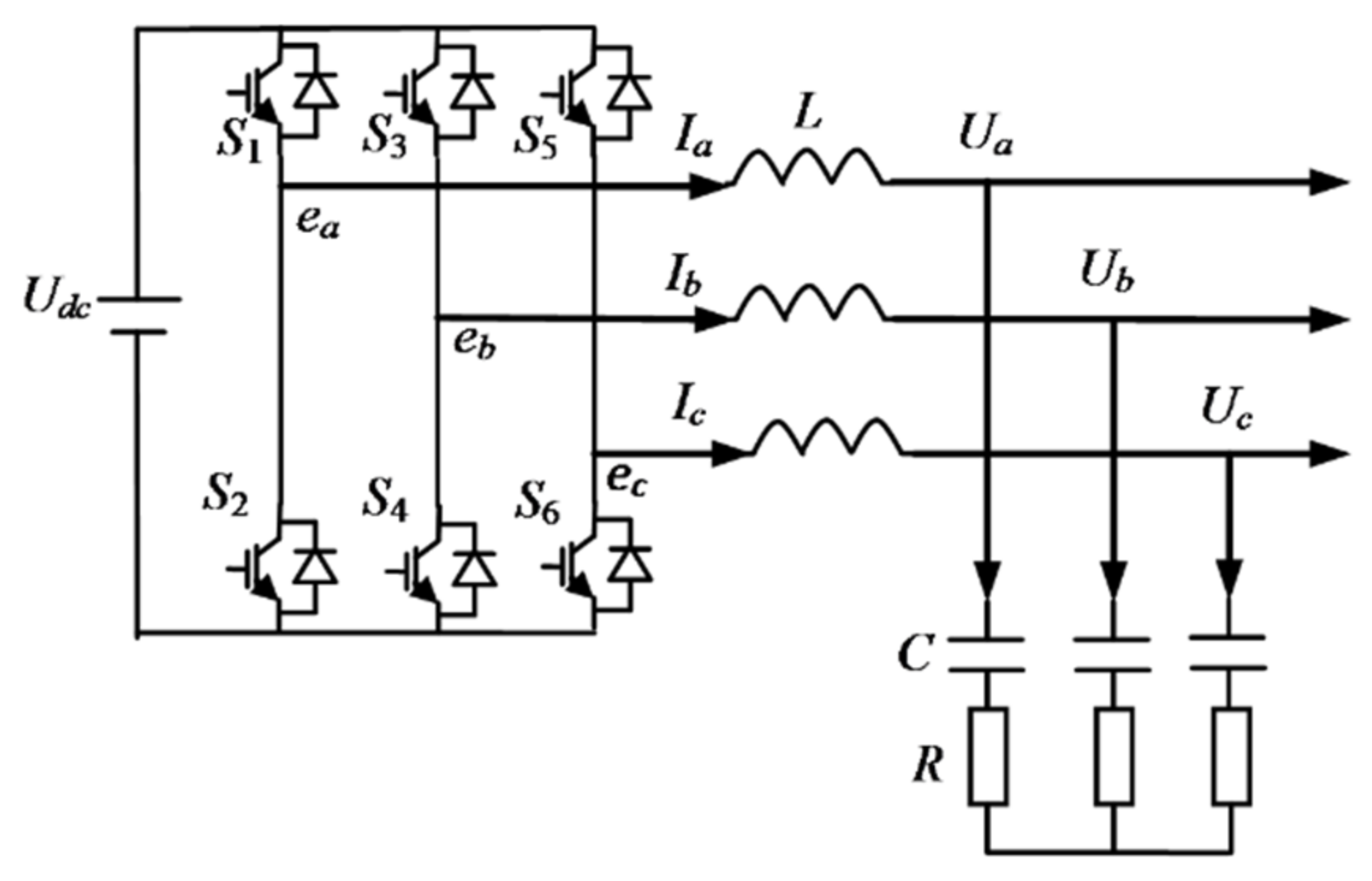
2.1. Structure of Invertor Unit

The main circuit of the inverter unit is shown in Figure 1. The U_dc is the output of energy storage unit, and can be regarded as a constant voltage source. S₁–S₆ are the power switching device that forms the three-phase bridge inverter circuit.

When the invertor is regarded as VSG, the inductance of the bridge arm is regarded as the stator winding of the generator. So L, R, I_a, and U_a are a phase reactance, resistance, current, and voltage of stator winding, respectively. e_a is the internal electric source of a phase of the generator, which can be expressed as E∠φ, E is the internal electromotive force, φ is the phase angle.

2.2. Virtual Stator Unit

According to the electromechanical coupling dynamics, the charge of capacitor e_a-c, e_b-c and e_c-c are the generalized displacement, then current I_abc= [I_a I_b I_c]^T are the generalized velocity. The energy of VSG include magnetic energy W_m = L(I_a² + I_b² + I_c²), electric field energy W_e = (e_a-b² + e_a-c² + e_b-c²)/(2C), and dissipated energy F_d = R(I_a² + I_b² + I_c²)/2. The voltage of line E_abc is regarded as an external force. The Lagrange function of VSG is L = W_m − W_e, and then the Lagrange equation is

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial {\mathit{I}}_{abc}}\right)-\frac{\partial L}{\partial {\mathit{U}}_{abc}}+\frac{\partial F_d}{\partial {\mathit{I}}_{abc}}={\mathit{E}}_{abc}$$

(1)

Noted to U_abc= ∂W_e/∂e_abc-c, Equation (1) can be expanded as follows.

$${\mathit{U}}_{abc}={\mathit{E}}_{abc}-L\frac{\mathrm{d}}{\mathrm{d}t}\left({\mathit{I}}_{abc}\right)-R{\mathit{I}}_{abc}$$

(2)

Equation (2) is the terminal voltage equation of VSG.

Considering e_abc-c= CU_abc, variables e_abc-c in the electric field energy W_e are replaced by U_abc. Using the X_ad basic value system and the Park transformation, and ignoring the 0 axis component, the generalized velocity selected as u_dq= [u_d u_q]^T, then the Lagrange function of the stator in per unit is:

$$L=\frac{1}{2}{i}_d^2{X}_L+\frac{1}{2}{i}_q^2{X}_L-\frac{1}{2}{u}_t^2{X}_C$$

(3)

where X_L and X_C are the reactance of inductance and capacitance converted into d, q coordinate in per unit, i_d, i_q, u_d, and u_q are current and voltage of stator d, q axis in per unit.

Equation (2) can be transformed into a normalized form of the d, q axis as follows.

$$\left[\begin{array}{c}\frac{\mathrm{d}{i}_d}{\mathrm{d}t}\\ \frac{\mathrm{d}{i}_q}{\mathrm{d}t}\end{array}\right]=\frac{1}{X_L}\left[\begin{array}{c}{e}_d\\ e_q\end{array}\right]-\frac{R}{X_L}\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\omega \left[\begin{array}{c}{i}_q\\ -i_d\end{array}\right]-\frac{1}{X_L}\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]$$

(4)

2.3. Virtual Excitation Unit

The excitation system of VSG can be simplified as a first-order link as follows.

$$\Delta E=\frac{K_E}{1+T_{E}s}(u_{\mathrm{ref}}-u_t)$$

(5)

where ∆E = E − E₀ is the increment of internal electric potential in per unit, E and E₀ is the electromotive force and its initial value in per unit, u_ref and u_t is the reference voltage and terminal voltage in per unit, K_E is the gain coefficient, T_E is the time constant of excitation.

The virtual excitation unit is constructed by combining the droop control of reactive power which is Q_ref − Q = −b_Q(u_ref − u_t). So the differential equation of excitation concluding droop control of reactive power can be expressed as follows.

$$T_E\frac{\mathrm{d}E}{\mathrm{d}t}=-E+E_0-\frac{K_E}{b_Q}{Q}_{\mathrm{ref}}+\frac{K_E}{b_Q}{Z}_Q{u}_{\mathrm{t}}$$

(6)

where Z_Q = i_dcosφ − i_qsinφ, Q and Q_ref are the reactive power of VSG and its reference value in per unit, respectively, u_ref is the reference value of voltage in per unit, b_Q is the droop coefficient of reactive power.

2.4. Rotor of VSG

While an inverter is constructed according to a virtual generator, the virtual generator with the salient pole effect ignored, one magnetic pole logarithm is adopted. A similar generator motion equation is

$$\left\{\begin{array}{l}\frac{\mathrm{d}\phi }{\mathrm{d}t}={\omega }_{\mathrm{B}}(\omega -{\omega }_{\mathrm{ref}})\hfill \\ \frac{\mathrm{d}\omega }{\mathrm{d}t}=\frac{1}{T_{\mathrm{B}}\omega }{p}_m-\frac{1}{T_{\mathrm{B}}\omega }D(\omega -{\omega }_{ref})-\frac{1}{T_{\mathrm{B}}\omega }{p}_e\hfill \end{array}\right.$$

(7)

where T_B is the inertia time constant of VSG in (s), p_m is the mechanical power in per unit, p_e is the active power in per unit, D is the damping coefficient, ω is the angular velocity in per unit.

The mechanical power of the invertor is obtained from droop control of active power, that is p_ref − p_m = − b_p(ω_ref − ω) where p_ref and ω_ref are reference value of active power and angular velocity in per unit, respectively, b_p is the droop coefficient of active power.

The Equation (7) can be transformed as follows.

$$\left\{\begin{array}{l}\frac{\mathrm{d}\phi }{\mathrm{d}t}=-{\omega }_{\mathrm{B}}{\omega }_{ref}+{\omega }_{\mathrm{B}}\omega \hfill \\ \frac{\mathrm{d}\omega }{\mathrm{d}t}=-\frac{1}{T_{\mathrm{B}}\omega }(D+b_p)\omega -\frac{1}{T_{\mathrm{B}}\omega }{p}_e+\frac{1}{T_{\mathrm{B}}\omega {\omega }_{\mathrm{in}}}[p_{ref}+(D+b_p){\omega }_{ref}]{\omega }_{i\mathrm{n}}\hfill \end{array}\right.$$

(8)

In the next section, it can be seen that this transformation can ensure the full rank of the input matrix and satisfy the transformation required in Hamiltonian structure modification.

2.5. Structure of VSG

From what has been discussed above, the framework structure of VSG can be constructed as Figure 2.

In Figure 2, the PWM and drive are execution units of VSG. VSG controls active power and reactive power output of the invertor according to changes of bus frequency and voltage and maintains the stability of bus frequency and voltage.

3. Hamiltonian Model of VSG

3.1. Hamiltonian Function

(1)

Virtual stator unit

According to the Hamiltonian principle, the generalized momentum is defined as p_d = ∂L/∂i_d and p_q = ∂L/∂i_q, then the Hamiltonian function is $H^{(1)}={\mathit{p}}^{\mathrm{T}}{{i}}_{dq}-L$. The Hamiltonian function of the virtual stator unit can be obtained from the Lagrange function Equation (3).

$$H^{(1)}=\frac{1}{2}{X}_L{i}_d^2+\frac{1}{2}{X}_L{i}_q^2+\frac{1}{2}{u}_{\mathrm{t}}^2{X}_C$$

(9)

(2)

Virtual excitation unit

The basic form of the virtual excitation unit is given in Equation (5). The transfer function of Equation (5) can be simulated by a classic RC circuit, where the electric energy of capacitance can be regarded as a Hamiltonian function [37]. Therefore, Hamiltonian function of virtual excitation unit can be obtained as follows.

$$H^{(2)}=\frac{1}{2}{T}_E\Delta E^2$$

(10)

(3)

Virtual rotor unit

The energy of the rotor unit is the inertia potential energy. According to the Hamiltonian principle, the inertia potential energy of the rotor is transformed from Lagrange to Hamiltonian, and the form of the Hamiltonian remains same. The Hamiltonian function of the virtual rotor unit is

$$H^{(3)}=\frac{1}{2}{T}_{\mathrm{B}}{\omega }^2$$

(11)

(4)

Hamiltoni an function of VGS

The Hamiltonian function of VSG is equal to the sum of the energies of the stator, rotor, and excitation, that is

$$H=\frac{1}{2}{T}_{\mathrm{B}}{\omega }^2+\frac{1}{2}{X}_L{i}_d^2+\frac{1}{2}{X}_L{i}_q^2+\frac{1}{2}{u}_{\mathrm{t}}^2{X}_C+\frac{1}{2}{T}_E\Delta E^2$$

(12)

3.2. Hamiltonian Model of VSG

There are transformation relationships based on the Hamiltonian function ∂H/∂φ = p_e, ∂H/∂ω = T_Bω, ∂H/∂i_d = X_Li_d, ∂H/∂i_q = X_Li_q, and ∂H/∂E = T_E(E − E₀). These Hamiltonian transformations can be used to replace state variables, and then differential equation can be written as Hamiltonian equation.

The Equation (4) can be rewritten as

$$\left\{\begin{array}{l}\frac{\mathrm{d}{i}_d}{\mathrm{d}t}=-\frac{R}{X_L^2}\frac{\partial H}{\partial i_d}+\frac{\omega }{X_L}\frac{\partial H}{\partial i_q}+\frac{1}{T_E{X}_L}\frac{\partial H}{\partial E}+(\frac{E_0}{X_L{u}_t}-\frac{\sin \phi }{X_L})u_{\mathrm{tin}}\hfill \\ \frac{\mathrm{d}{i}_q}{\mathrm{d}t}=-\frac{R}{X_L^2}\frac{\partial H}{\partial i_q}-\frac{\omega }{X_L}\frac{\partial H}{\partial i_d}-\frac{\cos \phi }{X_L}{u}_{\mathrm{tin}}\hfill \end{array}\right.$$

(13)

VSG adopts d-axis voltage orientation, that is e_q = 0, e_d = E. Considering the input control term is the bus voltage, denoted as u_tin. This treatment is to keep Equation (13) in an affine nonlinear equation form. In the network operation of the inverter, inverter outlet voltage u_t is equal to the voltage of the connected bus u_tin. Ignoring the salient pole effect of VSG and the line reactance, so X_q∑ = X_d’_∑ = X,u_d = u_tsinφ, u_q = u_tcosφ.

The Equation (8) can be rewritten as

$$\left\{\begin{array}{l}\frac{\mathrm{d}\phi }{\mathrm{d}t}=\frac{{\omega }_{\mathrm{B}}}{T_{\mathrm{B}}}\frac{\partial H}{\partial \omega }-\frac{{\omega }_{\mathrm{B}}{\omega }_{\mathrm{ref}}}{\omega }{\omega }_{\mathrm{in}}\hfill \\ \frac{\mathrm{d}\omega }{\mathrm{d}t}=-\frac{D+b_p}{T_{\mathrm{B}}^2\omega }\frac{\partial H}{\partial \omega }-\frac{1}{T_{\mathrm{B}}\omega }\frac{\partial H}{\partial \phi }+\frac{1}{T_{\mathrm{B}}{\omega }^2}[p_{\mathrm{ref}}+(D+b_p){\omega }_{\mathrm{ref}}]{\omega }_{\mathrm{in}}\hfill \end{array}\right.$$

(14)

Referring to the traditional third-order generator model, d, q axis current is i_d = (E − u_tcosφ)/X_L and i_q = u_tsinφ/X_L. In the Hamiltonian function, i_d and i_q imply the rotor variable φ, and the partial derivative of the implicit function is ∂H/∂φ = p_e.

From the principle of VSG, the bus frequency is the input controllable variable, denoted as ω_in. To keep Equation (14) in the form of affine nonlinear equation, in the last item of Equation (14), ω_in is approximately replaced by ω. Since the angular frequency changes very little in the connect-grid operation condition, this approximation makes the reference power term of VSG have some errors in the transient process, but the errors will not be too large. When it enters the steady state, ω = ω_in, the errors are eliminated.

The Equation (6) can be rewritten as

$$\frac{dE}{\mathrm{d}t}=-\frac{1}{T_E^2}\frac{\partial H}{\partial E}+\frac{K_E}{T_E{b}_Q}(-\frac{{\mathit{Q}}_{\mathrm{ref}}}{u_{\mathrm{t}}}+Z_Q)u_{\mathrm{tin}}$$

(15)

From the above transformation processes, they are all equivalent transformations based on differential equations. Therefore, the corresponding differential equations and Hamiltonian equations are mathematically equivalent.

Selected variables x = [φ ω i_d i_q E]^T, Equations (13)–(15) can be written in unification form. Considering matrix transformation J(x) = [T(x)−T^T(x)]/2 and R(x) = −[T(x) + T^T(x)]/2, the standard form of the generalized Hamiltonian system can be obtained as follows.

$$\dot{\mathit{x}}=[\mathit{J}(\mathit{x})-\mathit{R}(\mathit{x})]\frac{\partial H}{\partial \mathit{x}}+\mathit{g}(\mathit{x})\mathit{u}$$

(16)

$$\mathit{J}(\mathit{x})=\frac{1}{2}\left[\begin{array}{lllll}0\hfill & \frac{{\omega }_{\mathrm{B}}{x}_2+1}{T_{\mathrm{B}}{x}_2}\hfill & 0\hfill & 0\hfill & 0\hfill \\ -\frac{{\omega }_{\mathrm{B}}{x}_2+1}{T_{\mathrm{B}}{x}_2}\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 2\frac{{\omega }_{\mathrm{ref}}+x_2}{X_L}\hfill & \frac{1}{T_E{X}_L}\hfill \\ 0\hfill & 0\hfill & -2\frac{{\omega }_{\mathrm{ref}}+x_2}{X_L}\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & -\frac{1}{T_E{X}_L}\hfill & 0\hfill & 0\hfill \end{array}\right]$$

$$\mathit{R}(\mathit{x})=-\frac{1}{2}\left[\begin{array}{lllll}0\hfill & \frac{{\omega }_{\mathrm{B}}{x}_2-1}{T_{\mathrm{B}}{x}_2}\hfill & 0\hfill & 0\hfill & 0\hfill \\ \frac{{\omega }_{\mathrm{B}}{x}_2-1}{T_{\mathrm{B}}{x}_2}\hfill & -\frac{2(D+b_p)}{T_{\mathrm{B}}^2{x}_2}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & -\frac{2R}{X_L^2}\hfill & 0\hfill & \frac{1}{T_E{X}_L}\hfill \\ 0\hfill & 0\hfill & 0\hfill & -\frac{2R}{X_L^2}\hfill & 0\hfill \\ 0\hfill & 0\hfill & \frac{1}{T_E{X}_L}\hfill & 0\hfill & -\frac{2}{T_E^2}\hfill \end{array}\right],$$

$$\begin{array}{l}\mathit{g}(\mathit{x})=\left[\begin{array}{ll}-\frac{{\omega }_{\mathrm{B}}{\omega }_{\mathrm{ref}}}{x_2}\hfill & 0\hfill \\ \frac{1}{T_{\mathrm{B}}{x}_2^2}[p_{\mathrm{ref}}+(D+b_p){\omega }_{\mathrm{ref}}]\hfill & 0\hfill \\ 0\hfill & \frac{E_0}{X_L{u}_t}-\frac{\sin x_1}{X_L}\hfill \\ 0\hfill & -\frac{\cos x_1}{X_L}\hfill \\ 0\hfill & \frac{K_E}{T_E{b}_Q}(-\frac{Q_{\mathrm{ref}}}{u_t}+Z_Q)\hfill \end{array}\right]\\ \end{array}$$

$$\mathit{u}=\left[\begin{array}{c}{\omega }_{\mathrm{in}}\\ u_{\mathrm{tin}}\end{array}\right]$$

J(x) is the antisymmetric structure matrix, R(x) is the symmetric damping matrix, g(x) is the control input channel matrix, u is the input matrix, which includes bus frequency ω_in and bus voltage u_tin.

4. Structure Modification of Hamiltonian

4.1. Basic Theory

Antisymmetric matrix J_a(x) is used to modify the structure matrix, J_d(x) = J(x) + J_a(x), and J^T_a(x) = −J_a(x), where symmetric matrix R_a(x) is used to modify the damping matrix, R_d(x) = R(x) + R_a(x), and R^T_a(x) = R_a(x). Then the equivalence transformation of Hamiltonian system (16) can be given as follows.

$$\begin{array}{l}\dot{\mathit{x}}=\{[\mathit{J}(\mathit{x})+{\mathit{J}}_a(\mathit{x})]-[\mathit{R}(\mathit{x})+{\mathit{R}}_a(\mathit{x})]\}\frac{\partial H}{\partial \mathit{x}}-[{\mathit{J}}_a(\mathit{x})-{\mathit{R}}_a(\mathit{x})]\frac{\partial H}{\partial \mathit{x}}+\mathit{g}(\mathit{x})\mathit{u}\\ \begin{array}{l}\hfill \end{array}=[{\mathit{J}}_d(\mathit{x})-{\mathit{R}}_d(\mathit{x})]\frac{\partial H}{\partial \mathit{x}}+\mathit{g}(\mathit{x})\mathit{w}\end{array}$$

(17)

The above equation shows that, under appropriate conditions, the equivalent control w can be used to equivalent the change of The Hamiltonian structure, which is also the essence of the control design of Hamiltonian structure modification. The following equivalent transformations must be satisfied.

$$\mathit{g}(\mathit{x})\mathit{w}=\mathit{g}(\mathit{x})\mathit{u}-[{\mathit{J}}_a(\mathit{x})-{\mathit{R}}_a(\mathit{x})]\frac{\partial H}{\partial \mathit{x}}$$

(18)

Multiply both sides of the Equation (18) g^T(x). If the g(x) is column full rank matrix, then g^T(x)g(x) is reversible, so

$$\mathit{w}=\mathit{u}-{[{\mathit{g}}^T(\mathit{x})\mathit{g}(\mathit{x})]}^{-1}{\mathit{g}}^T(\mathit{x})[{\mathit{J}}_a(\mathit{x})-{\mathit{R}}_a(\mathit{x})]\frac{\partial H}{\partial \mathit{x}}=\mathit{u}+\mathit{\alpha }$$

(19)

$$\mathit{\alpha }=-{[{\mathit{g}}^T(\mathit{x})\mathit{g}(\mathit{x})]}^{-1}{\mathit{g}}^T(\mathit{x})[{\mathit{J}}_a(\mathit{x})-{\mathit{R}}_a(\mathit{x})]\frac{\partial H}{\partial \mathit{x}}$$

(20)

α is the additional control generated by the Hamiltonian structure modification.

In the Hamiltonian Equation (16), if u is replaced by w, it is mathematically equivalent to modifying the structure [J_a(x) − R_a(x)], because of the existence of additional control α.

4.2. Damping Injection

The stability of frequency and voltage are the key indexes of the isolated microgrid. However, there is no relevance between mechanical and electrical in the Hamiltonian system (16). This section attempts to increase the damping correlation between the bus voltage and the frequency so that the frequency and the voltage fluctuation are mutually restricted to better improve the stability of the isolated micro-grid. In the Hamiltonian model, the state variable x₂ is the angular velocity ω, and the state variable x₅ is the excitation electromotive force E. To increase the damping correlation between the ω and E, the corresponding position of the structure and the damping matrix is modified. Let J_a(x) = 0,R_a(x) is

$${\mathit{R}}_a(\mathit{x})=\left[\begin{array}{lllll}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & r_{25}\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & r_{25}\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]$$

(21)

According to Equation (20), the additional control can be obtained as

$$\mathit{\alpha }(\mathit{x})=\left[\begin{array}{c}\frac{A{T}_{\mathrm{B}}{x}_2^2}{A^2+(T_B{x}_2{\omega }_{\mathrm{B}}{\omega }_{ref}{)}^2}{r}_{25}\frac{\partial H}{\partial x_5}\\ B{r}_{25}\frac{\partial H}{\partial x_2}\end{array}\right]$$

(22)

where $A=p_{ref}+(D+b_p){\omega }_{ref}$, $B=\frac{T_E{b}_Q{K}_E{X}_L^2{u}_t(u_{ref}-u_t)}{E_0^2{T}_E{}^2{b}_Q-2T_E{}^2{b}_Q{u}_t{E}_0\sin x_1+T_E{}^2{b}_Q{u}_t^2+K_E^2{X}_L^2(u_{ref}-u_t{)}^2}$.

When the additional control could be calculated by Equation (20), g(x) must be column full rank matrix, so g^T(x)g(x) satisfies the reversible condition. This is why the transformation form of Equation (8) is adopted.

5. Simulation Experiment

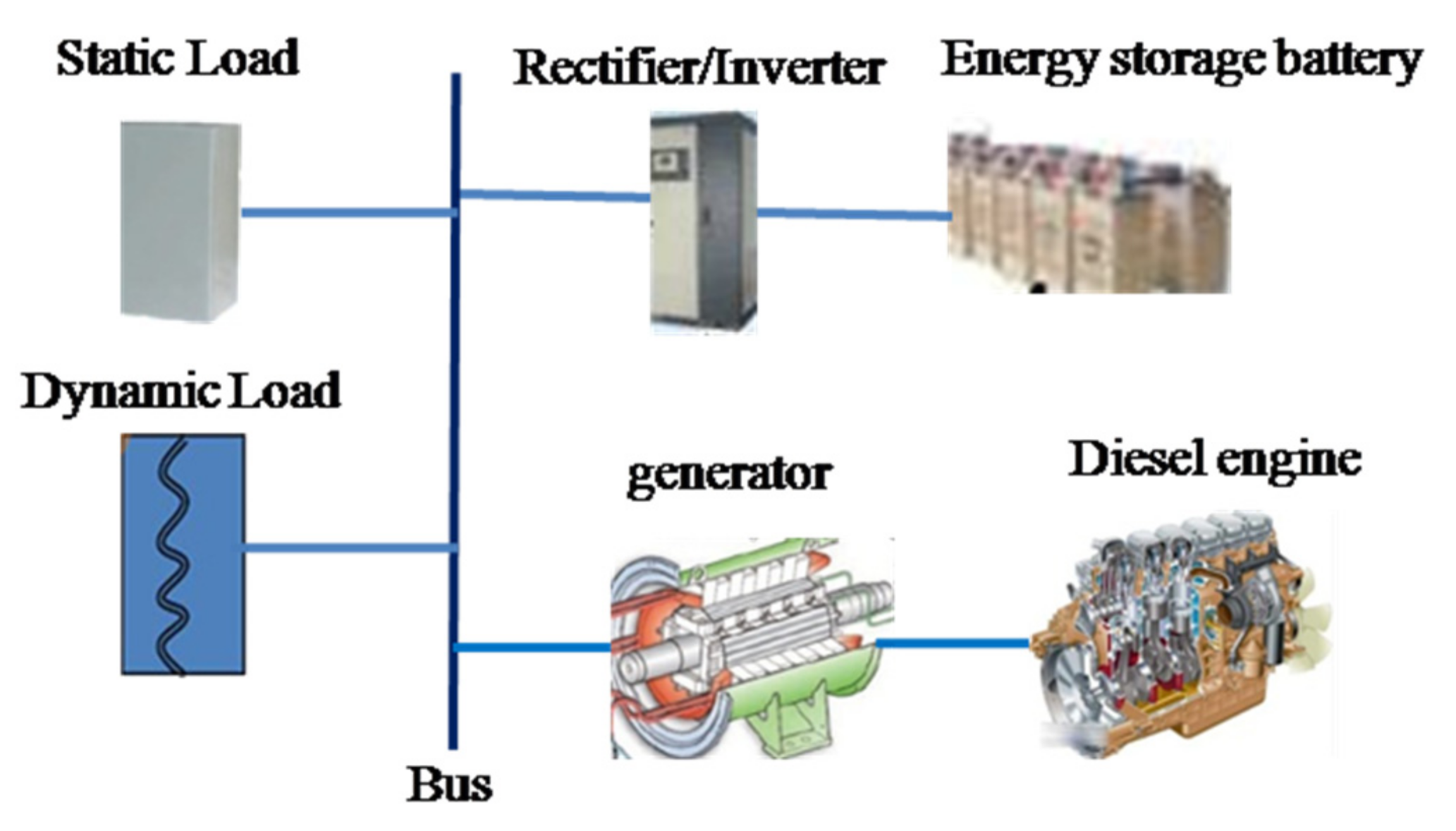
5.1. Simulation System

The isolated microgrid is shown in Figure 3.

In Figure 3, parameters of diesel generator sets (DGS), invertor unit, static load and dynamic load are all converted with power basic value of DGS. The model of dynamic load is the electromechanical transit model of electromotor [38], in which the active power of each motor is 0.1 pu and the reactive power is 0.047 pu. The change of dynamic load is simulated by the different numbers of electromotor.

The main parameters of the DGS: active power 1250 kW, rated speed n = 1500 r/min, m₁ = 0.8 kg, mechanical damping coefficient c₁ = 10.0 N.s/mm, spring stiffness k₁ = 3.6, the maximum stroke of the shaft output 10 mm, the moment of inertia J = 71.822 kg·m², the number of poles p = 2, and equivalent damping coefficient D = 2.1753. DGS use the traditional PID control, which the governor PID parameters are K_P = 2.0, K_I = 2.0, K_D = 0.1, excitation PID parameters are K_P = 2.0, K_I = 2.0, K_D = 0.1.

Using the Hamiltonian differential model of VSG replaced theinverter unit in the simulation calculation. LetD = 2, b_P = 10, and b_Q = −35.

Initial operation conditions: active power of DGS is 0.8 pu, reactive power of DGS is 0.6 pu; active power and reactive power of invertor are 0.0, the inverter works in a standby state; electromotors put in operation with active power 0.7 pu, reactive power 0.3291 pu. Other power is balanced by static loads to ensure the initial balance of bus power.

Simulation case: at t = 0.5 s, the motor is put into operation to simulate the nonlinear load mutation, the active power step is 0.1 pu, and the reactive power step is 0.047 pu.

The power changes of the invertor are shown in Figure 4.

When loads change suddenly, the invertor supplies the power vacancy rapidly due to the regulation lag of DGS. After the regulation of DGS is finished, the invertor operates at a standby state, in which active power and reactive power of output are zero. Figure 4 reflects such an operation mode of invertor in the isolated microgrid.

5.2. Damping Characteristic Analysis

(1)

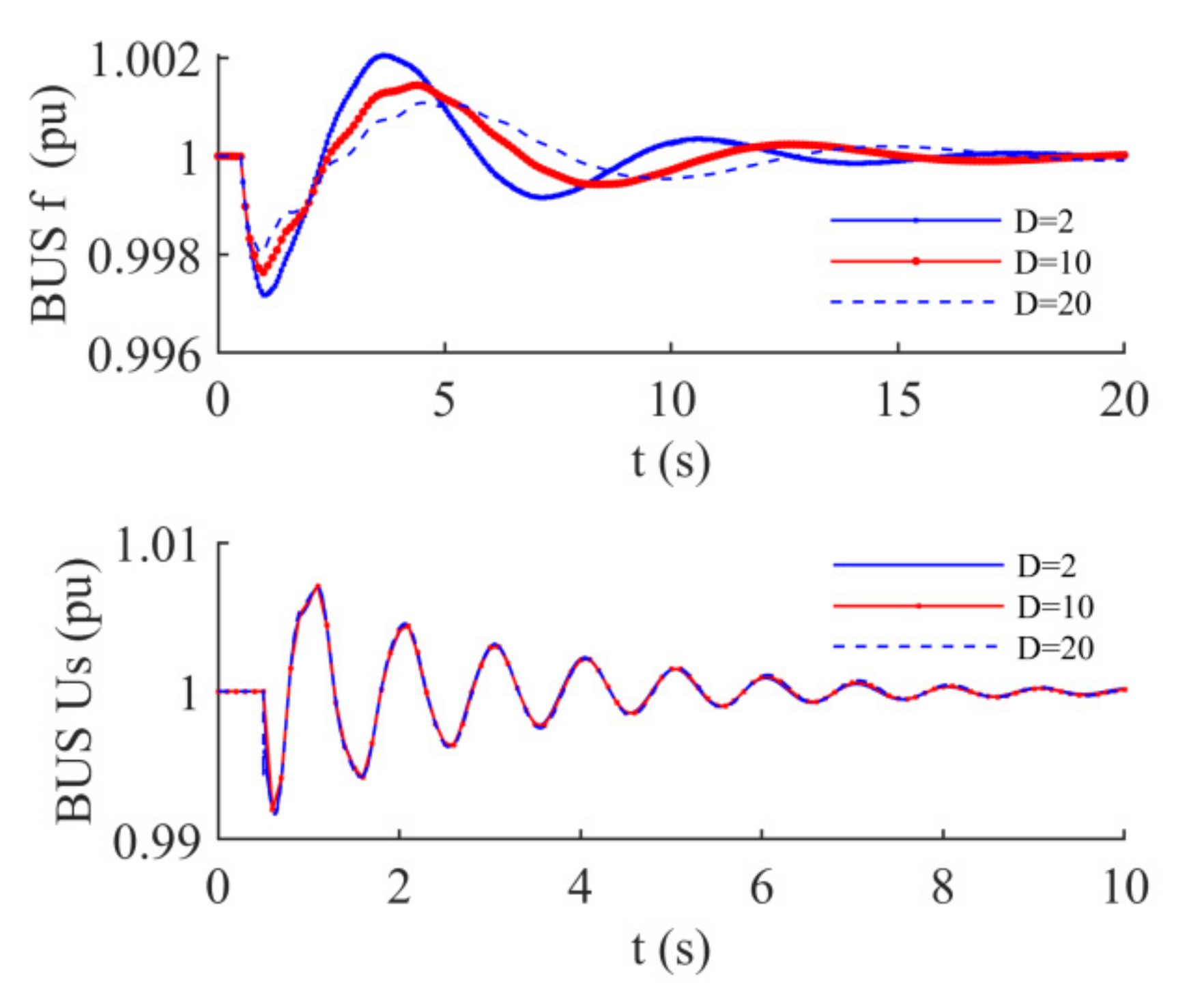
The damping coefficient D of VSG is located in row 2 and column 2 of damping matrix R(x), which represents the corresponding state variable of angular velocity. From the view of dynamics, the position that the factor located is self-correlation damping of angular velocity, on which only the damping characteristics of angular velocity have an effect. As the damping coefficient D increases, the oscillation amplitude of bus frequency decreases and the attenuation speeds up. In other words, the damping of angular frequency oscillation increases, while the change of bus voltage is not obvious. See Figure 5.

(2)

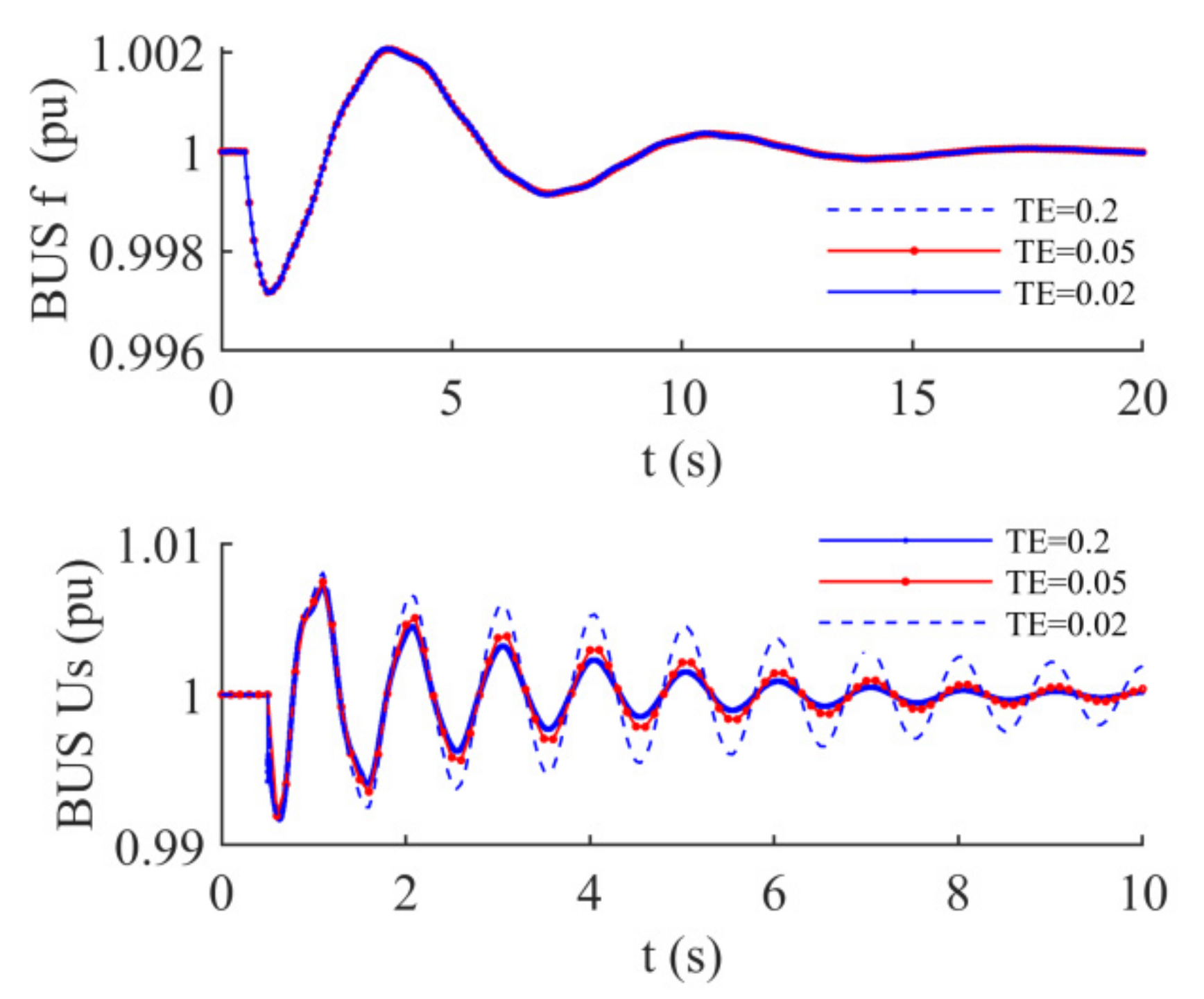
The time constant of excitation T_E relates to the state variables x₃ and x₅ in damping matrix R(x). Form the view of dynamics, where the element located at row 5 and column 5 is self-correction damping factor of x₅, where the element located at row 3 and column 5 is cross-correction damping factor of x₃ and x₅. Therefore, the change of T_E would affect the damping oscillation characteristics of bus voltage. Given different T_E, the change of bus frequency and voltage is shown in Figure 6.

When T_E decreases, the item in the damping matrix increases, and the bus voltage oscillation amplitude increases, which is equivalent to the decrease in the bus voltage oscillation damping. The value of T_E has positive damping property. Figure 6 also shows that different T_E given has little effect on the change of bus frequency.

Further simulation shows that T_E < 0.2, the value of T_E has little effect on the bus voltage, so it is not feasible to further increase the voltage oscillation damping by increasing T_E.

(3)

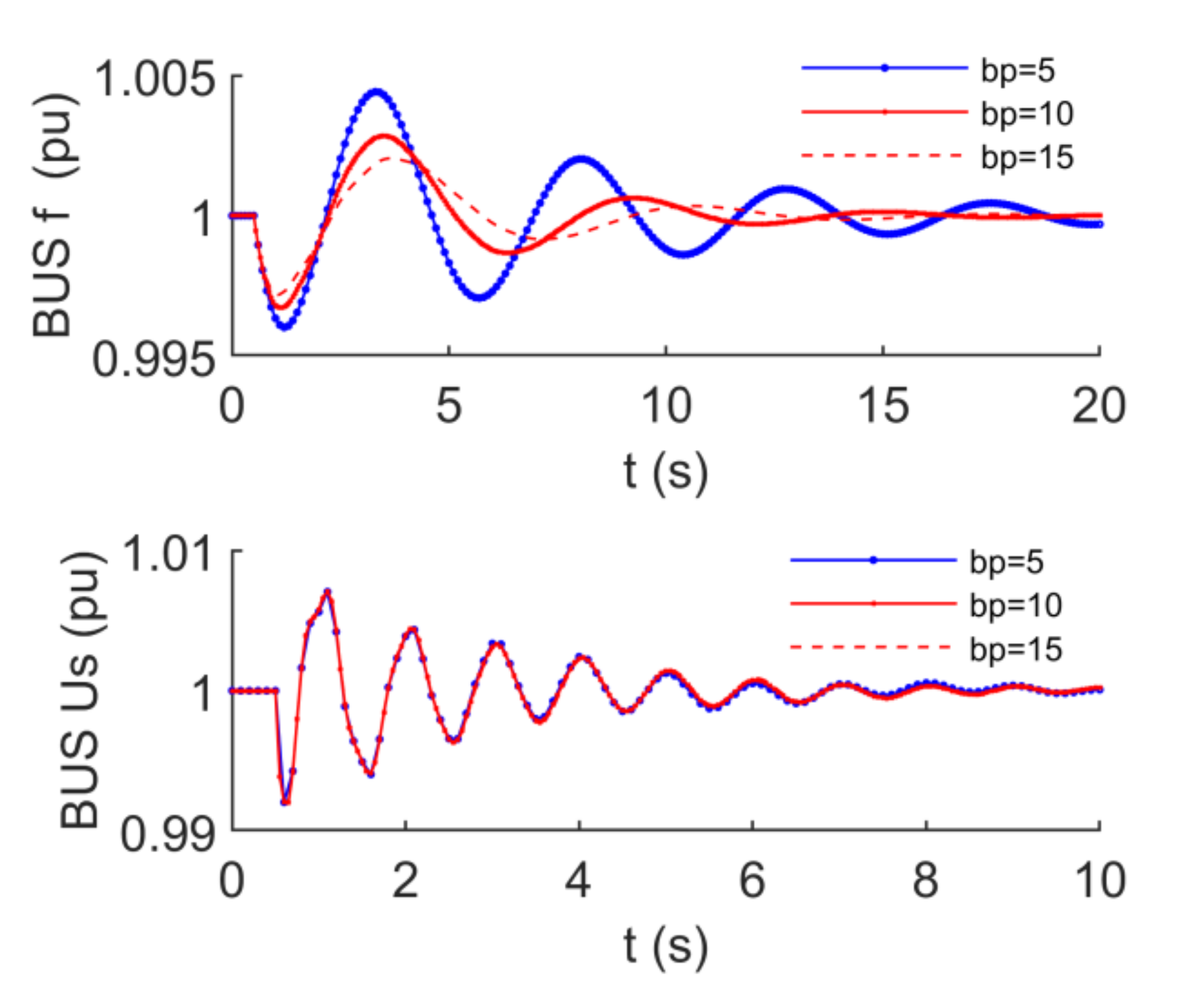
Effect of active power droop coefficient

The active power droop coefficient bp is located at the same position with the damping coefficient in the damping matrix R(x), which means that the bp has the same characteristics with damping coefficient. Given different bp values, the changes of bus frequency and voltage are shown in Figure 7.

Figure 7 shows that the effect of droop coefficient bp on oscillation damping of bus frequency is large. Its role is equivalent to the damping coefficient. However, the effect of bp on the oscillation of bus voltage can be ignored. The result is consistent with revealing by Hamiltonian structure dynamic.

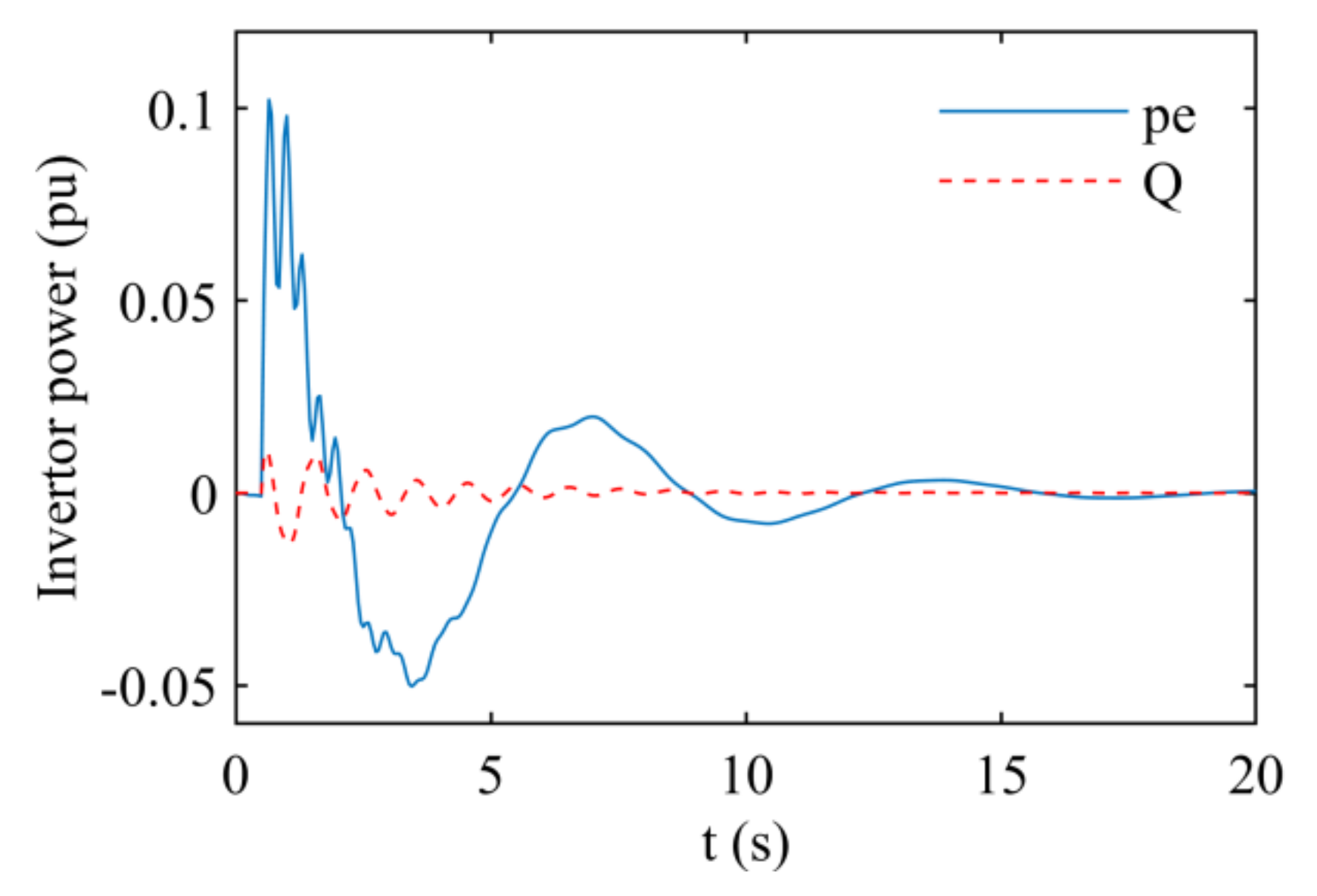
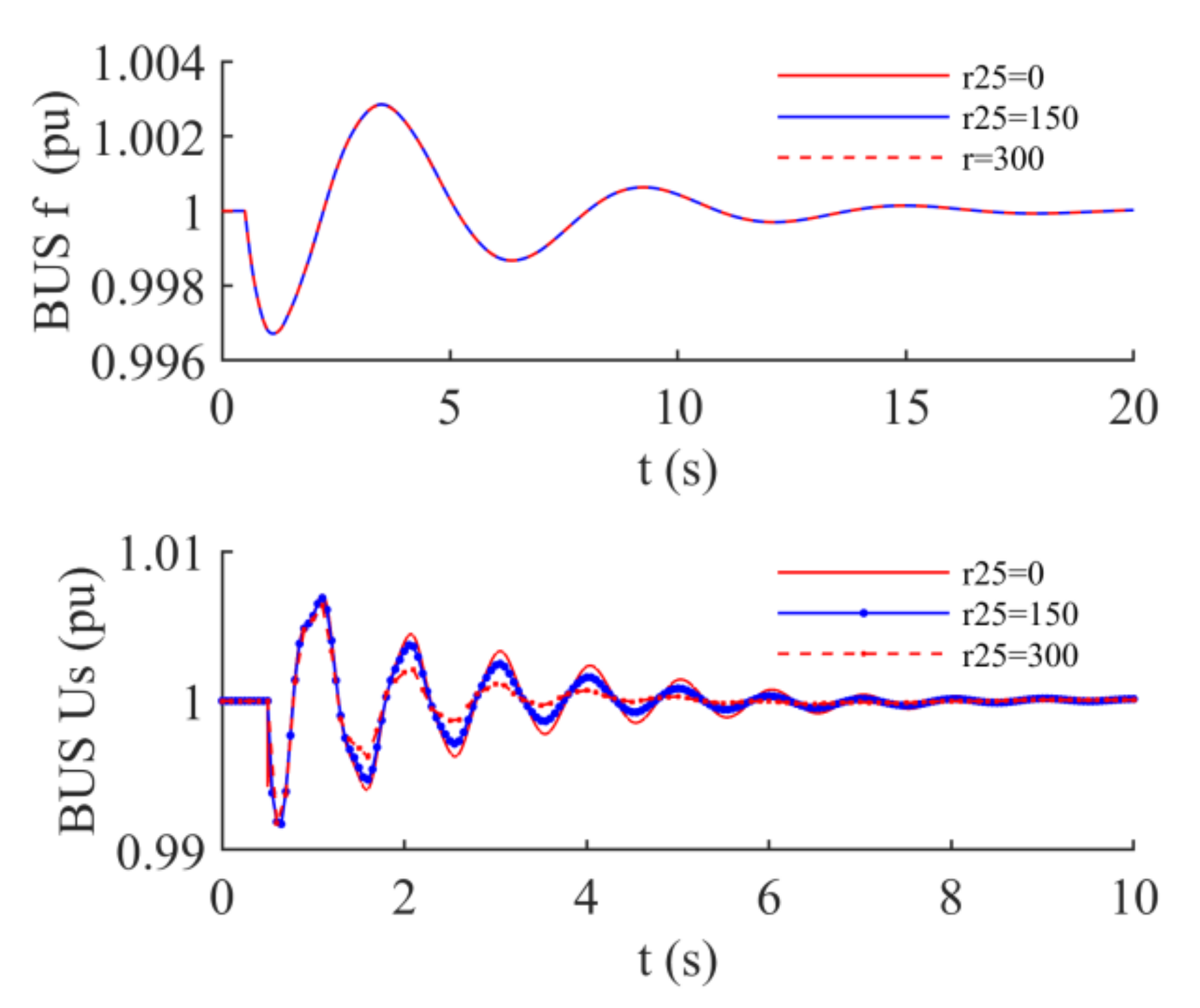
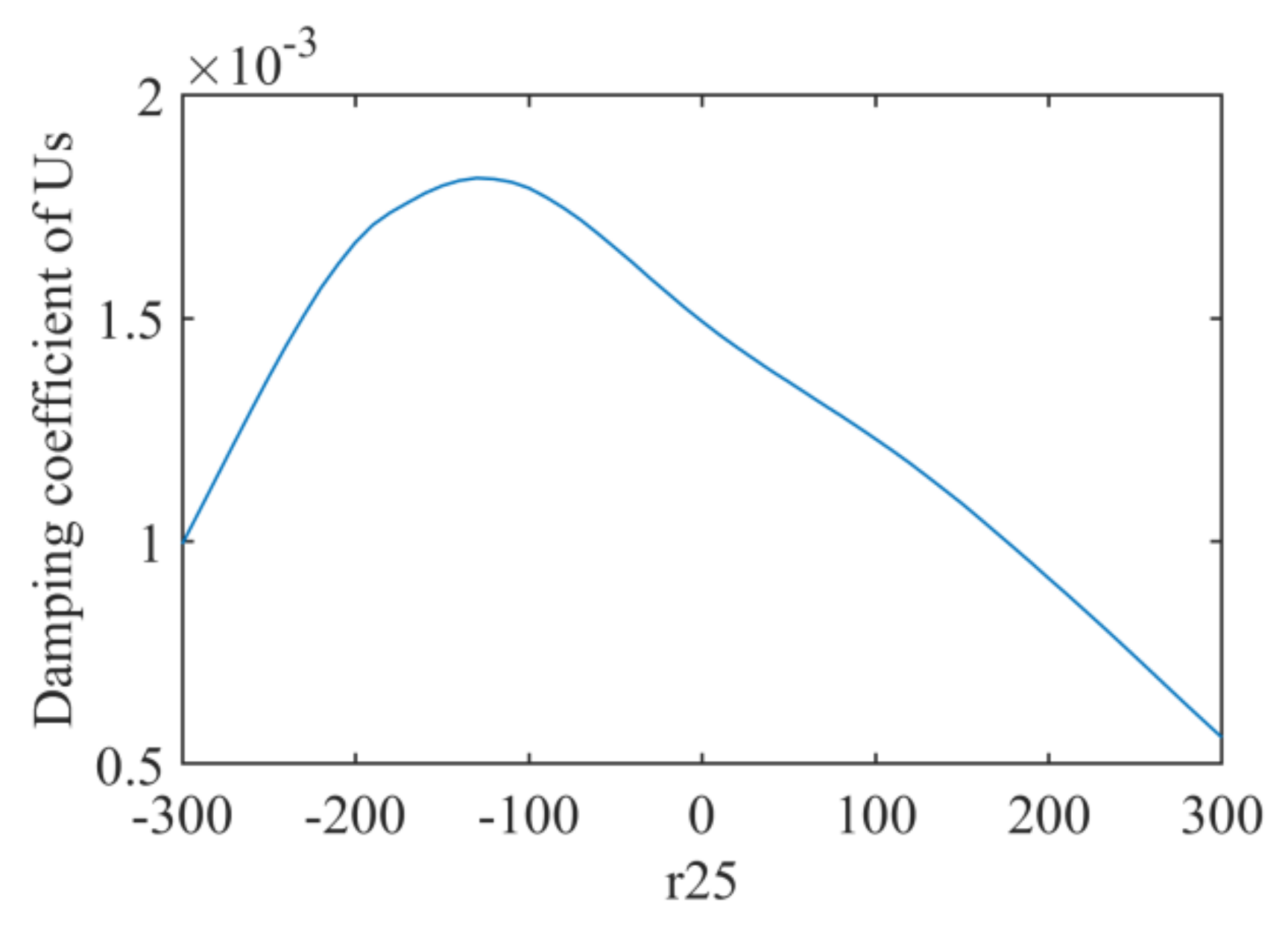
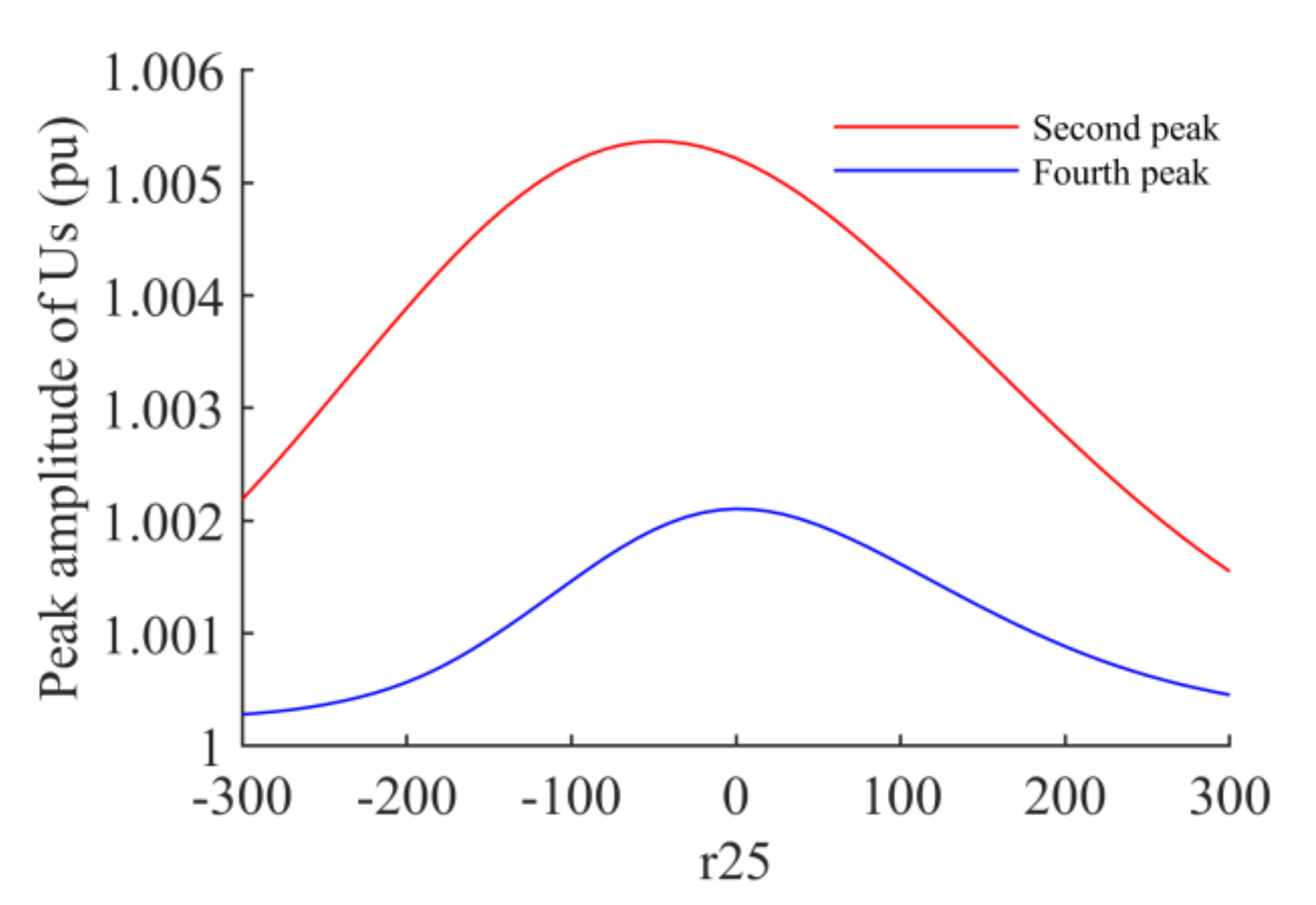
5.3. Damping Injection Control

In the damping matrix of the Hamiltonian model, the correlation factor r25 relative to the angular velocity ω and the excitation electromotive force E is added. After the damping correlation is added, the equivalent control corresponding to the structure modification is calculated by Equation (20).

Let the inverter damping coefficient D = 2, T_E = 0.2. Simulation analysis is carried out under the same simulation condition. The bus voltage and frequency changes under different values of r25 are shown in Figure 8.

In Figure 8, the bus frequency is little affected by the value of r25. From the damping modification additional control substituting the initial steady state data of the simulation condition into the damping modification additional control (20), the coefficient of the additional control item of the angular velocity in the first row is 1.7896 × 10⁻⁵. It is because this coefficient is very small, the structure modification has little influence on the angular frequency change when the given r25 is not very large. The damping correlation correction does not affect the change of the angular frequency, which is equivalent to get rid of the constraint of the angular frequency, and provides convenience for the selection of r25 to improve the bus voltage oscillation.

In Figure 8, the bus voltage oscillation attenuation varies greatly, and the attenuation varies with different values of r25, especially the voltage fluctuation amplitude changes greatly. Therefore, the change of bus voltage oscillation damping coefficient with different values of r25 is further studied, so the third and fourth peak values of voltage fluctuation are selected to investigate the change of amplitude as follows.

Figure 9 and Figure 10 show that the damping correlation factor r25 in an appropriate range can increase the damping of voltage oscillation and reduce the amplitude of voltage fluctuation. Its trend seems that the larger the value of r25 is, the smaller the oscillation amplitude will be. However, the further simulation shows that if r25 continues to increase, the off-beat phenomenon of voltage oscillation will occur, and the further increase will eventually lead to instability.

According to Figure 9 and Figure 10, increasing the value of damping factor r25 in the Hamiltonian damping matrix and using control to equalize the change of the system structure can effectively reduce the voltage fluctuation of the isolated microgrid.

6. Conclusions

In this paper, the Hamiltonian model of VSG is established. The damping formation mechanism and damping injection control of VSG are analyzed from the perspective of dynamics, and the isolated microgrid is constructed for simulation analysis. There are three conclusions as follows:

(1)

When the VSG is directly connected to the isolated microgrid bus, the influence of a single parameter of VSG on the oscillation damping of the bus voltage and frequency has decoupling characteristics, that is, the change of damping coefficient D and active power droop coefficient bp only affects the oscillation damping of the bus frequency; The excitation time constant T_E of VSG only affects the bus voltage oscillation damping. This decoupling characteristic greatly facilitates the design of virtual generator parameters.

(2)

The Hamiltonian damping injection control design method proposed in this paper can effectively reduce the bus voltage fluctuation amplitude by selecting an appropriate damping factor, which can make up for the deficiency of small virtual generator time constant T_E in reducing the bus voltage oscillation amplitude.

(3)

The Hamiltonian structure design method for VSG is a new approach. In this paper, the damping injection control is just an example. Further research can be carried out from the following aspects: the modified structure matrix, damping matrix, the single factor, and multiple factors to obtain more dynamic information and provide more means for control design.