2.3.1. Calculate Index Weight
Based on the above analysis, this paper focuses on Group1. There are six indicators in this indicator group. In order to distinguish and calculate easily, the indicators in the group are renamed as B1 research and development cost, B2 component production cost, B3 construction cost, B4 resource consumption, B5 building demolition cost, and B6 seasonal frozen effect. In order to further study the degree of influence of the above six indicators, the analytic hierarchy process (AHP) is used to calculate the weight of each indicator. This paper refers to the AHP analysis method used by Saaty [
36] in “Decision Making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World”. The AHP method can divide complex problems into different levels for processing, and is suitable for decision-making problems that are difficult to accurately measure and calculate. When using the AHP to solve problems, it is necessary to construct a hierarchical structure. For each index, the Saaty1–9 scaling method is used for expert scoring, and to assign values to the index influence degree. The Saaty1–9 scale table is shown in
Table 3.
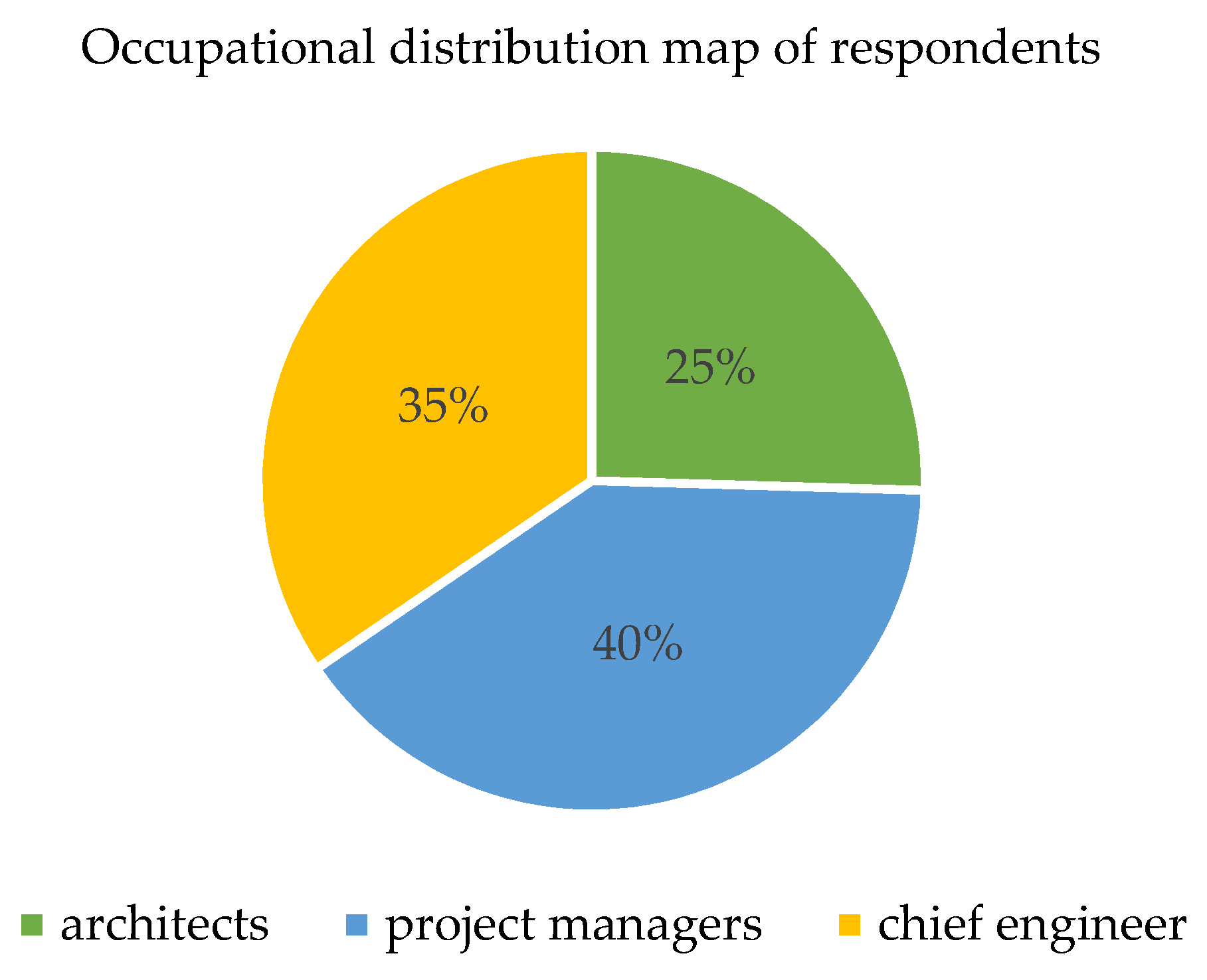
Using the Saaty1–9 scaling method, the indicators are assigned values through expert scores, qualitative factors are quantified, and the weights of various indicators are calculated. The weight of the impact of each indicator on the comprehensive benefits of the entire life cycle of the prefabricated building can be obtained by comparing the indicators in pairs and constructing a judgment matrix. In order to further ensure the accuracy of the research, this paper has increased the sample size and issued 300 questionnaires to senior leaders, project managers and domain experts in the prefabricated construction industry. The above-listed experts completed the questionnaires through the mobile application and a total of 237 valid questionnaires were received. The experts who responded to the effective questionnaire were architects, project managers, chief engineers, and scientific researchers with rich academic achievements in the field of prefabricated construction from China’s leading construction companies. They have worked or researched for a total of 3508 years (average 14.8 years). The occupational distribution chart is shown in
Figure 3.
According to the scoring results of each expert, a corresponding judgment matrix can be constructed, and the judgment matrix of each expert can be analyzed separately, and the index weight value given by each expert can be calculated. In order to ensure the accuracy of the calculation results, it is necessary to check the consistency of the judgment matrix, eliminate the questionnaire results that fail the consistency check, and then average the index weights given by each expert to obtain the average weight of each index.
The method of calculating the index weight according to the judgment matrix is as follows. First, multiply the data of each row of the judgment matrix to obtain the row product of each row, then calculate the 6th root of the row product, and normalize the calculation result by column to get the weight of each indicator. Finally, in order to test the accuracy of the weight calculation results, it is also necessary to calculate the maximum eigen value of the judgment matrix for consistency testing. The calculation process is as follows:
- (1)
Calculate the row product of each element of the matrix.
where
bij represents the element in the
i-th row and
j-th column of the matrix.
- (2)
Calculate the n-th root of Mi.
where
Mi represents the product of each element in each row of the matrix, and
n represents the number of rows in the matrix. In this paper, the value of
n is 6.
- (3)
Normalize wi by column to get the index weight.
where
wi′ is the sixth root of the product of the elements in each row.
- (4)
Calculate the maximum eigen value.
where
ri represents the
i-th row vector in the matrix and
wi represents the weight value corresponding to each indicator calculated by Formula (7).
Wi represents a column vector composed of each w value, and n represents the number of rows in the matrix. In this paper, the value of
n is 6.
Experts may have fuzzy judgments when scoring elements, leading to inconsistent influence of element values in the matrix. It is necessary to check the coordination between the importance of elements to avoid the occurrence of A is more important than B, B is more important than C, but C is more important than A. In order to ensure the accuracy of the weights, a consistency check is required. Determine whether there is a significant difference between the average value or the variance of each party at a certain level of significance. If there is no significant difference, the average value or variance of each party is consistent. When the CR calculation result is less than 0.1, it proves that there is no significant difference in the evaluation process, the index weight calculation is correct, and the result of the judgment matrix passes the consistency test. Refer to the inspection method proposed by Saaty [
37] in “The Analytic Hierarchy Process” and the calculation method of CI and CR is as follows:
- (1)
Calculate the consistency index CI.
where
λmax is the calculation result of Formula (8), and
n represents the number of rows in the matrix. In this paper, the value of
n is 6.
- (2)
The average consistency index is taken.
In the consistency test, the average consistency index RI needs to be used. RI is a constant used to calculate the consistency ratio CR of the judgment matrix, and the value is obtained according to the order of the matrix. By consulting the analytic hierarchy process (AHP) average consistency index value table, the RI values corresponding to different matrix orders can be obtained. This paper refers to the RI value table used by Zhang [
38] in the consistency test. RI values are shown in
Table 4.
- (3)
Calculate the consistency ratio CR.
The value of RI is obtained by looking up the table. This paper uses a 6-order matrix, so RI is 1.24.
When CR < 0.1, the matrix meets the consistency requirement.
Taking an expert’s scoring result as an example, the judgment matrix and calculation results constructed based on the expert’s scoring result are shown in
Table 5.
The calculation process is as follows. Taking B1 as an example, by multiplying the elements in the first column of the judgment matrix,
M1 = 0.74 corresponding to B1 can be obtained. Take the 6th root of the calculated
M1 to get
wi′ = 0.74. Using the same method, we can calculate the
wi′ corresponding to each indicator, and then divide the
wi′ corresponding to each indicator by Σ
wi′ to get the weight w
i corresponding to each indicator. The weight corresponding to index B1 is
w1 = 0.1. Similarly, the weight corresponding to other indexes can also be obtained. After obtaining the column vector
Wi composed of the index weights
wi, Formula (8) can be used to calculate the
λmax = 6.08. By substituting
λmax into Formula (9), CI = 0.016 can be calculated. By looking up
Table 4, RI = 1.24 can be determined, and then CI is divided by RI to get CR = 0.013.
Table 5 shows the evaluation results of this expert, CR = 0.013 < 0.1, which proves that the matrix passes the consistency test. Research and development costs (B1) weight is 0.10, component production cost (B2) weight is 0.25, construction cost (B3) weight is 0.38, resource consumption (B4) weight is 0.07, building demolition cost (B5) weight is 0.04, and seasonal freezing effect (B6) weight is 0.16. The influence degree of the indexes can be ranked according to the weight; the greater the weight, the greater the influence degree of the indexes. The ranking of the indexes of this expert is B3, B2, B6, B1, B4 and B5, and the influence degree decreases sequentially.
Based on the evaluation results of 237 questionnaires, a judgment matrix for each expert can be constructed. According to the above steps, the corresponding index weight value and CI can be calculated according to the scoring results of each expert. Through calculation, 24 questionnaire results failed the consistency test (CR > 0.1), and the 24 questionnaire results were removed and the average weight of each indicator was calculated. The calculation process of the average weight refers to the method adopted by Suganthi [
32], and the weights calculated from the remaining 213 questionnaire results are averaged to obtain the average weight of each indicator. The calculation results are shown in
Table 6.
In order to further verify the accuracy of the conclusions, this paper compares the ranking of the calculation results of various indicators with the ranking of the scoring results of the experts. We used Statistical Product and Service Solutions (SPSS) software (25.0.0, IBM, Armonk, NY, USA) to describe the distribution curve of the data set, and calculate the kurtosis and skewness to determine whether the expert scoring results conformed to the normal distribution. The judgment criteria are shown in
Table 7.
When making judgments, the distribution data set of expert opinions can be obtained by calculating the difference between the calculation ranking of each indicator and the expert scoring ranking. Taking B1 research and development cost as an example: According to the calculation results in
Table 6, the research and development costs index is ranked as 2. If the expert believes that the research and development costs ranking is 2, the corresponding ranking score is 0 points. If the expert believes that the research and development costs ranking is 3, which is 1 place lower than the calculated ranking, the corresponding ranking score is −1 point. Comparing the scoring results of each expert with the calculation results in this paper, a data set reflecting the gap between the opinions of all experts and the calculation results can be obtained. According to the kurtosis and skewness values of the data set, this determines whether the data obeys a normal distribution. The difference data set is shown in
Figure 4.
Figure 4 describes the distribution of the data set of expert opinion and average ranking difference, and lists the kurtosis and skewness values. It can be seen from the figure that the values of kurtosis and skewness are both close to zero. It can be judged that the data set obeys the normal distribution, and the calculation result of the weight of each indicator is correct.