1. Introduction
Knowledge of the electromechanical system model is important for many different reasons. It provides information regarding both the structure and parameters of the real system from the model point of view. This assists in understanding electromechanical system dynamic behavior in many practical cases. It also provides a tool to the simulate behavior of the electromechanical system in different conditions [
1,
2]. Deep knowledge of the model will be helpful in selecting a classical control method and tuning it and using a predictive control algorithm [
3,
4] or one of the adaptive control methods [
2,
5,
6]. Another wide range of applications that are based on model knowledge are fault diagnosis methods, where the model is used to calculate residuum between the model and the real system.
Mechatronic systems with a resonant mechanical part are difficult to control and are interesting subjects for many researchers worldwide. The difficulty is associated with the number of mechanical resonances and their frequencies. Mechatronic systems with one mechanical resonance (a two-mass drive system) and low frequency have been evaluated in recent years. This includes an example of one mechanical resonance (two-mass drive system) from 10.2 to 17.6 [
7], 9.6 [
8], and 70 Hz [
9]. The identification of two-mass drive systems has also been the subject of research. Online estimation of one mechanical resonance in the range of 54–80 Hz using pseudo-random binary signal (PRBS) and discrete-time transfer function (DTTF) was carried out in [
10] and in the range of 54–91 Hz using a chirp signal and DTTF model in [
11]. Furthermore, there has been identification of a resonating mechanical system in mobile road vehicles modeled as two-mass systems (one mechanical resonance of about 12 Hz) using PRBS, chirp, and stepped sine signals [
12]. The PRBS excitation signal was also used in [
13] to identify two-mass model parameters based on a DTTF model. The article [
13] also presents identification of two-mass mechanical systems with one mechanical resonance of about 80 Hz using PRBS and DTTF models. The identification of a drive system with one (64 or 100 Hz) and two mechanical resonance frequencies (around 60 and 100 Hz) was studied in [
14] using PRBS and a continuous-time model, with the cost function calculated as a module of the difference between the sampled frequency response and continuous-time model.
Previous research has focused on multi-mass drive systems with high mechanical resonance frequencies in ranges up to 500 Hz. The first approach of the author of [
15] used only output signal in frequency domains with a custom search algorithm. The dynamic search algorithm assists in finding appropriate resonance frequencies without a system model and an unknown number of resonances. However, anti-resonance frequencies were not identified by this algorithm, and a second drawback is its accuracy of around ±3 Hz. This algorithm was successfully tested and compared [
3] with manual identification used in control systems, with variable mechanical parameters with three resonance frequencies of 105, 251, and 417 Hz. Research was carried out by the author of [
16] to compare the identification of one resonance system in simulation and to identify laboratory setups with three mechanical resonances using PRBS and chirp signals as input and different means of identification of DTTF models (ARX—autoregressive with exogenous input and OE—output error). The usage of ARX and OE DTTF models gives fair results of identification and underlines the problem of the attraction of model parameters to high-frequency components by using a linear least-squares algorithm. In the next stage of development in this field of research, a nonlinear least-squares algorithm was used by the author of [
17] to find parameters that best fit frequency response data. The obtained identification results were positive only for the first two resonances of 81 and 202 Hz, without appropriate identification of the higher resonance component at 273 Hz because of the attraction of high-frequency components above the cutoff frequency of the current control loop. Studies [
15,
16,
17] showed that chirp signals give a smoother frequency response in comparison to PRBS, as the frequency range is banded and the magnitude is flat. A second conclusion from previous work is that linear least-squares with the DTTF model and nonlinear-least squares methods with the continuous-time transfer function model are attracted by higher frequency parts of the frequency response.
In this article, the author focuses on multi-mass drive systems with high frequencies. The laboratory stand is characterized by three main mechanical resonance frequencies in ranges of up to 500 Hz. The difficulty of the subject increases by the number of resonance frequencies, where tree mechanical resonances are characteristic of a four-mass system. Another difficulty is their high frequency values close to a region that exhibits no excitement in the frequency domain. The main finding of this article is the identification of a direct-drive system with a complex mechanical part, characterized by high frequency resonances as a continuous-time model directly within a frequency domain. Previous research has used a known nonlinear least-squares algorithms without constraints for less complex mechanical systems in a lower frequency range. This article shows the usage of a nonlinear least-squares algorithm with constraints to handle high-frequency attraction problems in the direct-drive system. The secondary findings presented in this article describe differences in cost functions based on complex number representation in the direct-drive system.
In practice, algorithms used for control and monitoring of electromechanical systems run on microcontrollers, or microprocessors, which process data with a constant sample time and with a limited bit resolution. Therefore, the data used for the model design will have constraints of value and time resolution. The model will be identified using sampled data; however, the model representation can still be chosen.
Model structure can be selected arbitrarily based on designer experience or by an algorithm. The first step of the identification workflow is to select a representation of the model structure. Classical identification methods use a discrete-time (DT) model structure and sampled data. In this paper, a continuous-time (CT) model structure processing sampled data is considered. CT system identification in the time domain requires special treatment of time derivatives [
18]. A suitable model of an electric drive with a multi-resonant mechanical part may be prepared in several model representations [
19]. If the mechanical part construction is known and well described by the equations of motion, the most suitable representation will be continuous-time state space (CTSS) with selected space variables. In practice, CTSS has multiple outputs and multiple inputs, but electric motor velocity and load velocity are most commonly selected as the outputs, and electric motor torque and load torque are selected as the inputs. Multi-input multi-output (MIMO) CTSS model representation can be transformed into a matrix of several continuous-time Laplace transfer functions (CTTF), where one CTTF describes the dynamic relationship of single input and single output (SISO), with zero condition of the other inputs [
19].
The next step of the identification workflow is the selection of inputs and outputs of an electric drive with a multi-resonant mechanical part, which are used further in the procedure. In real-world applications, not all inputs and outputs are available or measurable. Therefore, an MIMO model is constructed on a limited number of SISO sampled data. In this paper, the measured electric motor velocity and the current controller setpoint corresponding to the torque of the electric motor are used.
The final step is fitting the model to the measured data and validating the obtained results. This leads to a model fitting problem known in machine learning and curve fitting methods. One issue of fitting a model to measured sampled data is the optimization problem. If model parameters are bounded, there can be an optimization problem with constraints. Optimization solvers are a well known and present large group of methods, such as linear programming, quadratic programming, nonlinear programming, linear least squares, and nonlinear least squares [
20]. The identification of a discrete model from sampled time-domain data can be applied by linear programing [
13,
16]; however, in this approach, transformation to continuous representation after identification is required, and this method lacks frequency constraints. Many different methods have been developed to identify CT based on time-domain data [
18,
21,
22,
23,
24] or based on frequency-domain data [
25,
26,
27,
28]. As a fitting algorithm in the frequency domain, the methods of instrumental variable and linear least squares approximations [
28], instrumental variable and bi-orthonormal polynomial bases [
27], maximum likelihood [
25], and weighted nonlinear least squares [
26] have been applied.
In this paper, the nonlinear least-squares (NLS) method with constraints is applied to solve a nonlinear optimization problem of fitting the model to the frequency response dataset. Different complex number representations of the same datasets of frequency response data are thoroughly presented. All presented complex number representations are compared in a simulation test repeated one thousand times at different starting points. This allows for quality indicators of each representation to be prepared. A further novelty of the article is in bounding the NLS operating with frequency data to a specific range of frequencies of the excitation signal. A second constraint is added to the damping factor, so its assumed range is from zero to one. The presented identification workflow is verified by simulation and a dataset from the laboratory setup.
2. Frequency Model of Electric Drive with Multi-Resonant Mechanical Part
The model of the discussed electric direct drive has an electric part and a mechanical part. In the real application, a permanent magnet synchronous motor (PMSM) was used. The laboratory setup is presented in
Figure 1. The electric part consisted of a 3-phase supply, a 3-phase rectifier, and a 3-phase inverter. The mechanical part consisted of metal plates directly mounted to the motor shaft. The laboratory setup allowed for the measurement of 3-phase currents
and
which are transformed to rotating coordinates
and
based on the rotor electric position
which is calculated from the measured motor position
multiplied by the number of motor pole pairs equal to 12. Two proportional–integral (PI) controllers were used to track reference currents
and
. Actuating signals are voltages in rotating coordinates
and
, transformed to 3-phase stationary coordinates
, and
as an input for a pulse-width modulation (PWM) inverter. The PWM switches
voltage with a frequency of 10 kHz. The time constants of the electric part were significantly smaller than those of the mechanical part and had limited influence on the velocity and position of the mechanical part. In the current article, the author focused on the identification of the mechanical part with a known CTTF model of a current closed loop responsible for torque generation. The velocity of the motor
was calculated from the motor angular position
as a first time derivative
, where
is change in the motor angular position divided by change in time
. The calculated velocity of motor
contained high-frequency noise, and, therefore, a lowpass digital filter with a cutoff of 500 Hz frequency was applied. A low-pass filter is the first part of the digital filter shown in the diagram in
Figure 1. The second part of the digital filter is a bandstop filter, tuned to attenuate resonance frequencies in feedback signal
. The output of the used filter
was used as a feedback signal in the speed controller with a reference velocity of
. The velocity of the load
is not available in the measurements.
The mechanical part was modeled as four CTTFs:
and
, where only one pair of input and output was measurable, with motor current
(equivalent to motor torque
) and motor velocity
. The torque of load
and the velocity of load
were not measurable at the laboratory setup of direct drive. The model of the direct-drive mechanics is presented in
Figure 2, where the current constant k
T = 17.5 Nm/A, delays τ
cur = 300 μs, and τ
sam = 200 μs are known. The model of four CTTFs can be transformed to represent a MIMO-CTSS model if needed. At this point, a broader usage of the proposed method is worth mentioning. A reader who has a typical two-mass application [
29] or a multi-mass application [
3] can use the presented method after transforming CTSS to the matrix of CTTF. CTTF and
relationships between motor current
(equivalent to motor torque
) and motor velocity
are described in (1).
The Laplace CTTF model may be transformed into a continuous frequency response function (CFRF) by applying
s = jω, where
s is the Laplace operator and
ω is the angular frequency (
ω = 2
πf,
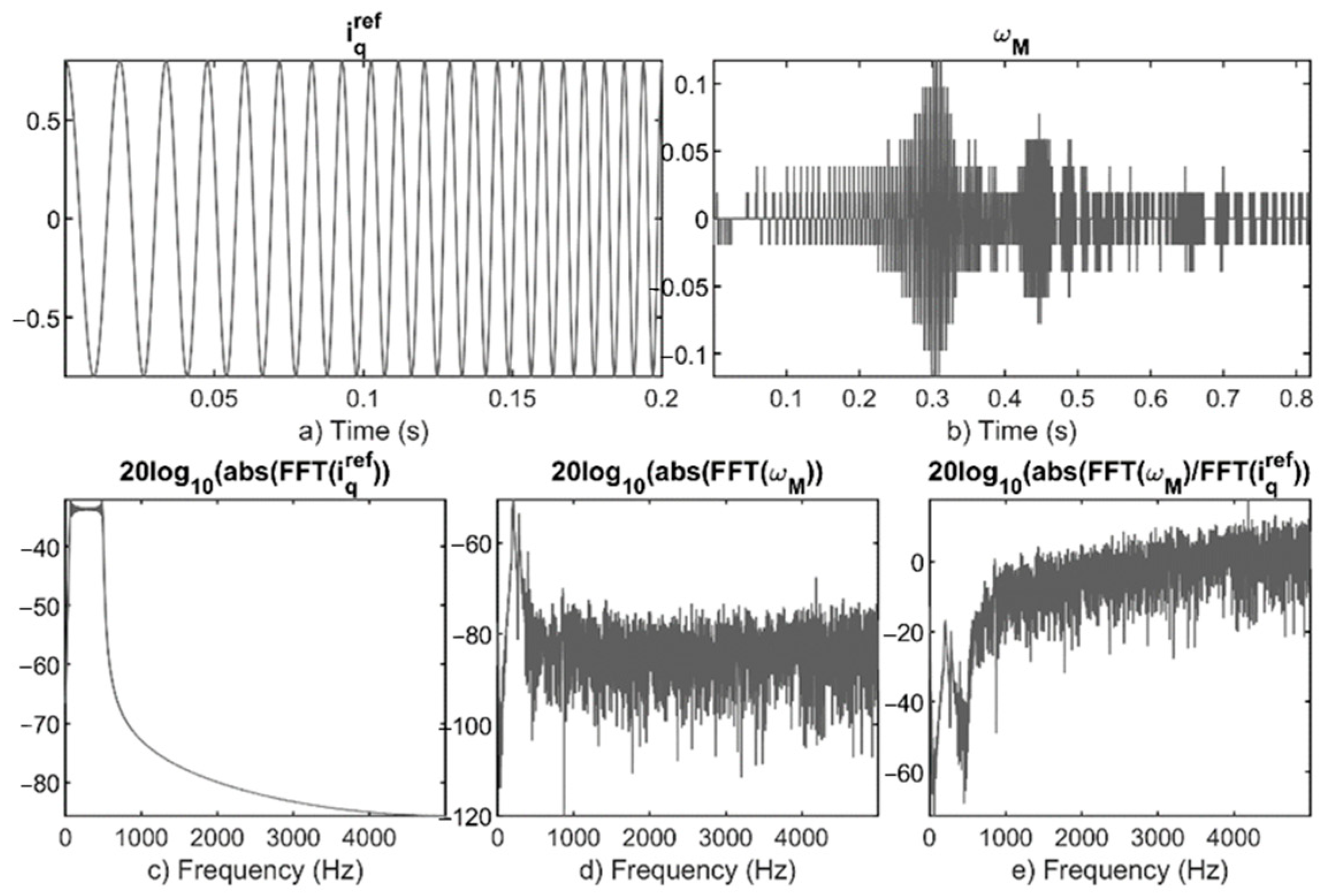
f—continuous frequency in Hz). In the result, (1) is transformed to (2). Sampled data (measurements) are delivered in the time domain and need to be transformed to the frequency domain by application of discrete Fourier transform (DFT). The transformed measurements were used to calculate discrete frequency response data (DFRD) by division of each complex number of the output and input. The CFRF model can be fitted to a complex number DFRD to find unknown parameters (3). In the real application, a linear chirp signal in the range of 50 to 500 Hz was used as the input, where change in frequency was achieved linearly in a time of 819.2 ms at the 100 μs sampling time. The linear chirp is a cosinusoidal signal with linearly increasing frequency in time. Part of the input signal change in time from 0 s to 200 ms is shown in
Figure 3a, and the magnitude of the whole input signal is shown in
Figure 3c. The linear chirp signal has flat magnitude characteristics and stimulates system frequencies equally in a selected frequency range (
Figure 3c). The time domain input-output data and the magnitude of Fourier transform are presented in
Figure 3.
Figure 3b presents motor velocity calculated from the motor angular position
as a first time derivative
, where
is changed by the motor angular position divided by change in time
. The change in the angular position is considerably small in laboratory direct drive because of the used low-speed PMSM with 12 pole pairs. The nominal motor speed is 145 rpm. An applied encoder sensor has 125,000 impulses per revolution. The resolution was increased four times by counting both edges of signal channel A XOR B of the encoder. This setup allowed for safe excitation at a very low speed of drive without damage.
Figure 3e presents DFRD of the laboratory direct drive in the frequency range from 0 to 5000 Hz (sampling frequency over two). The current control loop bandwidth of the laboratory stand is limited to about 530 Hz. Therefore, the part of DFRD above this frequency is useless because of a very small excitation that leads to an unreasonably large gain on output. The optimization of the model of resonance and anti-resonance frequencies was constrained to the range of the excitation spectrum.
4. Discussion
The identification of CT models that describe a laboratory setup of complex mechatronic system with limited knowledge of equations of motion is a difficult task. In previous research, the author encountered the problem of transformation to CT representation when identifying DT models. Therefore, to overcome this problem of identification, the CT model was selected based on frequency response data as complex numbers. The first fit of the CT model to the dataset is a nonlinear optimization problem, and the dataset is in complex number representation, which needs special treatment. Therefore, application of a real-number nonlinear optimization solver requires transformation of complex numbers to real numbers. Real representation of complex numbers can be achieved via several techniques. The selected representations of complex numbers were compared in a simulation evaluation. The best results were given by , , and ; however, other representations had also good performances if the starting point of optimization was appropriate. requires less memory for computation, because it has no information regarding the argument in comparison to and , which are twice its size. One drawback of neglecting the complex number argument is a loss of information about real system delays.
The presented identification workflow was verified using a direct-drive laboratory setup characterized by three high mechanical resonances and antiresonances that commonly meet in a four-mass system. The presented method is applicable in a broad context to identify a two-mass or multi-mass system. Future research directions in the field of development research may focus on moving algorithms directly into a microprocessor system as an algorithm in board and development work to extend the connectivity of the laboratory setup and prepare cloud connection for algorithms on the cloud. In terms of basic research, future work will be focused on appropriate selection of starting points for NLS optimization solvers.