Comparison of Machine Learning Methods for Image Reconstruction Using the LSTM Classifier in Industrial Electrical Tomography
Abstract
:1. Introduction
2. Materials and Methods
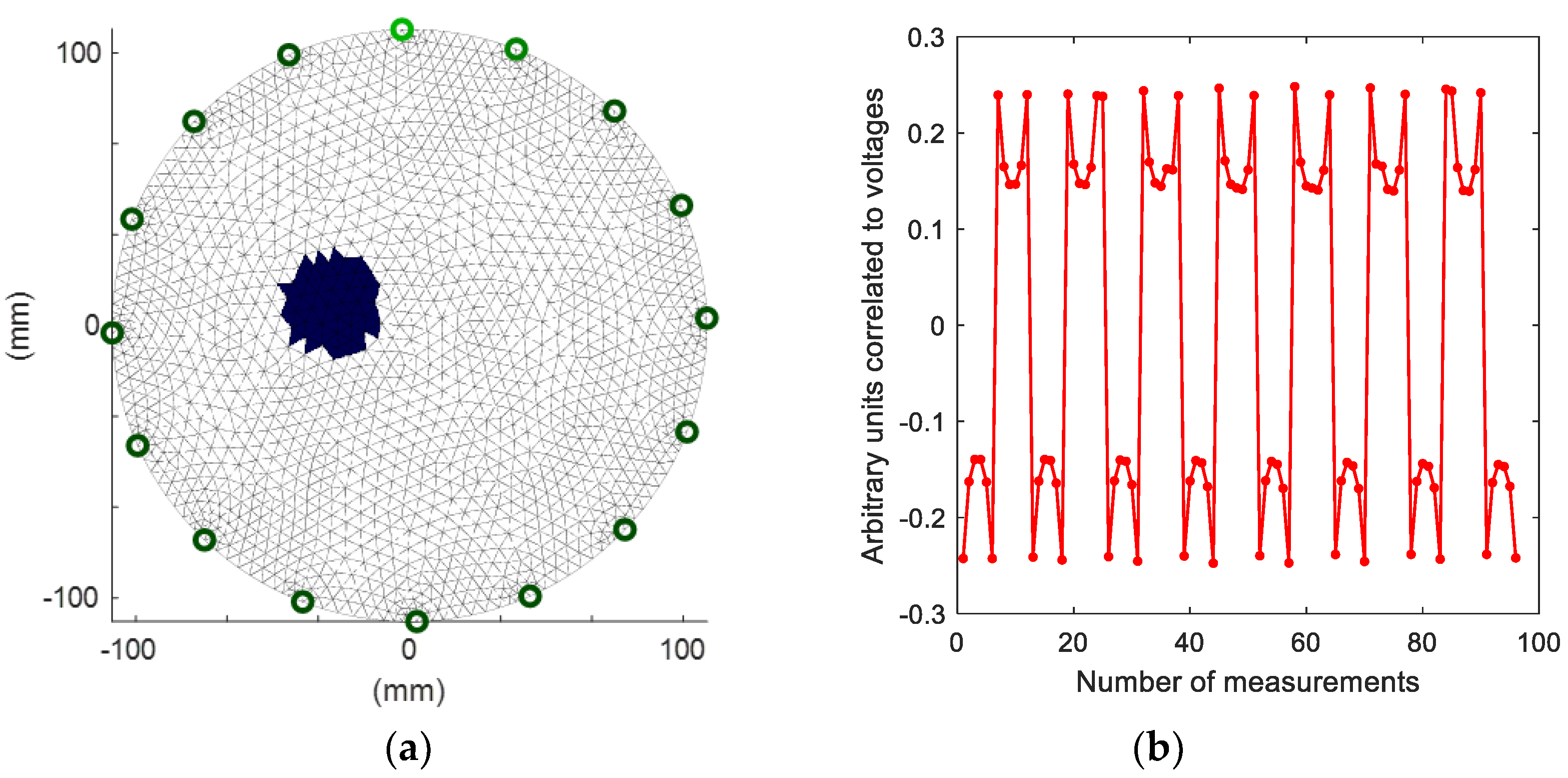
2.1. Research Object
2.2. Data Preparation
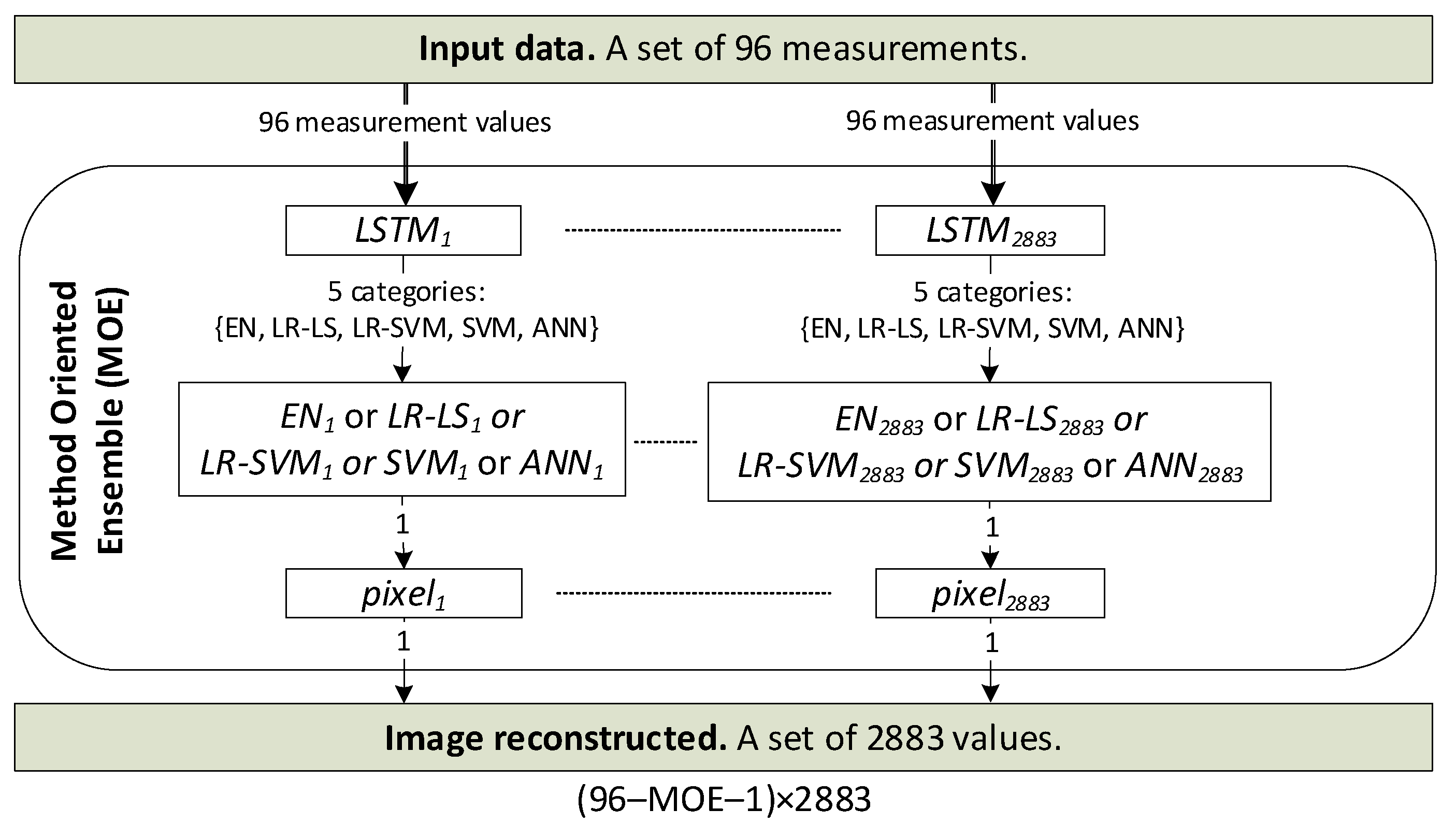
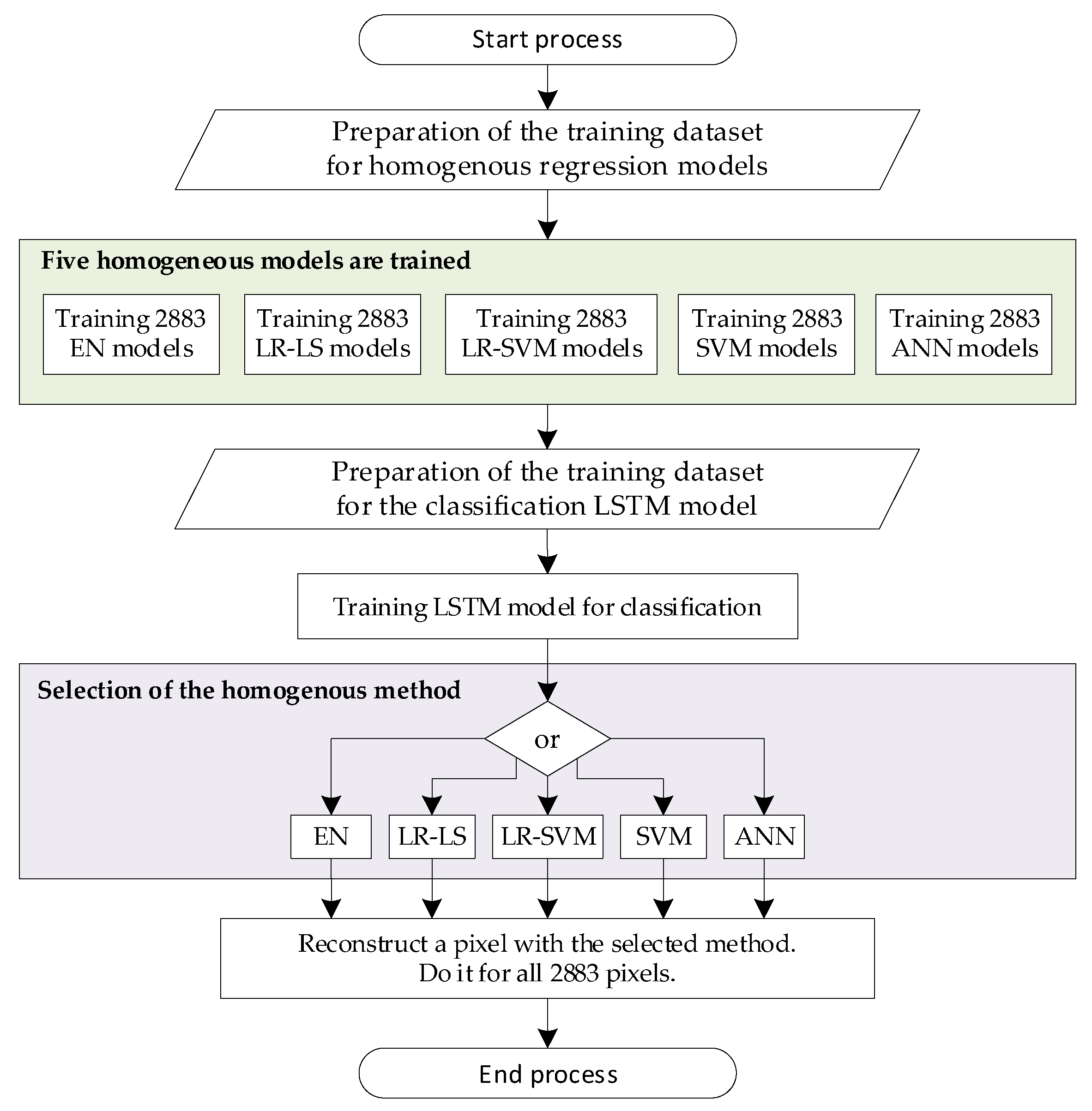
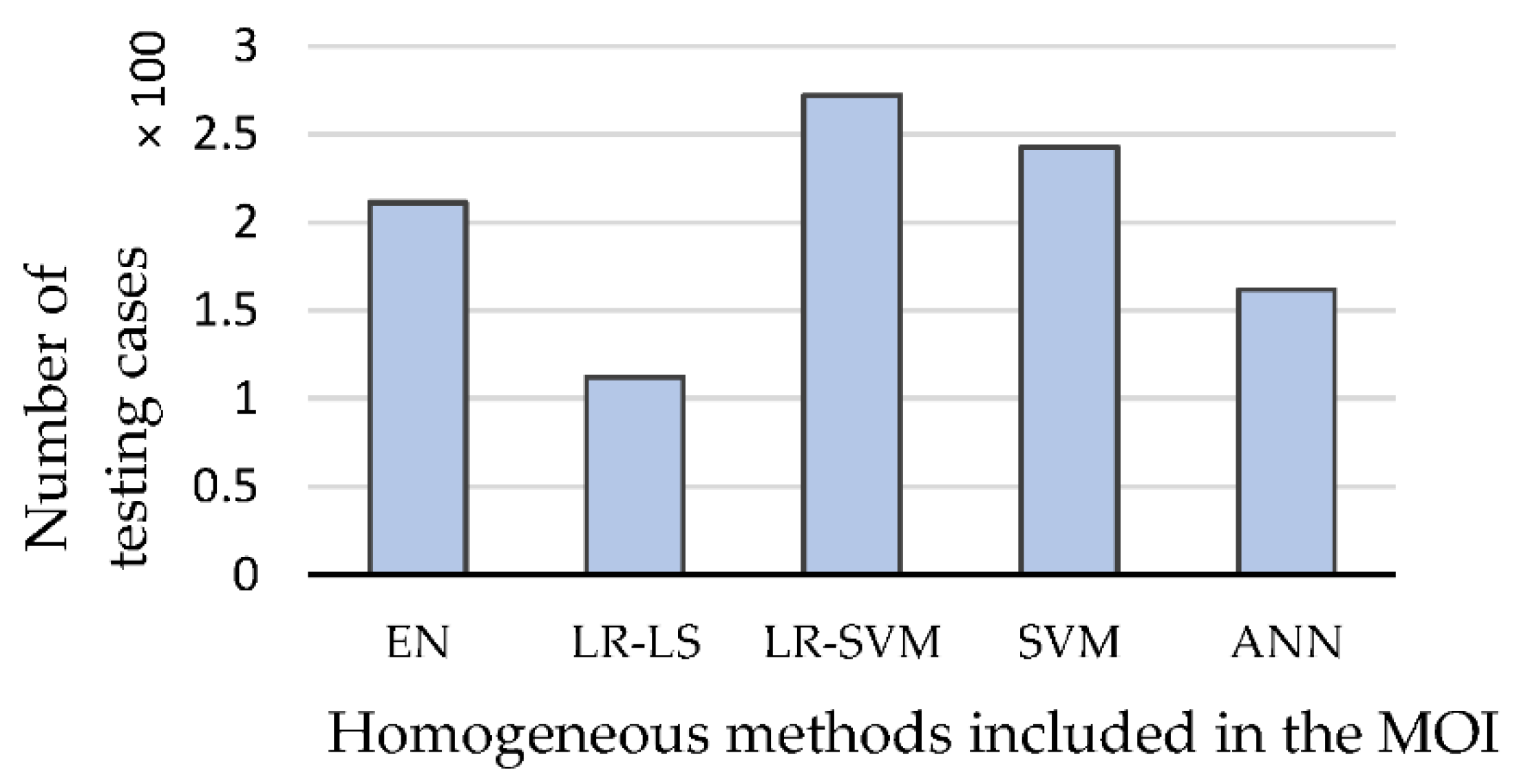
2.3. The Concept of the Method Oriented Ensemble (MOE)
| # | Algorithm 1. The pseudocode algorithm for training MOE |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. | m = 96 % number of measurements n = 2883 % number of finite elements in reconstruction mesh (pixels) Train n models with method # 1 (e.g., EN) Train n models with method # 2 (e.g., LR-LS) Train n models with method # 3 (e.g., LR-SVM) Train n models with method # 4 (e.g., SVM) Train n models with method # 5 (e.g., ANN) % Assigning the RMSE for each method and pixel for i = 1:5 % for 5 methods: EN, LR-LS, LR-SVM, SVM, ANN for j = 1:n % for n = 2883 pixels calculate RMSE(i, j) % assignment root mean square error for i-th method and j-th pixel end meanRMSE(i) = mean(RMSE(i,:)) % Calculate the mean RMSE for each of the 5 methods. end % Assignment meanRMSE for i-th method and all 2883 pixels. Prepare the training set to train the LSTM classifier. Inputs—96 measurements. Output—5 categories/classes. Select the method with the lowest meanRMSE. Reconstruct all n pixels using the selected method. |
2.4. Elastic Net (EN)
2.5. Linear Regression with Least-Squares Learner (LR-LS)
2.6. Linear Regression with Support Vector Machine Learner (LR-SVM)
2.7. Support Vector Machine (SVM)
2.8. Artificial Neural Network (ANN)
2.9. The Long Short-Term Memory (LSTM) Network for Classification
3. Results and Discussion
3.1. Visualizations of Real Measurements
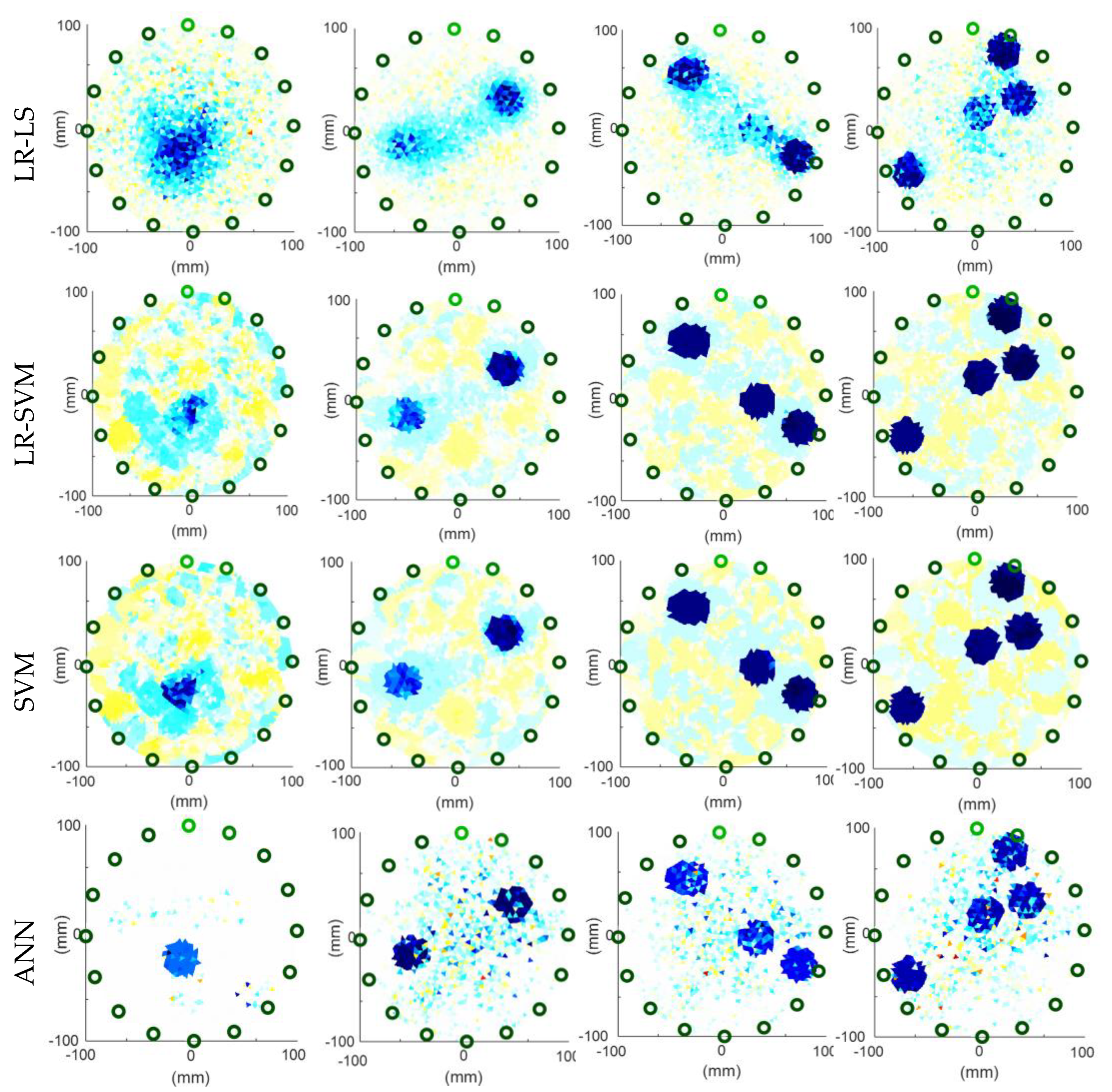
3.2. Comparison of the Reconstructions Based on Simulation Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, S.; Na, J.; Kim, M.; Lee, J.M. Multi-objective Bayesian optimization of chemical reactor design using computational fluid dynamics. Comput. Chem. Eng. 2018, 119, 25–37. [Google Scholar] [CrossRef]
- Kosicka, E.; Kozłowski, E.; Mazurkiewicz, D. Intelligent Systems of Forecasting the Failure of Machinery Park and Supporting Fulfilment of Orders of Spare Parts. In Proceedings of the First International Conference on Intelligent Systems in Production Engineering and Maintenance ISPEM, Wrocław, Poland, 28–29 September 2017; pp. 54–63. [Google Scholar]
- Wang, M. Industrial Tomography: Systems and Applications; Elsevier: Amsterdam, The Netherlands, 2015; ISBN 1782421181. [Google Scholar]
- Wajman, R.; Banasiak, R.; Babout, L. On the Use of a Rotatable ECT Sensor to Investigate Dense Phase Flow: A Feasibility Study. Sensors 2020, 20, 4854. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; Banasiak, R.; Soleimani, M. Planar array 3D electrical capacitance tomography. Insight Non-Destr. Test. Cond. Monit. 2013, 55, 675–680. [Google Scholar] [CrossRef]
- Mosorov, V.; Rybak, G.; Sankowski, D. Plug Regime Flow Velocity Measurement Problem Based on Correlability Notion and Twin Plane Electrical Capacitance Tomography: Use Case. Sensors 2021, 21, 2189. [Google Scholar] [CrossRef] [PubMed]
- Romanowski, A.; Chaniecki, Z.; Koralczyk, A.; Woźniak, M.; Nowak, A.; Kucharski, P.; Jaworski, T.; Malaya, M.; Rózga, P.; Grudzień, K. Interactive Timeline Approach for Contextual Spatio-Temporal ECT Data Investigation. Sensors 2020, 20, 4793. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Pour-Ghaz, M.; Vauhkonen, M.; Seppänen, A. Retrieval of the saturated hydraulic conductivity of cement-based materials using electrical capacitance tomography. Cem. Concr. Compos. 2020, 112, 103639. [Google Scholar] [CrossRef]
- Garbaa, H.; Jackowska-Strumiłło, L.; Grudzień, K.; Romanowski, A. Application of electrical capacitance tomography and artificial neural networks to rapid estimation of cylindrical shape parameters of industrial flow structure. Arch. Electr. Eng. 2016, 65, 657–669. [Google Scholar] [CrossRef]
- Grudzien, K.; Chaniecki, Z.; Romanowski, A.; Sankowski, D.; Nowakowski, J.; Niedostatkiewicz, M. Application of twin-plane ECT sensor for identification of the internal imperfections inside concrete beams. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference, Taipei, Taiwan, 23–26 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Kryszyn, J.; Smolik, W.T.; Radzik, B.; Olszewski, T.; Szabatin, R. Switchless charge-discharge circuit for electrical capacitance tomography. Meas. Sci. Technol. 2014, 25, 115009. [Google Scholar] [CrossRef]
- Kryszyn, J.; Smolik, W. Toolbox for 3D modelling and image reconstruction in electrical capacitance tomography. Inform. Control. Meas. Econ. Environ. Prot. 2017, 7, 137–145. [Google Scholar] [CrossRef]
- Majchrowicz, M.; Kapusta, P.; Jackowska-Strumiłło, L.; Sankowski, D. Acceleration of image reconstruction process in the electrical capacitance tomography 3D in heterogeneous, multi-GPU system. Inform. Control. Meas. Econ. Environ. Prot. 2017, 7, 37–41. [Google Scholar] [CrossRef]
- Romanowski, A. Big Data-Driven Contextual Processing Methods for Electrical Capacitance Tomography. IEEE Trans. Ind. Inform. 2019, 15, 1609–1618. [Google Scholar] [CrossRef]
- Soleimani, M.; Mitchell, C.N.; Banasiak, R.; Wajman, R.; Adler, A. Four-dimensional electrical capacitance tomography imaging using experimental data. Prog. Electromagn. Res. 2009, 90, 171–186. [Google Scholar] [CrossRef] [Green Version]
- Banasiak, R.; Wajman, R.; Jaworski, T.; Fiderek, P.; Fidos, H.; Nowakowski, J.; Sankowski, D. Study on two-phase flow regime visualization and identification using 3D electrical capacitance tomography and fuzzy-logic classification. Int. J. Multiph. Flow 2014, 58, 1–14. [Google Scholar] [CrossRef]
- Dusek, J.; Hladky, D.; Mikulka, J. Electrical impedance tomography methods and algorithms processed with a GPU. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium—Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017; pp. 1710–1714. [Google Scholar]
- Kłosowski, G.; Rymarczyk, T. Using neural networks and deep learning algorithms in electrical impedance tomography. Inform. Autom. Pomiary Gospod. Ochr. Sr. 2017, 7, 99–102. [Google Scholar] [CrossRef]
- Voutilainen, A.; Lehikoinen, A.; Vauhkonen, M.; Kaipio, J.P. Three-dimensional nonstationary electrical impedance tomography with a single electrode layer. Meas. Sci. Technol. 2010, 21, 35107. [Google Scholar] [CrossRef]
- Duraj, A.; Korzeniewska, E.; Krawczyk, A. Classification algorithms to identify changes in resistance. Przegląd Elektrotechn. 2015, 1, 82–84. [Google Scholar] [CrossRef]
- Szczesny, A.; Korzeniewska, E. Selection of the method for the earthing resistance measurement. Przegląd Elektrotechn. 2018, 94, 178–181. [Google Scholar]
- Dusek, J.; Mikulka, J. Measurement-Based Domain Parameter Optimization in Electrical Impedance Tomography Imaging. Sensors 2021, 21, 2507. [Google Scholar] [CrossRef]
- Chen, B.; Abascal, J.; Soleimani, M. Extended Joint Sparsity Reconstruction for Spatial and Temporal ERT Imaging. Sensors 2018, 18, 4014. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Huang, Y.; Wu, H.; Tan, C.; Jia, J. Efficient Multitask Structure-Aware Sparse Bayesian Learning for Frequency-Difference Electrical Impedance Tomography. IEEE Trans. Ind. Inform. 2021, 17, 463–472. [Google Scholar] [CrossRef] [Green Version]
- Ziolkowski, M.; Gratkowski, S.; Zywica, A.R. Analytical and numerical models of the magnetoacoustic tomography with magnetic induction. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 538–548. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Adamkiewicz, P.; Polakowski, K.; Sikora, J. Effective ultrasound and radio tomography imaging algorithm for two-dimensional problems. Przegląd Elektrotechn. 2018, 94, 62–69. [Google Scholar]
- Liang, G.; Dong, F.; Kolehmainen, V.; Vauhkonen, M.; Ren, S. Nonstationary Image Reconstruction in Ultrasonic Transmission Tomography Using Kalman Filter and Dimension Reduction. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Babout, L.; Grudzień, K.; Wiącek, J.; Niedostatkiewicz, M.; Karpiński, B.; Szkodo, M. Selection of material for X-ray tomography analysis and DEM simulations: Comparison between granular materials of biological and non-biological origins. Granul. Matter 2018, 20, 38. [Google Scholar] [CrossRef] [Green Version]
- Korzeniewska, E.; Sekulska-Nalewajko, J.; Gocławski, J.; Dróżdż, T.; Kiełbasa, P. Analysis of changes in fruit tissue after the pulsed electric field treatment using optical coherence tomography. Eur. Phys. J. Appl. Phys. 2020, 91, 30902. [Google Scholar] [CrossRef]
- Sekulska-Nalewajko, J.; Gocławski, J.; Korzeniewska, E. A method for the assessment of textile pilling tendency using optical coherence tomography. Sensors 2020, 20, 3687. [Google Scholar] [CrossRef] [PubMed]
- Sobaszek, Ł.; Gola, A.; Świć, A. Predictive Scheduling as a Part of Intelligent Job Scheduling System; Springer: Cham, Switzerland, 2018; pp. 358–367. [Google Scholar]
- Kłosowski, G.; Gola, A.; Świć, A. Application of fuzzy logic controller for machine load balancing in discrete manufacturing system. In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Wroclaw, Poland, 14–16 October 2015; Volume 9375, pp. 256–263. [Google Scholar]
- Rymarczyk, T.; Kłosowski, G.; Kozłowski, E. A Non-Destructive System Based on Electrical Tomography and Machine Learning to Analyze the Moisture of Buildings. Sensors 2018, 18, 2285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rymarczyk, T.; Kłosowski, G.; Hoła, A.; Sikora, J.; Wołowiec, T.; Tchórzewski, P.; Skowron, S. Comparison of Machine Learning Methods in Electrical Tomography for Detecting Moisture in Building Walls. Energies 2021, 14, 2777. [Google Scholar] [CrossRef]
- Lopato, P.; Chady, T.; Sikora, R.; Gratkowski, S.; Ziolkowski, M. Full wave numerical modelling of terahertz systems for nondestructive evaluation of dielectric structures. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2013, 32, 736–749. [Google Scholar] [CrossRef]
- Psuj, G. Multi-Sensor Data Integration Using Deep Learning for Characterization of Defects in Steel Elements. Sensors 2018, 18, 292. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kozłowski, E.; Mazurkiewicz, D.; Kowalska, B.; Kowalski, D. Binary linear programming as a decision-making aid for water intake operators. In Proceedings of the First International Conference on Intelligent Systems in Production Engineering and Maintenance ISPEM, Wrocław, Poland, 28–29 September 2017; Advances in Intelligent Systems and Computing Series. Springer: Cham, Switzerland, 2018; Volume 637, pp. 199–208. [Google Scholar]
- Yuen, B.; Dong, X.; Lu, T. Inter-Patient CNN-LSTM for QRS Complex Detection in Noisy ECG Signals. IEEE Access 2019, 7, 169359–169370. [Google Scholar] [CrossRef]
- Saadatnejad, S.; Oveisi, M.; Hashemi, M. LSTM-Based ECG Classification for Continuous Monitoring on Personal Wearable Devices. IEEE J. Biomed. Heal. Inform. 2019, 24, 515–523. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adler, A.; Lionheart, W.R.B. Uses and abuses of EIDORS: An extensible software base for EIT. Physiol. Meas. 2006, 27, S25–S42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rymarczyk, T.; Kłosowski, G.; Kozłowski, E.; Tchórzewski, P. Comparison of Selected Machine Learning Algorithms for Industrial Electrical Tomography. Sensors 2019, 19, 1521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kryszyn, J.; Wanta, D.M.; Smolik, W.T. Gain Adjustment for Signal-to-Noise Ratio Improvement in Electrical Capacitance Tomography System EVT4. IEEE Sens. J. 2017, 17, 8107–8116. [Google Scholar] [CrossRef]
- Xiao, L. Dual averaging methods for regularized stochastic learning and online optimization. J. Mach. Learn. Res. 2010, 11, 2543–2596. [Google Scholar]
- Ho, C.H.; Lin, C.J. Large-scale linear support vector regression. J. Mach. Learn. Res. 2012, 13, 3323–3348. [Google Scholar]
- Hsieh, C.J.; Chang, K.W.; Lin, C.J.; Keerthi, S.S.; Sundararajan, S. A dual coordinate descent method for large-scale linear SVM. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008. [Google Scholar]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Deep Learning Toolbox User’s Guide; The Mathworks Inc.: Herborn, Germany, 2018. [Google Scholar]
- Glorot, X.; Yoshua, B. Understanding the difficulty of training deep feedfor-ward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Kłosowski, G.; Rymarczyk, T.; Kania, K.; Świć, A.; Cieplak, T. Maintenance of industrial reactors supported by deep learning driven ultrasound tomography. Eksploat. Niezawodn. 2020, 22, 138–147. [Google Scholar] [CrossRef]
- Mikulka, J. GPU-Accelerated Reconstruction of T2 Maps in Magnetic Resonance Imaging. Meas. Sci. Rev. 2015, 15, 210–218. [Google Scholar] [CrossRef] [Green Version]
- Majchrowicz, M.; Kapusta, P.; Jackowska-Strumiłło, L.; Banasiak, R.; Sankowski, D. Multi-GPU, Multi-Node Algorithms for Acceleration of Image Reconstruction in 3D Electrical Capacitance Tomography in Heterogeneous Distributed System. Sensors 2020, 20, 391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rzasa, M.R.; Czapla-Nielacna, B. Analysis of the Influence of the Vortex Shedder Shape on the Metrological Properties of the Vortex Flow Meter. Sensors 2021, 21, 4697. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Tan, C.; Dong, F.; Santos, E.N.D.; Silva, M.J. Da Conductance Sensors for Multiphase Flow Measurement: A Review. IEEE Sens. J. 2021, 21, 12913–12925. [Google Scholar] [CrossRef]

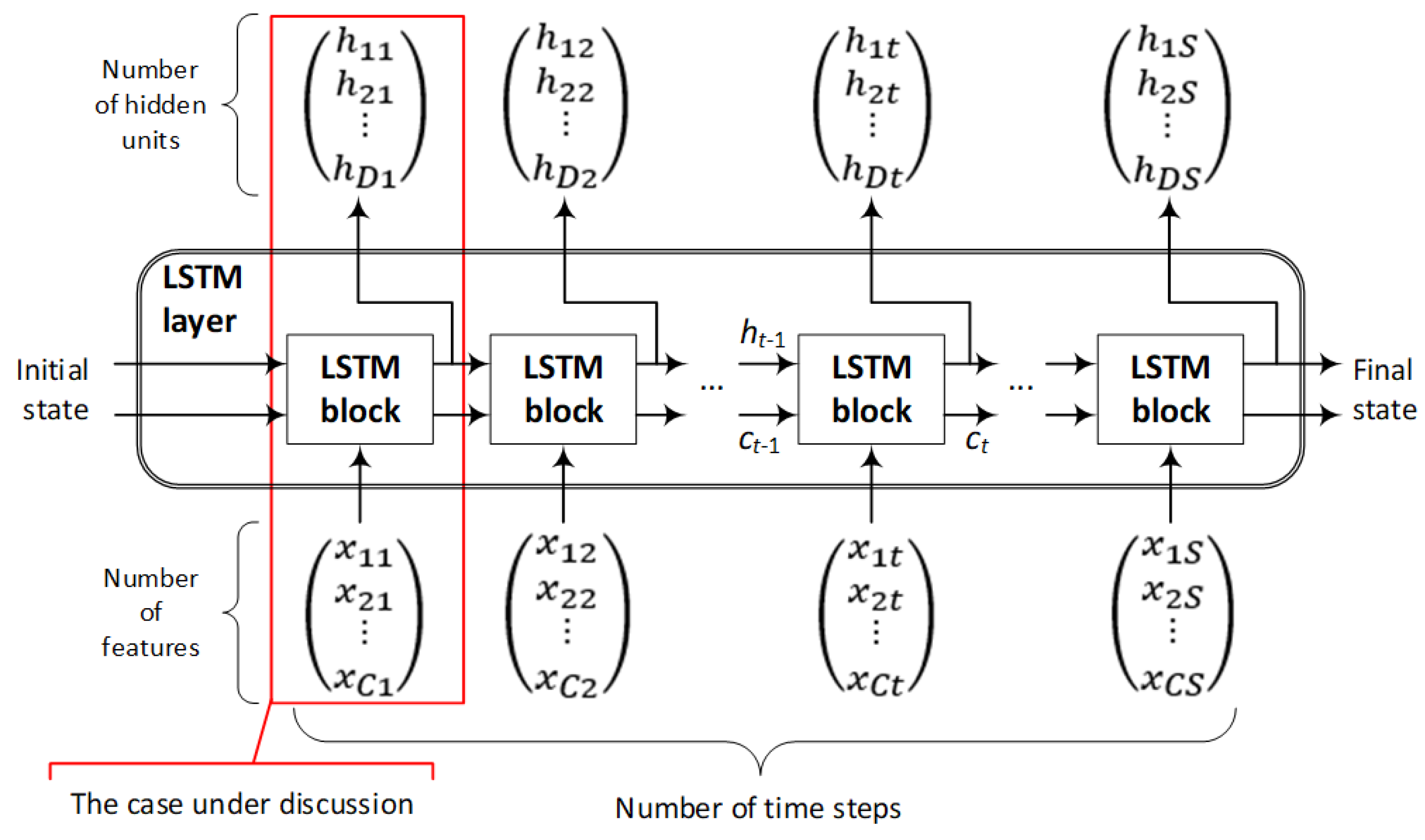

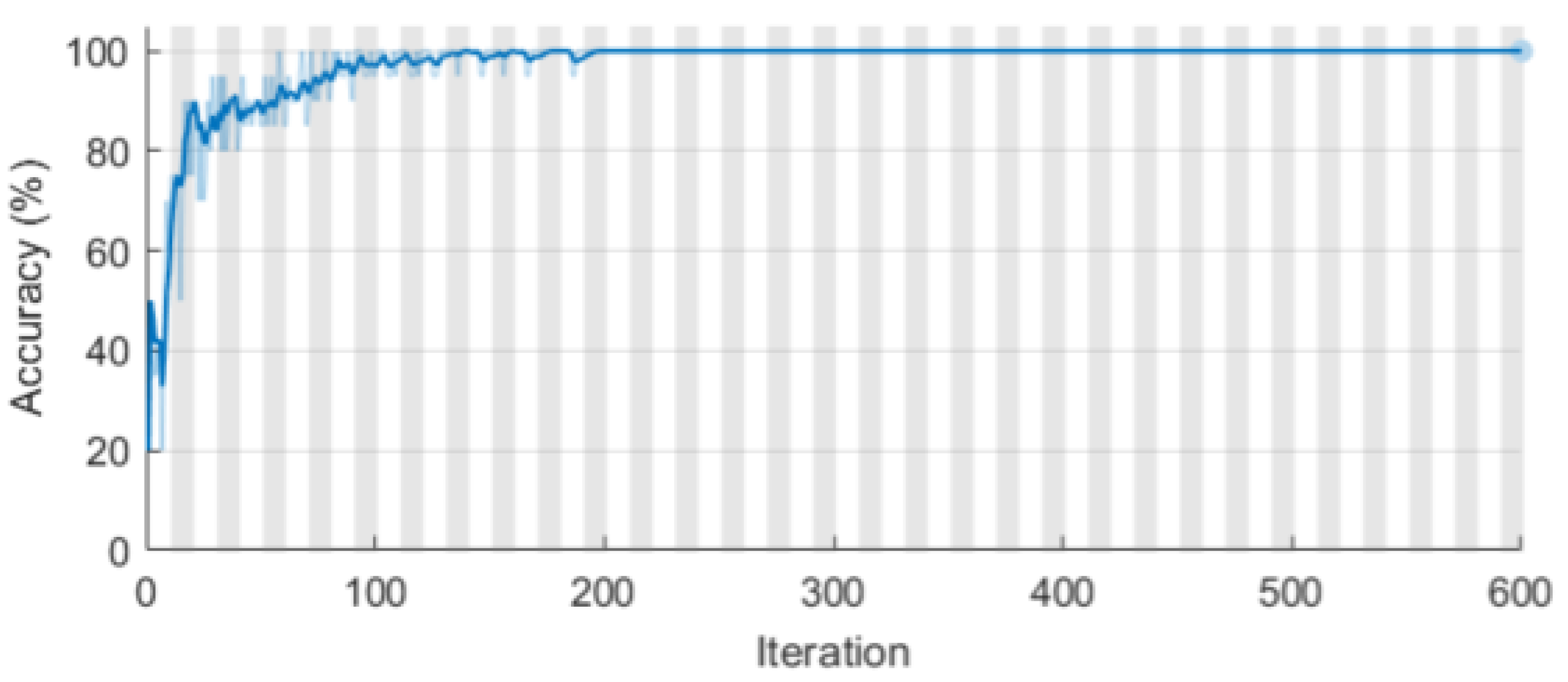
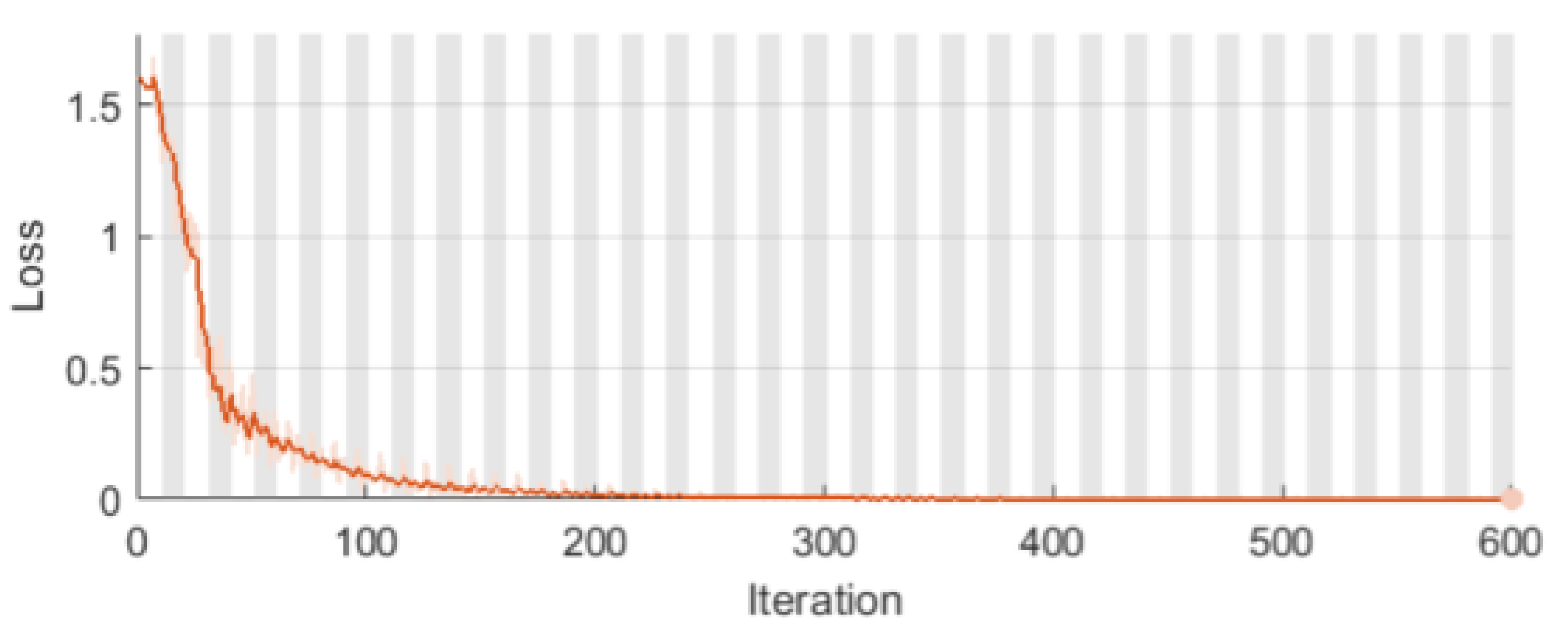
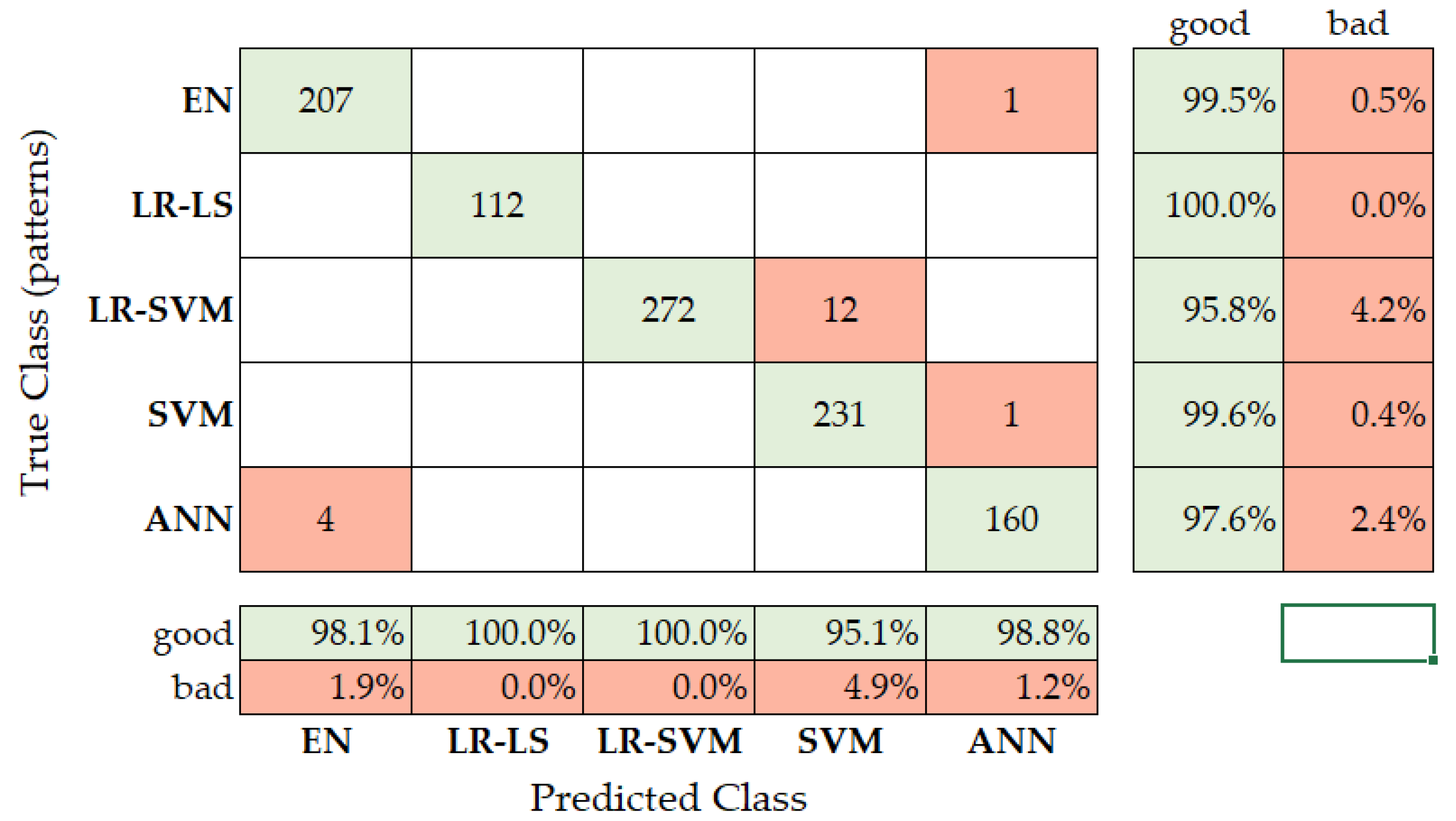


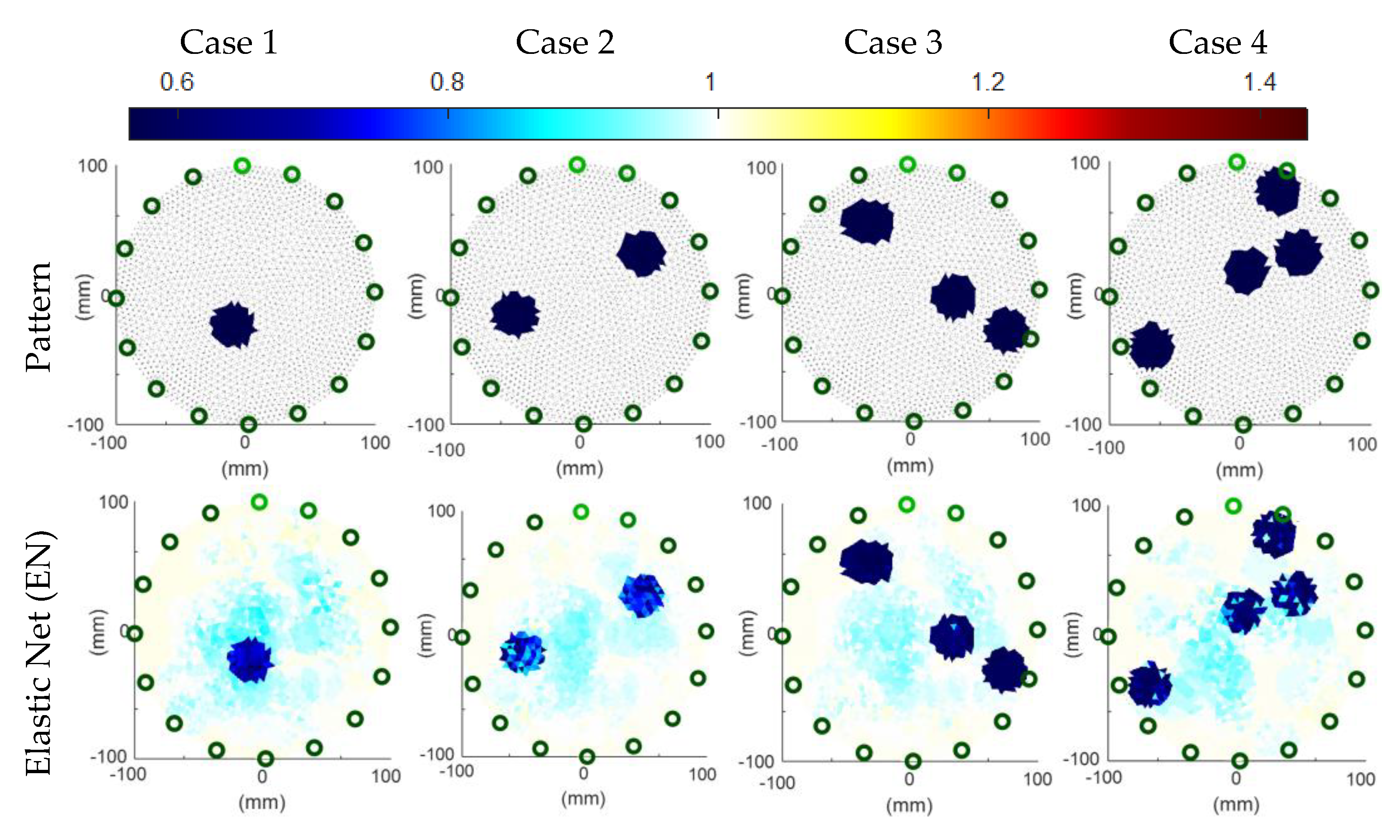
| # | Layer Description | Activations | Learnable Parameters (Weights and Biases) | Total Learnables | States |
|---|---|---|---|---|---|
| 1 | Sequence input with 96 dimensions | 96 | - | 0 | - |
| 2 | BiLSTM with 128 hidden units | 256 | Input weights: 1024 × 96 Recurrent weights: 1024 × 128 Bias: 1024 × 1 | 230,400 | Hidden state 256 × 1 Cell state 256 × 1 |
| 3 | Batch normalization | 256 | Offset: 256 × 1 Scale: 256 × 1 | 512 | - |
| 4 | BiLSTM with 128 hidden units | 256 | Input weights: 1024 × 256 Recurrent weights: 1024 × 128 Bias: 1024 × 1 | 364,240 | Hidden state 256 × 1 Cell state 256 × 1 |
| 5 | Fully connected layer | 5 | Weights: 5 × 256 Bias: 5 × 1 | 1285 | - |
| 6 | Softmax | 5 | - | 0 | - |
| 7 | Classification output (cross entropy) | 5 | - | 0 | - |
| Case Number | Indicator | Methods of Reconstruction | Best Homogenous Method (MOE Concept) | ||||
|---|---|---|---|---|---|---|---|
| EN | LR-LS | LR-SVM | SVM | ANN | |||
| 1 | RMSE | 0.289 | 0.133 | 0.145 | 0.135 | 0.068 | ANN |
| RIE | 0.293 | 0.135 | 0.147 | 0.137 | 0.069 | ANN | |
| MAPE | 1610.2 | 1880.7 | 2142.1 | 1988.4 | 126.6 | ANN | |
| ICC | 0.875 | 0.536 | 0.392 | 0.530 | 0.914 | ANN | |
| 2 | RMSE | 0.299 | 0.1519 | 0.123 | 0.117 | 0.132 | SVM |
| RIE | 0.306 | 0.155 | 0.126 | 0.120 | 0.135 | SVM | |
| MAPE | 2845.92 | 2659.4 | 2191.2 | 1990.1 | 1087.3 | ANN | |
| ICC | 0.905 | 0.709 | 0.843 | 0.853 | 0.794 | EN | |
| 3 | RMSE | 0.304 | 0.157 | 0.077 | 0.084 | 0.140 | LR-SVM |
| RIE | 0.318 | 0.164 | 0.081 | 0.087 | 0.147 | LR-SVM | |
| MAPE | 4467.8 | 2935.4 | 846.1 | 835.3 | 1239.5 | SVM | |
| ICC | 0.986 | 0.826 | 0.960 | 0.953 | 0.870 | EN | |
| 4 | RMSE | 0.317 | 0.135 | 0.076 | 0.085 | 0.152 | LR-SVM |
| RIE | 0.336 | 0.143 | 0.081 | 0.090 | 0.161 | LR-SVM | |
| MAPE | 5952.1 | 2536.1 | 916.7 | 988.2 | 1584.6 | LR-SVM | |
| ICC | 0.950 | 0.900 | 0.969 | 0.962 | 0.876 | LR-SVM | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kłosowski, G.; Rymarczyk, T.; Niderla, K.; Rzemieniak, M.; Dmowski, A.; Maj, M. Comparison of Machine Learning Methods for Image Reconstruction Using the LSTM Classifier in Industrial Electrical Tomography. Energies 2021, 14, 7269. https://doi.org/10.3390/en14217269
Kłosowski G, Rymarczyk T, Niderla K, Rzemieniak M, Dmowski A, Maj M. Comparison of Machine Learning Methods for Image Reconstruction Using the LSTM Classifier in Industrial Electrical Tomography. Energies. 2021; 14(21):7269. https://doi.org/10.3390/en14217269
Chicago/Turabian StyleKłosowski, Grzegorz, Tomasz Rymarczyk, Konrad Niderla, Magdalena Rzemieniak, Artur Dmowski, and Michał Maj. 2021. "Comparison of Machine Learning Methods for Image Reconstruction Using the LSTM Classifier in Industrial Electrical Tomography" Energies 14, no. 21: 7269. https://doi.org/10.3390/en14217269
APA StyleKłosowski, G., Rymarczyk, T., Niderla, K., Rzemieniak, M., Dmowski, A., & Maj, M. (2021). Comparison of Machine Learning Methods for Image Reconstruction Using the LSTM Classifier in Industrial Electrical Tomography. Energies, 14(21), 7269. https://doi.org/10.3390/en14217269







