Fuzzy Chaos Control of Fractional Order D-PMSG for Wind Turbine with Uncertain Parameters by State Feedback Design
Abstract
:1. Introduction
2. Preliminaries and D-PMSG Mathematical Model
2.1. Preliminaries
- (1).
- (2).
- (3).
2.2. Integer-Order Nonlinear Mathematical Model
2.3. Fractional-Order Nonlinear Mathematical Model
2.4. Fractional-Order T-S Fuzzy Model
3. Fuzzy Chaos Control for Fractional-Order D-PMSG
3.1. Fuzzy State Feedback Controller Scheme
3.2. Mittag–Leffler Stability
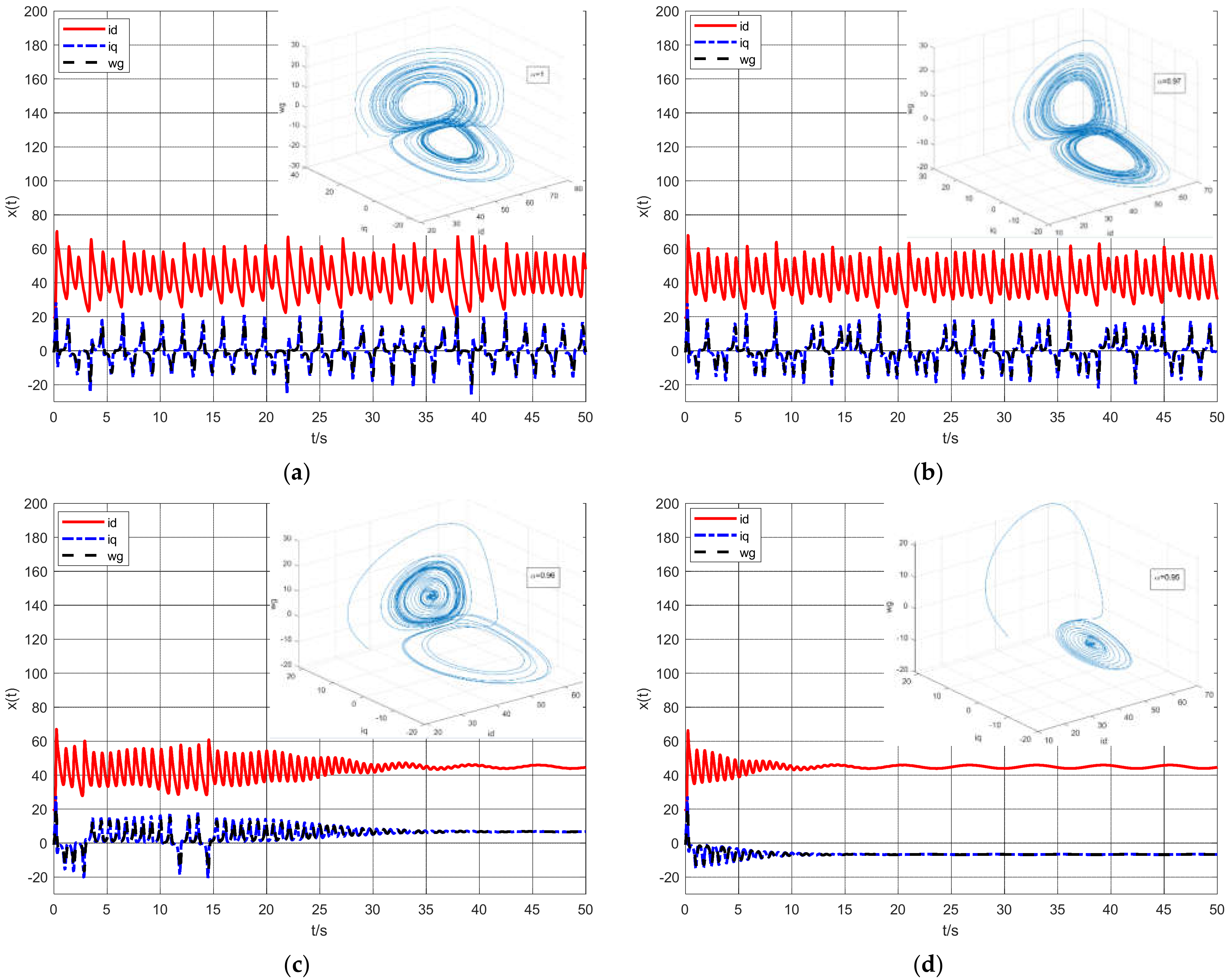
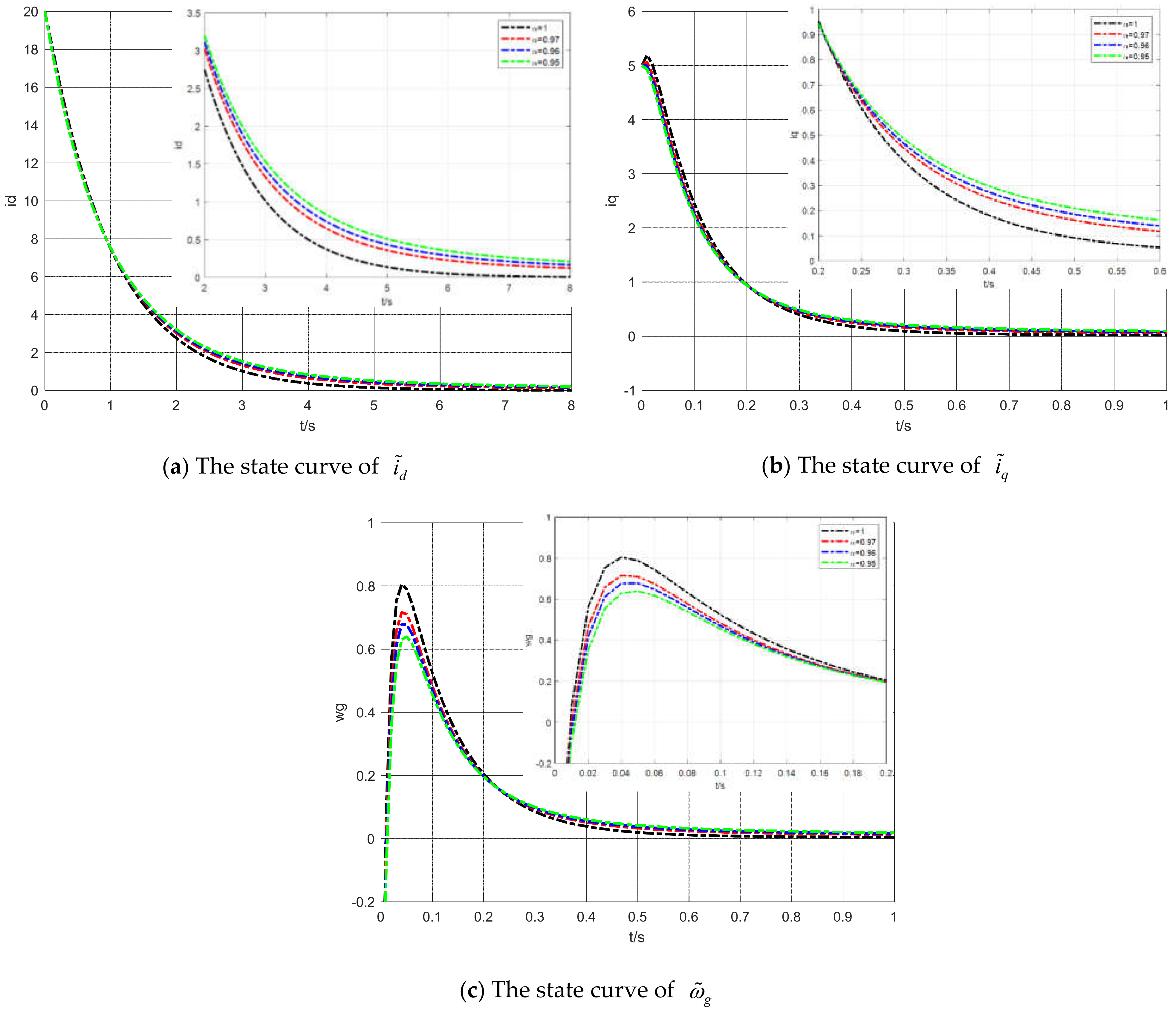
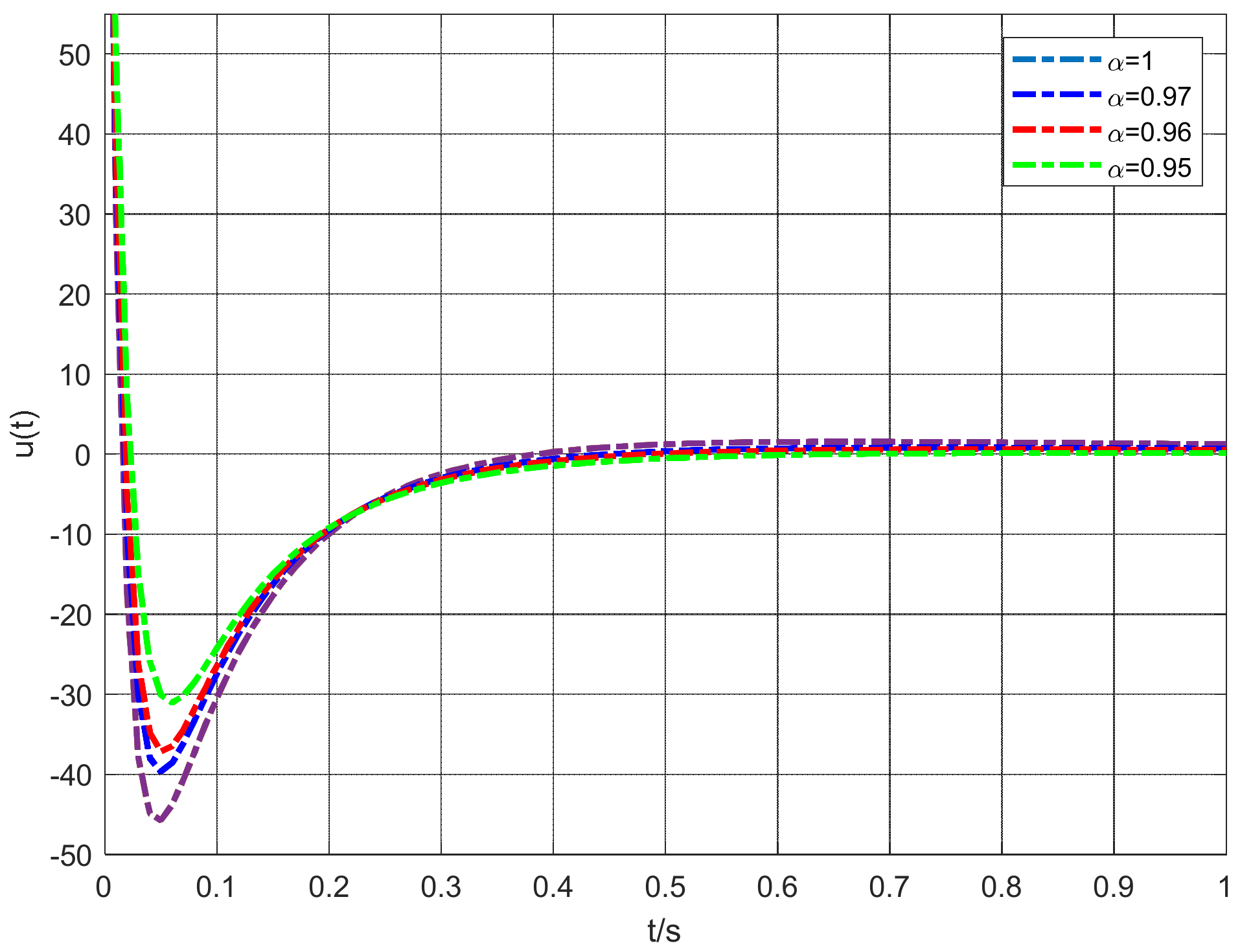
4. Simulation Results
4.1. Simulation Parameters
| System Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Direct/Quadrature inductance | mH | vary | |
| Stator resistance | R | Ω | 1.14 |
| Permanent magnet flux-linkage | mWb | vary | |
| Moment of inertia | kg⋅m2 | 0.089 | |
| Pole pairs | number | 17 |
4.2. System Simulation Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| D-PMSG | direct-drive permanent magnet synchronous generator |
| T-S | Takagi–Sugeno |
| FONSs | fractional order nonlinear systems |
| FLST | fractional Lyapunov stability theory |
| PDC | parallel distributed compensation |
| LMIs FONS | linear matrix inequalities fractional order nonlinear system |
| EPHA | European Public Health Alliance |
| GWEC | Global Wind Energy Council |
| WTSs | wind turbine systems |
| DFIG | doubly-fed induction generator |
| PMSG | permanent magnet synchronous generator |
| PMSM | permanent magnet synchronous motor |
| WTNS WECSs | wind turbine nonlinear system wind energy conversion systems |
| FOLDM | fractional order Lyapunov direct method |
References
- State Grid Energy Research Institute Co. LTD. Analysis Report on Energy and Power Development at Home and Abroad 2019; China Electric Power Press: Beijing, China, 2019. [Google Scholar]
- Biological Research. The Increase of Mortality Rate of SARS coc-1 in Air Polluted Cities. Available online: http://news.bioon.com/article/6752494.html (accessed on 23 March 2020).
- Jiang, Z.Y.; Hu, W.F.; Dong, W.B.; Gao, Z.; Ren, Z.R. Structural Reliability Analysis of Wind Turbines: A Review. Energies 2017, 10, 2099. [Google Scholar] [CrossRef] [Green Version]
- National Energy Administration. Analysis on Development Status of Wind Power Industry for Global and China. Available online: https://www.sohu.com/a/415029198_813209 (accessed on 26 August 2020).
- Li, S.Z.; Wang, H.P.; Tian, Y.; Aitouch, A.; Klein, J. Direct Power Control of DFIG Wind Turbine Systems based on an Intelligent Proportional-Integral Sliding Mode Control. ISA Trans. 2016, 64, 431–439. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.T.; Lee, D.C. Sensorless Control of DFIG Wind Turbine Systems based on SOGI and Rotor Position Correction. IEEE Trans. Power Electron. 2021, 36, 5486–5495. [Google Scholar] [CrossRef]
- Worku, M.Y.; Abido, M.A.; Iravani, R. PMSG based Wind System for Real-time Maximum Power Generation and Low Voltage Ride Through. J. Renew. Sustain. Energy 2017, 9, 013304–013319. [Google Scholar] [CrossRef]
- Mani, P.; Lee, J.H.; Kang, K.W.; Joo, Y.H. Digital Controller Design via LMIs for Direct-driven Surface Mounted PMSG-based Wind Energy Conversion System. IEEE Trans. Cybern. 2020, 50, 3056–3067. [Google Scholar] [CrossRef]
- Ren, L.Z.; Lei, T.F.; Chen, H.; Wang, R. Optimal Control Research for the Wind Turbine PMSG Chaos Motion. Appl. Mech. Mater. 2014, 543, 1291–1295. [Google Scholar] [CrossRef]
- Daróczy, L.; Janiga, G.; Thévenin, D. Analysis of the Performance of a H-Darrieus Rotor under Uncertainty using Polynomial Chaos Expansion. Energy 2016, 113, 399–412. [Google Scholar] [CrossRef]
- Huynh, T.T.; Lin, C.M.; Le, N.Q.K.; Vu, M.T.; Nguyen, N.P.; Chao, F. Intelligent Wavelet Fuzzy Brain Emotional Controller Using Dual Function-Link Network for Uncertain Nonlinear Control Systems. Appl. Intell. 2021, 17, 15–23. [Google Scholar]
- Huynh, T.T.; Lin, C.M.; Le, T.L.; Nguyen, N.P.; Hong, S.K.; Chao, F. Wavelet Interval Type-2 Fuzzy Quad-Function-Link Brain Emotional Control Algorithm for the Synchronization of 3D Nonlinear Chaotic Systems. Int. J. Fuzzy Syst. 2020, 22, 2546–2564. [Google Scholar] [CrossRef]
- Hemati, H. Strange Attractors in Brushless DC Motor. IEEE Trans. Circuits Syst.-I 1994, 41, 40–45. [Google Scholar] [CrossRef]
- Li, Z.; Park, J.B.; Joo, Y.H.; Zhang, B.; Chen, G.R. Bifurcations and Chaos in a Permanent-Magnet Synchronous Motor. IEEE Trans. Circuits Syst.-I: Fundam. Theory Appl. 2002, 49, 383–387. [Google Scholar]
- Wang, J.P.; Zhou, W.N.; Zhou, X.H. Chaos Control of Pulse-Disturbed Permanent Magnet Synchronous Motor with Uncertain Parameters. Trans. Inst. Meas. Control 2015, 8, 1–8. [Google Scholar] [CrossRef]
- Sun, L.X.; Lu, S.; Wen, Z.G.; Li, Y.F. Analysis of Chaotic Motion Mechanism of Permanent Magnet Synchronous Motors. Electr. Mach. Control 2019, 23, 97–104. [Google Scholar]
- Zhou, S.; Wang, D.Z.; Gao, Q.Z.; Liu, Y. Chaos Control of Permanent Magnet Synchronous Motor via Adaptive Sliding Mode Variable Structure Scheme. Int. J. Control. Autom. 2016, 9, 117–128. [Google Scholar] [CrossRef]
- Hu, J.; Qiu, Y.; Lu, H. Adaptive Robust Nonlinear Feedback Control of Chaos in PMSM System with Modeling Uncertainty. Appl. Math. Modeling 2016, 40, 8265–8275. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Joo, Y.H. Stochastic Sampled-data Controller for T-S Fuzzy Chaotic Systems and Its Application. IET Control. Theory Appl. 2019, 13, 1834–1843. [Google Scholar] [CrossRef]
- Jonscher, A.K. Dielectric Relaxation in Solids; Chelsea Dielectrics Press Ltd.: London, UK, 1983. [Google Scholar]
- Westerlund, S.; Ekstam, L. Capacitor Theory. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Daouac, R.A.Z.; Francisb, C.; Moreaua, X. Synthesis and Implementation of Non-integer Integrators using RLC Devices. Int. J. Electron. 2009, 96, 1207–1223. [Google Scholar]
- Petras, I.; Chen, Y.Q.; Coopmans, C. Fractional-order Memristive Systems. In Proceedings of the IEEE Conference on Emerging Technologies & Factory Automation, Palma de Mallorca, Spain, 22–25 September 2009. [Google Scholar]
- Zheng, W.J.; Luo, Y.; Chen, Y.Q.; Pi, Y.G. Fractional-order Modeling of Permanent Magnet Synchronous Motor Speed Servo System. J. Vib. Control 2016, 22, 2255–2280. [Google Scholar] [CrossRef]
- Xue, W.; Li, Y.L.; Cang, S.J.; Jia, H.Y.; Wang, Z.H. Chaotic Behavior and Circuit Implementation of a Fractional-order Permanent Magnet Synchronous Motor Model. J. Frankl. Inst. 2015, 352, 2887–2898. [Google Scholar] [CrossRef]
- Lu, S.K.; Wang, X.C.; Wang, L.D. Finite-time Adaptive Neural Network Control for Fractional-order Chaotic PMSM via Command Filtered Backstepping. Adv. Differ. Equ. 2020, 121, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.X.; Ma, B.L. Asymptotic Stabilization of Fractional Permanent Magnet Synchronous Motor. J. Comput. Nonlinear Dyn. 2017, 9, 1–18. [Google Scholar] [CrossRef]
- Wang, B.; Xue, J.Y.; Chen, D.Y. Takagi-Sugeno Fuzzy Control for a Wide Class of Fractional-order Chaotic Systems with Uncertain Parameters via Linear Matrix Inequality. J. Vib. Control 2016, 22, 2356–2369. [Google Scholar] [CrossRef]
- Li, N.; Li, Y.G.; Wang, H.X.; Sun, Y.G. Fuzzy Tracking Control for Fractional-order Permanent Magnet Synchronous Motor Chaotic System. Inf. Control 2016, 45, 8–13. [Google Scholar]
- Yang, G.L.; Li, H.G. Sliding Mode Variable-structure Control of Chaos in Direct-driven Permanent Magnet Synchronous Generators for Wind Turbines. Acta Phys. Sin. 2009, 58, 7552–7557. [Google Scholar]
- Cao, N.; Shi, W.X.; Zhu, C.H. Simulated Analysis of Dynamic Characteristics of Permanent Magnet Direct-Drive Synchronous Wind Turbine Generators. Electr. Mach. Control 2017, 44, 104–109. [Google Scholar]
- Yang, L.; Huang, T.M.; Deng, L.; Zeng, Y.F.; Huang, S.D. Analysis on Chaotic Mechanism of Direct-Drive Permanent Magnet Synchronous Generators based on Lyapunov Stability Theory. Eur. J. Electr. Eng. 2019, 21, 531–537. [Google Scholar] [CrossRef]
- Zheng, G.; Zou, J.X.; Xu, H.B.; Qin, G. Adaptive Backstepping Control of Chaotic Property in Direct-Driven Permanent Magnet Synchronous Generators for Wind Power. Acta Phys. Sin. 2011, 60, 060506–060513. [Google Scholar]
- Zeng, Z.Z.; Liu, F. Nonlinear Proportional Control of Chaotic Property in Direct-Driven Permanent Magnet Synchronous Generators for Wind Turbine. J. Electr. Power Sci. Technol. 2014, 29, 29–36. [Google Scholar]
- Wu, Z.Q.; Jia, W.J.; Zhao, L.R.; Wu, C.H. Maximum Wind Power Tracking for PMSG Chaos Systems-ADHDP Method. Appl. Soft Comput. 2015, 36, 204–209. [Google Scholar]
- Wang, L.; Li, Y.H.; Lu, G.L.; Zhu, X.H. Tracking Controller of D-PMSG Chaos Motion. Electr. Power Autom. Equip. 2011, 31, 45–49. [Google Scholar]
- Si, G.Q.; Zhu, J.W.; Diao, L.J.; Ding, Z.Q. Modeling, Nonlinear Dynamic Analysis and Control of Fractional PMSG of Wind Turbine. Nonlinear Dyn. 2017, 88, 985–1000. [Google Scholar] [CrossRef]
- Manashita, B.; Binoy, K.R. Dynamics of the Fractional-Order Chaotic PMSG, Its Stabilization using Predictive Control and Circuit Validation. IET Electr. Power Appl. 2017, 11, 707–716. [Google Scholar]
- Karthikeyan, R.; Anitha, K.; Prakash, D. Chaos Suppression in Fractional Order Permanent Magnet Synchronous Generator in Wind Turbine. Nonlinear Eng. 2016, 11, 1–9. [Google Scholar]
- Cantor, D.G. Computing in the Jacobian of a Hyperelliptic Curve. Math. Comput. 1987, 48, 95–101. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Krener, A.J. Approximate Linearization by State Feedback and Coordinate Change. Syst. Control. Lett. 1984, 5, 181–185. [Google Scholar] [CrossRef]
- Li, Y.T.; Li, J.M. Stability Analysis of Fractional Order Systems Based on T-S Fuzzy Model with the Fractional Order α: 0 < α < 1. Nonlinear Dyn. 2014, 78, 2909–2919. [Google Scholar]
- Wu, C. External Stability of Caputo Fractional-Order Nonlinear Control Systems: Advances in the Lyapunov Function Method. Nonlinear Dyn. 2021, 104, 429–438. [Google Scholar] [CrossRef]
- Fan, X.F.; Wang, Z.S. A Fuzzy Lyapunov Function Method to Stability Analysis of Fractional Order T-S Fuzzy Systems. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Tidjani, N.; Guessoum, A. Augmented Robust T-S Fuzzy Control Based PMSG Wind Turbine Improved with H∞ Performance. Int. J. Power Electron. Drive Syst. 2021, 12, 585–596. [Google Scholar]
- Mani, P.; Rajan, R.; Joo, Y.H. Design of Observer-Based Event-Triggered Fuzzy ISMC for T-S Fuzzy Model and Its Application to PMSG. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2221–2231. [Google Scholar] [CrossRef]
- Hwang, S.; Park, J.B.; Joo, Y.H. Disturbance Observer-Based Integral Fuzzy Sliding-Mode Control and Its Application to Wind Turbine System. IET Control. Theory Appl. 2019, 13, 1891–1900. [Google Scholar] [CrossRef]
- Herissi, B.; Boudjehem, D. Fractional-Order Fuzzy Controller for a PMSG Wind Turbine System. Int. J. Syst. Sci. 2020, 51, 3237–3250. [Google Scholar] [CrossRef]
- Mani, P.; Rajan, R.; Shanmugam, L.; Joo, Y.H. Adaptive Fractional Fuzzy Integral Sliding Mode Control for PMSM Model. IEEE Trans. Fuzzy Syst. 2019, 27, 1674–1686. [Google Scholar] [CrossRef]
- Xue, D.Y. Fractional Calculus and Fractional-Order Control; Science Press: Beijing, China, 2018. [Google Scholar]
- Xie, L.H. Output Feedback H∞ Control of Systems with Parameter uncertainty. Int. J. Control. 1996, 63, 741–750. [Google Scholar] [CrossRef]
- Boyd, S.; EL, G.L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of Fractional-Order nonlinear Dynamic Systems: Lyapunov Direct Method and Generalized Mittag-Leffler Stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.T. Stability and Stabilization of Fractional Order Systems Based on Takagi-Sugeno Fuzzy Model; Xidian University: Xi’an, China, 2015. [Google Scholar]
- Tavazoer, M.S.; Haeri, M. Chaotic Attractors in Incommensurate Fractional Order Systems. Phys. D 2008, 237, 2628–2637. [Google Scholar] [CrossRef]
- Rauh, A.; Seelert, W. The Betz Optimum Efficiency for Windmills. Appl. Energy 1984, 17, 15–23. [Google Scholar] [CrossRef]
- Ye, H.Y. Control Technology of Wind Turbine; China Machine Press: Beijing, China, 2015. [Google Scholar]
- Zhou, K.; Ai, M.; Sun, D.Y.; Jin, N.Z.; Wu, X.G. Field Weakening Operation Control Strategies of PMSM Based in Feedback Linearization. Energies 2019, 12, 4526. [Google Scholar] [CrossRef] [Green Version]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability; American Research Press: Santa Fe, NM, USA, 1998. [Google Scholar]
- Smarandache, F. Introduction to Neutrosophic Statistics; Infinite Study; Sitech & Education Publishing: Columbus, OH, USA, 2014. [Google Scholar]
- Hefenawy, N.E.; Metwally, M.A.; Ahmed, Z.M.; Henawy, I.M. A Review on the Applications of Neutrosophic Sets. J. Comput. Theor. Nanosci. 2014, 13, 936–944. [Google Scholar] [CrossRef]
- Aslam, M.; Bantan, R.A.R.; Khan, N. Design of a New Attribute Control Chart under Neutrosophic Statistics. Int. J. Fuzzy Syst. 2019, 21, 433–440. [Google Scholar] [CrossRef]
- Aslam, M. A New method to analyze rock joint roughness coefficient base on Neutrosophic Statistics. Measurement 2019, 146, 65–71. [Google Scholar] [CrossRef]
- Aslam, M.; Arif, O.H.; Sherwani, R.A.K. New Diagnosis Test under the Neutrosophic Statistics: An Application to Diabetic Patients. Biomed Res. Int. 2020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, Z.L.; Liu, C.P.; Ruan, S.Y.; Chen, K. Design of Neutrosophic Self-Tuning PID Controller for AC Permanent Magnet Synchronous Motor Based on Neutrosophic Theory. Math. Probl. Eng. 2021. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Yang, F.; Sheng, W.; Zhou, K.; Huang, T. Fuzzy Chaos Control of Fractional Order D-PMSG for Wind Turbine with Uncertain Parameters by State Feedback Design. Energies 2021, 14, 7369. https://doi.org/10.3390/en14217369
Yang L, Yang F, Sheng W, Zhou K, Huang T. Fuzzy Chaos Control of Fractional Order D-PMSG for Wind Turbine with Uncertain Parameters by State Feedback Design. Energies. 2021; 14(21):7369. https://doi.org/10.3390/en14217369
Chicago/Turabian StyleYang, Li, Fuzhao Yang, Weitao Sheng, Kun Zhou, and Tianmin Huang. 2021. "Fuzzy Chaos Control of Fractional Order D-PMSG for Wind Turbine with Uncertain Parameters by State Feedback Design" Energies 14, no. 21: 7369. https://doi.org/10.3390/en14217369






