Flexible Active Power Control for PV-ESS Systems: A Review
Abstract
:1. Introduction
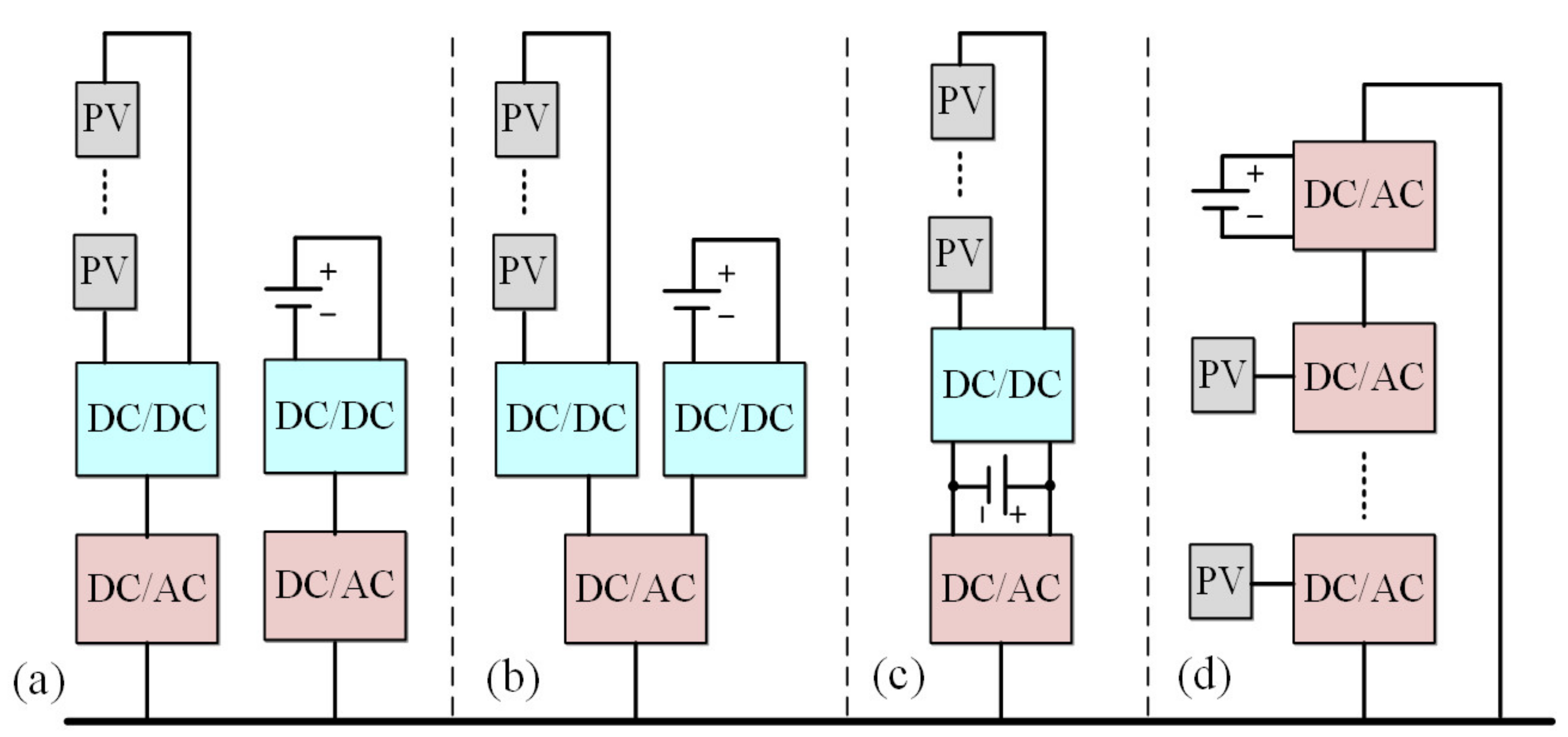
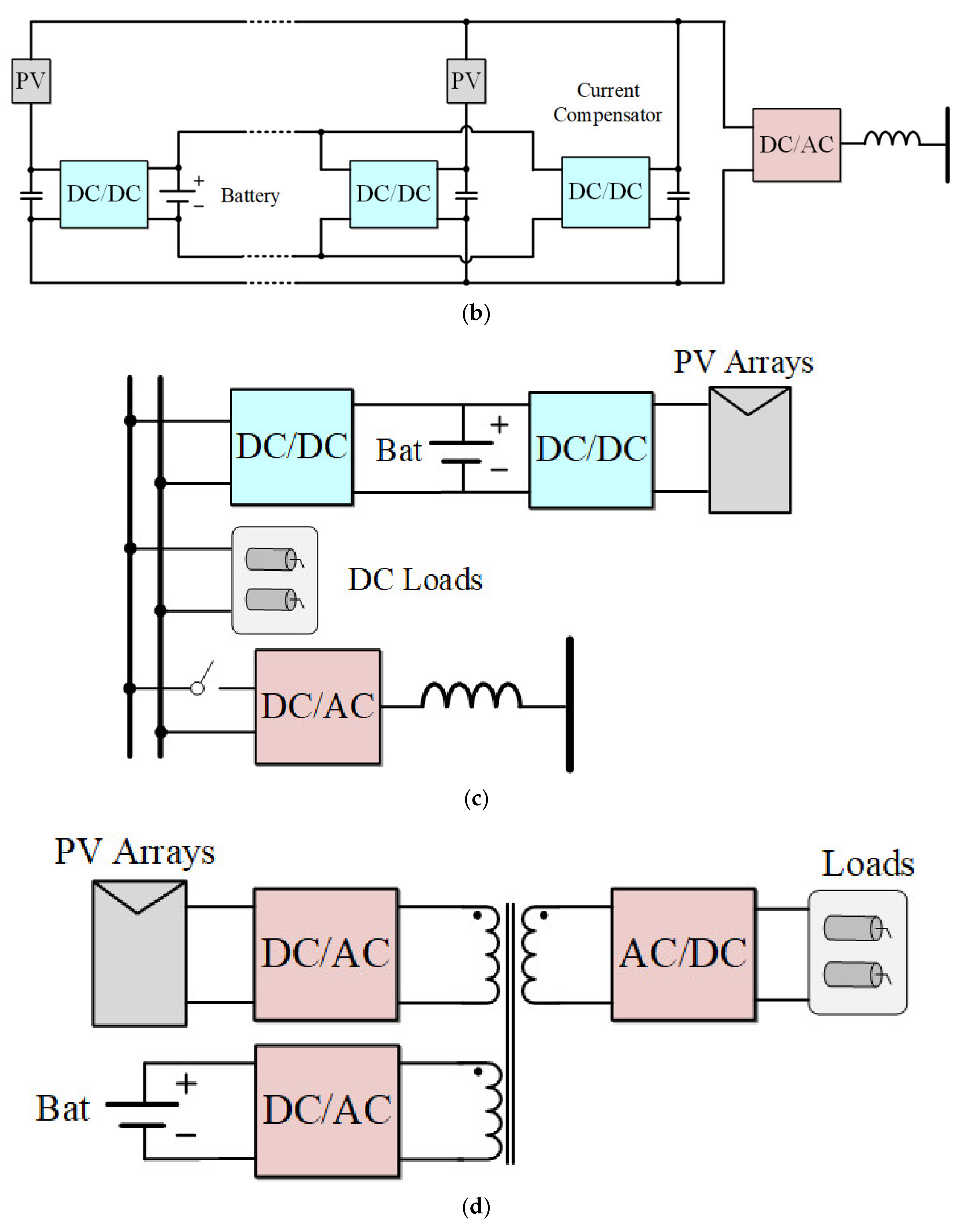
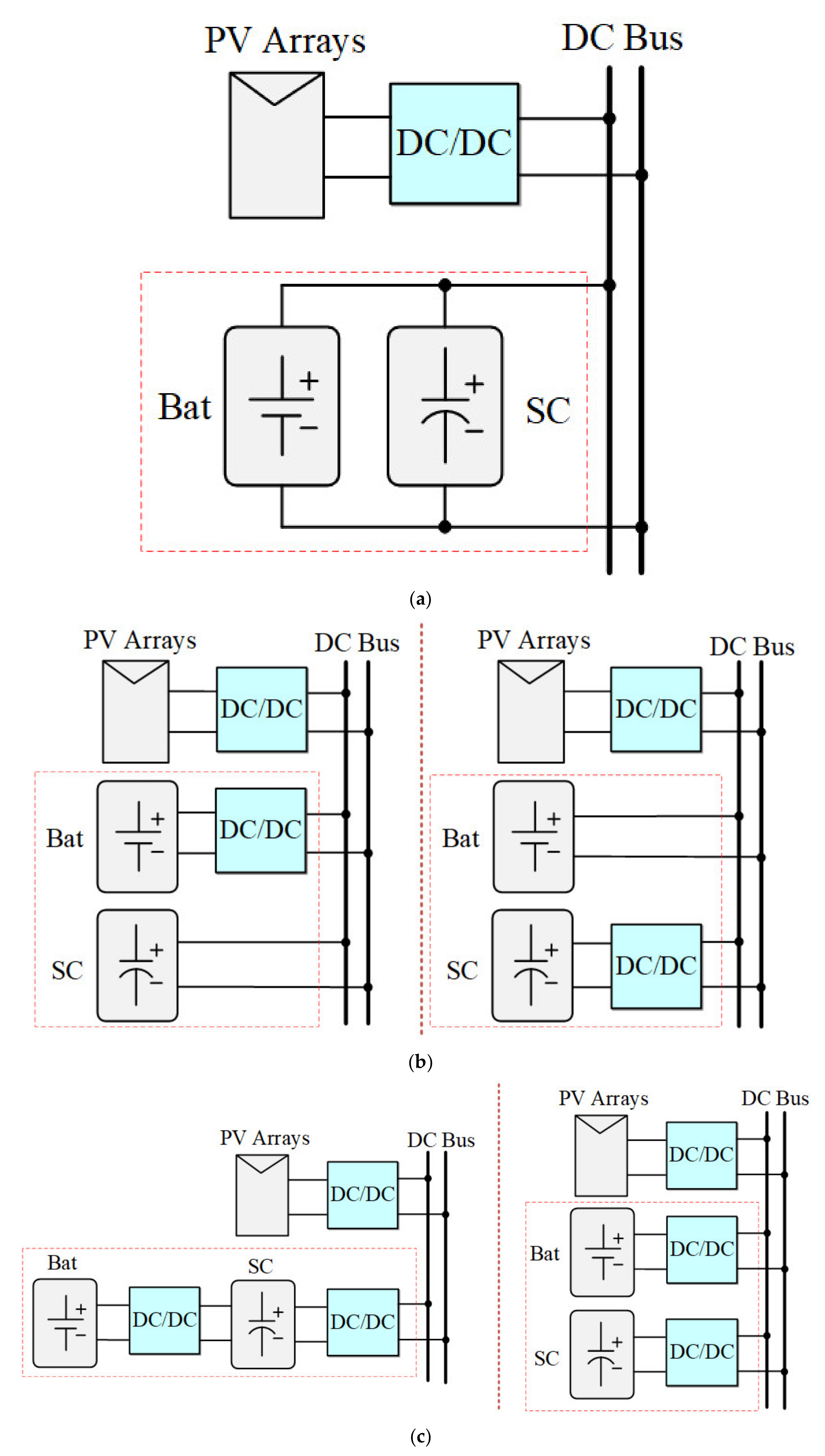
2. Configuration of PV-ESS Systems
3. Flexible Active Power Control Methods
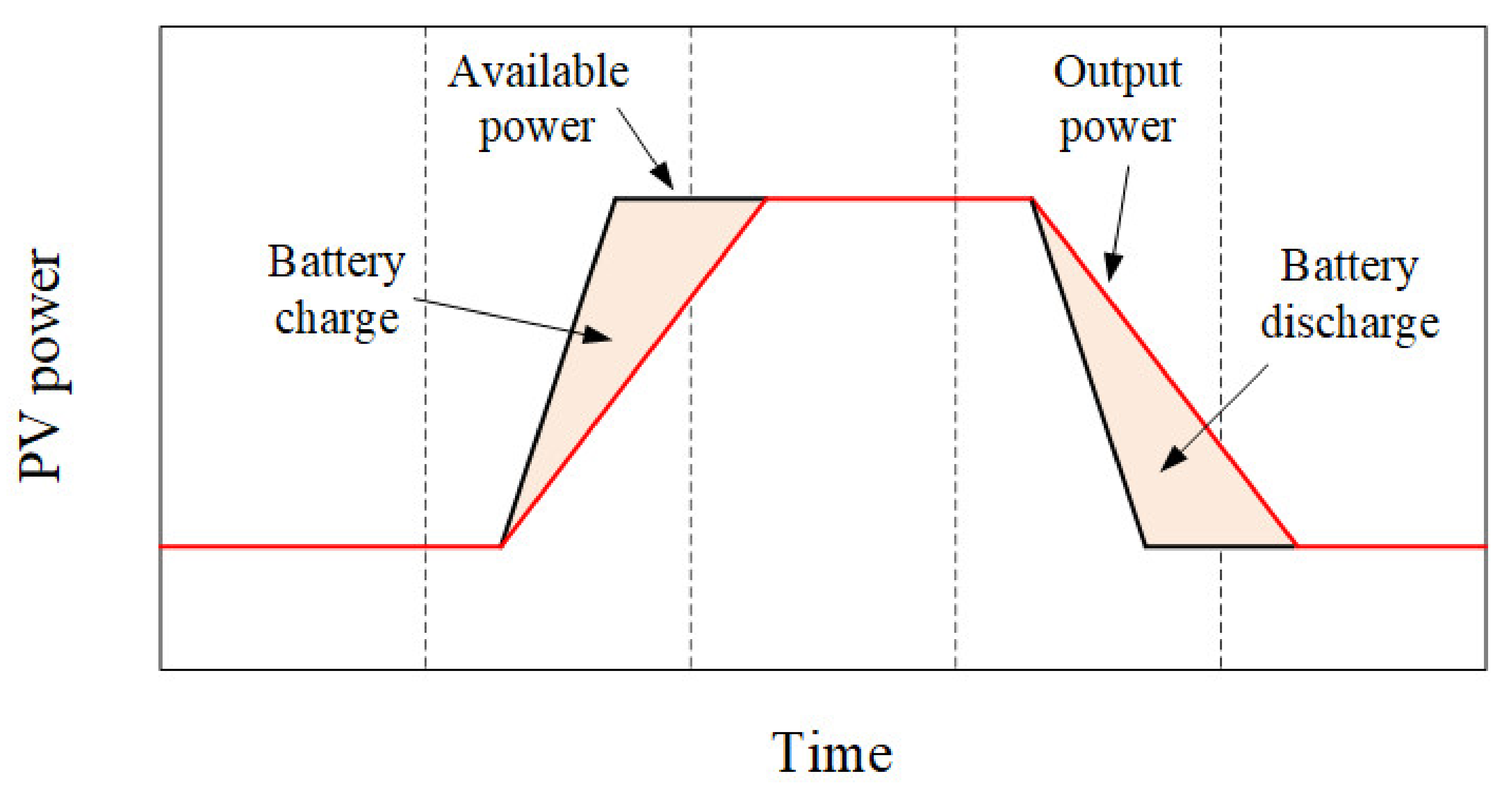
3.1. Power Reserve Control
3.2. Power Ramp-Rate Control
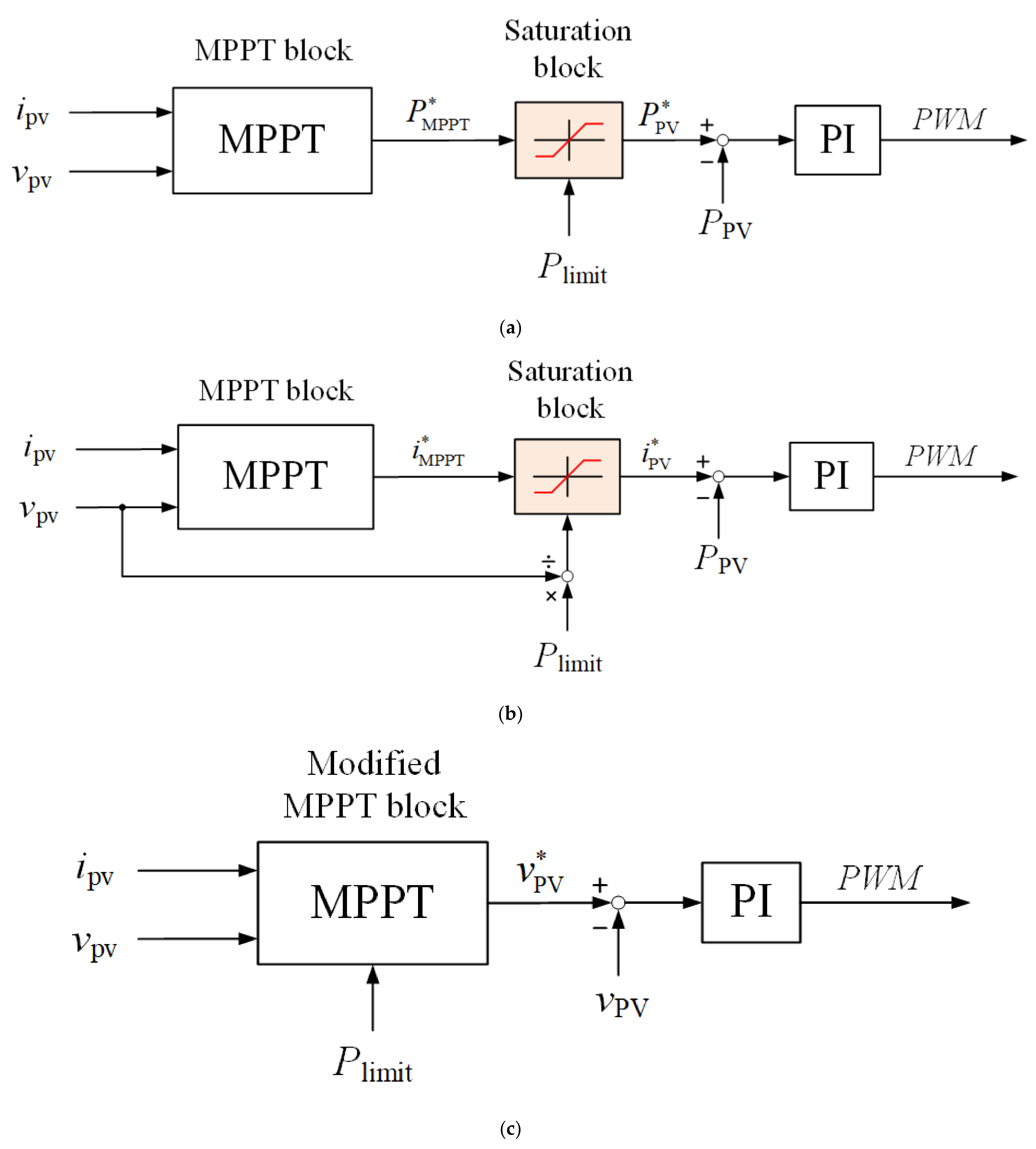
3.3. Power-Limiting Control
4. Frequency Regulation Methods
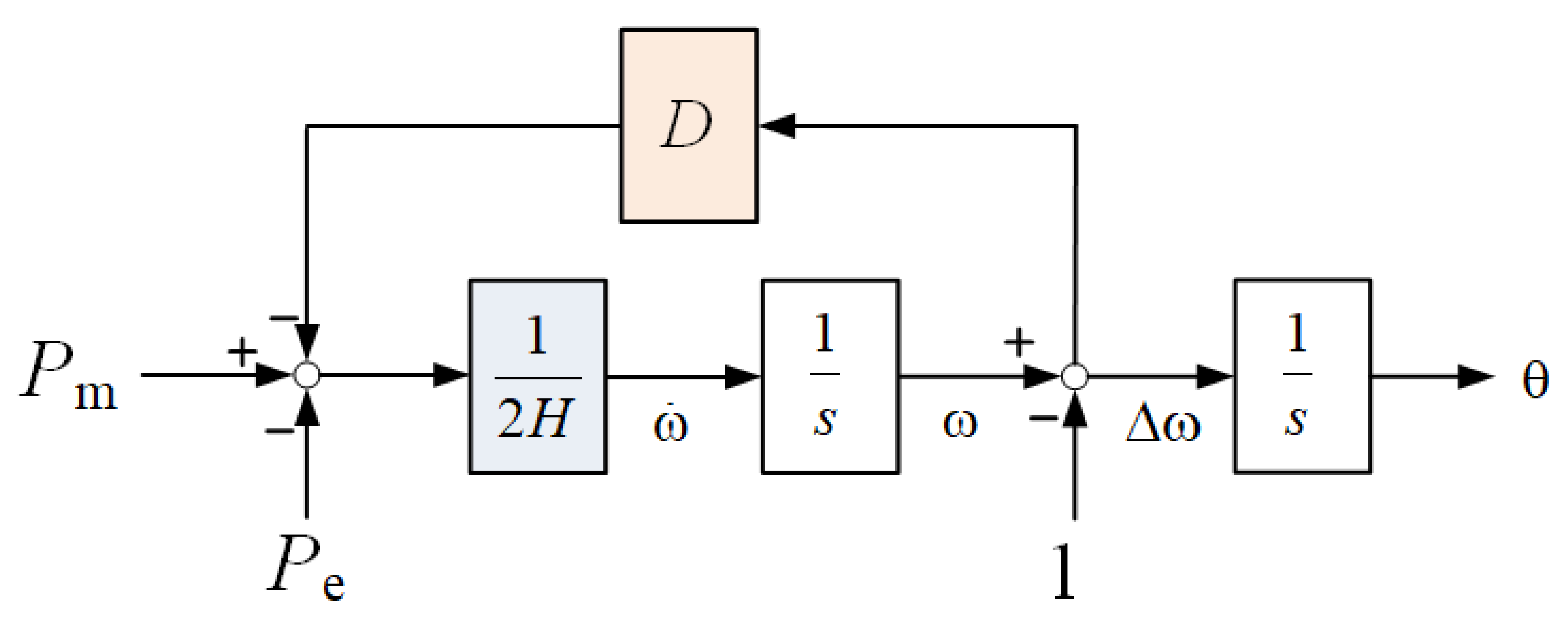
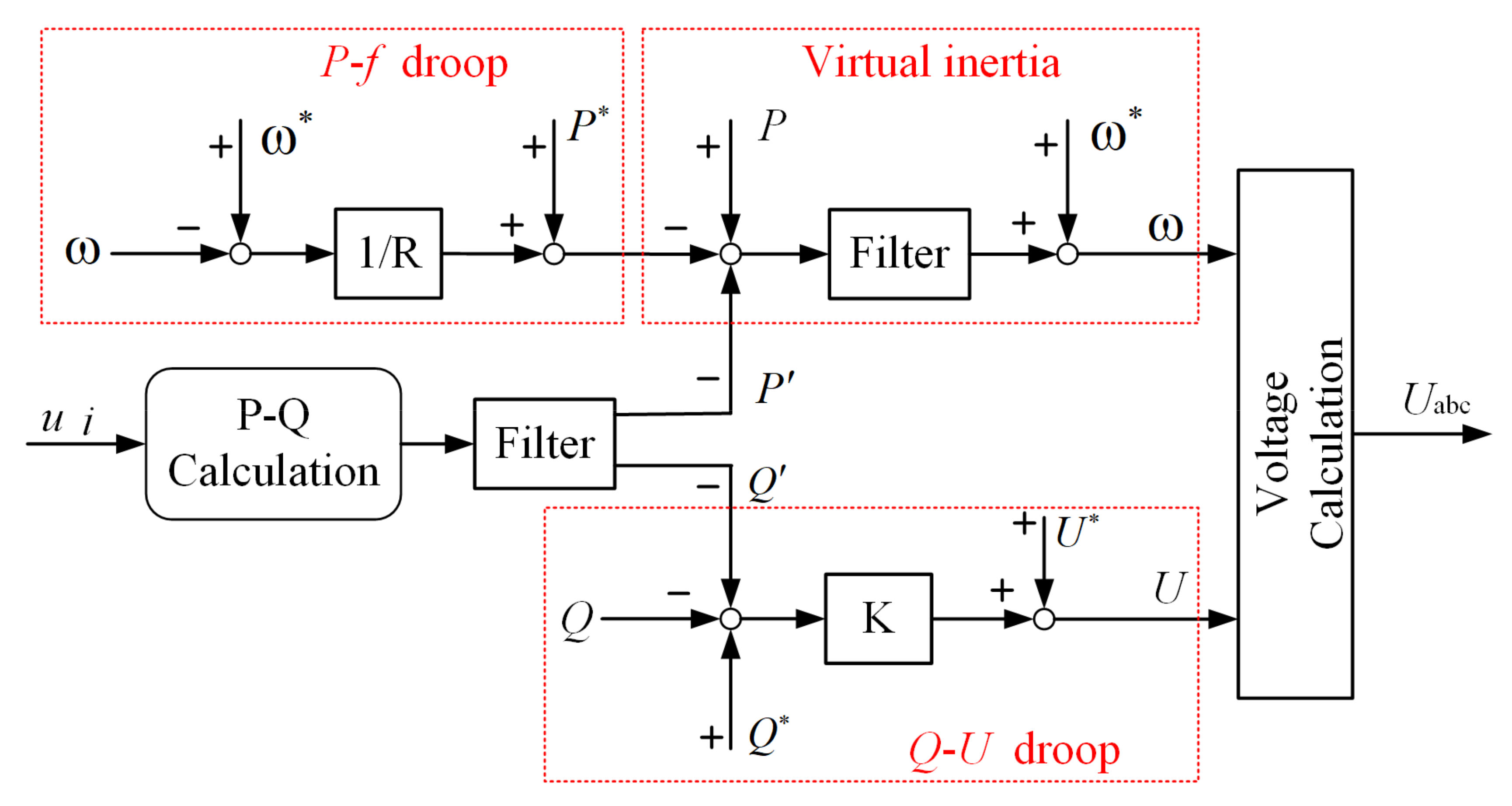
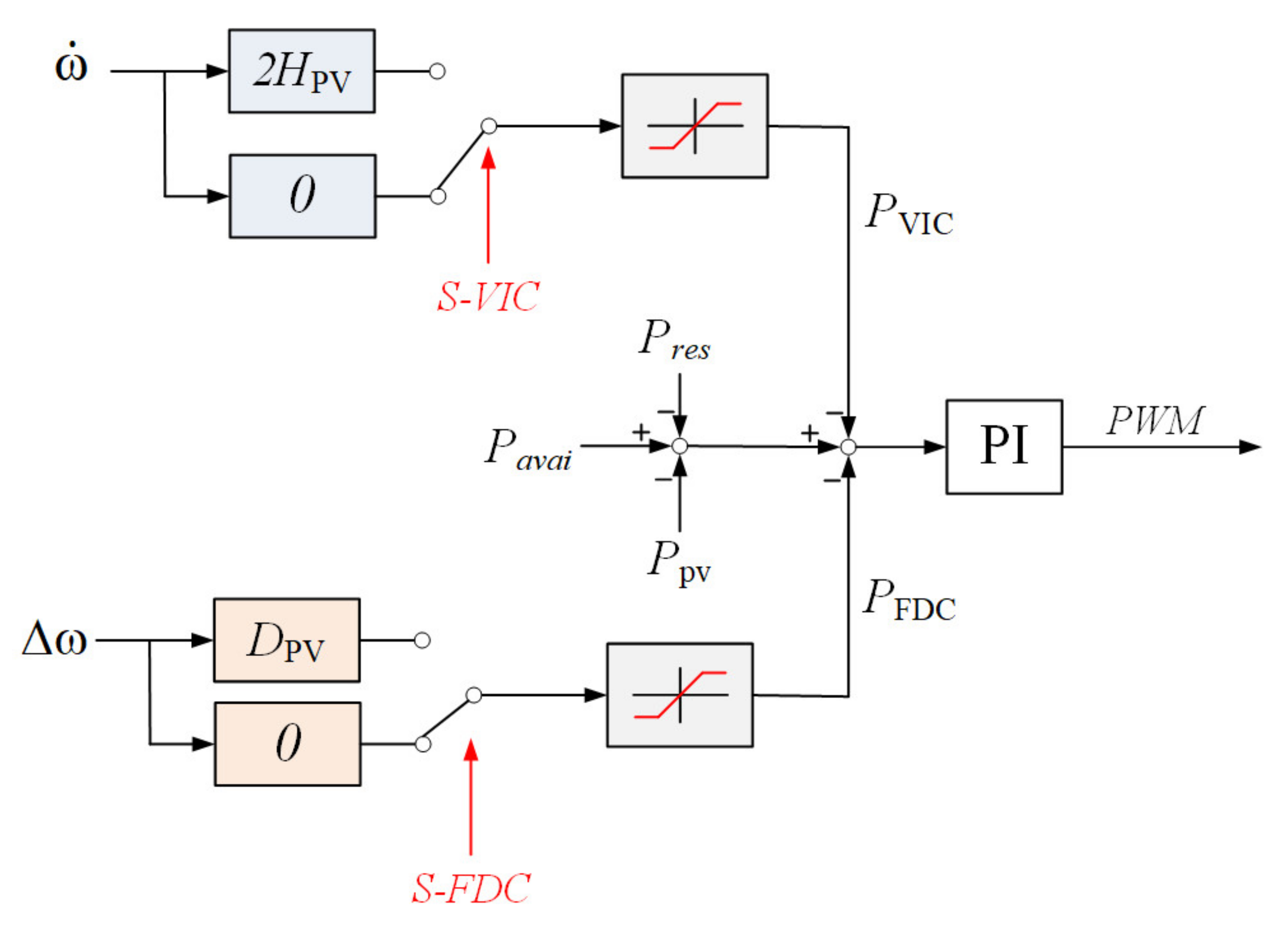
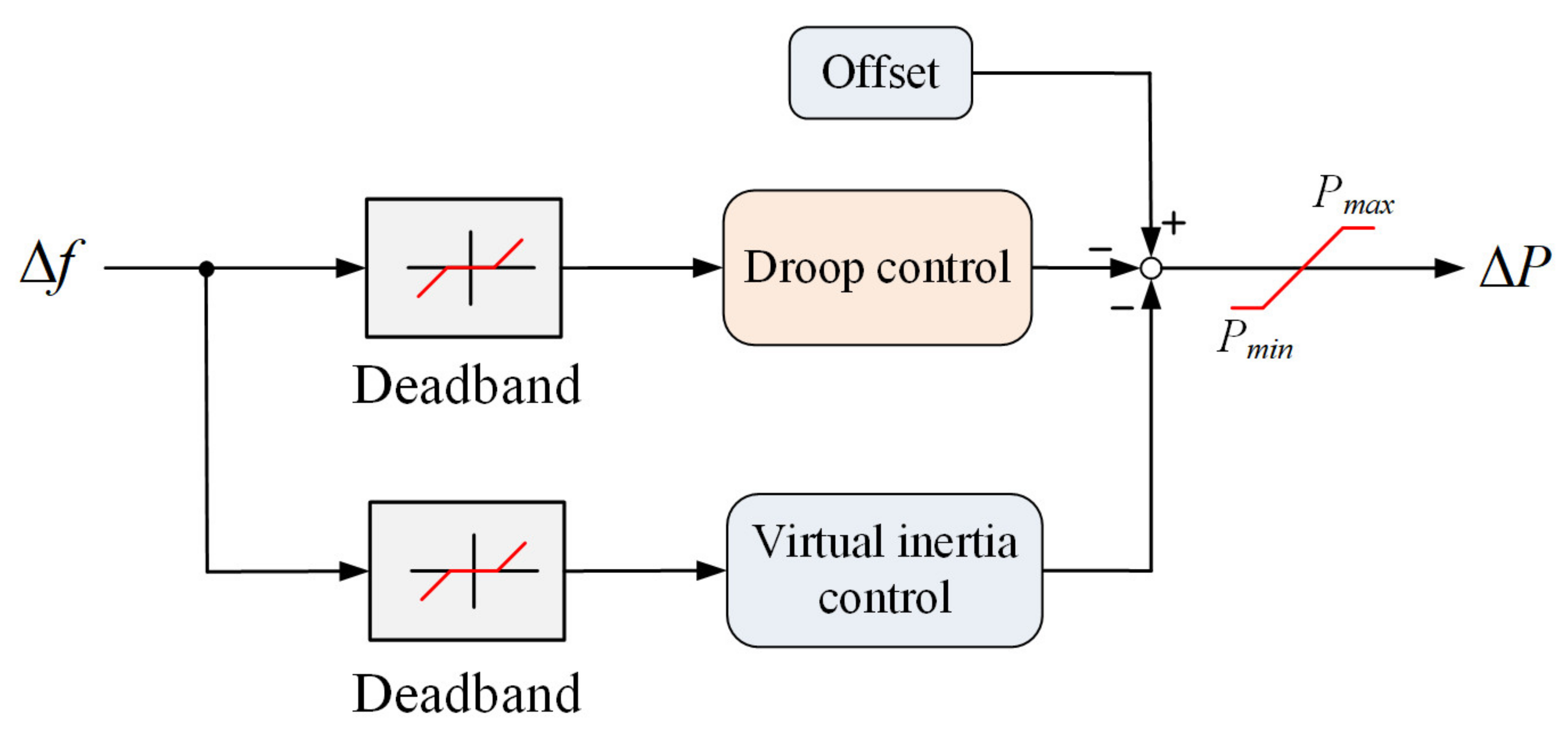
4.1. Virtual Inertia Control
4.2. Frequency-Damping Control
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EMA | Exponential moving average |
| ESS | Energy storage system |
| FAPC | Forecasting-based active power curtailment |
| FDC | Frequency-damping control |
| HESS | Hybrid energy storage system |
| LPF | Low-pass filter |
| MA | Moving average |
| MPPT | Maximum power point tracking |
| PCC | Point of common coupling |
| PLC | Power-limiting control |
| P&O | Perturb and observe |
| PRC | Power reserve control |
| PRRC | Power ramp-rate control |
| SC | Supercapacitor |
| SCR | Short circuit ratio |
| SG | Synchronous generators |
| VIC | Virtual inertia control |
| VRB | Vanadium redox battery |
| VSG | Virtual synchronous generator |
References
- Renewables 2021—Global Status Report. Available online: https://www.ren21.net/ (accessed on 15 June 2021).
- Yang, Y.; Enjeti, P.; Blaabjerg, F.; Wang, H. Wide-Scale Adoption of Photovoltaic Energy: Grid Code Modifications Are Explored in the Distribution Grid. IEEE Ind. Appl. Mag. 2015, 21, 21–31. [Google Scholar] [CrossRef] [Green Version]
- Shivashankar, S.; Mekhilef, S.; Mokhlis, H.; Karimi, M. Mitigating Methods of Power Fluctuation of Photovoltaic Sources—A Review. Renew. Sustain. Energy Rev. 2016, 59, 1170–1184. [Google Scholar] [CrossRef]
- Xu, J.; Bian, S.; Liu, M.; Zhang, Z.; Xie, S. Stability Analysis of Grid-Connected Inverters during the Transient of Grid Voltage Fluctuations in Weak Grid Cases. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 5185–5190. [Google Scholar]
- Stetz, T.; Appen, J.; Niedermeyer, F.; Scheibner, G.; Sikora, R.; Braun, M. Twilight of the Grids: The Impact of Distributed Solar on Germany’s Energy Transition. IEEE Power Energy Mag. 2015, 13, 50–61. [Google Scholar]
- Woyte, A.; Thong, V.; Belmans, R.; Nijs, J. Voltage Fluctuations on Distribution Level Introduced by Photovoltaic Systems. IEEE Trans. Energy Conver. 2006, 21, 202–209. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2130–2146. [Google Scholar] [CrossRef]
- Technical Regulation 3.2.2 for PV Power Plants with a Power Output above 11 kW; Energinet: Fredericia, Denmark, 2016.
- Technical Guideline—For Power Generating Units, Systems and Storage Systems as Well as for Their Components. Germany Grid Codes; Fördergesellschaft Windenergie und andere Dezentrale Energien: Berlin, Germany, 2019; Available online: https://wind-fgw.de/wp-content/uploads/2019/05/TG_Part8_Rev9_EN_preview.pdf (accessed on 29 October 2021).
- Australian Grid Code—National Electricity Rules Version 139. Available online: https://www.aemc.gov.au/sites/default/files/2020-05/NER%20v139%20full_1.pdf (accessed on 20 May 2020).
- Residential Grid-Connected Photovoltaic (PV) System; China Photovoltaic Industry Association: Beijing, China, 2019.
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F.; Sera, D. Delta Power Control Strategy for Multistring Grid-Connected PV Inverters. IEEE Trans. Ind. Appl. 2017, 53, 3862–3870. [Google Scholar] [CrossRef] [Green Version]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. A Cost-Effective Power Ramp-Rate Control Strategy for Single-Phase Two-Stage Grid-Connected Photovoltaic Systems. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–7. [Google Scholar]
- Yang, Y.; Blaabjerg, F.; Wang, H. Constant Power Generation of Photovoltaic Systems Considering the Distributed Grid Capacity. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition(APEC), Fort Worth, TX, USA, 16–20 March 2014; pp. 379–385. [Google Scholar]
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-Connected Photovoltaic Systems: An Overview of Recent Research and Emerging PV Converter Technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Indu Rani, B.; Saravana Ilango, G.; Nagamani, C. Control Strategy for Power Flow Management in a PV System Supplying DC Loads. IEEE Trans. Ind. Electron. 2013, 60, 3185–3194. [Google Scholar] [CrossRef]
- Chiang, S.J.; Chang, K.T.; Yen, C.Y. Residential Photovoltaic Energy Storage System. IEEE Trans. Ind. Electron. 1998, 45, 385–394. [Google Scholar] [CrossRef]
- Kim, N.; Parkhideh, B. Ramp-Rate Control Strategy for Distributed PV-ESS AC-Stacked Inverter Architecture. In Proceedings of the 2017 IEEE 8th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Florianopolis, Brazil, 17–20 April 2017; pp. 1–6. [Google Scholar]
- Kim, N.; Roy, C.; Parkhideh, B. A Single-Stage Capacitor-Bridge Boost Converter Topology for PV-Battery Series Integration in Regulated DC Microgrids. In Proceedings of the 2021 IEEE Applied Power Electronics Conference and Exposition (APEC), Phoenix, AZ, USA, 14–17 June 2021; pp. 2613–2619. [Google Scholar]
- Wang, Z.; Zhang, H.; He, B. Circuit Structure and Control Method of a Novel PV Energy Storage System. Guangdong Electr. Power 2020, 8, 1–8. [Google Scholar]
- Pullaguram, D.; Mudaliyar, S.R.; Mishra, S.; Senroy, N. Isolated PV Battery Management System to Power Home Appliances. In Proceedings of the 2017 7th International Conference on Power Systems (ICPS), Pune, India, 21–23 December 2017; pp. 755–760. [Google Scholar]
- Yong, H.; Li, X.; Wu, X.; Li, M.; Wang, Y. Stability Control Design for TAB-Based Three-Port Bidirectional DC/DC Converters in PV-Battery Grid-Connected Applications. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3469–3474. [Google Scholar]
- Showers, S.O.; Raji, A.K. Benefits and Challenges of Energy Storage Technologies in High Penetration Renewable Energy Power Systems. In Proceedings of the 2019 IEEE PES/IAS Power Africa, Abuja, Nigeria, 20–23 August 2019; pp. 209–214. [Google Scholar]
- Lin, D.; Zhao, B.; Li, P.; Wu, X.Z.; Gu, Y.N. Real-Time Fluctuation Smoothing Method for Photovoltaic Power Station Using Lead Carbon Battery. Power Syst. Technol. 2018, 42, 1518–1525. [Google Scholar]
- Şahin, M.E.; Blaabjerg, F. A Hybrid PV-Battery/Supercapacitor System and a Basic Active Power Control Proposal in MATLAB/Simulink. Electronics 2020, 9, 129. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Liu, Y. Analysis of Energy Storage Technology and Their Application for Micro Grid. In Proceedings of the 2017 International Conference on Computer Technology, Electronics and Communication (ICCTEC), Dalian, China, 19–21 December 2017; pp. 972–975. [Google Scholar]
- Lei, C.; Zhang, X.; Han, P. The Capacity Optimization of Hybrid Energy Storage System for Wind Power Smoothing. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 2106–2110. [Google Scholar]
- Jamahori, H.F.; Rahman, H.A. Hybrid Energy Storage System for Life Cycle Improvement. In Proceedings of the 2017 IEEE Conference on Energy Conversion (CENCON), Kuala Lumpur, Malaysia, 30–31 October 2017; pp. 196–200. [Google Scholar]
- Lin, X.; Lei, Y. Coordinated Control Strategies for SMES-Battery Hybrid Energy Storage Systems. IEEE Access 2017, 5, 23452–23465. [Google Scholar]
- Wang, G.; Ciobotaru, M.; Agelidis, V.G. Power Smoothing of Large Solar PV Plant Using Hybrid Energy Storage. IEEE Trans. Sustain. Energy 2014, 5, 834–842. [Google Scholar] [CrossRef]
- Tian, C.; Li, K.; Yan, Y.; Zhang, C. A Multi-Time Scale Control Strategy of Hybrid Energy Storage System in Wind Farm Based on Empirical Mode Decomposition. Power Syst. Technol. 2015, 39, 2167–2172. [Google Scholar]
- Jing, W.; Lai, C.H.; Wong, S.H.; Wong, M.L. Battery-Supercapacitor Hybrid Energy Storage System in Standalone DC Microgrids: A Review. IET Renew. Power Gener. 2017, 11, 461–469. [Google Scholar] [CrossRef]
- Jing, W.L.; Lai, C.H.; Wong, W.S.H.; Wong, M.L.D. Cost Analysis of Battery-Supercapacitor Hybrid Energy Storage System for Standalone PV Systems. In Proceedings of the 4th IET Clean Energy and Technology Conference (CEAT 2016), Kuala Lumpur, Malaysia, 14–15 November 2016; pp. 1–6. [Google Scholar]
- Roy, P.; He, J.; Liao, Y. Cost Minimization of Battery-Supercapacitor Hybrid Energy Storage for Hourly Dispatching Wind-Solar Hybrid Power System. IEEE Access 2020, 8, 210099–210115. [Google Scholar] [CrossRef]
- Batzelis, E.I.; Kampitsis, G.E.; Papathanassiou, S.A. Power Reserves Control for PV Systems with Real-Time MPP Estimation via Curve Fitting. IEEE Trans. Sustain. Energy 2017, 8, 1269–1280. [Google Scholar] [CrossRef]
- Li, X.; Wen, H.; Zhu, Y.; Jiang, L.; Hu, Y.; Xiao, W. A Novel Sensor-less Photovoltaic Power Reserve Control with Simple Real-Time MPP Estimation. IEEE Trans. Power Electron. 2019, 34, 7521–7531. [Google Scholar] [CrossRef]
- Scolari, E.; Sossan, F.; Paolone, M. Photovoltaic-Model-Based Solar Irradiance Estimators: Performance Comparison and Application to Maximum Power Forecasting. IEEE Trans. Sustain. Energy 2018, 9, 35–44. [Google Scholar] [CrossRef] [Green Version]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. A Sensorless Power Reserve Control Strategy for Two-Stage Grid-Connected PV Systems. IEEE Trans. Power Electron. 2017, 32, 8559–8569. [Google Scholar] [CrossRef] [Green Version]
- Peng, Q.; Tang, Z.; Yang, Y.; Blaabjerg, F. Event-Triggering Power Reserve Control for Grid-Connected PV Systems. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 417–423. [Google Scholar]
- Serban, I.; Marinescu, C. Flexible Solution for Grid-Connected Operation of Microgrids, Based on a Leading Inverter with Supercapacitor Energy Storage. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Garozzo, D.; Tina, G.M. Evaluation of the Effective Active Power Reserve for Fast Frequency Response of PV with BESS Inverters Considering Reactive Power Control. Energies 2020, 13, 3437. [Google Scholar] [CrossRef]
- Sarojini, R.K.; Palanisamy, K.; Sanjeevikumar, P.; Nielsen, J.B. Inertia Emulation Control Technique Based Frequency Control of Grid-Connected Single-Phase Rooftop Photovoltaic System with Battery and Supercapacitor. IET Renew. Power Gener. 2020, 14, 1156–1163. [Google Scholar]
- Chen, X.; Du, Y.; Wen, H.; Jiang, L.; Xiao, W. Forecasting-Based Power Ramp-Rate Control Strategies for Utility-Scale PV Systems. IEEE Trans. Ind. Electron. 2019, 66, 1862–1871. [Google Scholar]
- Hund, T.D.; Gonzalez, S.; Barrett, K. Grid-tied PV system energy smoothing. In Proceedings of the 2010 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 2762–2766. [Google Scholar]
- Wilson, A.R. Event Triggered Analog Data Acquisition Using the Exponential Moving Average. IEEE Sens. J. 2014, 14, 2048–2055. [Google Scholar]
- Koiwa, K.; Liu, K.; Tamura, J. Analysis and Design of Filters for the Energy Storage System: Optimal Tradeoff between Frequency Guarantee and Energy Capacity/Power Rating. IEEE Trans. Ind. Electron. 2018, 65, 6560–6570. [Google Scholar]
- Kazemi, M.V.; Sadati, S.J.; Gholamian, S.A. Adaptive Frequency Control Support of a DFIG Based on Second-Order Derivative Controller Using Data-Driven Method. Int. Trans. Elect. Energy Syst. 2020, 30, e12424. [Google Scholar]
- Alam, M.J.E.; Muttaqi, K.M.; Sutanto, D. A Novel Approach for Ramp-Rate Control of Solar PV Using Energy Storage to Mitigate Output Fluctuations Caused by Cloud Passing. IEEE Trans. Energy Convers. 2014, 29, 507–518. [Google Scholar]
- Tran, V.T.; Islam, M.R.; Sutanto, D.; Muttaqi, K.M. Mitigation of Solar PV Intermittency Using Ramp-Rate Control of Energy Buffer Unit. IEEE Trans. Energy Convers. 2019, 34, 435–445. [Google Scholar] [CrossRef]
- Jiang, Y.; Shi, X.; Lau, D.; Wang, D. Integration of Electrochemical Capacitors on Silicon Photovoltaic Modules for Rapid-Response Power Buffering. In Proceedings of the 2017 IEEE 44th Photovoltaic Specialist Conference (PVSC), Washington, DC, USA, 25–30 June 2017; pp. 3220–3223. [Google Scholar]
- Zhao, Q.; Xian, L.; Roy, S.; Kong, X.; Khambadkone, A.M. Optimal Control of PV Ramp Rate Using Multiple Energy Storage System. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017—ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017; pp. 928–931. [Google Scholar]
- Alvaro, D.; Arranz, R.; Aguado, J. Sizing and Operation of Hybrid Energy Storage Systems to Perform Ramp-Rate Control in PV Power Plants. Int. J. Electr. Power Energy Syst. 2019, 107, 589–596. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Blaabjerg, F.; Kerekes, T. A Hybrid Power Control Concept for PV Inverters with Reduced Thermal Loading. IEEE Trans. Power Electron. 2014, 29, 6271–6275. [Google Scholar] [CrossRef] [Green Version]
- Urtasun, A.; Sanchis, P.; Marroyo, L. Limiting the Power Generated by a Photovoltaic System. In Proceedings of the 10th International Multi-Conferences on Systems, Signals & Devices 2013 (SSD13), Hammamet, Tunisia, 18–21 March 2013; pp. 1–6. [Google Scholar]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. High-Performance Constant Power Generation in Grid-Connected PV Systems. IEEE Trans. Power Electron. 2016, 31, 1822–1825. [Google Scholar] [CrossRef] [Green Version]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F.; Wang, H. Benchmarking of Constant Power Generation Strategies for Single-Phase Grid-Connected Photovoltaic Systems. IEEE Trans. Ind. Appl. 2018, 54, 447–457. [Google Scholar] [CrossRef] [Green Version]
- Omran, W.A.; Kazerani, M.; Salama, M.M.A. Investigation of Methods for Reduction of Power Fluctuations Generated from Large Grid-Connected Photovoltaic Systems. IEEE Trans. Energy Convers. 2011, 26, 318–327. [Google Scholar]
- Liu, N.; Chen, Q.; Lu, X.; Liu, J.; Zhang, J. A Charging Strategy for PV-Based Battery Switch Stations Considering Service Availability and Self-Consumption of PV Energy. IEEE Trans. Ind. Electron. 2015, 62, 4878–4889. [Google Scholar] [CrossRef]
- Galilea, C.; Pascual, J.; Berrueta, A.; Ursua, A.; Marroyo, L. Economic Analysis of Residential PV Self-Consumption Systems with Li-ion Batteries Under Different Billing Scenarios. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Kelepouris, N.S.; Nousdilis, A.I.; Bouhouras, A.S.; Christoforidis, G.C.; Yerasimou, Y.; Chatzigeorgiou, N.G.; Georghiou, G.E.; Celli, G.; Mocci, S.; Gal, E.; et al. Impact of Demand Side Management on the Self-Sufficiency and Self-Consumption of Buildings with Photovoltaic and Storage Systems. In Proceedings of the 2021 9th International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 16–17 June 2021; pp. 1–6. [Google Scholar]
- Moshövel, J.; Kairies, K.; Magnor, D. Analysis of the Maximal Possible Grid Relief from PV-Peak-Power Impacts by Using Storage Systems for Increased Self-Consumption. Appl. Energy 2015, 137, 567–575. [Google Scholar] [CrossRef]
- Farinet, D.; Maurer, M.; Vacca, L.; Spataru, S.V.; Stroe, D. Battery Lifetime Analysis for Residential PV-Battery System used to Optimize the Self Consumption—A Danish Scenario. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 6693–6698. [Google Scholar]
- Sangwongwanich, A.; Angenendt, G.; Yang, Y.; Sera, D.; Sauer, D.; Blaabjerg, F. Enhancing PV Inverter Reliability with Battery System Control Strategy. CPSS Trans. Power Electron. Appl. 2018, 3, 93–101. [Google Scholar] [CrossRef]
- Technical Regulation 3.2.2 Signal List for PV Power Plant; Energinet: Fredericia, Denmark, 2015.
- Zhou, W.; Xiaosong, Z.; Xufeng, Y.; Wei, X. Review on Virtual Synchronous Generator Technologies. In Proceedings of the 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online, 2–3 July 2020; pp. 744–751. [Google Scholar]
- Rajan, R.; Fernandez, F.M. Grid Inertia Based Frequency Regulation Strategy of Photovoltaic System without Energy Storage. In Proceedings of the 2018 International CET Conference on Control, Communication, and Computing (IC4), Thiruvananthapuram, India, 5–7 July 2018; pp. 106–111. [Google Scholar]
- Qi, Y.; Yang, T.; Fang, J.; Tang, Y.; Rajashekara, K. Grid Inertia Support Enabled by Smart Loads. IEEE Trans. Power Electron. 2021, 36, 947–957. [Google Scholar] [CrossRef]
- Peng, Q.; Fang, J.; Yang, Y.; Liu, T.; Blaabjerg, F. Maximum Virtual Inertia from DC-Link Capacitors Considering System Stability at Voltage Control Timescale. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 79–89. [Google Scholar] [CrossRef]
- Zhang, R.; Fang, J.; Tang, Y. Inertia Emulation through Supercapacitor Energy Storage Systems. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Korea, 27–30 May 2019; pp. 1365–1370. [Google Scholar]
- Suul, J.A.; D’Arco, S.; Guidi, G. Virtual Synchronous Machine-Based Control of a Single-Phase Bi-Directional Battery Charger for Providing Vehicle-to-Grid Services. IEEE Trans. Ind. Appl. 2016, 52, 3234–3244. [Google Scholar]
- Yu, J.; Fang, J.; Tang, Y. Inertia Emulation by Flywheel Energy Storage System for Improved Frequency Regulation. In Proceedings of the 2018 IEEE 4th Southern Power Electronics Conference (SPEC), Singapore, 2018, 10–13 December; pp. 1–8.
- Fang, J.; Li, X.; Tang, Y.; Li, H. Power Management of Virtual Synchronous Generators through Using Hybrid Energy Storage Systems. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 2018, 4–8 March; pp. 1407–1411.
- Dajun, J.; Lei, Z.; Dawei, Z.; Ning, C.; Minhui, Q. Research on PV Generation Participating in Power Grid Frequency Regulation. In Proceedings of the 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; pp. 1713–1717. [Google Scholar]
- Zhao, D.; Qian, M.; Ma, J.; Jiang, D.; Ding, M.; Xiang, L. A Decentralized Frequency Regulation Strategy of PV Power Plant Based on Droop Control. In Proceedings of the 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; pp. 1824–1828. [Google Scholar]
- Yang, T.; Cui, H.; Zhang, L.; Yang, B.; Li, G.; Lu, Y. Active Frequency Support Control of Energy Storage Power Station Based on Photovoltaic and Energy-Storage Microgrid. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 2362–2367. [Google Scholar]
- Meng, J.; Wang, Y.; Fu, C.; Wang, H. Adaptive Virtual Inertia Control of Distributed Generator for Dynamic Frequency Support in Microgrid. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–5. [Google Scholar]
- Rajan, R.; Fernandez, F.M. Fuzzy Based Control of Grid-Connected Photovoltaic System for Enhancing System Inertial Response. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar]
- Okou, A.F.; Akhri, O.; Beguenane, R.; Tarbouchi, M. Nonlinear Control Strategy Insuring Contribution of PV Generator to Voltage and Frequency Regulation. In Proceedings of the 6th IET International Conference on Power Electronics, Machines and Drives (PEMD 2012), Bristol, UK, 27–29 March 2012; pp. 1–5. [Google Scholar]
- Kimpara, Y.; Kurimoto, M.; Manabe, Y.; Funabashi, T.; Kato, T. An Experimental Study on Active Power Control of Photovoltaic Power Generation for Supporting Grid Frequency Regulation. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Peng, Q.; Yang, Y.; Liu, T.; Blaabjerg, F. Coordination of Virtual Inertia Control and Frequency Damping in PV Systems for Optimal Frequency Support. CPSS Trans. Power Electron. Appl. 2020, 5, 305–316. [Google Scholar]
- Azhar, I.F.; Putranto, L.M.; Hadi, S.P. Design of Battery Energy Storage System Control Scheme for Frequency Regulation for PV Integrated Power System. In Proceedings of the 2020 FORTEI-International Conference on Electrical Engineering (FORTEI-ICEE), Bandung, Indonesia, 23–24 September 2020; pp. 7–12. [Google Scholar]







| Parameters | Lead-Acid Battery | Li-Ion Battery | VRB | Supercapacitor |
|---|---|---|---|---|
| Energy density (Wh/kg) | 10–100 | 150–400 | 20–70 | 10–20 |
| Power density (W/kg) | 90–700 | 1000–5000 | 1–10 | 4000–10,000 |
| Cycle life | 1000 | 5000 | >10,000 | >500,000 |
| Cycle efficiency | 70–90% | 90–99% | 60–85% | 85–98% |
| Charge/discharge time | min–h | min–h | h | s–min |
| Price (USD/kWh) | 100 | 600 | 150 | 2500 |
| Methods | Advantages | Disadvantages |
|---|---|---|
| P-V curve fitting [35] | Good robustness Reduced hardware cost | Heavy computational burden Sensitive to parameters of PV arrays Dependent on sampled points |
| Empirical model-based estimating [36] | Reduced hardware cost | Heavy computational burden Big data needed Sensitive to parameters of PV arrays |
| Sensor-based forecasting [37] | Real-time measurement | Extra cost of sensors Complexity |
| Master-slave strategy [12] | Simple Real-time measurement | Communication needed Dependent on entire system configuration |
| P&O method [38] | Good robustness Reduced hardware cost | Power and voltage impulses in DC link |
| Methods | Advantages | Disadvantages |
|---|---|---|
| MA [44] | Simplicity Small computational burden | Rely on previously sampled data |
| EMA [45] | Simplicity | Large ESS required Poor ability to regain SOC of ESS |
| LPF [46] | Suppress high-frequency power fluctuations | Large ESS required Sensitive to irradiance variations |
| 2-LPF [47] | Suppress higher-frequency power fluctuations ESS capacity reduced Long life expectancy of ESS Fast dynamics | Sensitive to irradiance variations |
| Gradient control [48] | Independent of past irradiance data | Complexity Short life expectancy of ESS |
| Methods | Dynamic Responses | Tracking Errors | Stability |
|---|---|---|---|
| Direct power control | fast | small | medium |
| Current-limiting control | fast | small | low |
| Modified MPPT strategy (left) | slow | medium | high |
| Modified MPPT strategy (right) | slow | large | medium |
| Methods | Advantages | Disadvantages |
|---|---|---|
| DC-link capacitor [68] | Without additional investment Simplicity Great numbers | Limited by the operation condition of the converter |
| Supercapacitor [69] | High power density Long lifetime Fast dynamics | Small capacity High cost |
| Battery [70] | Large capacity High energy density | Real-time RoCoF measurement required Potential instability concern |
| Flywheel [71] | High power density Long lifetime Easy control for inertia emulation | High cost Difficult operation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Kerekes, T. Flexible Active Power Control for PV-ESS Systems: A Review. Energies 2021, 14, 7388. https://doi.org/10.3390/en14217388
Wu X, Kerekes T. Flexible Active Power Control for PV-ESS Systems: A Review. Energies. 2021; 14(21):7388. https://doi.org/10.3390/en14217388
Chicago/Turabian StyleWu, Xiangqiang, and Tamas Kerekes. 2021. "Flexible Active Power Control for PV-ESS Systems: A Review" Energies 14, no. 21: 7388. https://doi.org/10.3390/en14217388






