Assessing Maximum Power Point Tracking Intelligent Techniques on a PV System with a Buck–Boost Converter
Abstract
:1. Introduction
2. Photovoltaic System
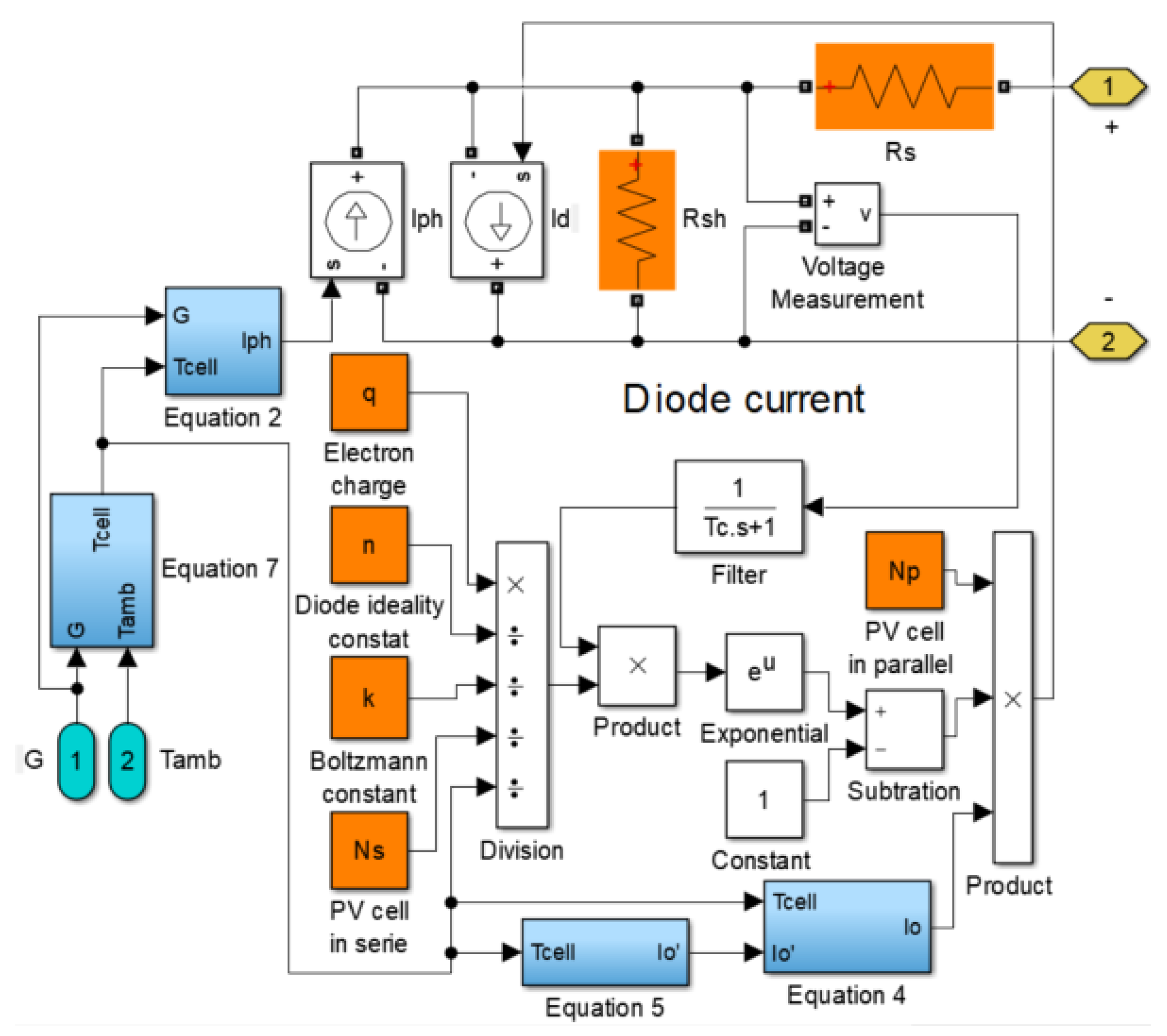
2.1. PV Module Modeling
2.2. Buck–Boost Converter
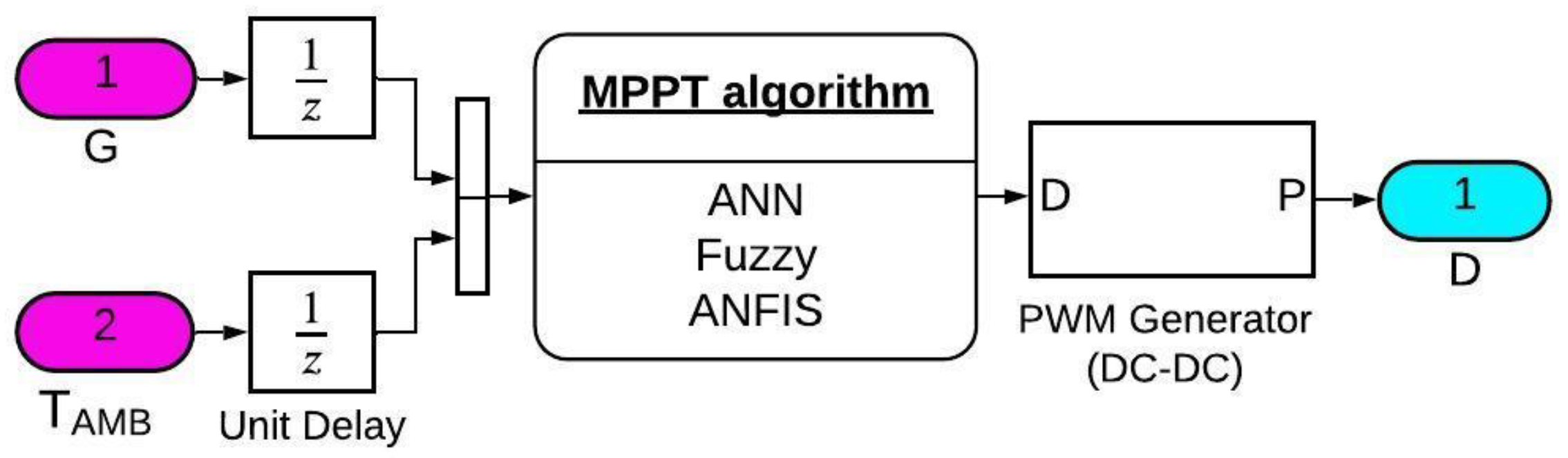
3. Methodology
3.1. MPPT Algorithms Based on ANN
3.2. MPPT Algorithms Based on Fuzzy Logic
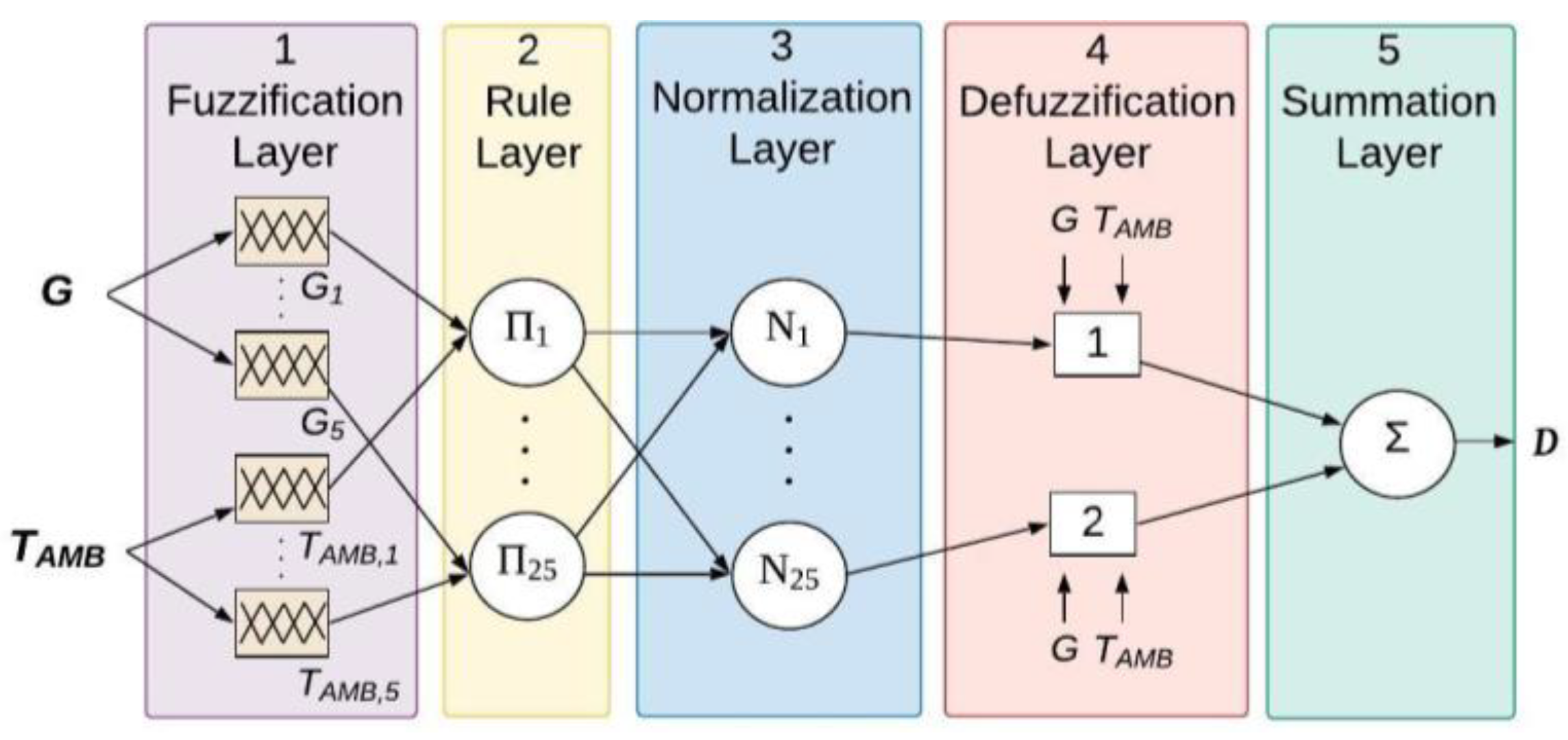
3.3. MPPT Algorithms Based on ANFIS
4. Results and Discussion
4.1. Validation of the Modeled PV System
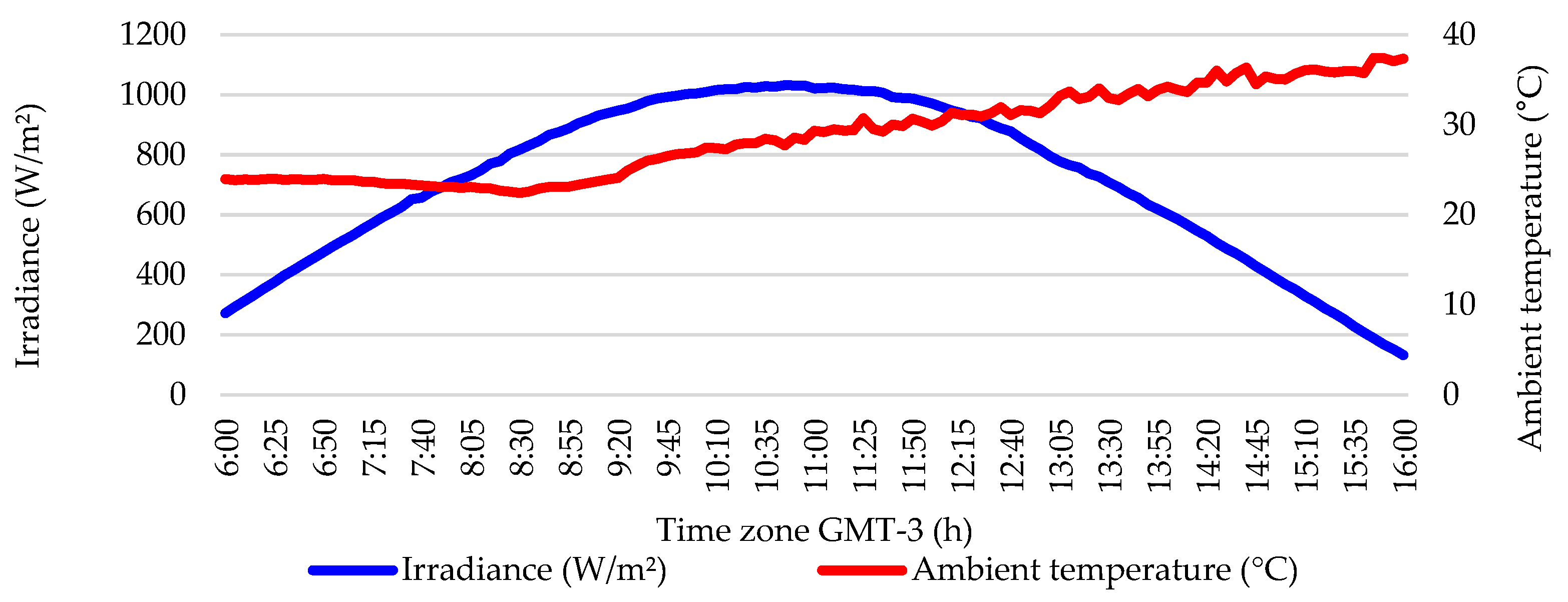
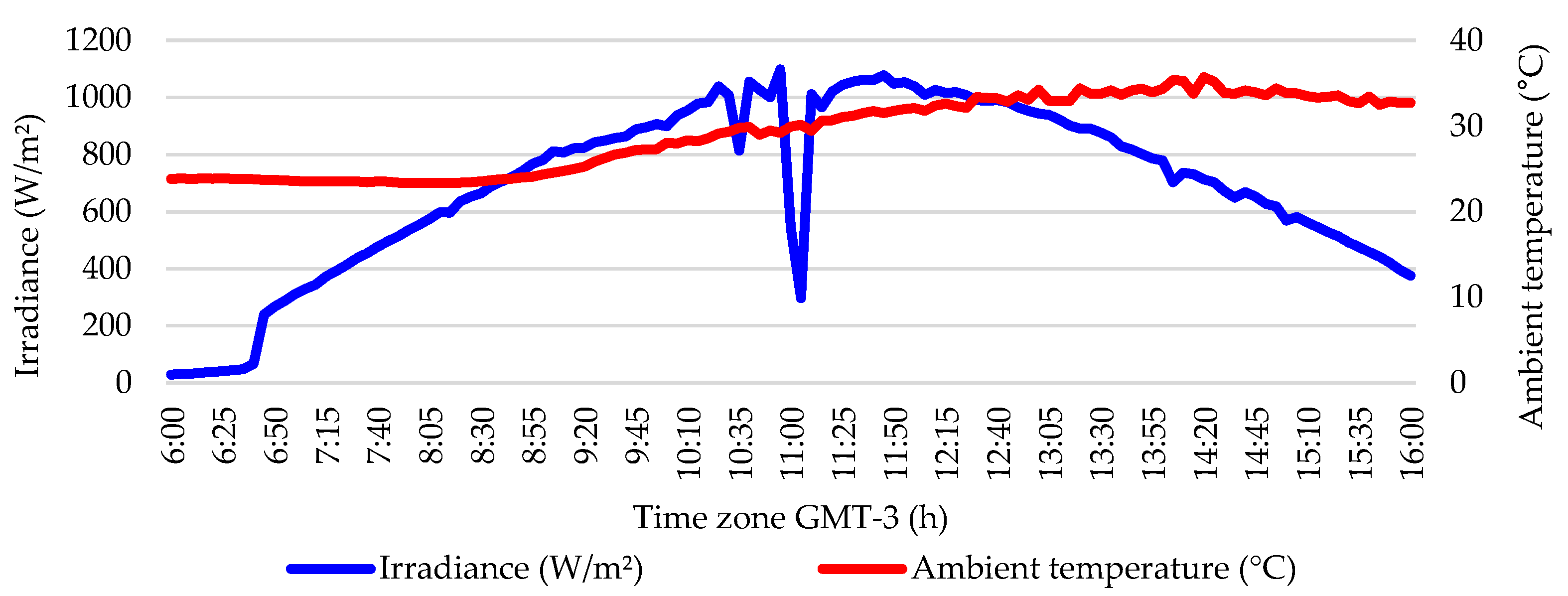
4.2. Definition of Ambient Conditions
4.2.1. Normal Condition
4.2.2. Shading Condition
4.2.3. Forecasting Condition
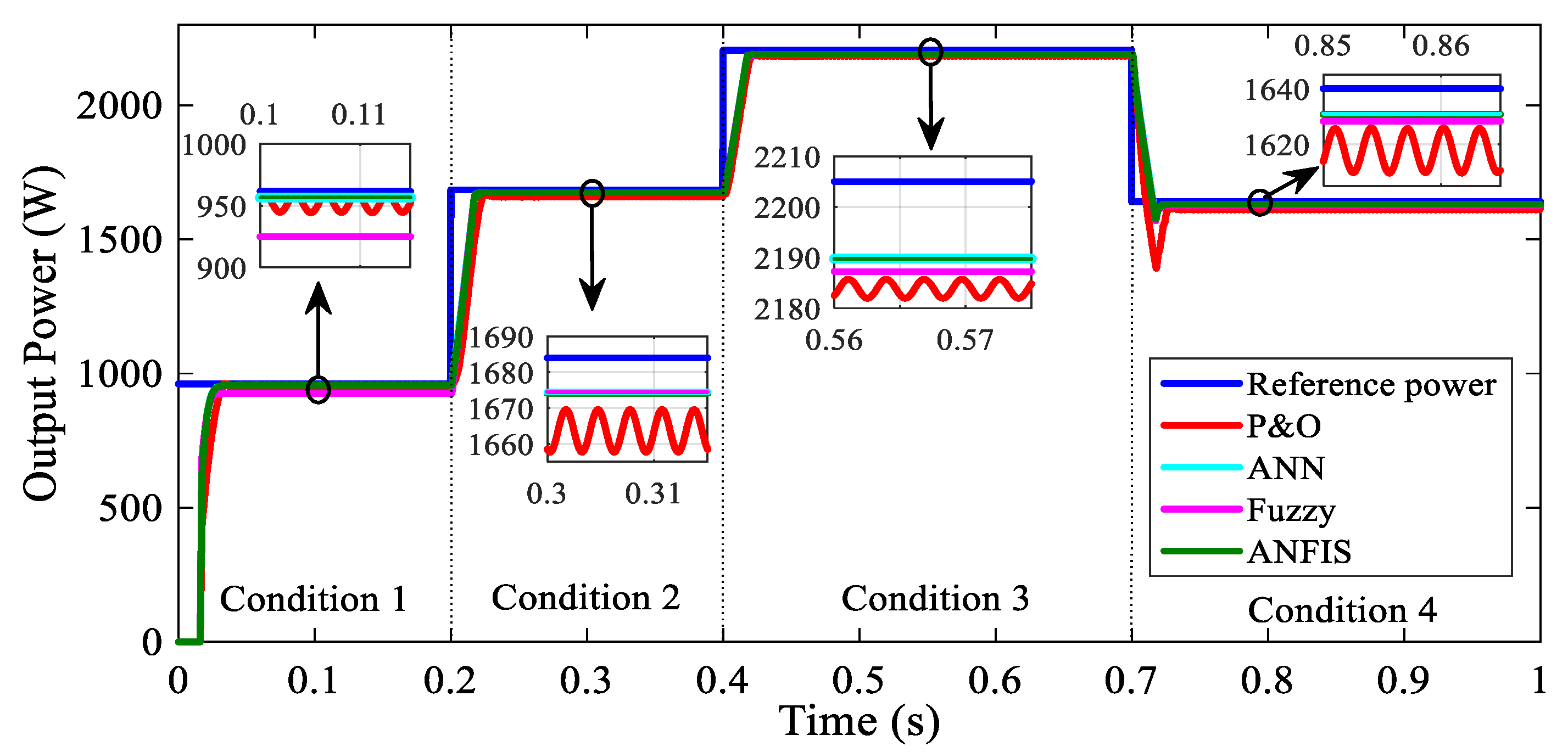
4.3. Dynamic Response Analysis
4.4. Comparative Study
4.5. Estimated Power Generation
5. Conclusions
- The proposed ANN and ANFIS MPPT techniques are considered an improvement of the classic P&O technique. If considering large-scale PV plants, they cause a subsequent increase in power generation.
- For all considered environmental conditions, the PV system with MPPT based on intelligent techniques achieved values close to the expected PMPP. Therefore, these techniques were able to track the MPP with great accuracy.
- A high tracking speed was also observed because the intelligent algorithm localized the true PMPP quickly in every irradiance change.
- Intelligent techniques showed negligible oscillations around the average power value in the steady state, when compared to the classic P&O technique. The amplitude of the oscillation is reflected in the system stability.
- The fuzzy intelligent technique showed less satisfactory results than the ANN and ANFIS techniques. However, more knowledge of the expert operators and a fine adjustment in the fuzzy controller parameters can improve the output power of the PV system with MPPT based on FL.
- Submitting the modeled PV system to ambient conditions of regions close to the Equator line, a more significant power generation was observed when using the ANN and ANFIS intelligent algorithms in the MPPT of the PV system. The power recovery was between 0.40% and 9.9%.
- The power recovery of the PV system with MPPT based on the ANN or ANFIS algorithm exceeded 1% when the ambient condition had a rapidly falling irradiance near noon in the shading condition. Furthermore, the power recovery achieved 9.9% in the forecasting condition (when the solar irradiance changes over time). The better dynamic response of these intelligent algorithms than that of the fuzzy and P&O algorithms justifies this recovery of power generation.
- Among the intelligent techniques simulated in the present paper, the ANN and ANFIS algorithms had a similar response. However, the ANN technique proposed a higher power generation. Moreover, the ANN algorithm has a less complex implementation, and it is more robust to noise.
- Using environmental parameters G and TAMB as input variables has the advantage of being able to track the MPP regardless of the geographic location of the PV system. Moreover, the global maximum power point is followed with high reliability. However, its cost of implementation and applicability remain a challenge due to the increased cost of implanting the sensors.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A

References
- Hanzaei, S.H.; Gorji, S.A.; Ektesabi, M. A Scheme-Based Review of MPPT Techniques With Respect to Input Variables Including Solar Irradiance and PV Arrays’ Temperature. IEEE Access 2020, 8, 182229–182239. [Google Scholar] [CrossRef]
- Sumathi, S.; Ashok Kumar, L.; Surekha, P. Solar PV and Wind Energy Conversion Systems; Springer: Cham, Switerland, 2015; ISBN 978-3-319-14940-0. [Google Scholar]
- Youssef, A.; El-Telbany, M.; Zekry, A. The role of artificial intelligence in photo-voltaic systems design and control: A review. Renew. Sustain. Energy Rev. 2017, 78, 72–79. [Google Scholar] [CrossRef]
- Vieira, G.; Ugulino de Araújo, F.M.; Dhimish, M.; Guerra, M.I.S. A Comprehensive Review on Bypass Diode Application on Photovoltaic Modules. Energies 2020, 13, 2472. [Google Scholar] [CrossRef]
- Enrique, J.M.; Durán, E.; Sidrach-de-Cardona, M.; Andújar, J.M. Theoretical assessment of the maximum power point tracking efficiency of photovoltaic facilities with different converter topologies. Sol. Energy 2007, 81, 31–38. [Google Scholar] [CrossRef]
- Reshma Gopi, R.; Sreejith, S. Converter topologies in photovoltaic applications—A review. Renew. Sustain. Energy Rev. 2018, 94, 1–14. [Google Scholar] [CrossRef]
- Aldobhani, A.M.S.; John, R. Maximum Power Point tracking under Different Environment Conditions for Solar Photovoltaic Panels Using ANFIS Model. J. Sci. Technol. 2007, 12, 31–47. [Google Scholar]
- Aldobhani, A.M.S.; John, R. Maximum Power Point Tracking of PV System Using ANFIS Prediction and Fuzzy Logic Tracking. Lect. Notes Eng. Comput. Sci. 2008, 2169, 1359–1366. [Google Scholar]
- Otieno, C.A.; Nyakoe, G.N.; Wekesa, C.W. A neural fuzzy based maximum power point tracker for a photovoltaic system. In Proceedings of the IEEE AFRICON Conference, Nairobi, Kenya, 23–25 September 2009; IEEE: Nairobi, Kenya, 2009; pp. 1–6. [Google Scholar]
- Panda, A.; Pathak, M.K.; Srivastava, S.P. Fuzzy Intelligent Controller for the Maximum Power Point Tracking of a Photovoltaic Module at Varying Atmospheric Conditions. J. Energy Technol. Policy 2011, 1, 6–9. [Google Scholar]
- Nabipour, M.; Razaz, M.; Seifossadat, S.G.; Mortazavi, S.S. A new MPPT scheme based on a novel fuzzy approach. Renew. Sustain. Energy Rev. 2017, 74, 1147–1169. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A soft computing MPPT for PV system based on Cuckoo Search algorithm. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 558–562. Available online: https://ieeexplore.ieee.org/document/6635669 (accessed on 5 August 2021). [CrossRef]
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P.K. Critical Review on PV MPPT Techniques: Classical, Intelligent and Optimisation. IET Renew. Power Gener. 2020, 14, 1433–1452. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Shiau, J.K.; Lee, M.Y.; Wei, Y.C.; Chen, B.C. Circuit Simulation for Solar Power Maximum Power Point Tracking with Different Buck-Boost Converter Topologies. Energies 2014, 7, 5027–5046. [Google Scholar] [CrossRef] [Green Version]
- Arora, A.; Gaur, P. Comparison of f ANN and ANFIS based MPPT controller for grid connected PV Systems. In Proceedings of the IEEE Indicon 2015, New Delhi, India, 17–20 December 2015; pp. 1–6. [Google Scholar]
- Martin, A.D.; Vazquez, J.R. MPPT algorithms comparison in PV systems: P&O, PI, neuro-fuzzy and backstepping controls. Proc. IEEE Int. Conf. Ind. Technol. 2015, 2015, 2841–2847. [Google Scholar] [CrossRef]
- Belhachat, F.; Larbes, C. Global maximum power point tracking based on ANFIS approach for PV array configurations under partial shading conditions. Renew. Sustain. Energy Rev. 2017, 77, 875–889. [Google Scholar] [CrossRef]
- Karagöz, M.K.; Demİrel, H. A Novel MPPT Method for PV Arrays Based on Modified Bat Algorithm with Partial Shading Capability. Int. J. Comput. Sci. Netw. Secur. 2017, 17, 61–66. [Google Scholar]
- Belhachat, F.; Larbes, C. A review of global maximum power point tracking techniques of photovoltaic system under partial shading conditions. Renew. Sustain. Energy Rev. 2018, 92, 513–553. [Google Scholar] [CrossRef]
- Khanam, J.J.; Foo, S.Y. Modeling of a Photovoltaic Array in MATLAB Simulink and Maximum Power Point Tracking Using Neural Network. J. Electr. Electron. Syst. 2018, 7, 1–8. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.Y. Artificial Intelligence Based MPPT Techniques for Solar Power System: A review. J. Mod. Power Syst. Clean Energy 2020, 8, 1043–1059. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. An Enhanced Adaptive P&O MPPT for Fast and Efficient Tracking Under Varying Environmental Conditions. IEEE Trans. Sustain. Energy 2018, 9, 1487–1496. [Google Scholar] [CrossRef]
- Ahmad, R.; Murtaza, A.F.; Sher, H.A. Power tracking techniques for efficient operation of photovoltaic array in solar applications—A review. Renew. Sustain. Energy Rev. 2019, 101, 82–102. [Google Scholar] [CrossRef]
- Kumar, J.; Rathor, B.; Bahrani, P. Fuzzy and P&O MPPT techniques for stabilized the efficiency of solar PV system. In Proceedings of the 2018 International Conference on Computing, Power and Communication Technologies (GUCON), Greater Noida, India, 28–29 September 2018; pp. 259–264. Available online: https://ieeexplore.ieee.org/document/8674909 (accessed on 10 August 2021). [CrossRef]
- Andrew-Cotter, J.; Uddin, M.N.; Amin, I.K. Particle Swarm Optimization based Adaptive Neuro-Fuzzy Inference System for MPPT Control of a Three-Phase Grid-Connected Photovoltaic System. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 2089–2094. [Google Scholar]
- Rajavel, A.; Rathina Prabha, N. Fuzzy logic controller-based boost and buck-boost converter for maximum power point tracking in solar system. Trans. Inst. Meas. Control 2021, 43, 945–957. [Google Scholar] [CrossRef]
- Leite, A.C.Q.B.; Salazar, A.O.; Carvalho, J.T. Maximum power point tracker based digital one cycle control applied in PV systems. Renew. Energy Power Qual. J. 2017, 1, 239–244. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Bayhan, H.; Bayhan, M. A simple approach to determine the solar cell diode ideality factor under illumination. Sol. Energy 2011, 85, 769–775. [Google Scholar] [CrossRef]
- Simon, M.; Meyer, E.L. Detection and analysis of hot-spot formation in solar cells. Sol. Energy Mater. Sol. Cells 2010, 94, 106–113. [Google Scholar] [CrossRef]
- Masters, G.M. Renewable and Efficient Electric Power Systems; Wiley-Interscience, John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 3175723993. [Google Scholar]
- Yingli Solar Datasheet YGE 60 Células Série 2; Yingli Green Energy do Brasil, S.A.: Brazil 2015, 2; Available online: https://www.neosolar.com.br/loja/fileuploader/download/download/?d=0&file=custom%2Fupload%2FFile-1438699024.pdf (accessed on 6 April 2021).
- Lappalainen, K.; Manganiello, P.; Piliougine, M.; Spagnuolo, G.; Valkealahti, S. Virtual Sensing of Photovoltaic Module Operating Parameters. IEEE J. Photovolt. 2020, 10, 852–862. [Google Scholar] [CrossRef]
- Spagnuolo, G.; Lappalainen, K.; Valkealaht, S.; Manganiello, P. Photovoltaic Module Parametric Identification. In Proceedings of the 2019 International Conference on Clean Electrical Power (ICCEP), Otranto, Italy, 2–4 July 2019; pp. 302–305. [Google Scholar] [CrossRef] [Green Version]
- Karatepe, E.; Boztepe, M.; Çolak, M. Development of a suitable model for characterizing photovoltaic arrays with shaded solar cells. Sol. Energy 2007, 81, 977–992. [Google Scholar] [CrossRef]
- Vieira, R.G.; Dhimish, M.; Ugulino de Araújo, F.M.; Guerra, M.I.S. PV module fault detection using combined artificial neural network and sugeno fuzzy logic. Electronics 2020, 9, 2150. [Google Scholar] [CrossRef]
- Gupta, A.; Chauhan, Y.K.; Pachauri, R.K. A comparative investigation of maximum power point tracking methods for solar PV system. Sol. Energy 2016, 136, 236–253. [Google Scholar] [CrossRef]
- Lamamra, K.; Batat, F.; Mokhtari, F. A new technique with improved control quality of nonlinear systems using an optimized fuzzy logic controller. Expert Syst. Appl. 2020, 145, 113148. [Google Scholar] [CrossRef]
- Meharrar, A.; Tioursi, M.; Hatti, M.; Boudghne Stambouli, A. A variable speed wind generator maximum power tracking based on adaptative neuro-fuzzy inference system. Expert Syst. Appl. 2011, 38, 7659–7664. [Google Scholar] [CrossRef]
- Kordos, M.; Rusiecki, A. Reducing noise impact on MLP training: Techniques and algorithms to provide noise-robustness in MLP network training. Soft Comput. 2016, 20, 49–65. [Google Scholar] [CrossRef] [Green Version]
- Yahyaoui, I. Advances in Renewable Energies and Power Technologies; Elsevier: Kidlington, UK, 2018; ISBN 9781626239777. [Google Scholar]
- Mohamed, S.A.; Tolba, M.A.; Eisa, A.A.; El-Rifaie, A.M. Comprehensive modeling and control of grid-connected hybrid energy sources using MPPT controller. Energies 2021, 14, 5142. [Google Scholar] [CrossRef]







| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|---|---|
| VOC | 37.5 V | kV | −0.1248 V/K | NP | 1 | VMPP | 29.6 V |
| ISC | 8.83 A | NOCT | 46 °C | PMPP | 245 W | RSH | 404.1 Ω |
| ki | 0.004415 A/K | NS | 60 | IMPP | 8.26 A | RS | 0.411 Ω |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| PV module | 14 | VOUT = VR | 480 V | C1 = C2 | |
| PMPP | 3430 W | R | 67.15 Ω | f | 50 kHz |
| VIN = VMPP | 414.4 V | L | 5.6 mH | ∆IMAX = ∆VMAX (Ripple) | 10% |
| Parameter | Data | Parameter | Data |
|---|---|---|---|
| Network type | Multilayer Perceptron | Number of neurons | (5,1) |
| Training algorithm | Levenberg–Marquardt | Activation function | (tansigmoid, pureline) |
| Inputs | [G TAMB] | Number of samples in dataset | 77 |
| Outputs | [D] | Epochs | 9 |
| Number of layers | 2 | MSE | |
| R2 | 1 |
| Input 2 | 15 [15 15 20] | 20 [15 20 25] | 25 [20 25 30] | 30 [25 30 35] | 35 [30 35 40] | 40 [35 40 45] | 45 [40 45 45] | |
|---|---|---|---|---|---|---|---|---|
| Input 1 | ||||||||
| 100 [100 100 200] | LO | LO | LO | LO | LO | LO | LO | |
| 200 [100 200 300] | LO | ML | ML | ML | ML | ML | ML | |
| 300 [200 300 400] | ML | ML | ML | ML | M | M | M | |
| 400 [300 400 500] | M | M | M | M | M | M | M | |
| 500 [400 500 600] | M | M | M | M | MH | MH | MH | |
| 600 [500 600 700] | MH | MH | MH | MH | MH | MH | MH | |
| 700 [600 700 800] | MH | MH | MH | MH | MH | MH | MH | |
| 800 [700 800 900] | MH | MH | MH | H | H | H | H | |
| 900 [800 900 1000] | H | H | H | H | H | H | H | |
| 1000 [900 1000 1100] | H | H | H | H | H | H | H | |
| 110 [1000 1100 1100] | H | H | H | H | H | H | H | |
| Parameter | Data | Parameter | Data | Parameter | Data |
|---|---|---|---|---|---|
| Type | Mamdani | Number of rules | 77 | Output range | [0.2582 0.6193] LO = [0.2583 0.3 0.34] ML = [0.331 0.3897 0.41] M = [0.4028 0.44 0.475] MH = [0.47 0.5085 0.547] H = [0.54 0.58 0.6195] |
| Inputs | [G TAMB] | Type of input MF | trimf | ||
| Output | [D] | Type of output MF | trimf | ||
| Number of input MFs | [11 7] | Input range 1 | [100 1100] | ||
| Number of output MFs | 5 | Input range 2 | [15 45] |
| Parameters | Data | Parameters | Data |
|---|---|---|---|
| Type | Sugeno | Type of output MF | constant |
| Inputs | [G TAMB] | Input range 1 | [100 1100] |
| Output | [D] | Input range 2 | [15 45] |
| Number of input MFs | [5 5] | Output range | [0.2582 0.6193] |
| Number of output MFs | 25 | Training | hybrid |
| Number of rules | 25 | Iterations | 3 |
| Type of input MF | trimf |
| Conditions | Ambient Conditions | Real System | Simulated System | ||
|---|---|---|---|---|---|
| G (W/m2) | TAMB (°C) | Pmeasured (W) | PMPP,simulation (W) | e% | |
| 1 | 294 | 23.86 | 919.25 | 935.2 | 1.73 |
| 2 | 303 | 31.74 | 906.83 | 893.9 | 1.43 |
| 3 | 548 | 24.65 | 1664.60 | 1629.0 | 2.14 |
| 4 | 868 | 31.46 | 2099.38 | 2105.0 | 0.27 |
| 5 | 957 | 31.41 | 2198.76 | 2223.0 | 1.10 |
| 6 | 1134 | 30.17 | 2397.52 | 2438.0 | 1.69 |
| Condition | G (W/m2) | TAMB (°C) | PMPP (W) |
|---|---|---|---|
| Condition 1 | 303 | 24 | 961.5 |
| Condition 2 | 631 | 32 | 1684.0 |
| Condition 3 | 957 | 32 | 2205.0 |
| Condition 4 | 548 | 24 | 1640.0 |
| Condition | ts (ms) | ∆P (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| P&O | ANN | FUZZY | ANFIS | P&O | ANN | FUZZY | ANFIS | |
| 1 | 29.16 | 23.44 | 22.24 | 23.54 | 0.57325 | 0.00020 | 0.00012 | 0.00016 |
| 2 | 19.90 | 15.60 | 15.70 | 15.8 | 0.33984 | 0.00031 | 0.00012 | 0.00028 |
| 3 | 15.70 | 14.10 | 14.10 | 14.3 | 0.00872 | 0.00023 | 0.00012 | 0.00026 |
| 4 | 22.50 | 13.40 | 13.20 | 13.0 | 0.22308 | 0.00011 | 0.00013 | 0.00013 |
| Condition | PMPP (W) | P&O | ANN | FUZZY | ANFIS | ||||
|---|---|---|---|---|---|---|---|---|---|
| PP&O (W) | e% | PANN (W) | e% | PFUZZY (W) | e% | PANFIS (W) | e% | ||
| 1 | 961.5 | 951.6 | 1.03 | 956.5 | 0.52 | 924.9 | 3.81 | 956.6 | 0.51 |
| 2 | 1684.0 | 1664.0 | 1.19 | 1674.0 | 0.59 | 1674.0 | 0.59 | 1674.0 | 0.59 |
| 3 | 2205.0 | 2184.0 | 0.95 | 2190.0 | 0.68 | 2187.0 | 0.82 | 2190.0 | 0.68 |
| 4 | 1640.0 | 1618.0 | 1.34 | 1631.0 | 0.55 | 1628.0 | 0.73 | 1631.0 | 0.55 |
| Reference | Algorithm | Settling Time (ms) | Accuracy (%) | Experimentally Tested | Dataset |
|---|---|---|---|---|---|
| Proposed research | ANN | 13.40–23.44 | 99.32–99.48 | No | 77 |
| Fuzzy | 13.20–22.24 | 96.19–99.41 | |||
| ANFIS | 13.00–23.54 | 99.32–99.49 | |||
| Aldobhani and John [7,8] | ANFIS | - | 98–99 | No | 39 |
| Panda, Pathak, and Srivastava [10] | Fuzzy | 12.20 | - | No | - |
| Arora and Gaur [16] | ANN | 125.00 | 99.83 | No | 300,001 |
| ANFIS | 105.00 | 100 | |||
| Martin and Vazquez [17] | Fuzzy | - | 98.2 | Yes | - |
| ANFIS | - | 98.2 | |||
| Belhachat and Larbes [18] | ANFIS | - | 99.92 | No | - |
| Andrew-Cotter, Uddin, and Amin [26] | ANFIS | - | 97 | No | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerra, M.I.S.; Ugulino de Araújo, F.M.; Dhimish, M.; Vieira, R.G. Assessing Maximum Power Point Tracking Intelligent Techniques on a PV System with a Buck–Boost Converter. Energies 2021, 14, 7453. https://doi.org/10.3390/en14227453
Guerra MIS, Ugulino de Araújo FM, Dhimish M, Vieira RG. Assessing Maximum Power Point Tracking Intelligent Techniques on a PV System with a Buck–Boost Converter. Energies. 2021; 14(22):7453. https://doi.org/10.3390/en14227453
Chicago/Turabian StyleGuerra, Maria I. S., Fábio M. Ugulino de Araújo, Mahmoud Dhimish, and Romênia G. Vieira. 2021. "Assessing Maximum Power Point Tracking Intelligent Techniques on a PV System with a Buck–Boost Converter" Energies 14, no. 22: 7453. https://doi.org/10.3390/en14227453
APA StyleGuerra, M. I. S., Ugulino de Araújo, F. M., Dhimish, M., & Vieira, R. G. (2021). Assessing Maximum Power Point Tracking Intelligent Techniques on a PV System with a Buck–Boost Converter. Energies, 14(22), 7453. https://doi.org/10.3390/en14227453








