Numerical and Experimental Investigation of Wire Cloth Heat Exchanger for Latent Heat Storages
Abstract
:1. Introduction
2. Materials and Methods
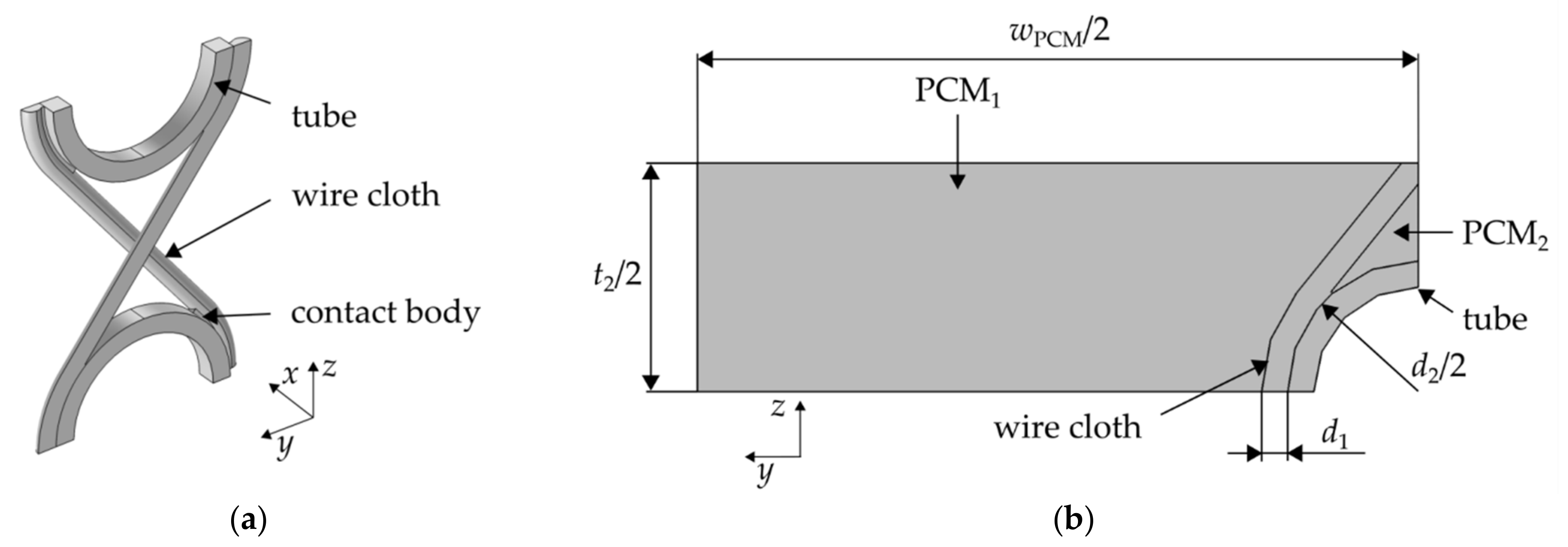
2.1. Wire Cloth Heat Exchanger
2.2. Phase Change Material
2.3. Performance Parameter
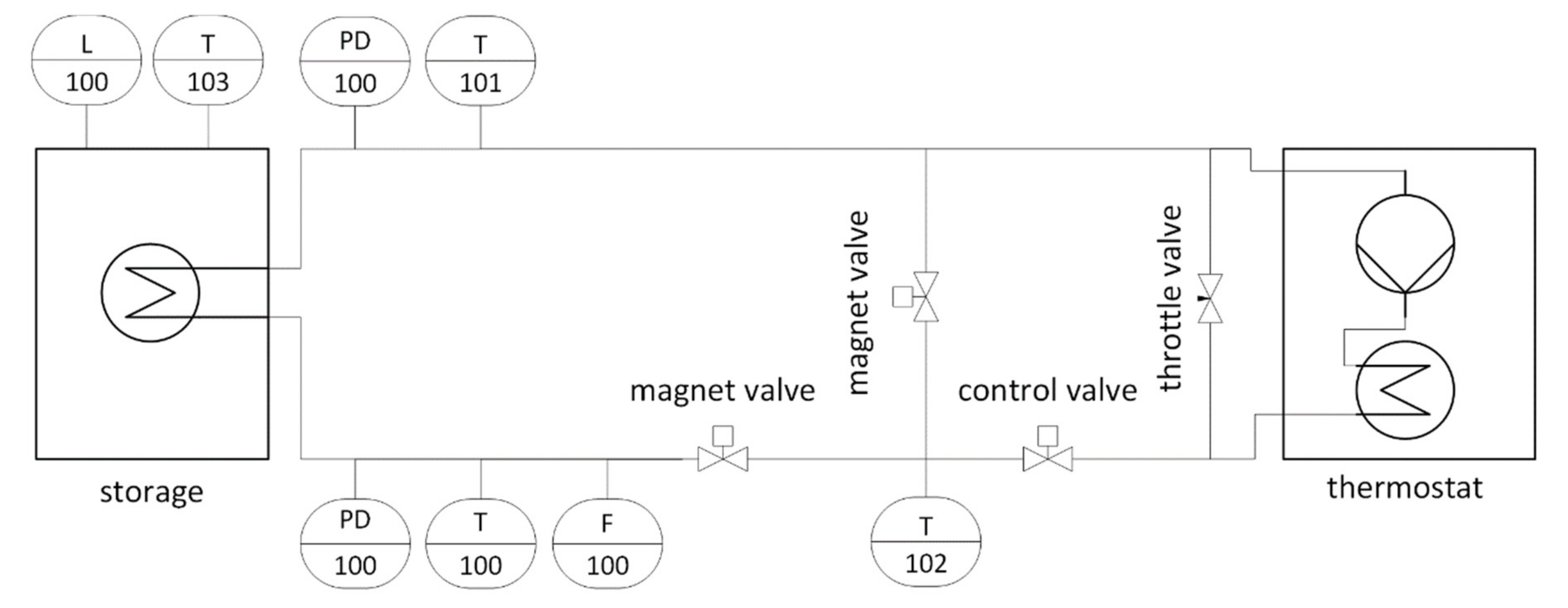
2.4. Experimental Setup
2.4.1. Storage System
2.4.2. Test Facility
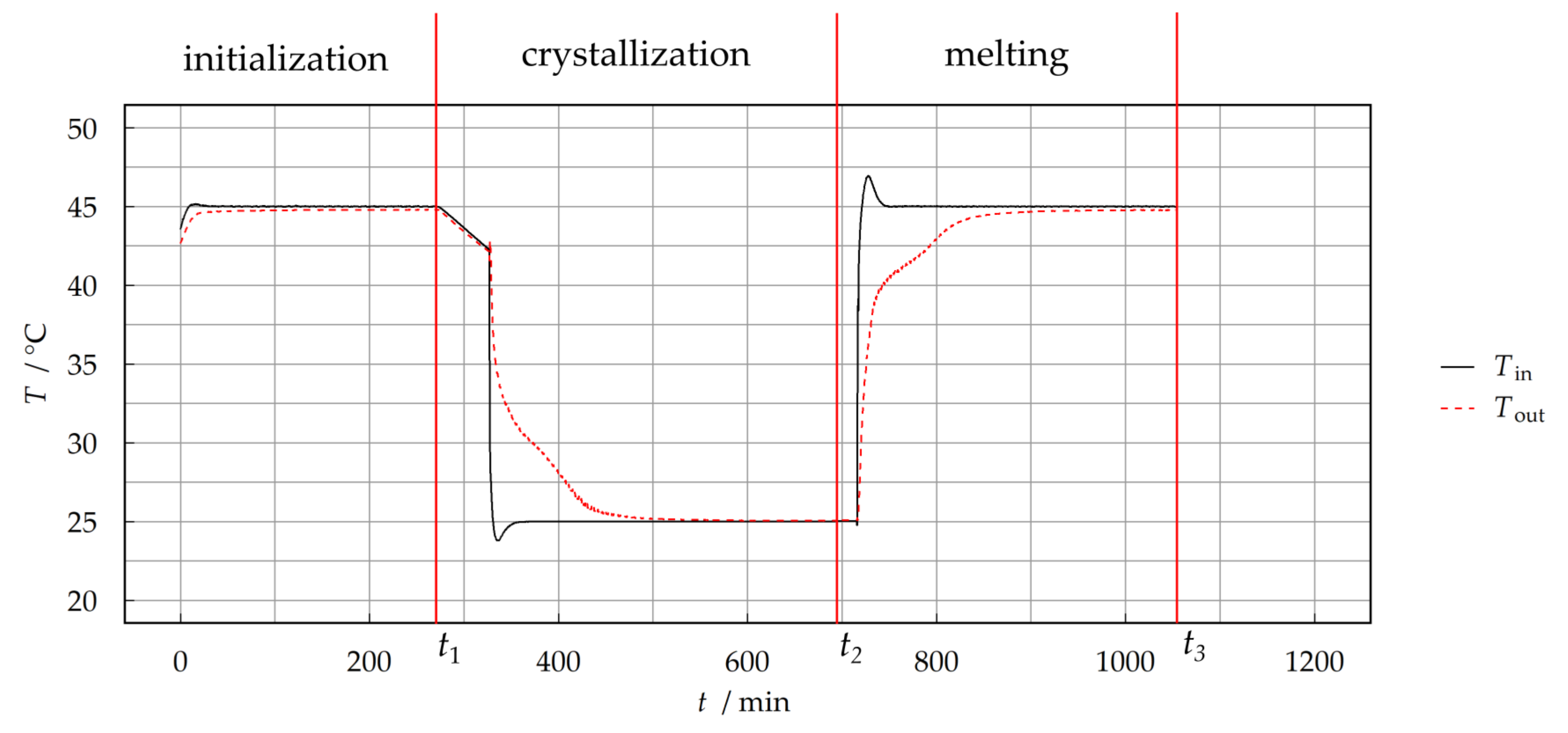
2.4.3. Measurement Procedure
2.4.4. Determination of Heat Losses
2.5. Model Description
- Volumetric expansion of the PCM during phase change is neglected.
- The PCM is treated as a solid body for both the solid and the liquid state.
- The heat transfer in PCM is based on heat conduction only.
- Natural convection is considered by an enhanced thermal conductivity method.
- Fully developed flow in the micro tubes.
- Negligible thermal gradient within the HTF perpendicular to flow direction, thus, 1D modeling is possible.
- Constant properties of HTF.
- Heat transfer between HTF and tube wall is defined by Nusselt—correlation from literature for constant wall temperature.
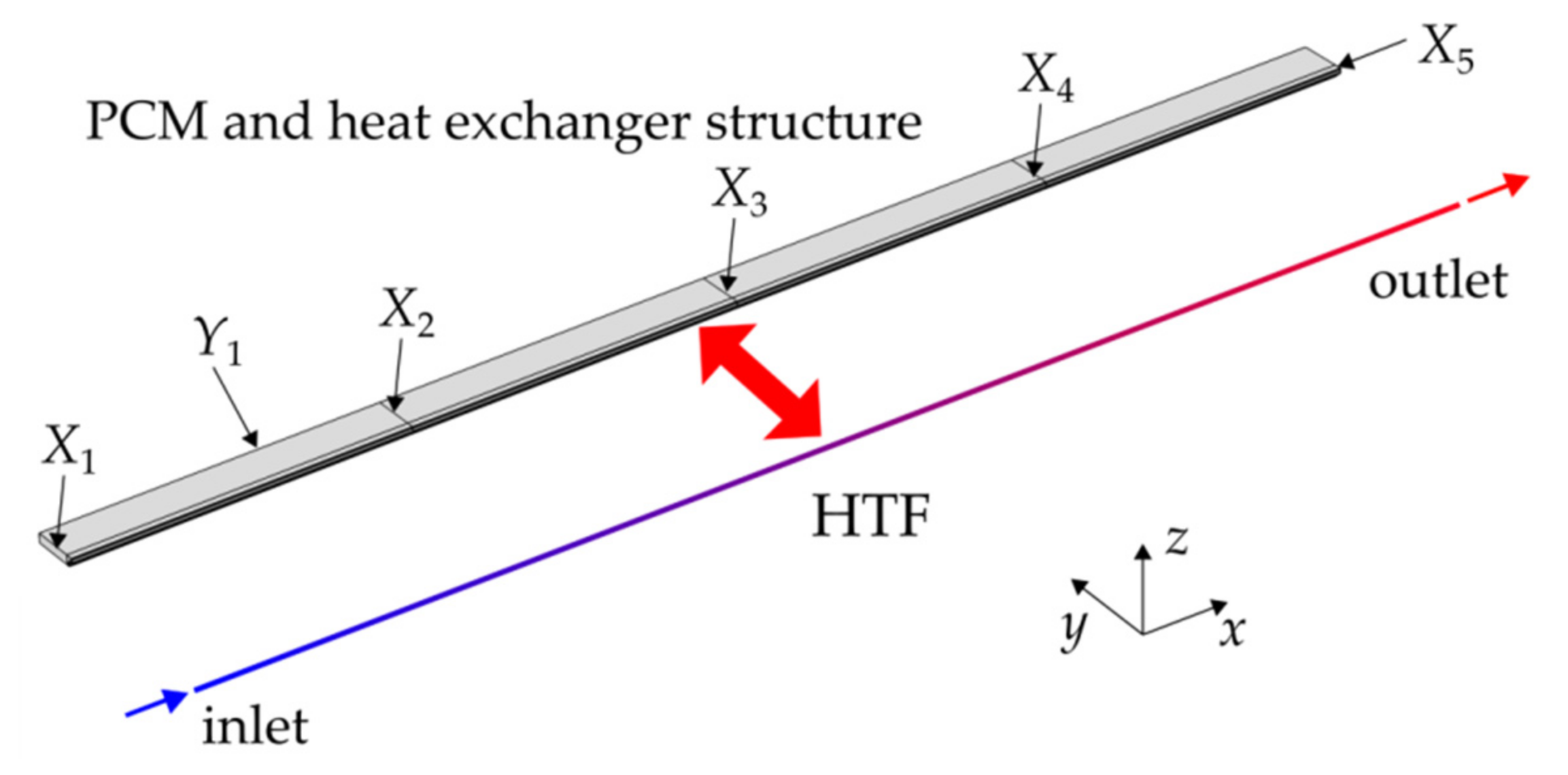
2.5.1. Geometry
2.5.2. Governing Equations
2.5.3. Boundary Conditions Validation Model
2.5.4. Simplification for Performance Evaluation Model
- Neglection of heat transfer in -direction;
- Constant HTF temperature;
- Neglection of heat losses;
- Neglection of auxiliary components like storage container and connection hoses.
2.5.5. Modeling of Phase Change
2.5.6. Discretization
3. Results and Discussion
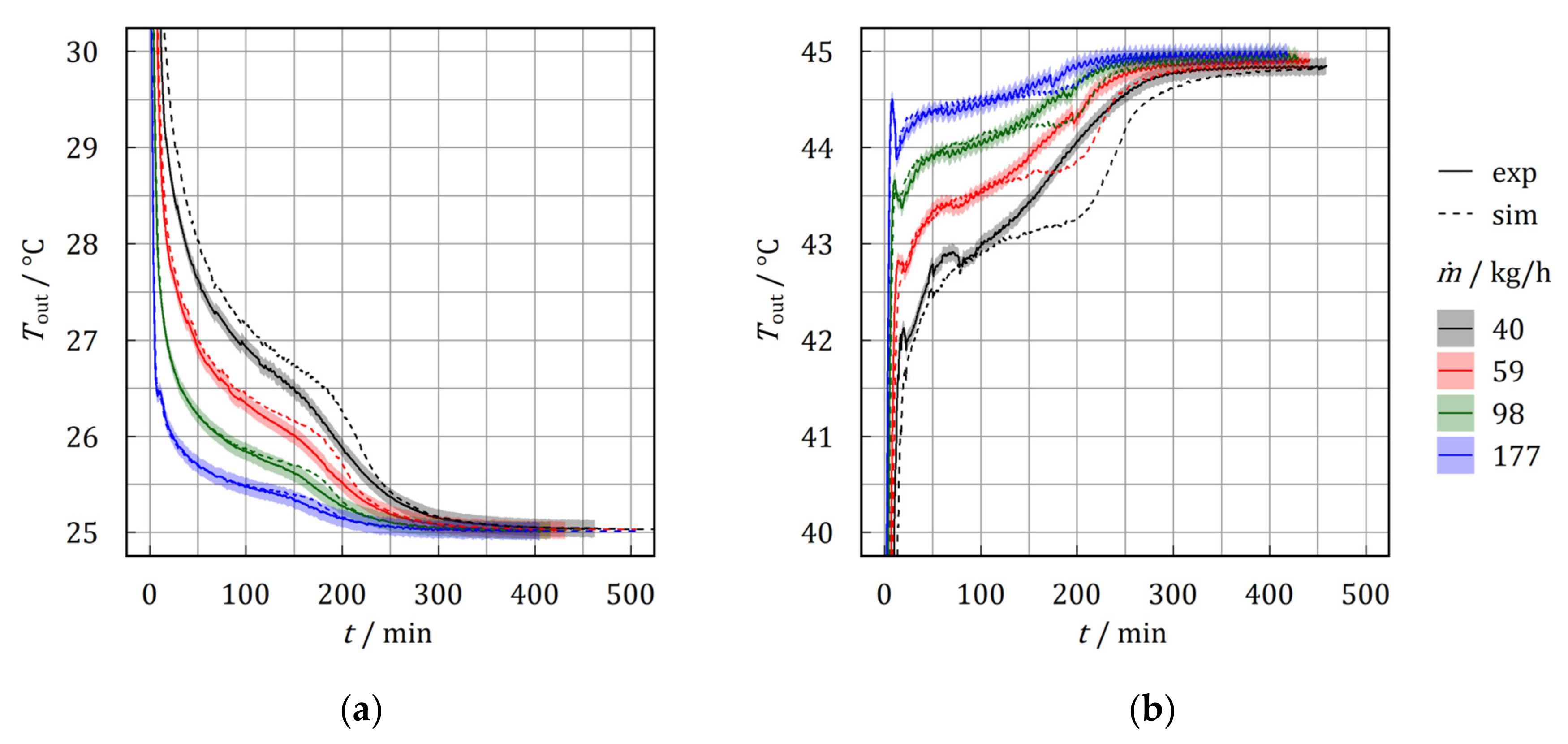
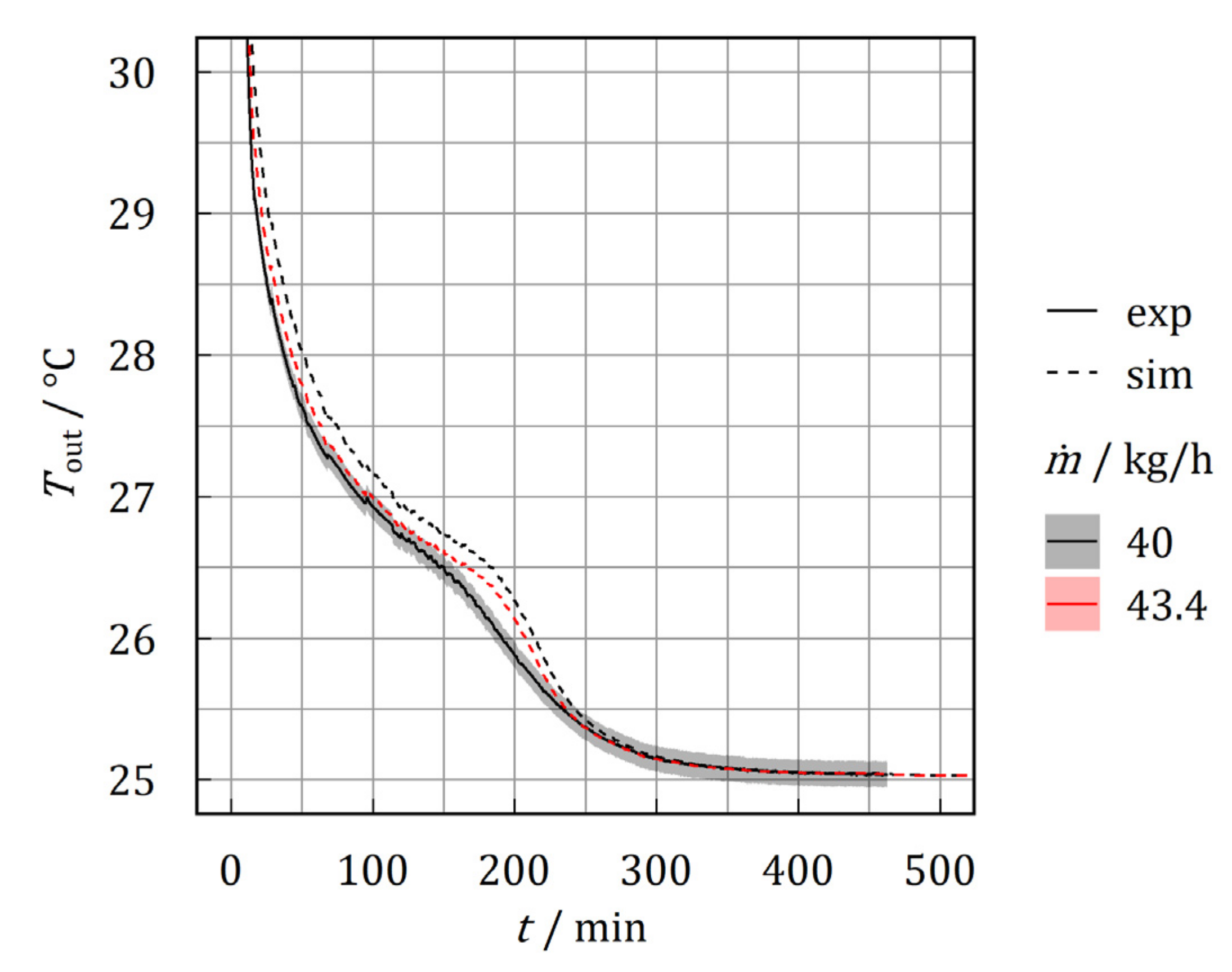
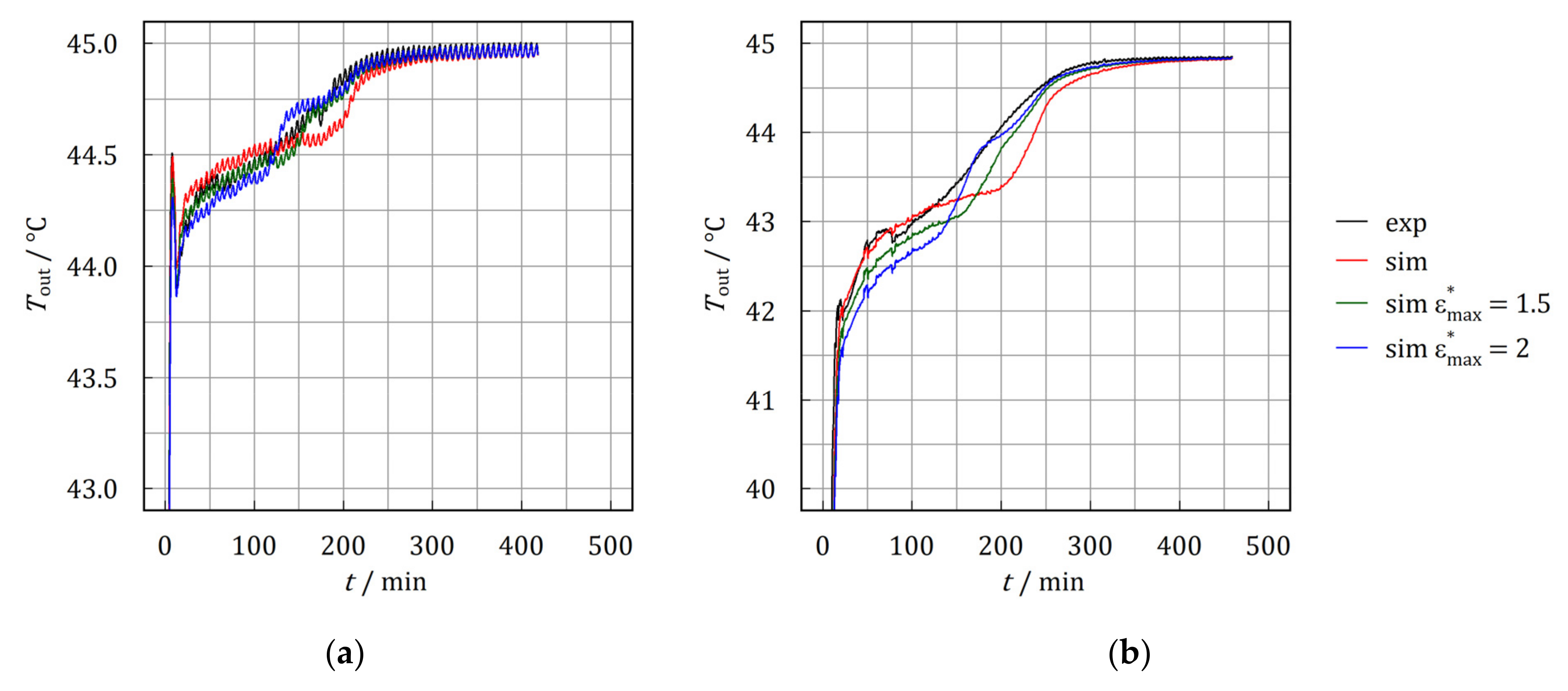
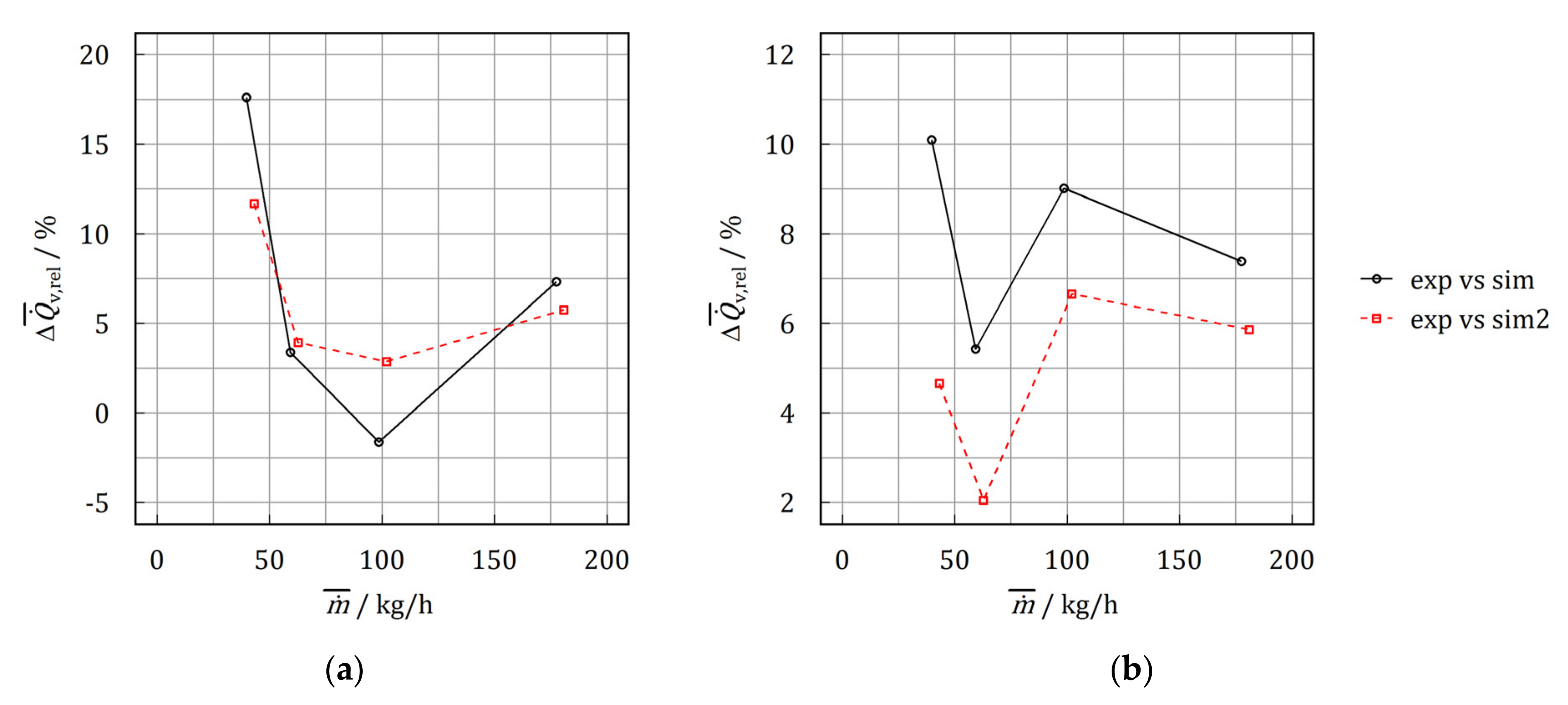
3.1. Model Validation
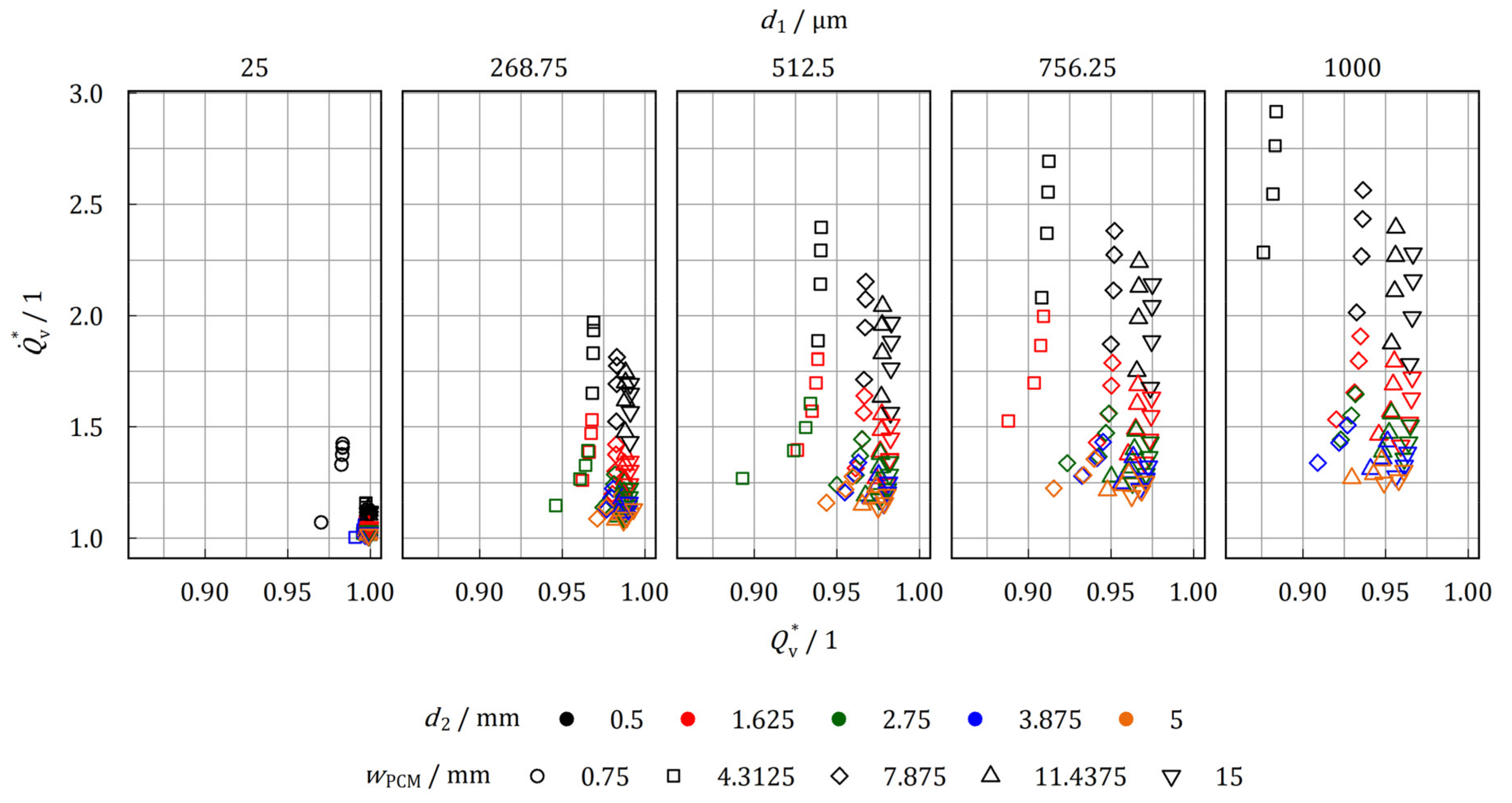
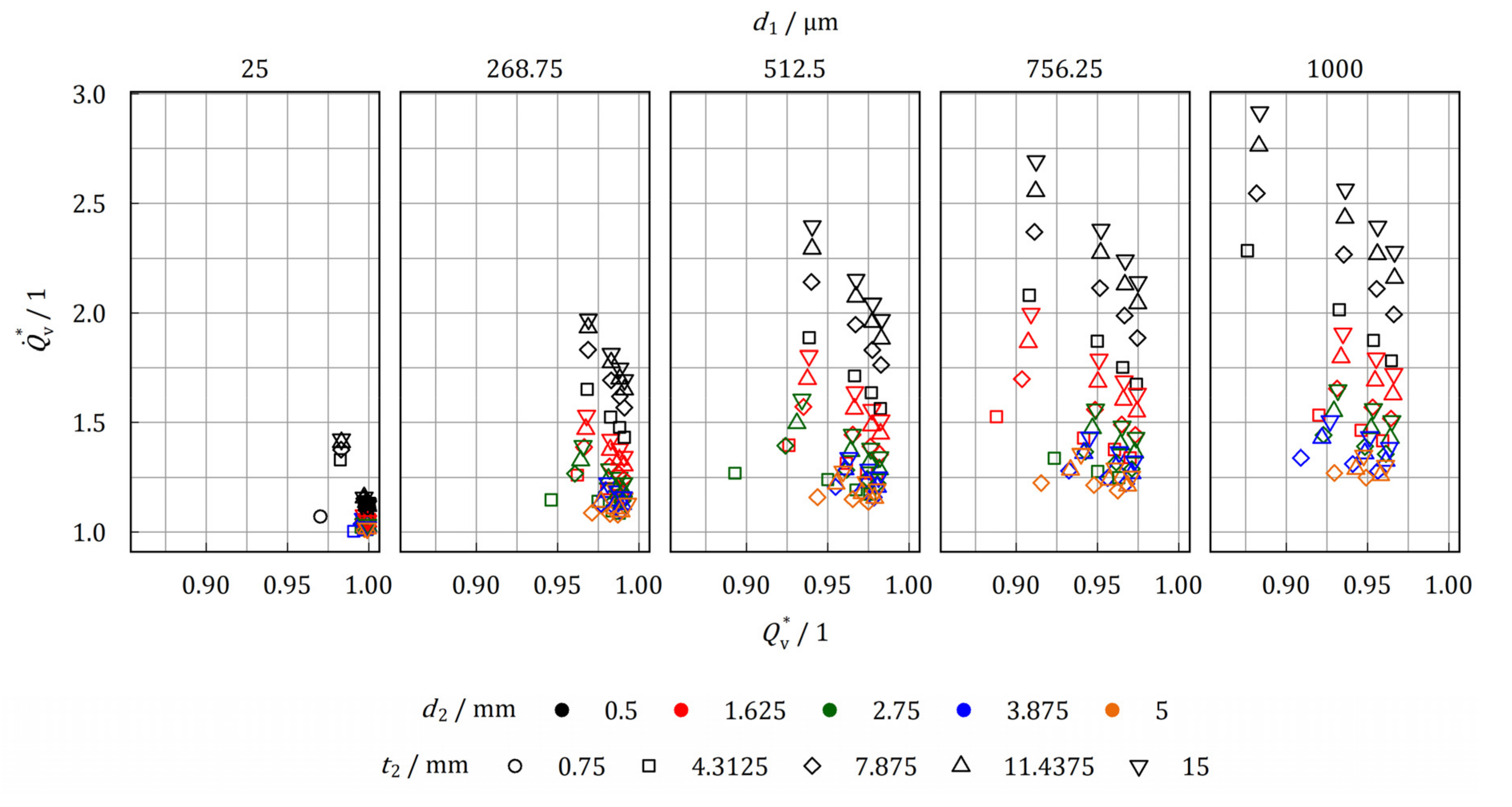
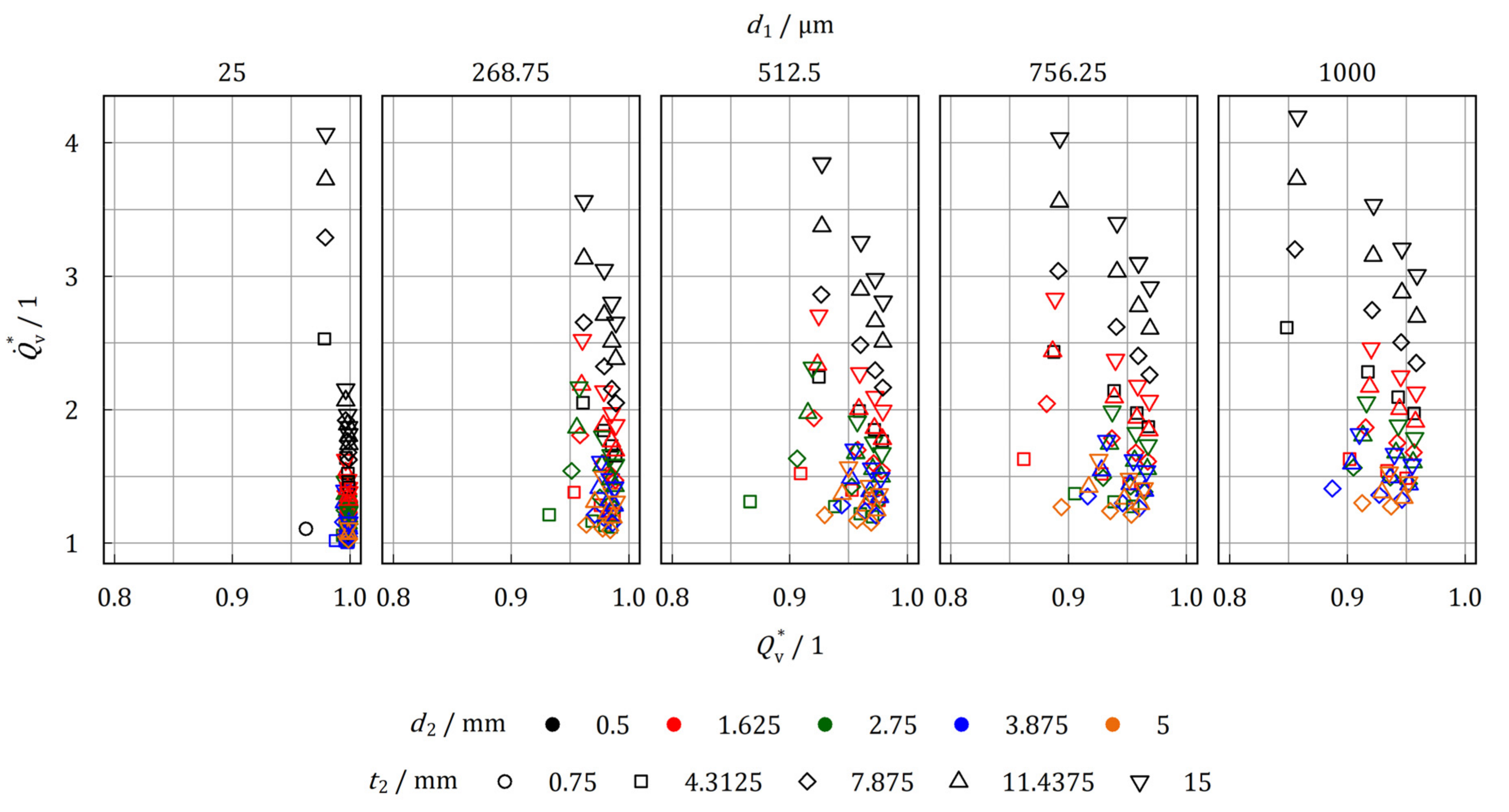
3.2. Performance Evaluation
3.2.1. Wire Cloth Heat Exchanger
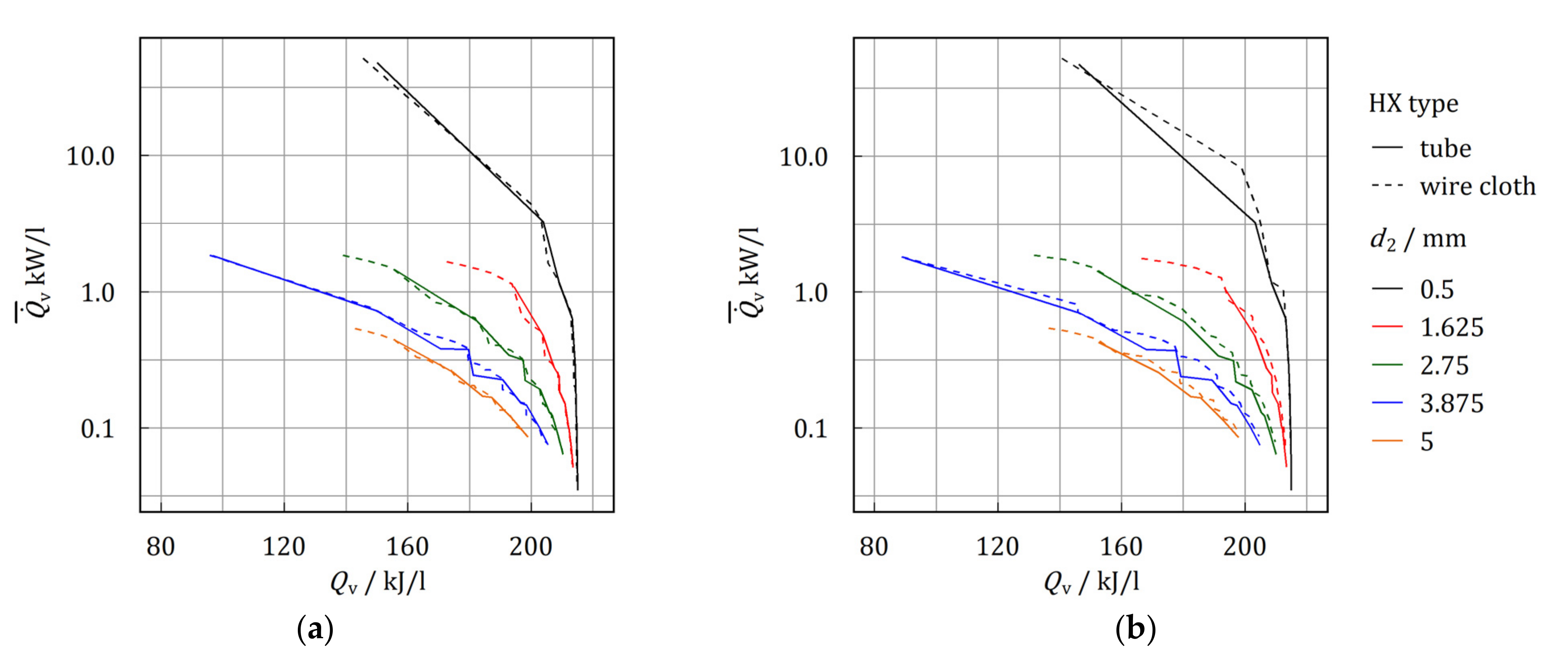
3.2.2. Comparison Wire Cloth and Tube Bundle Heat Exchanger
4. Discussion
5. Conclusions
- In this work, we evaluated planar wire cloth heat exchanger for the application in LTES with the Paraffin RT35HC as PCM. The wire cloth structure is investigated the first time for LTES. For the investigation, we developed and validated FEM models for crystallization and melting of the PCM. For the performance evaluation wire cloth heat exchanger are compared to tube bundle heat exchanger. The main conclusion is as follows: Wire cloth heat exchangers offer a high heat transfer area, small volume fraction of the heat exchanger, high pressure stability and are applicable for corrosive PCMs if they were made from stainless steel.
- A correction method for heat losses for experimental characterization of latent thermal energy storages based on stationary periods before and after the phase change period is introduced.
- Developed models are validated for parallel arranged of heat exchangers with maximum mean RMSE for crystallization and melting of 0.39 and 0.48 K, respectively. The deviation of the mean volumetric thermal power is within a range of 11.7 and 2.0%.
- Compared to tube bundle heat exchanger of equal tube arrangement the wire cloth can increase the thermal power by a maximum factor of 4.20, whereas the storage capacity is reduced to a minimum factor of 0.85.
- Comparing the Pareto-optimal configurations for high power and high storage capacity, the wire cloth heat exchanger performs similarly to tube bundle heat exchanger for stainless steel as heat exchanger material. There are benefits for the wire cloth if aluminum is used.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mehling, H.; Cabeza, L.F. Heat and Cold Storage with PCM: An up to Date Introduction into Basics and Applications; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-68556-2. [Google Scholar]
- Jegadheeswaran, S.; Pohekar, S.D. Performance enhancement in latent heat thermal storage system: A review. Renew. Sustain. Energy Rev. 2009, 13, 2225–2244. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, Z.; Ghafoor, A. A review of performance enhancement of PCM based latent heat storage system within the context of materials, thermal stability and compatibility. Energy Convers. Manag. 2016, 115, 132–158. [Google Scholar] [CrossRef]
- Liu, M.; Saman, W.; Bruno, F. Review on storage materials and thermal performance enhancement techniques for high temperature phase change thermal storage systems. Renew. Sustain. Energy Rev. 2012, 16, 2118–2132. [Google Scholar] [CrossRef]
- Neumann, H.; Gamisch, S.; Gschwander, S. Comparison of RC-model and FEM-model for a PCM-plate storage including free convection. Appl. Therm. Eng. 2021, 196, 117232. [Google Scholar] [CrossRef]
- Saeed, R.M.; Schlegel, J.P.; Sawafta, R.; Kalra, V. Plate type heat exchanger for thermal energy storage and load shifting using phase change material. Energy Convers. Manag. 2019, 181, 120–132. [Google Scholar] [CrossRef]
- Johnson, M.; Fiss, M.; Klemm, T.; Eck, M. Test and Analysis of a Flat Plate Latent Heat Storage Design. Energy Procedia 2014, 57, 662–671. [Google Scholar] [CrossRef] [Green Version]
- Johnson, M. Experimental Testing of Various Heat Transfer Structures in a Flat Plate Thermal Energy Storage Unit. In AIP Conference Proceedings; AIP Publishing LLC: Huntington, NY, USA, 2016; Volume 1734, p. 050022. [Google Scholar]
- Agyenim, F.; Eames, P.; Smyth, M. A comparison of heat transfer enhancement in a medium temperature thermal energy storage heat exchanger using fins. Solar Energy 2009, 83, 1509–1520. [Google Scholar] [CrossRef]
- Gil, A.; Barreneche, C.; Moreno, P.; Solé, C.; Inés Fernández, A.; Cabeza, L.F. Thermal behaviour of d-mannitol when used as PCM: Comparison of results obtained by DSC and in a thermal energy storage unit at pilot plant scale. Appl. Energy 2013, 111, 1107–1113. [Google Scholar] [CrossRef]
- Gil, A.; Oró, E.; Castell, A.; Cabeza, L.F. Experimental analysis of the effectiveness of a high temperature thermal storage tank for solar cooling applications. Appl. Therm. Eng. 2013, 54, 521–527. [Google Scholar] [CrossRef]
- Laing, D.; Bauer, T.; Steinmann, W.-D.; Lehmann, D. Advanced High Temperature Latent Heat Storage System—Design and Test Results. In Proceedings of the 11th International Conference on Thermal Energy Storage (Effstock 2009), Stockholm, Sweden, 14–17 June 2009. [Google Scholar]
- Anish, R.; Mariappan, V.; Mastani Joybari, M. Experimental investigation on the melting and solidification behavior of erythritol in a horizontal shell and multi-finned tube latent heat storage unit. Appl. Therm. Eng. 2019, 161, 114194. [Google Scholar] [CrossRef]
- Neumann, H.; Palomba, V.; Frazzica, A.; Seiler, D.; Wittstadt, U.; Gschwander, S.; Restuccia, G. A simplified approach for modelling latent heat storages: Application and validation on two different fin-and-tubes heat exchangers. Appl. Therm. Eng. 2017, 125, 41–52. [Google Scholar] [CrossRef]
- Rahimi, M.; Ranjbar, A.A.; Ganji, D.D.; Sedighi, K.; Hosseini, M.J.; Bahrampoury, R. Analysis of geometrical and operational parameters of PCM in a fin and tube heat exchanger. Int. Commun. Heat Mass Transf. 2014, 53, 109–115. [Google Scholar] [CrossRef]
- Kabbara, M.; Groulx, D.; Joseph, A. Experimental investigations of a latent heat energy storage unit using finned tubes. Appl. Therm. Eng. 2016, 101, 601–611. [Google Scholar] [CrossRef]
- Tay, N.; Belusko, M.; Bruno, F. An effectiveness-NTU technique for characterising tube-in-tank phase change thermal energy storage systems. Appl. Energy 2012, 91, 309–319. [Google Scholar] [CrossRef]
- Tay, N.; Bruno, F.; Belusko, M. Comparison of pinned and finned tubes in a phase change thermal energy storage system using 5CFD6. Appl. Energy 2013, 104, 79–86. [Google Scholar] [CrossRef]
- Hejčík, J.; Charvát, P.; Klimeš, L.; Astrouski, I. A PCM-water heat exchanger with polymeric hollow fibres for latent heat thermal energy storage: A parametric study of discharging stage. jtam 2016, 54, 1285–1295. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Yu, J.; Xiao, T.; Hu, Z.; He, Y.-L. Design and operating evaluation of a finned shell-and-tube thermal energy storage unit filled with metal foam. Appl. Energy 2020, 261, 114385. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, J.; Lei, D.; Liu, H.; Li, J.; Wu, Z. Experimental study on latent thermal energy storage system with gradient porosity copper foam for mid-temperature solar energy application. Appl. Energy 2020, 261, 114472. [Google Scholar] [CrossRef]
- Youssef, W.; Ge, Y.T.; Tassou, S.A. CFD modelling development and experimental validation of a phase change material (PCM) heat exchanger with spiral-wired tubes. Energy Convers. Manag. 2018, 157, 498–510. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, Z.A. Performance Evaluation of Coupled Thermal Enhancement through Novel Wire-Wound Fins Design and Graphene Nano-Platelets in Shell-and-Tube Latent Heat Storage System. Energies 2021, 14, 3743. [Google Scholar] [CrossRef]
- Schlott, A.; Hörstmann, J.; Tittes, K.; Andersen, O.; Meinert, J. High Power Latent Heat Storages with 3D Wire Structures–Numerical Evaluation of Phase Change Behavior. Energy Procedia 2017, 135, 75–81. [Google Scholar] [CrossRef]
- Koller, M.; Walter, H.; Hameter, M. Transient Numerical Simulation of the Melting and Solidification Behavior of NaNO3 Using a Wire Matrix for Enhancing the Heat Transfer. Energies 2016, 9, 205. [Google Scholar] [CrossRef]
- Nakaso, K.; Teshima, H.; Yoshimura, A.; Nogami, S.; Hamada, Y.; Fukai, J. Extension of heat transfer area using carbon fiber cloths in latent heat thermal energy storage tanks. Chem. Eng. Process. Process Intensif. 2008, 47, 879–885. [Google Scholar] [CrossRef]
- Medrano, M.; Yilmaz, M.O.; Nogués, M.; Martorell, I.; Roca, J.; Cabeza, L.F. Experimental evaluation of commercial heat exchangers for use as PCM thermal storage systems. Appl. Energy 2009, 86, 2047–2055. [Google Scholar] [CrossRef]
- Delgado-Diaz, W.; Stamatiou, A.; Maranda, S.; Waser, R.; Worlitschek, J. Comparison of Heat Transfer Enhancement Techniques in Latent Heat Storage. Appl. Sci. 2020, 10, 5519. [Google Scholar] [CrossRef]
- Balzer, R. Wärmetauschvorrichtung für Einen Wärmeaustausch Zwischen Medien und Webstruktur. Patent DE102006022629, 15 November 2007. [Google Scholar]
- Fugmann, H.; Martens, S.; Balzer, R.; Brenner, M.; Schnabel, L.; Mehring, C. Performance Evaluation of Wire Cloth Micro Heat Exchangers. Energies 2020, 13, 715. [Google Scholar] [CrossRef] [Green Version]
- Martens, S. Modellierung und Numerische Berechnung der Thermofluiddynamischen Eigenschaften Gewebebasierter Wärmeübertrager. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2019. [Google Scholar]
- Rösler, F. Modellierung und Simulation der Phasenwechselvorgänge in Makroverkapselten Latenten Thermischen Speichern. Ph.D. Thesis, Universität Bayreuth, Bayreuth, Germany, 2014. [Google Scholar]
- Gschwander, S.; Haussmann, T.; Hagelstein, G.; Sole, A.; Diarce, G.; Hohenauer, W.; Lager, D.; Rathgeber, C.; Hennemann, P.; Lazaro, A.; et al. Standard to Determine the Heat Storage Capacity of PCM Using hf-DSC with Constant Heating/Cooling Rate (Dynamic Mode). TASK 42. Available online: http://task42.iea-shc.org/data/sites/1/publications/Task4224-Standard-to-determine-the-heat-storage-capacity-of-PCM-vers150326.pdf (accessed on 31 January 2015).
- Kheirabadi, A.C.; Groulx, D. The Effect of the Mushy-Zone Constant on Simulated Phase Change Heat Transfer. In Proceedings of the ICHMT International Symposium on Advances in Computational Heat Transfer, Piscataway, NJ, USA, 25–29 May 2015. [Google Scholar]
- Barz, T.; Sommer, A. Modeling hysteresis in the phase transition of industrial-grade solid/liquid PCM for thermal energy storages. Int. J. Heat Mass Transf. 2018, 127, 701–713. [Google Scholar] [CrossRef]
- Lázaro, A.; Delgado, M.; König-Haagen, A.; Höhlein, S.; Diarce, G. Technical performance assessment of phase change material components. In Proceedings of the SHC 2019 International Conference on Solar Heating and Cooling for Building and Industry, Santiago, Chile, 4–7 November 2019. [Google Scholar]
- Evonik Industries AG. Technical Data Sheet-PLEXIGLAS® GS/XT.; Evonik Industries AG: Essen, Germany, 2013. [Google Scholar]
- DIN German Institute for Standardization. DIN EN ISO 10456: Baustoffe und Bauprodukte: Wärme- und feuchtetechnische Eigenschaften; Beuth Verlag GmbH: Berlin, Germany, 2010. [Google Scholar]
- 3D Systems GmbH. Technical Data Sheet-DuraForm PA; 3D Systems GmbH: York County, SC, USA, 2008. [Google Scholar]
- Armacell Enterprise GmbH & Co. KG. Technical Data Sheet-Armaflex; Armacell Enterprise GmbH & Co. KG: Schönefeld, Germany, 2017. [Google Scholar]
- BASF SE. Technical Data Sheet-Styrodur; BASF SE: Ludwigshafen, Germany, 2019. [Google Scholar]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [Green Version]
- Zipf, V.; Willert, D.; Neuhäuser, A. Active latent heat storage with a screw heat exchanger–experimental results for heat transfer and concept for high pressure steam. In AIP Conference Proceedings 1734; SolarPACES 2015; AIP Publishing: Melville, NY, USA, 2016; p. 50044. ISBN 073541386X. [Google Scholar]
- Wittstadt, U. Experimentelle und Modellgestützte Charakterisierung von Adsorptionswärmeübertragern. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2018. [Google Scholar]
- Gnielinski, V. VDI-Wärmeatlas-Teil G Wärmeübertragung bei Erzwungener Konvektion-G1 Durchströmte Rohre; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-19980-6. [Google Scholar]
- Farid, M.M.; Husian, R.M. An electrical storage heater using the phase-change method of heat storage. Energy Convers. Manag. 1990, 30, 219–230. [Google Scholar] [CrossRef]
- Vogel, J.; Felbinger, J.; Johnson, M. Natural convection in high temperature flat plate latent heat thermal energy storage systems. Appl. Energy 2016, 184, 184–196. [Google Scholar] [CrossRef] [Green Version]
- Deutsche Edelstahlwerke GmbH. Technical Data Sheet-1.4301; Deutsche Edelstahlwerke GmbH: Witten, Germany, 2015. [Google Scholar]
- Hesse, W. (Ed.) Aluminium-Werkstoff-Datenblätter: Aluminium Material Data Sheets, 7th ed.; Beuth Verlag GmbH: Berlin, Germany, 2016; ISBN 3410268758. [Google Scholar]
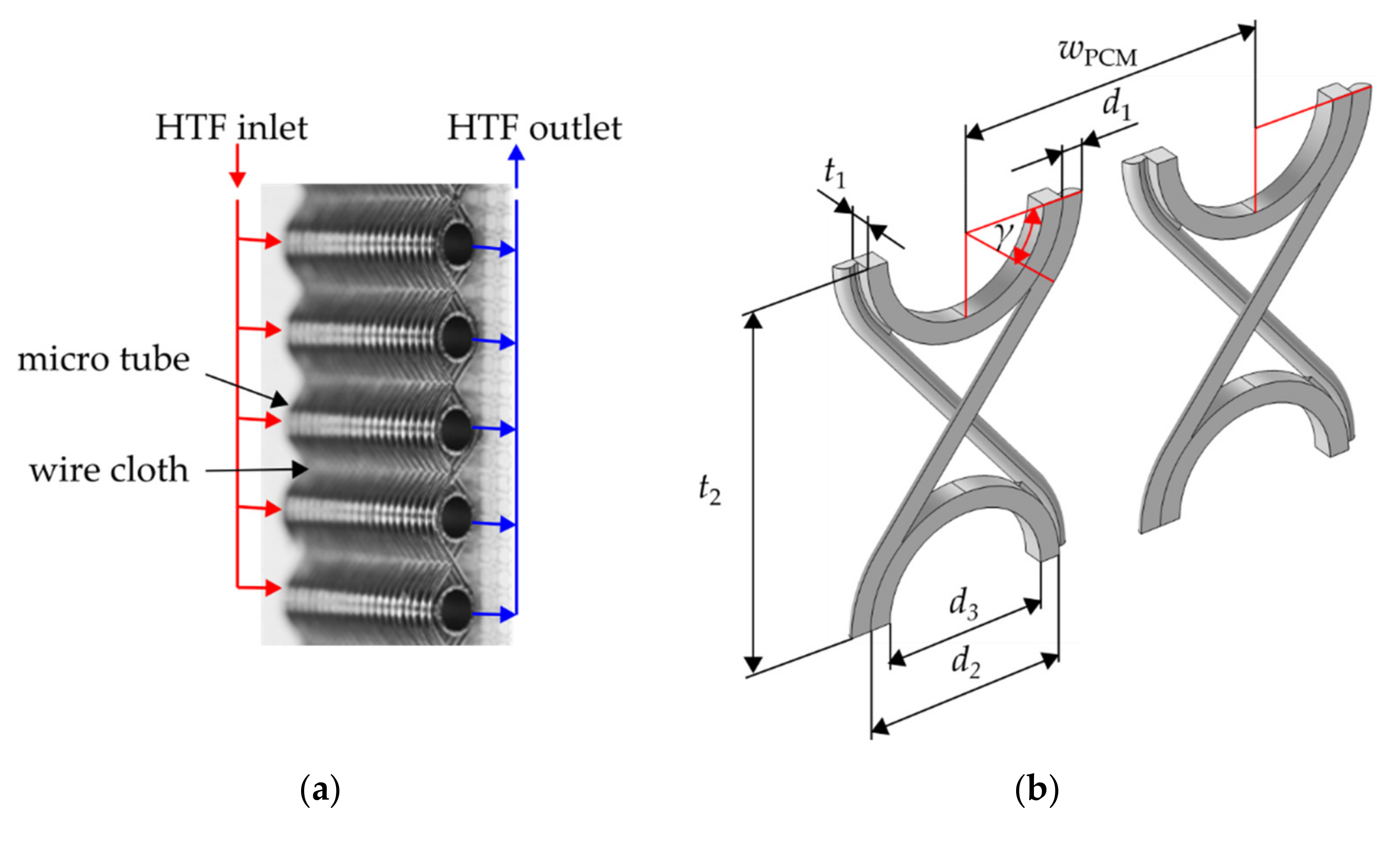

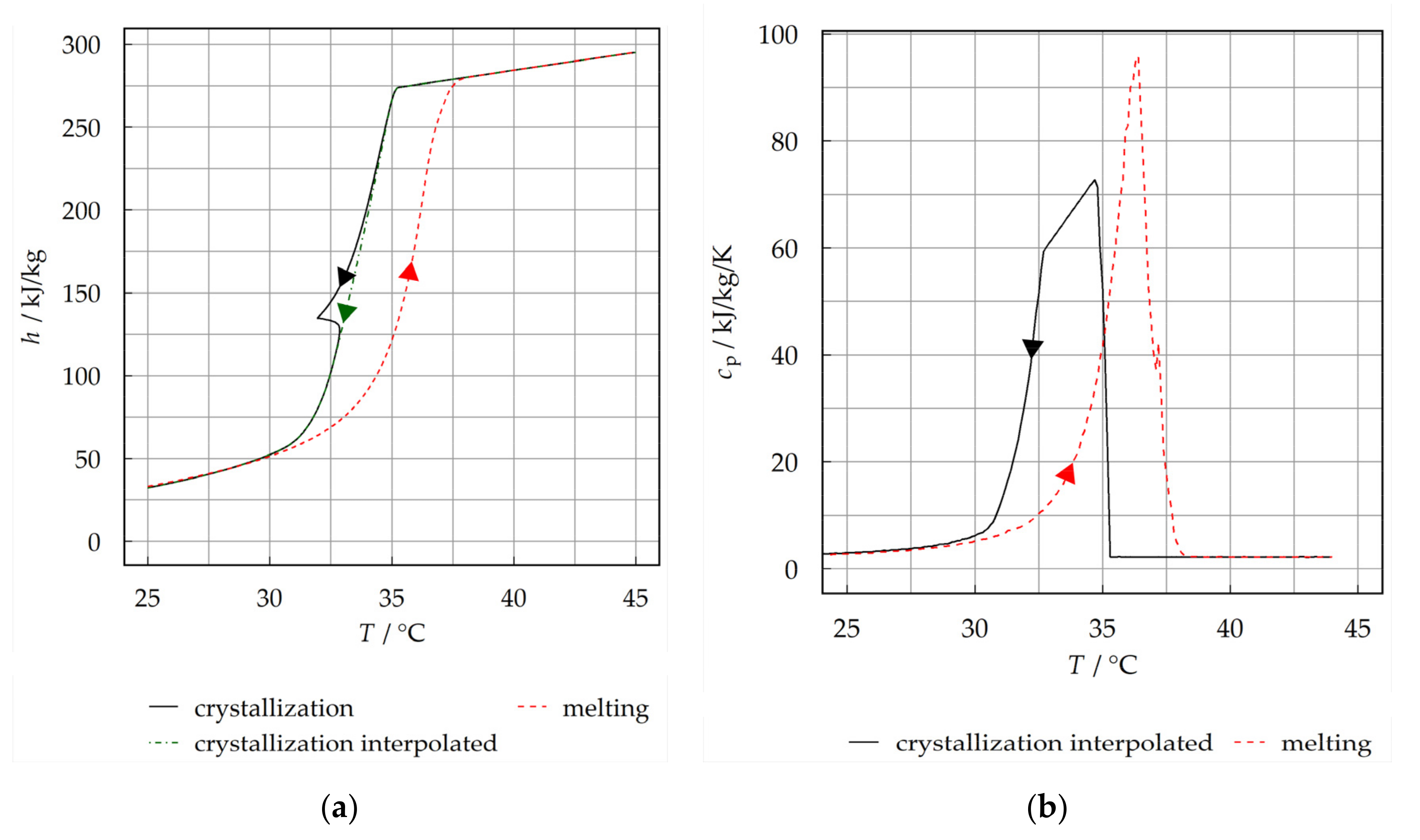
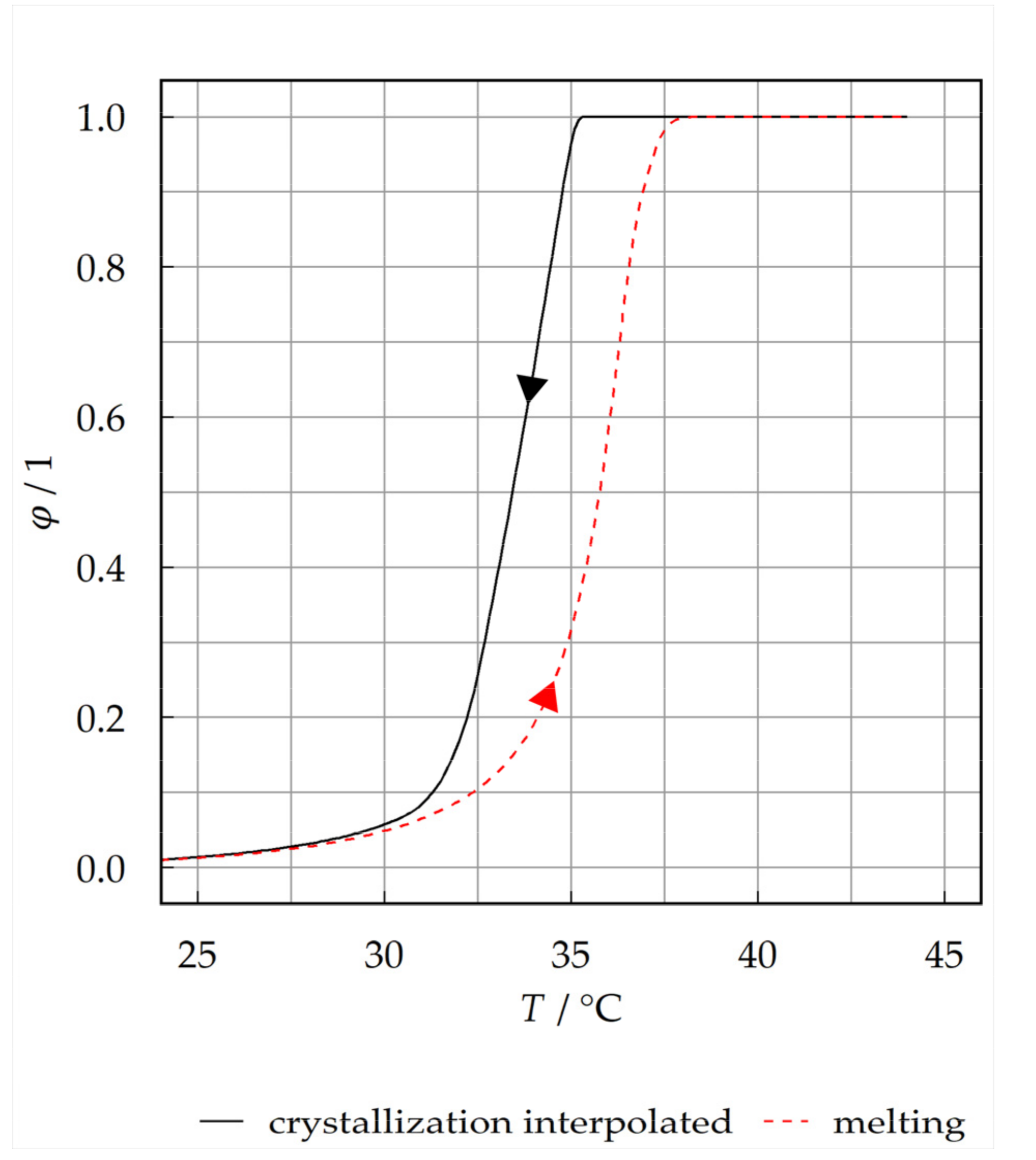
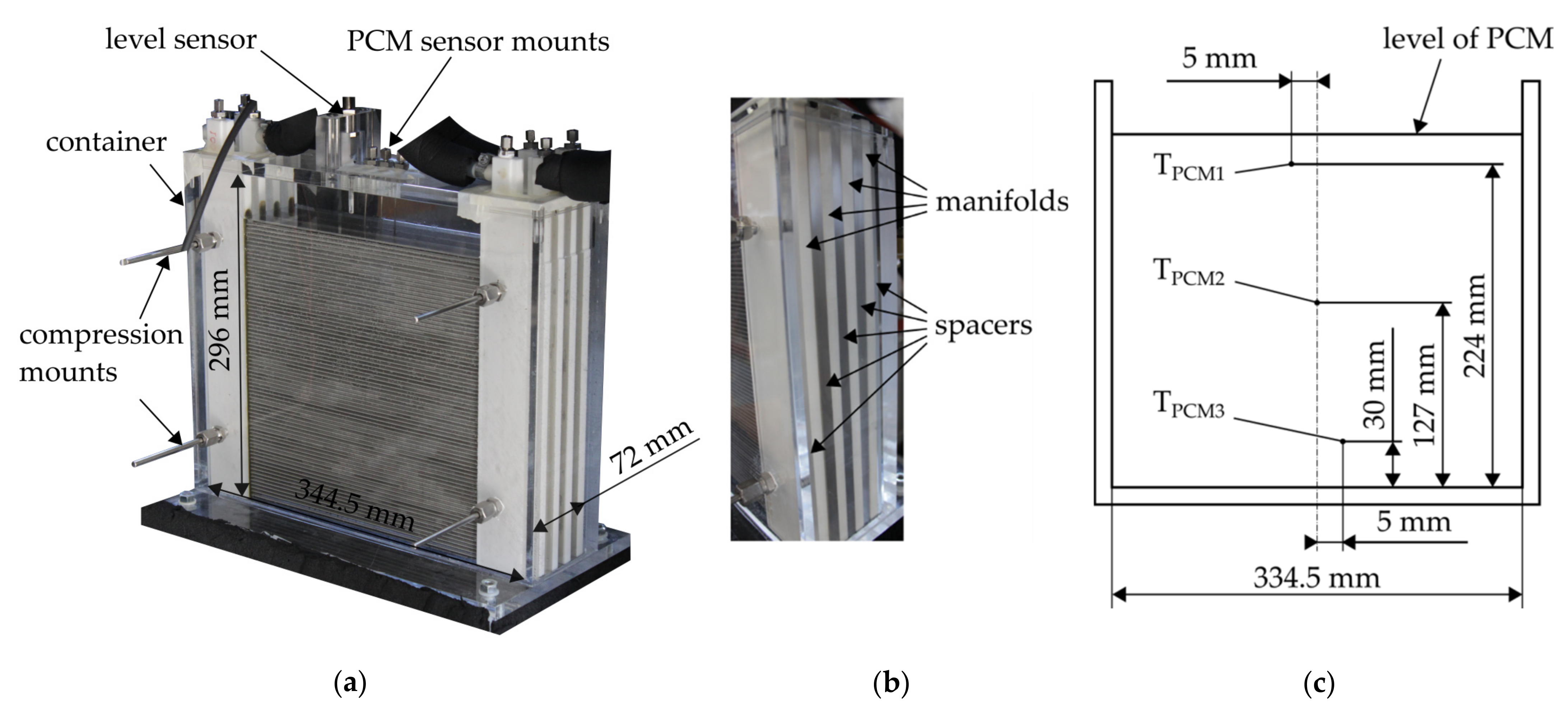





| Specification | Parameter | Unit | Value |
|---|---|---|---|
| number of tubes | 1 | 47 | |
| width of heat exchanger | mm | 250 | |
| height of heat exchanger | mm | 250 | |
| outer diameter tubes | mm | 2 | |
| wall thickness tubes | mm | 0.2 | |
| tube pitch perpendicular to flow direction | mm | 5.25 | |
| wire diameter | µm | 200 | |
| wire pitch in flow direction | µm | 200 | |
| heat transfer surface area PCM side | m2 | 0.2849 |
| Specification | Parameter | Unit | Value |
|---|---|---|---|
| thermal conductivity, solid state | W/m/K | 0.65 | |
| thermal conductivity, liquid state | W/m/K | 0.166 | |
| dynamic viscosity | Pas | 0.0044 | |
| density, solid state | kg/m3 | 830.9 | |
| density, liquid state | kg/m3 | 778.2 | |
| volumetric thermal expansion coefficient | 1/K | 8.65 × 10−4 | |
| melting enthalpy | kJ/kg | 222.44 | |
| melting temperature (peak) | °C | 36.2 |
| Parameter | Unit | PMMA [37] | Silicone [38] | Polyamide [39] | Elastomeric Foam [40] | PU Foam [41] |
|---|---|---|---|---|---|---|
| thermal conductivity, | W/m/K | 0.19 | 0.35 | 0.7 | 0.033 | 0.036 |
| density | kg/m3 | 1190 | 1200 | 1000 | - | - |
| J/kg/K | 1500 | 1000 | 1640 | - | - |
| Measured Variable | Technology | Range | Standard Uncertainty |
|---|---|---|---|
| temperature | Pt100 rod sensor | −30–60 °C | 0.075 K |
| mass flow rate | Coriolis sensor | 17–680 kg/h | 3.4 kg/h |
| pressure drop | differential pressure transmitter | 0–400 mbar | 0.3 mbar |
| PCM level change | ultrasonic level sensor | 2–82 mm | 0.6 mm |
| Boundary | Condition |
|---|---|
| convection according to Equation (18) | |
| conduction according to Equation (19) | |
| convection according to Equation (17) | |
| Additional PCM of experiment | considered as discretized volume |
| Outer surfaces | |
| Inlet of HTF | |
| Outlet of HTF |
| /kg/h | Crystallization | Melting | ||
|---|---|---|---|---|
| 40 | 0.21 | 0.39 | 0.30 | 0.48 |
| 59 | 0.09 | 0.17 | 0.16 | 0.29 |
| 98 | 0.04 | 0.14 | 0.10 | 0.20 |
| 177 | 0.02 | 0.09 | 0.06 | 0.13 |
| Parameter | Unit | Min | Max | |
|---|---|---|---|---|
| mm | 0.5 | 5 | 1.125 | |
| mm | 0.025 | 1 | 0.24375 | |
| mm | 0.75 | 15 | 3.5625 | |
| mm | 0.75 | 15 | 3.5625 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamisch, S.; Gschwander, S.; Rupitsch, S.J. Numerical and Experimental Investigation of Wire Cloth Heat Exchanger for Latent Heat Storages. Energies 2021, 14, 7542. https://doi.org/10.3390/en14227542
Gamisch S, Gschwander S, Rupitsch SJ. Numerical and Experimental Investigation of Wire Cloth Heat Exchanger for Latent Heat Storages. Energies. 2021; 14(22):7542. https://doi.org/10.3390/en14227542
Chicago/Turabian StyleGamisch, Sebastian, Stefan Gschwander, and Stefan J. Rupitsch. 2021. "Numerical and Experimental Investigation of Wire Cloth Heat Exchanger for Latent Heat Storages" Energies 14, no. 22: 7542. https://doi.org/10.3390/en14227542
APA StyleGamisch, S., Gschwander, S., & Rupitsch, S. J. (2021). Numerical and Experimental Investigation of Wire Cloth Heat Exchanger for Latent Heat Storages. Energies, 14(22), 7542. https://doi.org/10.3390/en14227542







