Design and Evaluation of High-Temperature Well Cementing Slurry System Based on Fractal Theory
Abstract
:1. Introduction
2. Fractal Theory and Grading Model
2.1. Fractal and Fractal Dimension
2.2. Basic Structure and General Properties of Fractal Model
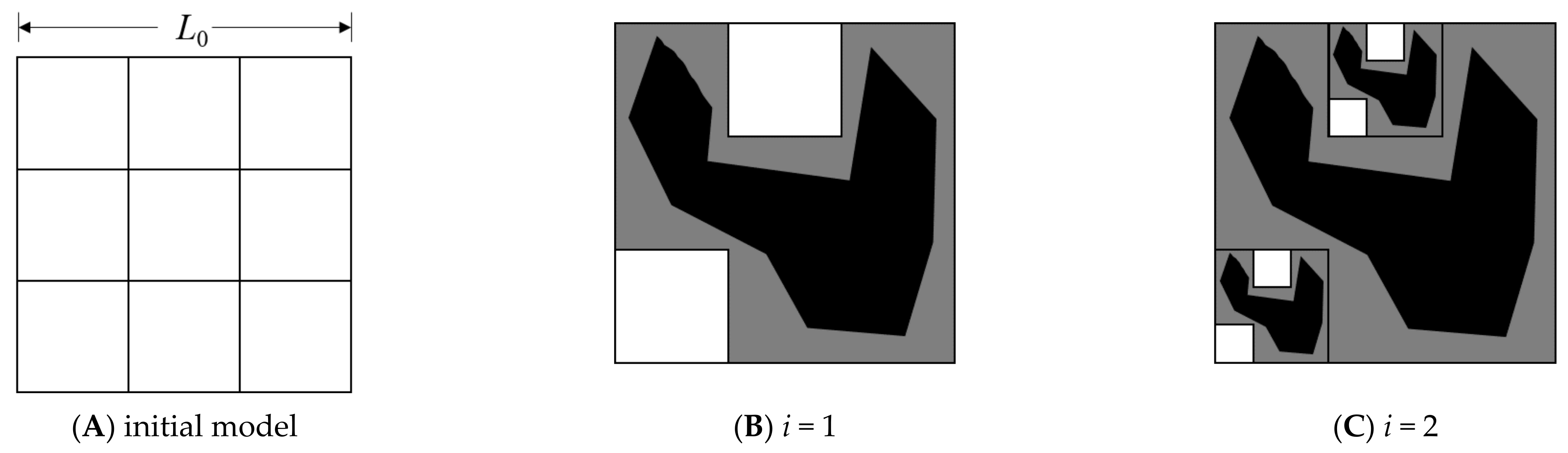
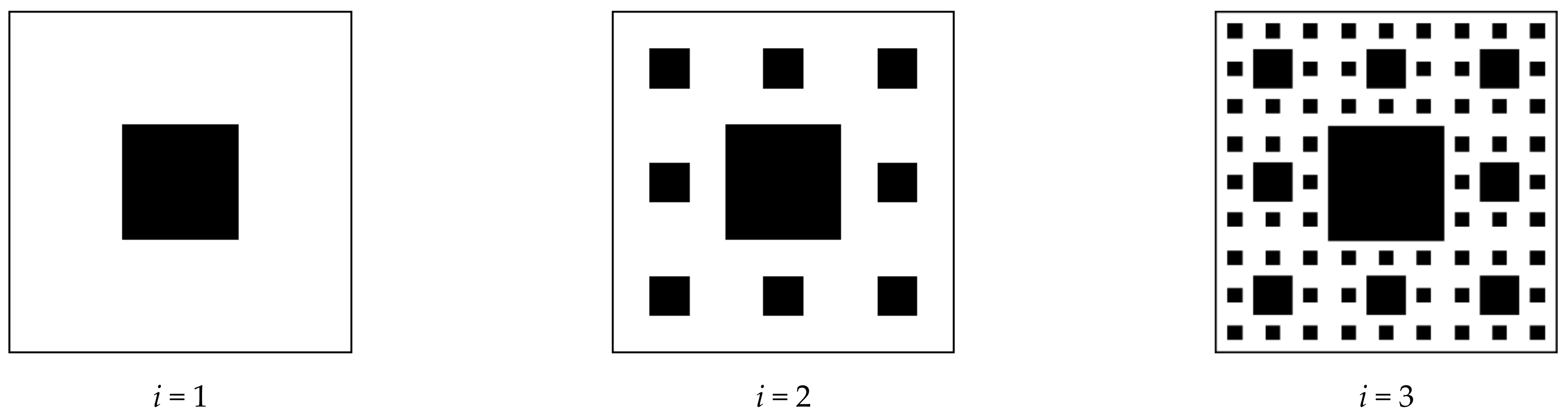
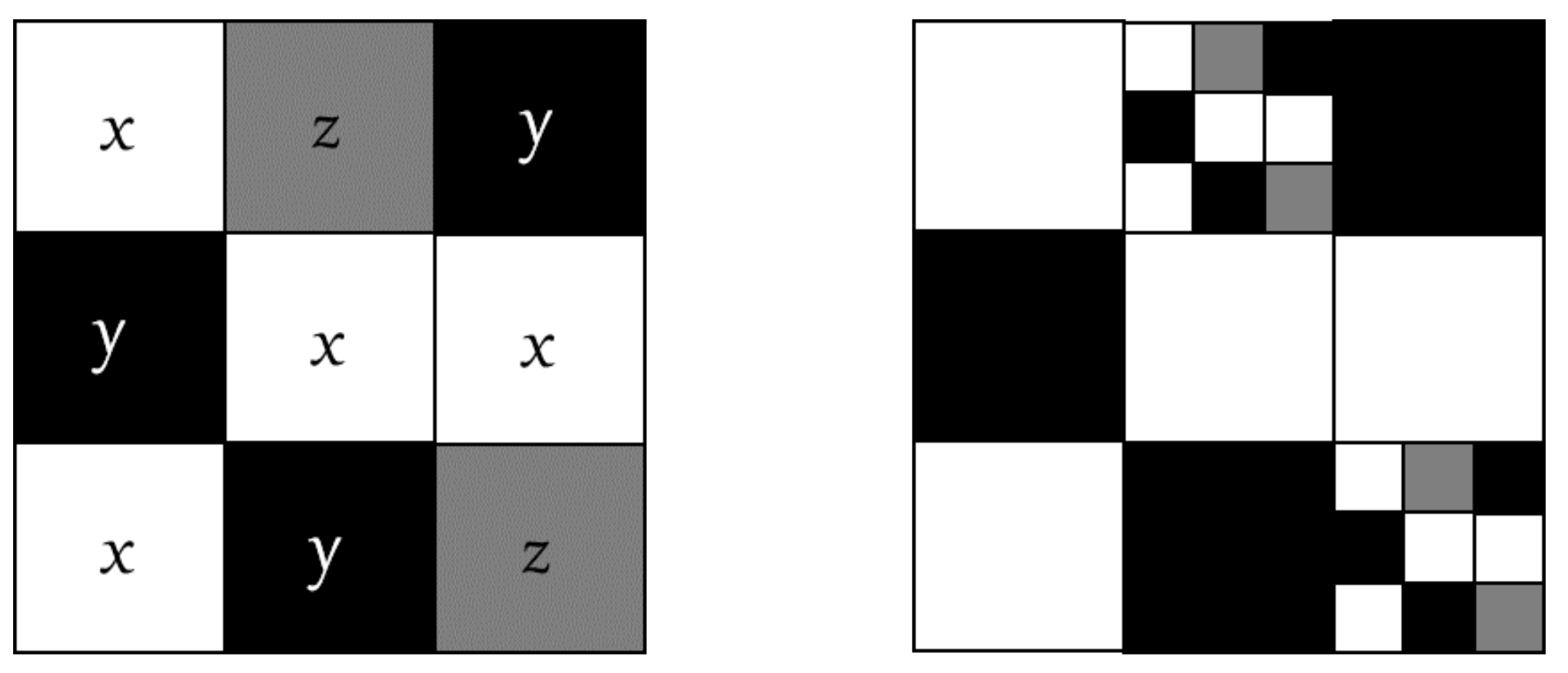
2.2.1. Pore Mass Fractal Model
2.2.2. Solid Mass Fractal Model
2.2.3. Pore Solid Fractal Model
2.3. Fractal Grading Model
3. Design of High-Temperature Well Cementing Slurry System
3.1. Design Principles
3.2. Experimental Materials
3.3. Design of Solid Phase Formula
3.4. Design of Fluid-Phase Formula
4. Performance Evaluation of High-Temperature Well Cementing Slurry System
4.1. Experimental Methods
4.2. Performance Evaluation of Cement Slurry
4.3. Evaluation of Temperature Resistance of Cement Slurry
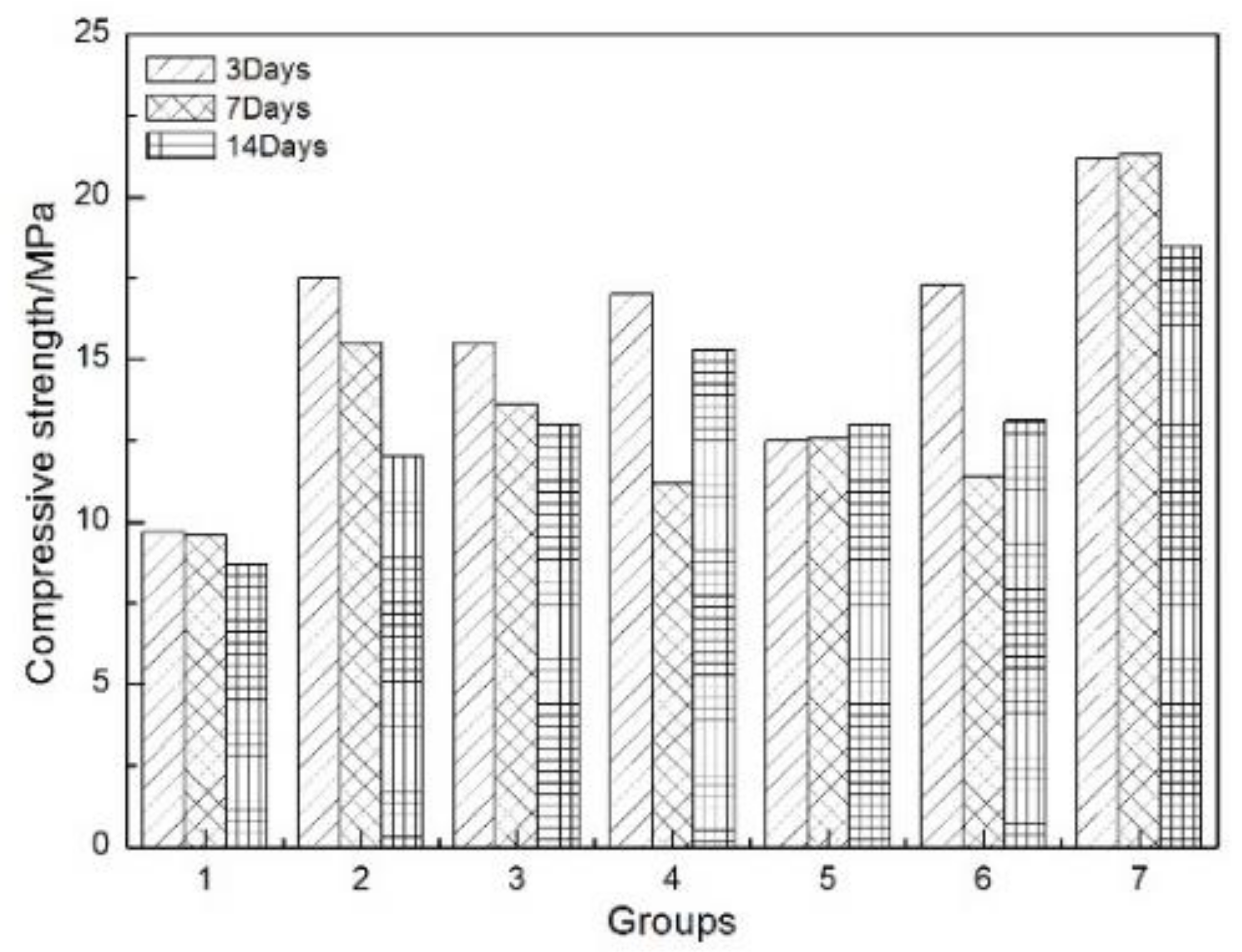
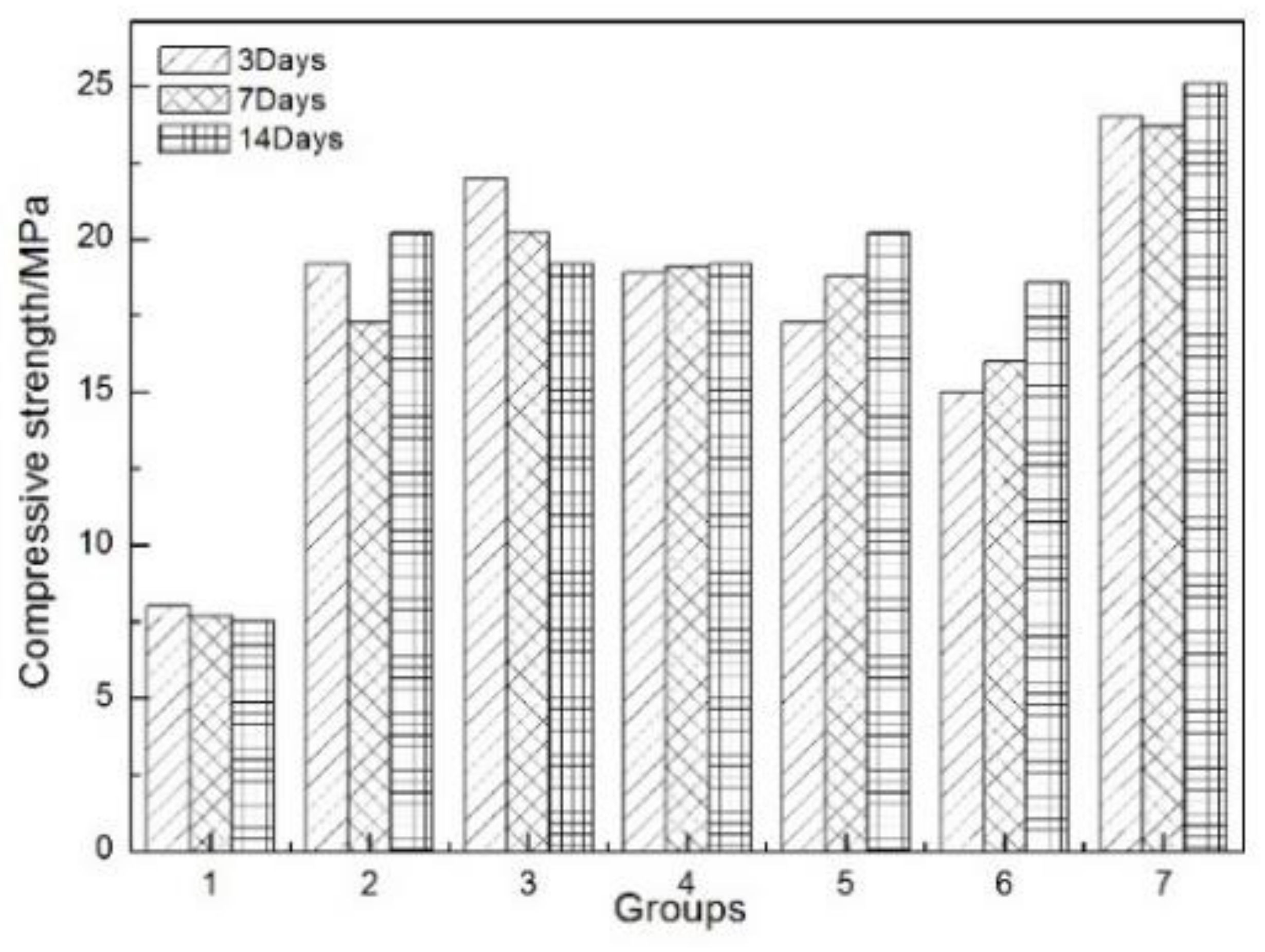
4.3.1. Compressive Strength of Cement Stone
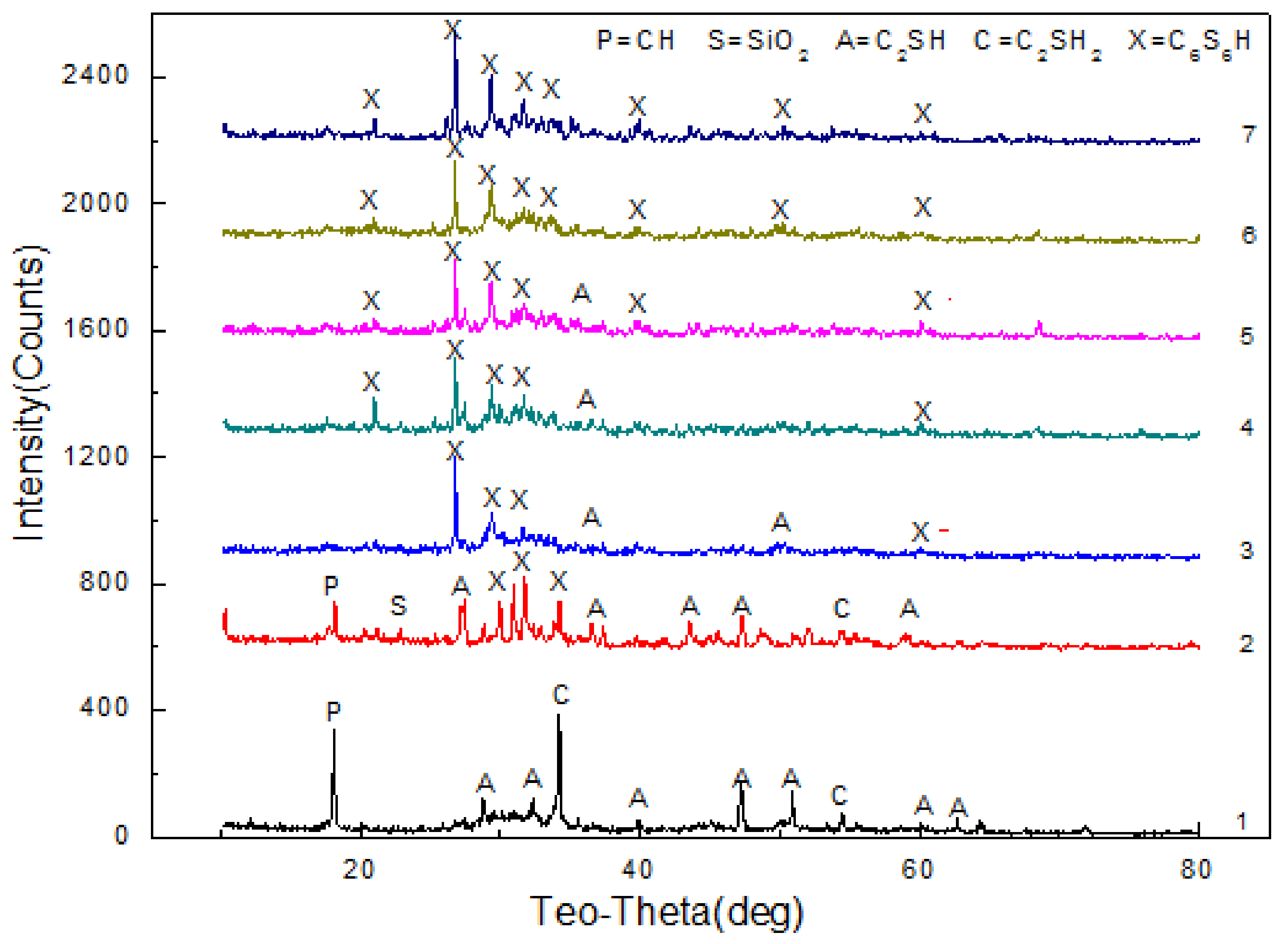
4.3.2. Phase Analysis
4.3.3. Analysis of Micromorphology
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Ahn, Y.; Kim, J.; Kwon, J.S.-I. Optimal design of supply chain network with carbon dioxide injection for enhanced shale gas recovery. Appl. Energy 2020, 274, 115334. [Google Scholar] [CrossRef]
- Liu, Y.; Jin, S.-D.; Cao, Q.; Zhou, W. Tertiary hydrothermal activity and its effect on reservoir properties in the Xihu Depression, East China Sea. Pet. Sci. 2019, 16, 14–31. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.-Z.; Li, J.; Wu, W.-T.; Cao, Q.; Bai, Y.-B.; Er, C. The petroleum system: A new classification scheme based on reservoir qualities. Pet. Sci. 2019, 16, 229–251. [Google Scholar] [CrossRef] [Green Version]
- Lan, W.-J.; Wang, H.-X.; Zhang, X.; Chen, S.-S. Sealing properties and structure optimization of packer rubber under high pressure and high temperature. Pet. Sci. 2019, 16, 632–644. [Google Scholar] [CrossRef]
- Xu, T.; Liu, C.; Huang, B.; Liu, X. Theory and Application of Cementing in Oil and Gas Wells; Petroleum Industry Press: Beijing, China, 2001. [Google Scholar]
- Jimenez, W.C.; Urdaneta, J.A.; Pang, X.; Garzon, J.R.; Nucci, G.; Arias, H. Innovation of Annular Sealants during the Past Decades and Their Direct Relationship with On/Offshore Wellbore Economics; SPE-180041; SPE Bergen One Day Seminar: Bergen, Norway, 2016. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Surfaces. J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Moskovits, M. The fractal nature of particle size distributions of grounds clinker. Cem. Concr. Res. 1990, 20, 499–505. [Google Scholar] [CrossRef]
- Thompson, A.H.; Katz, A.J.; Krohn, C.E. The microgeometry and transport properties of sedimentary rock. Adv. Phys. 1987, 36, 625–694. [Google Scholar] [CrossRef]
- Xia, C.; Liu, H. Research on Fractal Characteristics of the Size-Distribution of Concrete Aggregates. J. Southwest Jiaotong Univ. 2002, 2, 186–189. (In Chinese) [Google Scholar]
- Wang, Q.; Hu, J. Concrete aggregate gradation and fractal. Rock Soil Mech. 1997, 3, 93–99. (In Chinese) [Google Scholar]
- Katz, A.; Thompson, A. Fractal sandstone pores: Implications for conductivity and formation. Phys. Lett. 1985, 54, 1325–1328. [Google Scholar] [CrossRef]
- Dathe, A.; Eins, S.; Niemeyer, J.; Gerold, G. The surface fractal dimension of the soil–pore interface as measured by image analysis. Geoderma 2001, 103, 203–229. [Google Scholar] [CrossRef]
- Arandigoyen, M.; Alvarez, J.I. Pore structure and mechanical properties of cement–lime mortars. Cem. Concr. Res. 2007, 37, 767–775. [Google Scholar] [CrossRef] [Green Version]
- Arandigoyen, M.; Alvarez, J.I. Blended pastes of cement and lime: Pore structure and capillary porosity. Appl. Surf. Sci. 2006, 252, 8077–8085. [Google Scholar] [CrossRef] [Green Version]
- Huang, B. Cementing materials and process system optimized close packing theory. Drill. Fluid Completion Fluid 2001, 6, 4–12. [Google Scholar]
- Horsfield, H.T. The strength of asphalt mixtures. J. Soc. Chem. Ind. 1934, 53, 107–115. [Google Scholar]
- Liu, H. Particle size distribution and accumulation theory. J. Silic. 1991, 19, 164–172. [Google Scholar]
- Abid, K.; Gholami, R.; Tiong, M.; Nagaratnam, B.; Sarmadivaleh, M.; Mostofi, M.; Bing, C.H.; Muktadir, G. A Pozzolanic Supplementary Material to Reinforce Class G Cement Used for Drilling and Completion Operations. J. Pet. Sci. Eng. 2019, 177, 79–92. [Google Scholar] [CrossRef]
- Vidal, A.V.; Araujo, R.G.; Freitas, J.C. Sustainable Cement Slurry Using Rice Husk Ash for High Temperature Oil Well. J. Clean. Prod. 2018, 204, 292–297. [Google Scholar] [CrossRef]
- Swayze, M. Effect of High Temperature on Strength of Oil-Well Cements (Mid-Continent District Study Committee on Cementing Practices and Testing of Oil-Well Cements); Drilling and Production Practice: New York, NY, USA, 1954; API-54-072. [Google Scholar]
- Rust, C.F.; Wood, W.D. Laboratory Evaluations and Field Testing of Silica-CMHEC-Cement Mixtures. J. Pet. Technol. 1960, 12, 25–29. [Google Scholar] [CrossRef]
- Krakowiak, K.J.; Thomas, J.J.; Musso, S.; James, S.; Akono, A.-T.; Ulm, F.-J. Nano-Chemo-Mechanical Signature of Conventional Oil-Well Cement Systems: Effects of Elevated Temperature and Curing Time. Cem. Concr. Res. 2015, 67, 103–121. [Google Scholar] [CrossRef]
- Krakowiak, K.J.; Thomas, J.J.; James, S.; Abuhaikal, M.; Ulm, F.-J. Development of Silica-Enriched Cement-Based Materials with Improved Aging Resistance for Application in High-Temperature Environments. Cem. Concr. Res. 2018, 105, 91–110. [Google Scholar] [CrossRef]
- Reddy, B.R.; Zhang, J.; Ellis, M. Cement Strength Retrogression Issues in Offshore Deep Water Applications—Do We Know Enough for Safe Cementing. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2016. [Google Scholar] [CrossRef]
- Thomas, J.; James, S.; Ortega, J.A.; Musso, S.; Auzerais, F.; Krakowiak, K.; Akono, A.-T.; Ulm, F.-J.; Pellenq, R. Fundamental Investigation of the Chemical and Mechanical Properties of High-Temperature-Cured Oilwell Cements. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2012. [Google Scholar] [CrossRef]
- José Maria Gómez de Salazar, A.; Ureña, M.; Dolores, E. Diffusion Bonding of Discontinuously Reinforced SiC/Al Matrix Composites: The Role of Interlayers. Key Eng. Mater. 1995, 104, 523–540. [Google Scholar]
- Tsivilis, S.; Parissakis, G. A mathematical model for the prediction of cement strength. Cem. Concr. Res. 1995, 25, 9–14. [Google Scholar] [CrossRef]
- Ji, X.; Chan, S.Y.N.; Feng, N. Fractal model for simulating the space-filling process of cement hydrates and fractal dimensions of pore structure of cement-based materials. Cem. Concr. Res. 1997, 27, 1691–1699. [Google Scholar] [CrossRef]
- Yin, H. Study the Fractal Characteristic of Concrete’s Pore Structure; Guangxi University: Nanning, China, 2006. [Google Scholar]
- Chen, Y.; Li, Y.; He, X.; Wei, J.; Zhang, W.; Zhang, H.; Guo, S. Pore volume fractal dimension of fly ash-cement paste and its relationship between the pore srtucture and strength. J. Chin. Ceram. Soc. 2003, 31, 774–779. [Google Scholar]
- Tang, M. Study on the fractal characteristics of concrete pores. Concrete 2000, 8, 3–5. [Google Scholar]
- Orford, J.D.; Whalley, W.B. The use of the fractal dimension to quantify the morphology of irregular-shaped particles. Sedimentology 1983, 30, 655–668. [Google Scholar] [CrossRef]
- Chen, Y.P.; Shi, M.H. Determination of permeability using fractal method far porous media. Sci. China (Ser. E Technol. Sci.) 2001, 44, 625–630. [Google Scholar]
- Wang, Y.; Diamond, S. A fractal study of the fracture surfaces of cement pastes and mortars using a stereoscopic SEM method. Cem. Concr. Res. 2001, 31, 1385–1392. [Google Scholar] [CrossRef]
- Mandelbrot Benoit, B. The Fractal Geometry of Nature, Updated ed.; Times Books: New York, NY, USA, 1982. [Google Scholar]
- Mandelbrot Benoit, B. Fractals: Form, Chance and Dimension; W. H. Freeman: San Francisco, CA, USA, 1977. [Google Scholar]
- Yu, B.; Li, J. Some fractal characters of porous media. Fractals 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Falconer, K.J. The Hausdorff dimension of self-affine fractals. Math. Proc. Camb. Philos. Soc. 2008, 103, 339–350. [Google Scholar] [CrossRef]
- Yu, B. Fractal dimensions for multiphase fractal media. Fractals 2006, 14, 111–118. [Google Scholar] [CrossRef]
- Crawford, J.; Matsui, N.; Young, I. The relation between the moisture-release curve and the structure of soil. Eur. J. Soil Sci. 1995, 46, 369–375. [Google Scholar] [CrossRef]
- Perrier, E.M.A.; Bird, N.R.A. Modelling soil fragmentation: The pore solid fractal approach. Soil Tillage Res. 2002, 64, 91–99. [Google Scholar] [CrossRef]
- Gmachowski, L. Transport properties of fractal aggregates calculated by permeability. Colloids Surf. A Physicochem. Eng. Asp. 2003, 215, 173–179. [Google Scholar] [CrossRef]
- Li, X.; Logan Bruce, E. Permeability of fractal aggregates. Water Res. 2001, 35, 3373–3380. [Google Scholar] [CrossRef]
- Bird, N.R.A.; Perrier, E.M.A. The pore–solid fractal model of soil density scaling. Eur. J. Soil Sci. 2003, 54, 467–476. [Google Scholar] [CrossRef]
- Yu, B. Fractal Porous Media Transport Physics; Science Press: Beijing, China, 2014; pp. 21–25. [Google Scholar]
- API RP 10B. Recommended Method for Testing Well Cement, version 2; American Petroleum Institute: Washington, DC, USA, 1997. [Google Scholar]
- GB/T 19139-2012. Oil Well Cement Test Method; Standards Press of China: Beijing, China, 2012. [Google Scholar]
- Maxson, J.; Bour, D.; Iverson, B. Strength Retrogression in Cements under High-Temperature Conditions. In Proceedings of the Thirty-Fifth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 1–3 February 2010. [Google Scholar]
- Swayze, M.A. Effects of High Pressures and Temperatures on Strength of Oil-Well Cements. In API Spring Meeting of the Mid-Continent District; Division of Production: Oklahoma City, OK, USA, 1954. [Google Scholar]
- Meyer, C.; Pang, X.; Darbe, R.; Darbe, R.; Funkhouser, G.P. Modeling the Effect of Curing Temperature and Pressure on Cement Hydration Kinetics. ACI Mater. J. 2013, 110, 137–148. [Google Scholar]
- Wilkinson, A.P.; Jupe, A.C.; Luke, K.; Funkhouser, G.P. Class H Cement Hydration at 180 °C and High Pressure in the Presence of Added Silica. Cem. Concr. Res. 2008, 38, 660–666. [Google Scholar]
- Yu, Y.; Liu, H.; Liu, H.; Jin, J.; Liu, S. Hybrid Effects of Nano-Silica and Graphene Oxide on Mechanical Properties and Hydration Products of Oil Well Cement. Constr. Build. Mater. 2018, 191, 311–319. [Google Scholar]


| Granularity | Well Cement (μm) | Fine Sand (μm) | Coarse Sand (μm) |
|---|---|---|---|
| D(0.1) | 0.454 | 0.538 | 21.838 |
| D(0.5) | 2.825 | 2.390 | 97.209 |
| D(0.9) | 19.196 | 19.678 | 174.992 |
| D[4, 3] | 26.484 | 34.139 | 132.205 |
| / | D | ||||||
|---|---|---|---|---|---|---|---|
| 2.52 | 2.55 | 2.58 | 2.61 | 2.64 | 2.67 | ||
| Formula | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Slurry | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Fine Sand | 0 | 0 | 5.6 | 10.6 | 15.6 | 20.6 | 25.6 |
| Coarse Sand | 0 | 35 | 29.4 | 24.4 | 19.4 | 14.4 | 9.4 |
| / | D | ||||||
|---|---|---|---|---|---|---|---|
| 2.52 | 2.55 | 2.58 | 2.61 | 2.64 | 2.67 | ||
| Formula | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Slurry | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Fine Sand | 0 | 0 | 5.7 | 10.7 | 15.7 | 20.7 | 26.7 |
| Coarse Sand | 0 | 45 | 39.3 | 34.3 | 29.3 | 24.3 | 18.3 |
| Fluid Loss Agent | Intrinsic Viscosity | Rate of Molecular Weight Change (%) | |
|---|---|---|---|
| Before Heat Treatment | After Heat Treatment | ||
| A | 2.124 | 1.776 | 25.79 |
| B | 6.276 | 2.824 | 73.58 |
| C | 5.381 | 2.978 | 62.70 |
| Retarder | Intrinsic Viscosity | Rate of Molecular Weight Change (%) | |
|---|---|---|---|
| Before Heat Treatment | After Heat Treatment | ||
| A | 0.280 | 0.214 | 36.14 |
| B | 1.348 | 1.186 | 19.20 |
| C | 0.765 | 0.596 | 33.97 |
| Formula | Density/ (g/cm3) | Temperature/ °C | Fluidity/ cm | Stability/ (g/cm3) | Fluid Loss /mL | Initial Consistency/Bc | Thickening Time/min | Transient Time/min | SPN | Compressive Strength (74 h)/MPa |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.9 | 140 | 21 | 0.01 | 20 | 12 | 472 | 14 | 1.02 | 16 |
| 2 | 2.0 | 140 | 20 | 0.01 | 16 | 26 | 330 | 18 | 1.63 | 17.3 |
| 2.0 | 160 | 21 | 0.01 | 29 | 20 | 312 | 2 | 0.32 | 15 | |
| 2.0 | 180 | 20 | 0.01 | 47 | 24 | 512 | 2 | 0.57 | 23 | |
| 3 | 2.1 | 170 | 20 | 0.01 | 35 | 21 | 317 | 7 | 1.27 | 15.8 |
| 2.1 | 180 | 20 | 0.01 | 35 | 18 | 495 | 2 | 0.43 | 21 | |
| 4 | 2.2 | 190 | 20 | 0.02 | 37 | 25 | 457 | 1 | 0.32 | 25 |
| 5 | 2.3 | 200 | 20 | 0.02 | 42 | 29 | 471 | 1 | 0.15 | 25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, G.; Guo, X.; Li, Z.; Sun, J. Design and Evaluation of High-Temperature Well Cementing Slurry System Based on Fractal Theory. Energies 2021, 14, 7552. https://doi.org/10.3390/en14227552
Zheng G, Guo X, Li Z, Sun J. Design and Evaluation of High-Temperature Well Cementing Slurry System Based on Fractal Theory. Energies. 2021; 14(22):7552. https://doi.org/10.3390/en14227552
Chicago/Turabian StyleZheng, Guanyi, Xiaoyang Guo, Zaoyuan Li, and Jinfei Sun. 2021. "Design and Evaluation of High-Temperature Well Cementing Slurry System Based on Fractal Theory" Energies 14, no. 22: 7552. https://doi.org/10.3390/en14227552
APA StyleZheng, G., Guo, X., Li, Z., & Sun, J. (2021). Design and Evaluation of High-Temperature Well Cementing Slurry System Based on Fractal Theory. Energies, 14(22), 7552. https://doi.org/10.3390/en14227552





