Numerical Simulation via CFD Methods of Nitrogen Flooding in Carbonate Fractured-Vuggy Reservoirs
Abstract
:1. Introduction
2. Numerical Model
2.1. Model Simplification and Simulation Conditions
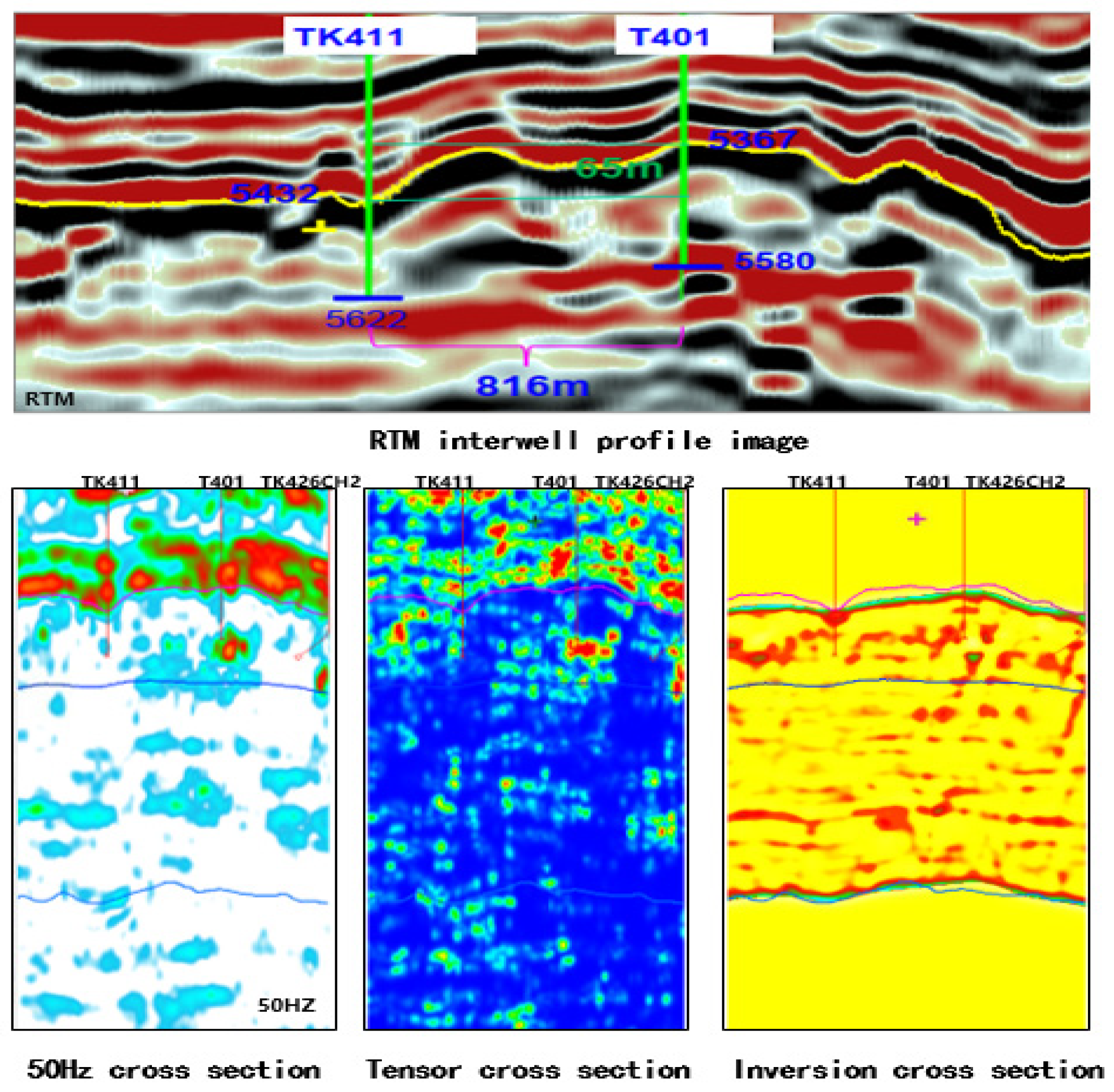
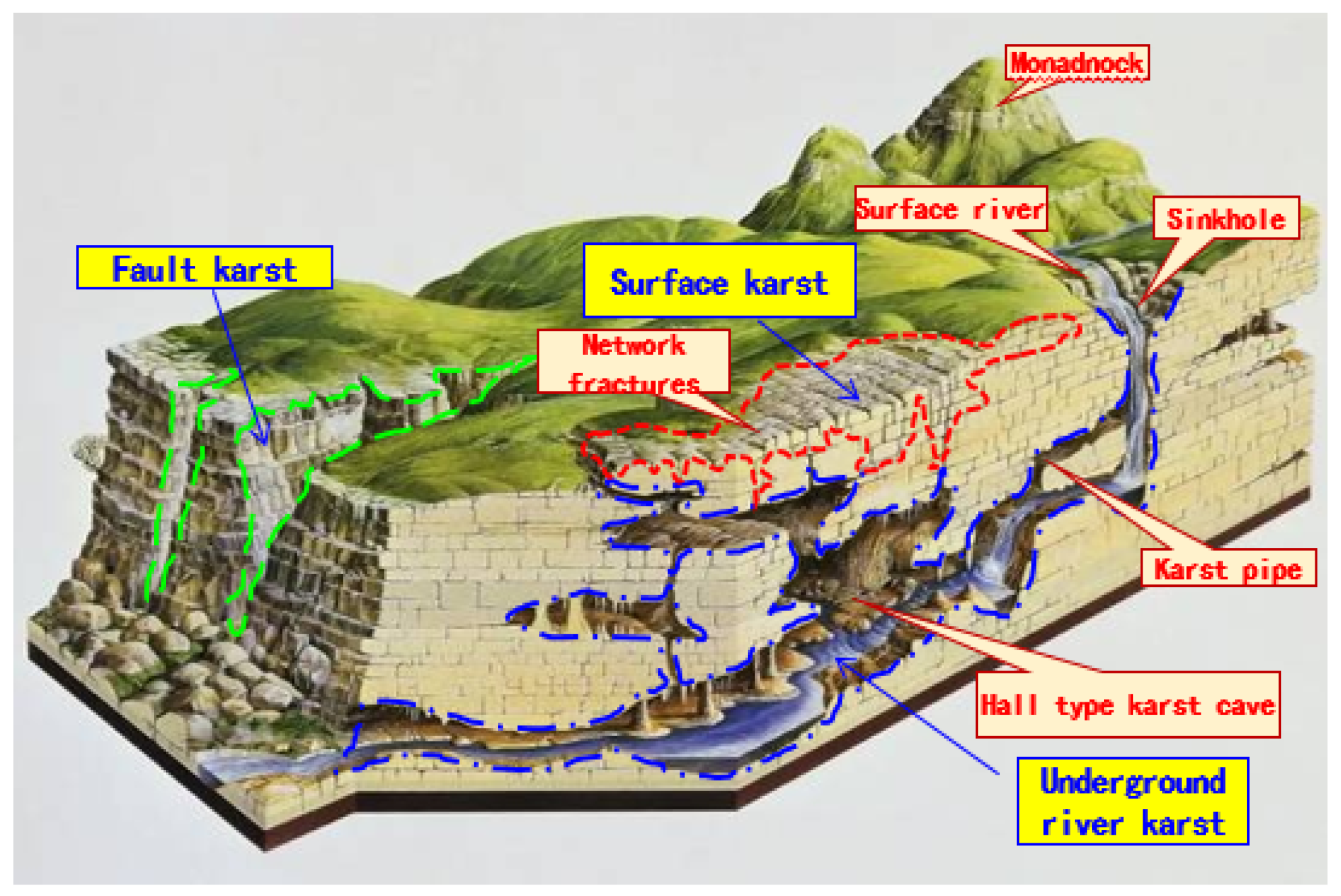
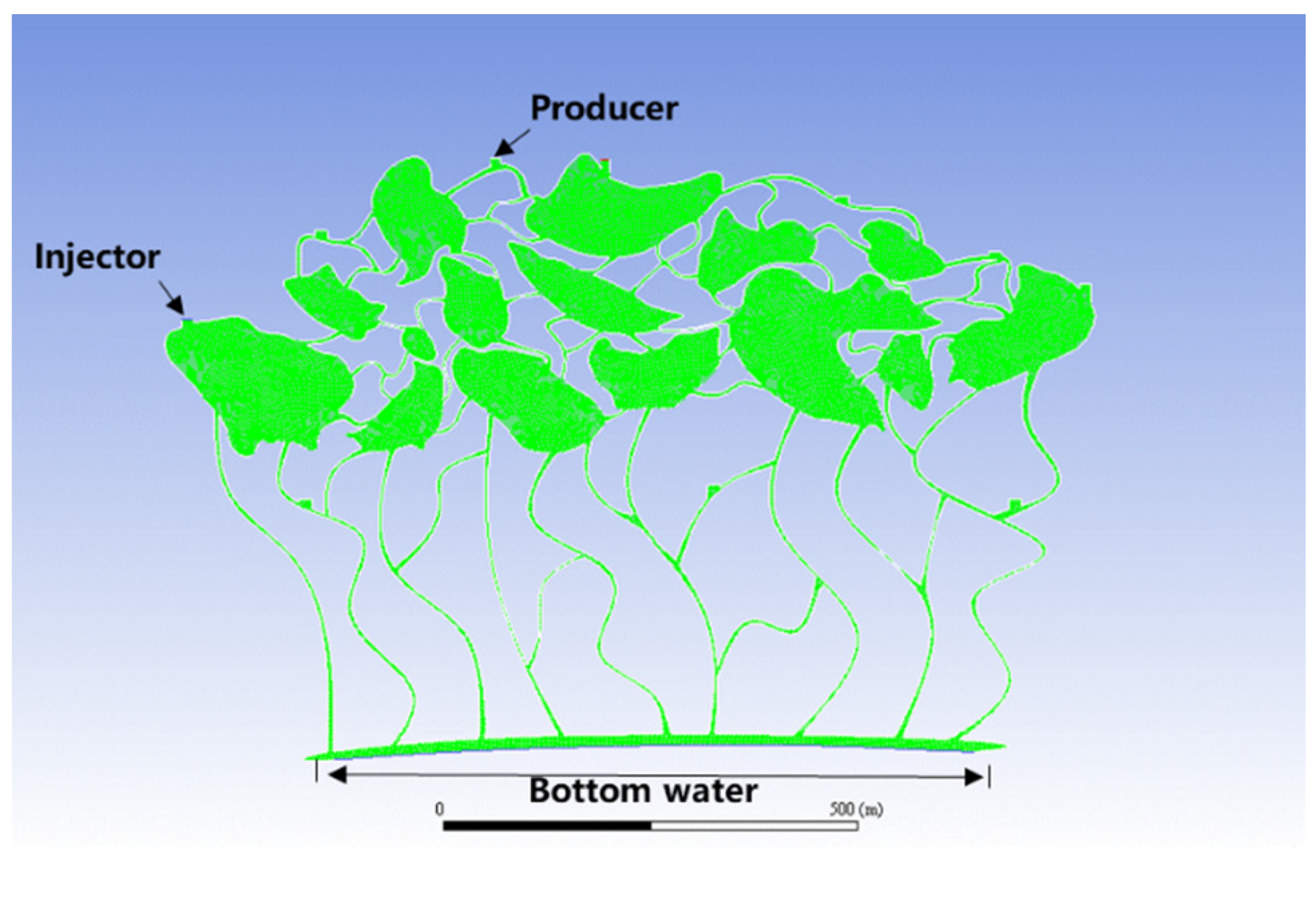
- 3D modeling of fracture-vuggy structure.
- Initial oil–water distribution simulation.
- Natural water flooding.
- Artificial water flooding simulation.
- Nitrogen flooding simulation.
2.2. Numerical Method
2.2.1. Assumptions
2.2.2. Governing Equations
2.2.3. Darcy Law in Porous Medium
2.2.4. Governing Equations of Porous Medium in Multiphase Field
3. Results and Discussion
3.1. Original Oil–Water Distribution
3.2. Natural Water Flooding
3.3. Artificial Water Injection
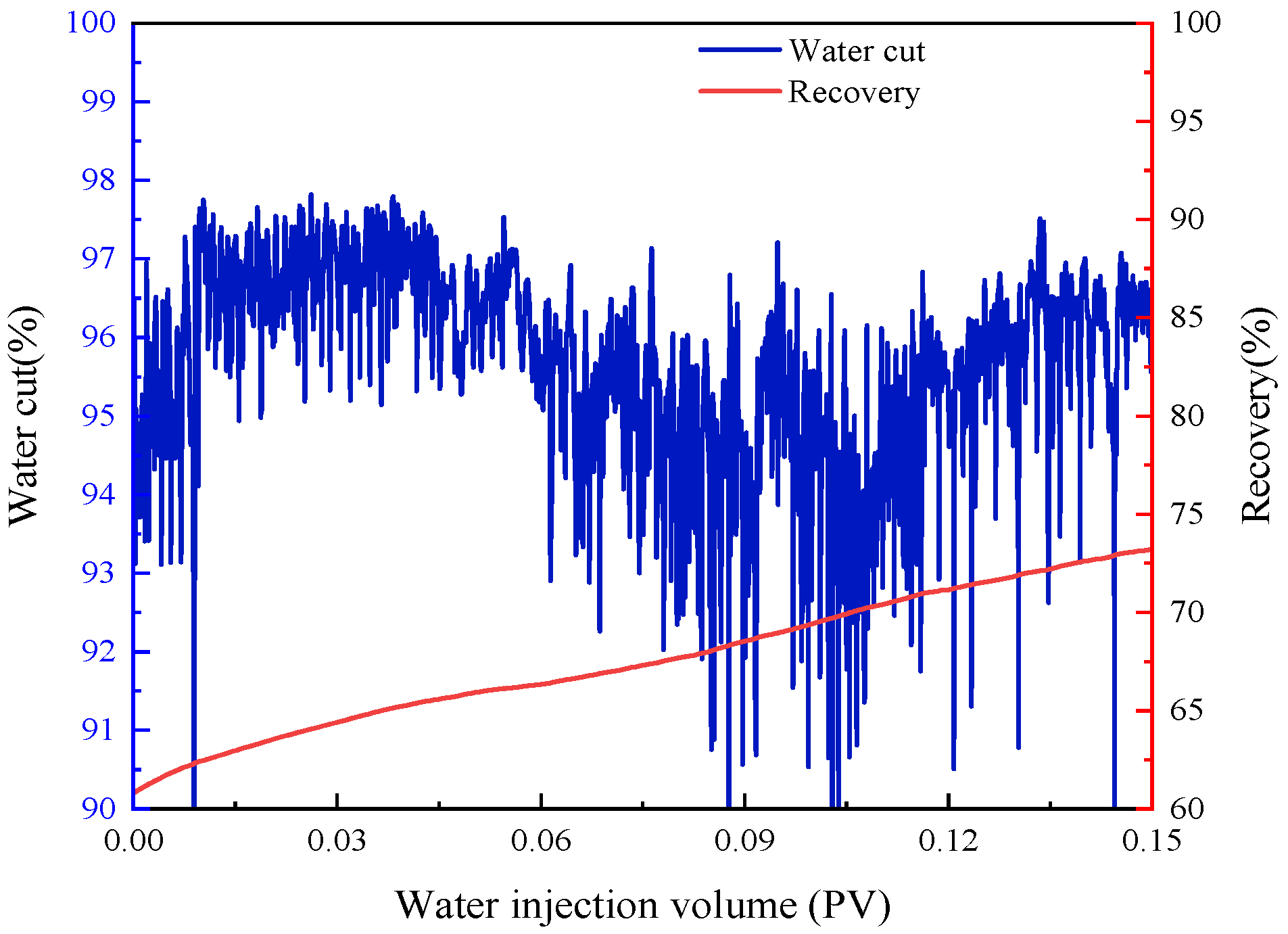
3.4. Nitrogen Flooding
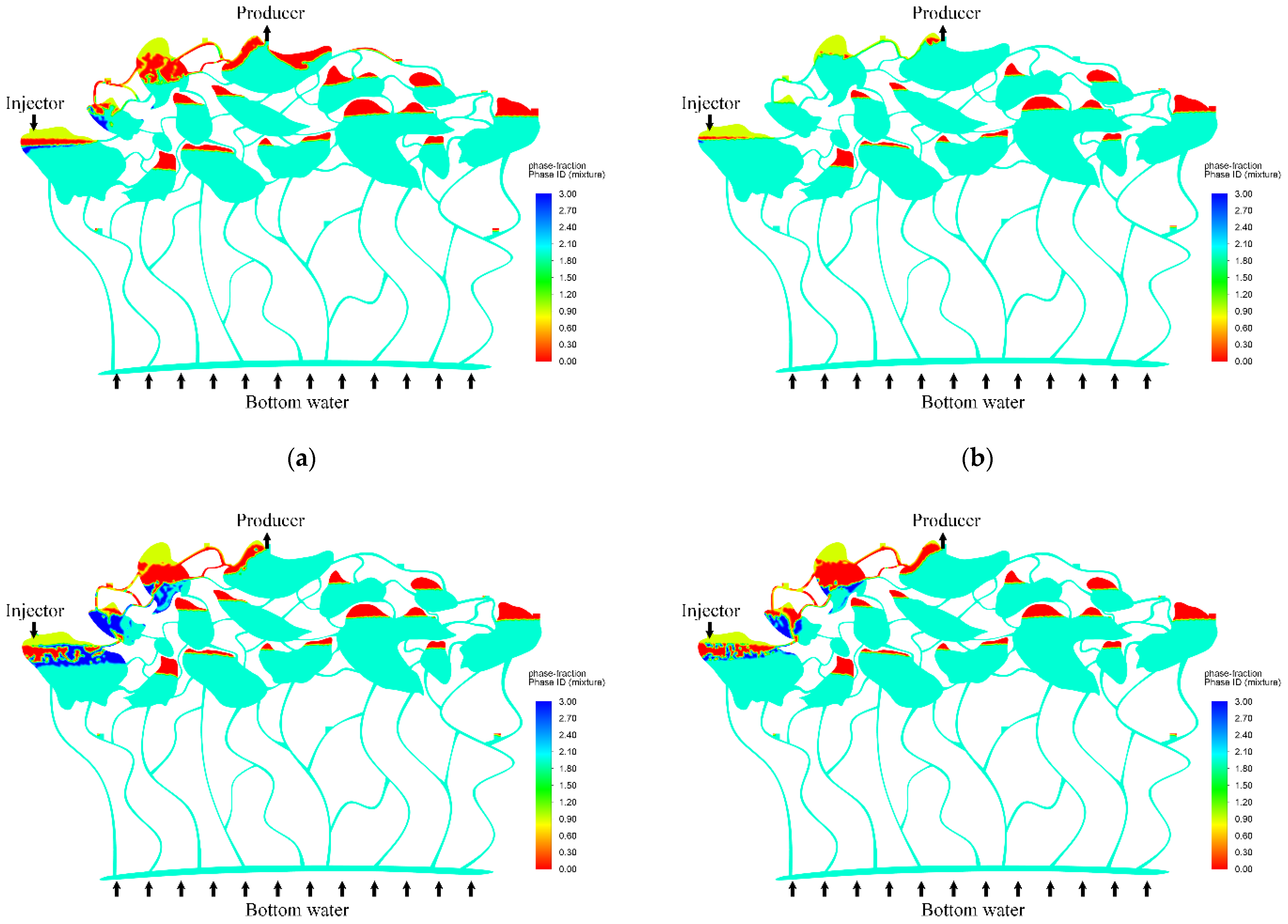
3.4.1. Effect of Injection Flow Rate
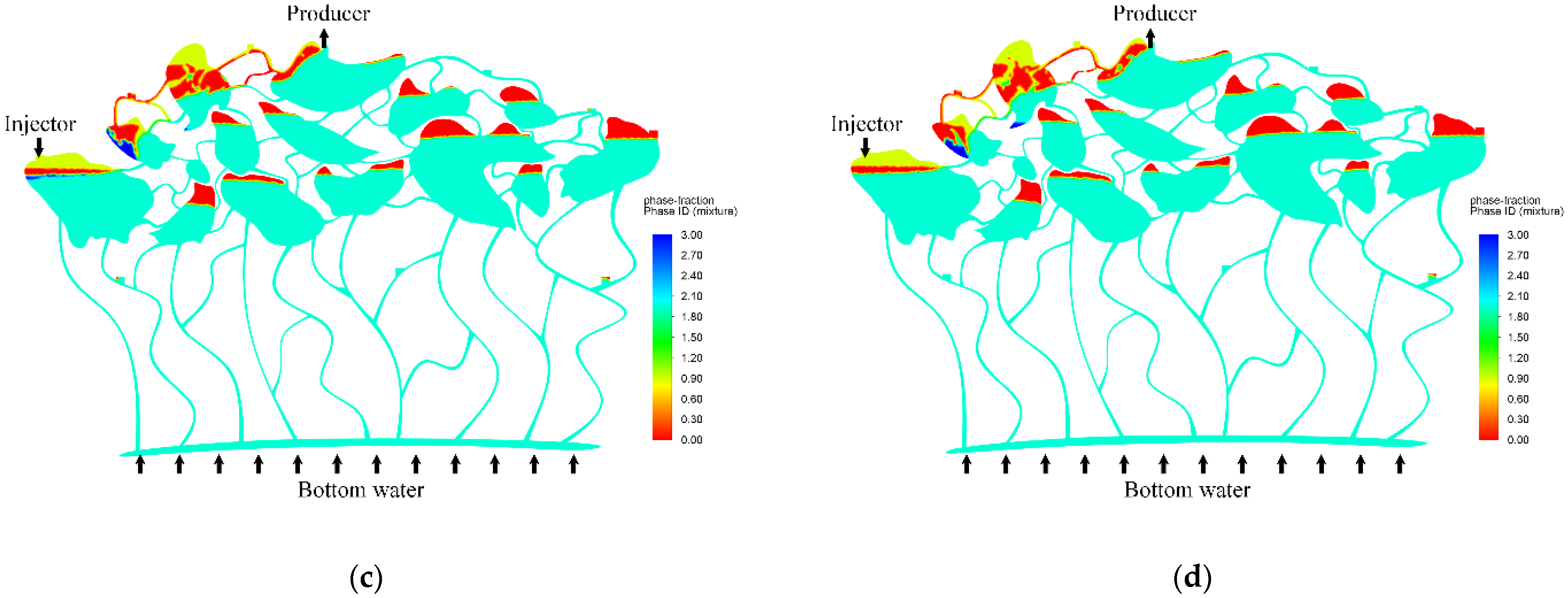
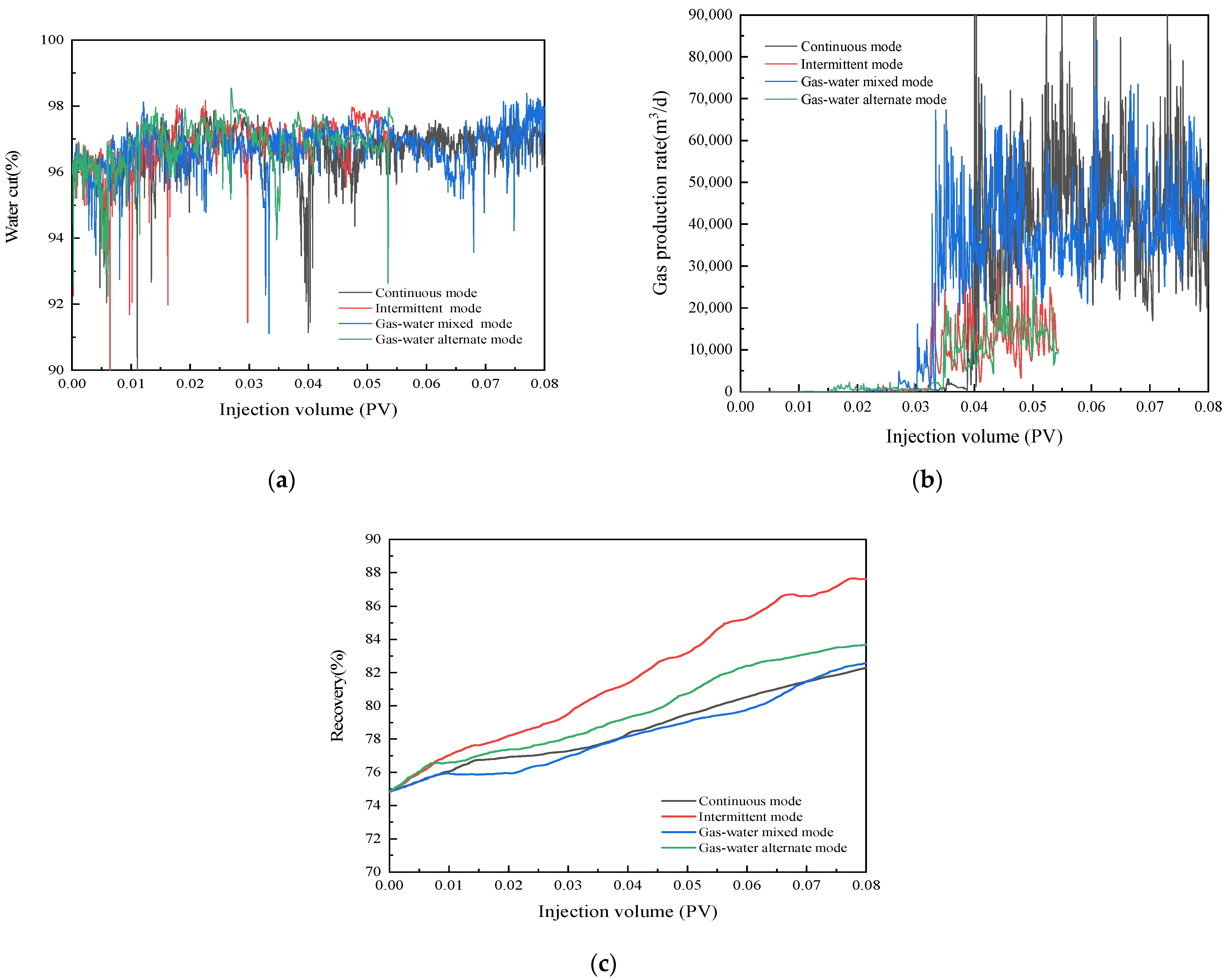
3.4.2. Effect of Injection Mode
- Continuous mode.
- Intermittent mode.
- Gas–water mixed injection mode.
- Gas–water alternate mode.
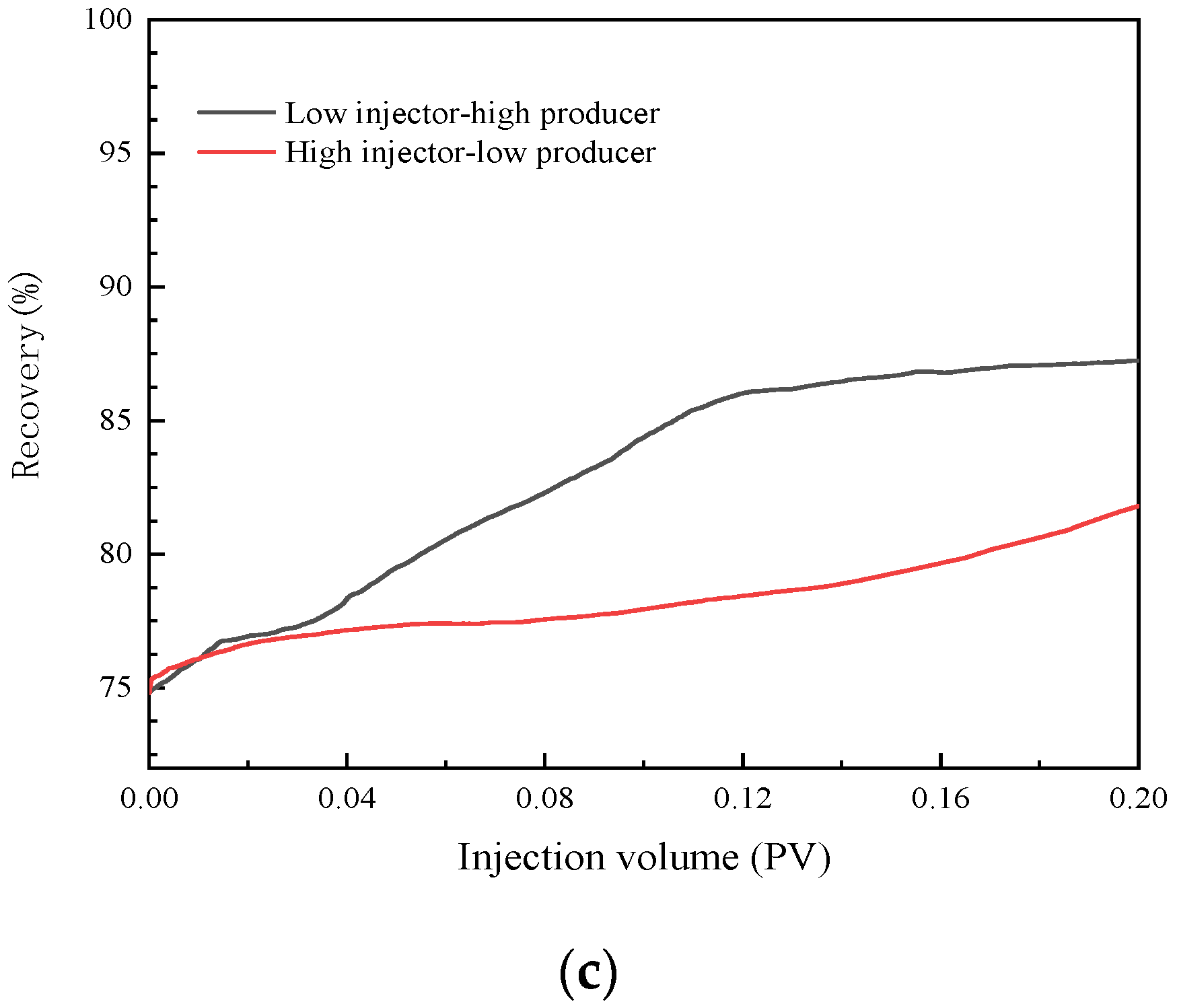
3.4.3. Effect of Injection–Production Relationship
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jiao, F. Practice and knowledge of volumetric development of deep fractured-vuggy carbonate reservoirs in Tarim Basin, NW China. Shiyou Kantan Yu Kaifa/Pet. Explor. Dev. 2019, 46, 552–558. [Google Scholar] [CrossRef]
- Hu, W. Development technology and research direction of fractured- vuggy carbonate reservoirs in Tahe OilfieldDevelopment technology and research direction of fractured- vuggy carbonate reservoirs in Tahe Oilfield. Reserv. Eval. Dev. 2020, 10, 1–10. [Google Scholar]
- Wei, Z.; Gang, H.A.I.; Ying, Z. Gas-Water Composite Flooding Technology for Fractured and Vuggy Carbonate Reservoirs in Tahe Oilfield. Pet. Drill. Tech. 2020, 48, 61–65. [Google Scholar] [CrossRef]
- Tan, T.; Guo, C.; Chen, Y.; Dou, L.; Company, O. Study and practice on mechanism of EOR by N2 flooding in fractured-vuggy reservoirs with high temperature and high pressure. Reserv. Eval. Dev. 2020, 10, 60–64. [Google Scholar]
- Lyu, X.; Liu, Z.; Hou, J.; Lyu, T. Mechanism and influencing factors of EOR by N2 injection in fractured-vuggy carbonate reservoirs. J. Nat. Gas Sci. Eng. 2017, 40, 226–235. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, L.; Li, H.; Li, W.; Yuan, D.; Yuan, Y.; Zheng, Z. Influencing factors on EOR nitrogen flooding in fractured-vuggy carbonate reservoir. Pet. Geol. Recover. Effic. 2015, 22, 64–68. [Google Scholar]
- Xiaojun, C. Visualized Gas Drive EOR Experiments in Fractured-Vuggy Reservoirs after Waterflooding in Tahe Oilfield. Xinjiang Pet. Geol. 2018, 39, 473–479. [Google Scholar]
- Zheng, Z.; Zhu, T.; Hou, J.; Luo, M.; Gao, Y. Visible research on remaining oil after nitrogen flooding in fractured-cavity carbonate reservoir. Pet. Geol. Recover. Effic. 2016, 23, 93–97. [Google Scholar]
- Qu, M.; Hou, J.; Zhao, F.; Song, Z.; Ma, S.; Wang, Q.; Li, M.; Yang, M. 3-D visual experiments on fluid flow behavior of water flooding and gas flooding in fractured-vuggy carbonate reservoir. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017; p. SPE187273. [Google Scholar]
- Yang, J.; Hou, J. Experimental study on gas channeling characteristics of nitrogen and foam flooding in 2-D visualized fractured-vuggy model. J. Pet. Sci. Eng. 2020, 192, 107337. [Google Scholar] [CrossRef]
- Yang, J.; Hou, J.; Qu, M.; Liang, T.; Wen, Y. Experimental study the flow behaviors and mechanisms of nitrogen and foam assisted nitrogen gas flooding in 2-D visualized fractured-vuggy model. J. Pet. Sci. Eng. 2020, 194, 107501. [Google Scholar] [CrossRef]
- Wang, J.; Ji, Z.; Liu, H.; Huang, Y.; Wang, Y.; Pu, Y. Experiments on nitrogen assisted gravity drainage in fractured-vuggy reservoirs. Pet. Explor. Dev. 2019, 46, 355–366. [Google Scholar] [CrossRef]
- Qu, M.; Hou, J.; Wen, Y.; Liang, T. Nitrogen gas channeling characteristics in fracture-vuggy carbonate reservoirs. J. Pet. Sci. Eng. 2020, 186, 106723. [Google Scholar] [CrossRef]
- He, J.; Killough, J.E.; Gao, S.; Fadlelmula, M.M.; Michael Fraim, F. Confronting the simulation of fluid flow in naturally fractured carbonate karst reservoirs. In Proceedings of the Society of Petroleum Engineers—Abu Dhabi International Petroleum Exhibition and Conference 2016, Abu Dhabi, United Arab Emirates, 7–10 November 2016; p. SPE183143. [Google Scholar]
- Zhang, H.; Lv, X.; Liu, Z.; Han, K. A Study on Fracture Vuggy Reservoir Multi-scale Flow Simulation Based on Pseudo-particle Method. J. Southwest Pet. Univ. Technol. Ed. 2014, 36, 93–100. [Google Scholar]
- Wu, Y.S.; Di, Y.; Kang, Z.; Fakcharoenphol, P. A multiple-continuum model for simulating single-phase and multiphase flow in naturally fractured vuggy reservoirs. J. Pet. Sci. Eng. 2011, 78, 13–22. [Google Scholar] [CrossRef]
- Gao, Y.; Li, X.; Peng, X. Study on Equivalent Simulation Method of Large-scale Fracture Cavity Body in Fracture Cavity Reservoir. J. Yangtze Univ. Sci. Ed. 2016, 13, 66–69. [Google Scholar]
- Yong, L.; Baozhu, L.; Qi, W.; Xingliang, D. Different equivalent simulation methods for fractured-vuggy carbonate gas condensate reservoirs. In Proceedings of the Society of Petroleum Engineers—SPE Europec featured at 79th EAGE Conference and Exhibition, Paris, France, 12–15 June 2017; pp. 1393–1404. [Google Scholar] [CrossRef]
- Yan, X.; Huang, Z.; Yao, J.; Zhang, Z.; Liu, P.; Li, Y.; Fan, D. Numerical simulation of hydro-mechanical coupling in fractured vuggy porous media using the equivalent continuum model and embedded discrete fracture model. Adv. Water Resour. 2019, 126, 137–154. [Google Scholar] [CrossRef]
- Kang, Z.; Li, Y.; Ji, B. Key technologies for EOR in fracture-vuggy carbonate reservoirs. OIL GAS Geol. 2020, 41, 434–441. [Google Scholar]
- Kang, Z.; Wu, Y.S.; Li, J.; Wu, Y.; Zhang, J.; Wang, G. Modeling multiphase flow in naturally fractured vuggy petroleum reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006; Volume 3, pp. 1794–1803. [Google Scholar] [CrossRef]
- Wu, Y.S.; Qin, G.; Ewing, R.E.; Efendiev, Y.; Kang, Z.; Ren, Y. A multiple-continuum approach for modeling multiphase flow in naturally fractured vuggy petroleum reservoirs. In Proceedings of the International Oil & Gas Conference and Exhibition in China, Beijing, China, 5–7 December 2006; Volume 2, pp. 739–750. [Google Scholar] [CrossRef]
- Kiran, R.; Ahmed, R.; Salehi, S. Experiments and CFD modelling for two phase flow in a vertical annulus. Chem. Eng. Res. Des. 2020, 153, 201–211. [Google Scholar] [CrossRef]
- Fu, H.; Yang, L.; Liang, H.; Wang, S.; Ling, K. Diagnosis of the single leakage in the fluid pipeline through experimental study and CFD simulation. J. Pet. Sci. Eng. 2020, 193, 107437. [Google Scholar] [CrossRef]
- Ge, Z.; He, D.; Huang, R.; Zuo, J.; Luo, X. Application of CFD-PBM coupling model for analysis of gas-liquid distribution characteristics in centrifugal pump. J. Pet. Sci. Eng. 2020, 194, 107518. [Google Scholar] [CrossRef]
- Yan, T.; Qu, J.; Sun, X.; Chen, Y.; Hu, Q.; Li, W.; Zhang, H. Numerical investigation on horizontal wellbore hole cleaning with a four-lobed drill pipe using CFD-DEM method. Powder Technol. 2020, 375, 249–261. [Google Scholar] [CrossRef]
- Zhang, R.; Bo, K.; Liu, Z. A method of sizing plugging nanoparticles to prevent water invasion for shale wellbore stability based on CFD-DEM simulation. J. Pet. Sci. Eng. 2021, 196, 107733. [Google Scholar] [CrossRef]
- Azadi, M.; Aminossadati, S.M.; Chen, Z. Large-scale study of the effect of wellbore geometry on integrated reservoir-wellbore flow. J. Nat. Gas Sci. Eng. 2016, 35, 320–330. [Google Scholar] [CrossRef] [Green Version]
- Sami, N.A.; Turzo, Z. Computational fluid dynamic (CFD) simulation of pilot operated intermittent gas lift valve. Pet. Res. 2020, 5, 254–264. [Google Scholar] [CrossRef]
- Sami, N.A.; Turzo, Z. Computational fluid dynamic (CFD) modelling of transient flow in the intermittent gas lift. Pet. Res. 2020, 5, 144–153. [Google Scholar] [CrossRef]
- Liu, C.; Li, J.; Song, Y. Study on the flow of water drive in cavern of fractured-cave reservoirs. Hebei J. Ind. Sci. Technol. 2018, 35, 171–177. [Google Scholar]
- Pinilla, A.; Asuaje, M.; Hurtado, C.; Hoyos, A.; Ramirez, L.; Padrón, A.; Ratkovich, N. 3D CFD simulation of a horizontal well at pore scale for heavy oil fields. J. Pet. Sci. Eng. 2021, 196, 107632. [Google Scholar] [CrossRef]
- Mehraban, M.F.; Rostami, P.; Afzali, S.; Ahmadi, Z.; Sharifi, M.; Ayatollahi, S. Brine composition effect on the oil recovery in carbonate oil reservoirs: A comprehensive experimental and CFD simulation study. J. Pet. Sci. Eng. 2020, 191, 107149. [Google Scholar] [CrossRef]
- Liu, C.; Liu, G.; Li, J.; Yan, Z. Anaylysis of mechanism and influential factors of water-driven-oil in fractured-vuggy reservoirs based on Fluent and Hernandez. J. Nanjing Univ. Sci. Technol. 2019, 43, 367–372. [Google Scholar]
- Mudunuru, M.K.; Carey, J.W.; Chen, L.; Kang, Q.; Karra, S.; Vesselinov, V.V.; Middleton, R.S.; Johnson, P.A.; Viswanathan, H.S. Subsurface energy: Flow and reactive-transport in porous and fractured media. In Handbook of Porous Materials: Synthesis, Properties, Modeling and Key Applications; World Scientific: Singapore, 2020; Volume 4, pp. 323–395. [Google Scholar] [CrossRef]
- Mudunuru, M.K.; O’Malley, D.; Srinivasan, S.; Hyman, J.D.; Sweeney, M.R.; Frash, L.; Carey, B.; Gross, M.R.; Welch, N.J.; Karra, S.; et al. Physics-informed machine learning for real-time unconventional reservoir management. CEUR Workshop Proc. (No. LA-UR-19-31611); Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2020; Volume 2587. [Google Scholar]
- Gross, M.R.; Hyman, J.D.; Srinivasan, S.; O’Malley, D.; Karra, S.; Mudunuru, M.K.; Sweeney, M.; Frash, L.; Carey, B.; Guthrie, G.D.; et al. A Physics-informed Machine Learning Workflow to Forecast Production in a Fractured Marcellus Shale Reservoir. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 26–28 July 2021; pp. 1–8. [Google Scholar] [CrossRef]








| Pressure (MPa) | Oil Viscosity (MPa·s) | Oil Density (g/cm3) | Brine Viscosity (MPa·s) | Brine Density (g/cm3) |
|---|---|---|---|---|
| 60 | 30 | 0.80 | 0.20 | 1.13 |
| Injection Rate (m3/d) | Cumulative Recovery | Recovery Increment |
|---|---|---|
| 20,000 | 89.94% | 15.14% |
| 40,000 | 87.59% | 12.79% |
| 50,000 | 87.24% | 12.44% |
| 60,000 | 86.84% | 12.04% |
| 80,000 | 85.84% | 11.04% |
| Injection Mode | Cumulative Recovery | Recovery Increment |
|---|---|---|
| Continuous | 82.29% | 7.49% |
| Intermittent | 87.61% | 12.81% |
| Gas–water mixed | 82.58% | 7.78% |
| Gas–water alternate | 83.69% | 8.89% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Chen, B.; Pu, W.; Wang, J.; Liu, Y.; Varfolomeev, M.; Yuan, C. Numerical Simulation via CFD Methods of Nitrogen Flooding in Carbonate Fractured-Vuggy Reservoirs. Energies 2021, 14, 7554. https://doi.org/10.3390/en14227554
Li K, Chen B, Pu W, Wang J, Liu Y, Varfolomeev M, Yuan C. Numerical Simulation via CFD Methods of Nitrogen Flooding in Carbonate Fractured-Vuggy Reservoirs. Energies. 2021; 14(22):7554. https://doi.org/10.3390/en14227554
Chicago/Turabian StyleLi, Kexing, Bowen Chen, Wanfen Pu, Jianhai Wang, Yongliang Liu, Mikhail Varfolomeev, and Chengdong Yuan. 2021. "Numerical Simulation via CFD Methods of Nitrogen Flooding in Carbonate Fractured-Vuggy Reservoirs" Energies 14, no. 22: 7554. https://doi.org/10.3390/en14227554
APA StyleLi, K., Chen, B., Pu, W., Wang, J., Liu, Y., Varfolomeev, M., & Yuan, C. (2021). Numerical Simulation via CFD Methods of Nitrogen Flooding in Carbonate Fractured-Vuggy Reservoirs. Energies, 14(22), 7554. https://doi.org/10.3390/en14227554








