Laminar Burning Velocities of Hydrogen-Blended Methane–Air and Natural Gas–Air Mixtures, Calculated from the Early Stage of p(t) Records in a Spherical Vessel
Abstract
:1. Introduction
2. Experimental Procedure
3. Computing Program
4. Data Evaluation
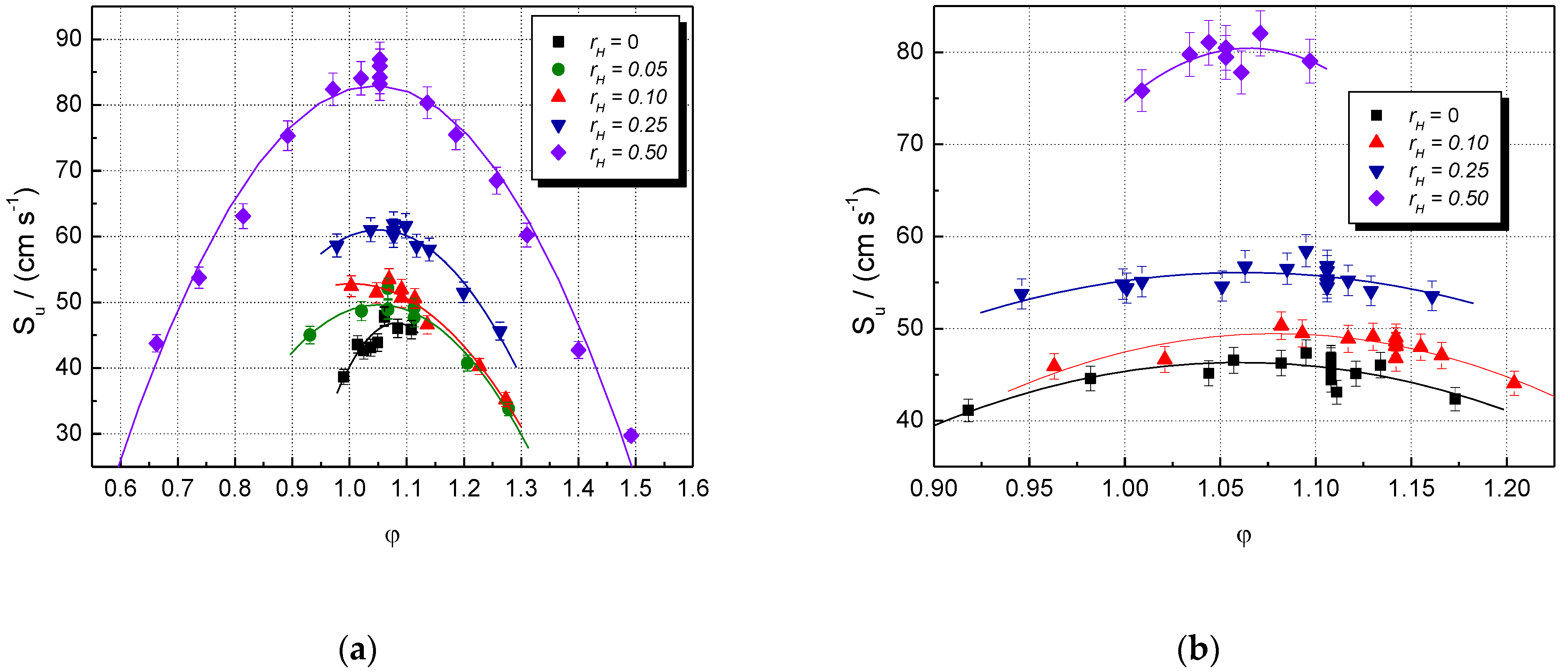
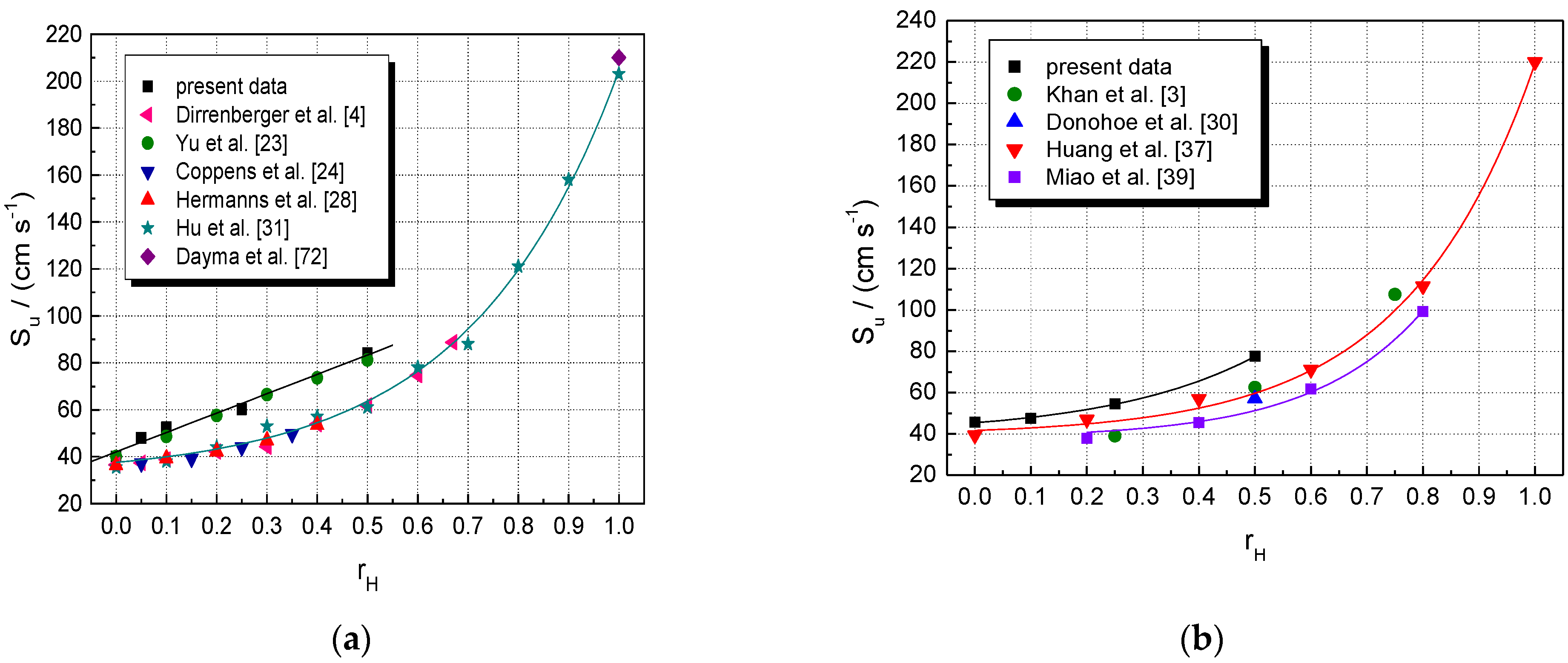
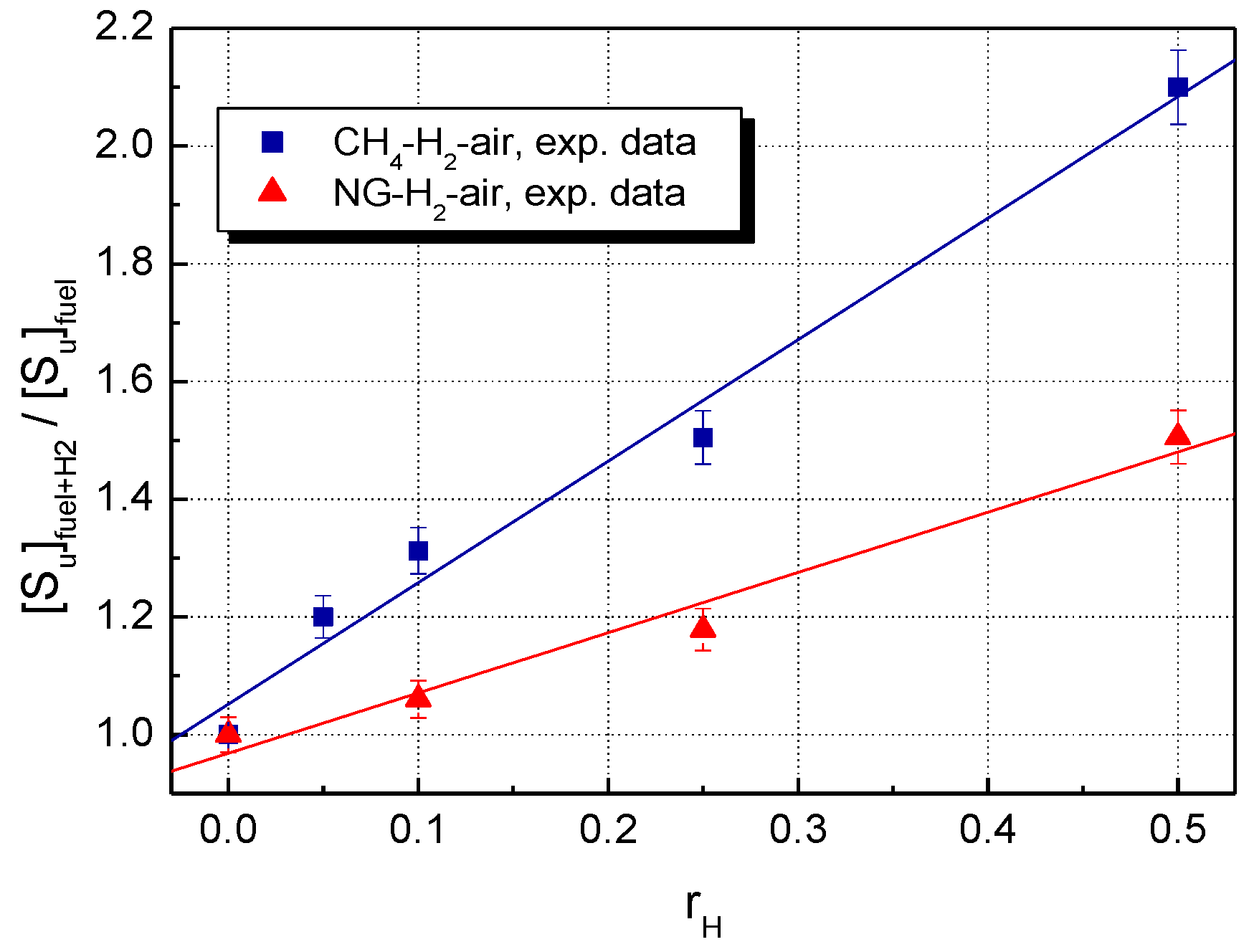
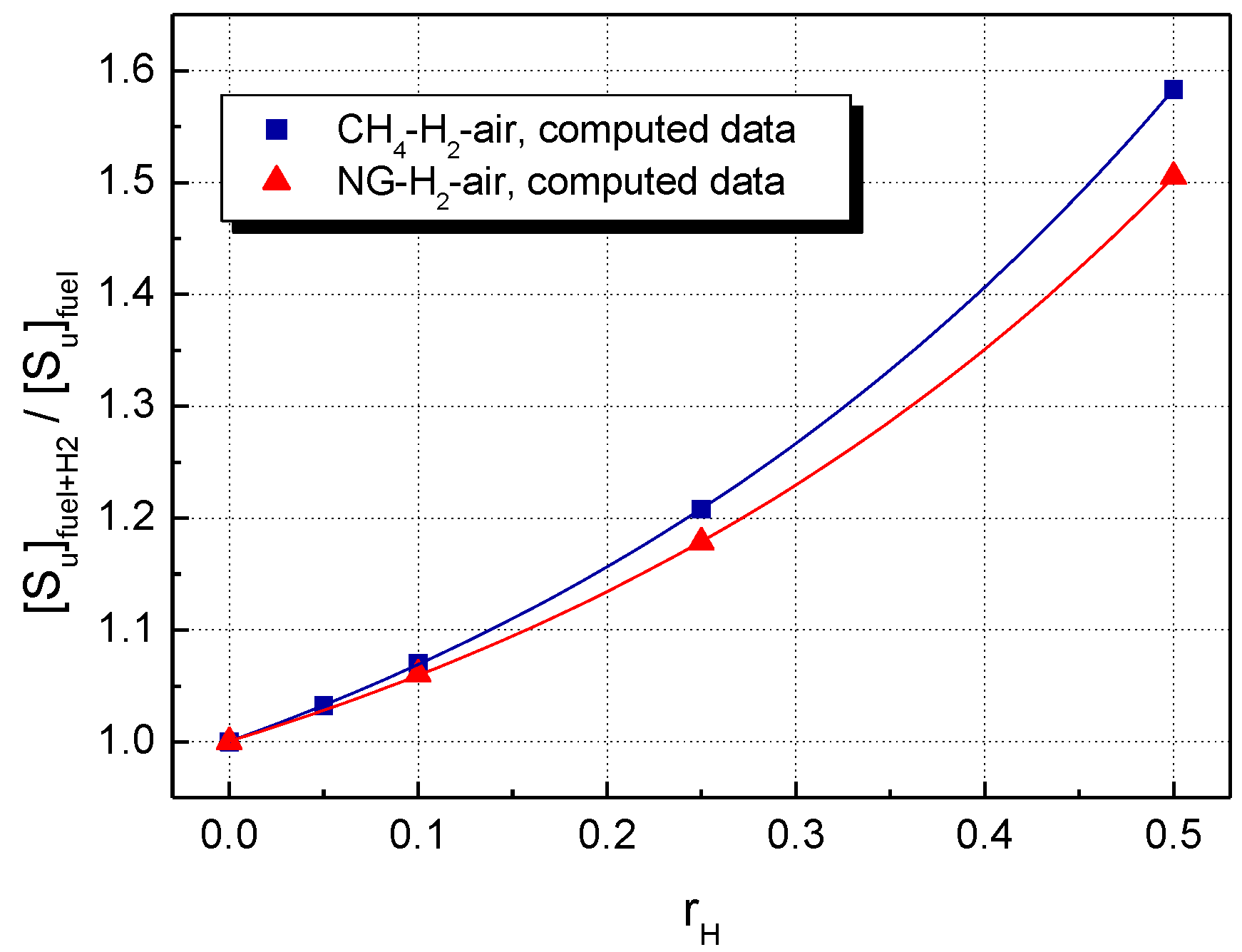
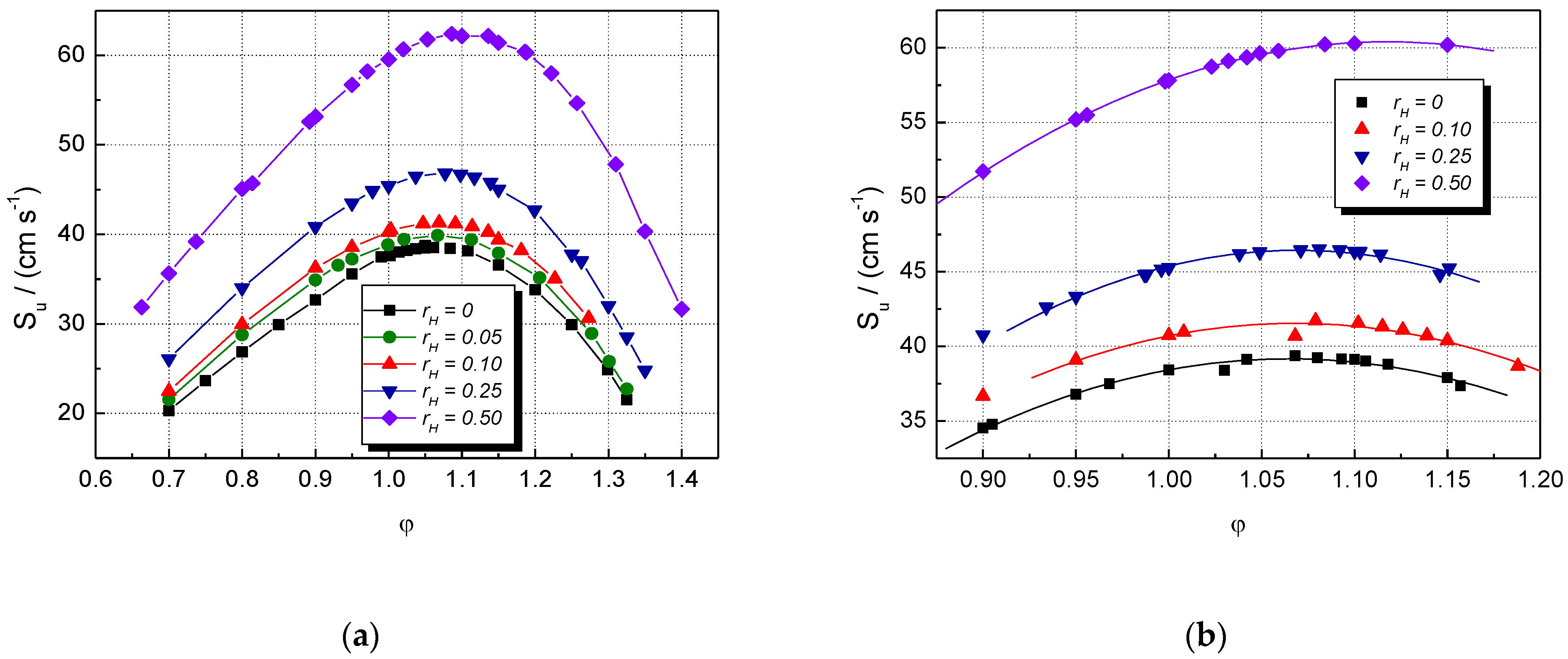
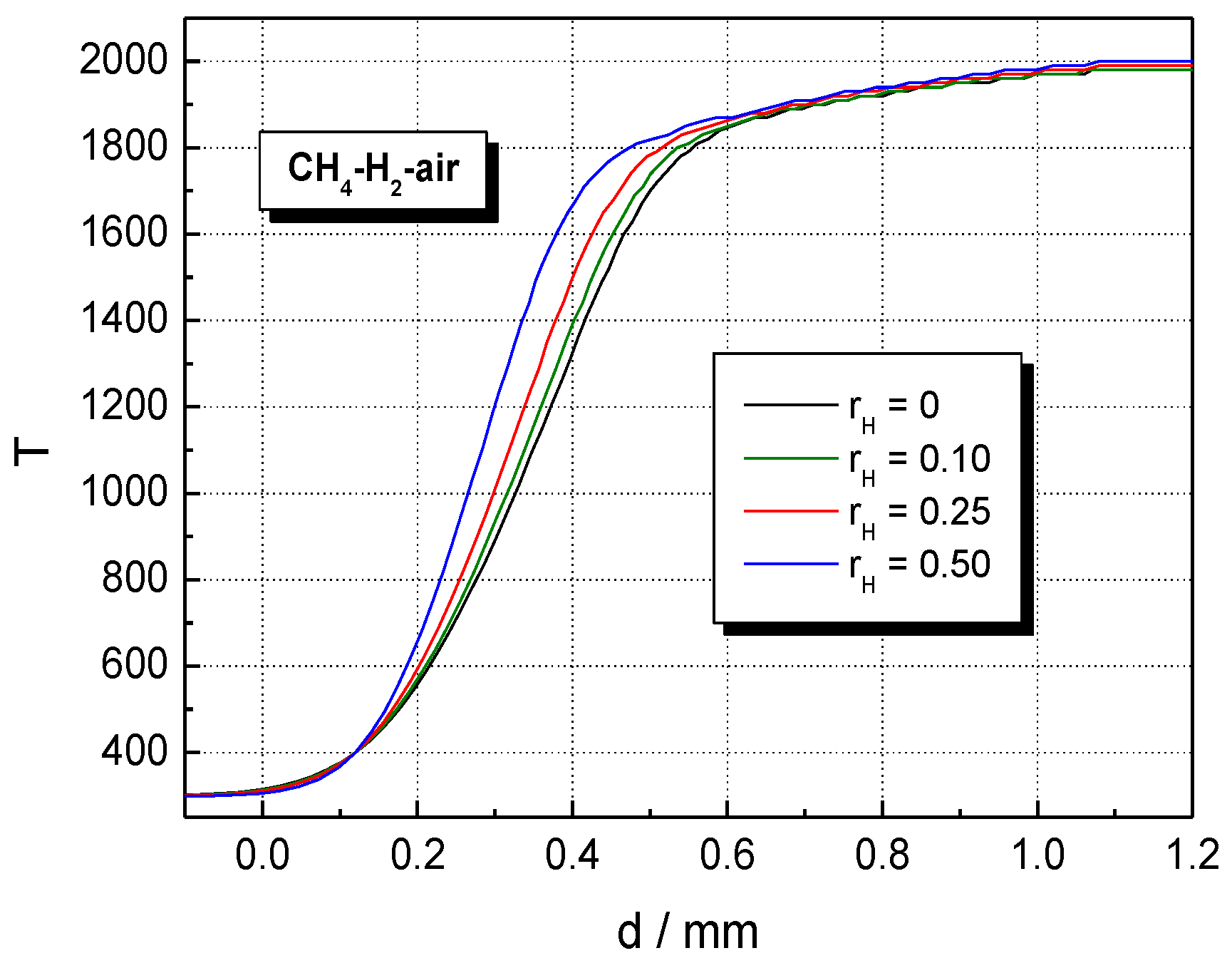
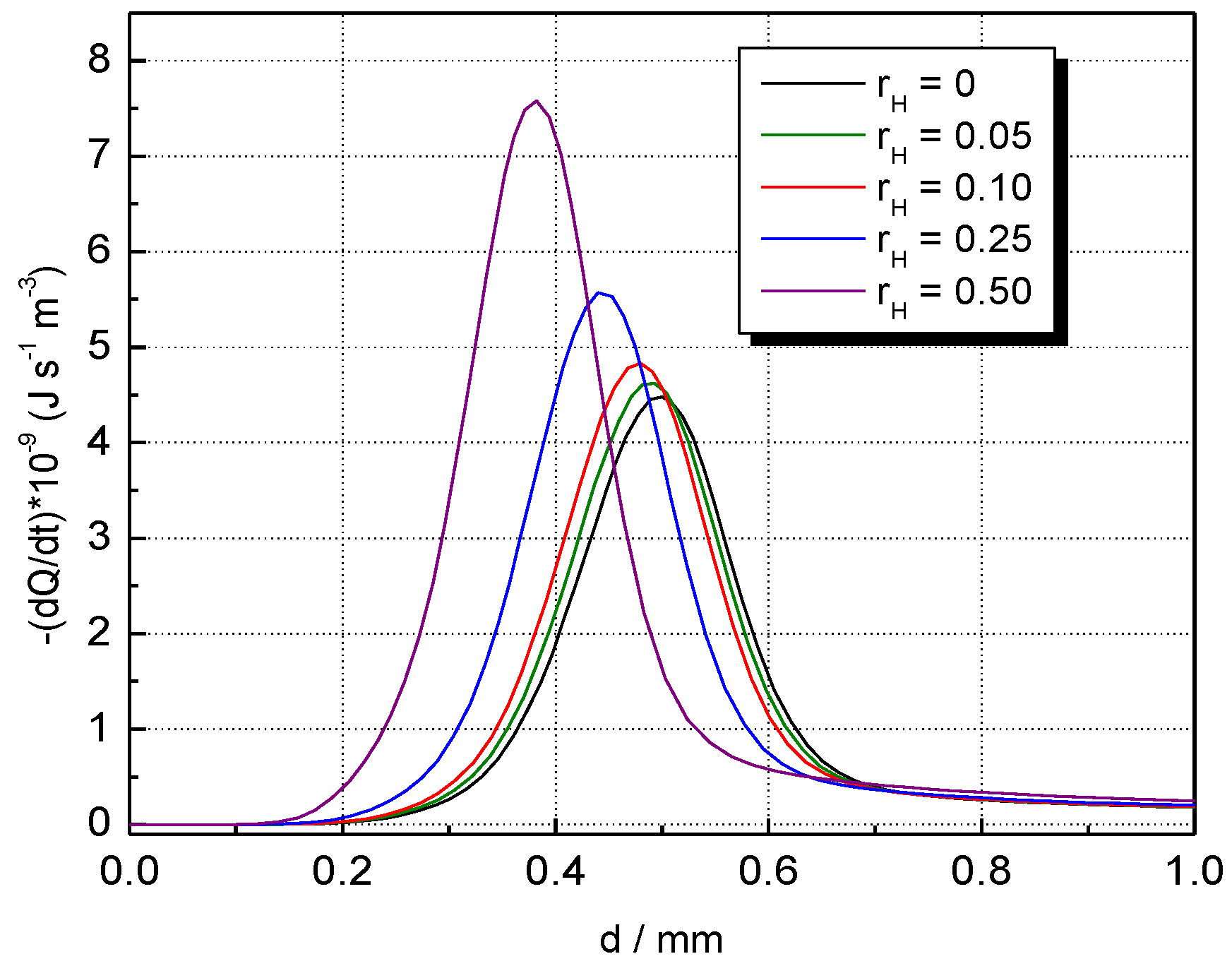
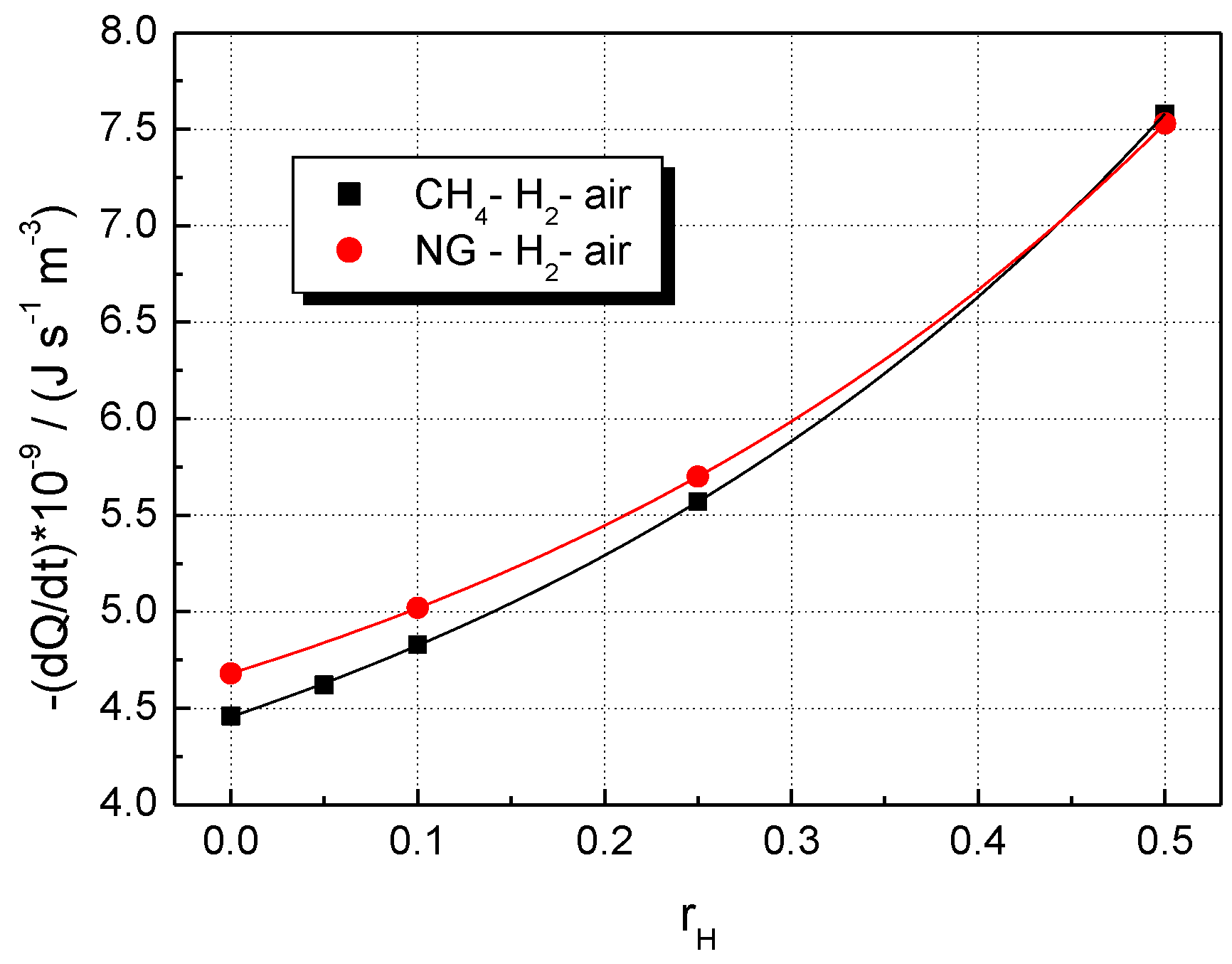
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gad, M.S.; Ismail, M.A. Effect of waste cooking oil biodiesel blending with gasoline and kerosene on diesel engine performance, emissions and combustion characteristics. Process Saf. Environ. Prot. 2021, 149, 1–10. [Google Scholar] [CrossRef]
- Gad, M.S.; El-Shafay, A.S.; Hashish, H.M. Assessment of diesel engine performance, emissions and combustion characteristics burning biodiesel blends from jatropha seeds. Process Saf. Environ. Prot. 2021, 147, 518–526. [Google Scholar] [CrossRef]
- Khan, A.R.; Ravi, M.R.; Ray, A. Experimental and chemical kinetic studies of the effect of H2 enrichment on the laminar burning velocity and flame stability of various multicomponent natural gas blends. Int. J. Hydrogen Energy 2019, 44, 1192–1212. [Google Scholar] [CrossRef]
- Dirrenberger, P.; Le Gall, H.; Bounaceur, R.; Herbinet, O.; Glaude, P.A.; Konnov, A.; Battin-Leclerc, F. Measurements of laminar flame velocity for components of natural gas. Energy Fuels 2011, 25, 3875–3884. [Google Scholar] [CrossRef] [Green Version]
- Liao, S.Y.; Jiang, D.M.; Cheng, Q. Determination of laminar burning velocities for natural gas. Fuel 2004, 83, 1247–1250. [Google Scholar] [CrossRef]
- Zhang, B.; Xiu, G.; Bai, C. Explosion characteristics of argon/nitrogen diluted natural gas—Air mixtures. Fuel 2014, 124, 125–132. [Google Scholar] [CrossRef]
- Ren, F.; Chu, H.; Xiang, L.; Han, W.; Gu, M. Effect of hydrogen addition on the laminar premixed combustion characteristics the main components of natural gas. J. Energy Inst. 2019, 92, 1178–1190. [Google Scholar] [CrossRef]
- Tang, C.L.; Huang, Z.H.; Law, C.K. Determination, correlation, and mechanistic interpretation of effects of hydrogen addition on laminar flame speeds of hydrocarbon—Air mixtures. Proc. Combust. Inst. 2011, 33, 921–928. [Google Scholar] [CrossRef]
- Brower, M.; Petersen, E.L.; Metcalfe, W.; Curran, H.J.; Fueri, M.; Bourque, G.; Aluri, N.; Guethe, F. Ignition delay time and laminar flame speed calculations for natural gas/hydrogen blends at elevated pressures. J. Eng. Gas Turbines Power 2013, 135, 021504. [Google Scholar] [CrossRef] [Green Version]
- Ma, Q.; Zhang, Q.; Chen, J.; Huang, Y.; Shi, Y. Effects of hydrogen on combustion characteristics of methane in air. Int. J. Hydrogen Energy 2014, 39, 11291–11298. [Google Scholar] [CrossRef]
- Askar, E.; Schröder, V.; Schütz, S.; Seemann, A. Power-to-gas: Safety characteristics of hydrogen/natural-gas mixtures. Chem. Eng. Trans. 2016, 48, 397–402. [Google Scholar] [CrossRef]
- Li, T.; Hampp, F.; Lindstedt, R.P. Experimental study of turbulent explosions in hydrogen enriched syngas related fuels. Process Saf. Environ. Prot. 2018, 116, 663–676. [Google Scholar] [CrossRef]
- Molnarne, M.; Schroeder, V. Hazardous properties of hydrogen and hydrogen containing fuel gases. Process Saf. Environ. Prot. 2019, 130, 1–5. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, Y.; Luo, Z.; Wen, H.; Zhao, J.; Su, B.; Cheng, F.; Deng, J. Flammability limit behavior of methane with the addition of gaseous fuel at various relative humidities. Process Saf. Environ. Prot. 2020, 140, 178–189. [Google Scholar] [CrossRef]
- Zhen, X.; Tian, Z.; Wang, Y.; Liu, D.; Li, X. A model to determine the effects of low proportion of hydrogen and the flame kernel radius on combustion and emission performance of direct injection spark ignition engine. Process Saf. Environ. Prot. 2021, 147, 1110–1124. [Google Scholar] [CrossRef]
- Chen, H.; He, J.J.; Chen, Z.M.; Geng, L.M. A comparative study of combustion and emission characteristics of dual-fuel engine fueled with diesel/methanol and diesel-polyoxymethylene dimethyl ether blend/methanol. Process Saf. Environ. Prot. 2021, 147, 714–722. [Google Scholar] [CrossRef]
- Mitu, M.; Brandes, E.; Hirsch, W. Mitigation effects on the explosion safety characteristic data of ethanol/air mixtures in closed vessel. Process Saf. Environ. Prot. 2018, 117, 190–199. [Google Scholar] [CrossRef]
- Dagaut, P.; Nicolle, A. Experimental and detailed kinetic modeling study of hydrogen-enriched natural gas blend oxidation over extended temperature and equivalence ratio ranges. Proc. Combust. Inst. 2005, 30, 631–638. [Google Scholar] [CrossRef]
- Nilsson, E.J.; van Sprang, A.; Larfeldt, J.; Konnov, A.A. The comparative and combined effects of hydrogen addition on the laminar burning velocities of methane and its blends with ethane and propane. Fuel 2017, 189, 369–376. [Google Scholar] [CrossRef]
- Kuppa, K.; Goldmann, A.; Schöffler, T.; Dinkelacker, F. Laminar flame properties of C1–C3 alkanes/hydrogen blends at gas engine conditions. Fuel 2018, 224, 32–46. [Google Scholar] [CrossRef]
- Mosisa Wako, F.; Pio, G.; Salzano, E. The Effect of Hydrogen Addition on Low-Temperature Combustion of Light Hydrocarbons and Alcohols. Energies 2020, 13, 3808. [Google Scholar] [CrossRef]
- Milton, B.E.; Keck, J.C. Laminar burning velocities in stoichiometric hydrogen and hydrogen- hydrocarbon gas mixtures. Combust. Flame 1984, 58, 13–22. [Google Scholar] [CrossRef]
- Yu, G.; Law, C.K.; Wu, C.K. Laminar flame speeds of hydrocarbon+ air mixtures with hydrogen addition. Combust. Flame 1986, 63, 339–347. [Google Scholar] [CrossRef] [Green Version]
- Coppens, F.H.V.; De Ruyck, J.; Konnov, A.A. Effects of hydrogen enrichment on adiabatic burning velocity and NO formation in methane+ air flames. Exp. Therm. Fluid Sci. 2007, 31, 437–444. [Google Scholar] [CrossRef]
- Di Sarli, V.; Di Benedetto, A. Laminar burning velocity of hydrogen–methane/air premixed flames. Int. J. Hydrogen Energy 2007, 32, 637–646. [Google Scholar] [CrossRef]
- Bourque, G.; Healy, D.; Curran, H.; Zinner, C.; Kalitan, D.; de Vries, J.; Aul, C.; Petersen, E. Ignition and Flame Speed Kinetics of Two Natural Gas Blends with High Levels of Heavier Hydrocarbons. J. Eng. Gas Turbines Power 2008, 132, 1051–1066, ASME Paper GT2008-51344. [Google Scholar] [CrossRef]
- Tahtouh, T.; Halter, F.; Samson, E.; Mounaïm-Rousselle, C. Effects of hydrogen addition and nitrogen dilution on the laminar flame characteristics of premixed methane—Air flames. Int. J. Hydrogen Energy 2009, 34, 8329–8338. [Google Scholar] [CrossRef]
- Hermanns, R.T.E.; Konnov, A.A.; Bastiaans, R.J.M.; De Goey, L.P.H.; Lucka, K.; Koehne, H. Effects of temperature and composition on the laminar burning velocity of CH4 + H2 + O2 + N2 flames. Fuel 2010, 89, 114–121. [Google Scholar] [CrossRef]
- Salzano, E.; Cammarota, F.; Di Benedetto, A.; Di Sarli, V. Explosion behavior of hydrogen–methane/air mixtures. J. Loss Prev. Process Ind. 2012, 25, 443–447. [Google Scholar] [CrossRef]
- Donohoe, N.; Heufer, A.; Metcalfe, W.K.; Curran, H.J.; Davis, M.L.; Mathieu, O.; Plichta, D.; Morones, A.; Petersen, E.L.; Güthe, F. Ignition delay times, laminar flame speeds, and mechanism validation for natural gas/hydrogen blends at elevated pressures. Combust. Flame 2014, 161, 1432–1443. [Google Scholar] [CrossRef] [Green Version]
- Dayma, G.; Zhang, S.; Li, Q.F.; Pan, X.B.; Liao, S.Y.; Wang, H.Q.; Yang, C.; Wei, S. Experimental investigation on the effects of hydrogen addition on thermal characteristics of methane/air premixed flames. Fuel 2014, 115, 232–240. [Google Scholar] [CrossRef]
- Jithin, E.V.; Varghese, R.J.; Velamati, R.K. Experimental and numerical investigation on the effect of hydrogen addition and N2/CO2 dilution on laminar burning velocity of methane/oxygen mixtures. Int. J. Hydrogen Energy 2020, 45, 16838–16850. [Google Scholar] [CrossRef]
- Di Sarli, V.; Di Benedetto, A.; Long, E.J.; Hargrave, G.K. Time-Resolved Particle Image Velocimetry of dynamic interactions between hydrogen-enriched methane/air premixed flames and toroidal vortex structures. Int. J. Hydrogen Energy 2012, 37, 16201–16213. [Google Scholar] [CrossRef] [Green Version]
- Di Sarli, V.; Di Benedetto, A. Effects of non-equidiffusion on unsteady propagation of hydrogen-enriched methane/air premixed flames. Int. J. Hydrogen Energy 2013, 38, 7510–7518. [Google Scholar] [CrossRef]
- El-Sherif, S.A. Control of emissions by gaseous additives in methane—Air and carbon monoxide—Air flames. Fuel 2000, 79, 567–575. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Y.; Zeng, K.; Liu, B.; Wang, Q.; Jiang, D. Measurements of laminar burning velocity for natural gas-hydrogen-air-mixtures. Combust. Flame 2006, 146, 302–311. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Y.; Wang, Q.; Wang, J.; Jiang, D.; Miao, H. Study on flame propagation characteristics of natural gas−hydrogen−air mixtures. Energy Fuels 2006, 20, 2385–2390. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Y.; Zeng, K.; Liu, B.; Wang, Q.; Jiang, D. Natural gas-hydrogen-air premixed mixture combustion with a constant volume bomb. Energy Fuels 2007, 21, 692–698. [Google Scholar] [CrossRef]
- Miao, H.; Jiao, Q.; Huang, Z.; Jiang, D. Measurement of laminar burning velocities and Markstein lengths of diluted hydrogen-enriched natural gas. Int. J. Hydrogen Energy 2009, 34, 507–518. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, X.; Xu, J.; Jin, B. Effects of initial pressure and hydrogen concentration on laminar combustion characteristics of diluted natural gas–hydrogen—Air mixture. Int. J. Hydrogen Energy 2012, 37, 12852–12859. [Google Scholar] [CrossRef]
- De Ferrières, S.; El Bakali, A.; Gasnot, L.; Montero, M.; Pauwels, J.F. Kinetic effect of hydrogen addition on natural gas premixed flames. Fuel 2013, 106, 88–97. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, X.; Hou, X.; Li, M. Effect of initial pressure, temperature and equivalence ratios on laminar combustion characteristics of hydrogen enriched natural gas. J. Energy Inst. 2018, 91, 887–893. [Google Scholar] [CrossRef]
- Schroeder, V.; Askar, E.; Habib, A.K.; Tashqin, T. Sicherheitstechnische Eigenschaften von Erdgas-Wasserstoff-Gemischen. Res. Rep. VH2539 2016. [Google Scholar]
- Cellek, M.S. Flameless combustion investigation of CH4/H2 in the laboratory-scaled furnace. Int. J. Hydrogen Energy 2020, 45, 35208–35222. [Google Scholar] [CrossRef]
- Ceriello, G.; Sorrentino, G.; Cavaliere, A.; Sabia, P.; de Joannon, M.; Ragucci, R. The role of dilution level and canonical configuration in the modeling of MILD combustion systems with internal recirculation. Fuel 2020, 264, 116840. [Google Scholar] [CrossRef]
- European Standard EN 15967. Determination of Maximum Explosion Pressure and the Maximum Rate of Pressure Rise of Gases and Vapours, 2011.
- Lowesmith, B.J.; Hankinson, G. Large scale high pressure jet fires involving natural gas and natural gas/hydrogen mixtures. Process Saf. Environ. Prot. 2012, 90, 108–120. [Google Scholar] [CrossRef]
- Janès, A.; Lesage, J.; Weinberger, B.; Carson, D. Experimental determination of minimum ignition current (MIC) ratio of hydrogen/methane (H2NG) blends up to 20 vol.% of hydrogen. Process Saf. Environ. Prot. 2017, 107, 299–308. [Google Scholar] [CrossRef]
- Amin, M.T.; Khan, F.; Amyotte, P. A bibliometric review of process safety and risk analysis. Process Saf. Environ. Prot. 2019, 126, 366–381. [Google Scholar] [CrossRef]
- European Standard EN 1839. Determination of Explosion Limits of Gases and Vapours, 2017.
- COSILAB, Version 3.0.3; Rotexo-Softpredict-Cosilab GmbH & Co KG: Bad Zwischenhahn, Germany, 2012.
- Giurcan, V.; Razus, D.; Mitu, M.; Oancea, D. Numerical study of the laminar flame propagation in ethane-air mixtures. Cent. Eur. J. Chem. 2014, 12, 391–402. [Google Scholar] [CrossRef]
- Mitu, M.; Giurcan, V.; Razus, D.; Oancea, D. Inert gas influence on the laminar burning velocity of methane-air mixtures. J. Hazard. Mater. 2017, 321, 440–448. [Google Scholar] [CrossRef]
- Razus, D.; Oancea, D.; Movileanu, C. Burning velocity evaluation from pressure evolution during the early stage of closed-vessel explosions. J. Loss Prev. Process Ind. 2006, 19, 334–342. [Google Scholar] [CrossRef]
- Dobashi, R. Experimental study on gas explosion behavior in enclosure. J. Loss Prev. Process Ind. 1997, 10, 83–89. [Google Scholar] [CrossRef]
- Knapton, J.; Stobie, I.; Krier, H. Burning Rate Studies of Fuel Air Mixtures at High Pressures. Combust. Flame 1973, 21, 211–220. [Google Scholar] [CrossRef]
- Sapko, M.; Furno, A.; Kuchta, J. Flame and Pressure Development of Large-Scale CH4-Air-N2 Explosions; U.S. Bureau of Mines Report No. 8176; Bureau of Mines, US Department of the Interior: Washington, DC, USA, 1976.
- Mitu, M.; Razus, D.; Giurcan, V.; Oancea, D. Normal burning velocity and propagation speed of ethane—Air: Pressure and temperature dependence. Fuel 2015, 147, 27–34. [Google Scholar] [CrossRef]
- Razus, D.; Oancea, D.; Brinzea, V.; Mitu, M.; Movileanu, C. Experimental and computed burning velocities of propane—Air mixtures. Energy Convers. Manag. 2010, 51, 2979–2984. [Google Scholar] [CrossRef]
- Giurcan, V.; Mitu, M.; Razus, D.; Oancea, D. Experimental study and kinetic modeling of laminar flame propagation in premixed stoichiometric n-butane-air mixture. Rev. Chim. (Bucharest) 2019, 70, 1125–1131. Available online: https://revistadechimie.ro/pdf/5%20GIURCAN%204%2019.pdf (accessed on 8 November 2021). [CrossRef]
- Razus, D.; Mitu, M.; Giurcan, V.; Movileanu, C.; Oancea, D. Methane-unconventional oxidant flames. Laminar burning velocities of nitrogen-diluted methane–N2O mixtures. Process Saf. Environ. Prot. 2018, 114, 240–250. [Google Scholar] [CrossRef]
- Dahoe, A.E.; de Goey, L.P.H. On the determination of the laminar burning velocity from closed vessel gas explosions. J. Loss Prev. Process Ind. 2003, 16, 457–478. [Google Scholar] [CrossRef]
- Metghalchi, M.A.K.J.; Keck, J.C. Laminar burning velocity of propane-air mixtures at high temperature and pressure. Combust. Flame 1980, 38, 143–154. [Google Scholar] [CrossRef]
- Elia, M.; Ulinski, M.; Metghalchi, M. Laminar burning velocity of methane—Air–diluent mixtures. J. Eng. Gas Turbines Power 2001, 123, 190–196. [Google Scholar] [CrossRef]
- Rahim, F.; Elia, M.; Ulinski, M.; Metghalchi, M. Burning velocity measurements of methane-oxygen-argon mixtures and an application to extend methane-air burning velocity measurements. Int. J. Engine Res. 2002, 3, 81–92. [Google Scholar] [CrossRef]
- Razus, D.; Brinzea, V.; Mitu, M.; Movileanu, C.; Oancea, D. Burning velocity of Propane-Air Mixtures from Pressure-time Records during Explosions in a Closed Spherical Vessel. Energy Fuels 2012, 26, 901–909. [Google Scholar] [CrossRef]
- Mitu, M.; Razus, D.; Giurcan, V.; Oancea, D. Experimental and Numerical Study of Laminar Burning Velocity of Ethane-Air Mixtures of Variable Initial Composition, Temperature and Pressure. Energy Fuels 2014, 28, 2179–2188. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, J.; Shu, J.; Xie, M.; Liu, J. A chemical kinetic investigation of laminar premixed burning characteristics for methane-hydrogen-air mixtures at elevated pressures. J. Taiwan Inst. Chem. Eng. 2020, 111, 141–154. [Google Scholar] [CrossRef]
- Salzano, E.; Pio, G.; Ricca, A.; Palma, V. The effect of a hydrogen addition to the premixed flame structure of light alkanes. Fuel 2018, 234, 1064–1070. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, Y.; Huang, Z. Progress in combustion investigations of hydrogen enriched hydrocarbons. Renew. Sustain. Energy Rev. 2010, 30, 195–216. [Google Scholar] [CrossRef]
- Zabetakis, M. Flammability Characteristics of Combustible Gases and Vapors; No. 627; US Bureau of Mines Bull, US Department of the Interior: Washington, DC, USA, 1965.
- Dayma, G.; Halter, F.; Dagaut, P. New insights into the peculiar behavior of laminar burning velocities of hydrogen—Air flames according to pressure and equivalence ratio. Combust. Flame 2014, 161, 2235–2241. [Google Scholar] [CrossRef]
- Su, B.; Luo, Z.; Wang, T.; Xie, C.; Cheng, F. Chemical kinetic behaviors at the chain initiation stage of CH4/H2/air mixture. J. Hazard. Mater. 2021, 403, 123680. [Google Scholar] [CrossRef] [PubMed]
- Glassman, I.; Yetter, R. Combustion, 4th ed.; Chapter 4; Academic Press: Burlington, MA, USA, 2008. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics. Internet Version. 2005. Available online: http://www.hbcpnetbase.com (accessed on 9 October 2020).

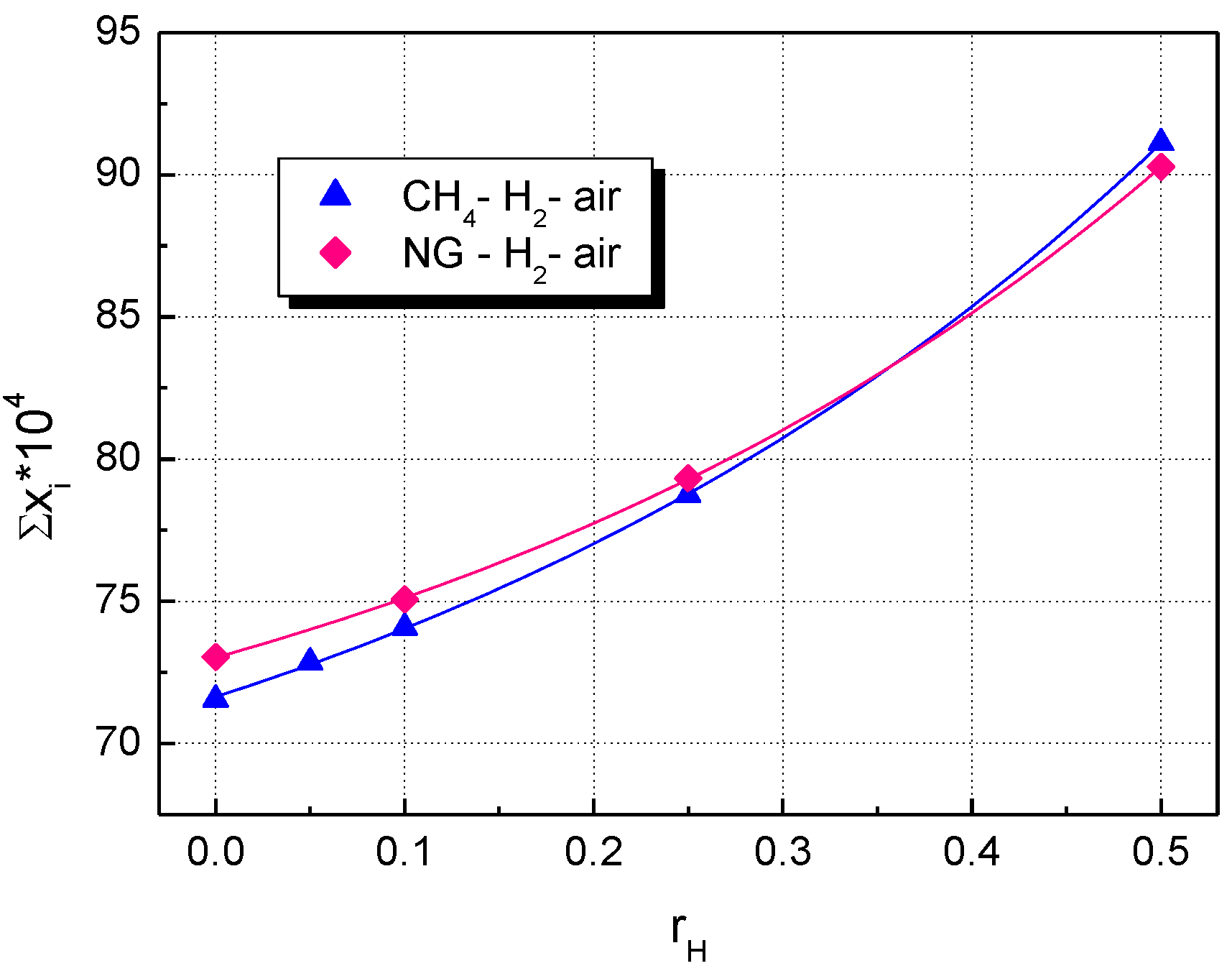
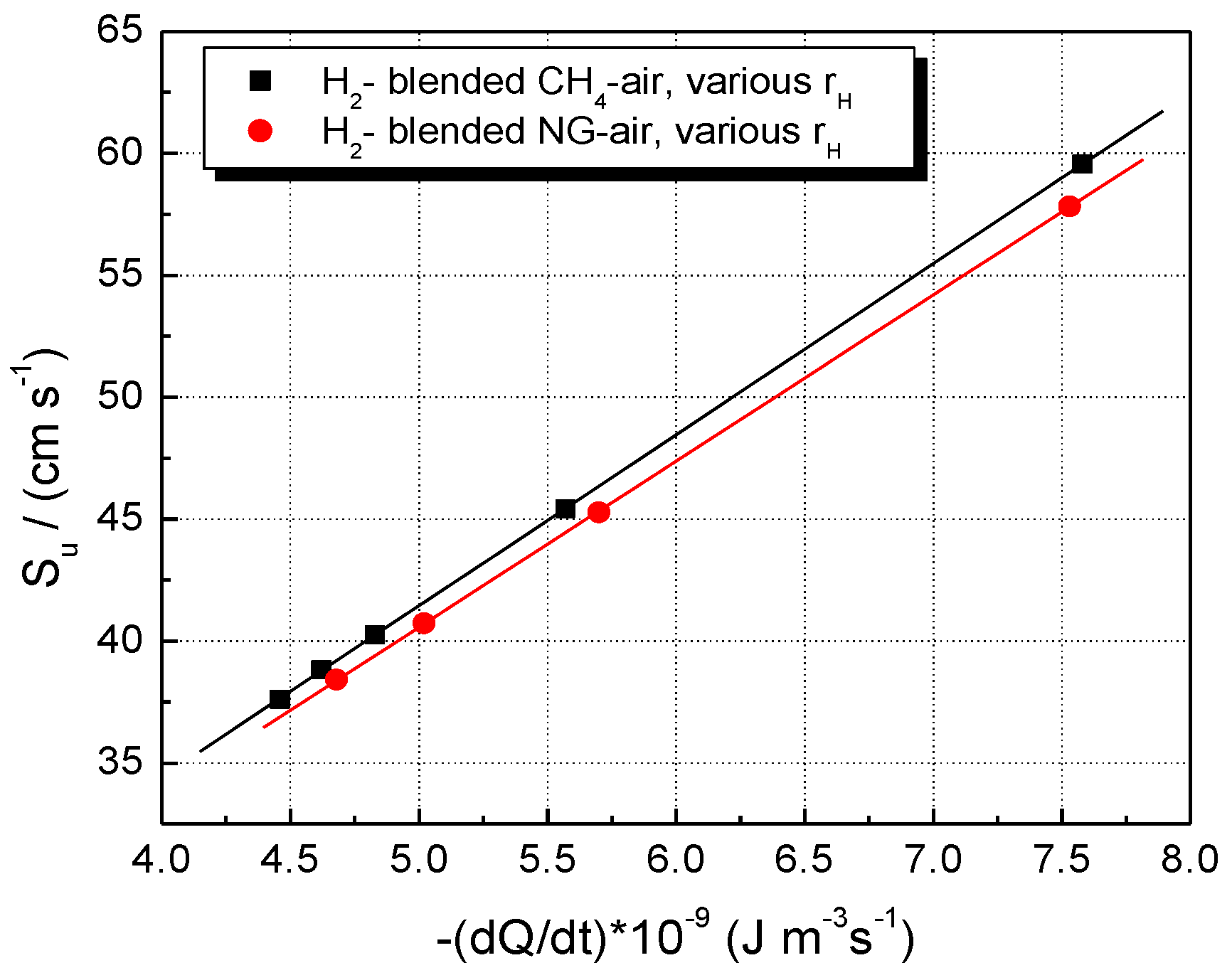
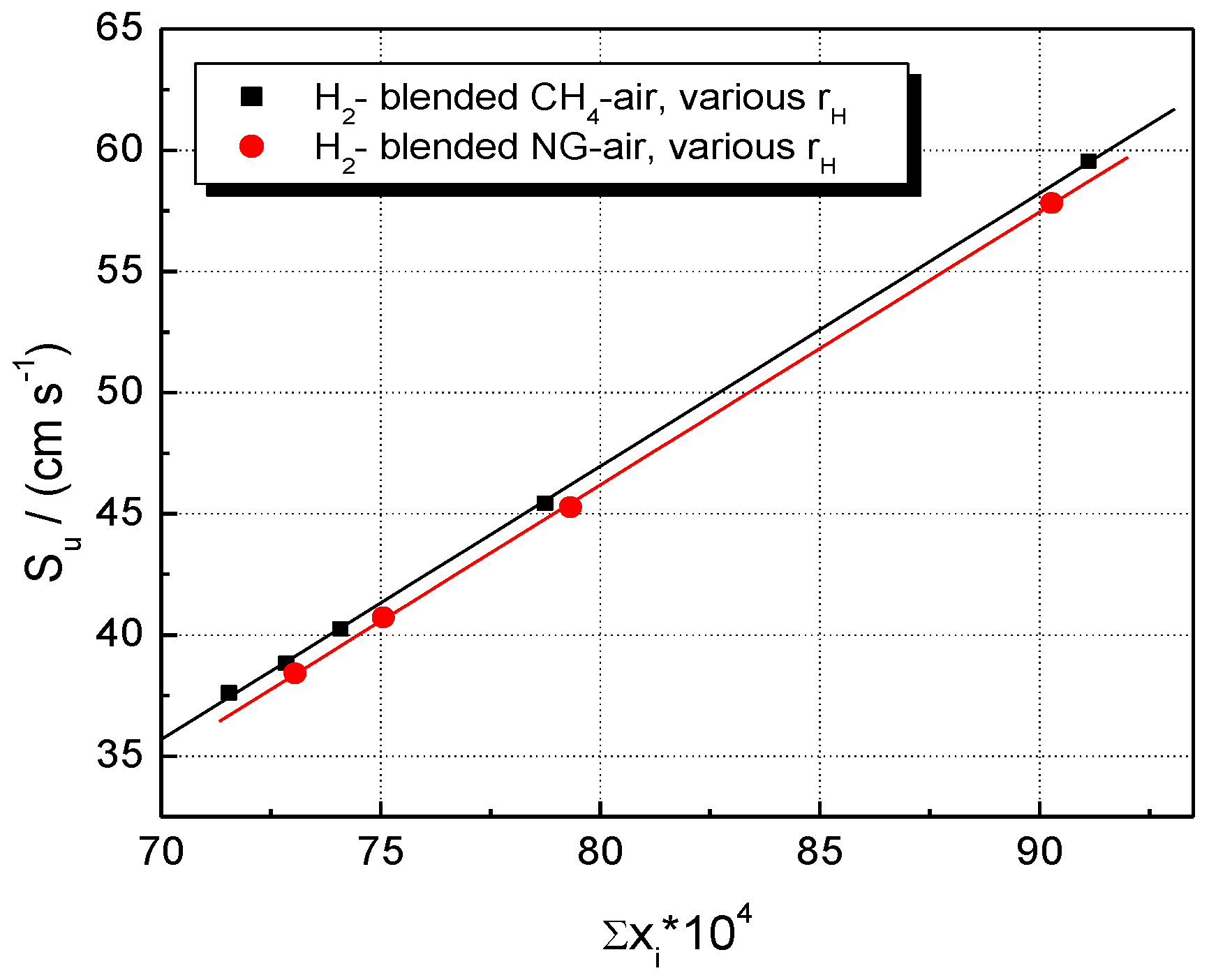
| Component | CH4 | C2H6 | C3H8 | n-C4H10 |
|---|---|---|---|---|
| Fraction in NG, mol% | 89.3 | 8.0 | 2.0 | 0.7 |
| Fuel | Equivalence Ratios, φ | |
|---|---|---|
| CH4–air | 0 | 0.95–1.15 |
| CH4–H2–air | 0.05; 0.10; 0.25; 0.50 | 0.90–1.30 |
| Natural gas (NG)–air | 0 | 0.90–1.20 |
| Natural gas (NG)–H2–air | 0.10; 0.25; 0.50 | 0.95–1.15 |
| [CH4]/mol% | [H2]/mol% | [CH4 + H2]/mol% | Equivalence Ratio, φ | Su/(cm s−1) |
|---|---|---|---|---|
| 8.40 | 2.80 | 11.20 | 0.978 | 58.6 |
| 8.84 | 2.96 | 11.80 | 1.037 | 61.0 |
| 9.14 | 3.06 | 12.20 | 1.077 | 60.2 |
| 9.14 | 3.06 | 12.20 | 1.077 | 60.9 |
| 9.14 | 3.06 | 12.20 | 1.077 | 61.9 |
| 9.30 | 3.10 | 12.40 | 1.098 | 61.6 |
| 9.44 | 3.16 | 12.60 | 1.117 | 58.6 |
| 9.60 | 3.20 | 12.80 | 1.139 | 58.0 |
| 10.04 | 3.33 | 13.40 | 1.199 | 51.5 |
| 10.50 | 3.50 | 14.00 | 1.263 | 45.6 |
| Additive | CH4 | H2 | O2 | N2 |
|---|---|---|---|---|
| cp/(J·mol−1·K−1) | 35.70 | 28.84 | 29.38 | 29.12 |
| cp/(J·kg−1·K−1) | 2231 | 14,420 | 918 | 1040 |
| ρ (kg m−3) | 0.717 | 0.0899 | 1.429 | 1.251 |
| /(mW·m−1·K−1) | 33.0 | 180.5 | 26.6 | 25.8 |
| D·106 (m2 s−1) | 20.63 | 129.2 | 20.28 | 19.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitu, M.; Razus, D.; Schroeder, V. Laminar Burning Velocities of Hydrogen-Blended Methane–Air and Natural Gas–Air Mixtures, Calculated from the Early Stage of p(t) Records in a Spherical Vessel. Energies 2021, 14, 7556. https://doi.org/10.3390/en14227556
Mitu M, Razus D, Schroeder V. Laminar Burning Velocities of Hydrogen-Blended Methane–Air and Natural Gas–Air Mixtures, Calculated from the Early Stage of p(t) Records in a Spherical Vessel. Energies. 2021; 14(22):7556. https://doi.org/10.3390/en14227556
Chicago/Turabian StyleMitu, Maria, Domnina Razus, and Volkmar Schroeder. 2021. "Laminar Burning Velocities of Hydrogen-Blended Methane–Air and Natural Gas–Air Mixtures, Calculated from the Early Stage of p(t) Records in a Spherical Vessel" Energies 14, no. 22: 7556. https://doi.org/10.3390/en14227556
APA StyleMitu, M., Razus, D., & Schroeder, V. (2021). Laminar Burning Velocities of Hydrogen-Blended Methane–Air and Natural Gas–Air Mixtures, Calculated from the Early Stage of p(t) Records in a Spherical Vessel. Energies, 14(22), 7556. https://doi.org/10.3390/en14227556







