A Fast Response Robust Deadbeat Predictive Current Control for Permanent Magnet Synchronous Motor
Abstract
:1. Introduction
2. Models of SPMSM and Analysis of Conventional Methods
2.1. Mathematical Model of SPMSM and Conventional Observer-Based DBPCC
2.2. Problems with Conventional Observer-Based DBPCC Methods
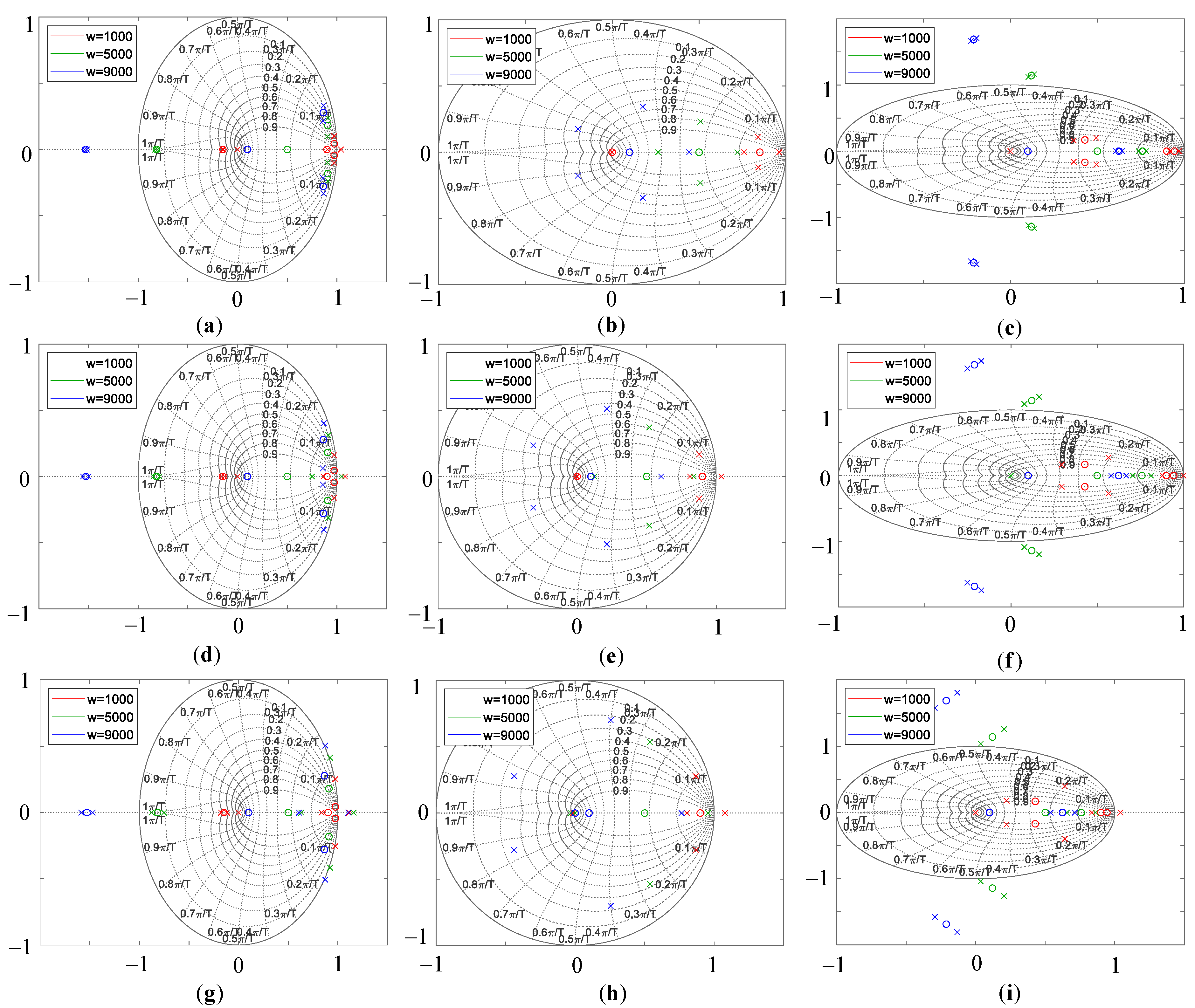
2.3. Stability Analysis of the ESO-Based DBPCC
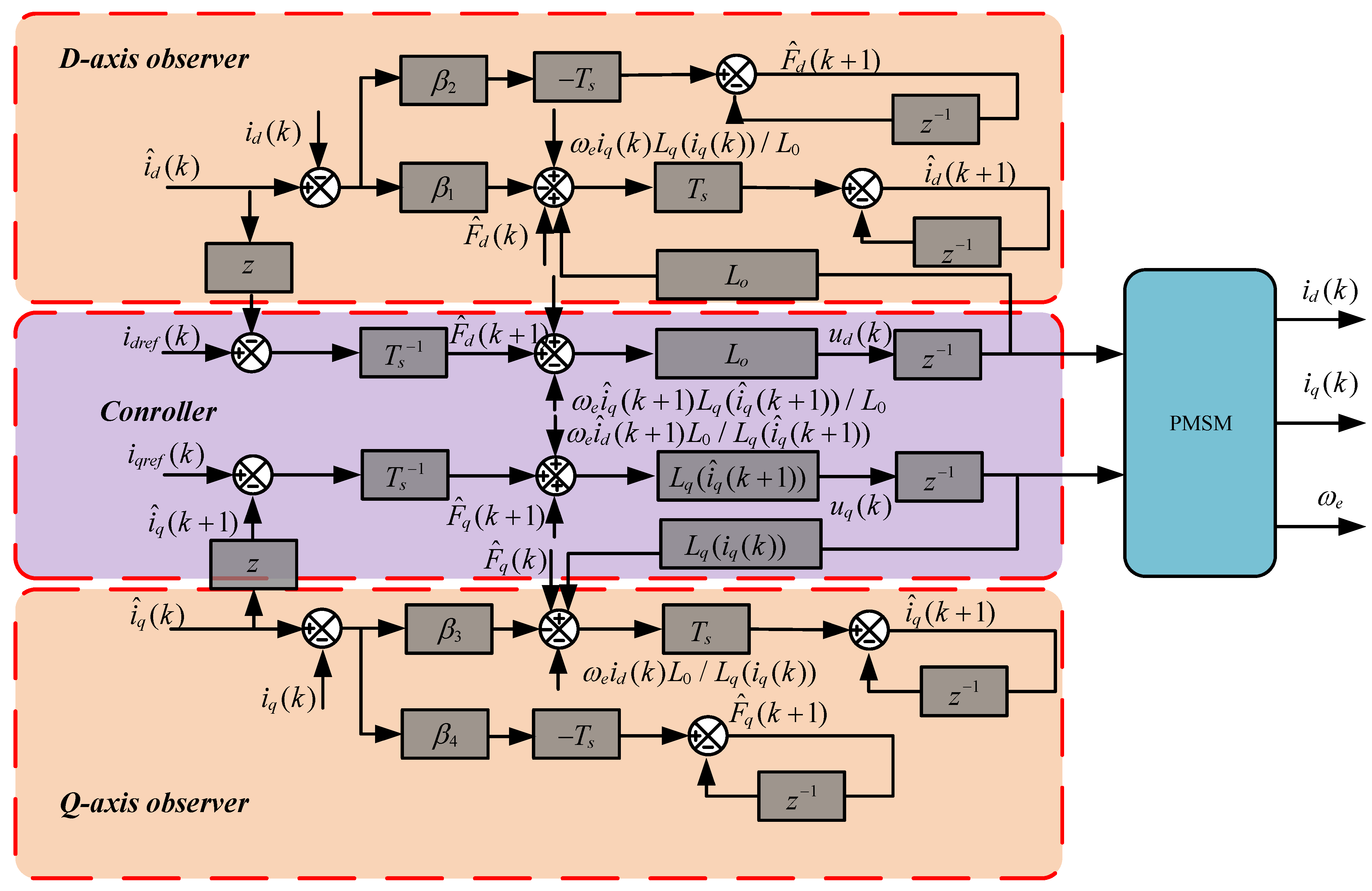
3. Proposed Methods
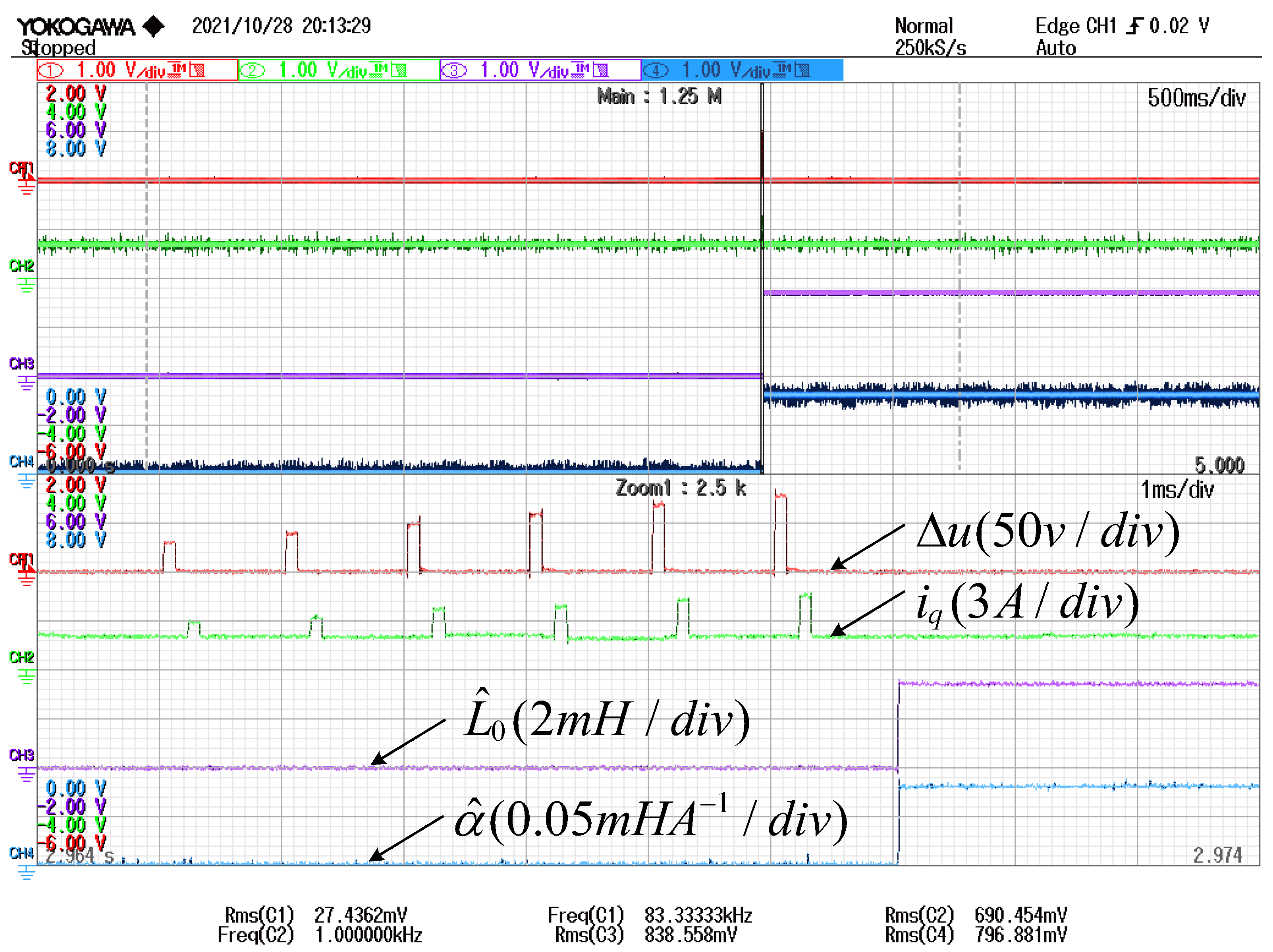
3.1. Online Inductance Identification Algorithm Considering Saturation
3.2. Proposed FRRDBPCC Method
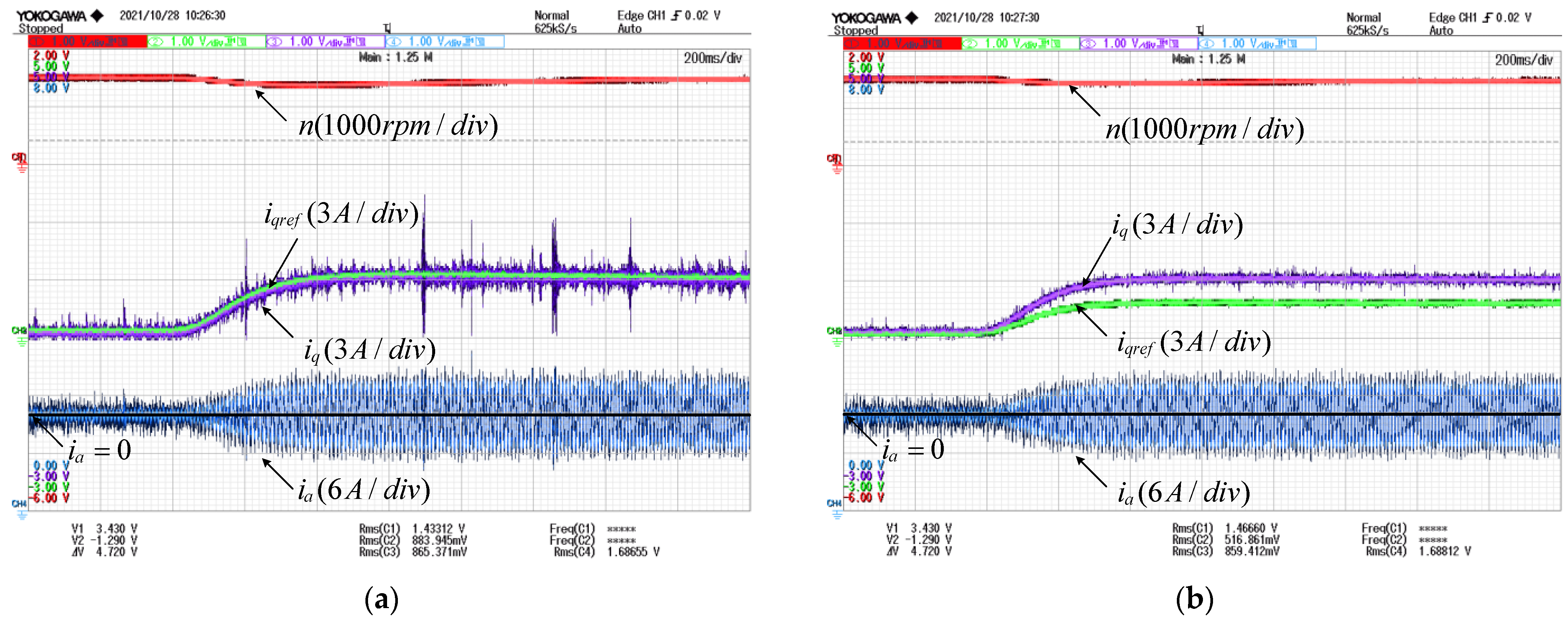
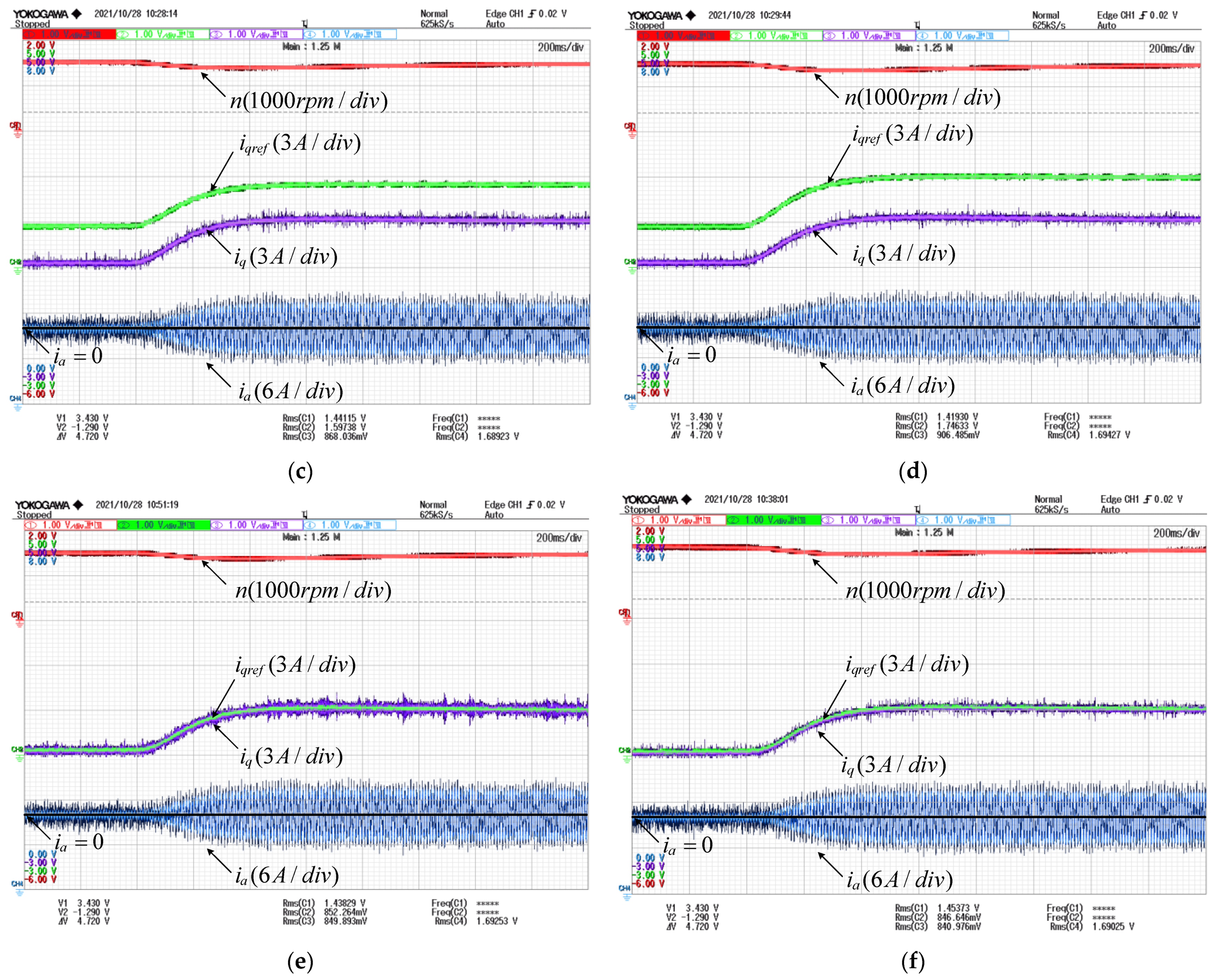
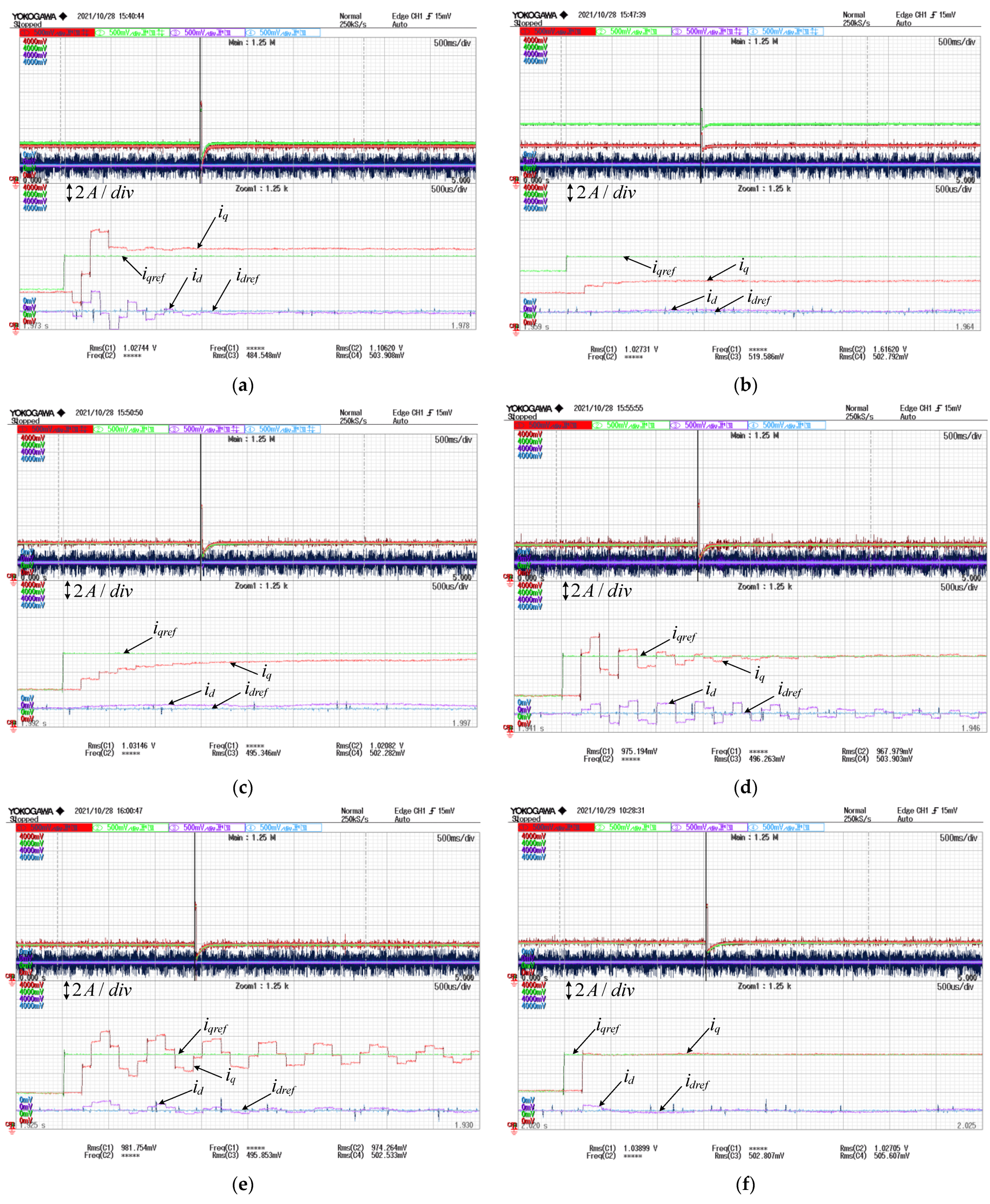
4. Experiments
4.1. Tracking Performance of Current under Loads
4.2. Tracking Performance of Current under Step Response
4.3. Inductance Identification
5. Conclusions
- (1)
- An ESO is proposed to estimate the lumped disturbance. The stability and tracking performance of the current loop are analyzed in detail.
- (2)
- An online inductance identification algorithm considering saturation is proposed to improve the dynamic response of the current loop.
- (3)
- An improved prediction model is proposed. The dq-axis can be completely decoupled. The motor resistance and flux linkage are excluded in the proposed model which simplifies the selection of parameters and reduces the computation burden in digital implementation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| SPMSM | Surface mounted permanent magnet synchronous motor |
| DBPCC | Deadbeat predictive current control |
| FRRDBPCC | Fast response robust deadbeat predictive current control |
| ESO | Extended state observer |
| PI | Proportional–integral |
| Voltage | |
| Current | |
| Resistance | |
| Inductance | |
| Flux linkage | |
| Electrical angular velocity | |
| Control period | |
| , , , | Gains of ESO |
| Lumped disturbance | |
| Derivative of lumped disturbance | |
| Saturation coefficient | |
| Reference value | |
| Nominal value | |
| , | Components in dq coordinates |
References
- Jung, J.-W.; Leu, V.Q.; Do, T.D.; Kim, E.-K.; Choi, H.H. Adaptive PID Speed Control Design for Permanent Magnet Synchronous Motor Drives. IEEE Trans. Power Electron. 2015, 30, 900–908. [Google Scholar] [CrossRef]
- Ali, M.N.; Soliman, M.; Mahmoud, K.; Guerrero, J.M.; Lehtonen, M.; Darwish, M.M.F. Resilient Design of Robust Multi-Objectives PID Controllers for Automatic Voltage Regulators: D-Decomposition Approach. IEEE Access 2021, 9, 106589–106605. [Google Scholar] [CrossRef]
- Qu, L.; Qiao, W.; Qu, L. Active-Disturbance-Rejection-Based Sliding-Mode Current Control for Permanent-Magnet Synchronous Motors. IEEE Trans. Power Electron. 2021, 36, 751–760. [Google Scholar] [CrossRef]
- Chen, Q.; Yu, X.; Sun, M.; Wu, C.; Fu, Z. Adaptive Repetitive Learning Control of PMSM Servo Systems with Bounded Nonparametric Uncertainties: Theory and Experiments. IEEE Trans. Ind. Electron. 2021, 68, 8626–8635. [Google Scholar] [CrossRef]
- Huang, M.; Deng, Y.; Li, H.; Wang, J. Torque Ripple Suppression of PMSM Using Fractional-Order Vector Resonant and Robust Internal Model Control. IEEE Trans. Transp. Electrif. 2021, 7, 1437–1453. [Google Scholar] [CrossRef]
- Niu, S.; Luo, Y.; Fu, W.; Zhang, X. Robust Model Predictive Control for a Three-Phase PMSM Motor With Improved Control Precision. IEEE Trans. Ind. Electron. 2021, 68, 838–849. [Google Scholar] [CrossRef]
- Petkar, S.G.; Eshwar, K.; Thippiripati, V.K. A Modified Model Predictive Current Control of Permanent Magnet Synchronous Motor Drive. IEEE Trans. Ind. Electron. 2021, 68, 1025–1034. [Google Scholar] [CrossRef]
- Wang, F.; He, L. FPGA-Based Predictive Speed Control for PMSM System Using Integral Sliding-Mode Disturbance Observer. IEEE Trans. Ind. Electron. 2021, 68, 972–981. [Google Scholar] [CrossRef]
- Wu, M.; Sun, X.; Zhu, J.; Lei, G.; Guo, Y. Improved Model Predictive Torque Control for PMSM Drives Based on Duty Cycle Optimization. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar] [CrossRef]
- Elsisi, M.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Effective Nonlinear Model Predictive Control Scheme Tuned by Improved NN for Robotic Manipulators. IEEE Access 2021, 9, 64278–64290. [Google Scholar] [CrossRef]
- Zhou, Z.; Xia, C.; Shi, T.; Geng, Q. Model Predictive Direct Duty-Cycle Control for PMSM Drive Systems With Variable Control Set. IEEE Trans. Ind. Electron. 2021, 68, 2976–2987. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, L.; Wang, J.; Gao, X.; Li, Z.; Zhang, Z. Robust Predictive Current Control of Permanent-Magnet Synchronous Motors With Newly Designed Cost Function. IEEE Trans. Power Electron. 2020, 35, 10778–10788. [Google Scholar] [CrossRef]
- Wang, F.; Zuo, K.; Tao, P.; Rodriguez, J. High Performance Model Predictive Control for PMSM by Using Stator Current Mathematical Model Self-Regulation Technique. IEEE Trans. Power Electron. 2020, 35, 13652–13662. [Google Scholar] [CrossRef]
- Wang, F.; He, L.; Rodriguez, J. FPGA-Based Continuous Control Set Model Predictive Current Control for PMSM System Using Multistep Error Tracking Technique. IEEE Trans. Power Electron. 2020, 35, 13455–13464. [Google Scholar] [CrossRef]
- Wei, Y.; Wei, Y.; Sun, Y.; Qi, H.; Guo, X. Prediction Horizons Optimized Nonlinear Predictive Control for Permanent Magnet Synchronous Motor Position System. IEEE Trans. Ind. Electron. 2020, 67, 9153–9163. [Google Scholar] [CrossRef]
- Elsisi, M.; Tran, M.-Q.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Robust Design of ANFIS-Based Blade Pitch Controller for Wind Energy Conversion Systems Against Wind Speed Fluctuations. IEEE Access 2021, 9, 37894–37904. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, S.; Zhang, C. Enhanced Robust Deadbeat Predictive Current Control for PMSM Drives. IEEE Access 2019, 7, 148218–148230. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, B.; Mei, Y. Deadbeat Predictive Current Control of Permanent-Magnet Synchronous Motors with Stator Current and Disturbance Observer. IEEE Trans. Power Electron. 2017, 32, 3818–3834. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.-H.; Li, S.; Guo, L.; Yan, Y. Disturbance/Uncertainty Estimation and Attenuation Techniques in PMSM Drives—A Survey. IEEE Trans. Ind. Electron. 2017, 64, 3273–3285. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Chen, X.; Yu, Y.; Wang, G.; Xu, D. Robust Predictive Current Control With Online Disturbance Estimation for Induction Machine Drives. IEEE Trans. Power Electron. 2017, 32, 4663–4674. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, W.; Mu, C.; Liu, Y. Improved Deadbeat Predictive Current Control Combined Sliding Mode Strategy for PMSM Drive System. IEEE Trans. Veh. Technol. 2018, 67, 251–263. [Google Scholar] [CrossRef]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. A Robust Deadbeat Predictive Controller With Delay Compensation Based on Composite Sliding-Mode Observer for PMSMs. IEEE Trans. Power Electron. 2021, 36, 10742–10752. [Google Scholar] [CrossRef]
- Gong, Z.; Zhang, C.; Ba, X.; Guo, Y. Improved Deadbeat Predictive Current Control of Permanent Magnet Synchronous Motor Using a Novel Stator Current and Disturbance Observer. IEEE Access 2021, 9, 142815–142826. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Huang, L. Model-Free Predictive Current Control of PMSM Drives Based on Extended State Observer Using Ultralocal Model. IEEE Trans. Ind. Electron. 2021, 68, 993–1003. [Google Scholar] [CrossRef]
- Xu, L.; Chen, G.; Li, Q. Ultra-Local Model-Free Predictive Current Control Based on Nonlinear Disturbance Compensation for Permanent Magnet Synchronous Motor. IEEE Access 2020, 8, 127690–127699. [Google Scholar] [CrossRef]
- He, L.; Wang, F.; Wang, J.; Rodriguez, J. Zynq Implemented Luenberger Disturbance Observer Based Predictive Control Scheme for PMSM Drives. IEEE Trans. Power Electron. 2020, 35, 1770–1778. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Rated speed | 1500 r/min |
| Pole pairs | 4 |
| Rated current | 3 A |
| Rated torque | 1.68 N.m |
| Rotor flux | 0.09357 Wb |
| Stator resistance | 1.75 Ω |
| Stator inductance | 3.2 mH |
| DC bus voltage | 310 V |
| Control period | 100 μs |
| Methods | Time to Reach Steady State | Steady State Tracking Error | Cross Coupling Effect | Chatteringand Overshoot |
|---|---|---|---|---|
| Conventional DBPCC with , , | 0.5 ms | large | serious | serious |
| Conventional ESO-based DBPCC with , , | 0.6 ms | large | medium | no |
| ESO-based DBPCC with | 2.5 ms | no | serious | no |
| ESO-based DBPCC with | 2 ms | no | serious | serious |
| PI controller | >3 ms | no | serious | serious |
| FRRDBPCC | 0.2 ms | no | slight | no |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, H.; Yang, J.; Deng, R. A Fast Response Robust Deadbeat Predictive Current Control for Permanent Magnet Synchronous Motor. Energies 2021, 14, 7563. https://doi.org/10.3390/en14227563
Nie H, Yang J, Deng R. A Fast Response Robust Deadbeat Predictive Current Control for Permanent Magnet Synchronous Motor. Energies. 2021; 14(22):7563. https://doi.org/10.3390/en14227563
Chicago/Turabian StyleNie, Haowei, Jiaqiang Yang, and Rongfeng Deng. 2021. "A Fast Response Robust Deadbeat Predictive Current Control for Permanent Magnet Synchronous Motor" Energies 14, no. 22: 7563. https://doi.org/10.3390/en14227563






