Comparison of the Reactive Scalar Gradient Evolution between Homogeneous MILD Combustion and Premixed Turbulent Flames
Abstract
:1. Introduction
- A comparison between the SDF statistics in EGR-type homogeneous-mixture MILD combustion and conventional premixed combustion to understand how different strain rates influence the SDF evolution in MILD combustion under different turbulence intensities.
- Modelling implication of the differences in the SDF statistics between MILD and conventional premixed turbulent combustion.
2. Mathematical Background
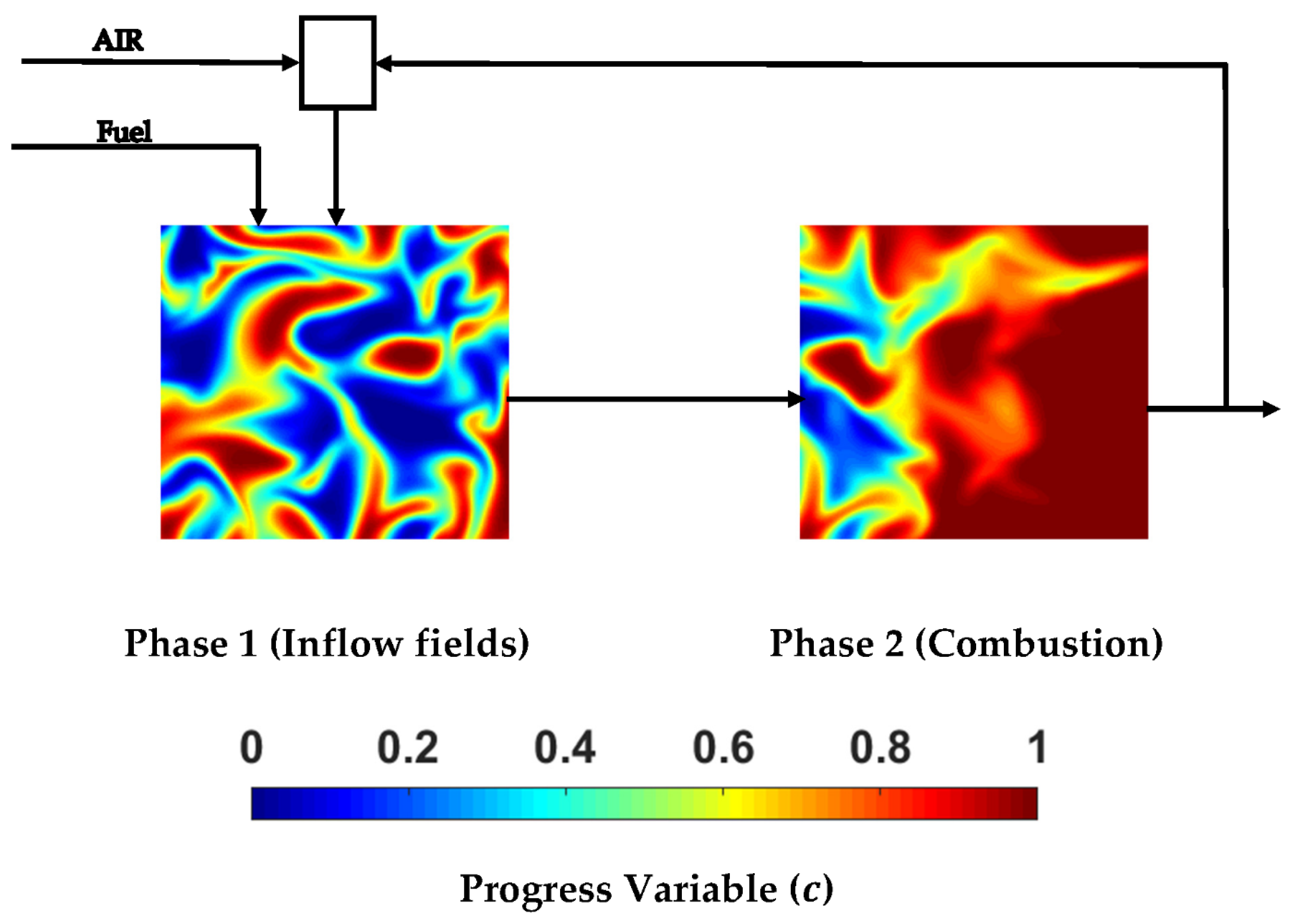
3. Numerical Implementation
- The thermochemical conditions shown in Table 1 are used to simulate a 1D laminar premixed flame for . An initial bimodal distribution of with prescribed integral length scale is then developed using the methodology by Eswaran and Pope [56]. The 1D laminar profiles of a species mass fraction for are specified as a function of the progress variable . These functions, alongside the bimodal distribution of , are used to initialise the density and species mass fractions corresponding to an atmospheric pressure and an unburned gas temperature of 1500 K (i.e., ).
- The generated bimodal scalar fields in the previous step are then allowed to evolve with turbulence for about 1 turnover time in a periodic domain mimicking the EGR in MILD combustion. At the end of this step the mean and variance of the preprocessed field are and respectively where is the mean value evaluated over the whole domain. The temperature in the preprocessed mixture has a variation of about of its mean value.
4. Results and Discussion
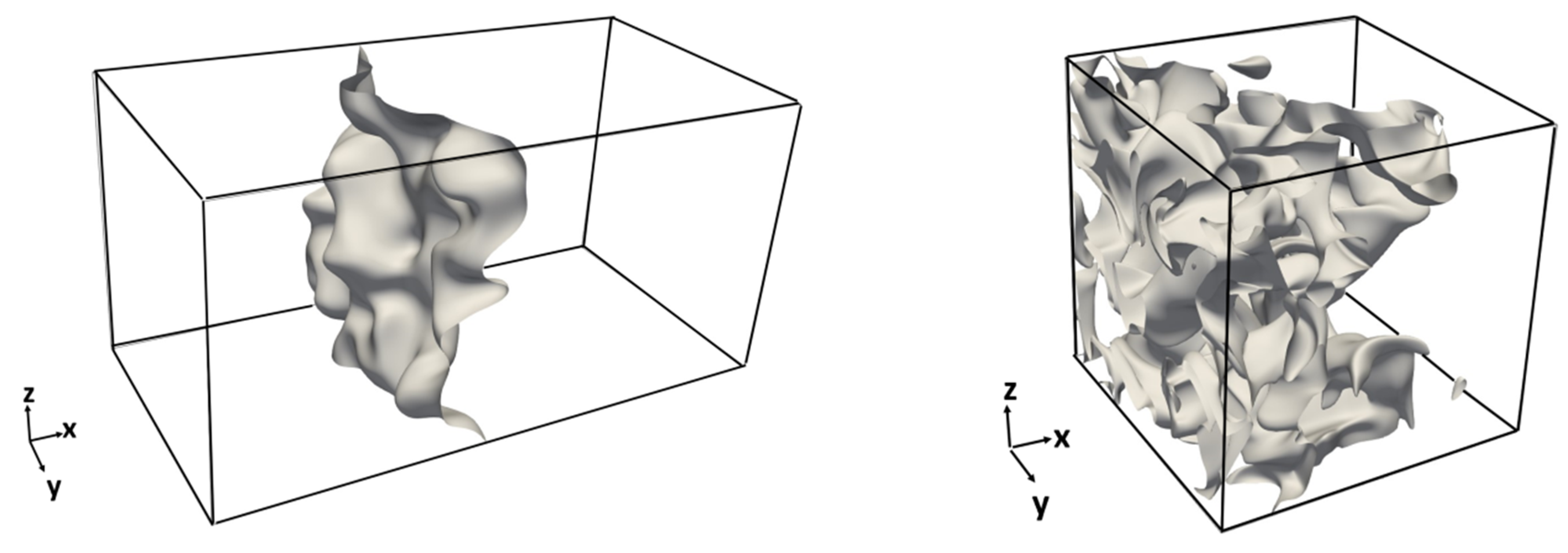
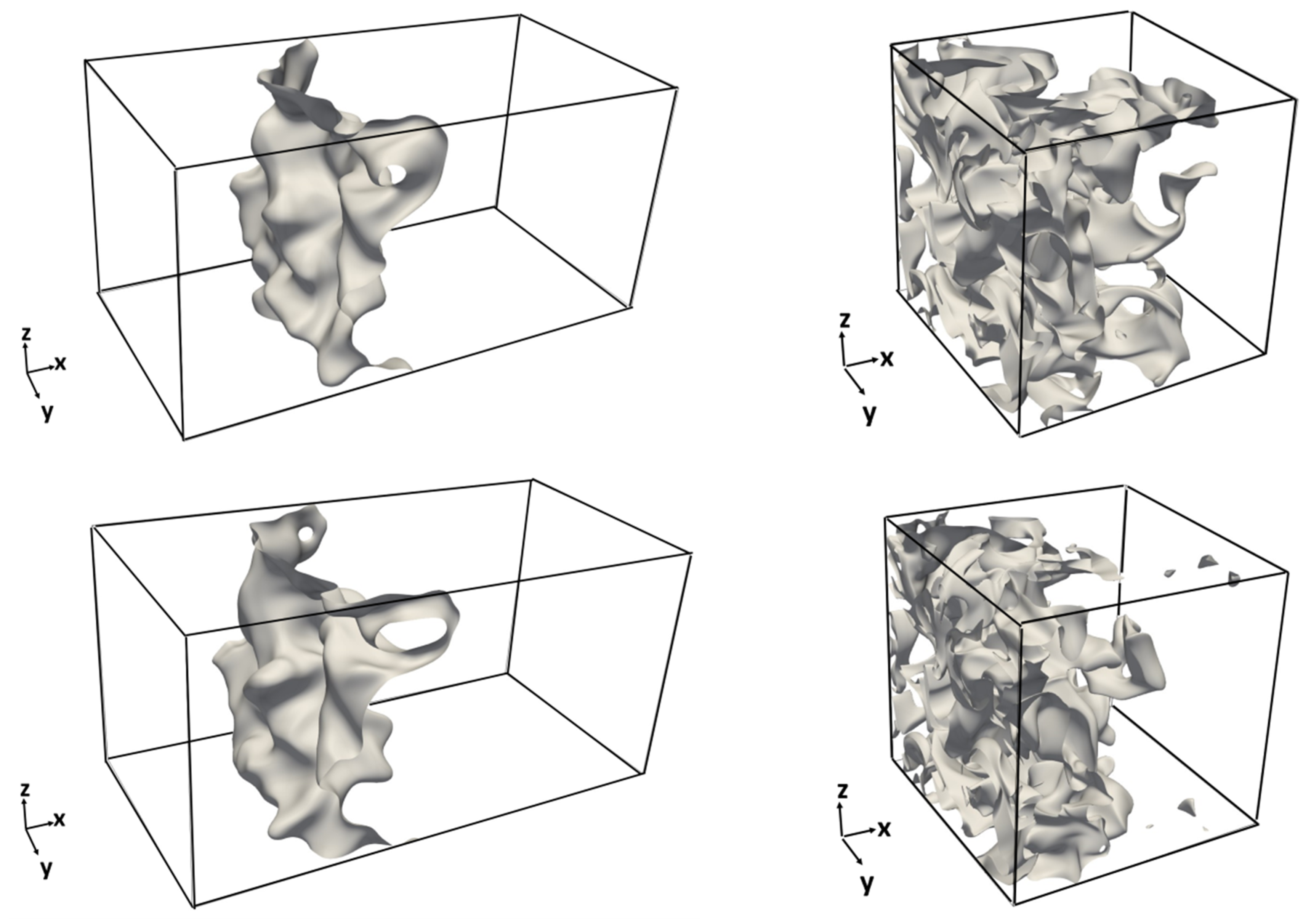
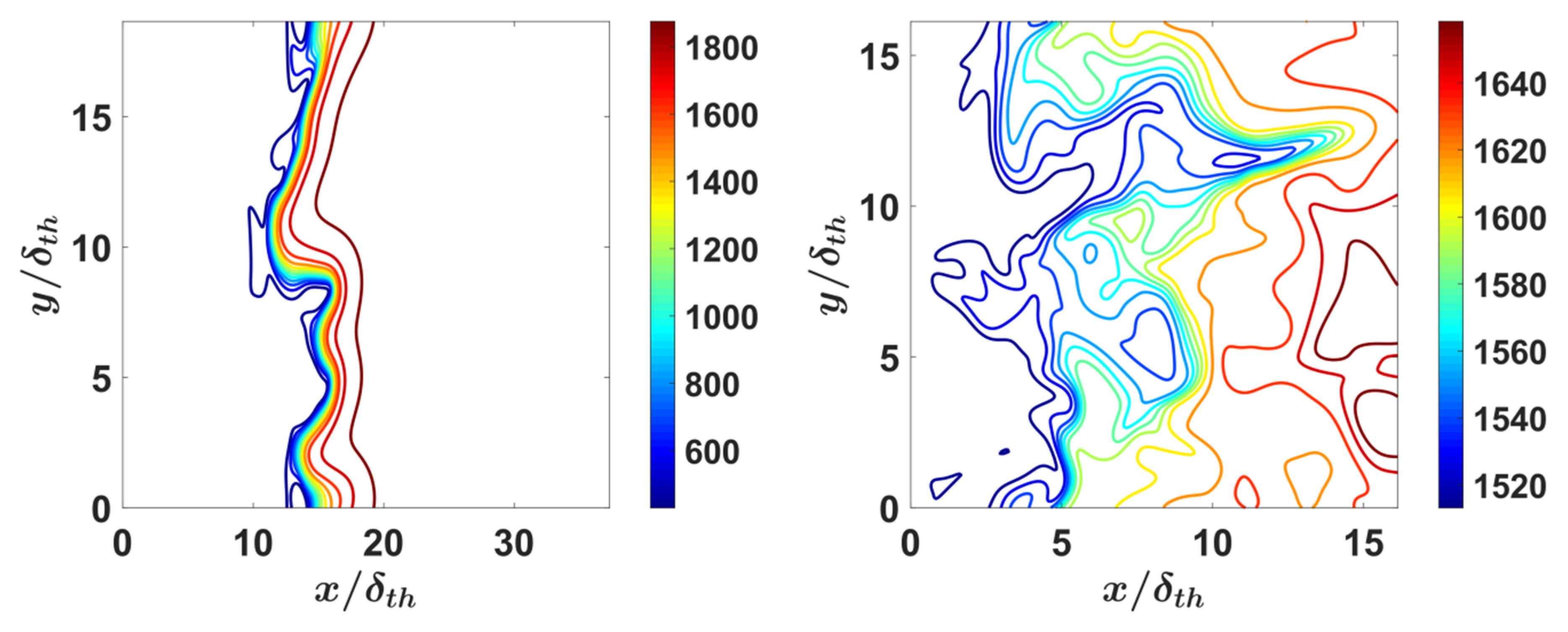
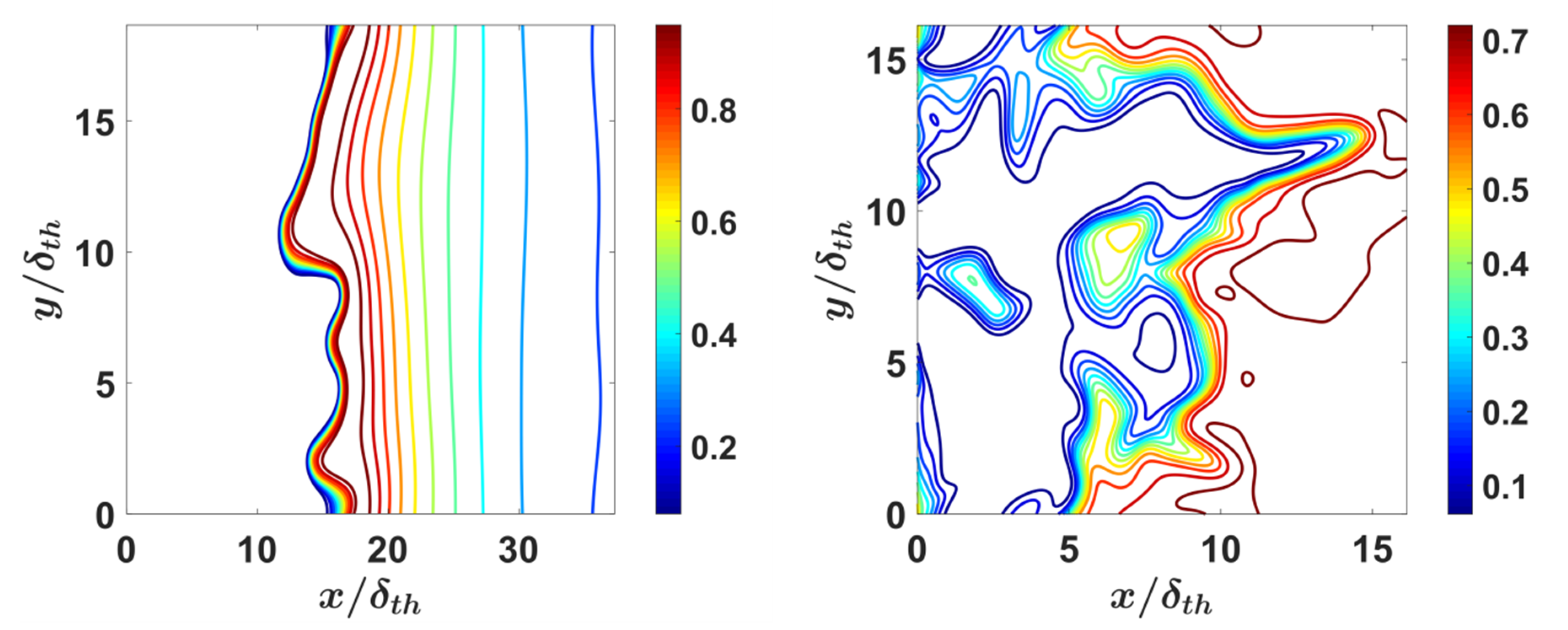
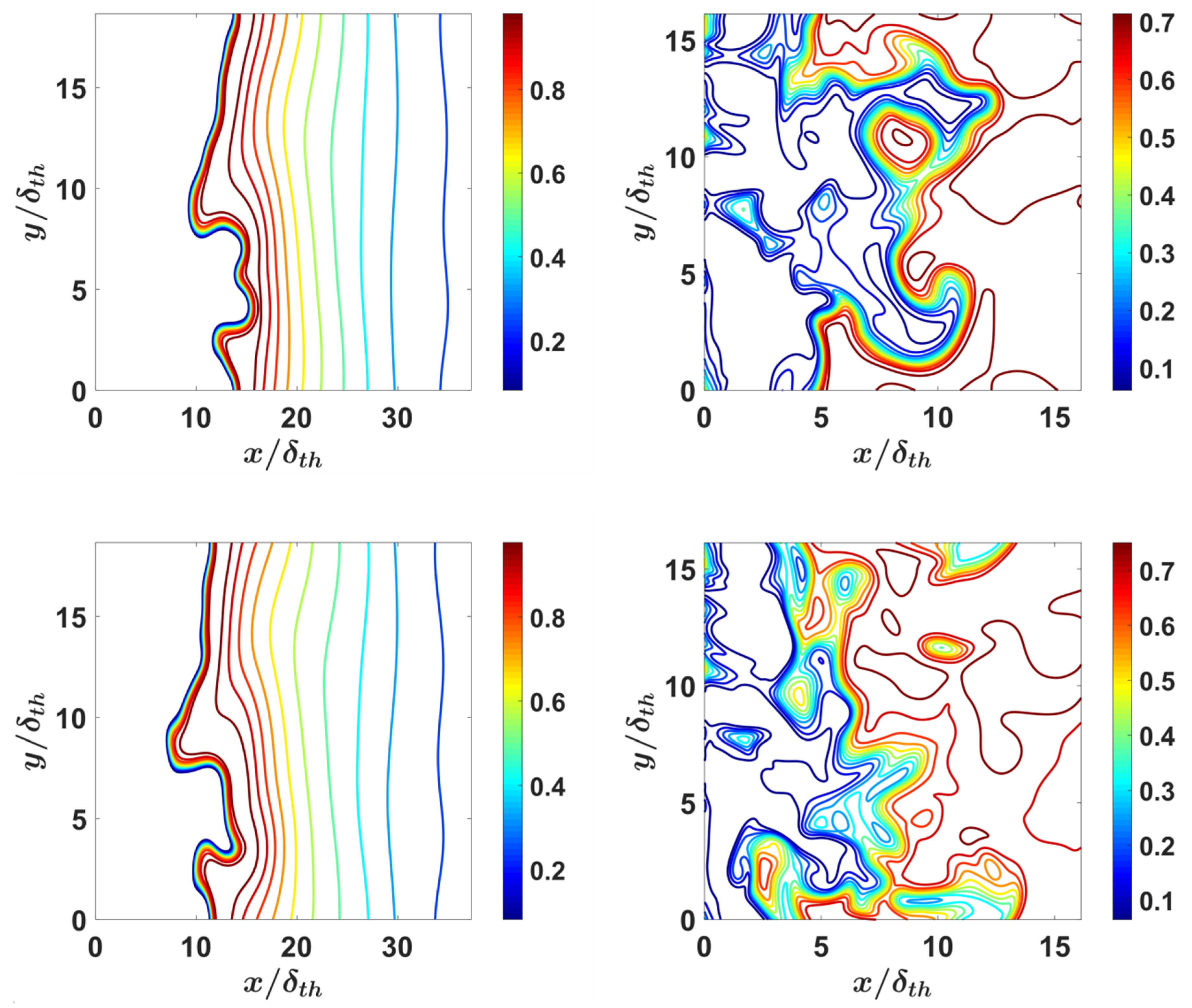
4.1. Flame Morphology
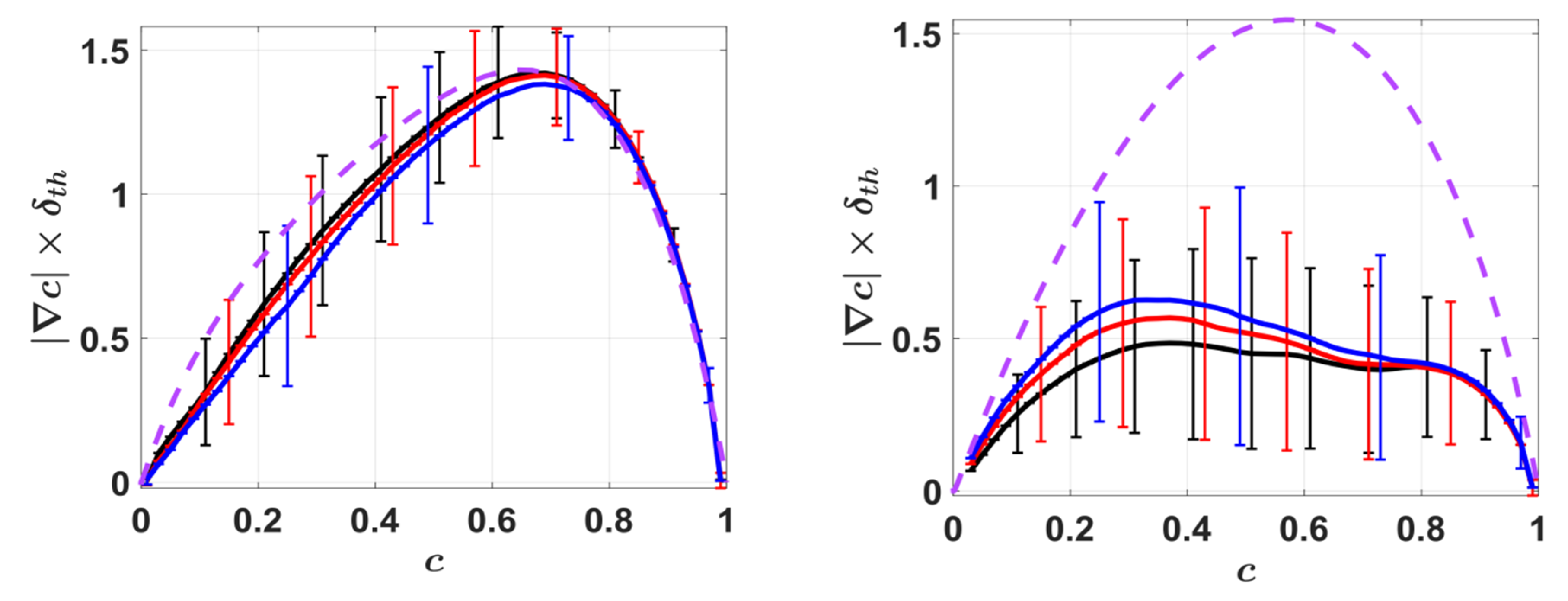
4.2. Mean Behaviour of the SDF
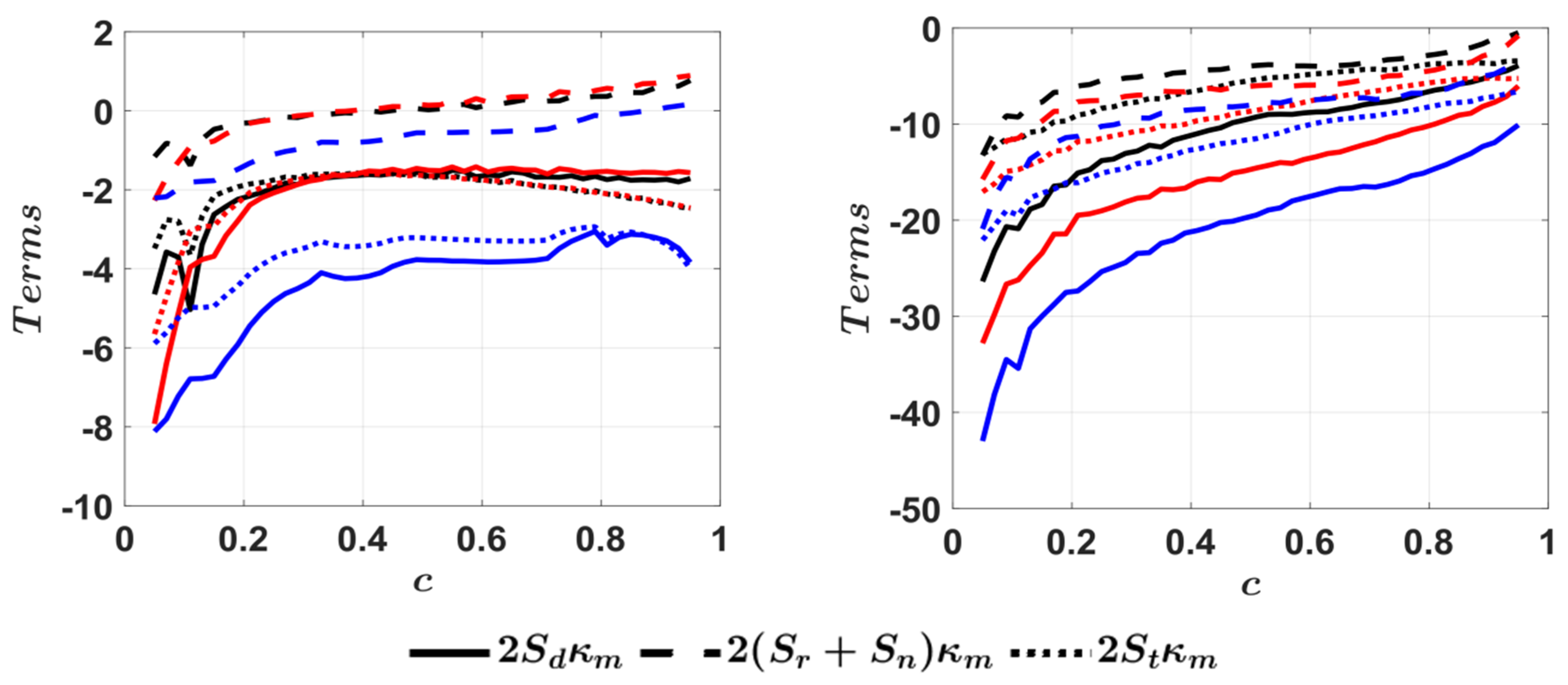
4.3. Mean Behaviour of Fluid-Dynamic Strain Rates
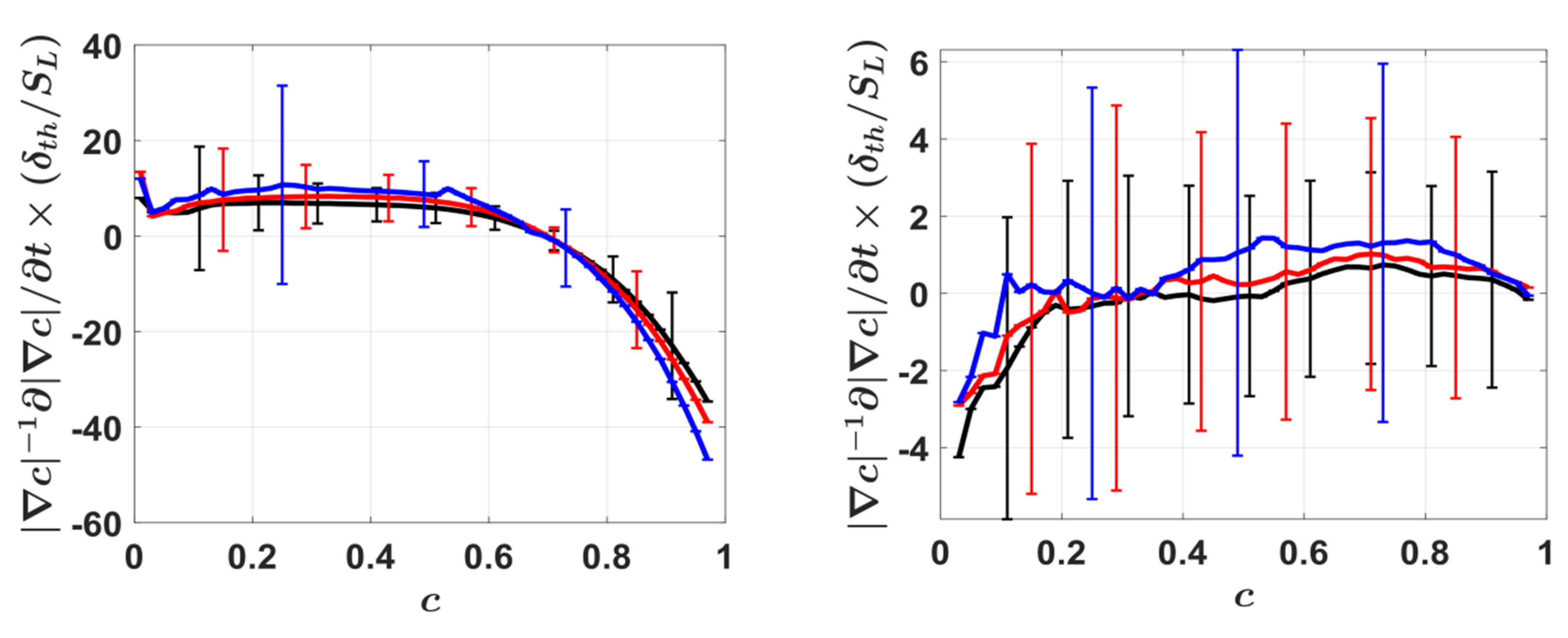
4.4. Mean Behaviour of Flame Displacement Speed
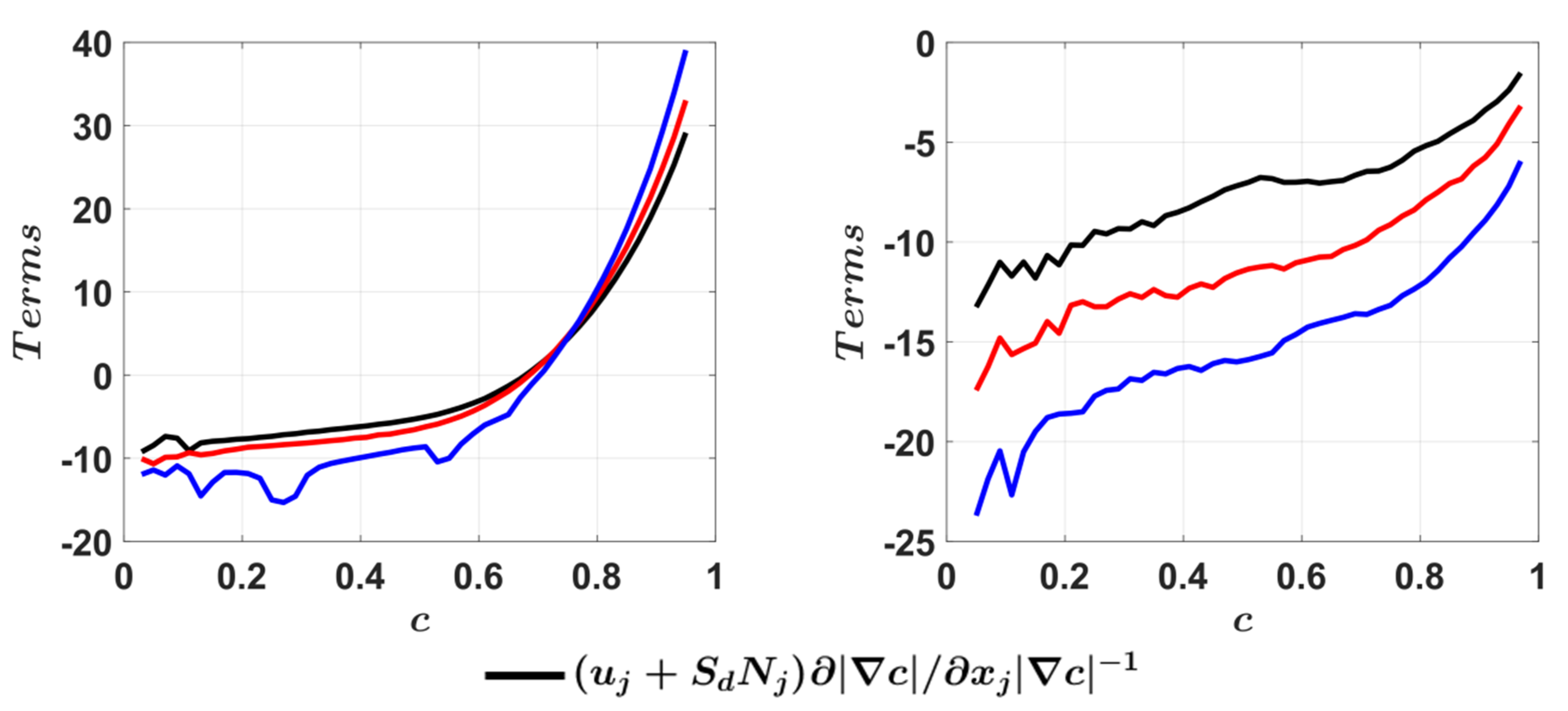
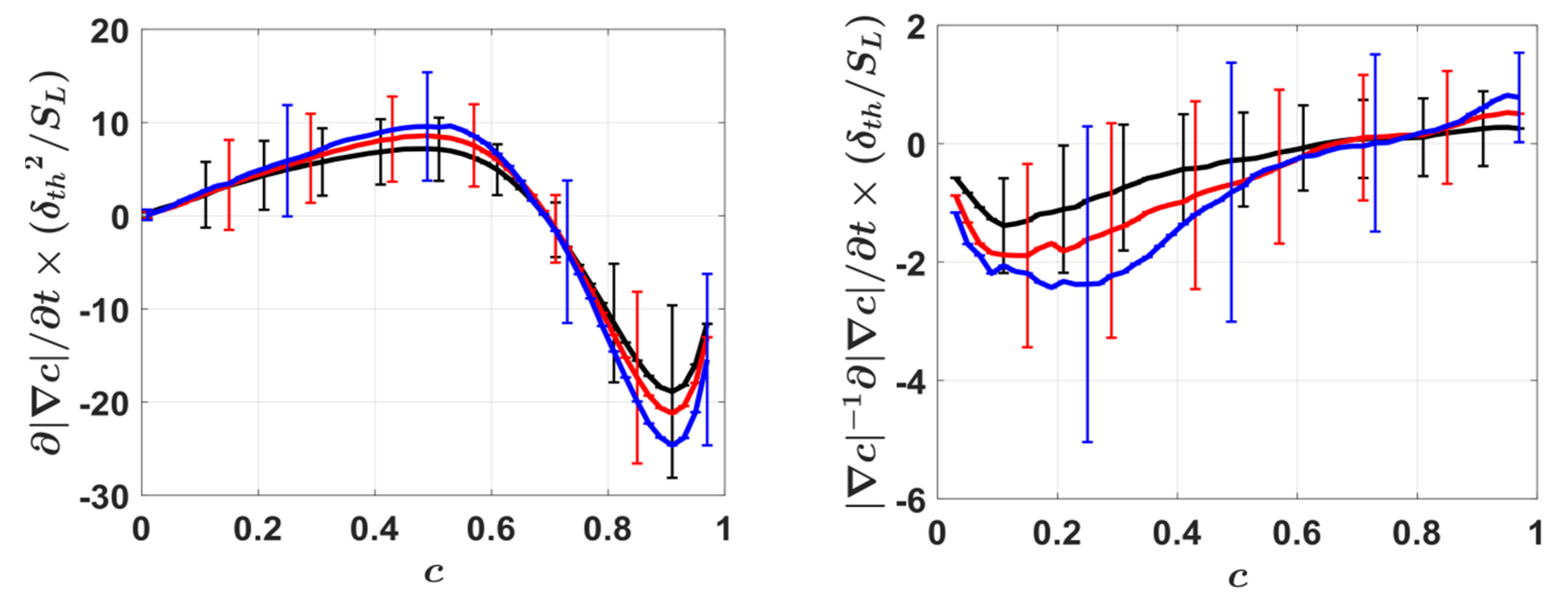
4.5. Mean Behaviour of Strain Rates Induced by Flame Propagation
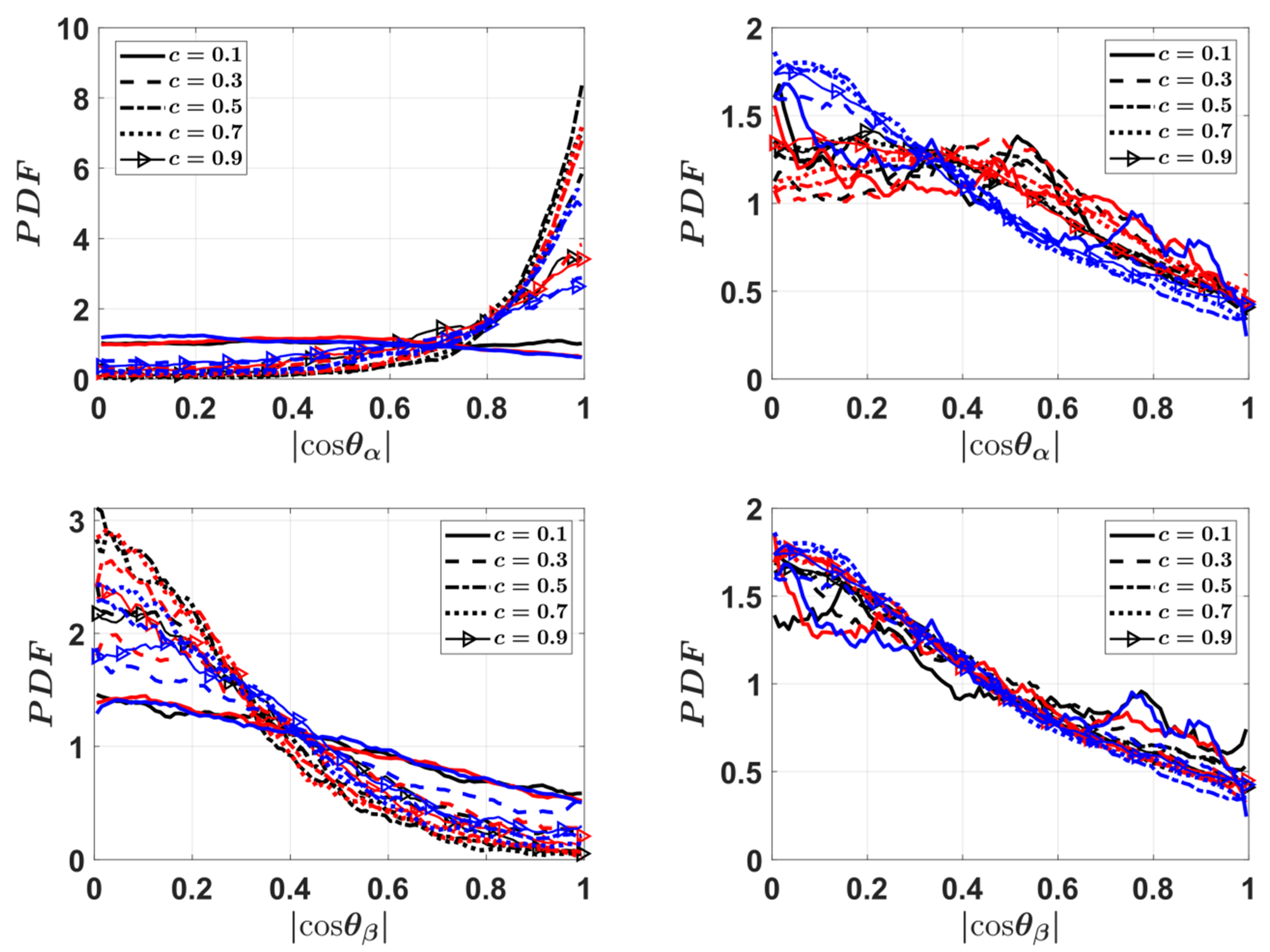
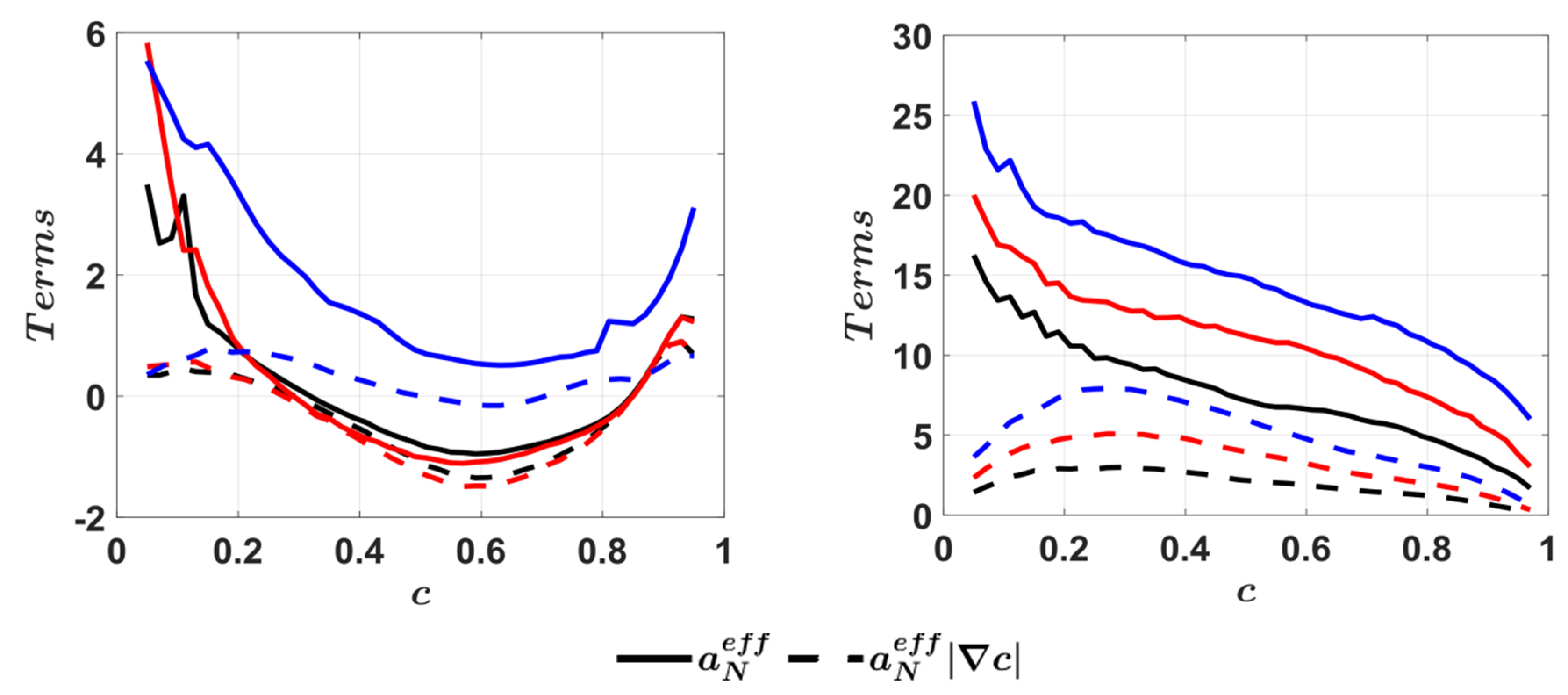
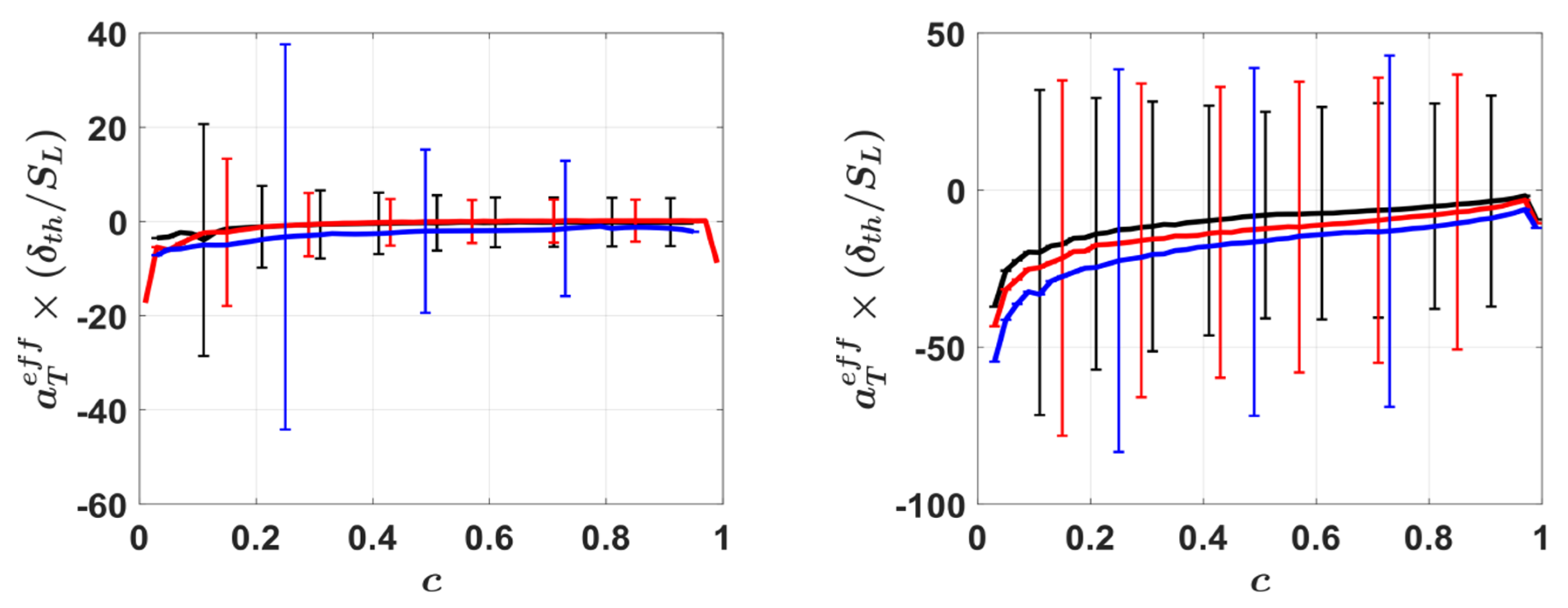
4.6. Mean Behaviour of Effective Strain Rates
4.7. Modelling Implications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leach, F.; Kalghatgi, G.; Stone, R.; Miles, P. The scope for improving the efficiency and environmental impact of internal combustion engines. Transp. Eng. 2020, 1, 100005. [Google Scholar] [CrossRef]
- Wünning, J.A.; Wünning, J.G. Flameless oxidation to reduce thermal NO-formation. Prog. Energy Combust. Sci. 1997, 23, 81–94. [Google Scholar] [CrossRef]
- Dally, B.B.; Karpetis, A.N.; Barlow, R.S. Structure of turbulent non-premixed jet flames in a diluted hot coflow. Proc. Combust. Inst. 2002, 29, 1147–1154. [Google Scholar] [CrossRef]
- Cavaliere, A.; De Joannon, M. Mild Combustion. Prog. Energy Combust. Sci. 2004, 30, 329–366. [Google Scholar] [CrossRef]
- Tsuji, H.; Gupta, A.K.; Hasegawa, T.; Katsuki, M. High Temperature Air Combustion: From Energy Conservation to Pollution Reduction; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Plessing, T.; Peters, N.; Wünning, J.G. Laser optical investigation of highly preheated combustion with strong exhaust gas recirculation. Proc. Combust. Inst. 1998, 27, 3197–3204. [Google Scholar] [CrossRef]
- de Joannon, M.; Saponaro, A.; Cavaliere, A. Zero-dimensional analysis of diluted oxidation of methane in rich conditions. Proc. Combust. Inst. 2000, 28, 1639–1646. [Google Scholar] [CrossRef]
- Aminian, J.; Galletti, C.; Shahhosseini, S.; Tognotti, L. Key modeling issues in prediction of minor species in diluted-preheated combustion conditions. Appl. Therm. Eng. 2011, 31, 3287–3300. [Google Scholar] [CrossRef]
- Coelho, P.J.; Peters, N. Numerical simulation of a mild combustion burner. Combust. Flame 2001, 124, 503–518. [Google Scholar] [CrossRef]
- Özdemir, I.B.; Peters, N. Characteristics of the reaction zone in a combustor operating at mild combustion. Exp. Fluids 2001, 30, 683–695. [Google Scholar] [CrossRef]
- Dally, B.B.; Riesmeier, E.; Peters, N. Effect of fuel mixture on moderate and intense low oxygen dilution combustion. Combust. Flame 2004, 137, 418–431. [Google Scholar] [CrossRef]
- Christo, F.C.; Dally, B.B. Modeling turbulent reacting jets issuing into a hot and diluted coflow. Combust. Flame 2005, 142, 117–129. [Google Scholar] [CrossRef]
- Krishnamurthy, N.; Paul, P.J.; Blasiak, W. Studies on low-intensity oxy-fuel burner. Proc. Combust. Inst. 2009, 32, 3139–3146. [Google Scholar] [CrossRef]
- Medwell, P.R.; Kalt, P.A.; Dally, B.B. Simultaneous imaging of OH, formaldehyde, and temperature of turbulent nonpremixed jet flames in a heated and diluted coflow. Combust. Flame 2007, 148, 48–61. [Google Scholar] [CrossRef]
- Duwig, C.; Li, B.; Li, Z.S.; Aldén, M. High resolution imaging of flameless and distributed turbulent combustion. Combust. Flame 2012, 159, 306–316. [Google Scholar] [CrossRef]
- Göktolga, M.U.; van Oijen, J.A.; de Goey, L.P.H. Modeling MILD combustion using a novel multistage FGM method. Proc. Combust. Inst. 2017, 36, 4269–4277. [Google Scholar] [CrossRef] [Green Version]
- Lewandowski, M.T.; Parente, A.; Pozorski, J. Generalised Eddy Dissipation Concept for MILD combustion regime at low local Reynolds and Damköhler numbers, Part 1: Model framework development. Fuel 2020, 278, 117743. [Google Scholar] [CrossRef]
- van Oijen, J.A. Direct numerical simulation of autoigniting mixing layers in MILD combustion. Proc. Combust. Inst. 2013, 34, 1163–1171. [Google Scholar] [CrossRef] [Green Version]
- Minamoto, Y.; Swaminathan, N.; Cant, S.R.; Leung, T. Reaction zones and their structure in MILD combustion. Combust. Sci. Technol. 2014, 186, 1075–1096. [Google Scholar] [CrossRef] [Green Version]
- Minamoto, Y.; Dunstan, T.D.; Swaminathan, N.; Cant, R.S. DNS of EGR-type turbulent flame in MILD condition. Proc. Combust. Inst. 2013, 34, 3231–3238. [Google Scholar] [CrossRef]
- Minamoto, Y.; Swaminathan, N.; Cant, R.S.; Leung, T. Morphological and statistical features of reaction zones in MILD and premixed combustion. Combust. Flame 2014, 161, 2801–2814. [Google Scholar] [CrossRef] [Green Version]
- Minamoto, Y.; Swaminathan, N. Scalar gradient behavior in MILD combustion. Combust. Flame 2014, 161, 1063–1075. [Google Scholar] [CrossRef] [Green Version]
- Minamoto, Y.; Swaminathan, N. Subgrid scale modelling for MILD combustion. Proc. Combust. Inst. 2015, 35, 3529–3536. [Google Scholar] [CrossRef] [Green Version]
- Doan, N.A.K.; Swaminathan, N.; Minamoto, Y. DNS of MILD combustion with mixture fraction variations. Combust. Flame 2018, 189, 173–189. [Google Scholar] [CrossRef]
- Doan, N.A.K.; Swaminathan, N. Role of radicals on MILD combustion inception. Proc. Combust. Inst. 2019, 37, 4539–4546. [Google Scholar] [CrossRef]
- Doan, N.A.K.; Swaminathan, N. Analysis of markers for combustion mode and heat release in MILD combustion using DNS data. Combust. Sci. Technol. 2019, 191, 1059–1078. [Google Scholar] [CrossRef]
- Swaminathan, N. Physical insights on MILD combustion from DNS. Front. Mech. Eng. 2019, 5, 549. [Google Scholar] [CrossRef]
- Mantel, T.; Borghi, R. A new model of premixed wrinkled flame propagation based on a scalar dissipation equation. Combust. Flame 1994, 96, 443–457. [Google Scholar] [CrossRef]
- Chakraborty, N.; Champion, M.; Mura, A.; Swaminathan, N. Scalar dissipation rate approach to reaction rate closure. In Turbulent Premixed Flame, 1st Ed.; Swaminathan, N., Bray, K.N.C., Eds.; Cambridge University Press: Cambridge, UK, 2011; pp. 74–102. [Google Scholar]
- Boger, M.; Veynante, D.; Boughanem, H.; Trouvé, A. Direct Numerical Simulation analysis of flame surface density concept for Large Eddy Simulation of turbulent premixed combustion. Proc. Combust. Inst. 1998, 27, 917–925. [Google Scholar] [CrossRef]
- Kollmann, W.; Chen, J.H. Pocket formation and the flame surface density equation. Proc. Combust. Inst. 1998, 27, 927–934. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, N.; Cant, R.S. Effects of strain rate and curvature on Surface Density Function transport in turbulent premixed flames in the thin reaction zones regime. Phys. Fluids 2005, 17, 065108. [Google Scholar] [CrossRef]
- Sankaran, R.; Hawkes, E.R.; Chen, J.H.; Lu, T.; Law, C.K. Structure of a spatially developing turbulent lean methane–air Bunsen flame. Proc. Combust. Inst. 2007, 31, 1291–1298. [Google Scholar] [CrossRef]
- Chakraborty, N.; Hawkes, E.R.; Chen, J.H.; Cant, R.S. Effects of strain rate and curvature on Surface Density Function transport in turbulent premixed CH4-air and H2-air flames: A comparative study. Combust. Flame 2008, 154, 259–280. [Google Scholar] [CrossRef]
- Chakraborty, N.; Klein, M. Influence of Lewis number on the Surface Density Function transport in the thin reaction zone regime for turbulent premixed flames. Phys. Fluids 2008, 20, 065102. [Google Scholar] [CrossRef]
- Chakraborty, N.; Klein, M. Effects of global flame curvature on Surface Density Function transport in turbulent premixed flame kernels in the thin reaction zones regime. Proc. Combust. Inst. 2009, 32, 1435–1443. [Google Scholar] [CrossRef]
- Dopazo, C.; Cifuentes, L.; Martin, J.; Jimenez, C. Strain rates normal to approaching isoscalar surfaces in a turbulent premixed flame. Combust. Flame 2015, 162, 1729–1736. [Google Scholar] [CrossRef]
- Dopazo, C.; Cifuentes, L.; Hierro, J.; Martin, J. Micro-scale mixing in turbulent constant density reacting flows and premixed combustion. Flow Turbul. Combust. 2015, 96, 547–571. [Google Scholar] [CrossRef]
- Dopazo, C.; Cifuentes, L. The physics of scalar gradients in turbulent premixed combustion and its relevance to modeling. Combust. Sci. Technol. 2016, 188, 1376–1397. [Google Scholar] [CrossRef]
- Wang, H.; Hawkes, E.R.; Chen, J.H.; Zhou, B.; Li, Z.; Alden, M. Direct numerical simulations of a high Karlovitz number laboratory premixed jet flame—An analysis of flame stretch and flame thickening. J. Fluid Mech. 2017, 815, 511–536. [Google Scholar] [CrossRef]
- Sandeep, A.; Proch, F.; Kempf, A.M.; Chakraborty, N. Statistics of strain rates and Surface Density Function in a flame-resolved high-fidelity simulation of a turbulent premixed bluff body burner. Phys. Fluids 2018, 30, 065101. [Google Scholar] [CrossRef]
- Dopazo, C.; Cifuentes, L.; Alwazzan, D.; Chakraborty, N. Influence of the Lewis number on effective strain rates in weakly turbulent premixed combustion. Combust. Sci. Technol. 2018, 190, 591–614. [Google Scholar] [CrossRef] [Green Version]
- Klein, M.; Alwazzan, D.; Chakraborty, N. A Direct Numerical Simulation analysis of pressure variation in turbulent premixed Bunsen burner flames-Part 1: Scalar gradient and strain rate statistics. Comput. Fluids 2018, 173, 178–188. [Google Scholar] [CrossRef] [Green Version]
- Klein, M.; Alwazzan, D.; Chakraborty, N. A Direct Numerical Simulation analysis of pressure variation in turbulent premixed Bunsen burner flames-Part 2: Surface Density Function transport statistics. Comput. Fluids 2018, 173, 147–156. [Google Scholar] [CrossRef] [Green Version]
- Smooke, M.D.; Giovangigli, V. Premixed and Nonpremixed Test Flame Results, Reduced Kinetic Mechanisms and Asymptotic Approximations for Methane-Air Flames; Springer: Berlin/Heidelberg, Germany, 1991; pp. 29–47. [Google Scholar]
- Malkeson, S.P.; Chakraborty, N. Statistical analysis of displacement speed in turbulent stratified flames: A direct numerical simulation study. Combust. Sci. Technol. 2010, 182, 1841–1883. [Google Scholar] [CrossRef]
- Peters, N.; Terhoeven, P.; Chen, J.H.; Echekki, T. Statistics of Flame Displacement Speeds from Computations of 2-D Unsteady Methane-Air Flames. Proc. Combust. Inst. 1998, 27, 833–839. [Google Scholar] [CrossRef] [Green Version]
- Echekki, T.; Chen, J.H. Analysis of the contribution of curvature to premixed flame propagation. Combust. Flame 1999, 118, 308–311. [Google Scholar] [CrossRef]
- Pope, S.B. The evolution of surfaces in turbulence. Int. J. Eng. Sci. 1998, 26, 445–469. [Google Scholar] [CrossRef]
- Candel, S.M.; Poinsot, T.J. Flame stretch and the balance equation for the flame area. Combust. Sci. Technol. 1990, 70, 1–15. [Google Scholar] [CrossRef]
- Cant, R.S. Technical Report CUED/A–THERMO/TR67; Cambridge University Engineering Department: Cambridge, UK, 2012. [Google Scholar]
- Poinsot, T.J.; Lele, S.K. Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion. In Cambridge Monograph on Mechanics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Rogallo, R.S. Numerical experiments in homogeneous turbulence. In NASA Technical Memorandum 81315; NASA Ames Research Center: Mountain View, CA, USA, 1981. [Google Scholar]
- Batchelor, G.K.; Townsend, A.A. Decay of turbulence in the final period. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 194, 527–543. [Google Scholar]
- Eswaran, V.; Pope, S.B. Direct numerical simulations of the turbulent mixing of a passive scalar. Phys. Fluids 1988, 31, 506–520. [Google Scholar] [CrossRef]
- Paul, P.H.; Najm, H.N. Planar laser-induced fluorescence imaging of flame heat release rate. Proc. Combust. Inst. 1998, 27, 43–50. [Google Scholar] [CrossRef] [Green Version]
- Najm, H.N.; Paul, P.H.; Mueller, C.J.; Wyckoff, P.S. On the adequacy of certain experimental observables as measurements of flame burning rate. Combust. Flame 1998, 113, 312–332. [Google Scholar] [CrossRef]
- Puri, R.; Moser, M.; Santoro, R.J.; Smyth, K.C. Laser-induced fluorescence measurements of OH concentrations in the oxidation region of laminar, hydrocarbon diffusion flames. Proc. Combust. Inst. 1992, 24, 1015–1022. [Google Scholar] [CrossRef]
- Cessou, A.; Stepowski, D. Planar Laser Induced Fluorescence Measurement of [OH] in the Stabilization Stage of a Spray Jet Flame. Combust. Sci. Technol. 1996, 118, 361–381. [Google Scholar]
- Schiessl, R.; Maas, U.; Hoffmann, A.; Wolfrum, J.; Schulz, C. Method for absolute OH-concentration measurements in premixed flames by LIF and numerical simulations. Appl. Phys. B 2004, 79, 759–766. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, N.; Swaminathan, N. Influence of the Damköhler number on turbulence-scalar interaction in premixed flames. I. Physical insight. Phys. Fluids 2007, 19, 045103. [Google Scholar] [CrossRef]
- Batchelor, G.K. The effect of homogeneous turbulence on material lines and surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1952, 231, 349–366. [Google Scholar]
- Batchelor, G.K. Small-scale variation of convected quantities like temperature in turbulent fluid Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 1959, 5, 113–133. [Google Scholar] [CrossRef]
- Gibson, C. Fine structure of scalar fields mixed by turbulence. I. Zero gradient points and minimal gradient surfaces. Phys. Fluids 1968, 11, 2305–2315. [Google Scholar] [CrossRef]
- Clay, J.P. Turbulent Mixing of Temperature in Water, Air and Mercury. Ph.D. Thesis, University of California, San Diego, CA, USA, 1973. [Google Scholar]
- Kerr, R.M. Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 1985, 153, 31–58. [Google Scholar] [CrossRef] [Green Version]
- Ruetsch, G.; Maxey, M. Small-scale features of vorticity and passive scalar fields in homogeneous isotropic turbulence. Phys. Fluids A Fluid Dyn. 1991, 3, 1587–1597. [Google Scholar] [CrossRef]
- Nomura, K.; Elghobashi, S. Mixing characteristics of an inhomogeneous scalar in isotropic and homogeneous sheared turbulence. Phys. Fluids A Fluid Dyn. 1992, 4, 606–625. [Google Scholar] [CrossRef] [Green Version]
- Leonard, A.D.; Hill, J.C. Scalar dissipation and mixing in turbulent reacting flows. Phys. Fluids A Fluid Dyn. 1991, 3, 1286–1299. [Google Scholar] [CrossRef]
- Ashurst, W.T.; Kerstein, A.; Kerr, R.; Gibson, C. Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 1987, 30, 2343. [Google Scholar] [CrossRef]
- Malkeson, S.P.; Chakraborty, N. Alignment statistics of active and passive scalar gradients in turbulent stratified flames. Phys. Rev. E 2011, 86, 046308. [Google Scholar] [CrossRef]
- Griffiths, R.A.C.; Chen, J.H.; Kolla, H.; Cant, R.S.; Kollmann, W. Three-dimensional topology of turbulent premixed flame interaction. Proc. Combust. Inst. 2015, 35, 1341–1348. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, N.; Cant, R.S. A Priori Analysis of the curvature and propagation terms of the Flame Surface Density transport equation for Large Eddy Simulation. Phys. Fluids 2007, 19, 105101. [Google Scholar] [CrossRef]
- Chakraborty, N.; Cant, R.S. Direct Numerical Simulation analysis of the Flame Surface Density transport equation in the context of Large Eddy Simulation. Proc. Combust. Inst. 2009, 32, 1445–1453. [Google Scholar] [CrossRef]
- Suillaud, E. Large-Eddy Simulation and Modelling of Highly Diluted Combustion in Spark-Ignition Engines. Ph.D. Thesis, Université Paris-Saclay, Orsay, France, 2021. [Google Scholar]
- Chakraborty, N.; Swaminathan, N. Influence of Damköhler number on turbulence-scalar interaction in premixed flames, Part II: Model Development. Phys. Fluids 2007, 19, 045104. [Google Scholar] [CrossRef]
- Gao, Y.; Chakraborty, N.; Swaminathan, N. Scalar dissipation rate transport and its modeling for Large Eddy Simulations of turbulent premixed combustion. Combust. Sci. Technol. 2015, 187, 362–383. [Google Scholar] [CrossRef]
- Gao, Y.; Chakraborty, N. Modeling of Lewis Number dependence of Scalar dissipation rate transport for Large Eddy Simulations of turbulent premixed combustion. Numer. Heat Transf. Part A Appl. 2016, 69, 1201–1222. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Minamoto, Y.; Tanahashi, M.; Chakraborty, N. A priori assessment of scalar dissipation rate closure for Large Eddy Simulations of turbulent premixed combustion using a detailed chemistry Direct Numerical Simulation database. Combust. Sci. Technol. 2016, 188, 1398–1423. [Google Scholar] [CrossRef] [Green Version]


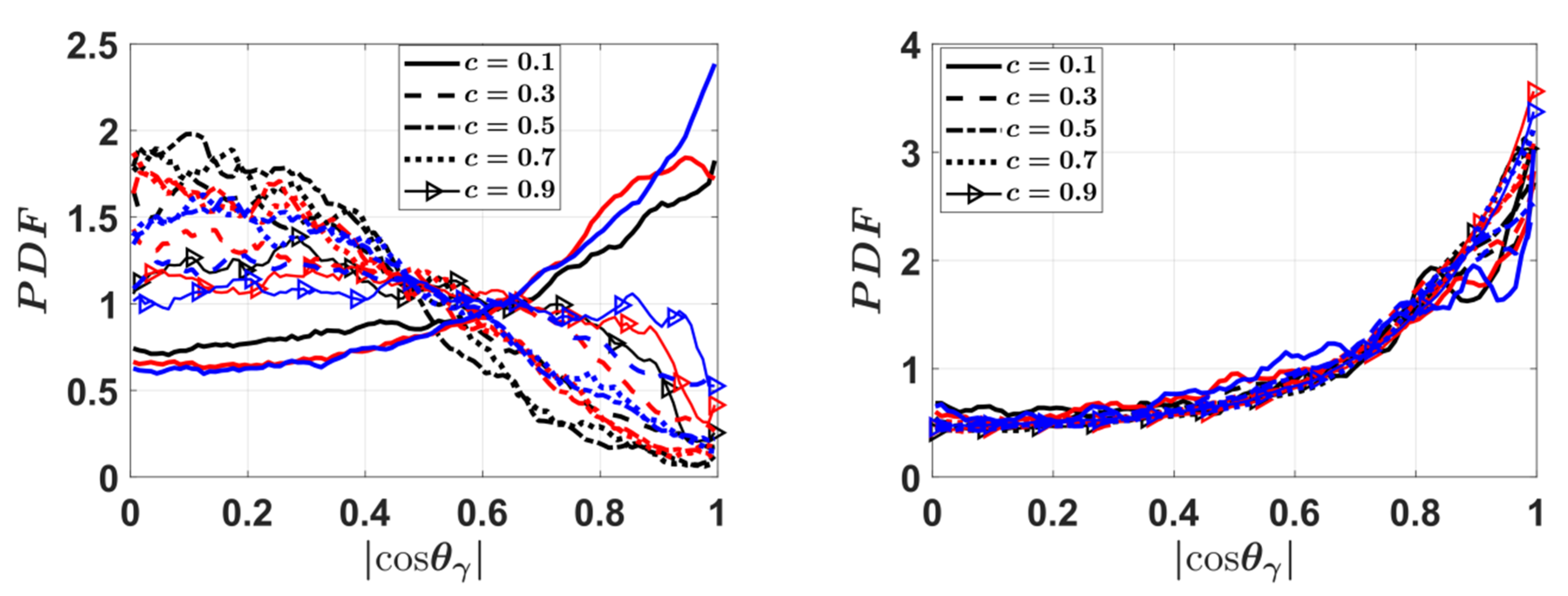
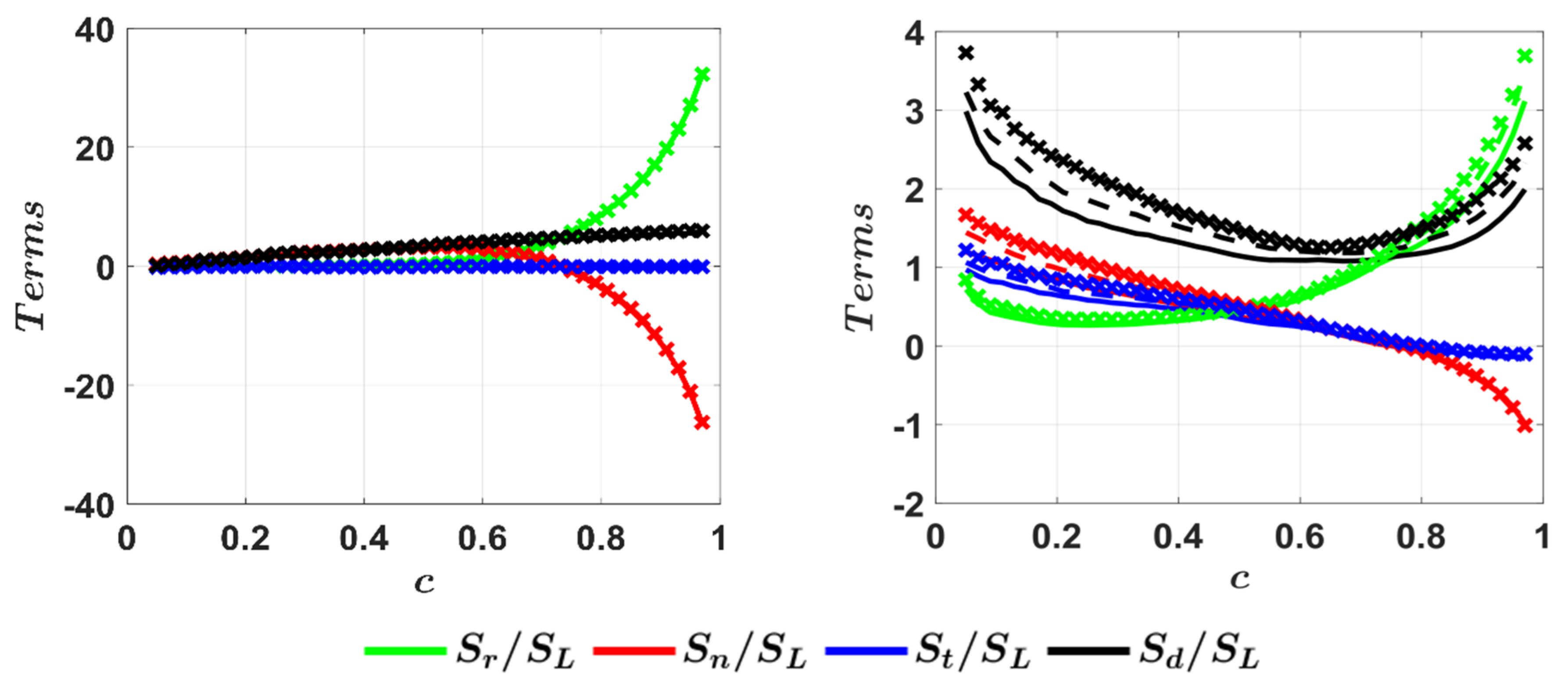
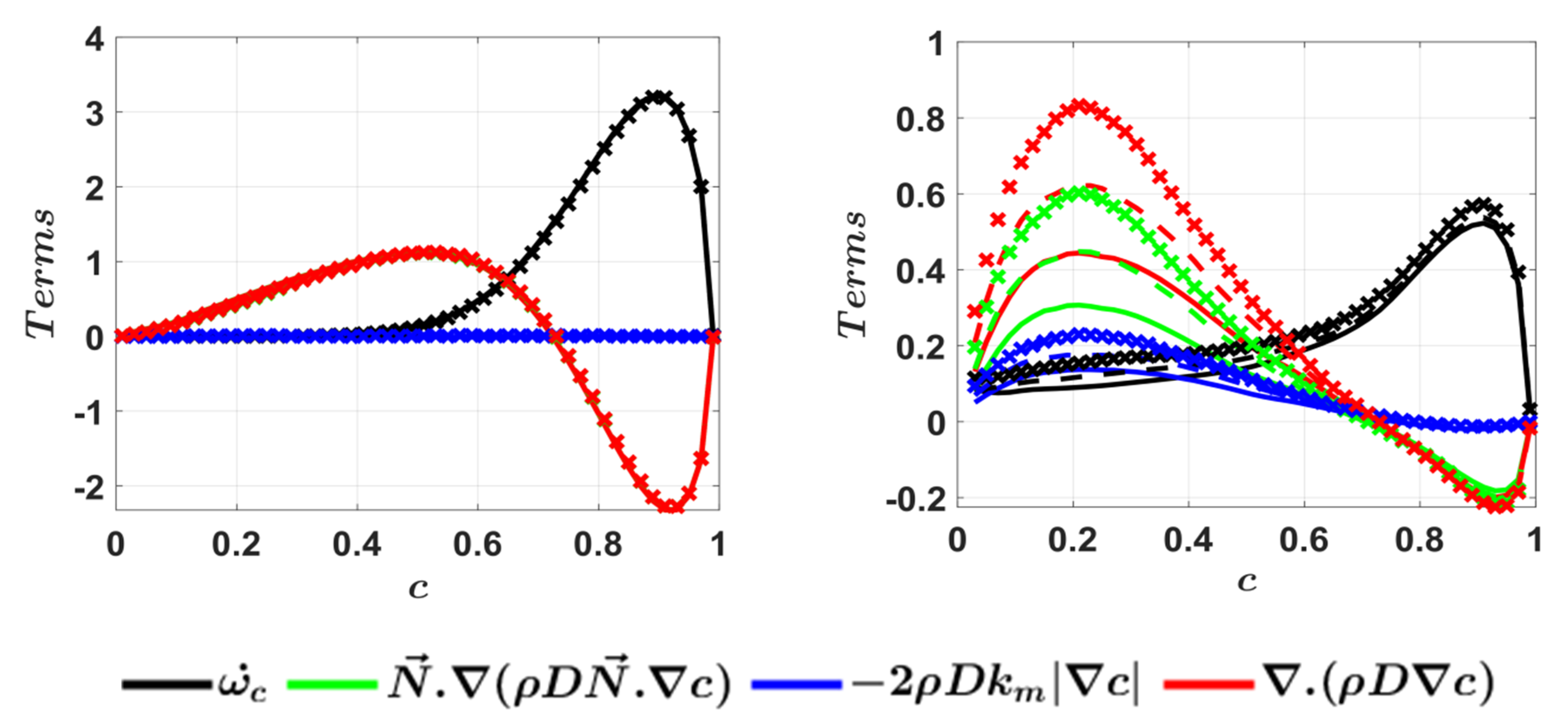
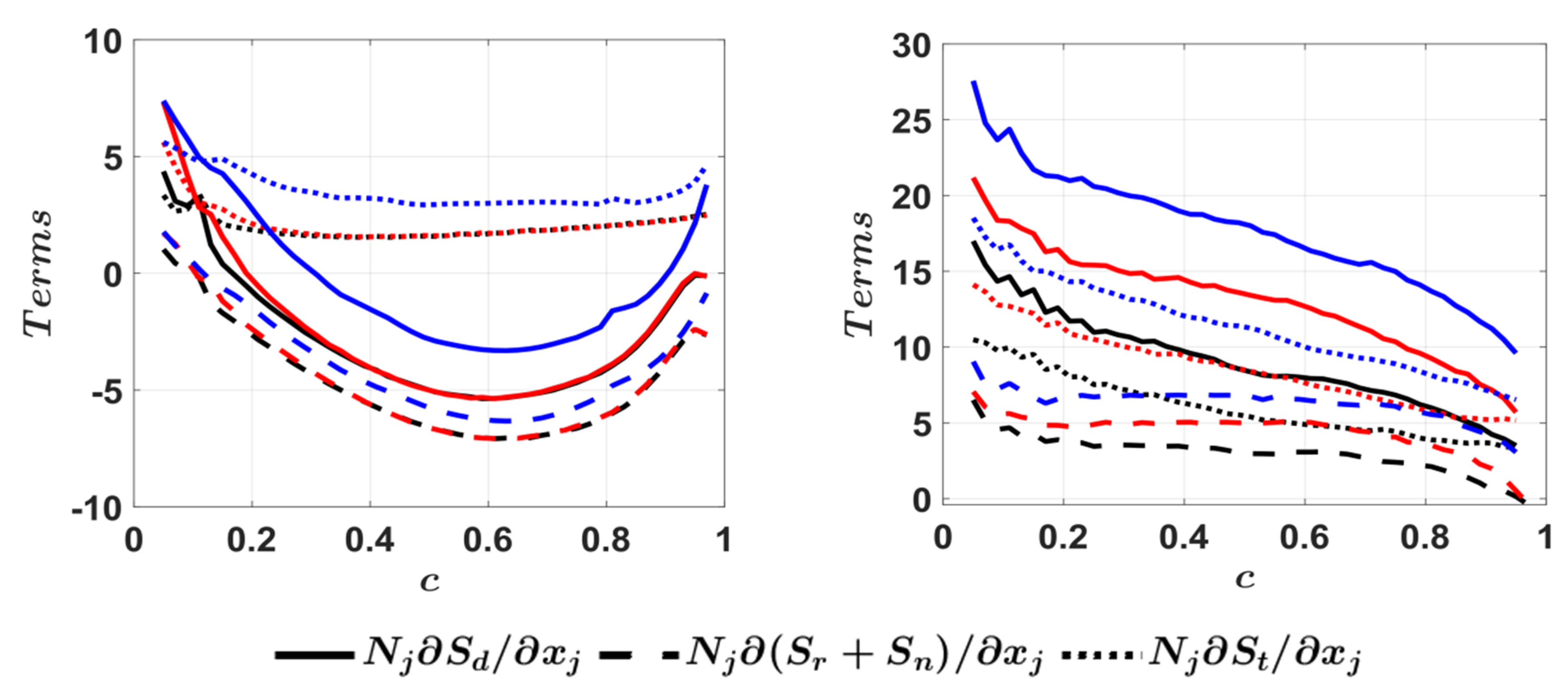
| Case | ||||||
|---|---|---|---|---|---|---|
| MILD | 0.048 | 0.061 | 0.121 | 0.019 | 0.751 | 1500 |
| Premixed | 0.194 | 0.0 | 0.0 | 0.077 | 0.729 | 300 |
| Case | ||||
|---|---|---|---|---|
| Premixed | 4.0 | 2.5 | 0.62 | 5.06 |
| 6.0 | 2.5 | 0.42 | 9.30 | |
| 8.0 | 2.5 | 0.31 | 14.31 | |
| MILD | 4.0 | 2.5 | 0.62 | 5.06 |
| 6.0 | 2.5 | 0.42 | 9.30 | |
| 8.0 | 2.5 | 0.31 | 14.31 |
| Case | and | and | and | and | |
|---|---|---|---|---|---|
| 4.0 | Premixed | 0.53 | −0.32 | 0.31 | −0.82 |
| MILD | 0.13 | 0.23 | −0.07 | −0.53 | |
| 6.0 | Premixed | 0.51 | −0.32 | 0.26 | −0.84 |
| MILD | 0.03 | −0.53 | −0.04 | −0.61 | |
| 8.0 | Premixed | 0.52 | −0.24 | 0.26 | −0.84 |
| MILD | 0.07 | −0.63 | 0.03 | −0.60 | |
| 4.0 | Premixed | 0.70 | −0.45 | 0.60 | −0.95 |
| MILD | 0.22 | 0.24 | −0.02 | −0.72 | |
| 6.0 | Premixed | 0.71 | −0.51 | 0.55 | −0.94 |
| MILD | 0.18 | −0.19 | 0.03 | −0.70 | |
| 8.0 | Premixed | 0.62 | −0.32 | 0.51 | −0.89 |
| MILD | 0.13 | −0.34 | 0.005 | −0.69 | |
| 4.0 | Premixed | 0.72 | −0.61 | 0.67 | −0.98 |
| MILD | 0.32 | 0.23 | −0.08 | −0.71 | |
| 6.0 | Premixed | 0.75 | −0.65 | 0.59 | −0.97 |
| MILD | 0.21 | 0.14 | −0.03 | −0.74 | |
| 8.0 | Premixed | 0.66 | −0.44 | 0.56 | −0.96 |
| MILD | 0.19 | 0.02 | 0.01 | −0.74 | |
| 4.0 | Premixed | 0.74 | −0.73 | 0.69 | −0.96 |
| MILD | 0.34 | 0.08 | −0.15 | −0.74 | |
| 6.0 | Premixed | 0.77 | −0.77 | 0.57 | −0.94 |
| MILD | 0.29 | 0.11 | −0.09 | −0.77 | |
| 8.0 | Premixed | 0.59 | −0.50 | 0.56 | −0.92 |
| MILD | 0.23 | 0.12 | −0.08 | −0.73 | |
| 4.0 | Premixed | 0.76 | −0.80 | 0.64 | −0.91 |
| MILD | 0.41 | −0.11 | −0.23 | −0.63 | |
| 6.0 | Premixed | 0.77 | −0.83 | 0.48 | −0.87 |
| MILD | 0.32 | −0.05 | −0.20 | −0.62 | |
| 8.0 | Premixed | 0.55 | −0.62 | 0.48 | −0.79 |
| MILD | 0.22 | 0.13 | −0.22 | −0.70 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awad, H.S.A.M.; Abo-Amsha, K.; Ahmed, U.; Chakraborty, N. Comparison of the Reactive Scalar Gradient Evolution between Homogeneous MILD Combustion and Premixed Turbulent Flames. Energies 2021, 14, 7677. https://doi.org/10.3390/en14227677
Awad HSAM, Abo-Amsha K, Ahmed U, Chakraborty N. Comparison of the Reactive Scalar Gradient Evolution between Homogeneous MILD Combustion and Premixed Turbulent Flames. Energies. 2021; 14(22):7677. https://doi.org/10.3390/en14227677
Chicago/Turabian StyleAwad, Hazem S.A.M., Khalil Abo-Amsha, Umair Ahmed, and Nilanjan Chakraborty. 2021. "Comparison of the Reactive Scalar Gradient Evolution between Homogeneous MILD Combustion and Premixed Turbulent Flames" Energies 14, no. 22: 7677. https://doi.org/10.3390/en14227677






