A Boosted Particle Swarm Method for Energy Efficiency Optimization of PRO Systems
Abstract
:1. Introduction
2. Materials and Methods
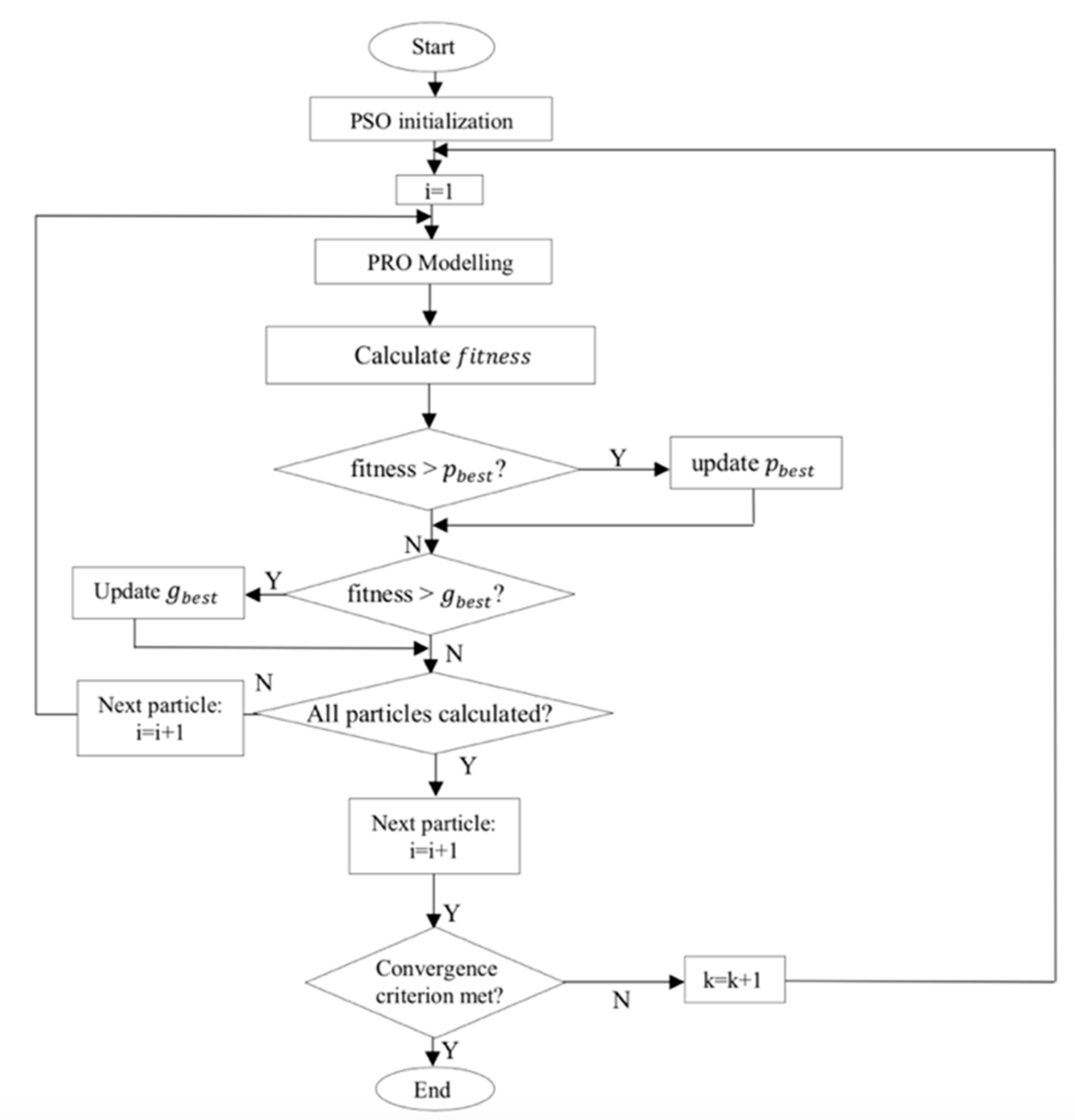
2.1. Particle Swarm Optimization
2.2. Boosted Particle Swarm Optimization
3. Formulation of the Optimization Problem in the PRO System
3.1. Pressure Retarded Osmosis Model
3.2. Optimization Performance Index
3.3. Problem Description
4. Results and Discussion
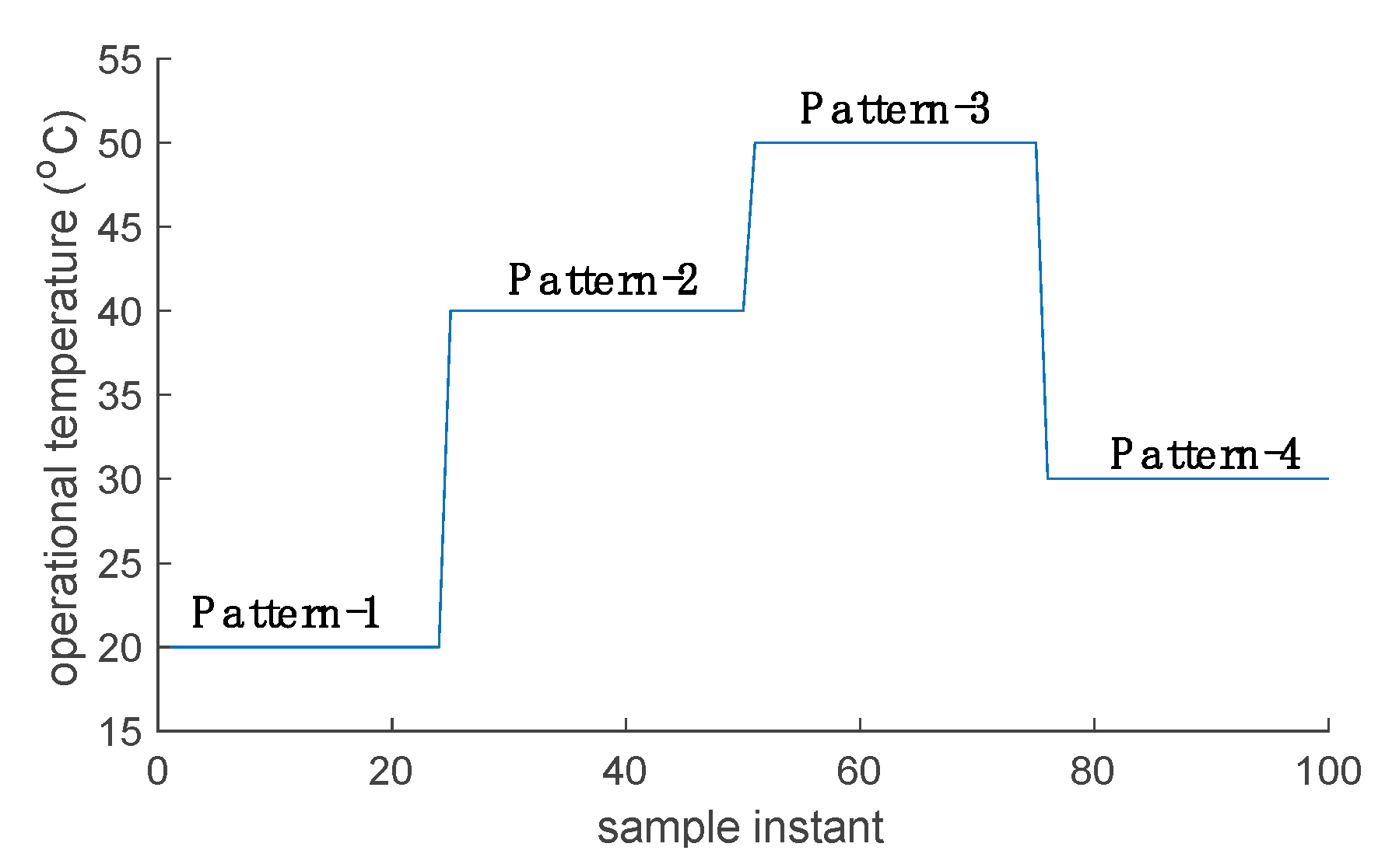
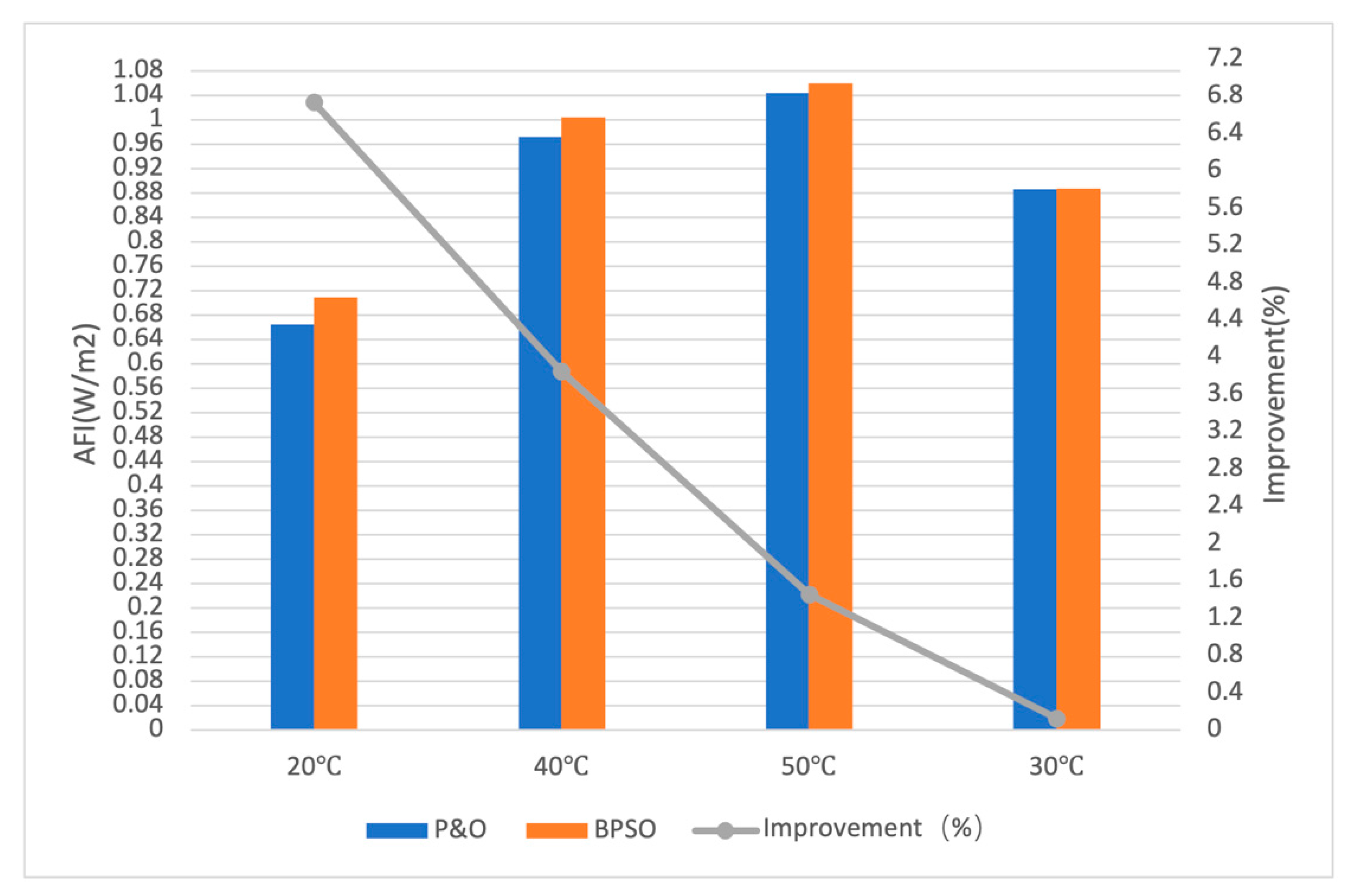
4.1. Scenario 1: Variations in the Operating Temperature
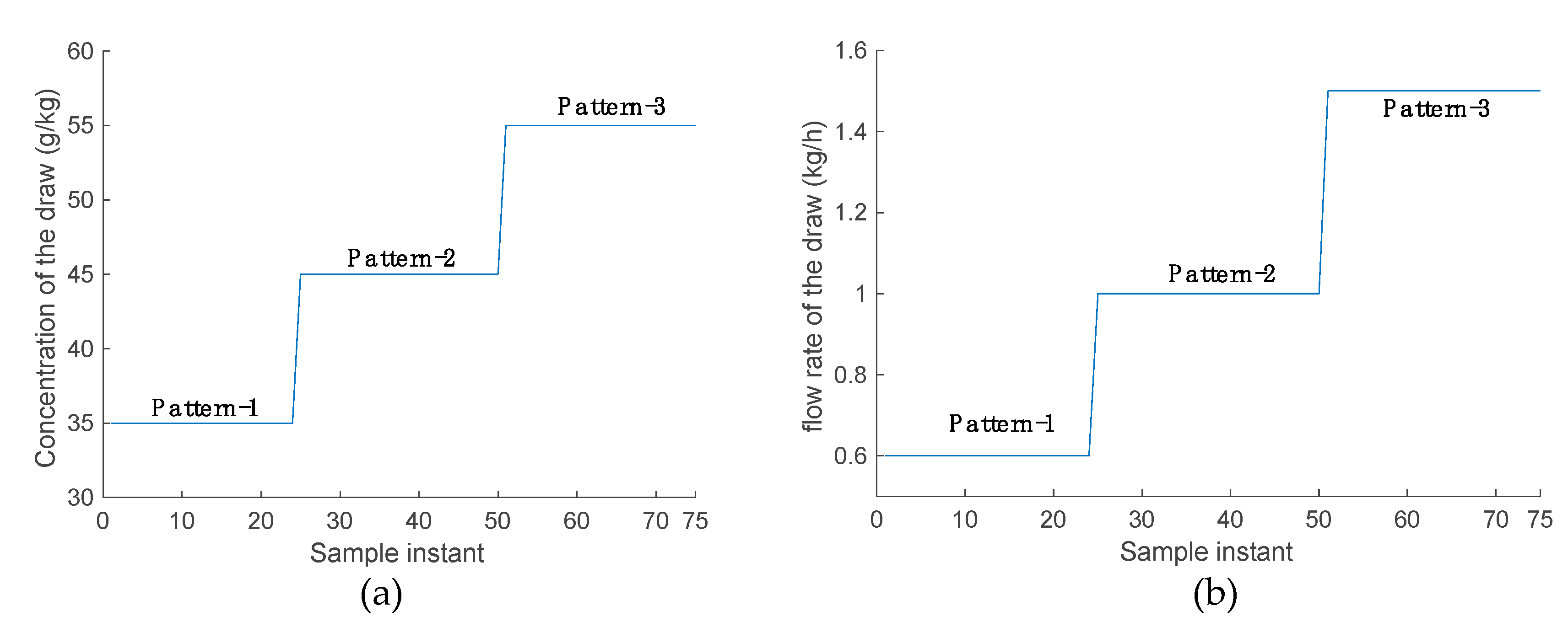
4.2. Scenario 2: Variations in Concentrations and Flow Rates
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| current iteration | |
| velocity of the ith particle | |
| position of the ith particle | |
| w | inertia weight parameter |
| r | normalized random values in the interval (0, 1) |
| the best position found in the ith iteration | |
| the best acquired global position | |
| d | dimension |
| upper bound | |
| lower bound | |
| the mean best solution in the iteration | |
| A | membrane permeability |
| Van’t Hoff factor | |
| osmotic pressure difference between two solutions | |
| draw solution concentrations | |
| the feed solution concentrations | |
| the draw flow rates | |
| the feed flow rates | |
| mass flow rates of the permeating solution | |
| mass flow rates of the reverse solute | |
| permeate density | |
| draw solution density | |
| membrane area | |
| the permeated solution flow rate | |
| water flux | |
| salt flux | |
| salt permeability factors | |
| S | membrane structural factor |
| D | solute diffusion factor |
| osmotic pressure on the draw side | |
| osmotic pressure on the feed side | |
| solute resistivity of the porous membrane support | |
| permeate volume | |
| applied energy | |
| available extracted energy | |
| the fitness function of the designed problem | |
| the best fitness | |
| the cpu time in seconds |
References
- Loeb, S. Production of energy from concentrated brines by pressure-retarded osmosis. I. Preliminary technical and economic correlations. J. Membr. Sci. 1976, 1, 49–63. [Google Scholar] [CrossRef]
- Marin-Coria, E.; Silva, R.; Enriquez, C.; Martínez, M.L.; Mendoza, E. Environmental assessment of the impacts and benefits of a salinity gradient energy pilot plant. Energies 2021, 14, 3252. [Google Scholar] [CrossRef]
- Chen, Y.; Alanezi, A.A.; Zhou, J.; Altaee, A.; Shaheed, M.H. Optimization of module pressure retarded osmosis membrane for maximum energy extraction. J. Water Process Eng. 2019, 32, 100935. [Google Scholar] [CrossRef]
- Gonzales, R.R.; Abdel-Wahab, A.; Adham, S.; Han, D.S.; Phuntsho, S.; Suwaileh, W.; Hilal, N.; Shon, H.K. Salinity gradient energy generation by pressure retarded osmosis: A review. Desalination 2021, 500, 114841. [Google Scholar] [CrossRef]
- Alvarez-Silva, O.; Winter, C.; Osorio, A.F. Salinity Gradient Energy at River Mouths. Environ. Sci. Technol. Lett. 2014, 1, 410–415. [Google Scholar] [CrossRef]
- Long, R.; Lai, X.; Liu, Z.; Liu, W. Pressure retarded osmosis: Operating in a compromise between power density and energy efficiency. Energy 2019, 172, 592–598. [Google Scholar] [CrossRef]
- Tawalbeh, M.; Al-Othman, A.; Abdelwahab, N.; Alami, A.H.; Olabi, A.G. Recent developments in pressure retarded osmosis for desalination and power generation. Renew. Sustain. Energy Rev. 2021, 138, 110492. [Google Scholar] [CrossRef]
- He, W.; Wang, Y.; Shaheed, M.H. Maximum power point tracking (MPPT) of a scale-up pressure retarded osmosis (PRO) osmotic power plant. Appl. Energy 2015, 158, 584–596. [Google Scholar] [CrossRef] [Green Version]
- Maisonneuve, J.; Chintalacheruvu, S. Increasing osmotic power and energy with maximum power point tracking. Appl. Energy 2019, 238, 683–695. [Google Scholar] [CrossRef]
- AlZainati, N.; Saleem, H.; Altaee, A.; Zaidi, S.J.; Mohsen, M.; Hawari, A.; Millar, G.J. Pressure retarded osmosis: Advancement, challenges and potential. J. Water Process Eng. 2021, 40, 101950. [Google Scholar] [CrossRef]
- Chen, Y.; Vepa, R.; Shaheed, M.H. Enhanced and speedy energy extraction from a scaled-up pressure retarded osmosis process with a whale optimization based maximum power point tracking. Energy 2018, 153, 618–627. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Miyatake, M.; Veerachary, M.; Toriumi, F.; Fujii, N.; Ko, H. Maximum power point tracking of multiple photovoltaic arrays: A PSO approach. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 367–380. [Google Scholar] [CrossRef]
- Einarsson, S.J.; Wu, B. Thermal associated pressure-retarded osmosis processes for energy production: A review. Sci. Total Environ. 2021, 757, 143731. [Google Scholar] [CrossRef] [PubMed]
- Pattle, R.E. Production of electric power by mixing fresh and salt water in the hydroelectric pile. Nature 1954, 174, 660. [Google Scholar] [CrossRef]
- He, W.; Luo, X.; Kiselychnyk, O.; Wang, J.; Shaheed, M.H. Maximum power point tracking (MPPT) control of pressure retarded osmosis (PRO) salinity power plant: Development and comparison of different techniques. Desalination 2016, 389, 187–196. [Google Scholar] [CrossRef] [Green Version]
- Van’t Hoff, J.H. The role of osmotic pressure in the analogy between solutions and gases. J. Membr. Sci. 1995, 100, 39–44. [Google Scholar] [CrossRef]
- Adhikary, S.; Islam, M.S.; Touati, K.; Sultana, S.; Ramamurthy, A.S.; Rahaman, M.S. Increased power density with low salt flux using organic draw solutions for pressure-retarded osmosis at elevated temperatures. Desalination 2020, 484, 114420. [Google Scholar] [CrossRef]
- Touati, K.; Tadeo, F.; Hänel, C.; Schiestel, T. Effect of the operating temperature on hydrodynamics and membrane parameters in pressure retarded osmosis. Desalin. Water Treat. 2016, 57, 10477–10489. [Google Scholar] [CrossRef]

| Metaheuristic Algorithms | Key Vectors | Essential Coefficients |
|---|---|---|
| PSO | velocity and position | current solution, current best solution, global best solution |
| GWO | position | current solution, top three best solution |
| DA | step vector and position | current solution, current best solution, worst solution |
| WOA | position | current solution, current best solution, global best solution |
| GOA | position | current solution, global best solution, population solution |
| HGSO | position | current solution, current best solution, global best solution, population solution, worst solution |
| Metaheuristic Algorithms | Key Vectors | Essential Coefficients |
|---|---|---|
| PSO | velocity and position | current solution, current best solution, global best solution |
| BPSO | velocity and position | current solution, current best solution, global best solution, population solution, worst solution |
| Temperature (°C) | A () | B () | D () | () | ICP Factor () |
|---|---|---|---|---|---|
| 20 | 1.06 × 10−7 | 2.62 × 10−8 | 3.50 × 10−9 | 4.27 × 10−4 | 1.32 × 106 |
| 30 | 1.43 × 10−7 | 4.25 × 10−8 | 4.54 × 10−9 | 9.74 × 10−4 | 1.00 × 106 |
| 40 | 1.74 × 10−7 | 5.87 × 10−8 | 5.74 × 10−9 | 10.88 × 10−4 | 0.822 × 106 |
| 50 | 1.98 × 10−7 | 8.00 × 10−8 | 7.09 × 10−9 | 11.98 × 10−4 | 0.71 × 106 |
| Temperature Profile | 20 °C | 40 °C | 50 °C | 30 °C |
|---|---|---|---|---|
| AFI | AFI | AFI | AFI | |
| P&O | 0.66416819 | 0.97153503 | 1.04421445 | 0.88632589 |
| IMR | 0.69696450 | 1.00331396 | 1.05242449 | 0.88698557 |
| PSO | 0.70885323 | 1.00416366 | 1.05937919 | 0.88741486 |
| GWO | 0.70885340 | 1.00416453 | 1.05938074 | 0.88741477 |
| WOA | 0.70885377 | 1.00416649 | 1.05938071 | 0.88741489 |
| HGSO | 0.70885380 | 1.00416666 | 1.05938089 | 0.88741489 |
| BPSO | 0.70885382 | 1.00416668 | 1.05938090 | 0.88741491 |
| Temperature Profile | 20 °C | 40 °C | 50 °C | 30 °C |
|---|---|---|---|---|
| AFI | AFI | AFI | AFI | |
| P&O | 0.66416819 | 0.97153503 | 1.04421445 | 0.88632589 |
| BPSO | 0.70885382 | 1.00416668 | 1.05938090 | 0.88741491 |
| Improvement (%) | 6.73 | 3.84 | 1.45 | 0.12 |
| Salinity Conditions (CS) | CS1 | CS2 | CS3 | |||
|---|---|---|---|---|---|---|
| AFI | ACT (s) | AFI | ACT (s) | AFI | ACT (s) | |
| P&O | 0.67859463 | 0.23 | 1.12592327 | 0.22 | 1.66253908 | 0.23 |
| PSO | 0.67871438 | 0.33 | 1.12648435 | 0.34 | 1.66288136 | 0.30 |
| GOA | 0.67871439 | 0.28 | 1.12642532 | 0.27 | 1.66287249 | 0.26 |
| WOA | 0.67871442 | 0.25 | 1.12648449 | 0.27 | 1.66288220 | 0.29 |
| DA | 0.67871438 | 0.31 | 1.12648348 | 0.28 | 1.66288201 | 0.32 |
| GWO | 0.67871440 | 0.29 | 1.12648430 | 0.31 | 1.66288197 | 0.25 |
| HGSO | 0.67871442 | 0.42 | 1.12648455 | 0.39 | 1.66288208 | 0.47 |
| BPSO | 0.67871445 | 0.21 | 1.12648455 | 0.18 | 1.66288247 | 0.22 |
| Salinity Conditions (CS) | CS1 | CS2 | CS3 |
|---|---|---|---|
| ACT (s) | ACT (s) | ACT (s) | |
| P&O | 0.33 | 0.34 | 0.30 |
| BPSO | 0.21 | 0.18 | 0.22 |
| Improvement (%) | 57.1 | 88.9 | 36.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Gou, L. A Boosted Particle Swarm Method for Energy Efficiency Optimization of PRO Systems. Energies 2021, 14, 7688. https://doi.org/10.3390/en14227688
Chen Y, Gou L. A Boosted Particle Swarm Method for Energy Efficiency Optimization of PRO Systems. Energies. 2021; 14(22):7688. https://doi.org/10.3390/en14227688
Chicago/Turabian StyleChen, Yingxue, and Linfeng Gou. 2021. "A Boosted Particle Swarm Method for Energy Efficiency Optimization of PRO Systems" Energies 14, no. 22: 7688. https://doi.org/10.3390/en14227688
APA StyleChen, Y., & Gou, L. (2021). A Boosted Particle Swarm Method for Energy Efficiency Optimization of PRO Systems. Energies, 14(22), 7688. https://doi.org/10.3390/en14227688






