Pulse-Width Modulation Template for Five-Level Switch-Clamped H-Bridge-Based Cascaded Multilevel Inverter
Abstract
:1. Introduction
2. Five-Level Switch-Clamped Inverter
3. Proposed Single Carrier SPWM for 5-Level Switch-Clamped Multilevel Inverter
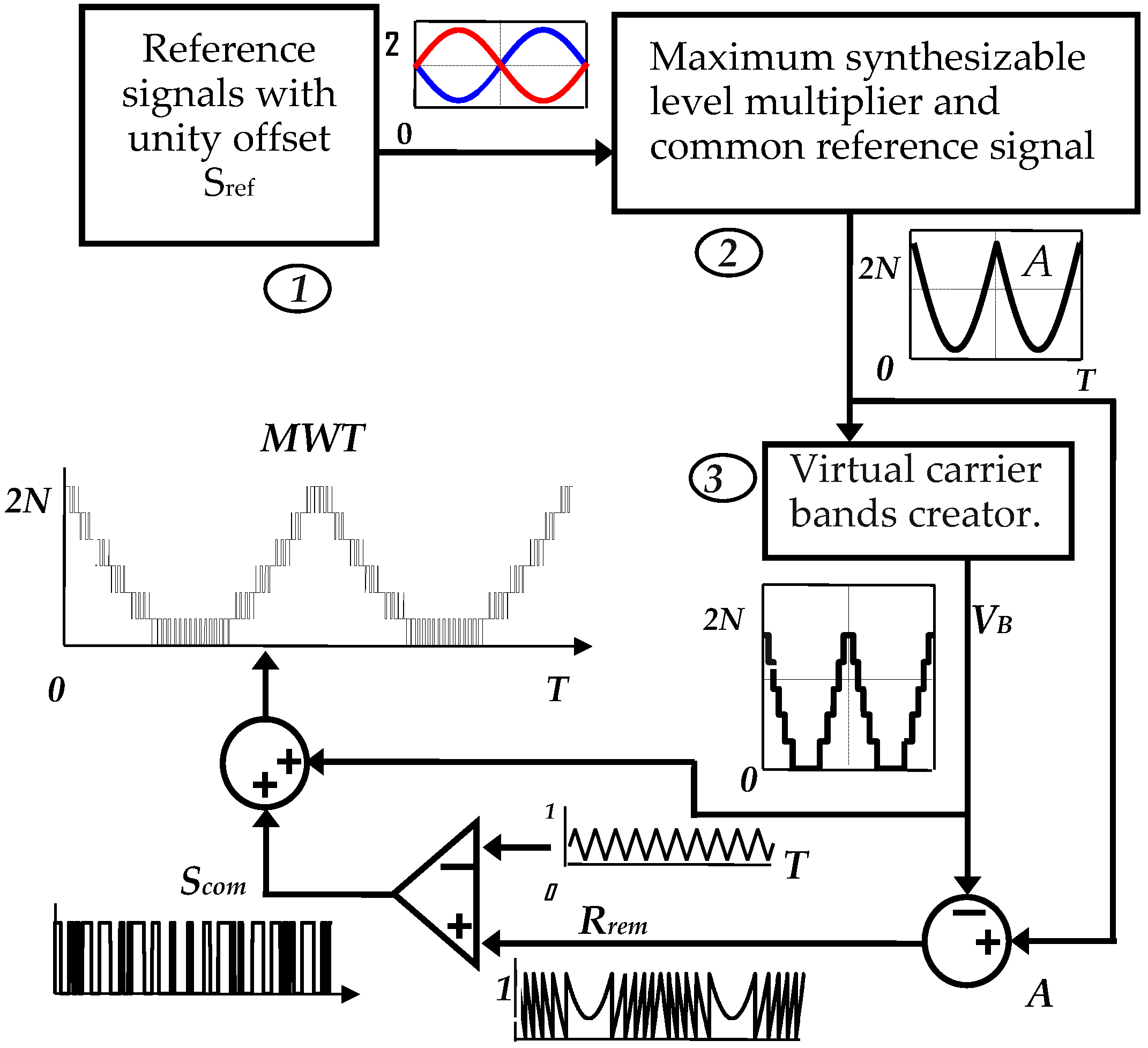
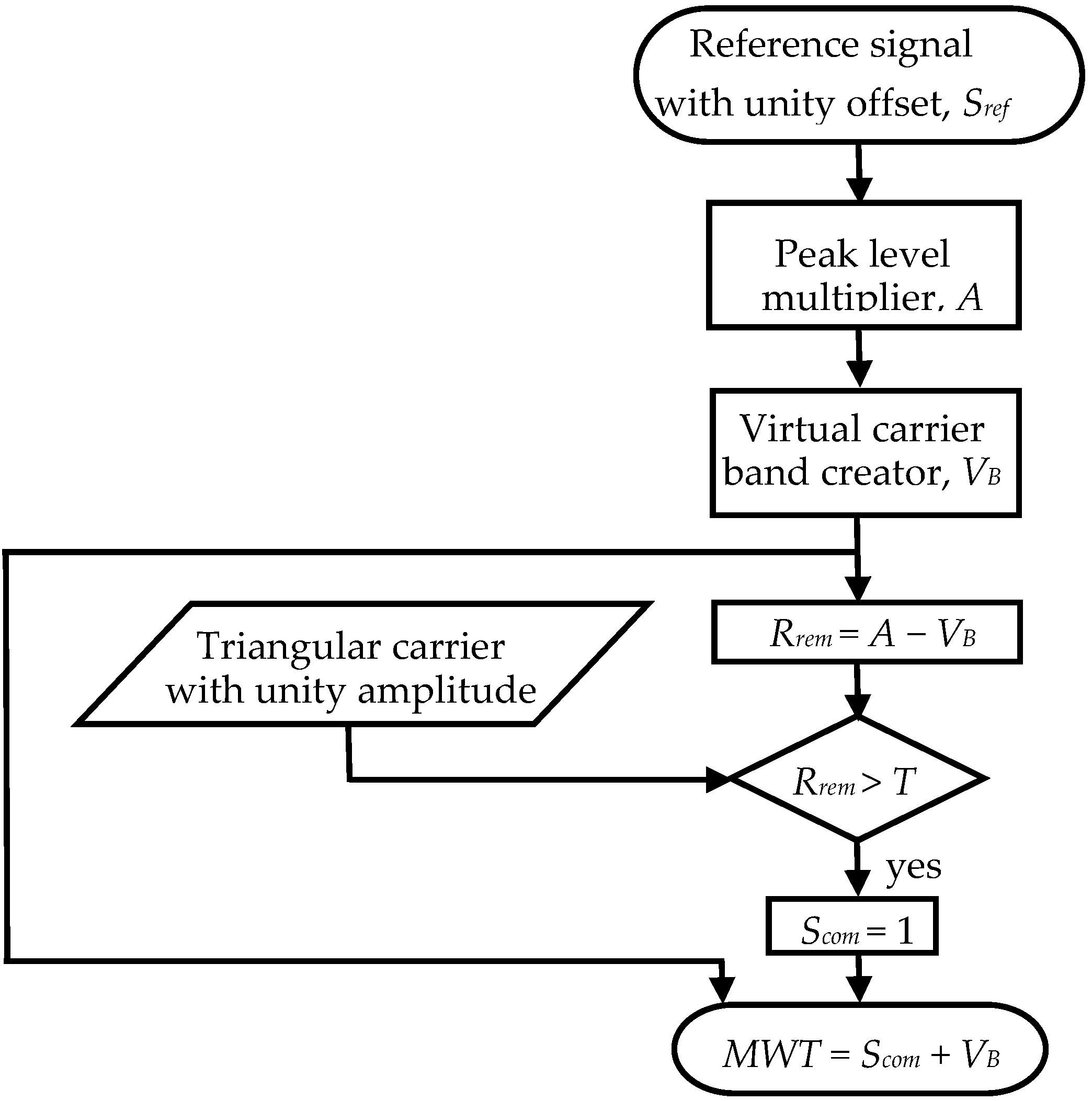
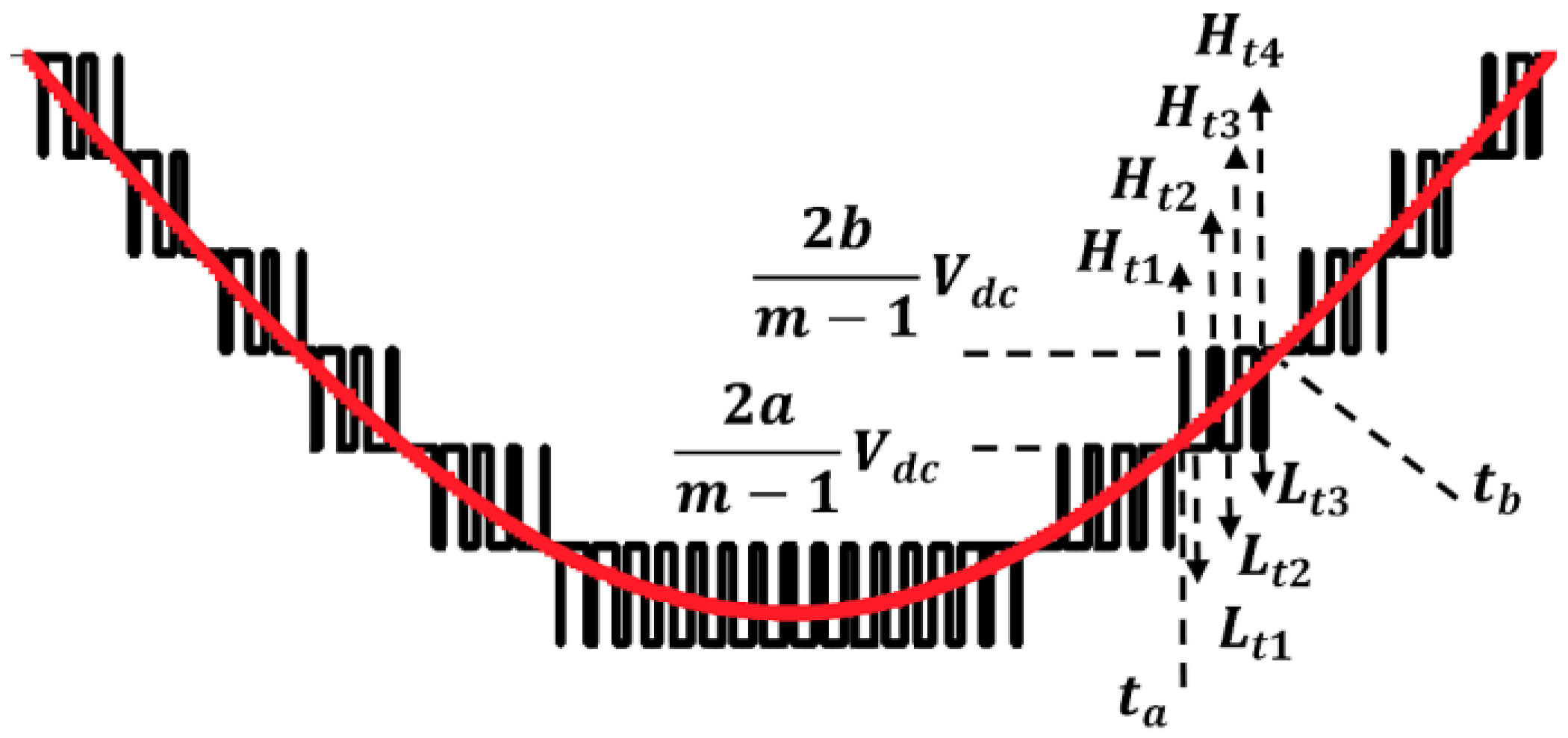
3.1. Reference Waveform Generation
3.2. Generation of the Virtual Carrier Bands
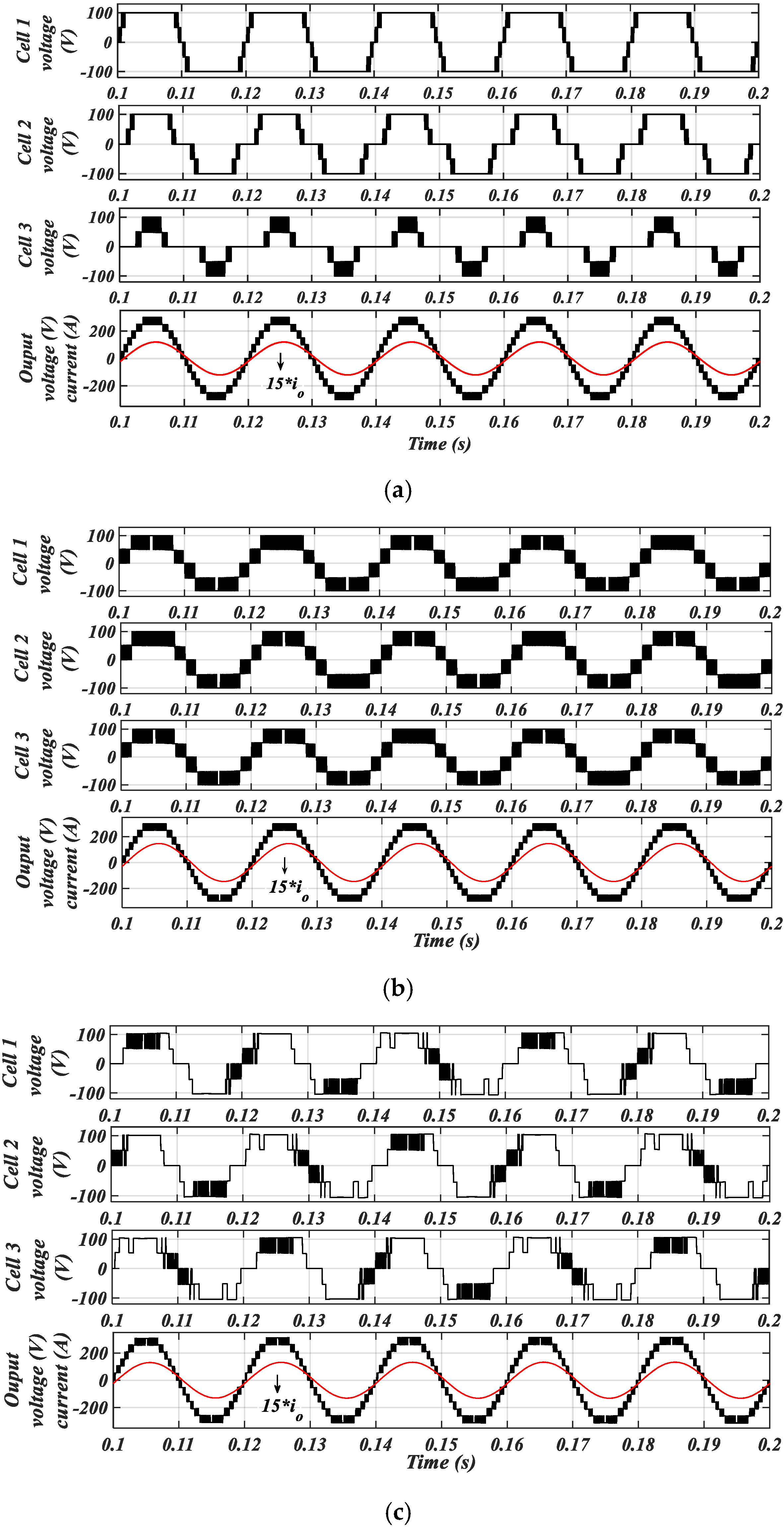
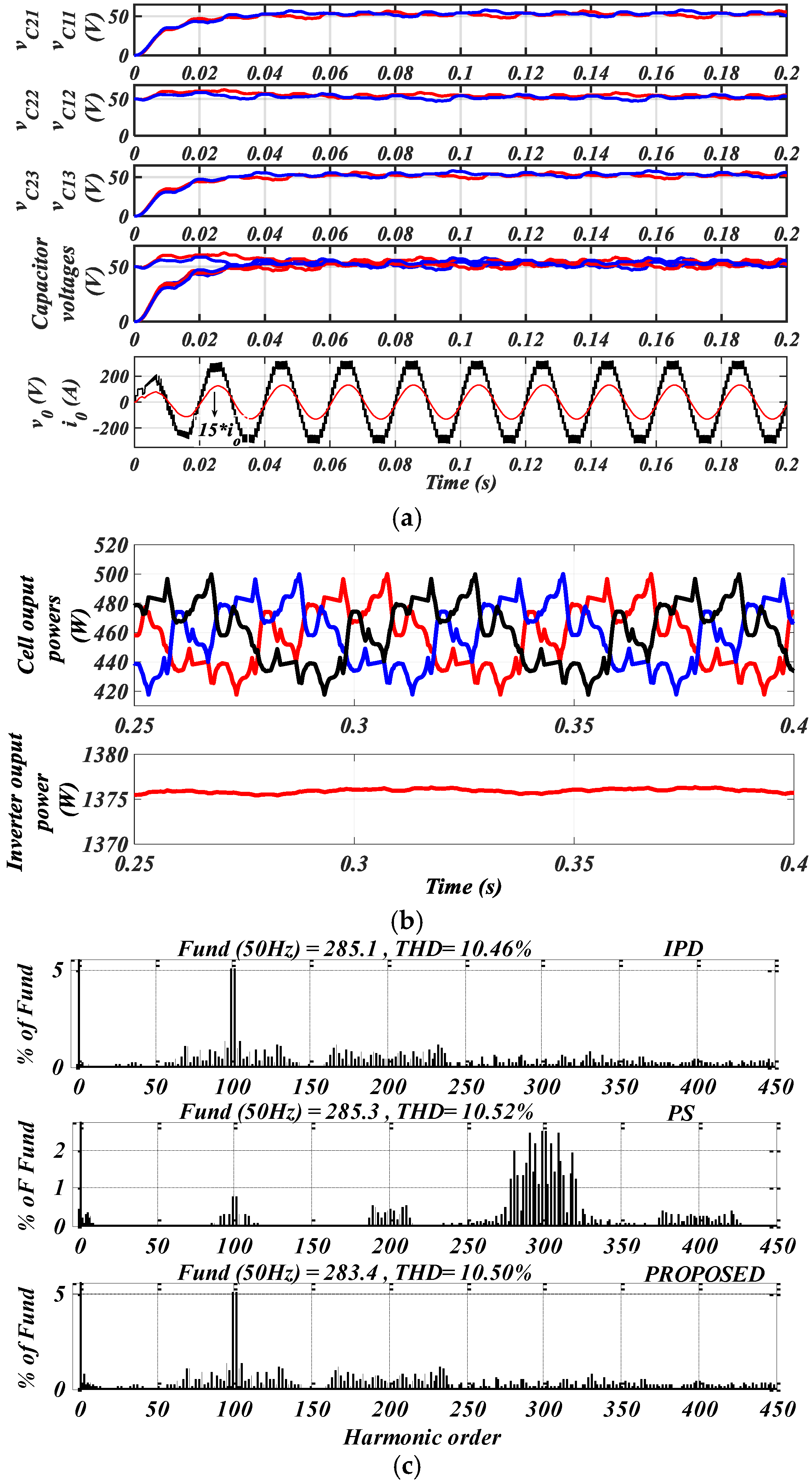
4. Simulation and Experimental Results
4.1. Simulation Results
4.2. THD of the Inverter Output Voltage
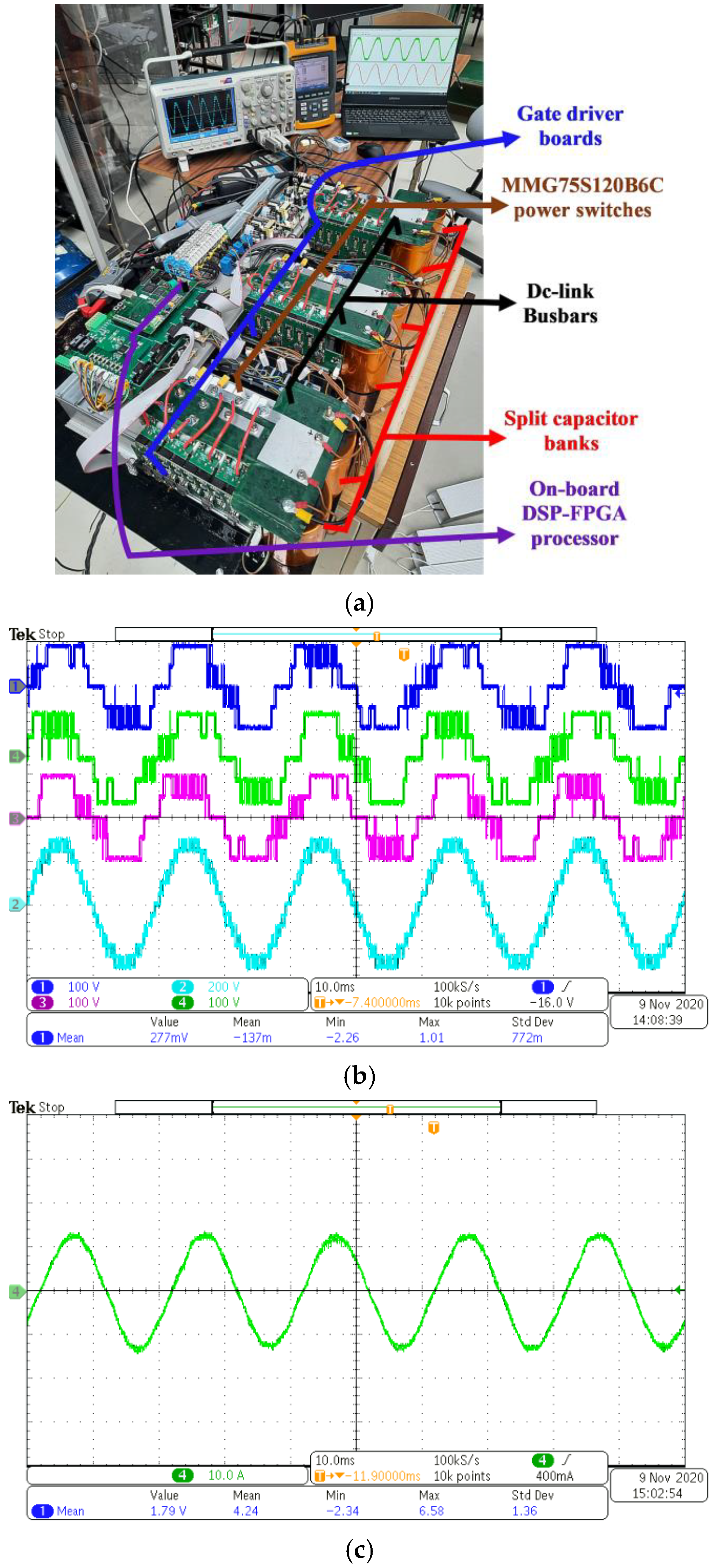
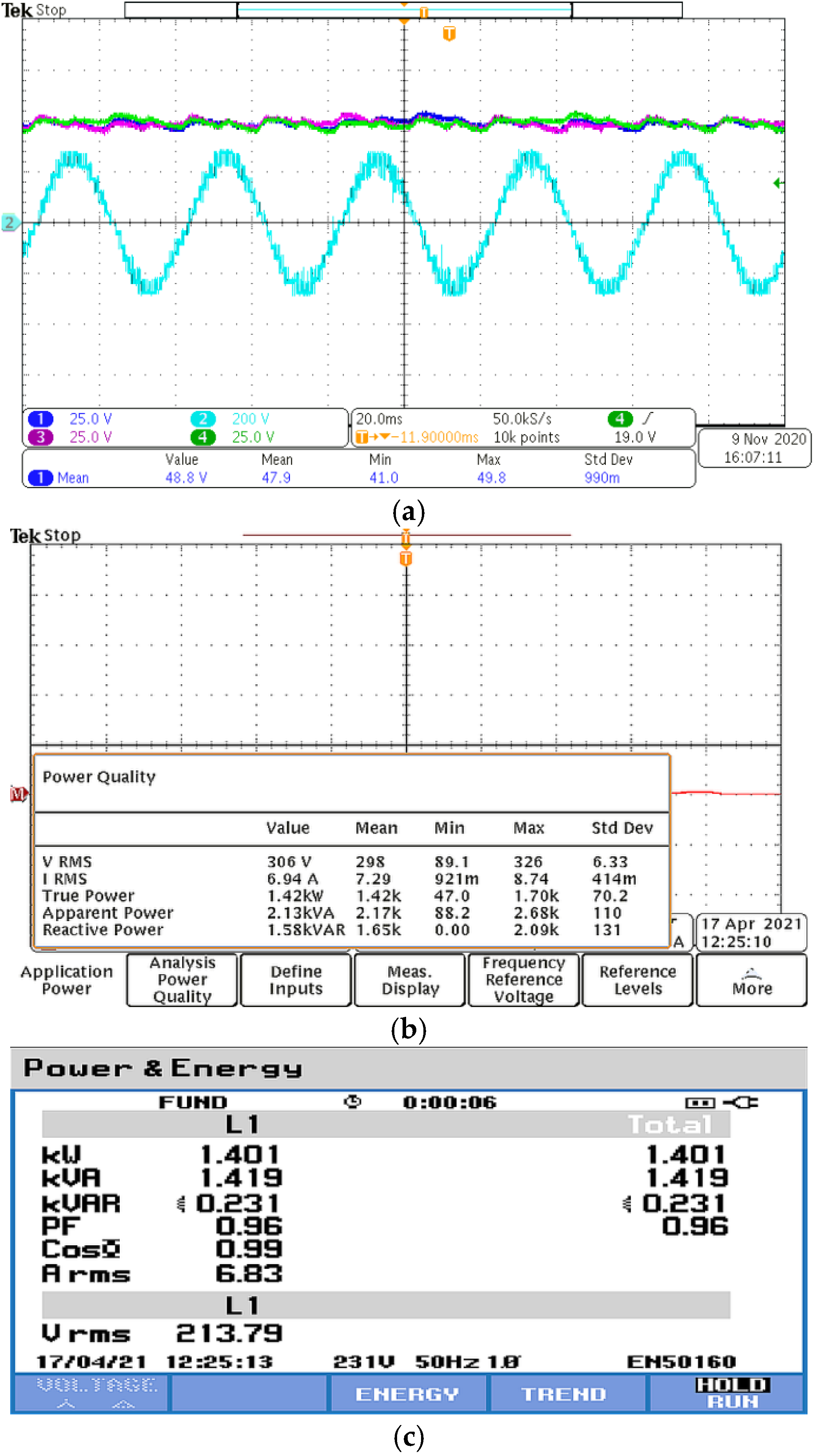
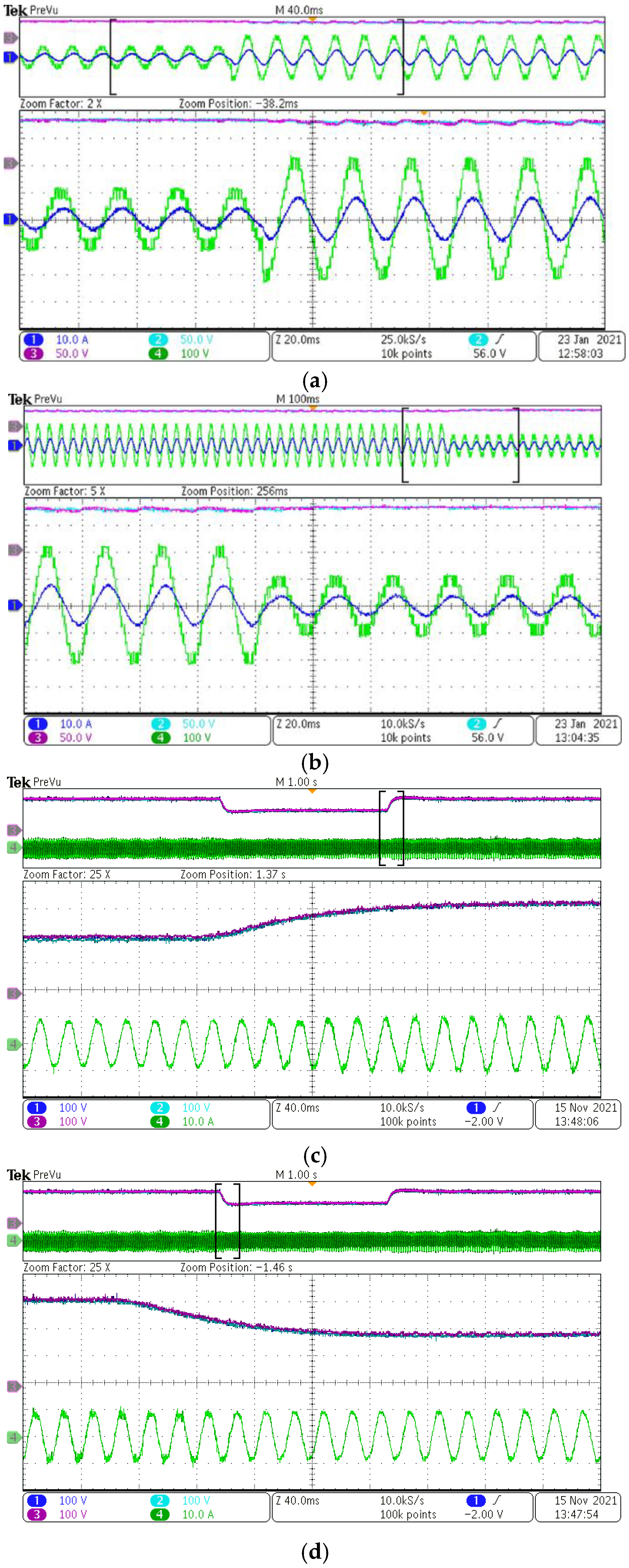
4.3. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, R.; Gupta, N.; Poole, K.F. Global green energy conversion revolution in 21st century through solid state devices. In Proceedings of the 26th International Conference on Microelectronics, Nis, Serbia, 11–14 May 2008. [Google Scholar]
- Jovcic, D.; Pahalawaththa, N.; Zavahir, M. Investigation of the use of Inverter Control Strategy Instead of Synchronous Condensers at Inverter Terminal of an HVDC System. IEEE Trans. Power Deliver. 2020, 15, 704–709. [Google Scholar] [CrossRef]
- Elserougi, A.A.; Massoud, A.M.; Abdel-Khalik, A.S.; Ahmed, S. Bidirectional Buck-Boost Inverter-Based HVDC Transmission System with AC-Side Contribution Blocking Capability during DC-Side Faults. IEEE Trans. Power Deliver. 2014, 29, 1249–1261. [Google Scholar] [CrossRef]
- Sotoodeh, P.; Miller, R.D. Design and Implementation of an 11-Level Inverter with FACTS Capability for Distributed Energy Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 87–96. [Google Scholar] [CrossRef]
- Chivite-Zabalza, J.; Izurza-Moreno, P.; Madariaga, D.; Calvo, G.; Rodríguez, M.A. Voltage Balancing control in 3-Level Neutral-Point Clamped Inverter Using Triangular Carrier PWM Modulation for FACTS Applications. IEEE Trans. Power Electron. 2013, 28, 4473–4484. [Google Scholar] [CrossRef]
- Sher, H.A.; Rizvi, A.A.; Addoweesh, K.E.; Al-Haddad, K. A single-stage stand-alone photovoltaic energy system with high tracking efficiency. IEEE Trans. Sustain. Energy 2016, 8, 755–762. [Google Scholar] [CrossRef]
- Sher, H.A.; Addoweesh, K.E.; Al-Haddad, K. An efficient and cost-effective hybrid MPPT method for a photovoltaic flyback microinverter. IEEE Trans. Sustain. Energy 2017, 9, 1137–1144. [Google Scholar] [CrossRef]
- Youssef, M.Z.; Woronowicz, K.; Aditya, K.; Azeez, N.A.; Williamson, S.S. Design and Development of an Efficient Multilevel DC/AC Traction Inverter Railway Transportation Electrification. IEEE Trans. Ind. Electron. 2016, 31, 3036–3042. [Google Scholar] [CrossRef]
- Haizhong, Y.; Emadi, A. A Six-Phase Current Reconstruction Scheme for Dual Traction Inverters in Hybrid Electric Vehicles with a Single DC-Link Current Sensor. IEEE Trans. Veh. Technol. 2014, 63, 3085–3093. [Google Scholar] [CrossRef]
- Kersten, A.; Theliander, O.; Grunditz, E.; Thiringer, T.; Bongiorno, M. Battery Loss and Stress Mitigation in a Cascaded H-bridge Multilevel Inverter for Vehicle bridge Multilevel Inverter for Vehicle Traction Applications by Filter Capacitors. IEEE Trans. Transp. Electric. 2019, 5, 659–671. [Google Scholar] [CrossRef]
- Chaitanya, M.A.; Maswood, A.I.; Yeong, L.M.; Gupta, K. Realisation of ‘more Electric Ships’ through a Modular, Efficient, Tank-less and Non-resonant Inverter. IET Power Electron. 2016, 9, 771–781. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Leopoldo, G.; Franquelo, B.W.; Rodriguez, J.; Pérez, M.A.; Leon, J.I. Recent advances and industrial applications of multilevel converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Omer, P.; Kumar, J.; Surjan, B.S. A review on reduced switch-count multilevel inverter topologies. IEEE Access 2020, 8, 22281–22302. [Google Scholar] [CrossRef]
- Vijeh, M.; Rezanejad, M.; Samadaei, E.; Bertilsson, K. A general review of multilevel inverters based on main submodules: Structural point of view. IEEE Trans. Power Electron. 2019, 34, 9479–9502. [Google Scholar] [CrossRef]
- Park, S.J.; Kang, F.-S.; Lee, M.H.; Kim, C.-U. A new single-phase, five-level PWM inverter employing a deadbeat control scheme. IEEE Trans. Power Electron. 2003, 18, 831–843. [Google Scholar] [CrossRef]
- Odeh, C.I.; Damian, B.; Nnadi, N. Single-phase 9-level Hybridized Cascaded Multilevel Inverter. IET Power. Electron. 2013, 6, 468–477. [Google Scholar] [CrossRef]
- Rahim, N.A.; Mohamad, E.M.F.; Hew, W.P. Transistor-Clamped H-Bridge Based Cascaded Multilevel Inverter with New Method of Capacitor Voltage Balancing. IEEE Trans. Ind. Electron. 2013, 60, 2943–2956. [Google Scholar] [CrossRef]
- Rodríguez, J.; Bernet, S.; Wu, B.; Pontt, J.O.; Kouro, S. Multilevel Voltage-Source-Converter Topologies for Industrial Medium-Voltage Drives. IEEE Trans. Ind. Electron. 2007, 54, 2930–2945. [Google Scholar] [CrossRef]
- Liu, X.; Lindemann, A.; Amiri, H.A. Theoretical and Experimental Analysis of N + 1 and 2N + 1 Phase-Shifted Carrier-Based PWM Strategies in Modular Multilevel Converters. In Proceedings of the International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 20–22 May 2014; pp. 1–8. [Google Scholar]
- Wu, B. High-Power Converters and AC Drives; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 127–138. [Google Scholar]
- Sreenivasarao, D.; Agarwal, P.; Das, B. Performance evaluation of carrier rotation strategy in level-shifted pulse-width modulation technique. IET Power Electron. 2014, 7, 667–680. [Google Scholar] [CrossRef]
- Venkata Rao, J.; Mahesh, A. Carrier rotation schemes for equal device conduction periods in Cascaded H-bridge Multilevel Inverter. In Proceedings of the International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, 5–6 May 2017; pp. 1578–1583. [Google Scholar]
- Nimmi; Mahesh, A. Carrier rotation schemes for equal device conduction periods in Cascaded H-bridge Multilevel Inverter. In Proceedings of the International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 13–14 April 2018; pp. 696–701. [Google Scholar]
- Ma, J.; Wang, X.; Blaabjerg, F.; Song, W.; Wang, S.; Liu, T. Real-Time Calculation Method for Single-Phase Cascaded H-bridge Inverters Based on Phase-Shifted Carrier Pulsewidth Modulation. IEEE Trans. Power Electron. 2020, 35, 977–987. [Google Scholar] [CrossRef]
- Sahoo, S.; Bhattacharya, T. Phase Shifted Carrier Based Synchronized Sinusoidal PWM Techniques for Cascaded H-Bridge Multi Level Inverter. IEEE Trans. Power Electron. 2018, 33, 513–524. [Google Scholar] [CrossRef]
- Ma, J.; Wang, X.; Blaabjerg, F.; Song, W.; Wang, S.; Liu, T. Multi-Sampling Method for Single-Phase Grid-Connected Cascaded H-bridge Inverters. IEEE Trans. Ind. Electron. 2020, 67, 8322–8334. [Google Scholar] [CrossRef]
- Ronanki, D.; Williamson, S. A Novel 2N+1 Carrier-Based Pulse Width Modulation Scheme for Modular Multilevel Converters with Reduced Control Complexity. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 908–915. [Google Scholar]
- Lingom, P.M.; Song-Manguelle, J.; Nyobe-Yome, J.M.; Mon-Nzongo, D.L.; Jin, T.; Doumbia, M.L. A Single-Carrier PWM Method for Multilevel Converters. In Proceedings of the IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; pp. 122–127. [Google Scholar]
- Odeh, C.I.; Lewicki, A.; Morawiec, M. A Single-Carrier-Based Pulse-width Modulation Template for Cascaded H-bridge multilevel inverters. IEEE Access 2021, 56, 42182–42191. [Google Scholar] [CrossRef]
- Selvaraj, J.; Rahim, N.A. Multilevel Inverter for Grid-Connected PV System Employing Digital PI Controller. IEEE Trans. Ind. Electron. 2009, 56, 149–158. [Google Scholar] [CrossRef]
- Rech, C.; Pinheiro, J.R. Hybrid multilevel converters: Unified analysis and design considerations. IEEE Trans. Ind. Electron. 2007, 54, 1092–1104. [Google Scholar] [CrossRef]
- Odeh, C.I. A Single-phase Hybrid Multi-level Inverter. Elect. Power Compon. Syst. 2015, 43, 252–259. [Google Scholar] [CrossRef]
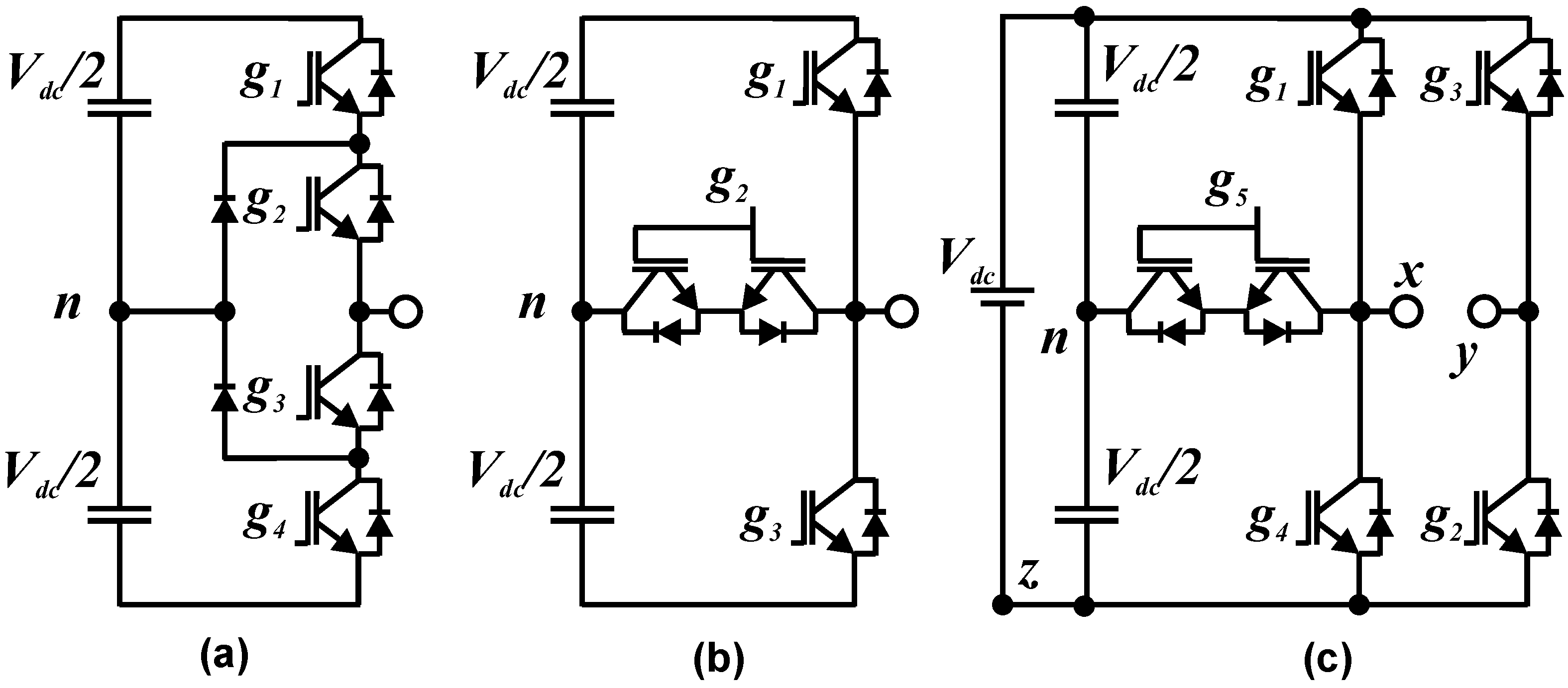
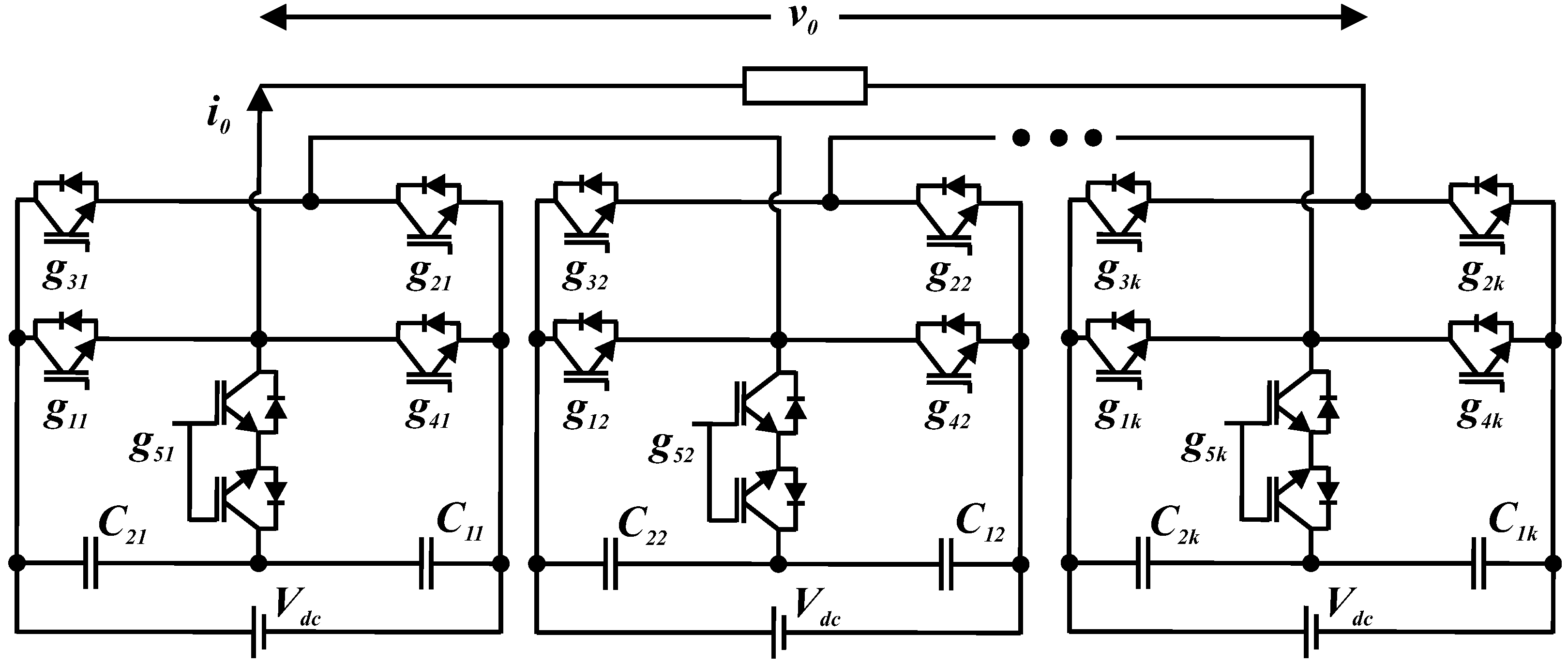


| s/n | g1 | g2 | g3 | g4 | g5 | vxz | vyz | vxy |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 1 | 0.5 Vdc | 0 | 0.5 Vdc |
| 3 | 1 | 1 | 0 | 0 | 0 | Vdc | 0 | Vdc |
| 4 | 1 | 0 | 1 | 0 | 0 | Vdc | Vdc | 0 |
| 5 | 0 | 0 | 1 | 0 | 1 | 0.5 Vdc | Vdc | −0.5 Vdc |
| 6 | 0 | 0 | 1 | 1 | 0 | 0 | Vdc | −Vdc |
| s/n | Compared Parameter | Modulation Schemes | ||
|---|---|---|---|---|
| IPD | PS | Proposed SPWM | ||
| 1 | Number of carriers | 2N | N | 1 |
| 2 | Number of sine signals | 1 | 2 | 1 |
| 3 | Algorithm execution time (µs) | 3.492 | 3.42 | 3.168 |
| s/n | Component | Specification |
|---|---|---|
| 1 | Power switches | MMG75S120B6 |
| 2 | Fundamental frequency | 50 Hz |
| 3 | Carrier frequency | 5 kHz |
| 4 | Capacitor banks | 2200 µF, 200 V |
| 5 | RL load | 35 Ω and 20 mH |
| 6 | Dc-link voltage | 100 V |
| 7 | Power | 1.5 kW |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Odeh, C.I.; Kondratenko, D.; Lewicki, A.; Morawiec, M.; Jąderko, A.; Baran, J. Pulse-Width Modulation Template for Five-Level Switch-Clamped H-Bridge-Based Cascaded Multilevel Inverter. Energies 2021, 14, 7726. https://doi.org/10.3390/en14227726
Odeh CI, Kondratenko D, Lewicki A, Morawiec M, Jąderko A, Baran J. Pulse-Width Modulation Template for Five-Level Switch-Clamped H-Bridge-Based Cascaded Multilevel Inverter. Energies. 2021; 14(22):7726. https://doi.org/10.3390/en14227726
Chicago/Turabian StyleOdeh, Charles Ikechukwu, Dmytro Kondratenko, Arkadiusz Lewicki, Marcin Morawiec, Andrzej Jąderko, and Janusz Baran. 2021. "Pulse-Width Modulation Template for Five-Level Switch-Clamped H-Bridge-Based Cascaded Multilevel Inverter" Energies 14, no. 22: 7726. https://doi.org/10.3390/en14227726
APA StyleOdeh, C. I., Kondratenko, D., Lewicki, A., Morawiec, M., Jąderko, A., & Baran, J. (2021). Pulse-Width Modulation Template for Five-Level Switch-Clamped H-Bridge-Based Cascaded Multilevel Inverter. Energies, 14(22), 7726. https://doi.org/10.3390/en14227726








