Joint Acquisition Time Design and Sensor Association for Wireless Sensor Networks in Microgrids
Abstract
:1. Introduction
- This paper comprehensively considers the factors that affect the quality of WSN monitoring, such as data collection time, sensor association and cluster heads (CHs) selection. A joint acquisition time and sensor association optimization algorithm (ATSAO) is proposed to prolong the lifetime of the WSN and enhance the stability of monitoring. The optimal topology and collection time control strategy are obtained.
- The joint optimization problem is formulated as a multi-constrained mixed integer programming problem, and an effective iterative algorithm is proposed based on block coordinate descent (BCD) technology to obtain its sub-optimal solution to achieve WSN energy consumption minimization and maximize the satisfaction of collecting data to extend the lifetime of the sensor network and ensure the accuracy and reliability of monitoring.
- The sensor association is modeled as a 0–1 multi-knapsack optimization problem. The methods with different complexity are proposed to address the problem, and their performance differences are compared by simulation so that they can be selected according to the actual needs in the project.
2. Literature Review
3. System Model
Energy Consumption Model
4. Problem Formulation and Problem Solution
4.1. Cluster Heads Selection
4.2. Problem Formulation
4.3. Problem Solution
4.3.1. Acquisition Time Optimization
4.3.2. Sensor Association Optimization
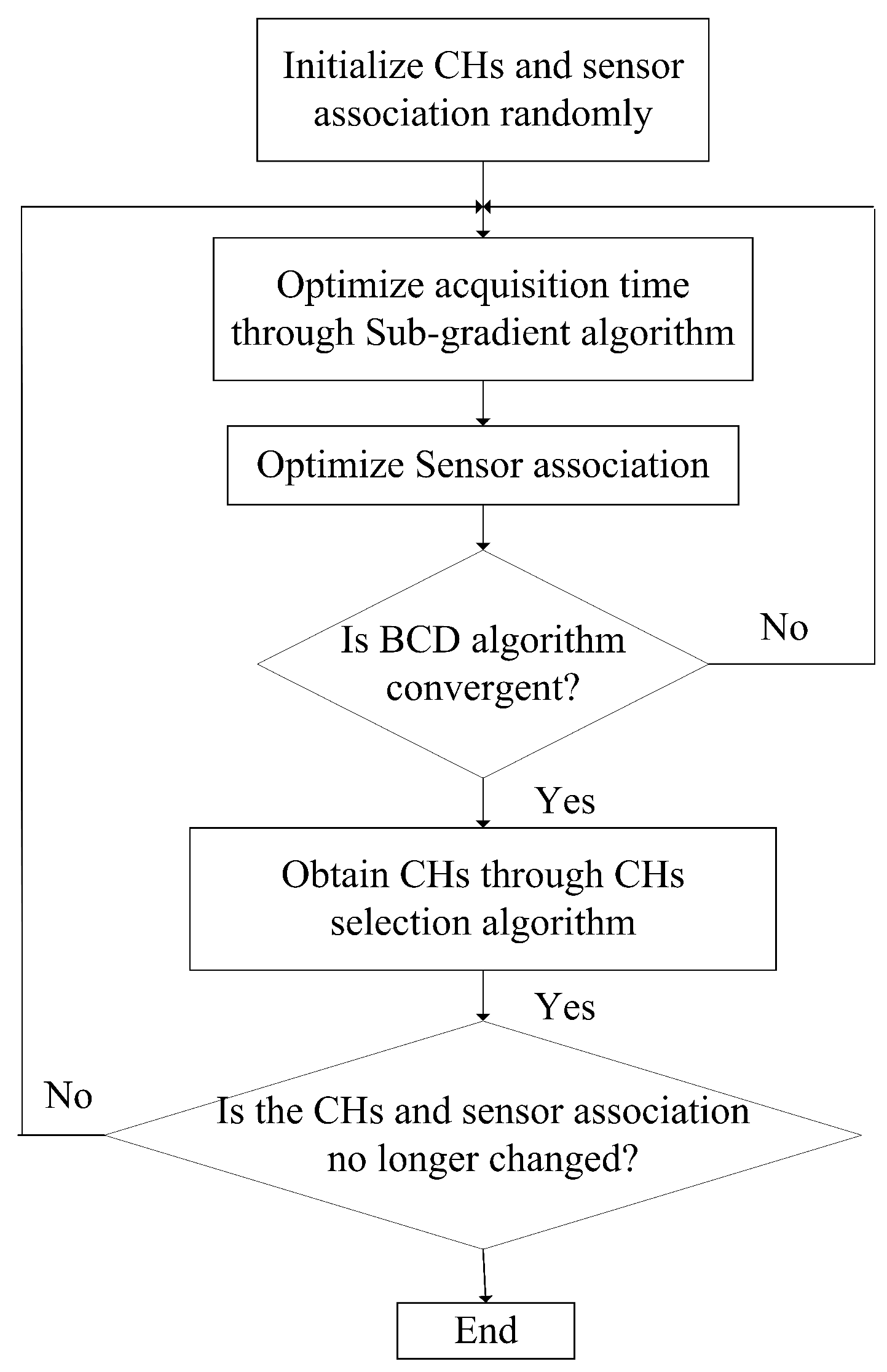
4.4. Overall Algorithm Design
| Algorithm 1 Acquisition Time and Sensor Association Optimization (ATSAO). |
|
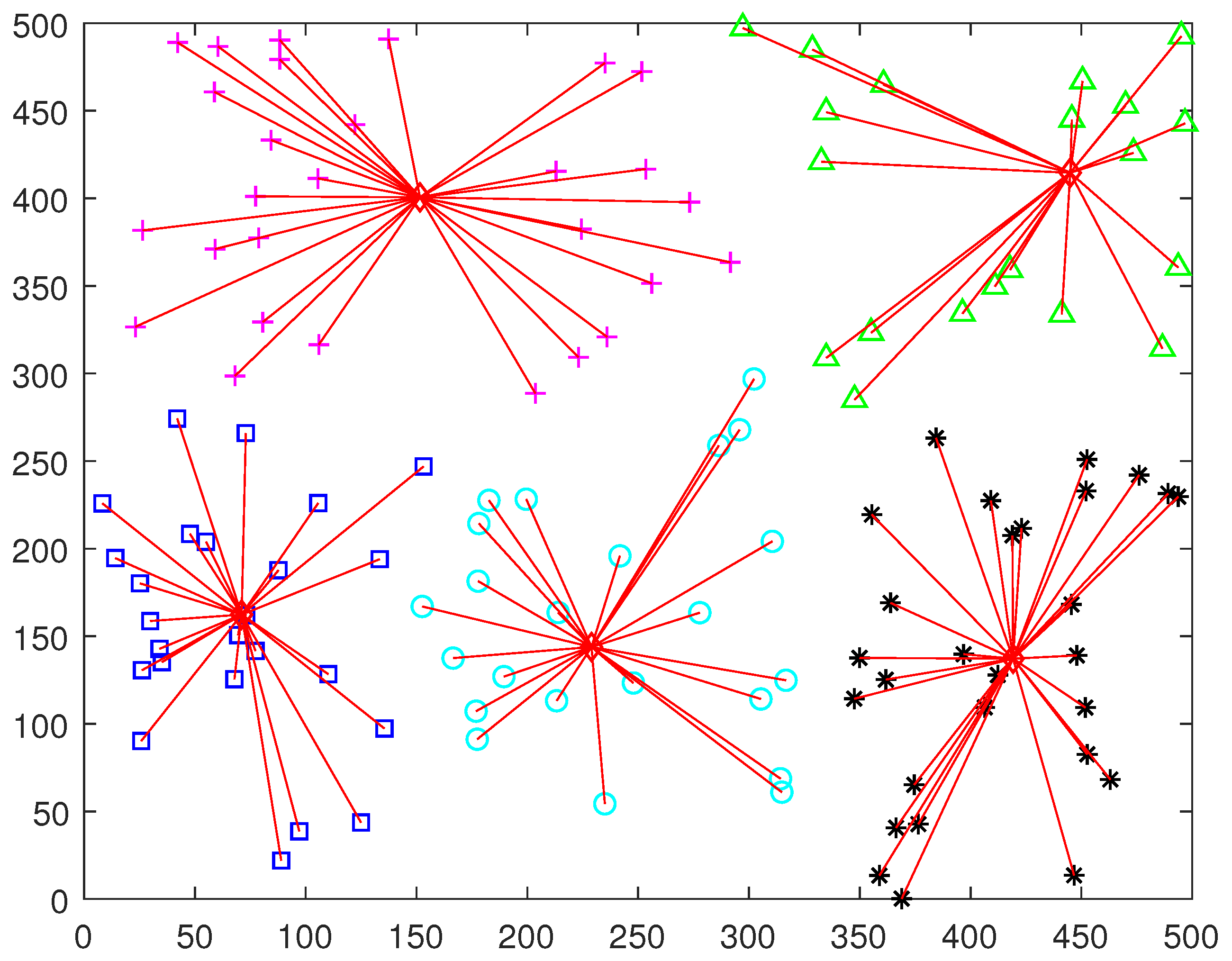
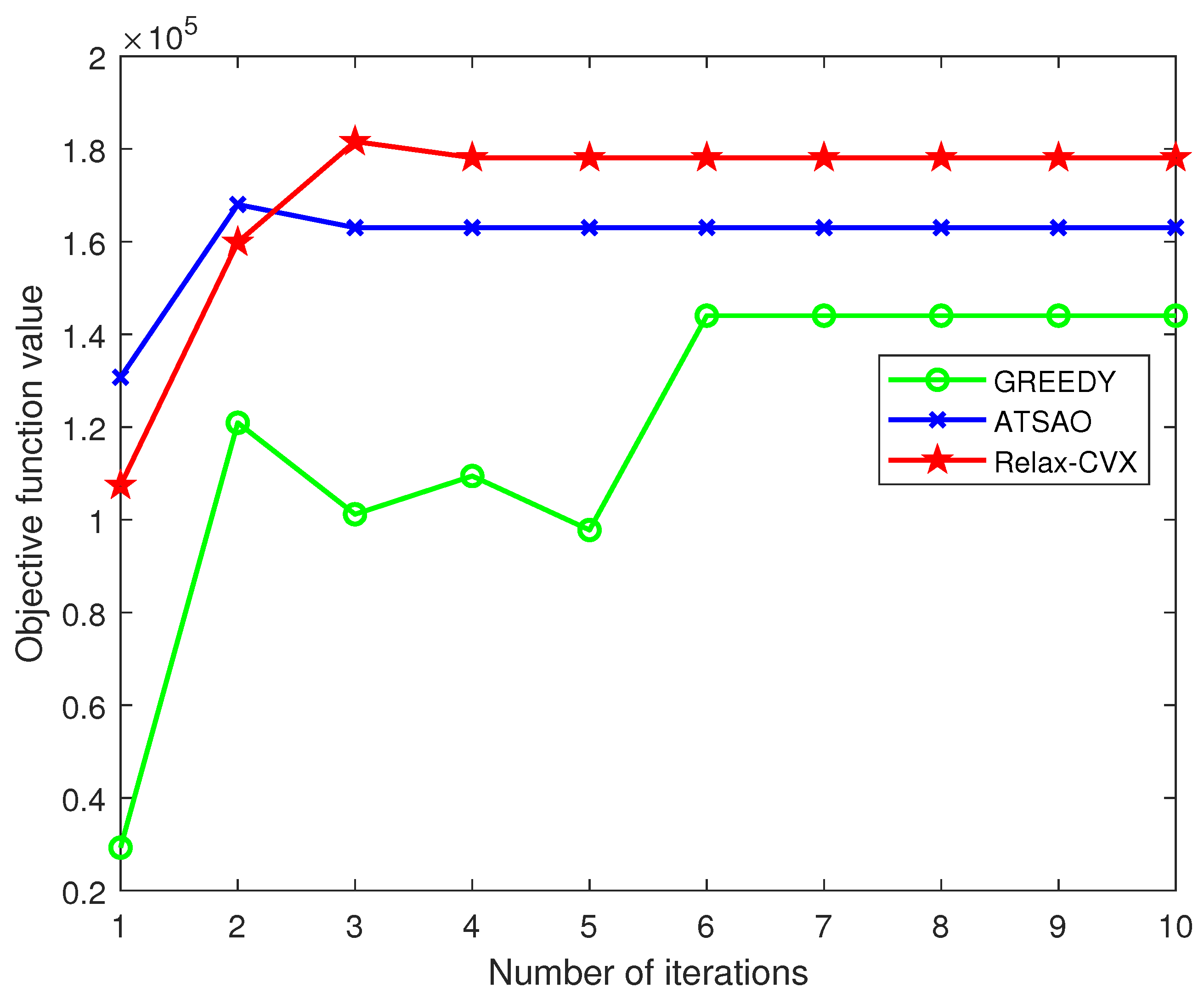
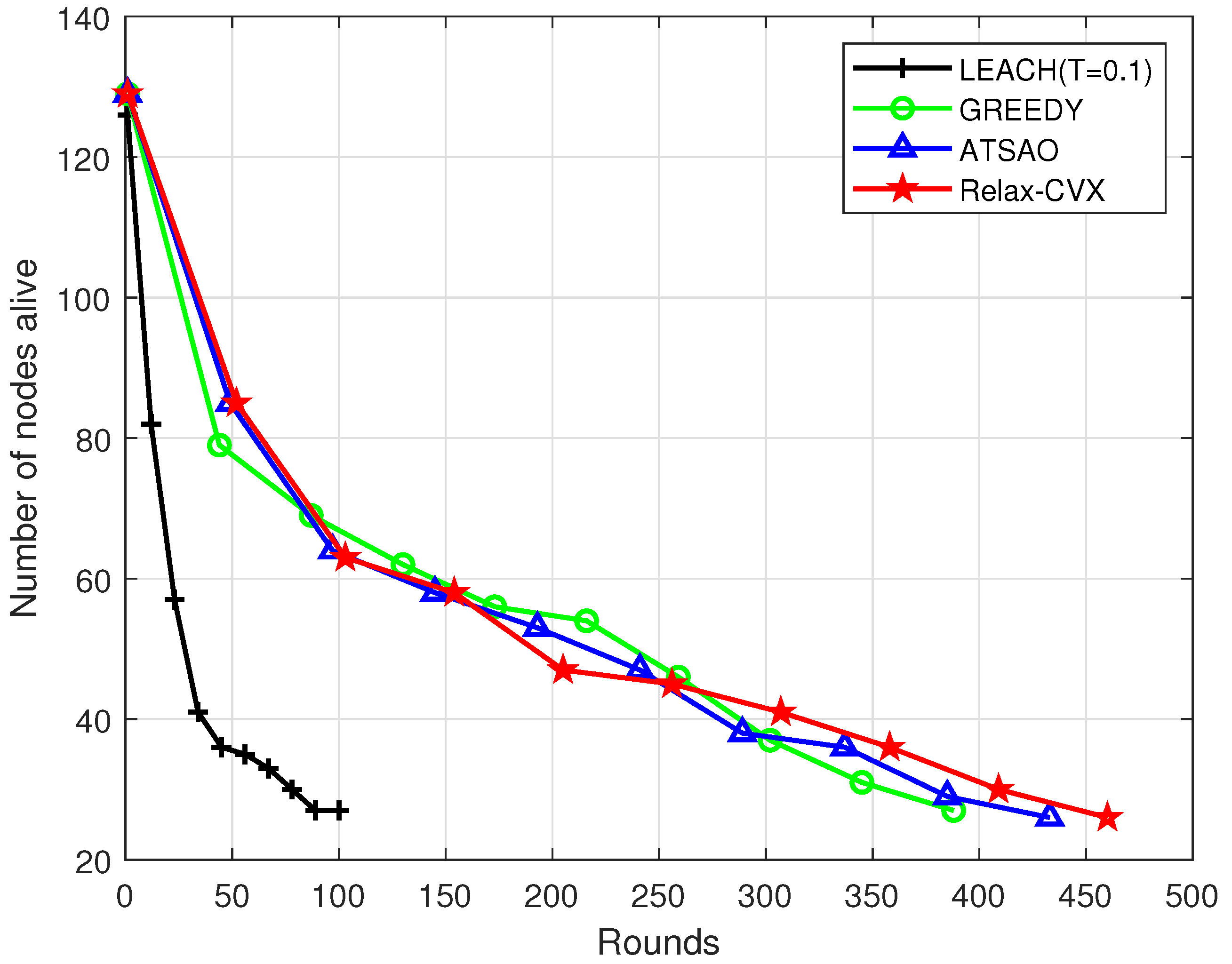
5. Experiment Simulation
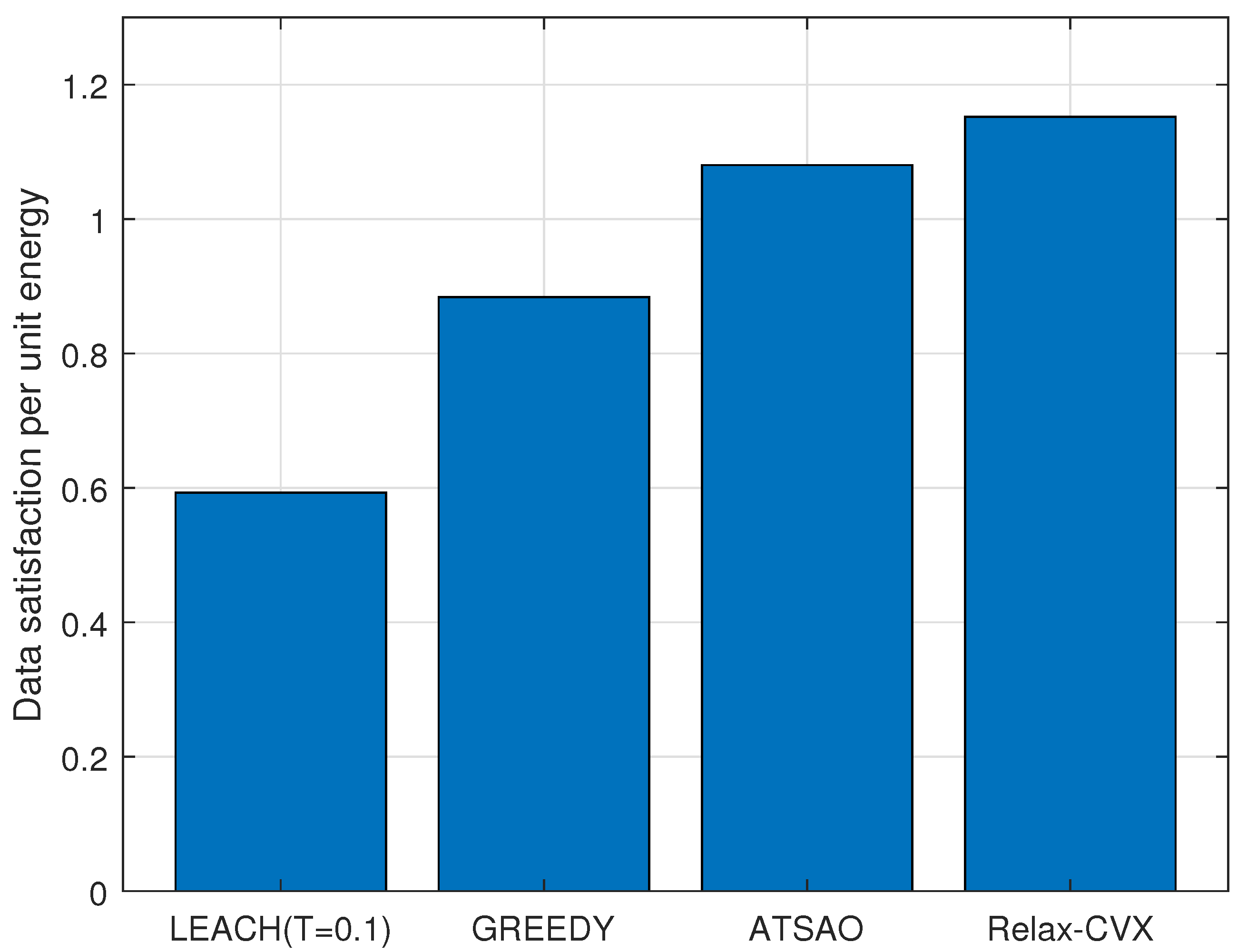
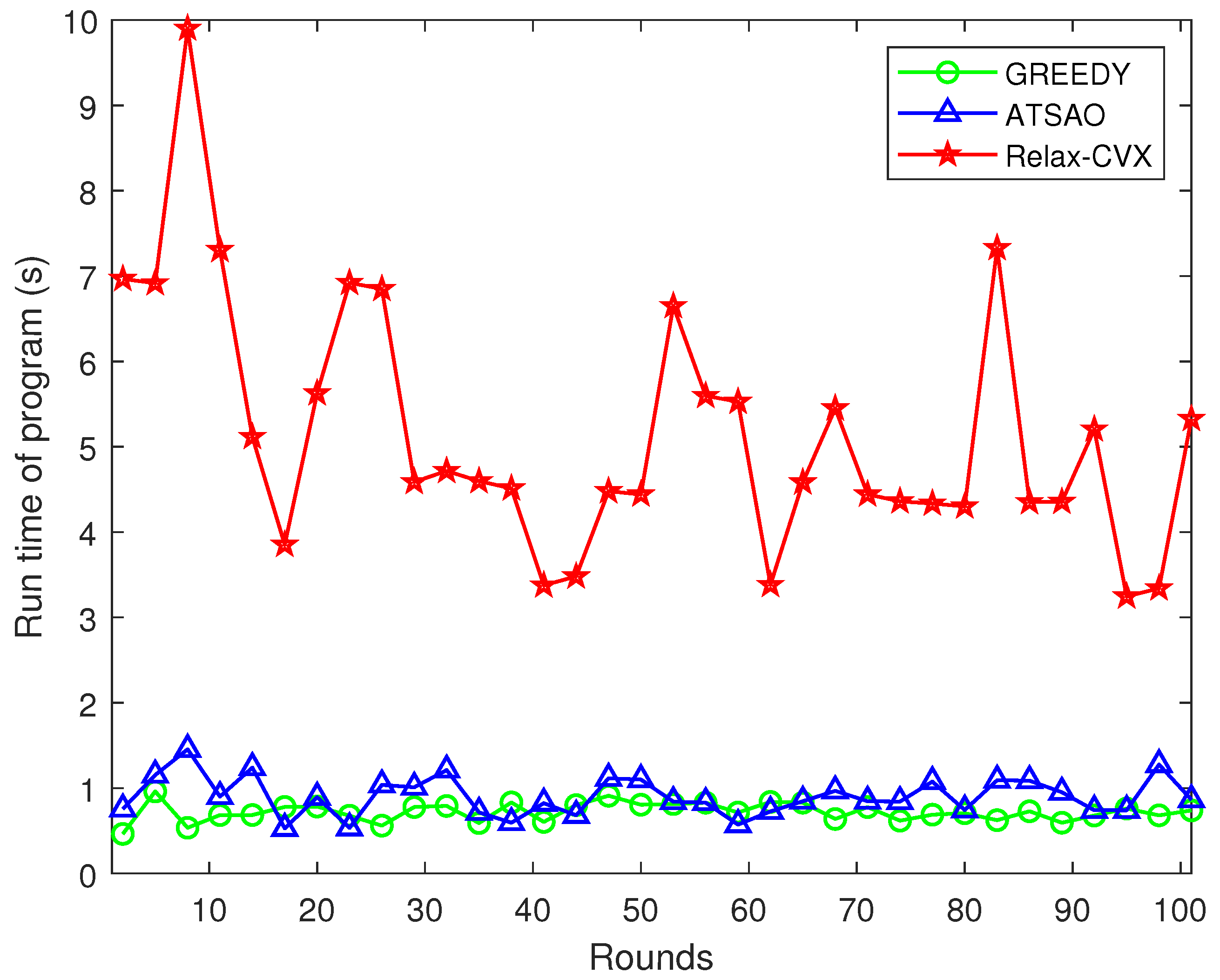
Simulation Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sharmila, N.; Nataraj, K.; Rekha, K. An Overview on Design and Control Schemes of Microgrid. In Proceedings of the 2019 Global Conference for Advancement in Technology (GCAT), Bangalore, India, 18–20 October 2019; pp. 1–4. [Google Scholar]
- Kim, H.M.; Lim, Y. A communication framework in multiagent system for islanded microgrid. Int. J. Distrib. Sens. Netw. 2012, 8, 382316. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, J.; Qiu, J.; Zhang, S.; Lai, M.; Dong, Z.Y. A practical pricing approach to smart grid demand response based on load classification. IEEE Trans. Smart Grid 2016, 9, 179–190. [Google Scholar] [CrossRef]
- Rana, M. Architecture of the internet of energy network: An application to smart grid communications. IEEE Access 2017, 5, 4704–4710. [Google Scholar] [CrossRef]
- Swain, A.; Salkuti, S.R.; Swain, K. An Optimized and Decentralized Energy Provision System for Smart Cities. Energies 2021, 14, 1451. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, B.; Pal, B.C.; Xu, L.; Al-Durra, A. Energy efficient three-phase utility interactive residential microgrid with mode transfer capabilities at weak grid conditions. IEEE Trans. Ind. Appl. 2019, 55, 7082–7091. [Google Scholar] [CrossRef]
- Lai, S.; Ravindran, B.; Cho, H. Heterogenous quorum-based wake-up scheduling in wireless sensor networks. IEEE Trans. Comput. 2010, 59, 1562–1575. [Google Scholar] [CrossRef]
- Kumar, G.A.; Shivashankar; Sujay, N.; Tejas, P.; Srikanth, P.; Yashavanth, T. Design and implementation of wireless sensor network based smart DC grid for smart cities. In Proceedings of the 2019 4th International Conference on Recent Trends on Electronics, Information, Communication & Technology (RTEICT), Bengaluru, India, 17–18 May 2019; pp. 1453–1458. [Google Scholar]
- Takriti, M.; Boussaada, Z.; Sansa, I.; Curea, O.; Bellaaj, N.M. Wireless Sensors Networks Applications For Micro-Grids Management: State of Art. In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCon), Tunis, Tunisia, 28 September–1 October 2020; pp. 1058–1061. [Google Scholar]
- Zhong, L.; Ge, M.; Zhang, S.; Liu, Y. Rate Aware Fuzzy Clustering and Stable Sensor Association for Load Balancing in WSNs. IEEE Internet Things J. 2021, 1. [Google Scholar] [CrossRef]
- Karthik, S.S.; Kavithamani, A. Fog computing-based deep learning model for optimization of microgrid-connected WSN with load balancing. Wirel. Netw. 2021, 27, 2719–2727. [Google Scholar] [CrossRef]
- Sampathkumar, A.; Mulerikkal, J.; Sivaram, M. Glowworm swarm optimization for effectual load balancing and routing strategies in wireless sensor networks. Wirel. Netw. 2020, 26, 4227–4238. [Google Scholar] [CrossRef]
- Yarinezhad, R.; Hashemi, S.N. Solving the load balanced clustering and routing problems in WSNs with an fpt-approximation algorithm and a grid structure. Pervasive Mobile Comput. 2019, 58, 101033. [Google Scholar] [CrossRef]
- Zhong, L.; Li, M.; Cao, Y.; Jiang, T. Stable User Association and Resource Allocation Based on Stackelberg Game in Backhaul-Constrained HetNets. IEEE Internet Veh. Technol. 2019, 68, 10239–10251. [Google Scholar] [CrossRef]
- Gandhi, G.S.; Vikas, K.; Ratnam, V.; Babu, K.S. Grid clustering and fuzzy reinforcement-learning based energy-efficient data aggregation scheme for distributed WSN. IET Commun. 2020, 14, 2840–2848. [Google Scholar] [CrossRef]
- Hemalatha, R.; Prakash, R.; Sivapragash, C. Analysis on energy consumption in smart grid WSN using path operator calculus centrality based HSA-PSO algorithm. Soft Comput. 2019, 1–13. [Google Scholar] [CrossRef]
- Dhunna, G.S.; Al-Anbagi, I. A low power WSNs attack detection and isolation mechanism for critical smart grid applications. IEEE Sens. J. 2019, 19, 5315–5324. [Google Scholar] [CrossRef]
- Faheem, M.; Butt, R.A.; Raza, B.; Ashraf, M.W.; Begum, S.; Ngadi, M.A.; Gungor, V.C. Bio-inspired routing protocol for WSN-based smart grid applications in the context of Industry 4.0. Trans. Emerg. Telecommun. Technol. 2019, 30, e3503. [Google Scholar] [CrossRef]
- Bouakkaz, F.; Derdour, M. Maximizing WSN life using power efficient grid-chain routing protocol (PEGCP). Wirel. Pers. Commun. 2021, 117, 1007–1023. [Google Scholar] [CrossRef]
- Wu, H.; Shahidehpour, M. Applications of wireless sensor networks for area coverage in microgrids. IEEE Trans. Smart Grid 2016, 9, 1590–1598. [Google Scholar]
- Ashraf, N.; Javaid, S.; Lestas, M. Logarithmic utilities for aggregator based demand response. In Proceedings of the 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aalborg, Denmark, 29–31 October 2018; pp. 1–7. [Google Scholar]
- Ghorbanzadeh, M.; Abdelhadi, A.; Clancy, C. A utility proportional fairness radio resource block allocation in cellular networks. In Proceedings of the 2015 International Conference on Computing, Networking and Communications (ICNC), Garden Grove, CA, USA, 16–19 February 2015; pp. 499–504. [Google Scholar]
- Ren, J.; Zhang, Y.; Zhang, N.; Zhang, D.; Shen, X. Dynamic channel access to improve energy efficiency in cognitive radio sensor networks. IEEE Internet Wirel. Commun. 2016, 15, 3143–3156. [Google Scholar] [CrossRef]
- Hong, M.; Razaviyayn, M.; Luo, Z.Q.; Pang, J.S. A unified algorithmic framework for block-structured optimization involving big data: With applications in machine learning and signal processing. IEEE Signal Process. Mag. 2015, 33, 57–77. [Google Scholar] [CrossRef] [Green Version]
- Martello, S.; Toth, P. An Algorithm for the Generalized Assignment Problem. 1981. Available online: http://scholar.google.com/scholar_lookup?title=An%20algorithm%20for%20the%20generalized%20assignment%20problem&author=S..%20Martello&author=P..%20Toth&pages=589-603&publication_year=1981 (accessed on 9 November 2021).
- Ye, Q.; Rong, B.; Chen, Y.; Al-Shalash, M.; Caramanis, C.; Andrews, J.G. User association for load balancing in heterogeneous cellular networks. IEEE Internet Wirel. Commun. 2013, 12, 2706–2716. [Google Scholar] [CrossRef] [Green Version]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2000. [Google Scholar]
- Neamatollahi, P.; Abrishami, S.; Naghibzadeh, M.; Moghaddam, M.H.Y.; Younis, O. Hierarchical clustering-task scheduling policy in cluster-based wireless sensor networks. IEEE Trans. Ind. Inform. 2017, 14, 1876–1886. [Google Scholar] [CrossRef]
- Behera, T.M.; Mohapatra, S.K.; Samal, U.C.; Khan, M.S.; Daneshmand, M.; Gandomi, A.H. Residual energy-based cluster-head selection in WSNs for IoT application. IEEE Internet Things J. 2019, 6, 5132–5139. [Google Scholar] [CrossRef] [Green Version]
- Chidean, M.I.; Morgado, E.; del Arco, E.; Ramiro-Bargueno, J.; Caamaño, A.J. Scalable data-coupled clustering for large scale WSN. IEEE Internet Wirel. Commun. 2015, 14, 4681–4694. [Google Scholar] [CrossRef]
- Ni, Q.; Pan, Q.; Du, H.; Cao, C.; Zhai, Y. A novel cluster head selection algorithm based on fuzzy clustering and particle swarm optimization. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 14, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Pan, J.; Xie, D.; Wang, F. NDCMC: A hybrid data collection approach for large-scale WSNs using mobile element and hierarchical clustering. IEEE Internet Things J. 2015, 3, 533–543. [Google Scholar] [CrossRef]


| Variable | Parameter | Value |
|---|---|---|
| S | Distribution area | |
| Deployment density of WSN nodes | 250 | |
| Maximum access number of CH | 30 | |
| Satisfaction coefficient | ||
| l | Amount of data generated per unit time | 40 bit |
| Trade-off parameter | 100 | |
| Data acquisition power | 1 mW | |
| Data transmission power | 20 mW | |
| Power amplifier efficiency | 0.9 | |
| Circuit power | 5 mW | |
| Energy consumption for data receiving | 5 nJ/bit | |
| Energy cost for data aggregation | 0.5 nJ/bit | |
| Maximum acquisition time | 10 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong , L.; Zhang , S.; Zhang , Y.; Chen , G.; Liu , Y. Joint Acquisition Time Design and Sensor Association for Wireless Sensor Networks in Microgrids. Energies 2021, 14, 7756. https://doi.org/10.3390/en14227756
Zhong L, Zhang S, Zhang Y, Chen G, Liu Y. Joint Acquisition Time Design and Sensor Association for Wireless Sensor Networks in Microgrids. Energies. 2021; 14(22):7756. https://doi.org/10.3390/en14227756
Chicago/Turabian StyleZhong , Liang, Shizhong Zhang , Yidu Zhang , Guang Chen , and Yong Liu . 2021. "Joint Acquisition Time Design and Sensor Association for Wireless Sensor Networks in Microgrids" Energies 14, no. 22: 7756. https://doi.org/10.3390/en14227756
APA StyleZhong , L., Zhang , S., Zhang , Y., Chen , G., & Liu , Y. (2021). Joint Acquisition Time Design and Sensor Association for Wireless Sensor Networks in Microgrids. Energies, 14(22), 7756. https://doi.org/10.3390/en14227756






