4.1. Effect of Convection and Diffusion Mechanism on the Lateral Mixing Process
The aspect ratio of the fluidized bed used in the present research is 1.0. Generally, there is only one bubble bursting at the surface of the fluidized bed at one time in the mixing process. This is confirmed by a visual analysis of the snapshots of fluidized bed, as shown in
Figure 4. The eruption of bubbles is not limited by the walls of the bed. Therefore, the fluidized bed can be assumed as one so-called “mixing cell”. The micro mixing ratios at different lateral positions are measured, from which the detailed mechanism about lateral mixing within the mixing cell can be revealed.
In bubbling fluidized beds, the lateral mixing resulted from convective bubble flow and random motion of particles [
11,
12,
13,
14,
15]. On the one hand, as particles in the fluidized beds are quite random, diffusion mixing results from the local relative motion of particles. On the other hand, when a bubble rises, it carries a large number of particles up together in its wake and simultaneously pushes emulsion solids aside, resulting in ascending and descending emulsion solids. The relative motion of emulsion solids causes convection mixing. The diffusion and convection mechanisms are related to the motion of particles. In the convection mixing caused by the ascending and descending emulsion solids, diffusion mixing also exists due to the local relative motion of particles. The particle cluster size and particle velocity will change at different positions, which means that diffusion may develop into convection with the variation of position and vice versa.
In order to figure out the effect of convection and diffusion mechanism on the mixing process, first, the relationship between the micro mixing ratio and convection/diffusion must be established. According to the discussions above, when convection mixing happens, the micro mixing ratio will change largely with time because particle clusters that containing different types of particles flow through the measurement point. The particle cluster here means a large number of particles that are driven by bubbles and having similar velocity. On the contrary, the diffusion mixing is believed to be induced by the exchanging of positions of particles with their nearest neighbors. Therefore, when diffusion mixing happens, the micro mixing ratio will change slightly with time because there is no sudden change of mixing state at the measurement point.
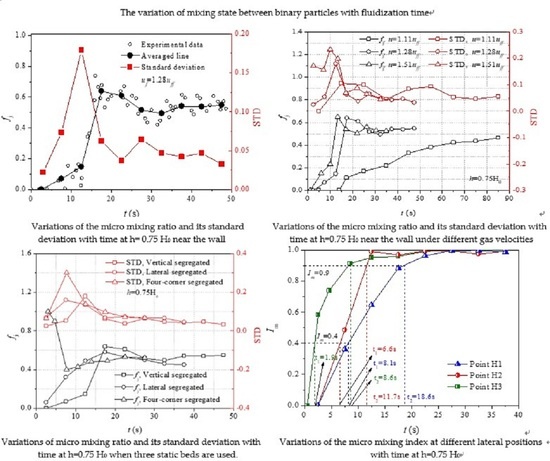
The mixing processes at different lateral positions are analyzed in detail to characterize the role of convection and diffusion in the lateral mixing process of solids. Silicon carbide particles and quartz sands are vertically segregated in the static bed and the gas velocity is 1.28 times the fully fluidization velocity (
uff) which is determined by bed pressure drop method. The evolutions of the micro mixing ratio of dense particle (
fj) with time at different lateral positions when the bed height is 0.25 H
0 are shown in
Figure 5. In the mixing process, when emulsion solids flow through the measurement point, the section of signal from when emulsion solids reach the measurement point to when emulsion solids leave the measurement point are picked out. The averaged value of this section of signal is used to calculate the mixing ratio at the measurement point according to Equation (7) and the mixing ratio is shown as a scatter in
Figure 5. The averaged line is calculated by averaging the
fj in each five seconds. The standard deviations (STD) of
fj in each five seconds are calculated to characterize the fluctuation of
fj with time, from which the effect of convection and diffusion on the mixing process is analyzed.
Figure 5a shows that
fj near the wall decreases quickly from 1 to 0 between
t = 0 s and 12.5 s, and then increases quickly to 0.65 at
t = 27.5 s. The significant variation of
fj results in a large STD in the beginning of mixing. As can be seen from the figure that the STD is higher before
t = 22.5 s, which means that convection plays a more important role in the mixing process near the wall. The phenomenon can be explained in the way that from a macro perspective, it has been found that bubbles tend to rise along the center line of fluidized bed and carry a large number of particles to the top [
2]. According to the principle of conservation, particles near the wall will gather and flow down [
38]. Therefore, solids mixing near the wall is mainly accomplished through the coordinated motion of particle clusters. From a micro perspective, because in bubbling fluidized bed gas velocity near the wall is much lower than that in the main flow region, the drag force exerted on the particles near the wall is smaller and there is a poor mobility of particles [
39,
40]. The above factors result in that convective is the main mechanism of solids mixing near the wall. After
t = 27.5 s, quasi-steady mixing is formed in which the averaged line is about 0.56 and nearly does not vary with time. Moreover, STD decreases slowly with time after
t = 22.5 s, indicating that the latter part of the mixing process is mainly accomplished by diffusion. The explanation may be that the component in different particle clusters is similar and solids mixing is mainly accomplished by the relative motion of particles.
Figure 5b,c show that the evolutions of
fj and its STD with time at half radius (measurement point L2) and center line (measurement point L3) of the fluidized bed are similar, but very different from that near the wall. After a stagnant of about 10 s, the averaged
fj at the half radius and center line of fluidized bed decreases directly with time and show moderate fluctuation. The STD at the half radius and center line is smaller than that near the wall, which means that diffusion mixing is enhanced at the half radius and center line. The explanation may be that the particles at the half radius and center line have a better mobility due to the larger drag force compared with the particles near the wall [
39]. In this way, the relative motion between particles is enhanced and diffusion becomes more important in the mixing process.
In addition, STD at the center line is higher than that at the half radius, which means that convection mixing is more significant at the center line. The phenomenon can be explained in the way that the mixing behavior at the half radius is mainly determined by the mobility of particles. As mentioned above, particles at the center line are carried up by bubbles and then particles near the wall flow down. The half radius is at the interface between the upstream and downstream of particles. Chanchal et al. [
1] found that at the lower part of the bubbling fluidized bed, a vortex of particles exists at the half radius where the trajectory of particle changes greatly. Therefore, diffusion mixing is more evident at the half radius. Meanwhile, a large number of particles around the center line are carried up by the bubbles in the wake, the coordinated motion of particle clusters are enhanced and convection mixing is more significant at the center line.
The evolutions of
fj and its STD with time at different lateral positions when the bed height is 0.75 H
0 are shown in
Figure 6.
Figure 6a,b shows that the averaged
fj near the wall and half radius follow a similar trend. The STD near the wall and half radius also follow similar distribution that both large and small STD is observed before
t = 22.5 s. Therefore, the mixing near the wall and at half radius is accomplished by both convection and diffusion. At the higher part of fluidized bed, the bubbles become larger and have a wider influence on the motion of particles. During the rise of big bubble, particles at the radius and near the wall are in the cloud of the bubble and flow down around the boundary of bubble to the wake, which give a rise to diffusion mixing. In addition, because the coordinated motion of larger particle clusters is induced by the bubbles at a higher part of the fluidized bed, convection mixing is also enhanced. After
t = 27.5 s, the smaller STD means that diffusion plays a more important role in the later part of mixing process. The mixing mechanism of the later part of the mixing process is similar with that discussed above and not repeated here.
Figure 6c shows that
fj at the center line varies largely from 0 to 0.8 from the beginning of mixing. Correspondingly, the STD is very high which means that convection plays a major role in solids mixing process at the center line. Moreover, STD is much larger than that at half radius and near the wall. Sette et al. [
15] concluded that many dense particles at the center of the fluidized bed are carried up by bubbles in the wake. Meanwhile, light particles around rising bubbles drift in a downward direction to fill the gap created by the bubbles. In this way, the coordinated motion of particle clusters is significant and convection is the main mixing mechanism at the center line. In addition, the STD decreases quickly with time, which may be due to the fact that in the beginning, particle mixing is very fast and after
t = 17.5 s the compositions of particles in different particle clusters are similar.
Gas velocity is one of the major factors that influence the mixing behavior of solids in fluidized bed. In order to study the effect of gas velocity on the lateral mixing of solids, the variations of
fj and its STD with time at different lateral positions (
h = 0.75 H
0) when the gas velocity increases from 1.11
uff to 1.51
uff are shown in
Figure 7.
Figure 7a shows that when the gas velocity increases from 1.11
uff to 1.28
uff, a significant difference between the evolutions of
fj near the wall is observed. However, the evolution of
fj changes a little when the gas velocity increases from 1.28
uff to 1.51
uff. Moreover, it is observed that STD of
fj is larger at a higher gas velocity, indicating that convection becomes more important in solids mixing with the increase of gas velocity. It has been proven that [
41] with the increase of gas velocity, the circulation of solids in bubbling fluidized beds is accelerated and particles near the wall flow down more quickly. Therefore, the coordinated motion of particle clusters near the wall is enhanced and convection becomes more important in the mixing process.
For the mixing process at center line, it can be observed from
Figure 7b that a significant difference resulted both when the gas velocity increases from 1.1
uff to 1.28
uff and from 1.28
uff to 1.51
uff. Moreover, a larger STD of
fj is observed at a higher gas velocity, indicating that convection plays a more important role in the mixing process with the increase in gas velocity. As discussed above, at the higher part of the bubbling fluidized bed, the mixing at center line is mainly accomplished by the dragging of particles from surrounding dense phase into the wake behind the rising bubbles. Because the diameter of the bubble will increase exponentially with the increase of gas velocity [
2], more particles are dragged into the wake of bubbles. Therefore, a large difference between the evolutions of
fj at different gas velocities results for the mixing at the center line. However,
Figure 7b also shows that at the center line, when
u = 1.51
uff, the STD is smaller than that when
u = 1.28
uff, indicating that diffusion is more evident despite the increase in bubble size. The reason may be that coalesce and creak of bubbles are more frequent at higher gas velocities, which results in instability of the fluidization system and inconsistency of the motion of particles is caused.
A comprehensive understanding about the effect of static bed on lateral mixing of binary solids may provide useful guidance for determining the feeding way of fluidized bed reactor. In order to get a quantitative understanding about the effect of static bed on lateral mixing, the evolutions of
fj and its STD at different lateral positions are shown in
Figure 8.
Figure 8a shows that when the lateral and vertical segregated static beds are used, a quick increase of
fj near the left wall is observed in the beginning of mixing and then
fj decreases with time. A faster increase of
fj is found when lateral segregated static bed is used. On the contrary, when four-corner segregated static bed is used, a sudden decreases of
fj near the left wall results in the beginning and then
fj increases slowly to about 0.52 when
t = 27.5 s. At the beginning of mixing, larger STD is observed when the four-corner segregated static bed is used.
Figure 8b shows that at the center line of fluidized bed, when different static beds are used, the variations of
fj are similar with that near the left wall except for two things. On the one hand, in the beginning, the increase of
fj is faster when a vertical segregated static fixed bed is used. On the other hand, when a four-corner segregated static bed is used, the averaged
fj varies inversely with time. Because of the accumulation of dense particles at the right side when the lateral segregated static bed is used, the final value of
fj at measurement points H1 and H3 is approximately 0.44, which is smaller than that when the other two types of static beds are used.
4.2. Micro Lateral Dispersion Coefficient of Solids
From the discussions above, it is found that the mixing mechanism of solids is very different at various positions of the mixing cell. Therefore, it is necessary to characterize the local solids dispersion at different positions of the fluidized bed. In the present research, the fluidized bed is assumed as one mixing cell and the diffusion-like equation is inapplicable to describe the solids dispersion. Moreover, the local mixing ratio of dense particles measured by the novel measurement method is dimensionless. Under these conditions, in order to characterize the local solids dispersion, a new micro dispersion coefficient is proposed which is based on Fick’s first law. The definition of micro dispersion coefficient is given below:
where
DmL is the local lateral micro dispersion coefficient at the measurement point;
JL is the local lateral flux of dense particles through per unit area in unit time at the measurement point, respectively. The
JL near the wall is evaluated by the increase of micro mixing ratio of dense particles in unit time since the wall is the boundary of mixing in lateral direction. The
JL near the wall is calculated by the time-averaged increase of micro mixing ratio in each five-second interval. Then, the
JL at half radius is evaluated by summing up the time-averaged increase of micro mixing ratio at half radius and the
JL near the wall.
The lateral gradients of mixing ratio on the right sides of Equation (11) are calculated based on the time-averaged micro mixing ratio in each five-second interval. Although the measured micro mixing ratio at one measurement point is scattered, the time-averaged mixing ratio can reflect the effective local mixing state at this measurement point. The rationale in calculating the lateral micro dispersion coefficient is same with that of the macro dispersion coefficient in the literature. However, because the measured micro mixing ratio by the novel method is dimensionless, the unit of lateral micro dispersion coefficient is m/s, which is different from that of macro dispersion coefficient. The micro dispersion coefficient can be used to evaluate the local lateral dispersion of solids in fluidized bed given local mixing ratios or volume fractions of dense particles.
Figure 9 and
Figure 10 show the variations of
Dm with STD at different bed heights and gas velocities, respectively. The static bed is composed of silicon carbide particles and quartz sands which are vertically segregated. In our experiments, the micro lateral dispersion coefficient within the mixing cell mainly falls between 0.005 and 0.025 m/s. It can be observed from
Figure 9 that when the bed height is 0.25 H
0, the variations of
Dm with STD are different at different lateral positions. The
Dm is higher when there is a larger STD near the wall, which means that convection play a major role in the lateral mixing of solids. The reason may be that the voidage near the wall is lower and the lateral mixing is mainly accomplished through the coordinated motion of particle clusters. However, the variation of
Dm with STD at the half radius is opposite with that near the wall. The STD at the half radius is generally lower than 0.12 and
Dm is higher when there is a smaller STD. This means that diffusion is more important for lateral mixing at half radius. As mentioned above, the half radius is at the interface between the upstream and downstream of particles and a vortex of particles is formed where the trajectory of particle changes greatly, which results in the mixing being mainly accomplished by diffusion.
When the bed height is 0.75 H0, the Dm near the wall and at half radius increase with STD, indicating that convection has a more important influence on lateral mixing with the increase of bed height. Because bubbles grow larger with the increase of bed height, the bubble induced coordinated motion of particle clusters becomes very important in the lateral mixing at the upper part. In addition, when there is a larger STD, Dm at half radius is higher than that near the wall, meanwhile when there is a smaller STD, Dm at the half radius is lower. This means that convection is more important for lateral mixing at the half radius than that near the wall, which may be due to the rising bubbles having a more important influence on the particles at the half radius.
The influence of gas velocity on the micro lateral dispersion coefficient is shown in
Figure 10. It can be observed from
Figure 10a that at a lower gas velocity, the STD near the wall is smaller and
Dm is generally lower than 0.013. With the increase of gas velocity,
Dm increases quickly with STD, which means that convection plays a more important role in lateral mixing at a higher gas velocity. The variation of
Dm with gas velocity is mainly caused by the change of bubble dynamics. At a higher gas velocity, bubbles become larger and rise faster in the fluidized bed, which will make the particle clusters near the wall flow down faster [
41]. In this way, the lateral dispersion of solids is enhanced. This finding is in accordance with the experimental results acquired by Castilla et al. [
16] and Liu and Chen [
19].
Figure 10b shows that at the half radius,
Dm increases quickly when the gas velocity changes from 1.11 to 1.28
uff, indicating that convection becomes more important in the lateral mixing of solids. However, when increasing the gas velocity to 1.51
uff, a higher
Dm is found when there is a smaller STD. This means that when
u = 1.51
uff, apart from convection, diffusion also plays an important role in the lateral mixing of solids. The enhancement of diffusion mixing at a higher gas velocity may be due to the fact that on the one hand, bubbles become larger and rise faster at higher gas velocity. During the rise of large bubble, particles flow down quickly around the boundary of the big bubble to the wake, which enhances the diffusion mixing. On the other hand, the coalesce and creak of bubbles are more frequent at a higher gas velocity, which results in instability of the fluidization system. Therefore, inconsistency of the motion of particles is caused and diffusion becomes more important in the lateral mixing of solids.
4.3. Lateral Mixing Quality of Solids
The above discussion gives knowledge about the effect of convection and diffusion on lateral dispersion process/coefficient in fluidized beds. However, higher dispersion coefficient does not always represent better mixing [
25]. Therefore, an effective evaluation of the lateral mixing quality is necessary in the present work. In the literature, there are mainly four methods used to calculate the mixing index of binary mixtures, namely average-height method [
42], nearest-neighbors method [
43], Lacey’s method [
44] and particle concentration method [
45]. A brief introduction to these methods is given below.
In the average-height method, the average height of the dense particles is calculated and normalized by the average height of all particles in the fluidized bed. Then, the normalized average vertical position of the dense particles is used to calculate the mixing index. The average-height method is used to calculate the mixing index of particles in the whole fluidized bed. The equation for the average-height method is
where
is the normalized average vertical position of the dense particles. The mixing index is defined as:
which means that
M is 0 for totally unmixed bed and 1 for fully mixed bed.
In the nearest-neighbors method, the number of particles surrounding a target particle is acquired. The mixing index is calculated by counting the number of particles having the same density or color as the target particle. The definition of the mixing index is expressed as follows:
where
ndiff is the number of nearest neighbors having different density or color,
nnb is the number of nearest neighbors.
In the average-height method and nearest-neighbors method, the mixing index is calculated given the coordinated of all the particles. Therefore, they are mainly used in numerical simulations.
In Lacey’s method, the fluidized bed is divided into many cells and the variance for the concentration of dense particles in each cell is calculated according to the following equation:
where
N is the number of cells in fluidized bed,
is the concentration of dense particles in cell
i, and
is the average concentration of dense particles in the bed.
and
are defined as
Then the mixing index can be calculated as
Lacey’s method is mainly used to calculate the mixing index of particles in the whole fluidized bed given the concentration of dense particles in all cells. It can be used in numerical simulation and experimental research.
In the particle concentration method, the mixing index is calculated knowing the percentage of concentration of jetsam at different parts of the fluidized bed. The definition of mixing index is expressed as
where
X is % of dense particles at the measurement point,
Xbed is % of dense particles in the bed.
The particle concentration method is mainly used to calculate the mixing index when the mixing reaches steady. But in the present research, the whole mixing process of binary mixtures in fluidized bed is studied. When there are only dense particles or light particles at the measurement point, the mixing index for such totally unmixed states calculated by concentration method is 0 or 2. Therefore, it is difficult to evaluate the local mixing quality of binary mixtures effectively in the mixing process.
It can be found that the methods mentioned above are inapplicable when evaluating the local mixing quality in the dynamic mixing process. For this problem, a new mixing index is proposed based on Shannon entropy in this article. The formula is given in Equation (20).
where
Im is the micro mixing index at the measurement point, which will be 0.0 for the totally segregated state and 1.0 for any completely mixed state;
n is the number of kind of particles, and the value is 2 in this study;
fi is the micro mixing ratio of
ith particle in the measuring field of capacitance probe sensor. Compared with the existing methods for mixing index, an effective evaluation of the local mixing quality of binary mixtures in the whole mixing process can be acquired through the new solids mixing index.
The evolutions of
Im with time at different lateral positions when the bed height is 0.25 H
0 and 0.75 H
0 are shown in
Figure 11a,b, respectively. More specifically, the time required for the mixing indices at different lateral positions to reach 0.4 and 0.9 is also illustrated in the figures. The gas velocity is 1.28
uff.
Figure 11a shows that when the bed height is 0.25 H
0, the fastest mixing is found at the half radius. Although the bubbles have a more important influence on the mixing at center line, the mixing at center line is the slowest. The phenomenon can be explained in the way that the half radius is at the interface between the upstream of particles at center line and downstream of particles near the wall, and a vortex of particles is formed at the half radius where the trajectory of particle changes significantly. The flow pattern at the half radius is very suitable for solids mixing. As for the mixing at the center line, because of the large drag force exerted on the particles, particles are forced to move in approximately the same velocity and the mixing is slowed down. After about
t = 45 s, steady lateral mixing is reached, and it is found that the final mixing quality at different lateral positions is similar.
The evolutions of
Im at different lateral positions when the bed height is 0.75 H
0 are shown in
Figure 11b. The time required to reach certain mixing quality at different lateral positions is also illustrated in the figure. It can be seen from the figure that fastest mixing is acquired at the center line and mixing rate slows down quickly with the increase of the distance from the center line. The phenomenon can be explained by the way that at the higher part of the bubbling fluidized bed, because of the growth of bubbles, more particles are carried to the top by bubbles in the wake. Meanwhile, the particles above will fall due to the creak of bubbles. The relative motion between particle clusters is more evident, which is good for the mixing at the center line. It has been proven that at the higher part of bubbling fluidized beds, the gas velocity near the wall is much smaller than that in the main flow region [
40,
41,
42]. Therefore, smaller drag force is exerted on the particles near the wall and poor mobility of the particles is resulted, which slows down the mixing.
Furthermore, the lateral distributions of
Im under different gas velocities when the bed height is 0.75 H
0 are shown in
Figure 12 to evaluate the lateral mixing quality.
Figure 12a depicts that at
t = 5 s, a peak is found at the middle of the distribution curve of
Im when
u = 1.11
uff or 1.28
uff, whereas the lateral distribution of
Im when
u = 1.51
uff is more like a parabolic. The simultaneous rise of
Im at measurement points H2, H3 and H4 when
u = 1.51
uff may be due to the bubbles being larger and the mobility of particles at a wider range is improved by the bubbles.
Figure 12b shows that at
t= 10 s, the lateral distribution of mixing index is quite flat when
u = 1.51
uff. With the decrease of gas velocity,
Im at the center line changes slightly, but
Im near the walls decrease very fast.
Figure 12c shows that at
t = 20 s, the lateral distributions of
Im are quite flat when
u = 1.28
uff and 1.51
uff, whereas when
u = 1.11
uff, the overall
Im is still lower specifically near the walls. In general, the influence of gas velocity on the lateral mixing of solids is more important in the mixing process, but the final mixing extent is similar.
Figure 13 shows the lateral distributions of
Im at
h = 0.75 H
0 when different static beds are used and the gas velocity is 1.28
uff. At
t = 5 s, a symmetric lateral distribution of
Im with a peak at the middle is formed when the vertical segregated static bed is used. By contrast, asymmetric distributions of
Im are formed when the other two types of static bed are used. When the lateral segregated static bed is used, lateral mixing at the left side is much better than that at the right side. Because when the lateral segregated static bed is used, the flow resistance on the left (light particles) is lower than that on the right (dense particles), the gas flows through the bed mainly along the left wall which improves the mobility of particles at the left side. In general, better lateral mixing is observed when the four-corner segregated binary solids are used at
t = 5 s, which may be due to there being more interfaces between binary solids and dissimilar particles have more opportunities to contact with each other.
Figure 13b shows that at
t = 10 s, when the lateral and four-corner segregated static beds are used, the particle mixing quality at the left side is similar, which is higher than that when the vertical segregated static bed is used. However, dead areas of mixing are formed when the lateral and four-corner segregated static beds are used near the right wall, and the dead area is larger when lateral segregated static bed is used.
A deeper understanding about the lateral mixing mechanism can be acquired through the combination of dynamic modeling and this experiment. A dynamic modeling of the lateral mixing process of binary mixtures in a fluidized bed can complement the understanding about the mixing mechanism acquired by this experiment. Moreover, the experimental results in the present research can provide useful data for model validation in the dynamic modeling. The dynamic modeling of the lateral mixing of binary solids in bubbling fluidized beds will be conducted in our on-going research.