Numerical Investigation of Transient Flow Characteristics in a Centrifugal Compressor Stage with Variable Inlet Guide Vanes at Low Mass Flow Rates
Abstract
:1. Introduction
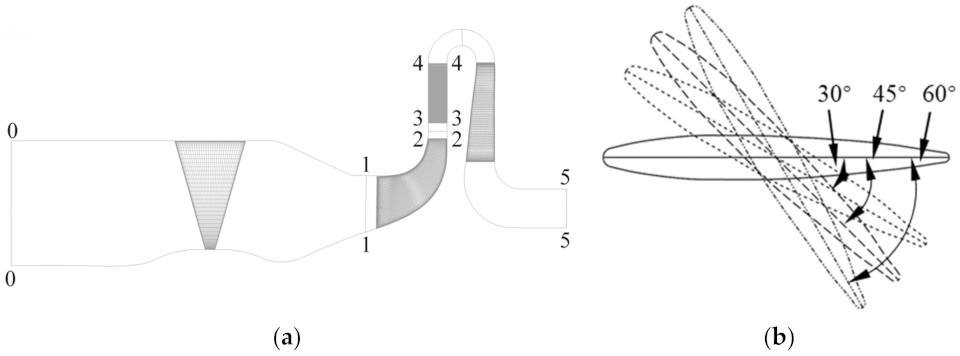
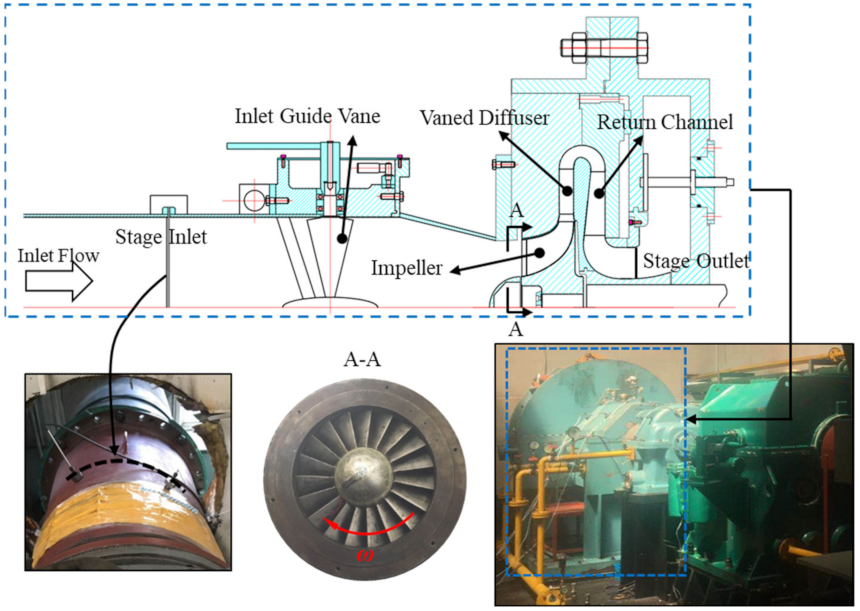
2. Centrifugal Compressor Stage Geometry Investigated
3. Numerical Method
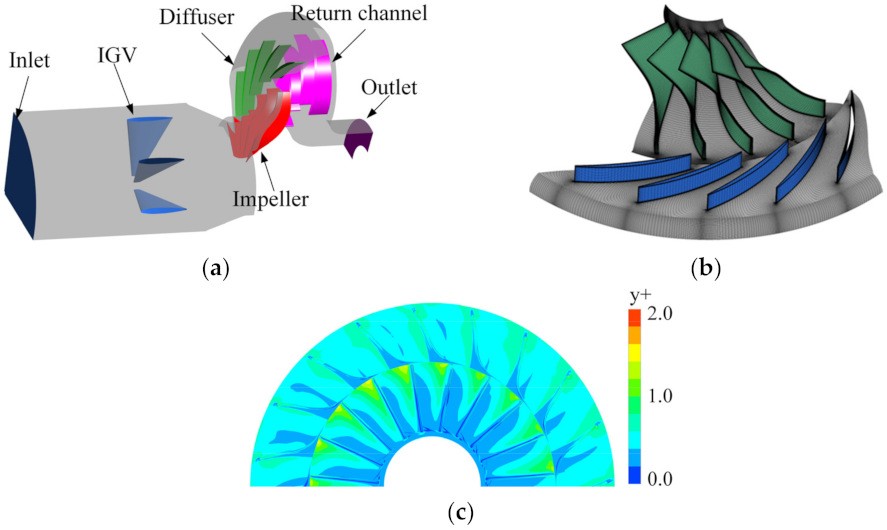
3.1. Numerical Model and Grid
3.2. Numerical Scheme
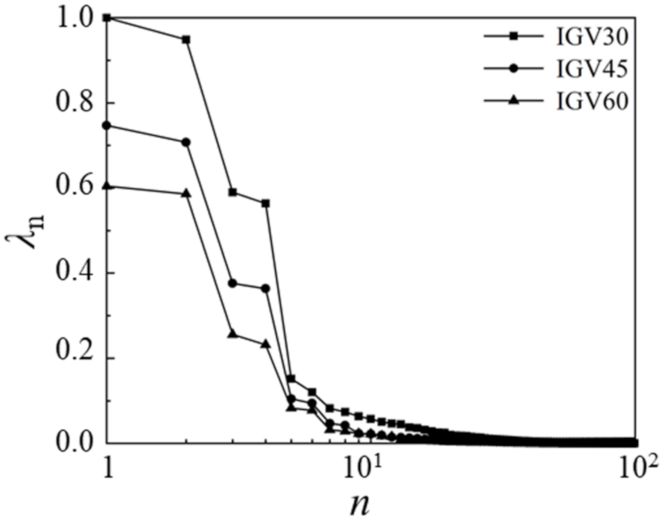
3.3. Modal Decomposition Method
4. Numerical Results and Analysis
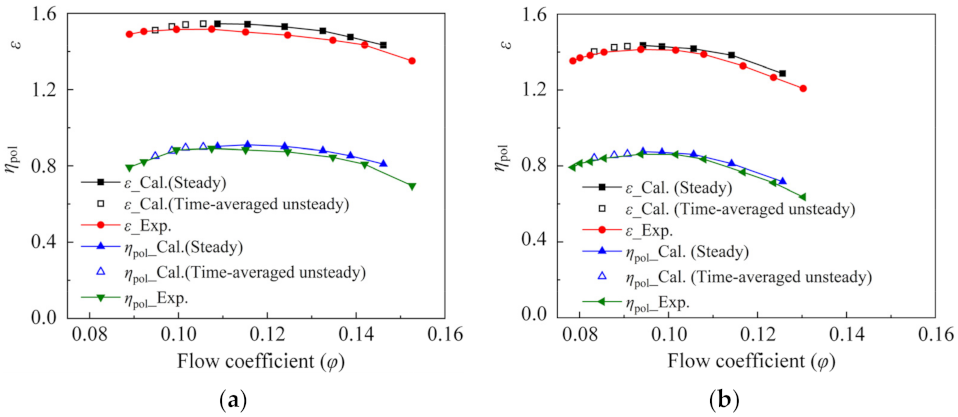
4.1. Validation of the Numerical Methods
4.2. Effects of Positive Pre-Swirls on Aerodynamic Performance of the Stage
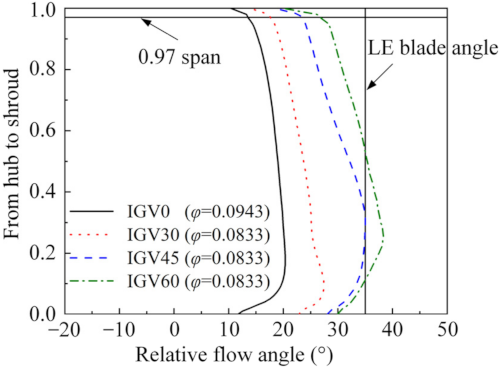
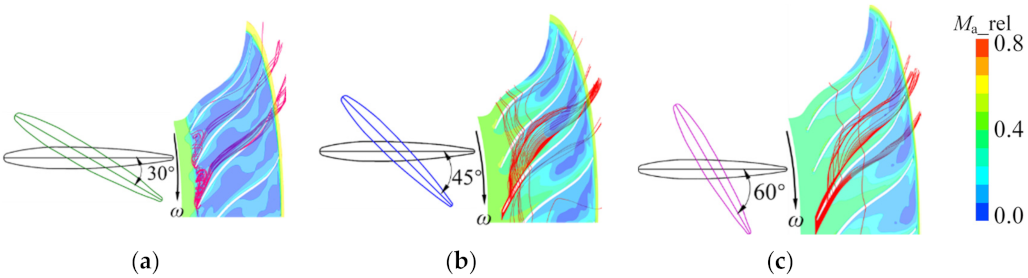
4.3. Effects of Guide Vane Opening on the Internal Flow of the Impeller
4.4. Effects of Guide Vane Openings on the Flow Field of the Vaned Diffuser
5. Conclusions
- (1)
- With increasing positive pre-swirl, the minimum mass flow rate at which the compressor can operate becomes smaller. Therefore, a stall margin gets larger when coupled with a decreased pressure ratio. Compared with the IGV0 case, the IGV30, IGV45, and IGV60 improve approximately 9.95% of stall (surge) margin;
- (2)
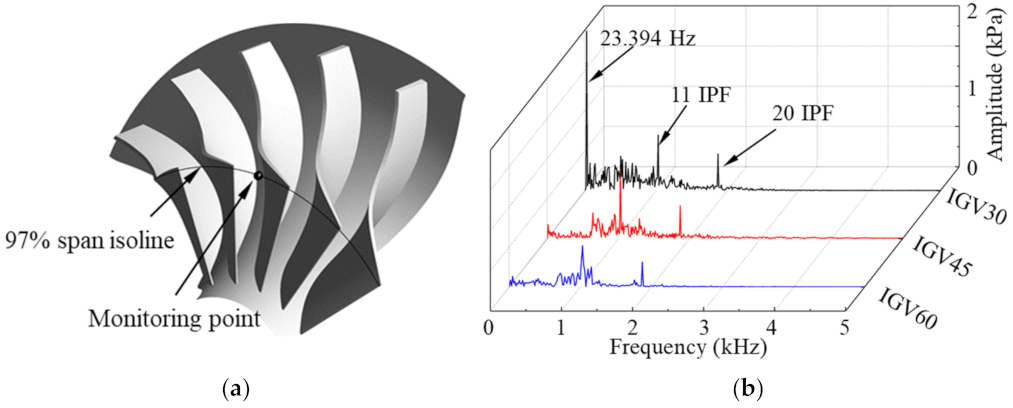
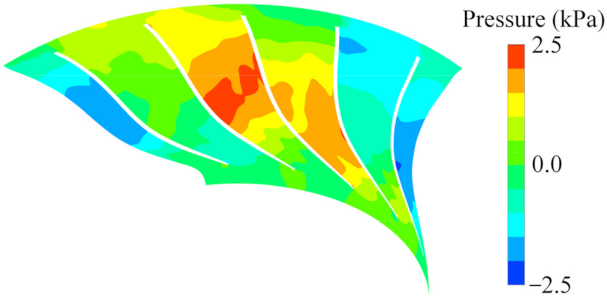
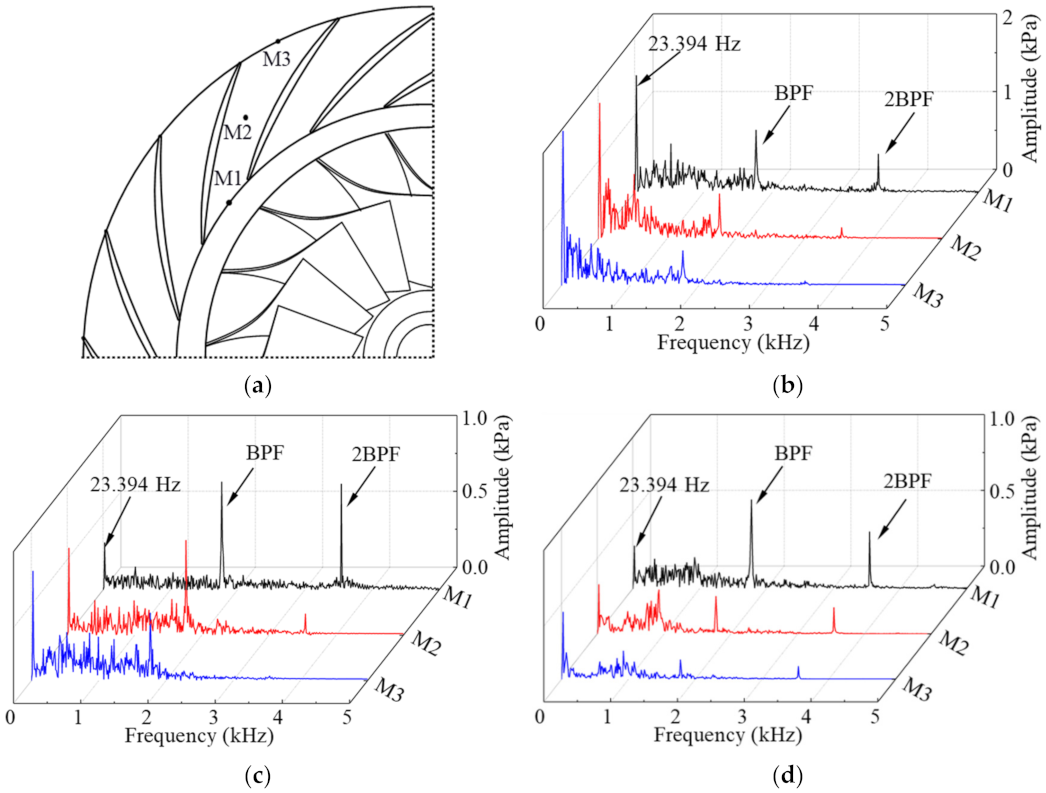
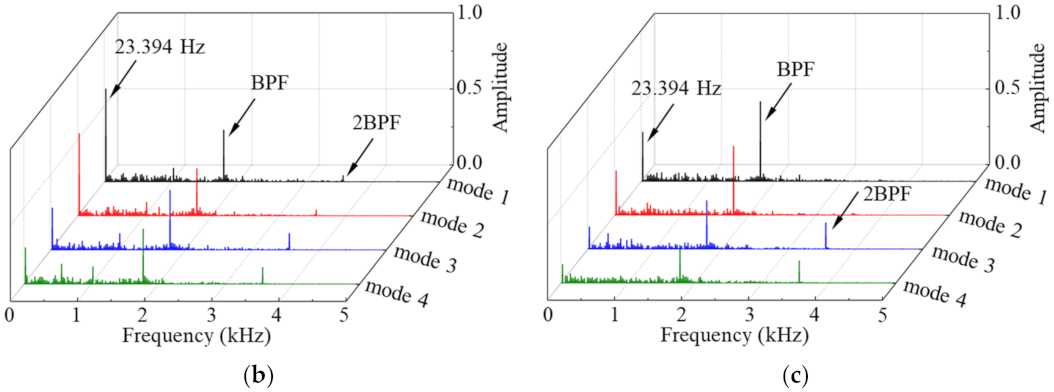
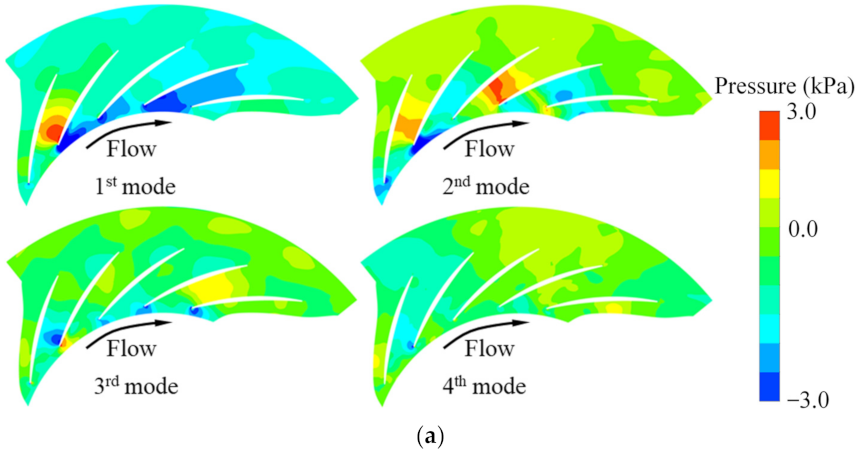
- The unstable flow phenomenon caused by the low frequency (23.394 Hz) in the impeller of the IGV30 case at φ = 0.0833 (72.9% design flow point) was determined by the methods of streamline distribution, spectrum analysis, vector, entropy increase, and modal decomposition, and the unstable flow structure propagates in the impeller at a speed of nearly 25.07% of the machine shaft frequency along the reverse direction of the impeller rotation. However, there was no similar unstable flow phenomenon by the low frequency in the impeller under the other two guide vane openings. The regulation of IGV improves the flow inside the impeller and then broadens the stable operating range of the compressor stage;
- (3)
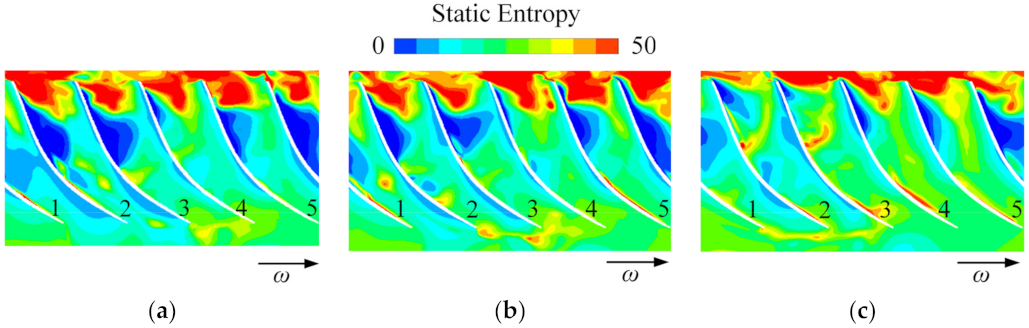
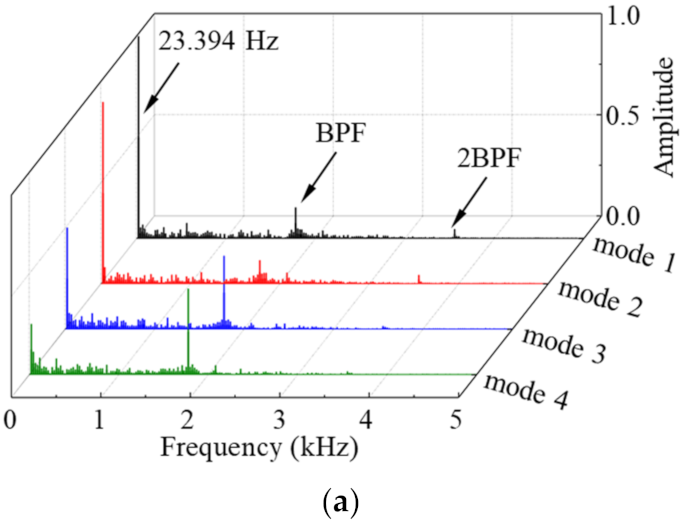
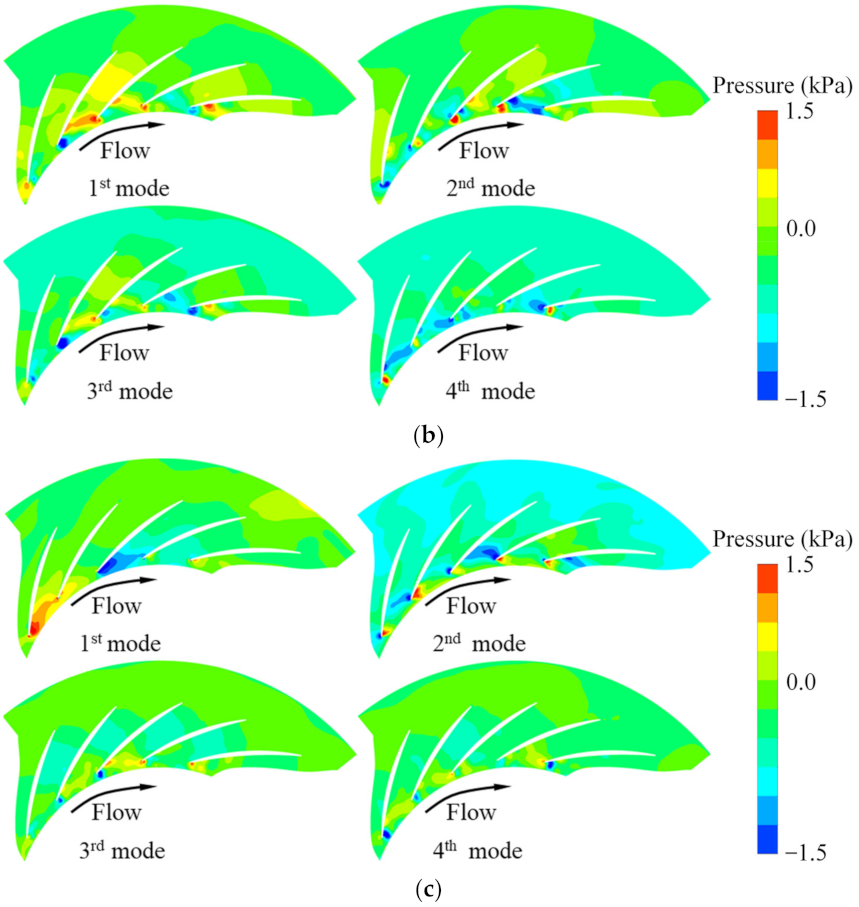
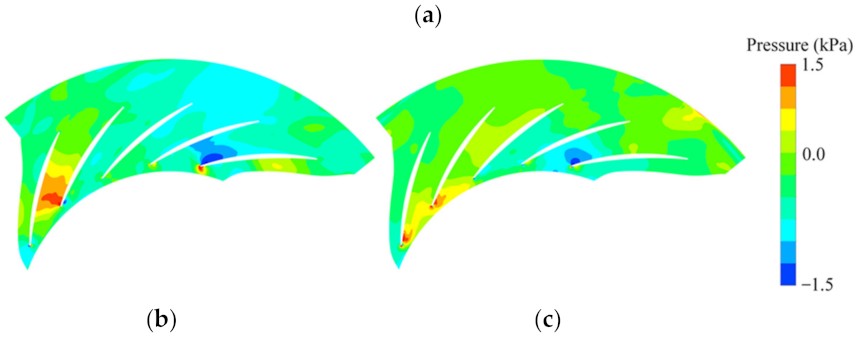
- Combined with the monitoring point spectrum analysis and modal decomposition method, it is determined that the unstable flow phenomenon caused by the low frequency appears in the diffuser with three guide vane’s openings at φ = 0.0833. The unstable flow in the diffuser is mainly caused by the low frequency and impeller-diffuser interaction. When the positive pre-swirl of the guide vanes is small, the unstable flow caused by low frequency dominates the flow inside the diffuser, while the positive pre-swirl of the guide vane increases, the flow inside the diffuser is dominated by low frequency and the impeller-diffuser interaction, and the strength of the unstable flow is significantly weakened. As a result, the risk of the diffuser passages blockage is reduced, which is also a fundamental reason for the guide vane’s regulation to broaden the operating range of the compressor. Moreover, the unstable flow caused by the low frequency attenuation/release process of the diffuser can be predicted with the DMD method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| VIGV | variable inlet guide vane |
| IGV | inlet guide vane |
| POD | proper orthogonal decomposition |
| DMD | dynamic modal decomposition |
| k | adiabatic exponent |
| Pt | total pressure (Pa) |
| Tt | total temperature (K) |
| Qm | mass flow rate (kg/s) |
| D | diameter |
| BPF | blade passing frequency |
| IPF | impeller passing frequency |
| FFT | fast Fourier transform |
| t | time |
| Δt | time step |
| 0 | centrifugal compressor stage inlet |
| 1 | impeller inlet |
| 2 | impeller outlet |
| 3 | diffuser inlet |
| 4 | diffuser outlet |
| 5 | centrifugal compressor stage outlet |
| λ | POD eigenvalue |
| n | number |
| φ | mass flow coefficient |
| ε | total pressure ratio |
| ηpol | total–total polytropic efficiency |
| ω | direction of impeller rotation |
References
- Sun, Q.; Ji, C.J.; Fang, J.Y.; Li, C.Y.; Zhang, X.L. Optimization design of IGV profile in centrifugal compressor. Math. Probl. Eng. 2017, 2017, 8437325. [Google Scholar] [CrossRef] [Green Version]
- Cui, M.M. Effect of Suction Elbow and Inlet Guide Vanes on Flow Field in a Centrifugal Compressor Stage. In ASME Paper No. GT2002-30376; American Society of Mechanical Engineers: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Becciani, M.; Bianchini, A.; Checcucci, M.; Ferrara, G.; Deluca, M.; Marmorini, L.; Arnone, A.; Ferrara, G. A pre-design model to estimate the effect of variable inlet guide vanes on the performance map of a centrifugal compressor for automotive applications. In Proceedings of the SAE 13th International Conference on Engines and Vehicles, Capri, Italy, 10–14 September 2017; Volume 24. [Google Scholar] [CrossRef]
- Rodgers, C. Centrifugal compressor inlet guide vanes for increased surge margin. J. Turbomach. 1991, 113, 696–702. [Google Scholar] [CrossRef]
- Coppinger, M.; Swain, E. Performance prediction of an industrial centrifugal compressor inlet guide vane system. Proc. Inst. Mech. Eng. Part A J. Power Energy 2000, 214, 153–164. [Google Scholar] [CrossRef]
- Mohseni, A.; Goldhahn, E.; Braembussche, R.A.V.D.; Van den Braembussche, R.A.; Seume, J.R. Novel IGV designs for centrifugal compressors and their interaction with the impeller. J. Turbomach. 2012, 134, 021006. [Google Scholar] [CrossRef]
- Zhou, L.; Xi, G.; Cai, Y. Numerical investigation of unsteady IGV-impeller-diffuser interaction in a centrifugal compressor. J. Northwest. Polytech. Univ. 2010, 22, 1715–1721. [Google Scholar] [CrossRef]
- Biela, C.; Brandstetter, C.; Holzinger, F.; Schiffer, H. Influence of inlet guide vane wakes on performance and stability of a transonic compressor. In Proceedings of the 20th International Symposium on Air Breathing Engines, Gothenburg, Sweden, 12–16 September 2011; 2011. Article ID: ISABE-2011-1209. [Google Scholar]
- Xu, C.; Fan, C.; Zhang, Z.P.; Mao, Y.J. Numerical study of wake and potential interactions in a two-stage centrifugal refrigeration compressor. Eng. Appl. Comput. Fluid Mech. 2021, 15, 313–327. [Google Scholar] [CrossRef]
- Galindo, J.; Serrano, J.R.; Margot, X.; Tiseira, A.; Schorn, N.; Kindl, H. Potential of flow pre-whirl at the compressor inlet of automotive engine turbochargers to enlarge surge margin and overcome packaging limitations. Int. J. Heat Fluid Flow 2007, 28, 374–387. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Q. Potential of the range extension of compressors with a variable inlet pre-whirl for automotive turbocharged engines with an ultra-high-power density. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2015, 229, 1959–1968. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, J.; Wang, Z.; Xi, G. Numerical investigation of diffuser. In ASME Paper No. GT2017-63913; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Grondin, J.; Trébinjac, I.; Rochuon, N. Rotating instabilities versus rotating stall in a high-speed centrifugal compressor. In ASME Paper No. GT2018-76916; American Society of Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Zhao, J.; Xi, G.; Wang, Z.; Zhao, Y. The unsteady pre-stall behaviour of the spike-type rotating stall within an airfoil vaned-diffuser. In ASME Paper GT2018-76145; American Society of Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Day, I.J. Stall, surge, and 75 years of research. J. Turbomach. 2015, 138, 011001. [Google Scholar] [CrossRef]
- Giovanni, F.; Lorenzo, F.; Leonardo, B. Rotating stall in centrifugal compressor vaneless diffuser: Experimental analysis of geometrical parameters influence on phenomenon evolution. Int. J. Rotating Mach. 2004, 10, 576764. [Google Scholar] [CrossRef] [Green Version]
- Fujisawa, N.; Hara, S.; Ohta, Y. Unsteady behavior of leading-edge vortex and diffuser stall in a centrifugal compressor with vaned diffuser. J. Therm. Sci. 2016, 25, 13–21. [Google Scholar] [CrossRef]
- Semlitsch, B.; Mihăescu, M. Flow phenomena leading to surge in a centrifugal compressor. Energy 2016, 103, 572–587. [Google Scholar] [CrossRef]
- Witte, M.; Torner, B.; Wurm, F.H. Analysis of unsteady flow structures in a radial turbomachine by using proper orthogonal decomposition. In ASME Paper No. GT2018-76596; American Society of Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Sharma, S.; Broatch, A.; García, T.J.; Allport, J.M.; Nickson, A.K. Acoustic characteristics of a ported shroud turbocompressor operating at design conditions. Inter. J. Engine Res. 2018, 21, 1454–1468. [Google Scholar] [CrossRef]
- Sajadmanesh, S.M.; Mojaddam, M.; Mohseni, A.; Nikparto, A. Numerical identification of separation bubble in an ultra-high-lift turbine cascade using URANS simulation and proper orthogonal decomposition. Aerosp. Sci. Technol. 2019, 93, 105329. [Google Scholar] [CrossRef]
- Sharma, S.; Broatch, A.; García, T.J.; Nickson, A.K.; Allport, J.M. Acoustic and pressure characteristics of a ported shroud turbocompressor operating at near surge conditions. Appl. Acoust. 2019, 148, 434–447. [Google Scholar] [CrossRef] [Green Version]
- Rochuon, N.; Trébinjac, I.; Billonnet, G. An extraction of the dominant rotor-stator interaction modes by the use of Proper Orthogonal Decomposition (POD). J. Therm. Sci. 2006, 15, 109–114. [Google Scholar] [CrossRef]
- Zhang, L.; Mi, D.; Yan, C.; Tang, F. Multidisciplinary Design Optimization for a Centrifugal Compressor Based on Proper Orthogonal Decomposition and an Adaptive Sampling Method. Appl. Sci. 2018, 8, 2608. [Google Scholar] [CrossRef] [Green Version]
- Ji, C.; Wang, Z.; Tang, Y.; Xi, G. A Flow Information-Based Prediction Model Applied to the Nonaxisymmetric Hub Optimization of a Centrifugal Impeller. J. Mech. Des. 2021, 143, 103502. [Google Scholar] [CrossRef]
- Sundström, E.; Mihaescu, M. Centrifugal compressor: The sound of surge. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef]
- Li, X.; Zhao, Y.; Liu, Z.; Zhao, M. Dynamic mode decomposition analysis of the flow characteristics in a centrifugal compressor with vaned diffuser. Pro. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 154–168. [Google Scholar] [CrossRef]
- Hu, C.; Yang, C.; Yi, W.; Hadzic, K.; Xie, L.; Zou, R.; Zhou, M. Numerical investigation of centrifugal compressor stall with compressed dynamic mode decomposition. Aerosp. Sci. Technol. 2020, 106, 106153. [Google Scholar] [CrossRef]
- Xue, X.; Wang, T.; Shao, Y.; Yang, B.; Gu, C. Experimental and numerical analysis of unsteady flow structure in a centrifugal compressor with variable vaned diffuser. In ASME Paper GT2018-76597; American Society of Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Omidi, M.; Li, H. Numerical study of the improvement in stability and performance by use of a partial vaned diffuser for a centrifugal compressor stage. Appl. Sci. 2021, 11, 6980. [Google Scholar] [CrossRef]
- Zhao, P.F.; Liu, Y.; Li, H.K.; Wang, X.F.; Yang, J.G. The effect of impeller–diffuser interactions on diffuser performance in a centrifugal compressor. Eng. Appl. Comput. Fluid Mech. 2016, 10, 565–577. [Google Scholar] [CrossRef] [Green Version]
- Crevel, F.; Gourdain, N.; Moreau, S. Numerical simulation of aerodynamic instabilities in a multistage high-speed high-pressure compressor on its test-rig—part I: Rotating stall. J. Turbomach. 2014, 136, 101003. [Google Scholar] [CrossRef]
- Zamiri, A.; Lee, B.J.; Chung, J.T. Numerical evaluation of transient flow characteristics in a transonic centrifugal compressor with vaned diffuser. Aerosp. Sci. Technol. 2017, 70, 244–256. [Google Scholar] [CrossRef]
- Chen, S.; Zuo, S.; Wei, K. Numerical investigation of the centrifugal compressor stability improvement by half vaned low solidity diffusers. J. Therm. Sci. 2021, 30, 696–706. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130, 07800. [Google Scholar]
- ANSYS. ANSYS CFX Version 17.0. 2015. Available online: http://www.ansys.com/ (accessed on 16 July 2021).
- Sirovich, L. Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Hutchinson, P. Stochastic tools in turbulence. Phy. Bull. 1971, 22, 161. [Google Scholar] [CrossRef]
- Sirovich, L.; Rodriguez, J.D. Coherent structures and chaos: A model problem. Phy. Lett. A 1987, 120, 211–214. [Google Scholar] [CrossRef]
- Lengani, D.; Simoni, D.; Pichler, R.; Sandberg, R.D.; Michelassi, V.; Bertini, F. On the identification and decomposition of the unsteady losses in a turbine cascade. J. Turbomach. 2019, 141, 031005. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Zhou, Q.; Yang, S.; Li, H. Rotating stall induced non-synchronous blade vibration analysis for an unshrouded industrial centrifugal compressor. Sensors 2019, 19, 4995. [Google Scholar] [CrossRef] [PubMed] [Green Version]




| Parameters | Value | |
|---|---|---|
| Impeller outlet diameter | D2 | 810 mm |
| Diffuser inlet diameter | D3 | 900 mm |
| Diffuser outlet diameter | D4 | 1240 mm |
| Return channel diameter | Dret | 620 mm |
| Impeller exit width | b2 | 57.5 mm |
| Tip clearance | τ | 3.5 mm |
| Number of guide vanes | Zgui | 11 |
| Number of impellers | Zimp | 19 |
| Number of diffuser vanes | Zdif | 20 |
| Number of return channels | Zret | 18 |
| Rotational speed | ω | 5600 rpm |
| Coarse | Medium | Fine | GCI | Experimental | |
|---|---|---|---|---|---|
| Total pressure ratio | 1.4948 | 1.5426 | 1.5466 | 1.07% | 1.5322 |
| Total-total efficiency | 90.13% | 90.88% | 90.92% | 0.86% | 89.39% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Liu, Y.; Omidi, M.; Zhang, C.; Li, H. Numerical Investigation of Transient Flow Characteristics in a Centrifugal Compressor Stage with Variable Inlet Guide Vanes at Low Mass Flow Rates. Energies 2021, 14, 7906. https://doi.org/10.3390/en14237906
Li S, Liu Y, Omidi M, Zhang C, Li H. Numerical Investigation of Transient Flow Characteristics in a Centrifugal Compressor Stage with Variable Inlet Guide Vanes at Low Mass Flow Rates. Energies. 2021; 14(23):7906. https://doi.org/10.3390/en14237906
Chicago/Turabian StyleLi, Shuai, Yan Liu, Mohammad Omidi, Chuang Zhang, and Hongkun Li. 2021. "Numerical Investigation of Transient Flow Characteristics in a Centrifugal Compressor Stage with Variable Inlet Guide Vanes at Low Mass Flow Rates" Energies 14, no. 23: 7906. https://doi.org/10.3390/en14237906
APA StyleLi, S., Liu, Y., Omidi, M., Zhang, C., & Li, H. (2021). Numerical Investigation of Transient Flow Characteristics in a Centrifugal Compressor Stage with Variable Inlet Guide Vanes at Low Mass Flow Rates. Energies, 14(23), 7906. https://doi.org/10.3390/en14237906







