Assessment of Organic Rankine Cycle Part-Load Performance as Gas Turbine Bottoming Cycle with Variable Area Nozzle Turbine Technology
Abstract
:1. Introduction
2. Mathematical Models and Method
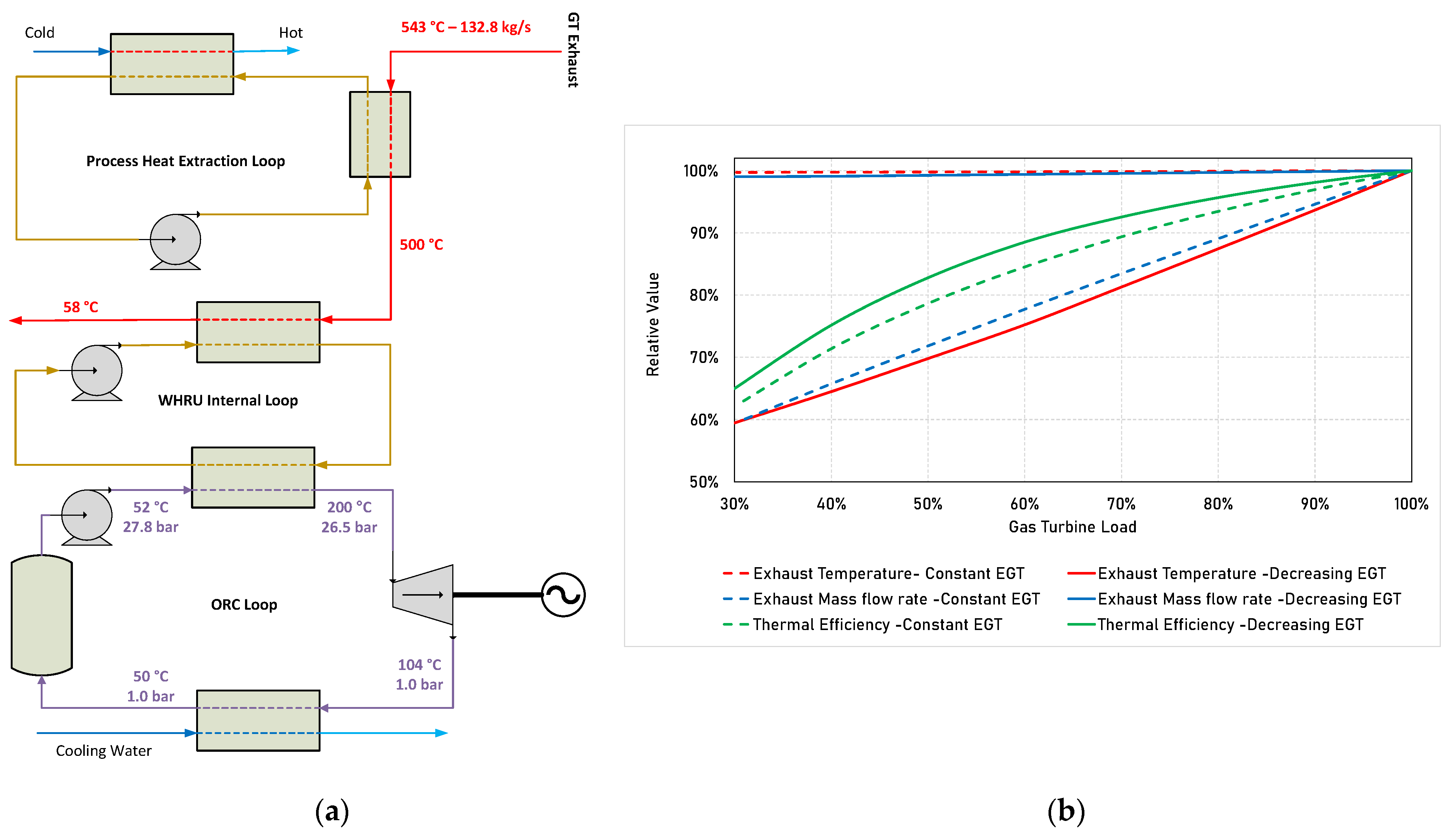
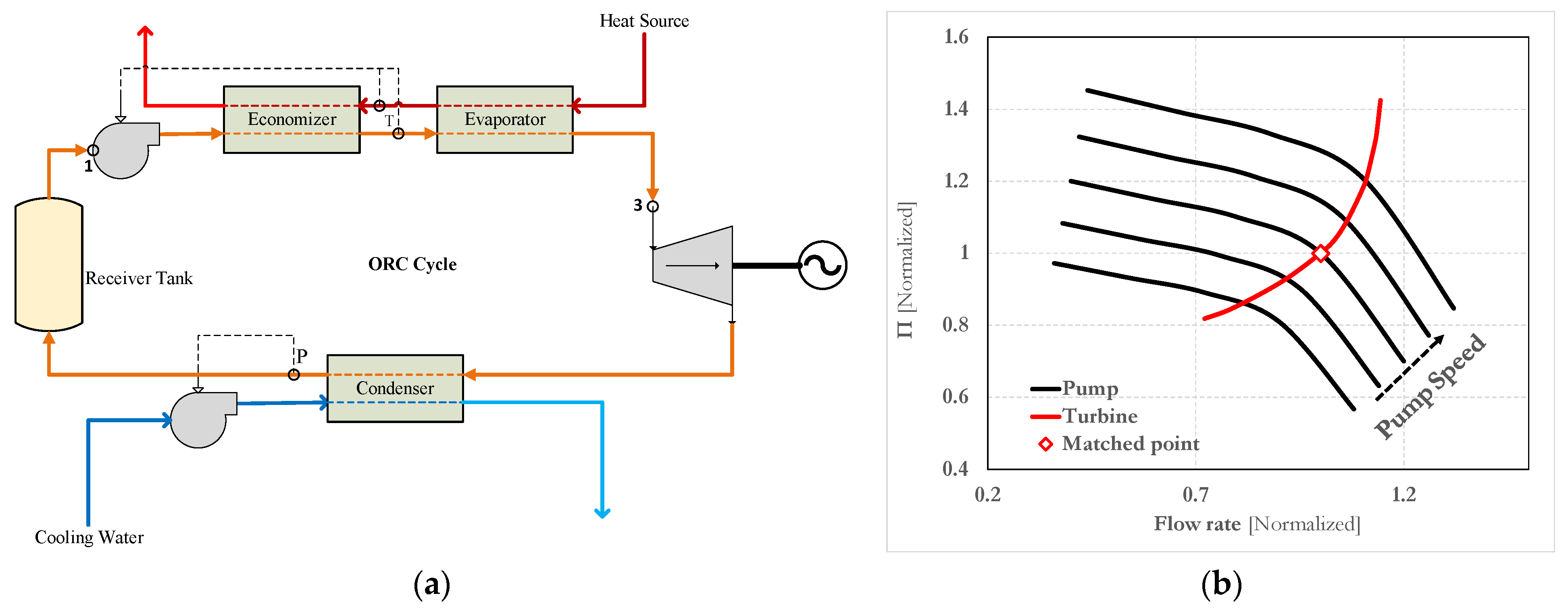
2.1. System Configuration Selection
2.2. Component Modelling
2.2.1. Gas Turbine
2.2.2. Pump
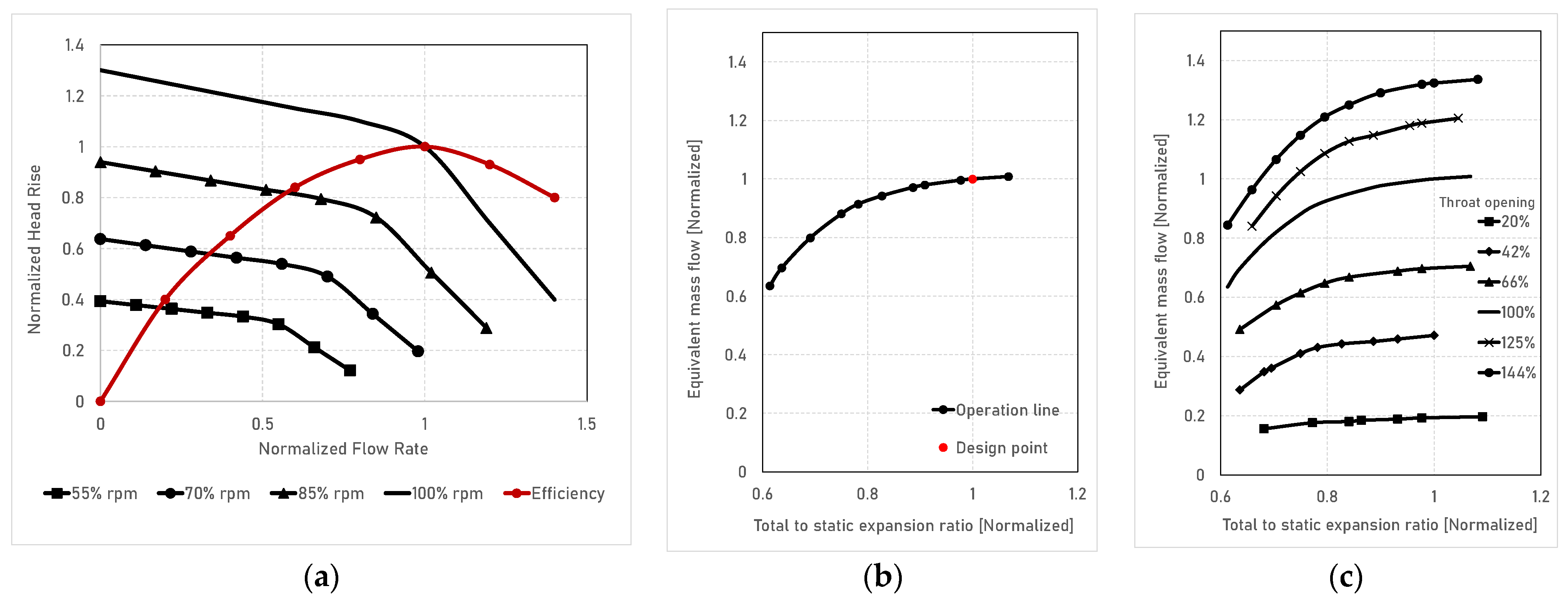
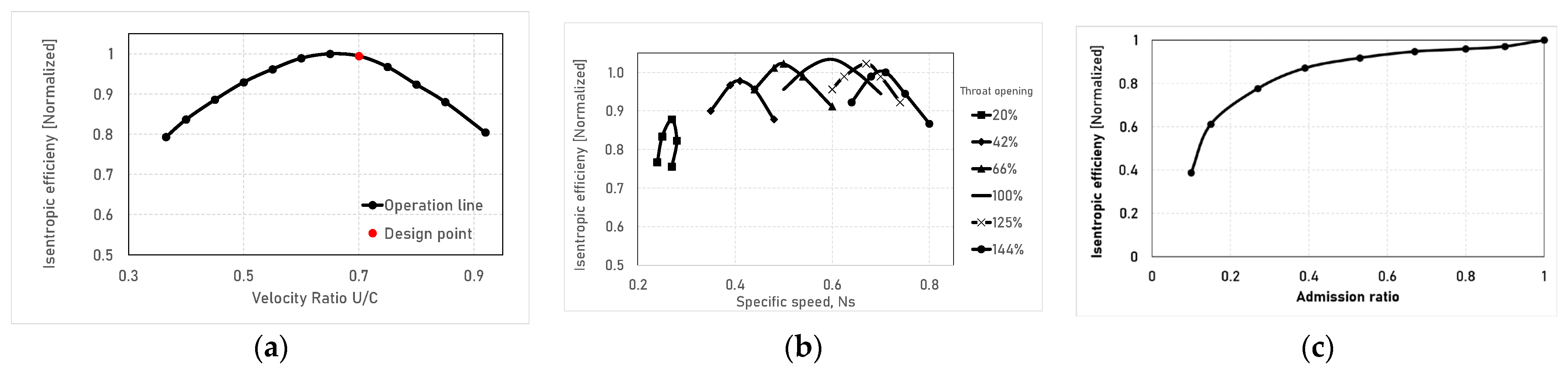
2.2.3. Radial Inflow Turbine
2.2.4. Variable Area Nozzle Turbine
2.2.5. Partial Admission Turbine
2.2.6. Heat Exchangers
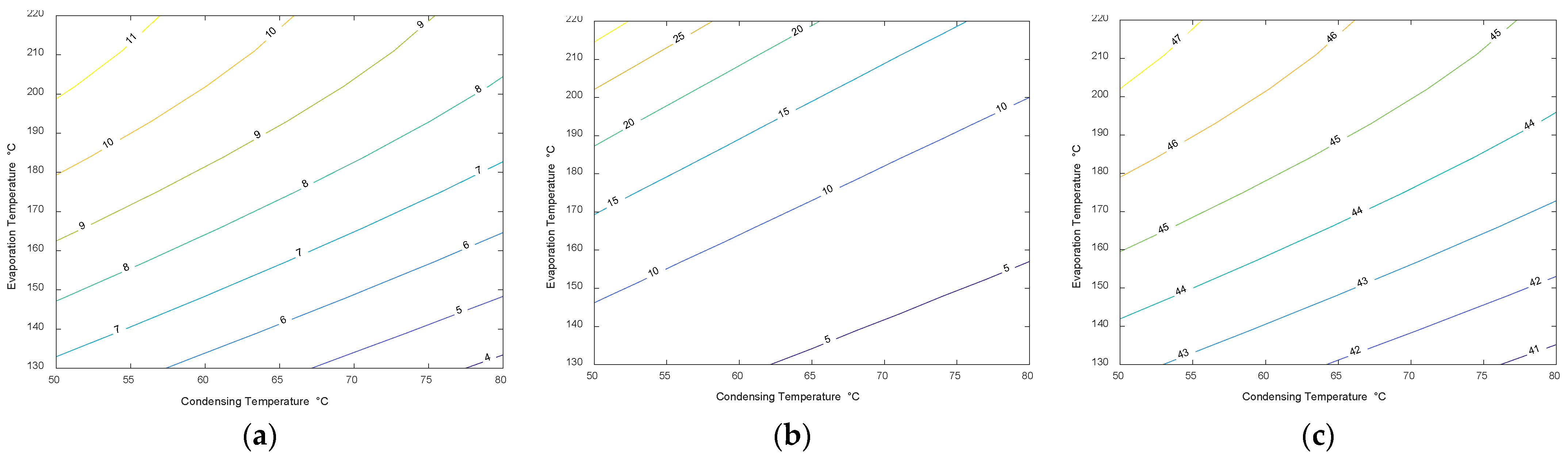
2.3. Cycle Design Point
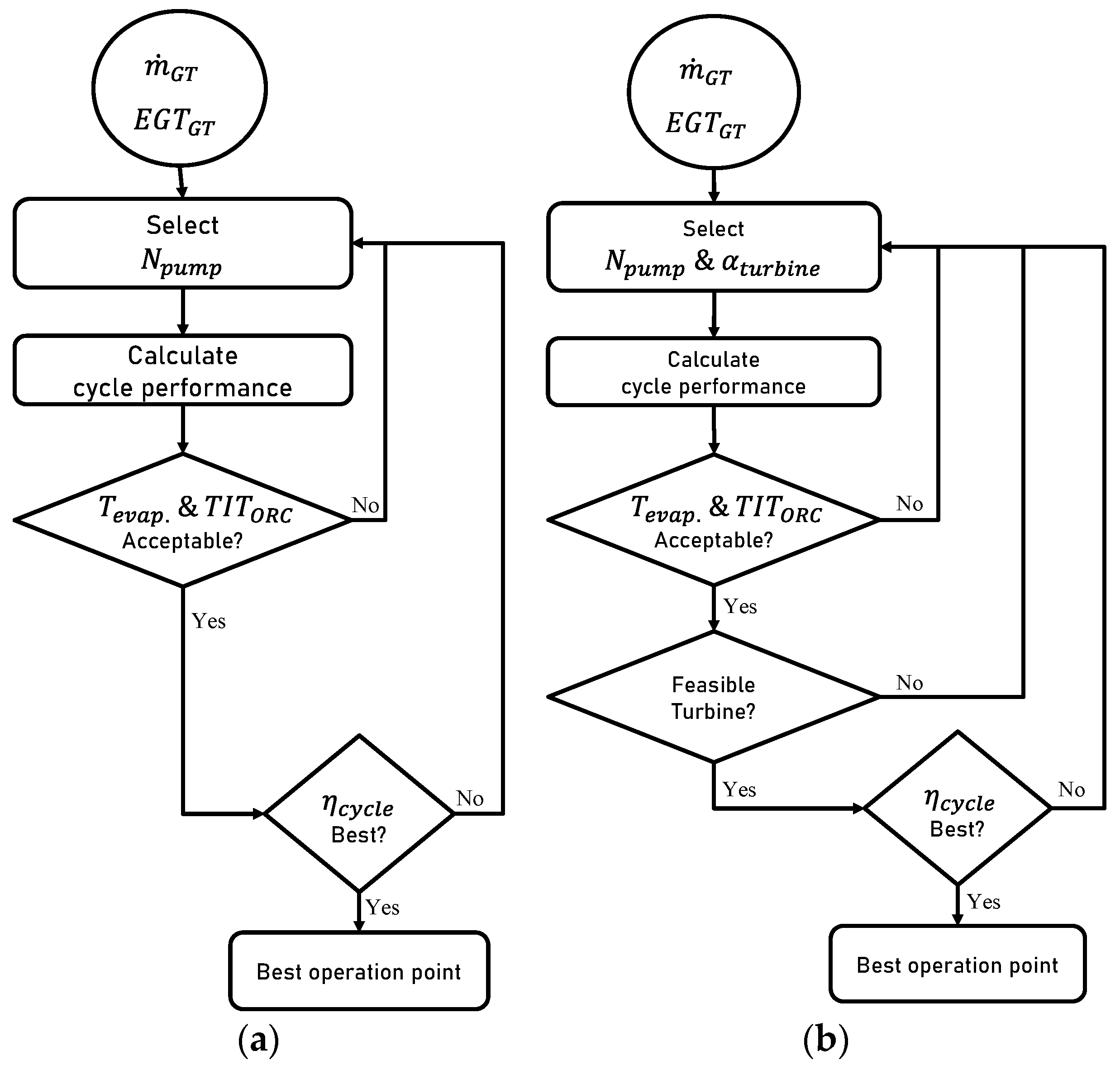
2.4. Part-Load Strategy Development
2.4.1. Sliding Pressure
2.4.2. Variable Geometry Turbine
2.4.3. Valve Throttling
2.5. Method and Tool Verification
3. Results and Discussions
3.1. Design Point
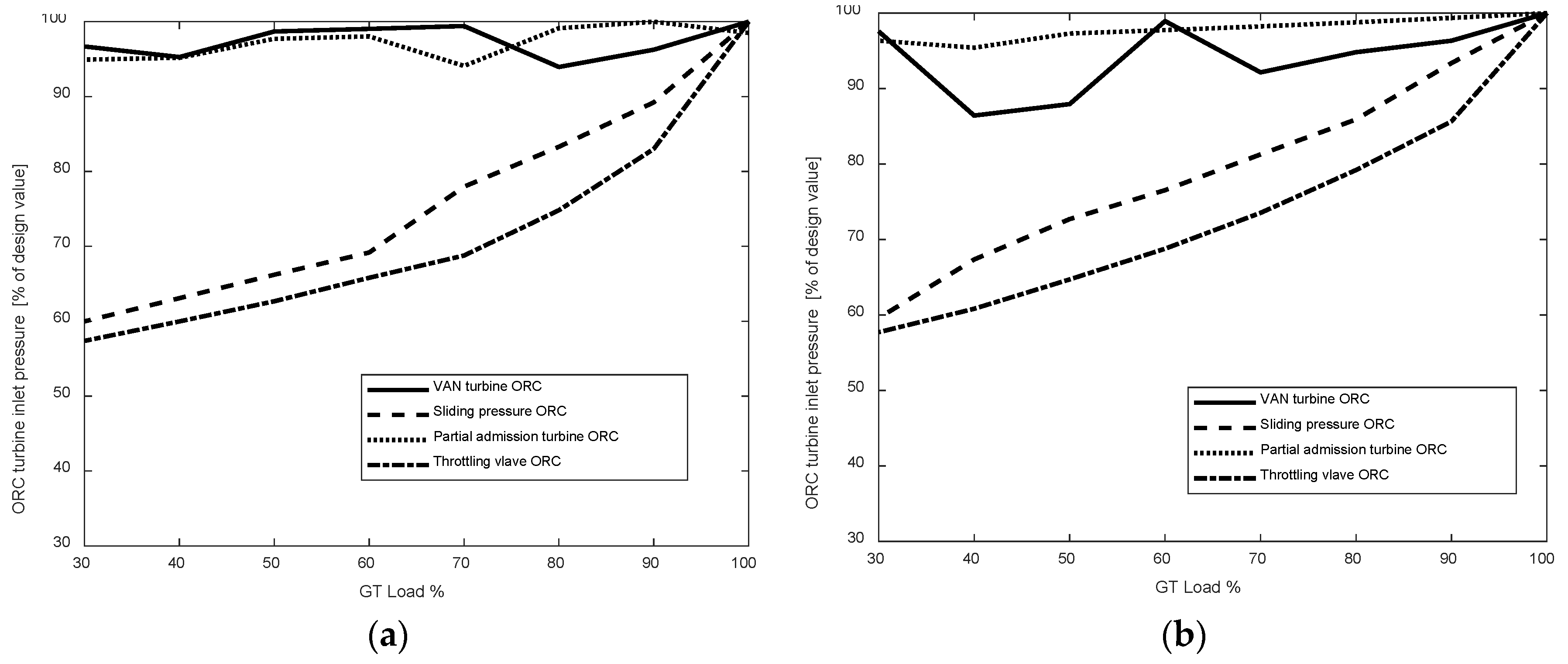
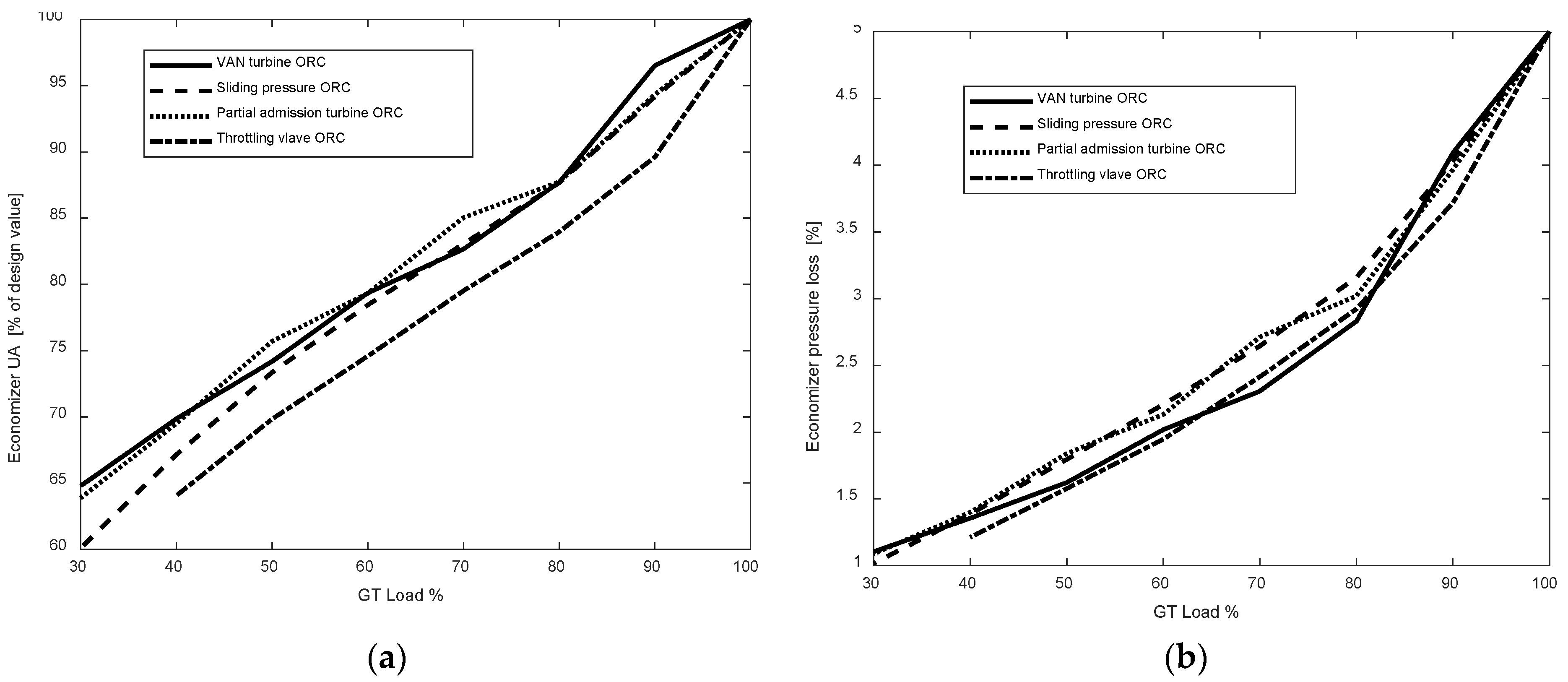
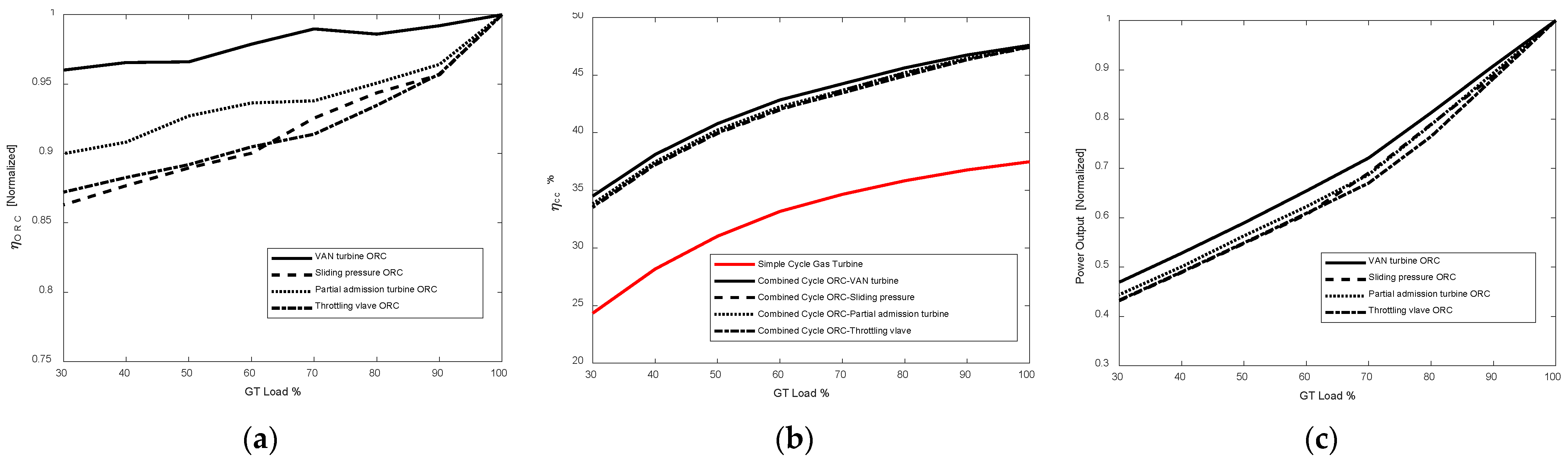
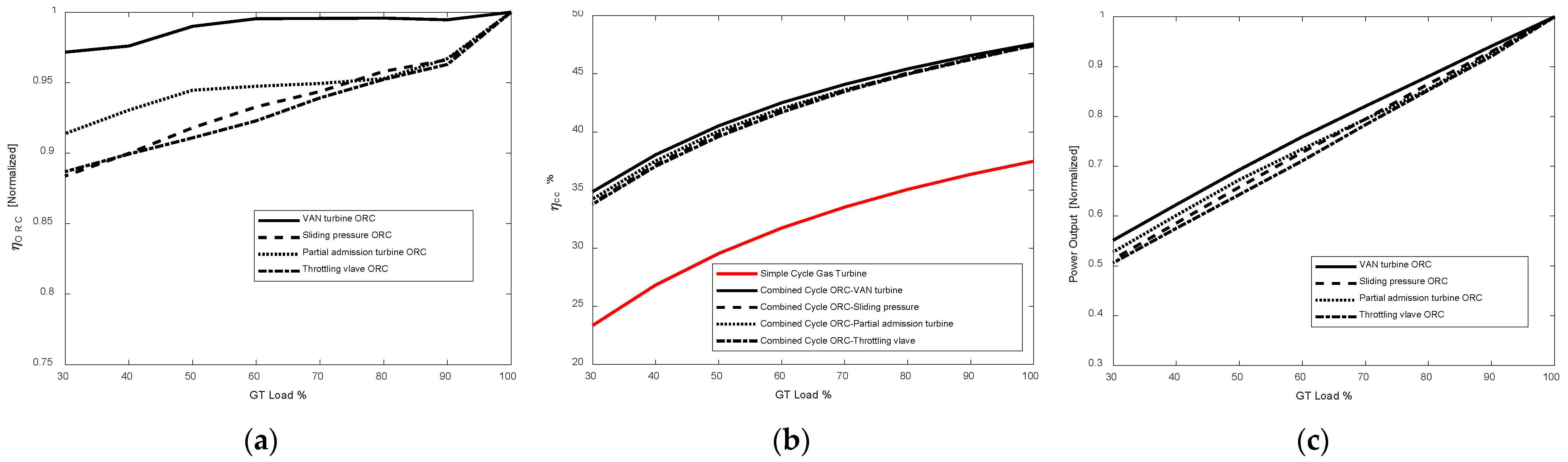
3.2. Part-Load Operation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | heat exchanger area |
| C | heat capacity |
| CR | heat exchanger heat capacity ratio |
| turbine isentropic speed (m/s) | |
| skin friction factor | |
| D | diameter (m) |
| f | Fanning friction factor |
| enthalpy (J/kg) | |
| K | thermal conductivity |
| mass flow rate (kg/s) | |
| N | rotational speed |
| Nu | Nusselt number |
| P | pressure (Pa) |
| Pr | Prandtl number |
| PR | component pressure ratio |
| Q | volume flow rate |
| Re | Reynolds number |
| T | temperature (K) |
| U | impeller tip speed (m/s) or overall heat transfer coefficient |
| x | length (m) |
| turbine specific speed | |
| velocity (m/s) | |
| power (W) | |
| Greek letters | |
| part-load turbine manipulating variable | |
| heat transfer coefficient ratio | |
| efficiency | |
| cycle pressure ratio | |
| density | |
| surface roughness | |
| Subscripts | |
| 0 | Total |
| c | heat exchanger cold side, or corrected |
| cond. | related to condenser |
| D | based on diameter |
| ds | design point |
| econ. | related to economizer |
| evap. | related to evaporator |
| h | heat exchanger hot side |
| i | inlet |
| max | maximum |
| min | minimum |
| o | outlet |
| pump | related to pump |
| rel | relative |
| s | isentropic |
| turb. | related to turbine |
References
- Walnum, H.T.; Nekså, P.; Nord, L.O.; Andresen, T. Modelling and simulation of CO2 (carbon dioxide) bottoming cycles for offshore oil and gas installations at design and off-design conditions. Energy 2013, 59, 513–520. [Google Scholar] [CrossRef]
- Sølvberg, I. Resource Report—Fields and Discovery; The Norwegian Petroleum Directorate: Stavanger, Norway, 2019; pp. 47–53. [CrossRef] [Green Version]
- IEA. The Future of Hydrogen: Seizing Today’s Opportunities. In Proceedings of the G20 Summit, Osaka, Japan, 28–29 June 2019; p. 203. [Google Scholar]
- Omar, A.; Saghafifar, M.; Mohammadi, K.; Alashkar, A.; Gadalla, M. A review of unconventional bottoming cycles for waste heat recovery: Part II—Applications. Energy Convers. Manag. 2019, 180, 559–583. [Google Scholar] [CrossRef]
- Pierobon, L.; Benato, A.; Scolari, E.; Haglind, F.; Stoppato, A. Waste heat recovery technologies for offshore platforms. Appl. Energy 2014, 136, 228–241. [Google Scholar] [CrossRef] [Green Version]
- Del Turco, P.; Asti, A.; Scotti Del Greco, A.; Bacci, A.; Landi, G.; Seghi, G. The ORegen™ Waste Heat Recovery Cycle: Reducing the CO2 Footprint by Means of Overall Cycle Efficiency Improvement. In Proceedings of the ASME Turbo Expo, Vancouver, BC, Canada, 6–10 June 2011; pp. 547–556. [Google Scholar]
- Pierobon, L.; Larsen, U.; van Nguyen, T.; Haglind, F. Optimization of organic rankine cycles for off-shore applications. Proceedings of ASME Turbo Expo, San Antonio, TX, USA, 3–7 June 2013; pp. 1–11. [Google Scholar] [CrossRef]
- Riboldi, L.; Nord, L.O. Concepts for lifetime efficient supply of power and heat to offshore installations in the North Sea. Energy Convers. Manag. 2017, 148, 860–875. [Google Scholar] [CrossRef]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Barnhart, C.J. Energy and Carbon Intensities of Stored Wind Energy. In Wind Energy Engineering: A Handbook for Onshore and Offshore Wind Turbines; Elsevier Inc.: Amsterdam, The Netherlands, 2017; pp. 377–387. [Google Scholar]
- Mazzetti, M.J.; Ladam, Y.; Walnum, H.T.; Hagen, B.L.; Skaugen, G.; Nekså, P. Flexible Combined Heat and Power Systems for Offshore Oil and Gas. In Proceedings of the ASME Power Conference (POWER2014-32169), Baltimore, MD, USA, 28–31 July 2014; pp. 1–8. [Google Scholar]
- Nord, L.O.; Montañés, R.M. Compact steam bottoming cycles: Model validation with plant data and evaluation of control strategies for fast load changes. Appl. Therm. Eng. 2018, 142, 334–345. [Google Scholar] [CrossRef]
- van Nguyen, T.; Voldsund, M.; Breuhaus, P.; Elmegaard, B. Energy efficiency measures for offshore oil and gas platforms. Energy 2016, 117, 325–340. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Dai, Y. Comparative analysis on off-design performance of a gas turbine and ORC combined cycle under different operation approaches. Energy Convers. Manag. 2017, 135, 84–100. [Google Scholar] [CrossRef]
- Fu, B.R.; Hsu, S.W.; Lee, Y.R.; Hsieh, J.C.; Chang, C.M.; Liu, C.H. Effect of off-design heat source temperature on heat transfer characteristics and system performance of a 250-kW organic Rankine cycle system. Appl. Therm. Eng. 2014, 70, 7–12. [Google Scholar] [CrossRef]
- Casartelli, D.; Binotti, M.; Silva, P.; Macchi, E.; Roccaro, E.; Passera, T. Power Block Off-design Control Strategies for Indirect Solar ORC Cycles. Energy Procedia 2015, 69, 1220–1230. [Google Scholar] [CrossRef] [Green Version]
- de Escalona, J.M.M.; Sánchez, D.; Chacartegui, R.; Sánchez, T. Part-load analysis of gas turbine & ORC combined cycles. Appl. Therm. Eng. 2012, 36, 63–72. [Google Scholar] [CrossRef]
- Cao, Y.; Gao, Y.; Zheng, Y.; Dai, Y. Optimum design and thermodynamic analysis of a gas turbine and ORC combined cycle with recuperators. Energy Convers. Manag. 2016, 116, 32–41. [Google Scholar] [CrossRef]
- Chacartegui, R.; Sánchez, D.; Muñoz, J.M.; Sánchez, T. Alternative ORC bottoming cycles FOR combined cycle power plants. Appl. Energy 2009, 86, 2162–2170. [Google Scholar] [CrossRef]
- Carcasci, C.; Ferraro, R.; Miliotti, E. Thermodynamic analysis of an organic Rankine cycle for waste heat recovery from gas turbines. Energy 2014, 65, 91–100. [Google Scholar] [CrossRef]
- Khaljani, M.; Saray, R.K.; Bahlouli, K. Thermodynamic and thermoeconomic optimization of an integrated gas turbine and organic Rankine cycle. Energy 2015, 93, 2136–2145. [Google Scholar] [CrossRef]
- Nami, H.; Ertesvåg, I.S.; Agromayor, R.; Riboldi, L.; Nord, L.O. Gas turbine exhaust gas heat recovery by organic Rankine cycles (ORC) for offshore combined heat and power applications—Energy and exergy analysis. Energy 2018, 165, 1060–1071. [Google Scholar] [CrossRef]
- GT MASTER Version 29.0; Thermoflow Inc.: Fayville, MA, USA, 2016; Available online: http://www.thermoflow.com/UpdateLetters/TF8_UPDATE_LETTER.html (accessed on 11 November 2021).
- Hu, D.; Li, S.; Zheng, Y.; Wang, J.; Dai, Y. Preliminary design and off-design performance analysis of an Organic Rankine Cycle for geothermal sources. Energy Convers. Manag. 2015, 96, 175–187. [Google Scholar] [CrossRef]
- Manente, G.; Toffolo, A.; Lazzaretto, A.; Paci, M. An Organic Rankine Cycle off-design model for the search of the optimal control strategy. Energy 2013, 58, 97–106. [Google Scholar] [CrossRef]
- Meitner, P.L.; Glassman, A.J. Off-Design Performance Loss Model for Radial Turbines with Pivoting, Variable-Area Stators; National Aeronautics and Space Administration Cleveland Oh Lewis Research Center: Cleveland, OH, USA, 1980. [Google Scholar]
- Hagen, B.A.L.; Agromayor, R.; Nekså, P. Equation-oriented methods for design optimization and performance analysis of radial inflow turbines. Energy 2021, 237, 121596. [Google Scholar] [CrossRef]
- Wang, H.; Luo, K.; Huang, C.; Zou, A.; Li, D.; Qin, K. Numerical investigation of partial admission losses in radial inflow turbines. Energy 2022, 239, 121870. [Google Scholar] [CrossRef]
- Hagen, B.A.L.; Nikolaisen, M.; Andresen, T. A novel methodology for Rankine cycle analysis with generic heat exchanger models. Appl. Therm. Eng. 2020, 165, 114566. [Google Scholar] [CrossRef]
- Dhar, P.L. Thermal System Design and Simulation; Elsevier Ltd.: Amsterdam, The Netherlands, 2016. [Google Scholar]
- NPhu, M.; Trinh, N.T.M. Modelling and experimental validation for off-design performance of the helical heat exchanger with LMTD correction taken into account. J. Mech. Sci. Technol. 2016, 30, 3357–3364. [Google Scholar] [CrossRef]
- Selander, W.N. Explicit Formulas for the Computation of Friction Factors in Turbulent Pipe Flow; Energy Can Ltd. AECL Rep., No. 6354; Atomic Energy of Canada Ltd.: Chalk River, ON, Canada, 1978. [Google Scholar]
- Bell, I.H.; Wronski, J.; Lemort, Q.; Lemort, V. Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [Green Version]
- Rajabloo, T.; Bonalumi, D.; Iora, P. Effect of a partial thermal decomposition of the working fluid on the performances of ORC power plants. Energy 2017, 133, 1013–1026. [Google Scholar] [CrossRef]

| Gas Turbine | Bottoming Cycle | ||
|---|---|---|---|
| power output [MW] | 47.05 | hex pinch point limit [°C] | 10 |
| thermal efficiency [%] | 37.48 | pump isentropic efficiency [%] | 70 |
| exhaust gas mass flow rate [kg/s] | 132.8 | turbine isentropic efficiency [%] | 80 |
| Exhaust gas temperature [°C] | 452.7 | condenser/economizer pressure loss [%] | 5 |
| process heat extraction [MW] | 4 | evaporator pressure loss [%] | 1 |
| Parameters | Verification Cases | ||
|---|---|---|---|
| Case 1 | Case 2 | Case 3 | |
| gas turbine load [%] | 100 | 100 | 50 |
| ORC working fluid | MDM2 | Toluene | Toluene |
| gas turbine exhaust gas temperature [°C] | 520 | 520 | 358 |
| gas turbine exhaust mass flow rate [kg/s] | 19.2 | 19.2 | 19.2 |
| gas turbine thermal efficiency [% LHV] | 28.9 | 28.9 | 23.8 |
| ORC thermal efficiency, reference value [%] | 17.1 | 27.8 | 26.7 |
| ORC thermal efficiency, simulation results [%] | 17.2 | 27.9 | 27.0 |
| relative error [%] | 0.5 | 0.3 | 1.1 |
| Properties | Value | Properties | Value | Properties | Value |
|---|---|---|---|---|---|
| health/physical/fire hazard | 2/3/1 | [K] | 511.7 | 580 | |
| EQ)/kg] | 3 | [kPa] | 4515 | [mol/L] | 70.13 |
| Cycle Properties | Value | Cycle Properties | Value |
|---|---|---|---|
| evaporation temperature [°C] | 200 | power output [MW] | 11.1 |
| condensing temperature [°C] | 50 | evaporator pinch point temperature [°C] | 138 |
| pump pressure ratio | 27 | mass flow rate [kg/s] | 106 |
| turbine pressure ratio | 24.2 | air exhaust temperature [°C] | 58 |
| superheating [°C] | 5 | economizer pinch point temperature [°C] | 8 |
| thermal efficiency [%] | 18.1 | combined-cycle efficiency [%] | 46.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Motamed, M.A.; Nord, L.O. Assessment of Organic Rankine Cycle Part-Load Performance as Gas Turbine Bottoming Cycle with Variable Area Nozzle Turbine Technology. Energies 2021, 14, 7916. https://doi.org/10.3390/en14237916
Motamed MA, Nord LO. Assessment of Organic Rankine Cycle Part-Load Performance as Gas Turbine Bottoming Cycle with Variable Area Nozzle Turbine Technology. Energies. 2021; 14(23):7916. https://doi.org/10.3390/en14237916
Chicago/Turabian StyleMotamed, Mohammad Ali, and Lars O. Nord. 2021. "Assessment of Organic Rankine Cycle Part-Load Performance as Gas Turbine Bottoming Cycle with Variable Area Nozzle Turbine Technology" Energies 14, no. 23: 7916. https://doi.org/10.3390/en14237916







