A Unified Controller for Multi-State Operation of the Bi-Directional Buck–Boost DC-DC Converter
Abstract
:1. Introduction
2. The Multi-State Carrier-Based Modulation Scheme
3. Mathematical Model of the Converter
3.1. Output Voltage Control Loop with Feedback Linearization
3.2. Inductor Current Control Loop with Feedback Linearization
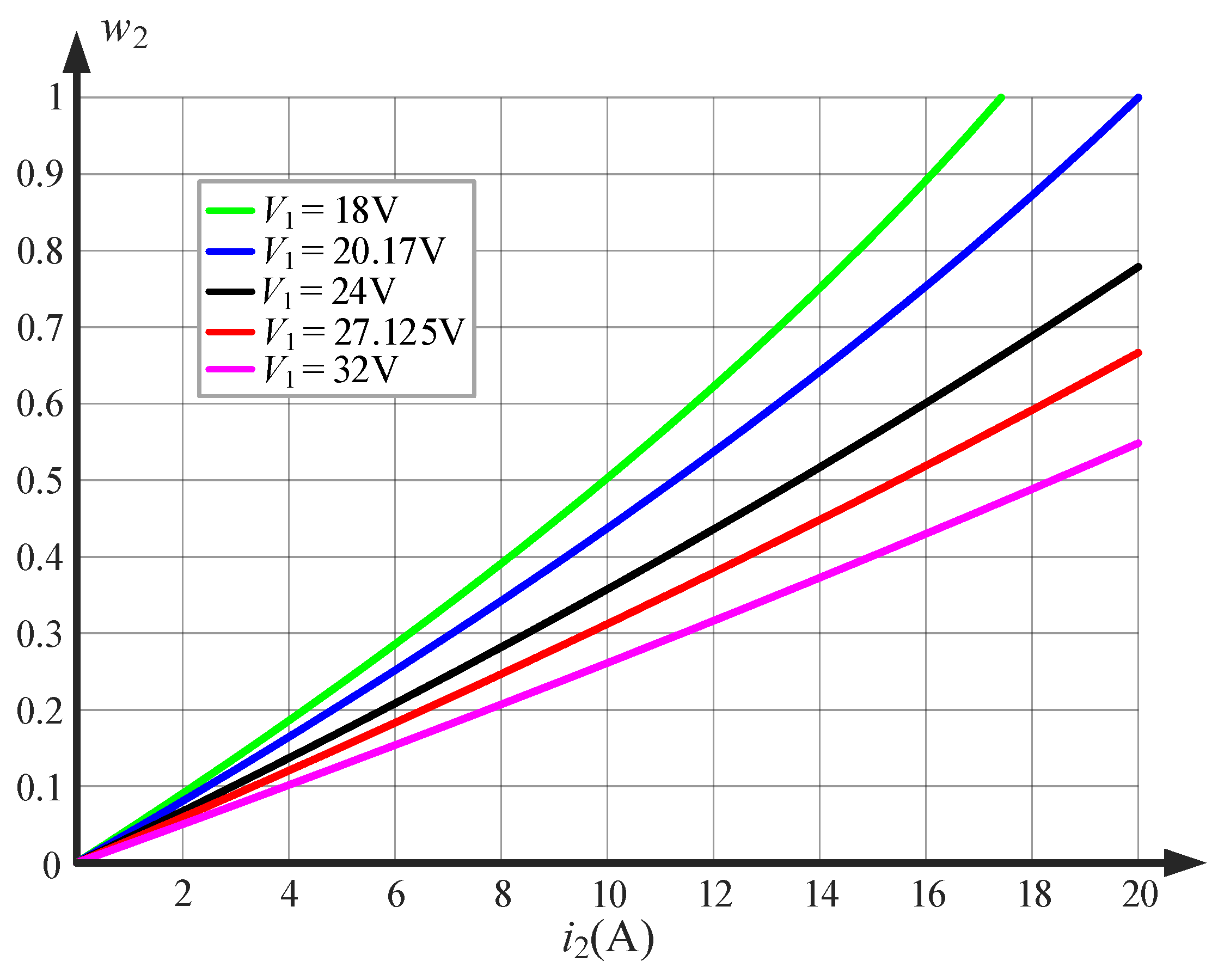
3.3. Impact of the Output Current and Input Voltage on the Choice of the Reference Inductor Current
3.4. Reference Value for the Inductor Current
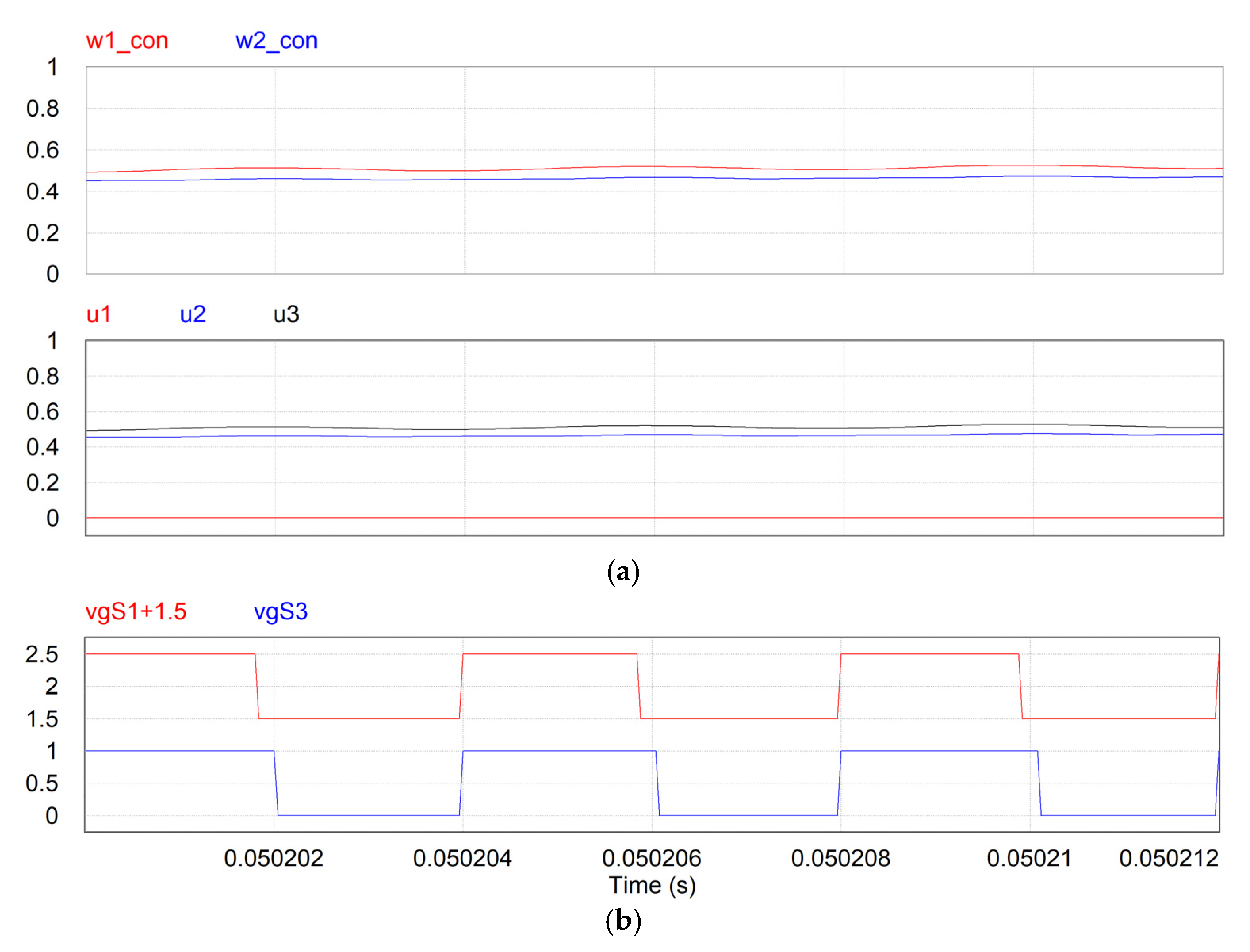
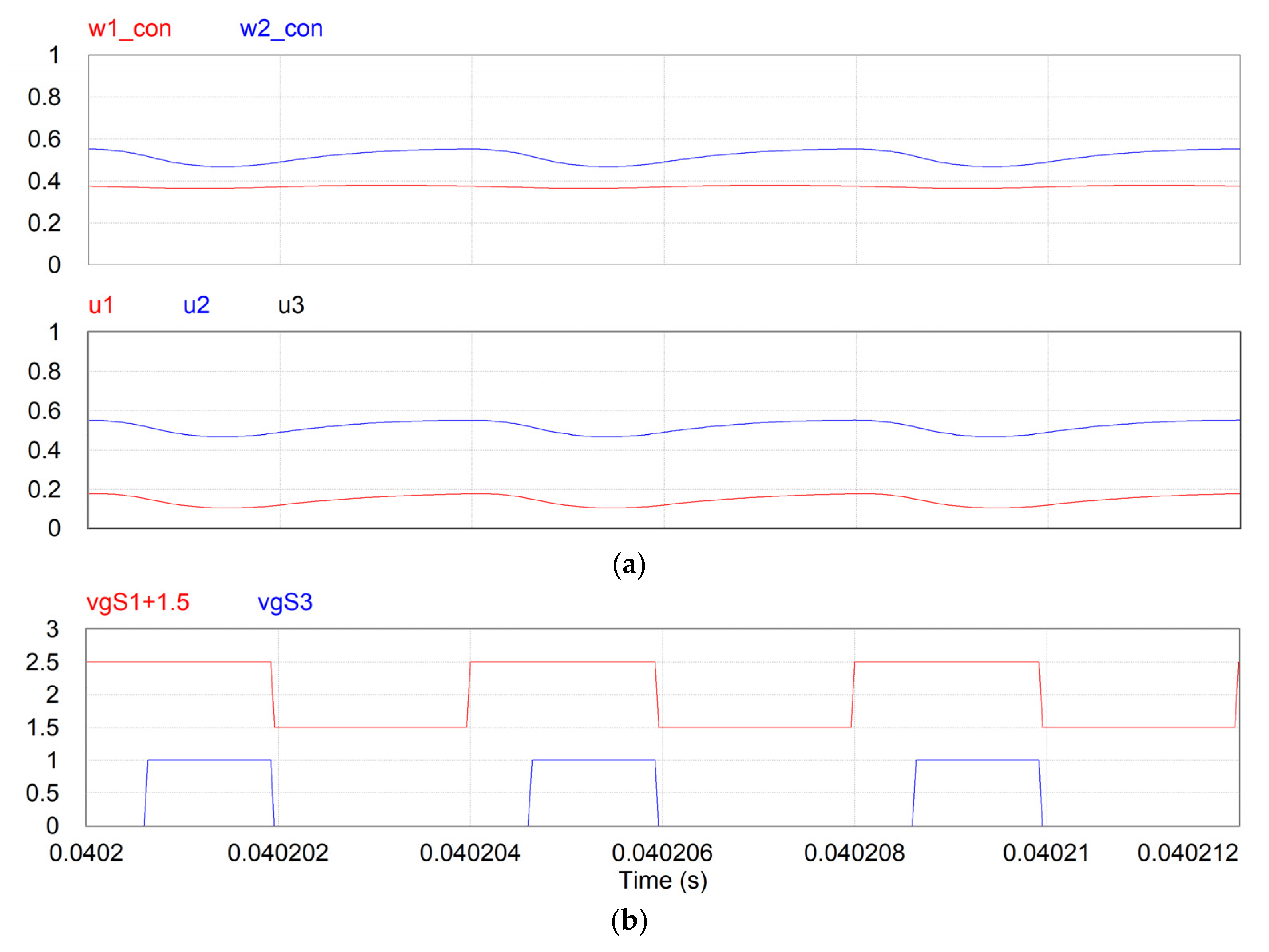
4. Obtaining u1, u2, and u3 from w1 and w2
5. Design Example
Controller Design
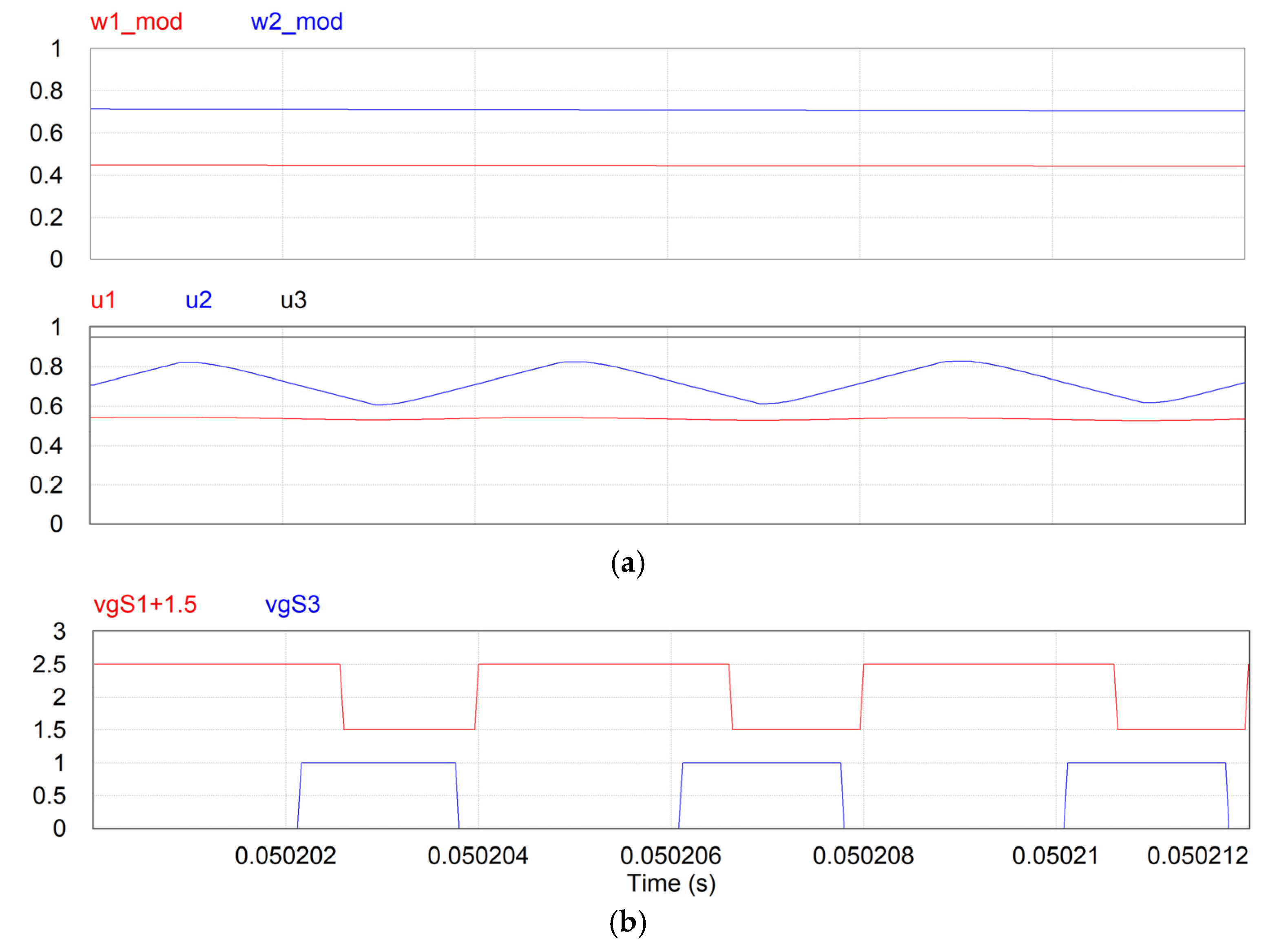
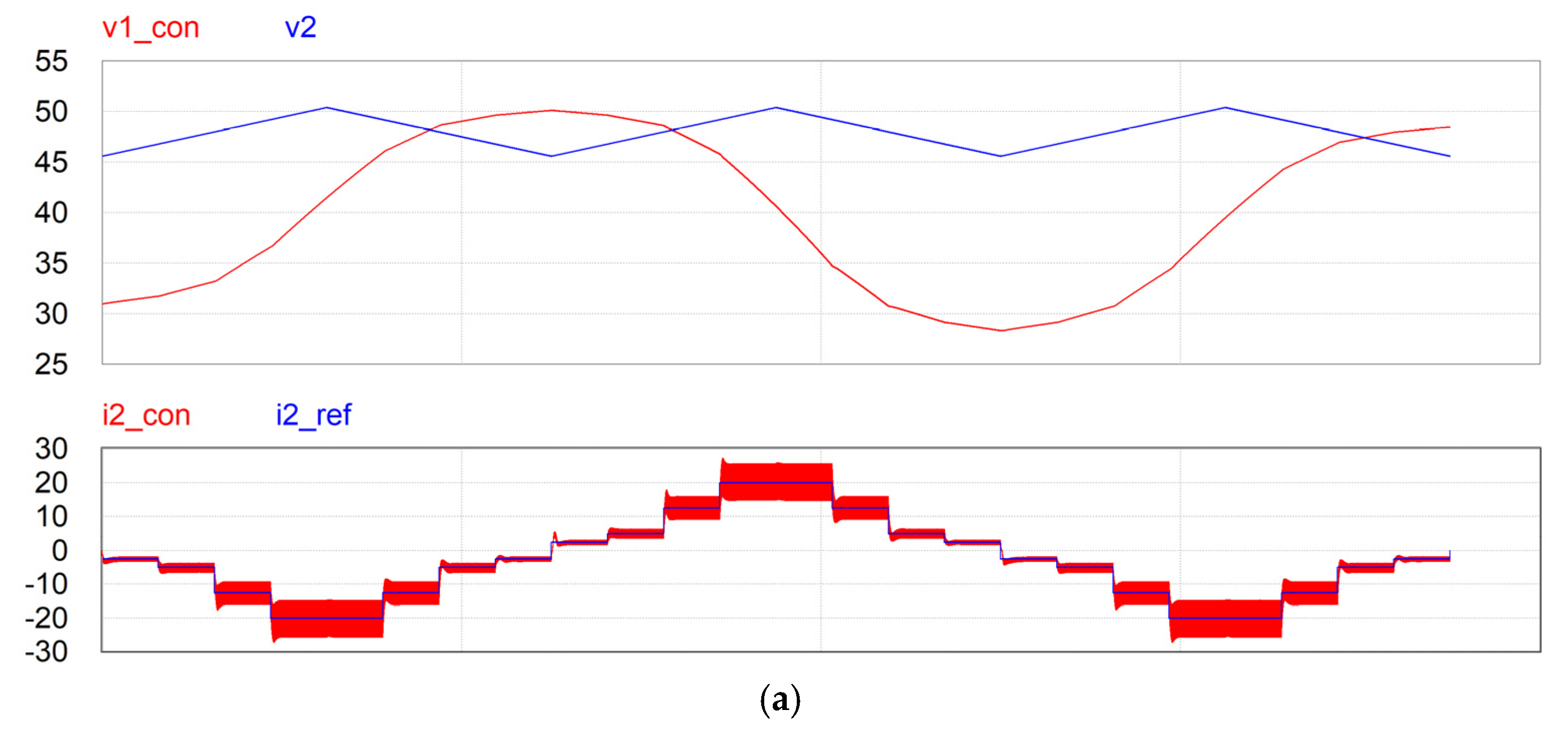
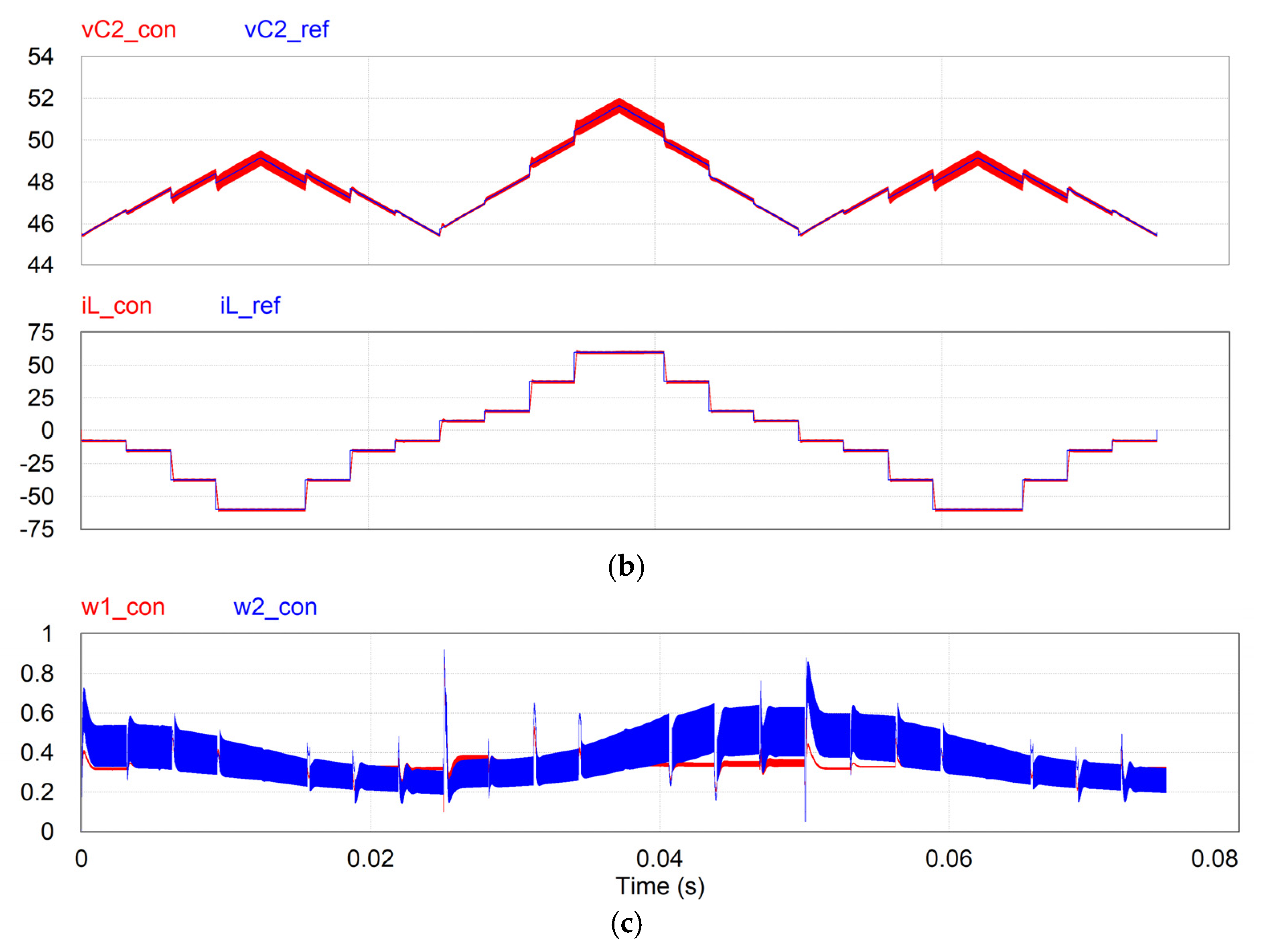
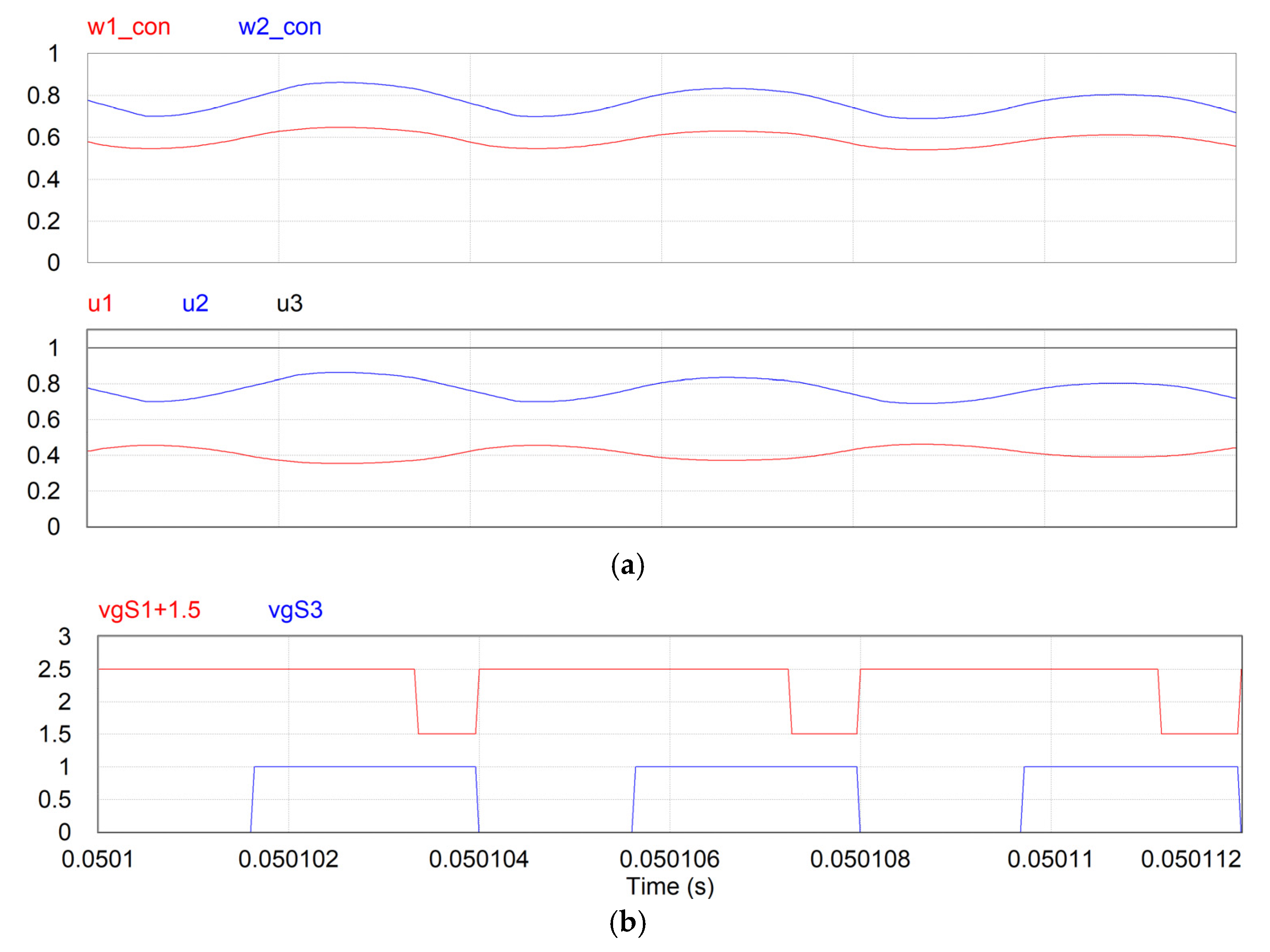
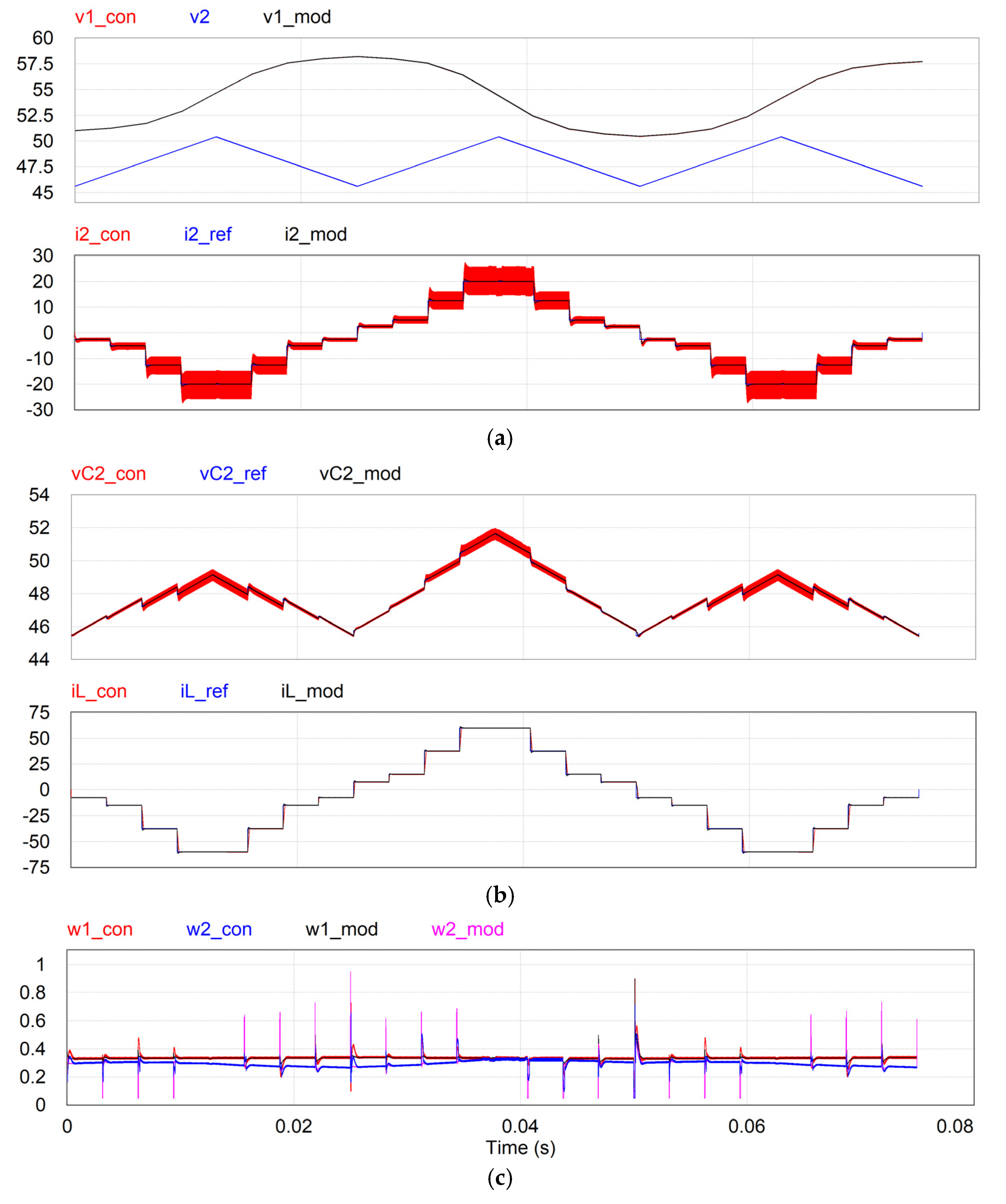
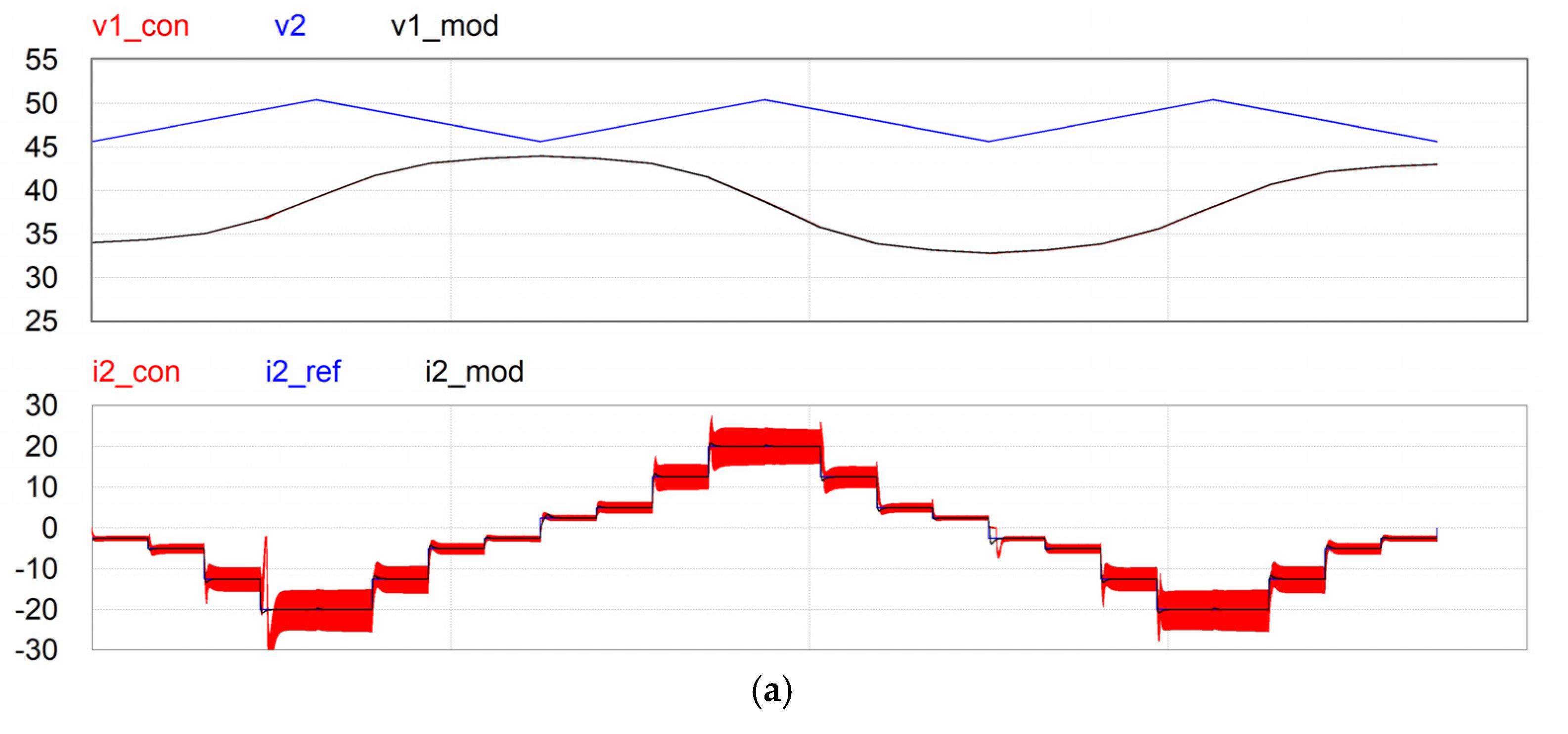
6. Performance Verification and Discussion
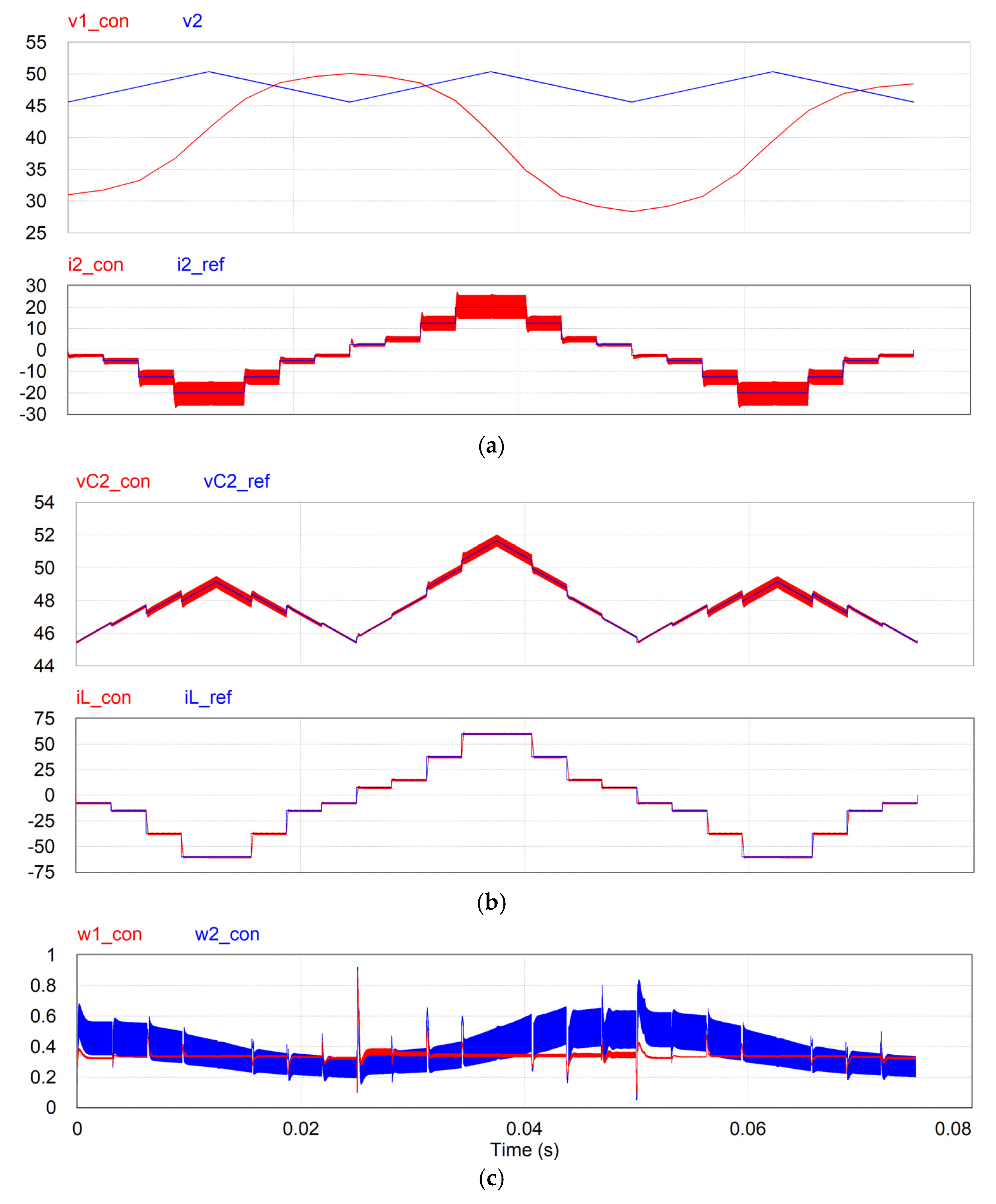
6.1. Control Scheme with PI Controllers and Feedback Linearization
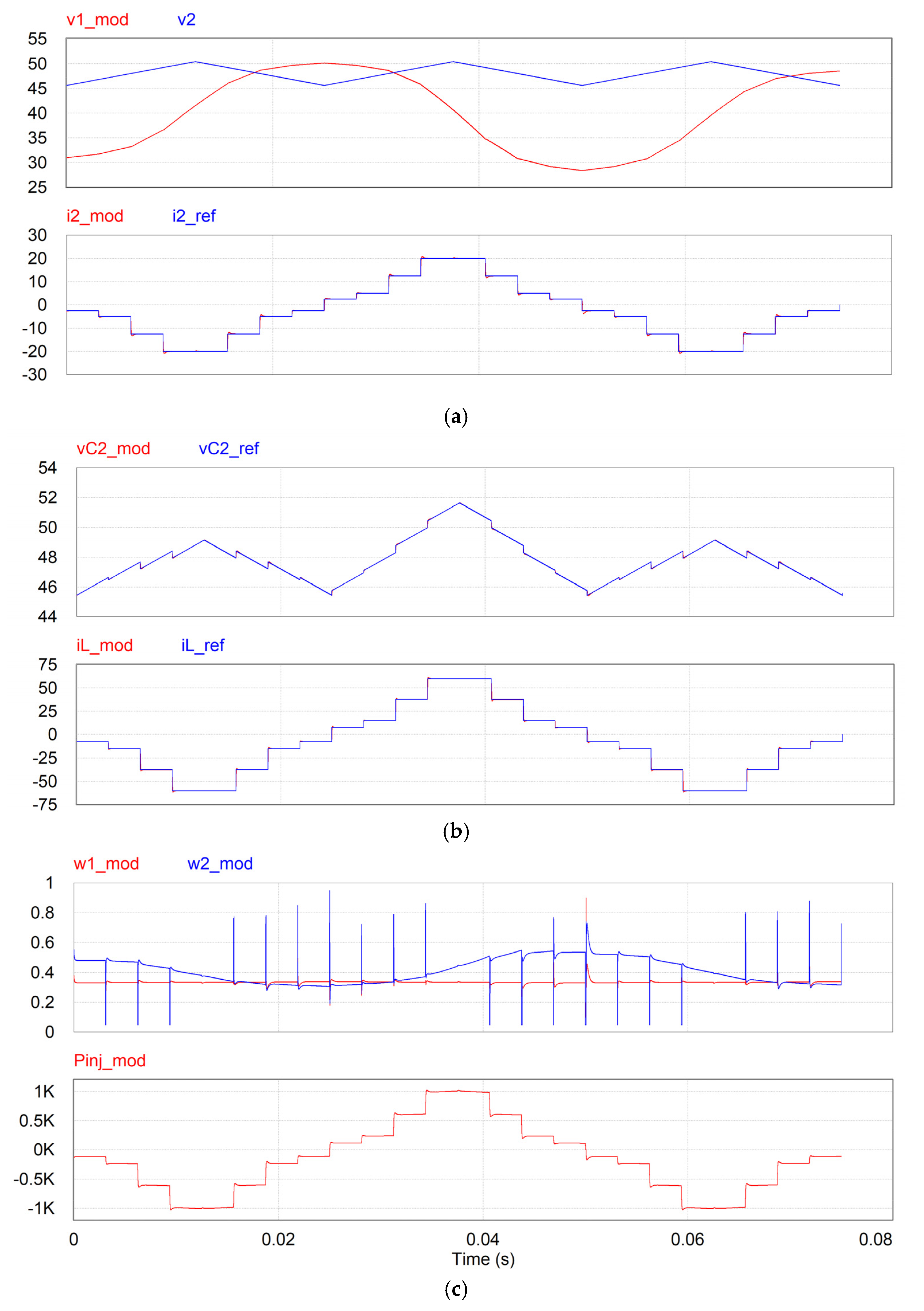
6.2. Simulation Results with the Switched Converter
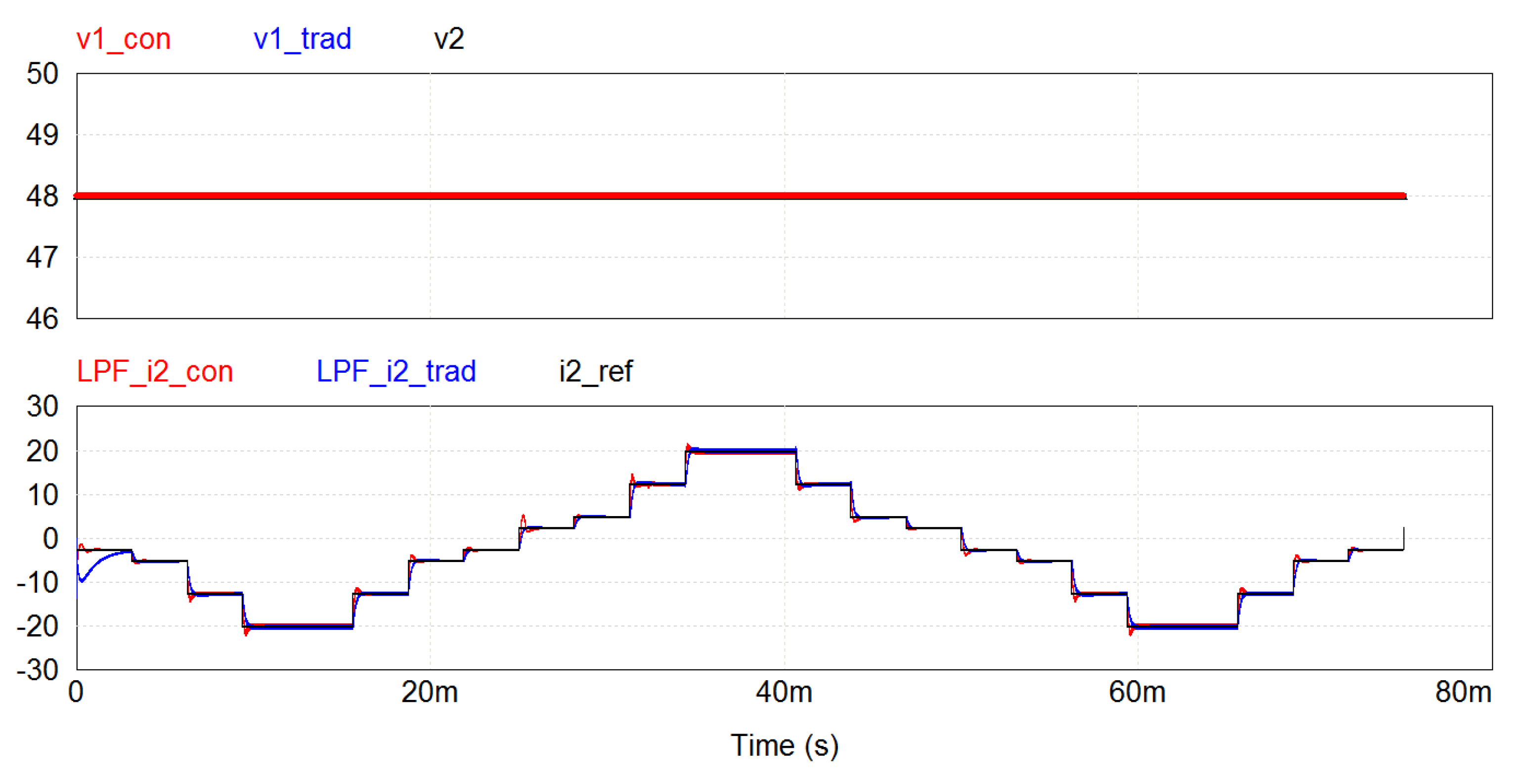
6.3. Comparison to a Conventional Technique
6.4. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Ferahtia, S.; Djeroui, A.; Mesbahi, T.; Houari, A.; Zeghlache, S.; Rezk, H.; Paul, T. Optimal Adaptive Gain LQR-Based Energy Management Strategy for Battery–Supercapacitor Hybrid Power System. Energies 2021, 14, 1660. [Google Scholar] [CrossRef]
- Viswanathan, K.; Oruganti, R.; Srinivasan, D. A novel tri-state boost converter with fast dynamics. IEEE Trans. Power Electron. 2002, 17, 677–683. [Google Scholar] [CrossRef]
- Georgious, R.; Garcia, J.; Sumner, M.; Saeed, S.; Garcia, P. Fault Ride-Through Power Electronic Topologies for Hybrid Energy Storage Systems. Energies 2020, 13, 257. [Google Scholar] [CrossRef] [Green Version]
- Saeed, S.; Lopes, L.A. Fault Protection Scheme for DC Nanogrids Based on the Coordination of Fault-Insensitive Power Electronic Interfaces and Contactors. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 5789–5794. [Google Scholar]
- Waffler, S.; Kolar, J.W. An Enhanced Control Algorithm for Improving the Light-Load Efficiency of Noninverting Synchronous Buck-Boost Converters. IEEE Trans. Power Electron. 2016, 31, 3395–3399. [Google Scholar]
- Kim, D.-H.; Lee, B.-K. A Novel Low-Loss Modulation Strategy for High-Power Bidirectional Buck + Boost Converters. IEEE Trans. Power Electron. 2009, 24, 1589–1599. [Google Scholar]
- Tsai, Y.-Y.; Tsai, Y.-S.; Tsai, C.-W.; Tsai, C.-H. Digital Noninverting Buck-Boost Converter with Enhanced Duty-Cycle-Overlap Control. IEEE Trans. Circuits Syst.-II Express Briefs 2017, 64, 41–45. [Google Scholar] [CrossRef]
- Jones, D.C.; Erickson, R.W. Buck-Boost Converter Efficiency Maximization via a Nonlinear Digital Control Mapping for Adaptive Effective Switching Frequency. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 153–165. [Google Scholar] [CrossRef]
- Choubey, A.; Lopes, L.A.C. A Tri-State 4-Switch Bi-Directional Converter for Interfacing Supercapacitors to DC Micro-Grids. In Proceedings of the PEDG 2017—8th International Symposium on Power Electronics for Distributed Generation Systems, Florianopolis, Brazil, 17–20 April 2017; pp. 1–6. [Google Scholar]
- He, M.; Zhang, F.; Xu, J.; Yang, P.; Yan, T. High Efficiency Two-Switch Tri-State Buck-Boost Power Factor Correction Converter with Fast Dynamic Response and Low-Inductor Current Ripple. IET Power Electron. 2013, 6, 1544–1554. [Google Scholar] [CrossRef]
- Viswanathan, K.; Oruganti, R.; Srinivasan, D. A Dual-Mode Control of Tri-state Boost Converter for Improved Performance. IEEE Trans. Power Electron. 2005, 20, 790–797. [Google Scholar] [CrossRef]
- Aharon, I.; Kuperman, A.; Shmilovitz, D. Analysis of Dual-Carrier Modulator for Bidirectional Noninverting Buck-Boost Converter. IEEE Trans. Power Electron. 2015, 30, 840–848. [Google Scholar] [CrossRef]
- Luo, X.; Barreras, J.V.; Chambon, C.L.; Wu, B.; Batzelis, E. Hybridizing Lead–Acid Batteries with Supercapacitors: A Methodology. Energies 2021, 14, 507. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Farsizadeh, H.; Tavana, M.-R.; Khooban, M.H. A Novel Deep Learning Controller for DC–DC Buck–Boost Converters in Wireless Power Transfer Feeding CPLs. IEEE Trans. Ind. Electron. 2021, 68, 6379–6384. [Google Scholar] [CrossRef]
- Boutebba, O.; Semcheddine, S.; Krim, F.; Corti, F.; Reatti, A.; Grasso, F. A Nonlinear Back-stepping Controller of DC-DC Non Inverting Buck-Boost Converter for Maximizing Photovoltaic Power Extraction. In Proceedings of the EEEIC/I&CPS Europe 2020—IEEE International Conference on Environment and Electrical Engineering and IEEE Industrial and Commercial Power Systems Europe, Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Iovine, A.; Carrizosa, M.J.; Damm, G.; Alou, P. Nonlinear Control for DC Microgrids Enabling Efficient Renewable Power Integration and Ancillary Services for AC Grids. IEEE Trans. Power Syst. 2019, 34, 5136–5146. [Google Scholar] [CrossRef]
- Perez, F.; Iovine, A.; Damm, G.; Galai-Dol, L.; Ribeiro, P.F. Stability Analysis of a DC MicroGrid for a Smart Railway Station Integrating Renewable Sources. IEEE Trans. Control. Syst. Technol. 2020, 28, 1802–1816. [Google Scholar] [CrossRef]
- Li, X.; Chen, X. A Multi-Index Feedback Linearization Control for a Buck-Boost Converter. Energies 2021, 14, 1496. [Google Scholar] [CrossRef]
- Callegaro, L.; Ciobotaru, M.; Pagano, D.J.; Fletcher, J.E. Feedback Linearization Control in Photovoltaic Module Integrated Converters. IEEE Trans. Power Electron. 2019, 34, 6876–6889. [Google Scholar] [CrossRef]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics: Converters, Applications and Design, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Mohan, N. Power Electronics: A First Course, 1st ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]

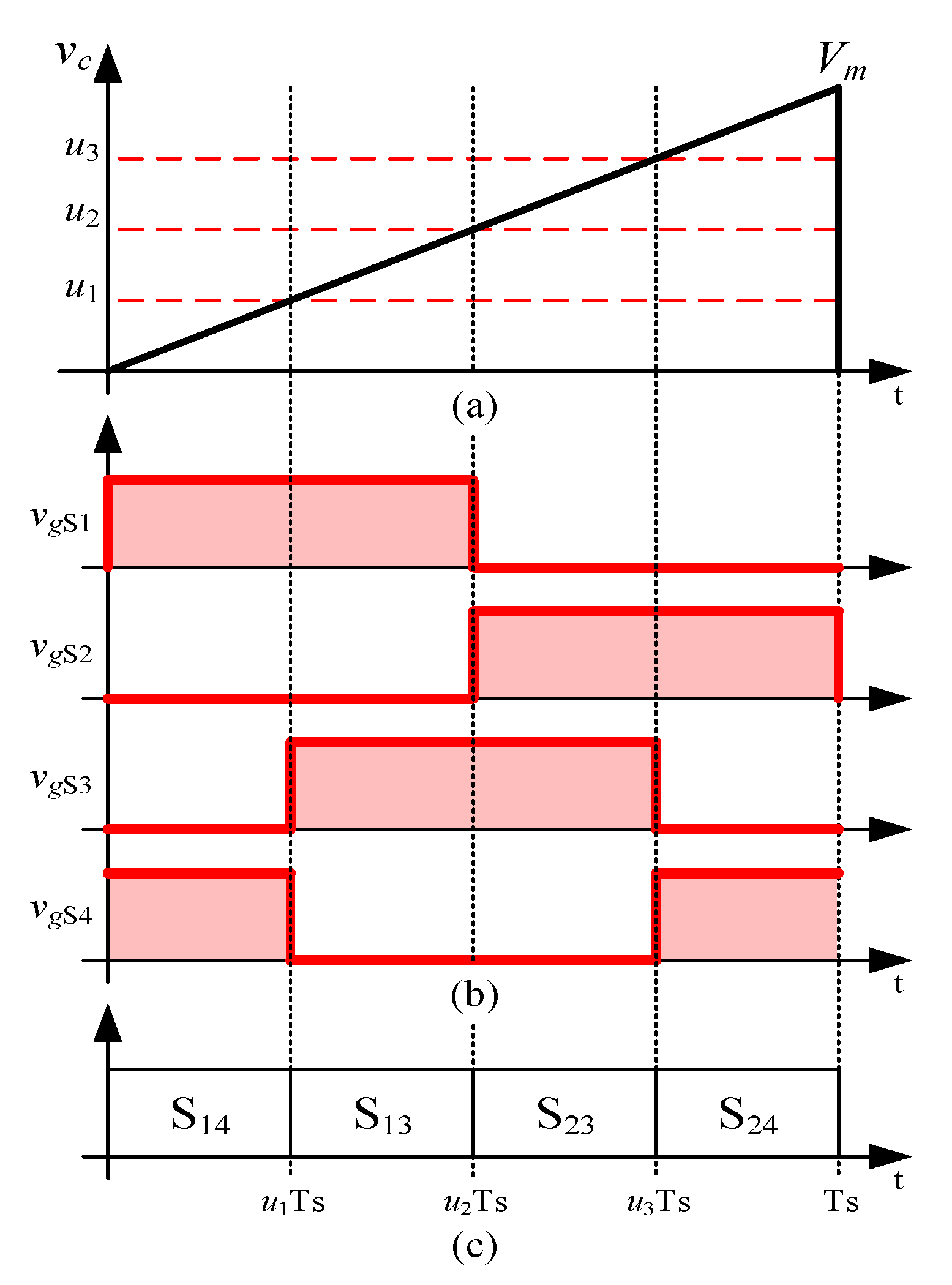
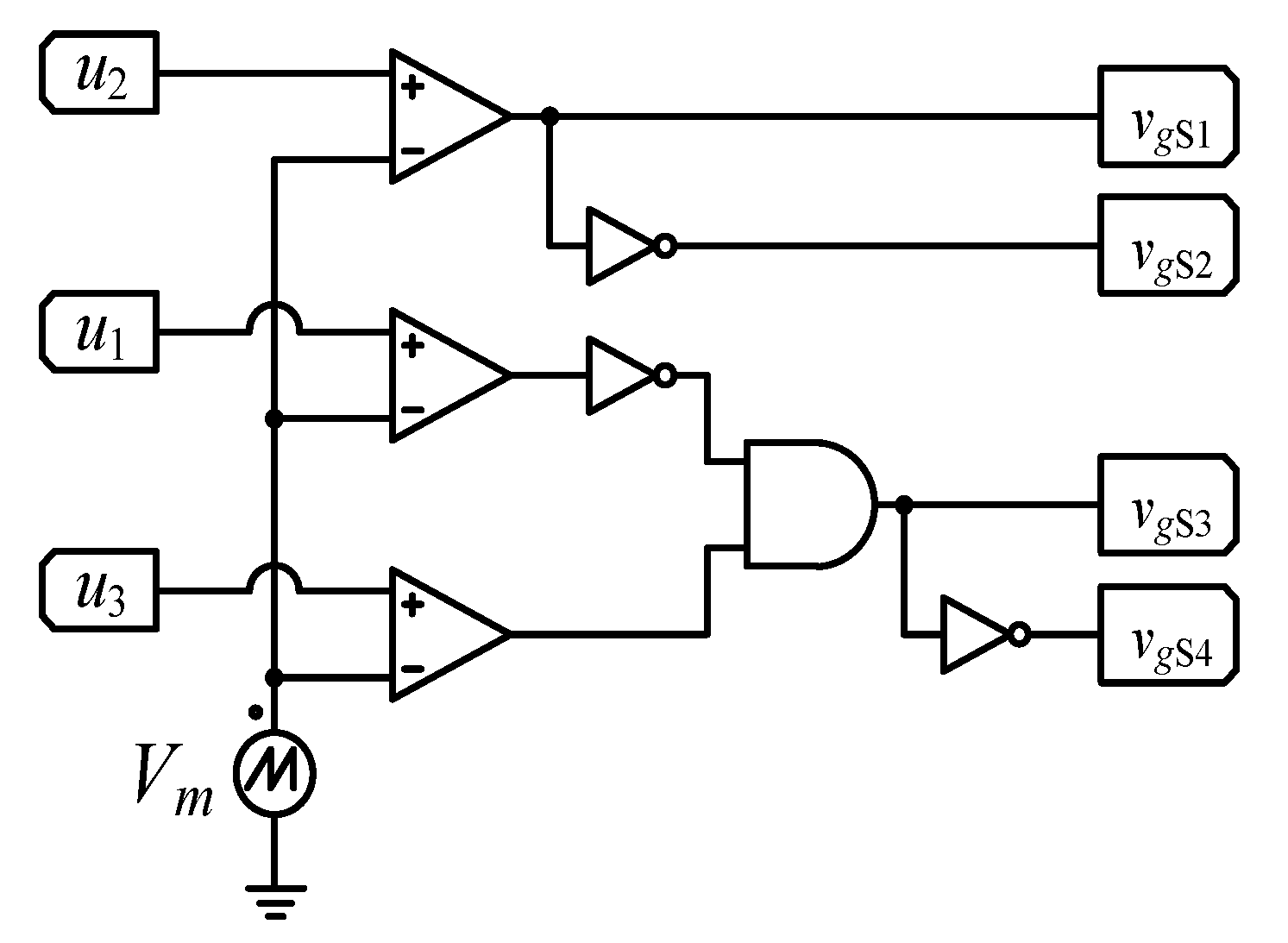
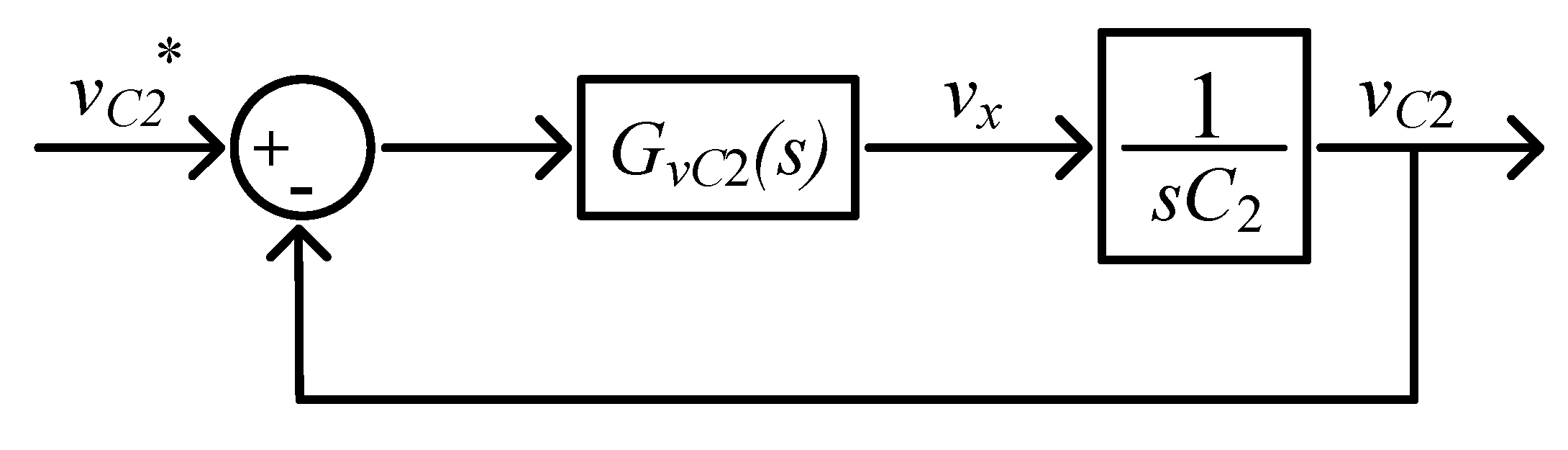


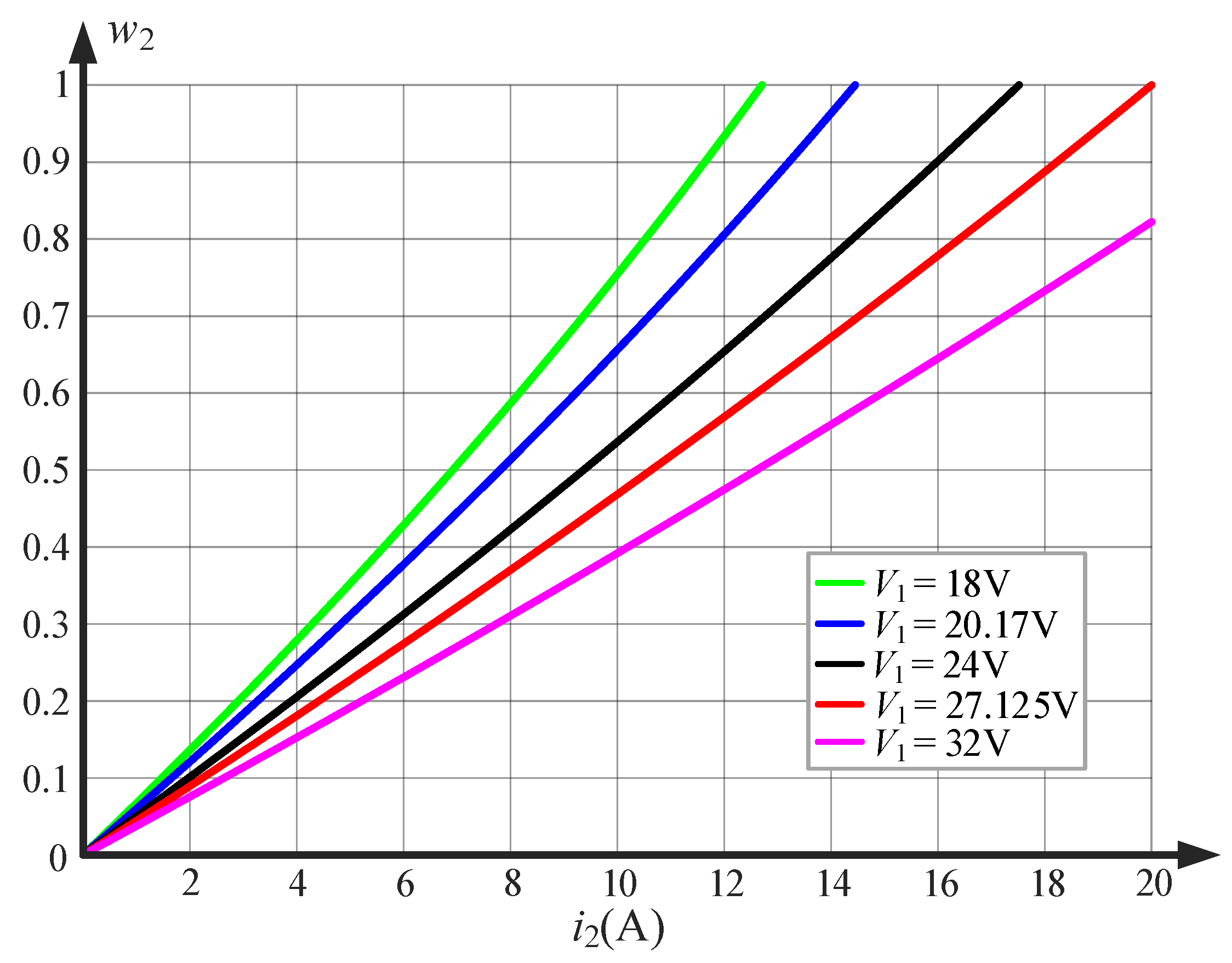
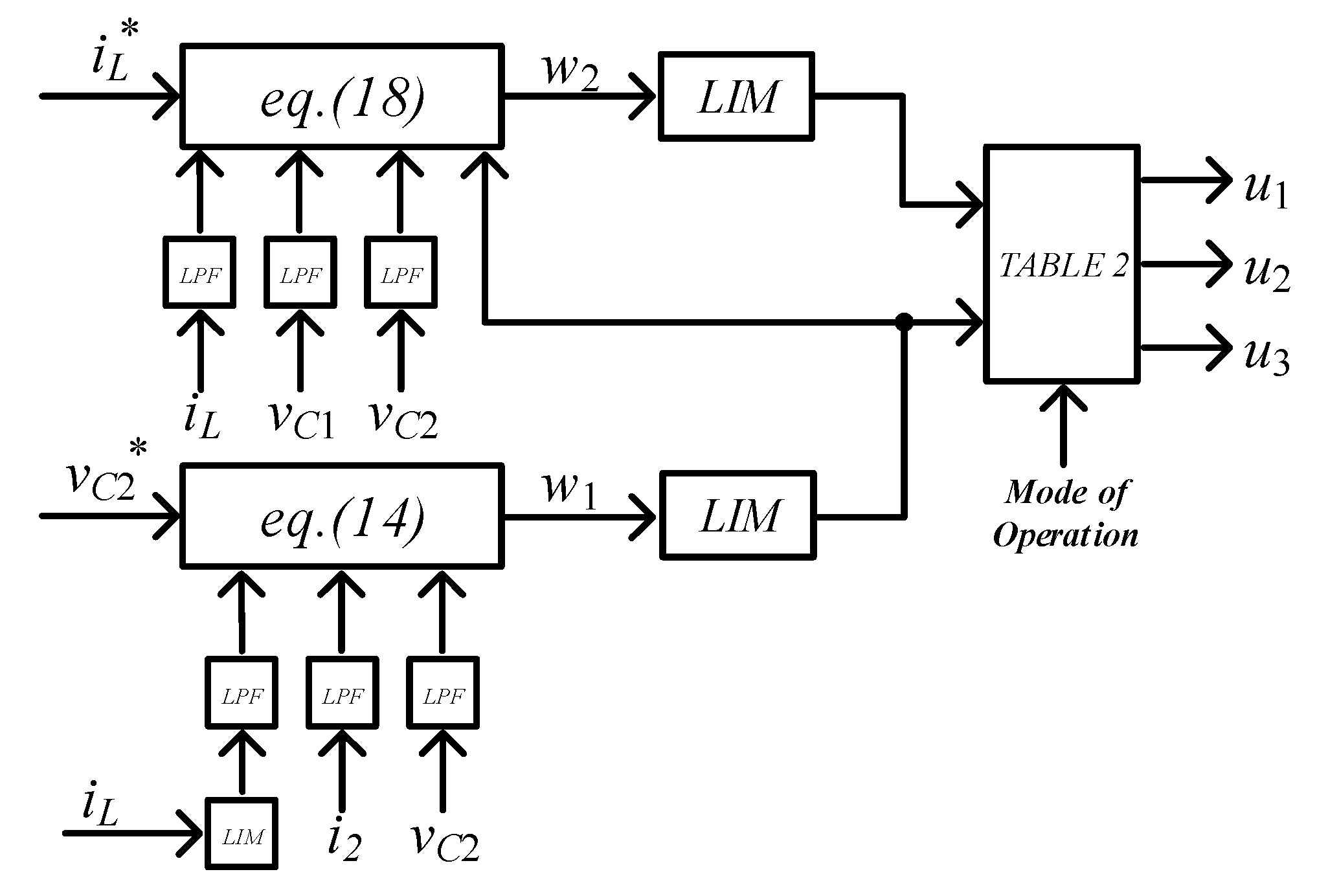


| u1 | u2 | u3 | States | Mode of Operation |
|---|---|---|---|---|
| 0 | 0 | u3 | S23–S24 | Not useful—Disregard |
| 0 | u2,3 | u2,3 | S13–S24 | Not useful—Disregard |
| 0 | u2 | 1 | S13–S23 | 1—Dual-State Buck |
| u1,2 | u1,2 | 1 | S14–S23 | 2—Dual-State Buck–Boost |
| u1 | 1 | 1 | S14–S13 | 3—Dual-State Boost |
| 0 | u2 | u3 | S13–S23–S24 | 4—Tri-state Buck with free-wheeling (fw) |
| u1 | u2 | 1 | S14–S13–S23 | 5—Tri-state Buck–Boost with no fw |
| u1 | u2,3 | u2,3 | S14–S13–S24 | 6—Tri-state Boost with fw (u2,3 ≥ u1) |
| u1,2 | u1,2 | u3 | S14–S23–S24 | 7—Tri-state Buck–Boost with fw (u3 ≥ u1,2) |
| u1 | u2 | u3 | S14–S13–S23–S24 | 8—Quad-state |
| u1 | u2 | u3 | Mode of Operation |
|---|---|---|---|
| 0 | w2 | w1 | 4—Tri-state Buck with free-wheeling (fw) |
| 1-w1 | w2 | 1 | 5—Tri-state Buck–Boost with no fw |
| w2-w1 | w2 | w2 | 6—Tri-state Boost with fw |
| w2 | w2 | w2 + w1 | 7—Tri-state Buck–Boost with fw |
| c-w1 | w2 | c | 8—Quad-state |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Broday, G.R.; Damm, G.; Pasillas-Lépine, W.; Lopes, L.A.C. A Unified Controller for Multi-State Operation of the Bi-Directional Buck–Boost DC-DC Converter. Energies 2021, 14, 7921. https://doi.org/10.3390/en14237921
Broday GR, Damm G, Pasillas-Lépine W, Lopes LAC. A Unified Controller for Multi-State Operation of the Bi-Directional Buck–Boost DC-DC Converter. Energies. 2021; 14(23):7921. https://doi.org/10.3390/en14237921
Chicago/Turabian StyleBroday, Gabriel R., Gilney Damm, William Pasillas-Lépine, and Luiz A. C. Lopes. 2021. "A Unified Controller for Multi-State Operation of the Bi-Directional Buck–Boost DC-DC Converter" Energies 14, no. 23: 7921. https://doi.org/10.3390/en14237921






