Reservoir Simulation of CO2 Storage Using Compositional Flow Model for Geological Formations in Frio Field and Precaspian Basin
Abstract
:1. Introduction
2. Model Description
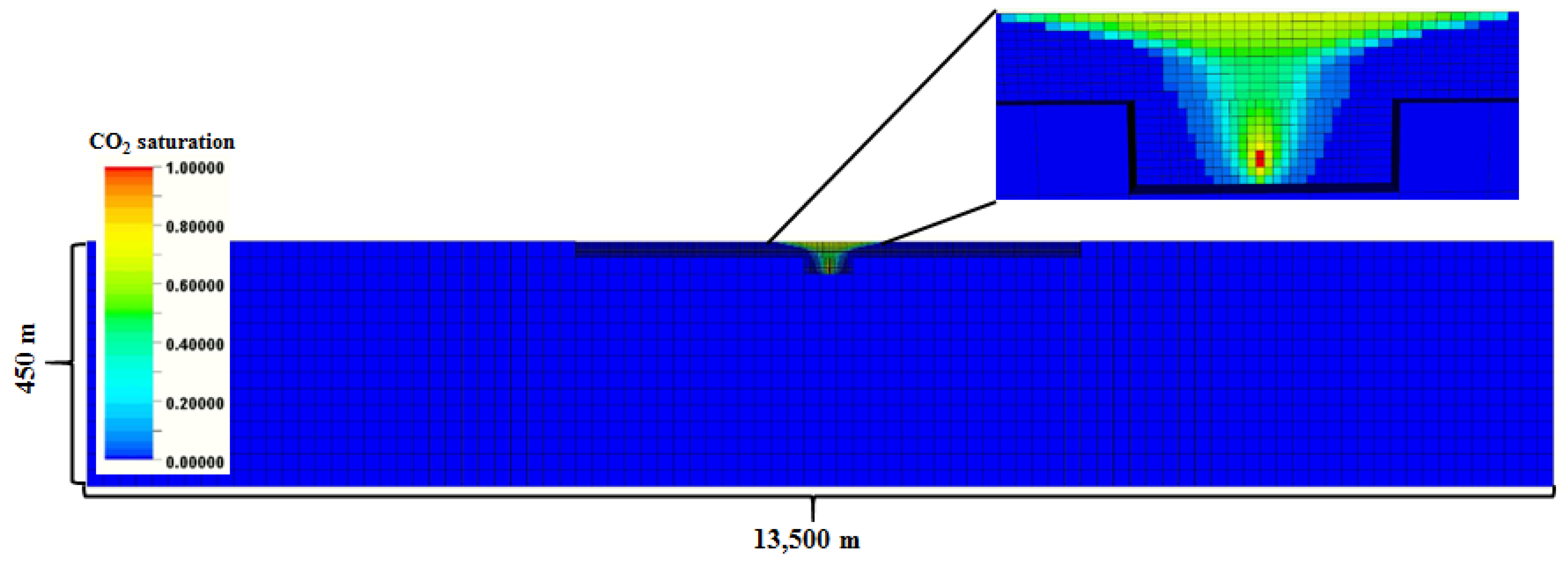
2.1. Overview of the Frio CO Model
2.2. Compositional Reservoir Simulation Model Set-Up
3. Numerical Results
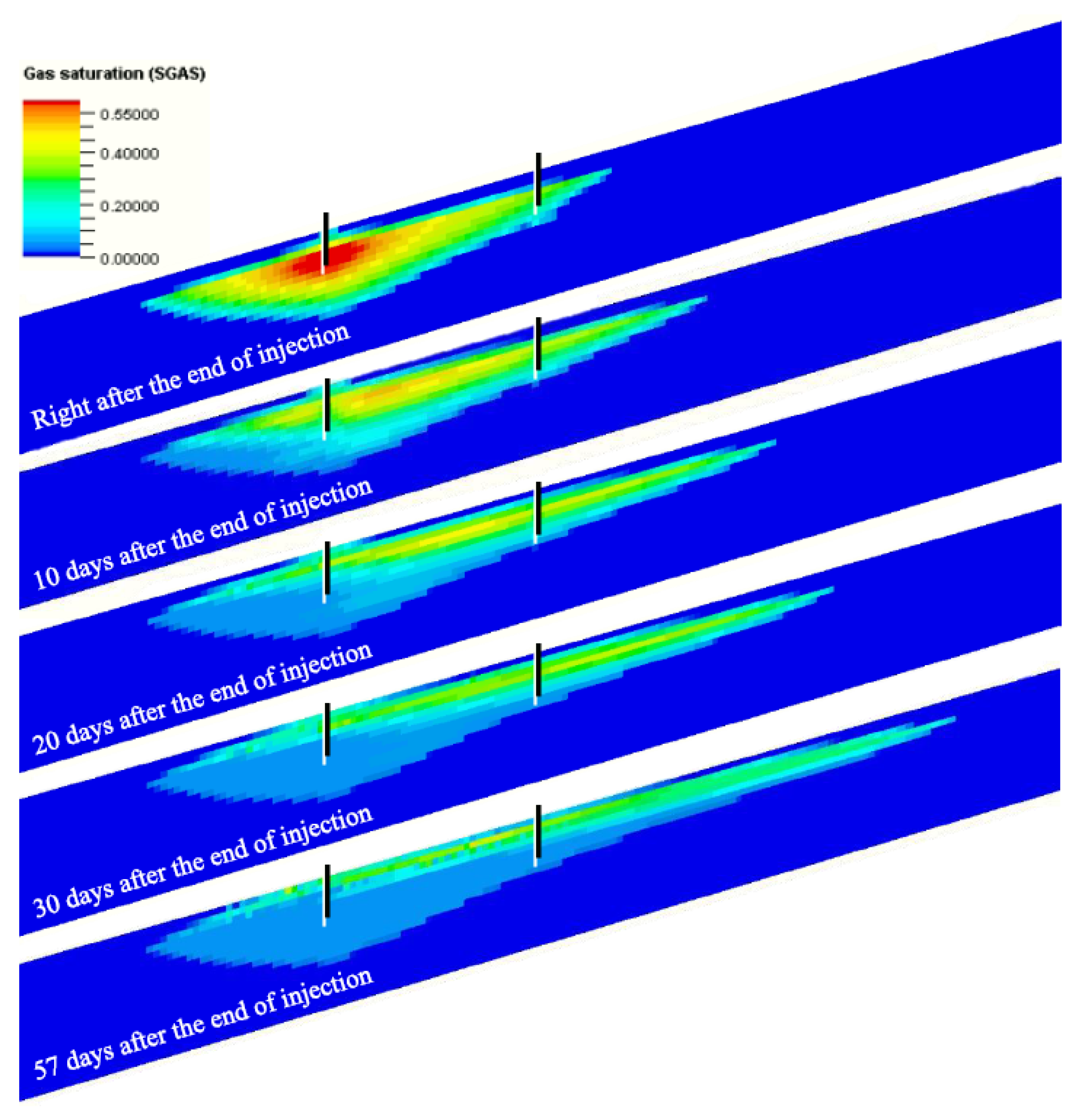
3.1. History Matching of the Well Pressure for Frio Project
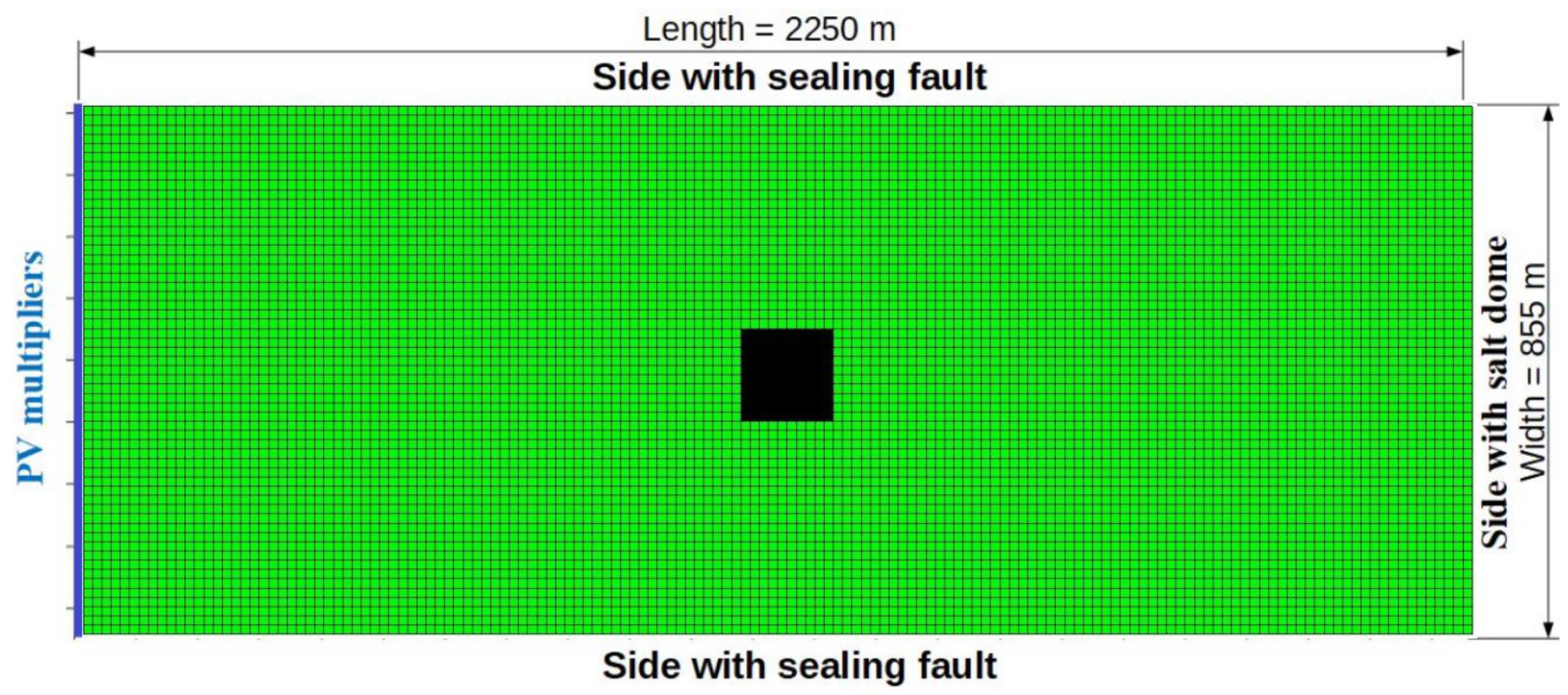
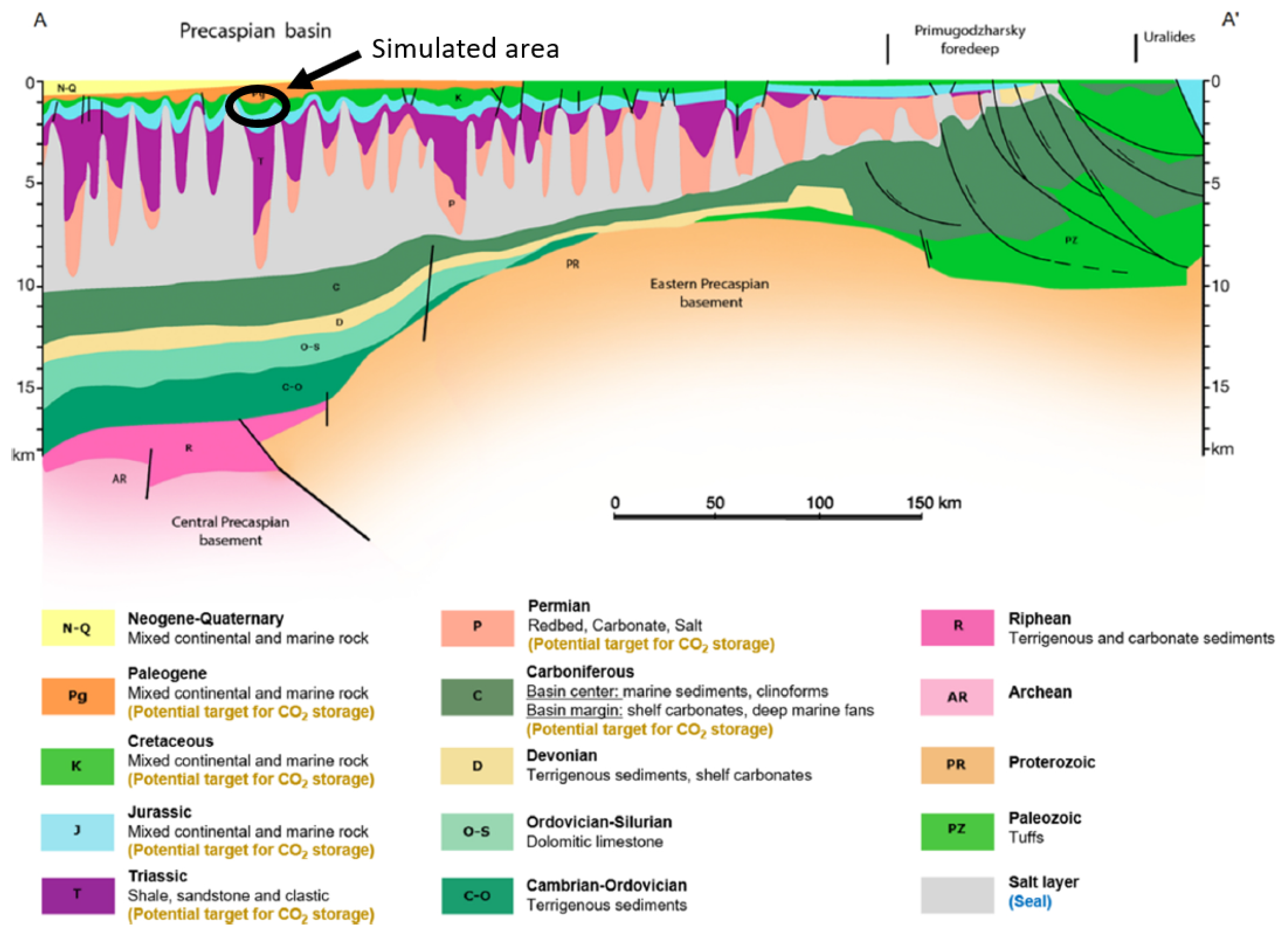
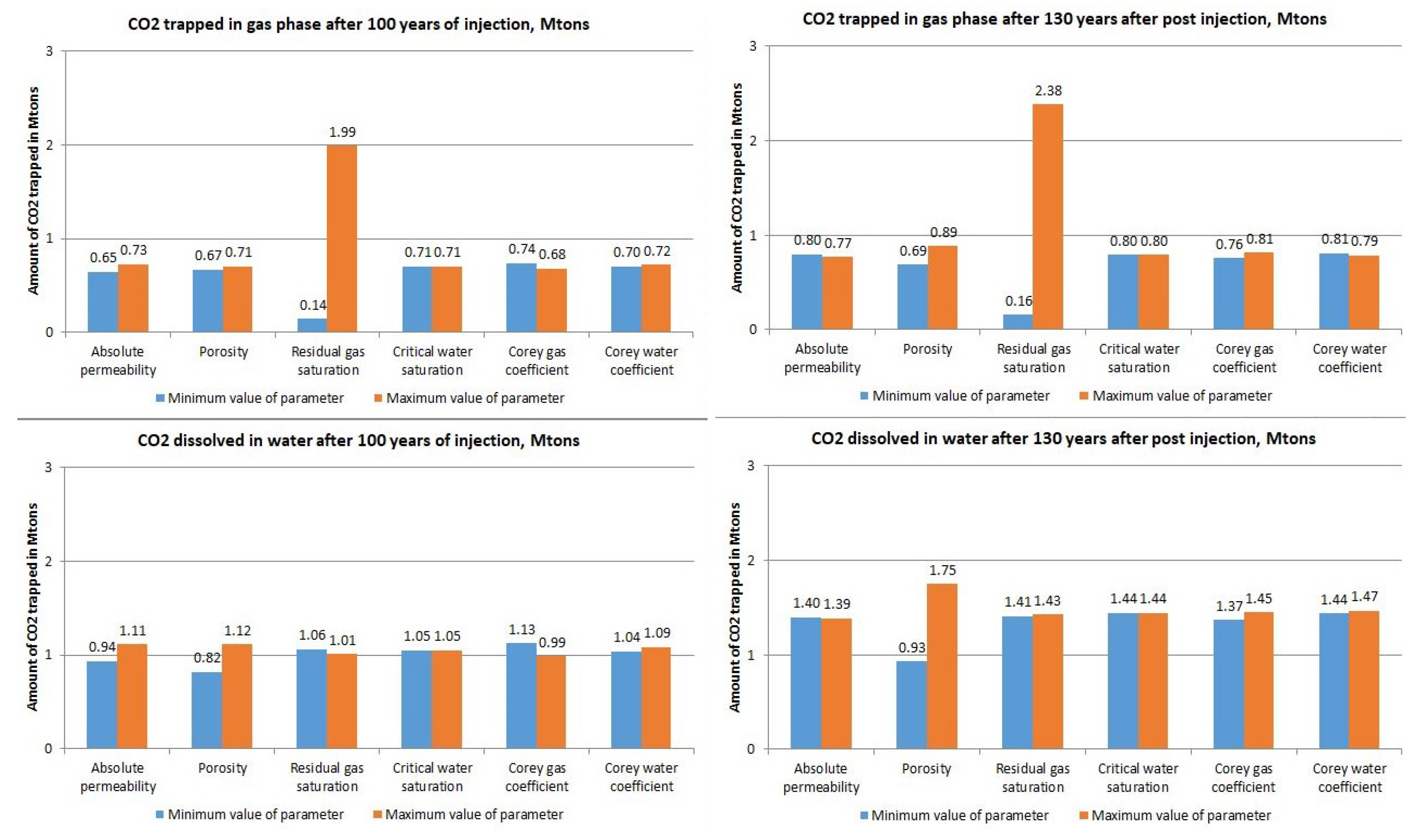
3.2. Application of the CO Storage Model Using Data from Kazakhstan
- Sensitivity analysis to determine how different parameters affect the trapped amount of CO;
- Monte Carlo Latin Hypercube sampling method was used as experimental design in order to cover the entire range of uncertainty for six parameters;
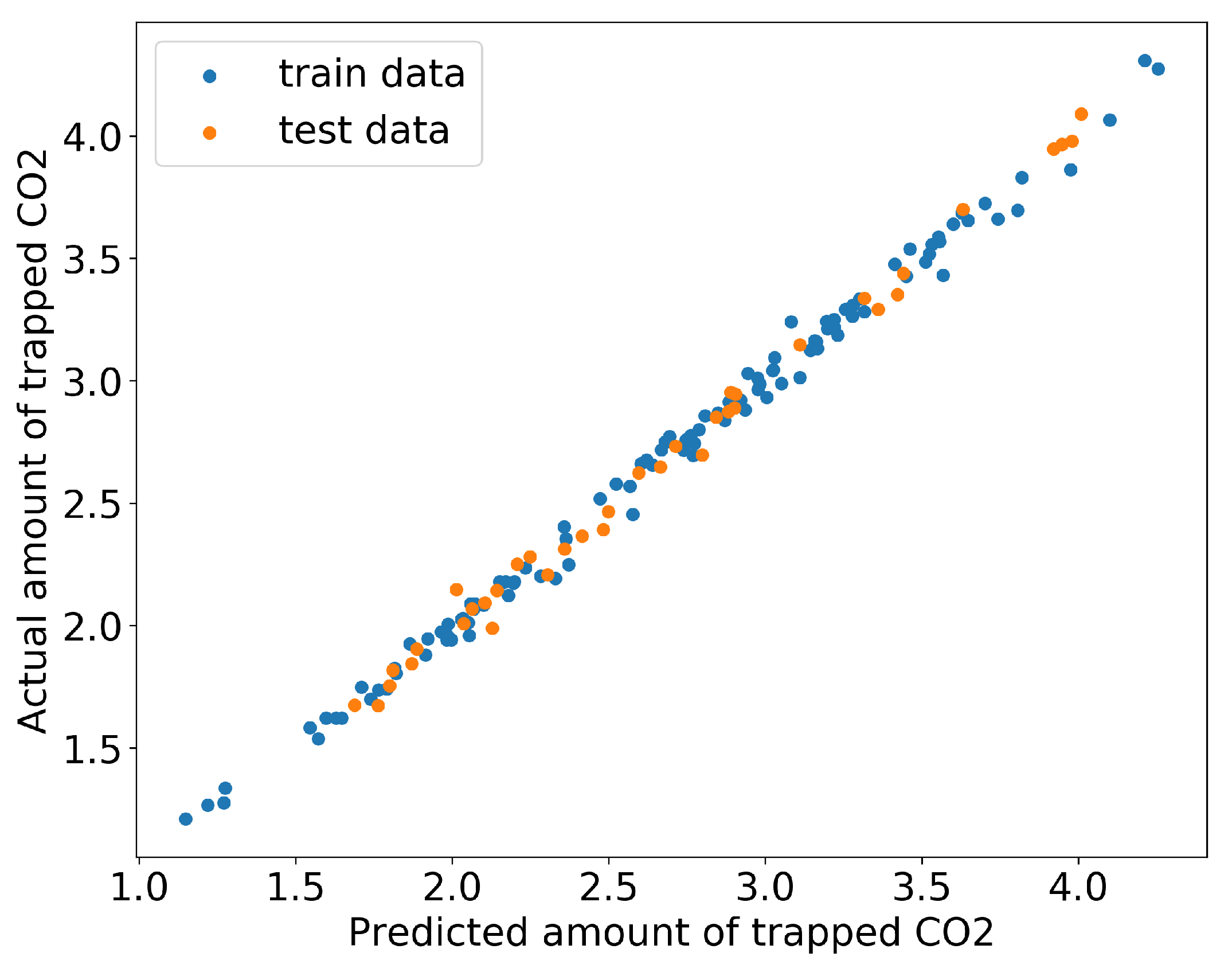
- The supervised learning algorithm was used to train the model using 75% of data taken from Monte Carlo simulation results;
- The trained model was used to explore the uncertainty range in more detail by generating an additional 10,000 cases;
- The probability density function was built based on results of the Monte Carlo simulation and regression model, which gave us P10, P50 and P90 cases.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ringrose, P.S.; Meckel, T.A. Maturing global CO2 storage resources on offshore continental margins to achieve 2DS emissions reductions. Sci. Rep. 2019, 9, 1–10. [Google Scholar]
- Aminu, M.D.; Nabavi, S.A.; Rochelle, C.A.; Manovic, V. A review of developments in carbon dioxide storage. Appl. Energy 2017, 208, 1389–1419. [Google Scholar] [CrossRef] [Green Version]
- Min, B.; Sun, A.Y.; Wheeler, M.F.; Jeong, H. Utilization of Multiobjective Optimization for Pulse Testing Dataset from a CO2-EOR/Sequestration Field. J. Pet. Sci. Eng. 2018, 170, 244–266. [Google Scholar] [CrossRef]
- Ringrose, P. How to Store CO2 Underground: Insights from Early-Mover CCS Projects; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Eigestad, G.T.; Dahle, H.K.; Hellevang, B.; Riis, F.; Johansen, W.T.; Øian, E. Geological modeling and simulation of CO2 injection in the Johansen formation. Comput. Geosci. 2009, 13, 435. [Google Scholar] [CrossRef]
- Nilsen, H.M.; Lie, K.A.; Andersen, O. Analysis of CO2 trapping capacities and long-term migration for geological formations in the Norwegian North Sea using MRST-co2lab. Comput. Geosci. 2015, 79, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Delshad, M.; Kong, X.; Tavakoli, R.; Hosseini, S.A.; Wheeler, M.F. Modeling and simulation of carbon sequestration at Cranfield incorporating new physical models. Int. J. Greenh. Gas Control. 2013, 18, 463–473. [Google Scholar] [CrossRef]
- Lu, X.; Lotfollahi, M.; Ganis, B.; Min, B.; Wheeler, M.F. An integrated flow-geomechanical analysis of flue gas injection in cranfield. In Proceedings of the SPE Improved Oil Recovery Conference. Society of Petroleum Engineers, Tulsa, OK, USA, 14–18 April 2018. [Google Scholar]
- Ghomian, Y.; Pope, G.A.; Sepehrnoori, K. Reservoir simulation of CO2 sequestration pilot in Frio brine formation, USA Gulf Coast. Energy 2008, 33, 1055–1067. [Google Scholar] [CrossRef]
- Kerimray, A.; Suleimenov, B.; De Miglio, R.; Rojas-Solórzano, L.; Gallachóir, B.Ó. Long-term climate change mitigation in Kazakhstan in a post Paris agreement context. In Limiting Global Warming to Well Below 2 °C: Energy System Modelling and Policy Development; Springer: Berlin/Heidelberg, Germany, 2018; pp. 297–314. [Google Scholar]
- Heidug, W.; Lipponen, J.; McCoy, S.; Benoit, P. Storing CO2 through Enhanced Oil Recovery: Combining EOR with CO2 Storage (EOR+) for Profit; IEA: Paris, France, 2015. [Google Scholar]
- Nurseitova, D. Carbon capture and storage in geological formations: The potential for Kazakhstan 1. In Sustainable Energy in Kazakhstan; Routledge: Milton, UK, 2017; pp. 134–143. [Google Scholar]
- Abuov, Y.; Seisenbayev, N.; Lee, W. CO2 storage potential in sedimentary basins of Kazakhstan. Int. J. Greenh. Gas Control. 2020, 103, 103186. [Google Scholar] [CrossRef]
- Hovorka, S.D.; Benson, S.M.; Doughty, C.; Freifeld, B.M.; Sakurai, S.; Daley, T.M.; Kharaka, Y.K.; Holtz, M.H.; Trautz, R.C.; Nance, H.S. Measuring permanence of CO2 storage in saline formations: The Frio experiment. Environ. Geosci. 2006, 13, 105–121. [Google Scholar] [CrossRef]
- Spycher, N.; Pruess, K. CO2-H2O mixtures in the geological sequestration of CO2. II. Partitioning in chloride brines at 12–100 °C and up to 600 bar. Geochim. Cosmochim. Acta 2005, 69, 3309–3320. [Google Scholar] [CrossRef]
- Amanbek, Y.; Singh, G.; Wheeler, M.F.; van Duijn, H. Adaptive numerical homogenization for upscaling single phase flow and transport. J. Comput. Phys. 2019, 387, 117–133. [Google Scholar] [CrossRef]
- Amanbek, Y.; Singh, G.; Pencheva, G.; Wheeler, M.F. Error indicators for incompressible Darcy Flow problems using Enhanced Velocity Mixed Finite Element Method. Comput. Methods Appl. Mech. Eng. 2020, 363, 112884. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Leung, W.T.; Wheeler, M.F. Sequential local mesh refinement solver with separate temporal and spatial adaptivity for non-linear two-phase flow problems. J. Comput. Phys. 2020, 403, 109074. [Google Scholar] [CrossRef] [Green Version]
- Doughty, C.; Freifeld, B.M.; Trautz, R.C. Site characterization for CO2 geologic storage and vice versa: The Frio brine pilot, Texas, USA as a case study. Environ. Geol. 2008, 54, 1635–1656. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Skjaeveland, S.; Siqveland, L.; Kjosavik, A.; Hammervold, W.; Virnovsky, G. Capillary Pressure Correlation for Mixed-Wet Reservoirs. SPE Reserv. Eval. Eng. 2000, 3, 60–67. [Google Scholar] [CrossRef]
- Jung, H.; Singh, G.; Espinoza, D.N.; Wheeler, M.F. Quantification of a maximum injection volume of CO2 to avert geomechanical perturbations using a compositional fluid flow reservoir simulator. Adv. Water Resour. 2018, 112, 160–169. [Google Scholar] [CrossRef]
- Fanchi, J.R. 4-Porosity and Permeability. In Integrated Reservoir Asset Management; Fanchi, J.R., Ed.; Gulf Professional Publishing: Boston, MA, USA, 2010; pp. 49–69. [Google Scholar] [CrossRef]
- Hovorka, S.D.; Sakurai, S.; Kharaka, Y.K.; Nance, H.S.; Doughty, C.; Benson, S.M.; Freifeld, B.M.; Trautz, R.C.; Phelps, T.; Daley, T.M. Monitoring CO2 Storage in Brine Formations: Lessons Learned from the Frio Field Test One Year Post Injection. 2006. Available online: https://www.beg.utexas.edu/gccc/bookshelf/Final%20Papers/06-06-Final.pdf (accessed on 6 March 2021).
- Amanbek, Y.; Merembayev, T.; Srinivasan, S. Framework of Fracture Network Modeling using Conditioned Data with Sequential Gaussian Simulation. arXiv 2020, arXiv:2003.01327. [Google Scholar]
- Almani, T.; Kumar, K.; Singh, G.; Wheeler, M.F. Stability of multirate explicit coupling of geomechanics with flow in a poroelastic medium. Comput. Math. Appl. 2019, 78, 2682–2699. [Google Scholar] [CrossRef]
- Latin Hypercube Sampling. Wikipedia. 23 June 2021. Available online: https://en.wikipedia.org/wiki/Latin_hypercube_sampling (accessed on 16 August 2021).


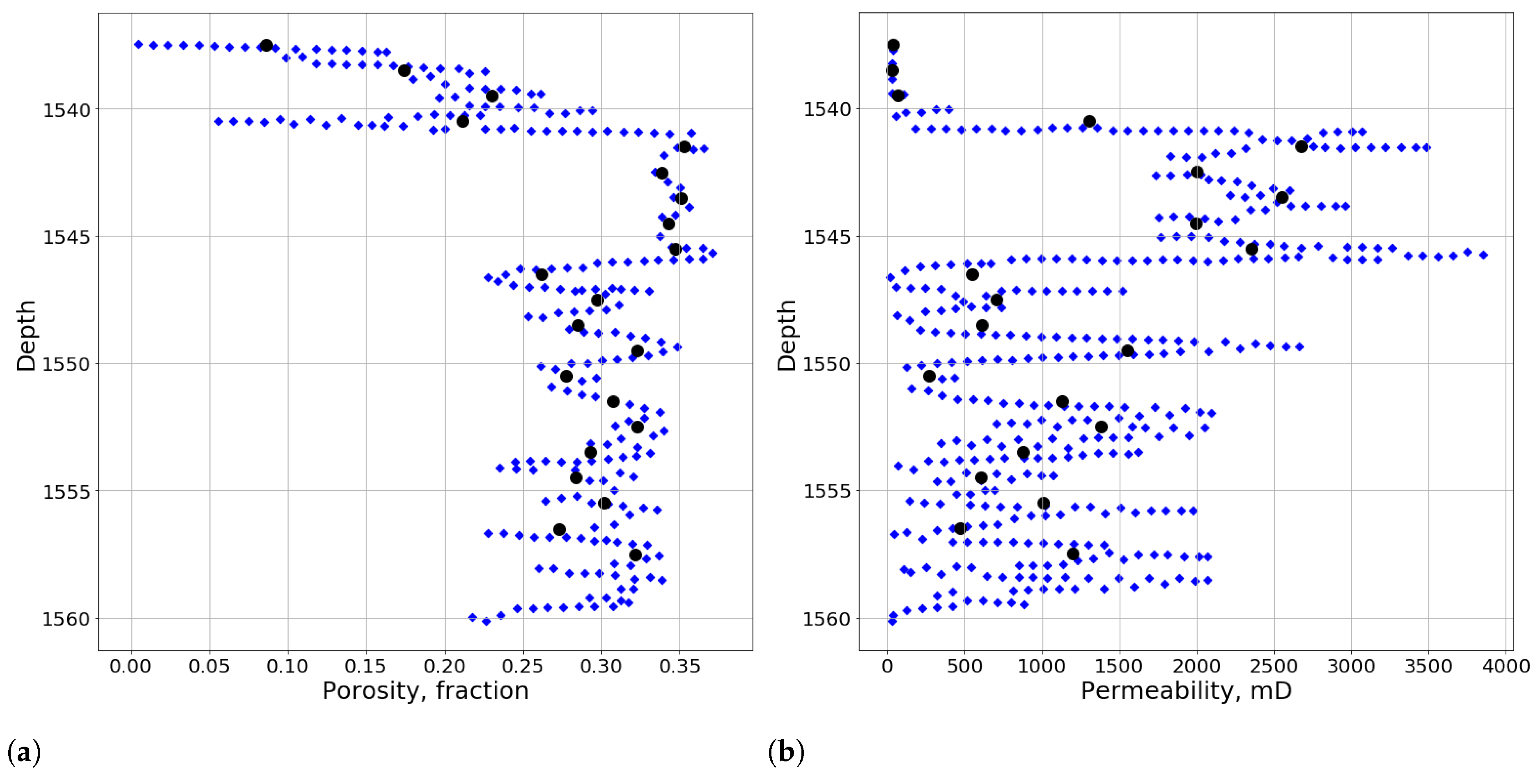
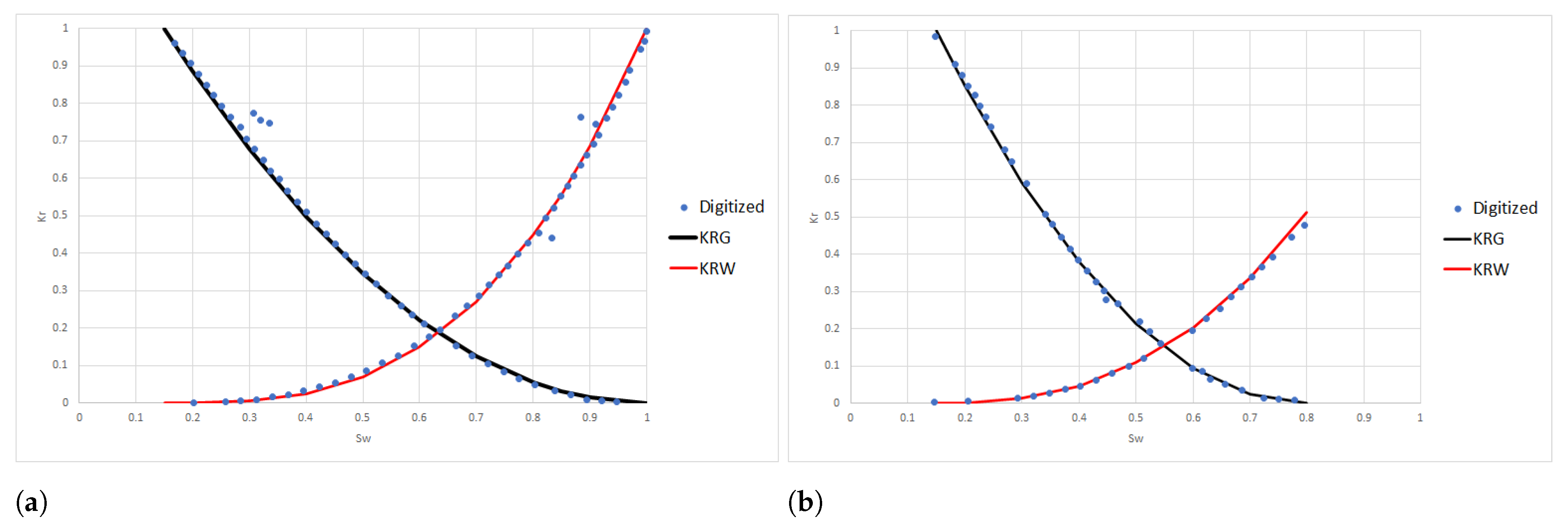
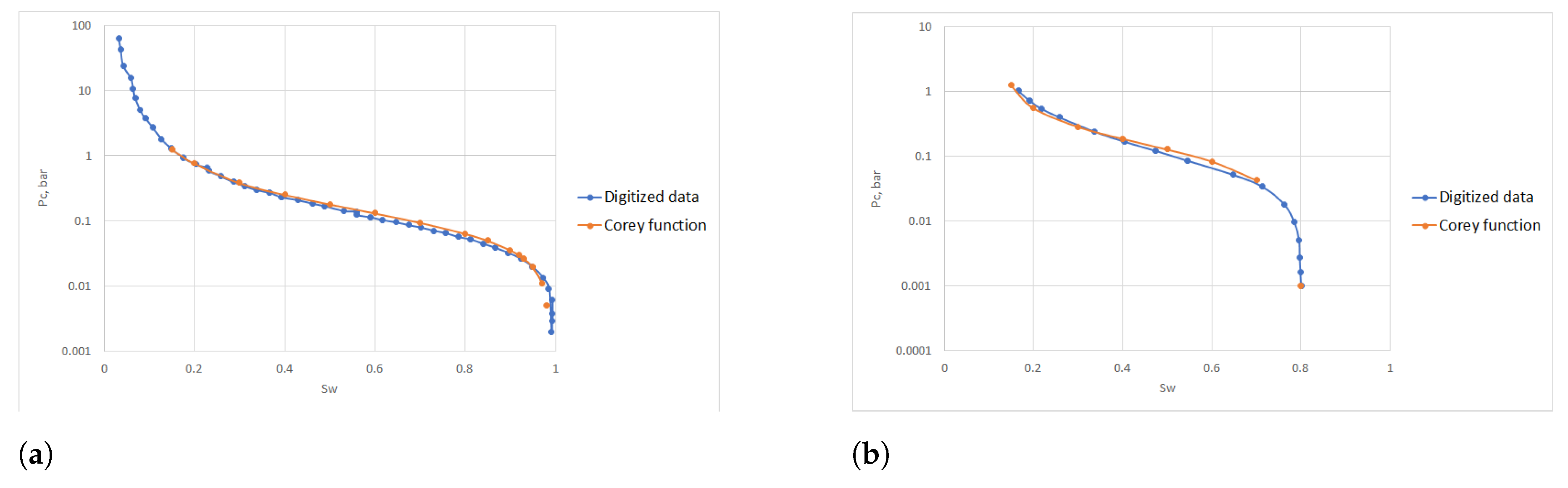
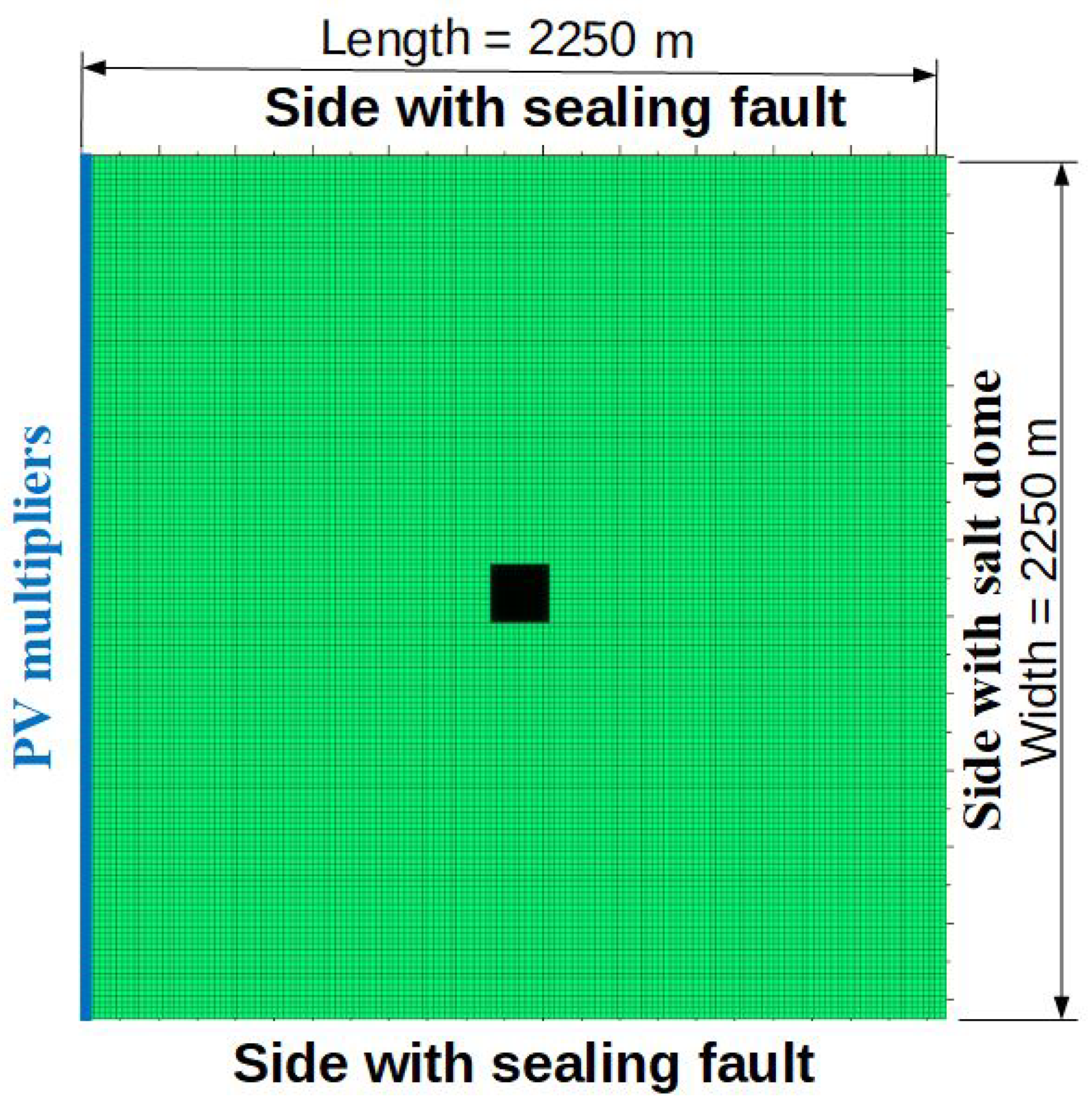





| Parameter | Value |
|---|---|
| Depth of reservoir top, m | 1073 |
| Top perforation depth, m | 1121 |
| Pore pressure at reservoir top depth, bar | 109 |
| Overburden pressure at 1073 m and 1121 m, bar | 232, 242 |
| Reservoir temperature, C | 55.7 |
| Porosity, % | 20 |
| Horizontal permeability, mD | 115 |
| Kv/Kh ratio | 0.1 |
| Number of cells in I and J directions | 90 |
| Number of layers | 15 |
| Cell dimensions in I and J directions, m | 150 |
| Layer thickness, m | 30 |
| Injection rate, tons/day | 223 |
| Injection period, years | 100 |
| Post injection period, years | 130 |
| Total amount injected, millon tons | 8.14 |
| Algorithm | R2 | MAE | MSE | MRST |
|---|---|---|---|---|
| Random forest | 0.94 | 0.15 | 0.03 | 0.17 |
| Linear regression | 0.97 | 0.09 | 0.01 | 0.12 |
| Second order polynomial regression | 0.99 | 0.04 | 0.003 | 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamashev, A.; Amanbek, Y. Reservoir Simulation of CO2 Storage Using Compositional Flow Model for Geological Formations in Frio Field and Precaspian Basin. Energies 2021, 14, 8023. https://doi.org/10.3390/en14238023
Kamashev A, Amanbek Y. Reservoir Simulation of CO2 Storage Using Compositional Flow Model for Geological Formations in Frio Field and Precaspian Basin. Energies. 2021; 14(23):8023. https://doi.org/10.3390/en14238023
Chicago/Turabian StyleKamashev, Aibar, and Yerlan Amanbek. 2021. "Reservoir Simulation of CO2 Storage Using Compositional Flow Model for Geological Formations in Frio Field and Precaspian Basin" Energies 14, no. 23: 8023. https://doi.org/10.3390/en14238023
APA StyleKamashev, A., & Amanbek, Y. (2021). Reservoir Simulation of CO2 Storage Using Compositional Flow Model for Geological Formations in Frio Field and Precaspian Basin. Energies, 14(23), 8023. https://doi.org/10.3390/en14238023






