Experimental Investigation of Rotating Instability in an Axial Compressor with a Steady Swirl Distortion Inlet
Abstract
:1. Introduction
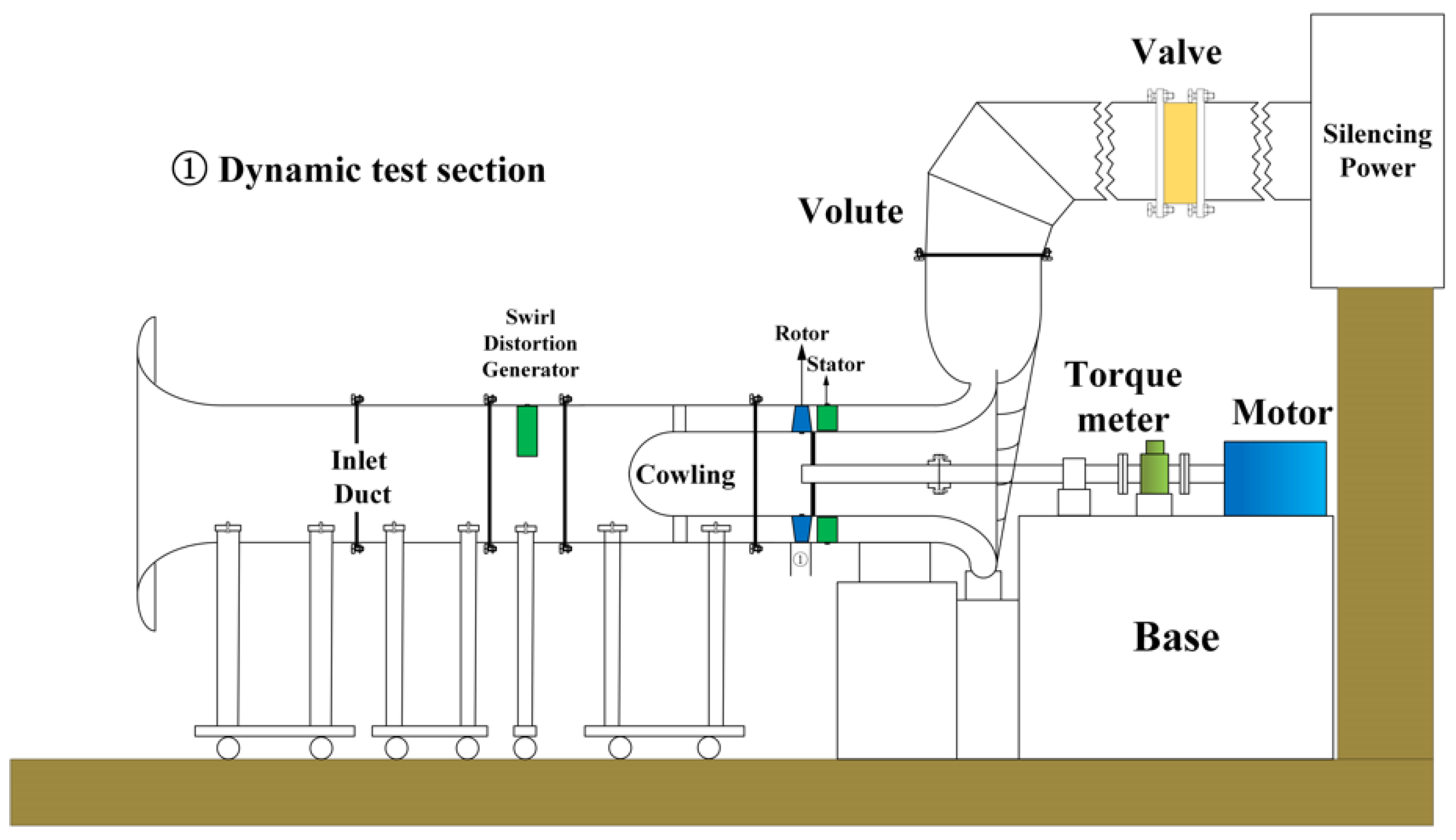
2. Experimental Equipment and Scheme
2.1. Brief Introduction of the Compressor Test Bench
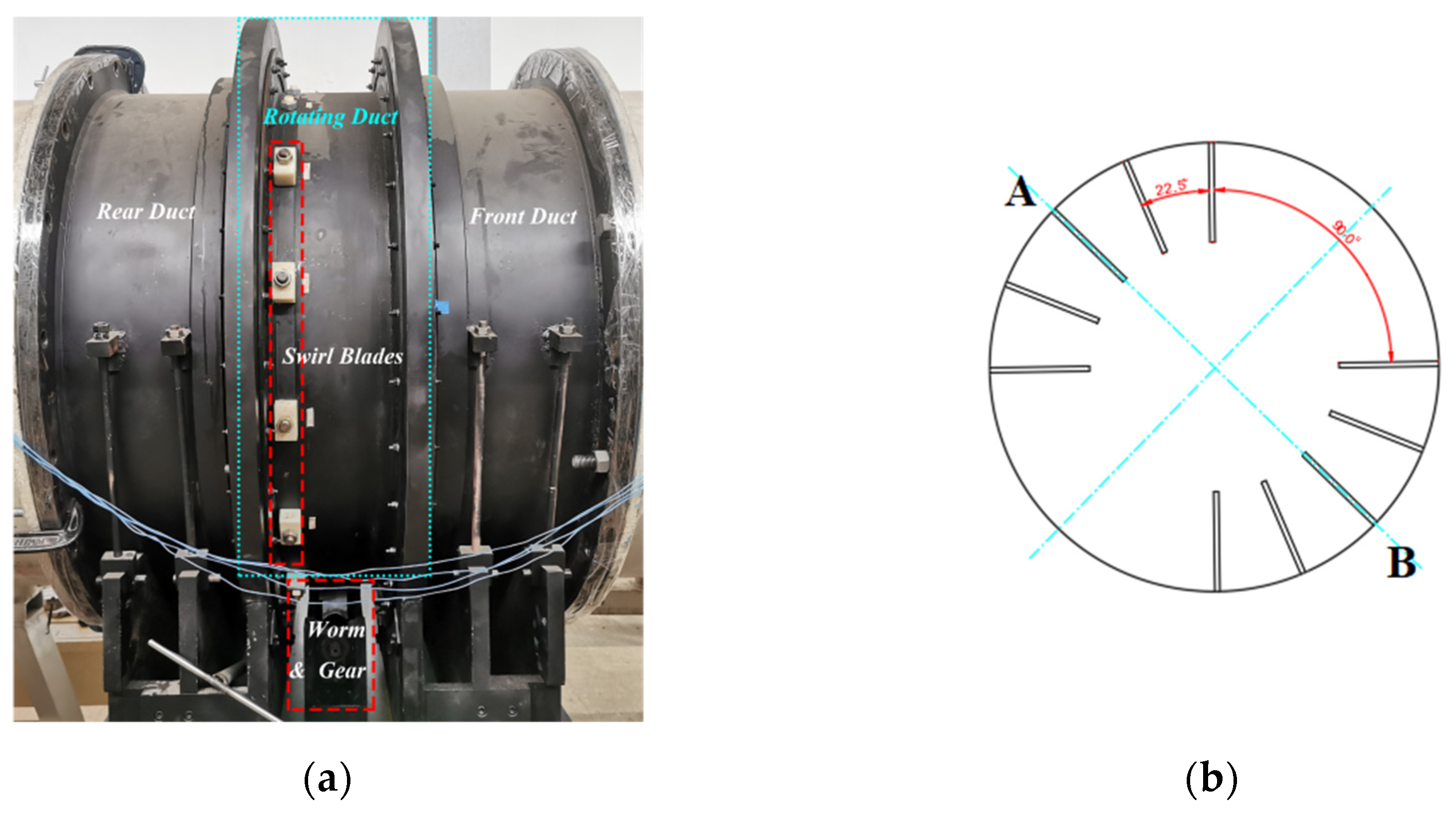
2.2. Swirl Distortion Generator
2.3. Experimental Methods
3. Results and Discussion
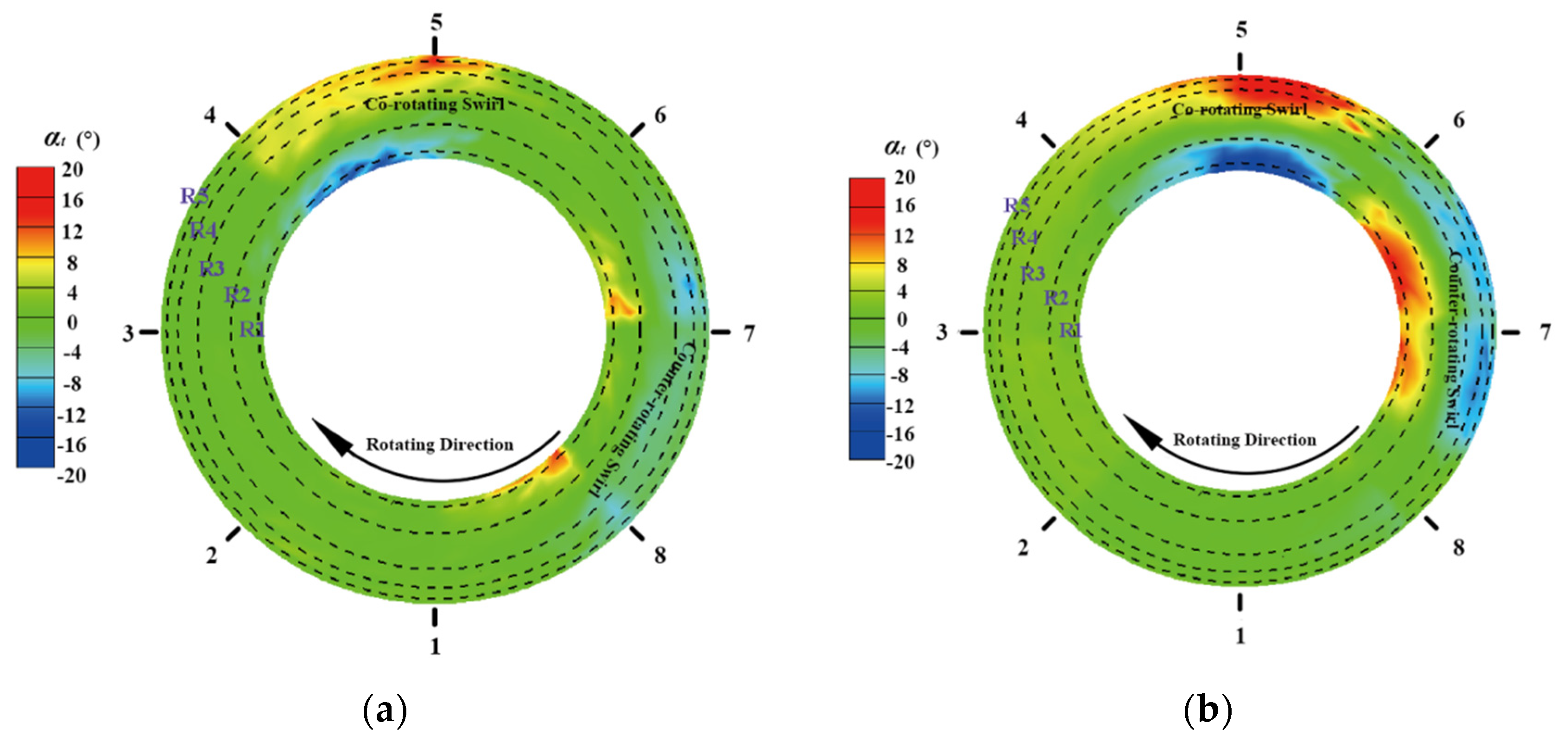
3.1. Description of the Swirl Flow
3.2. Compressor Performance
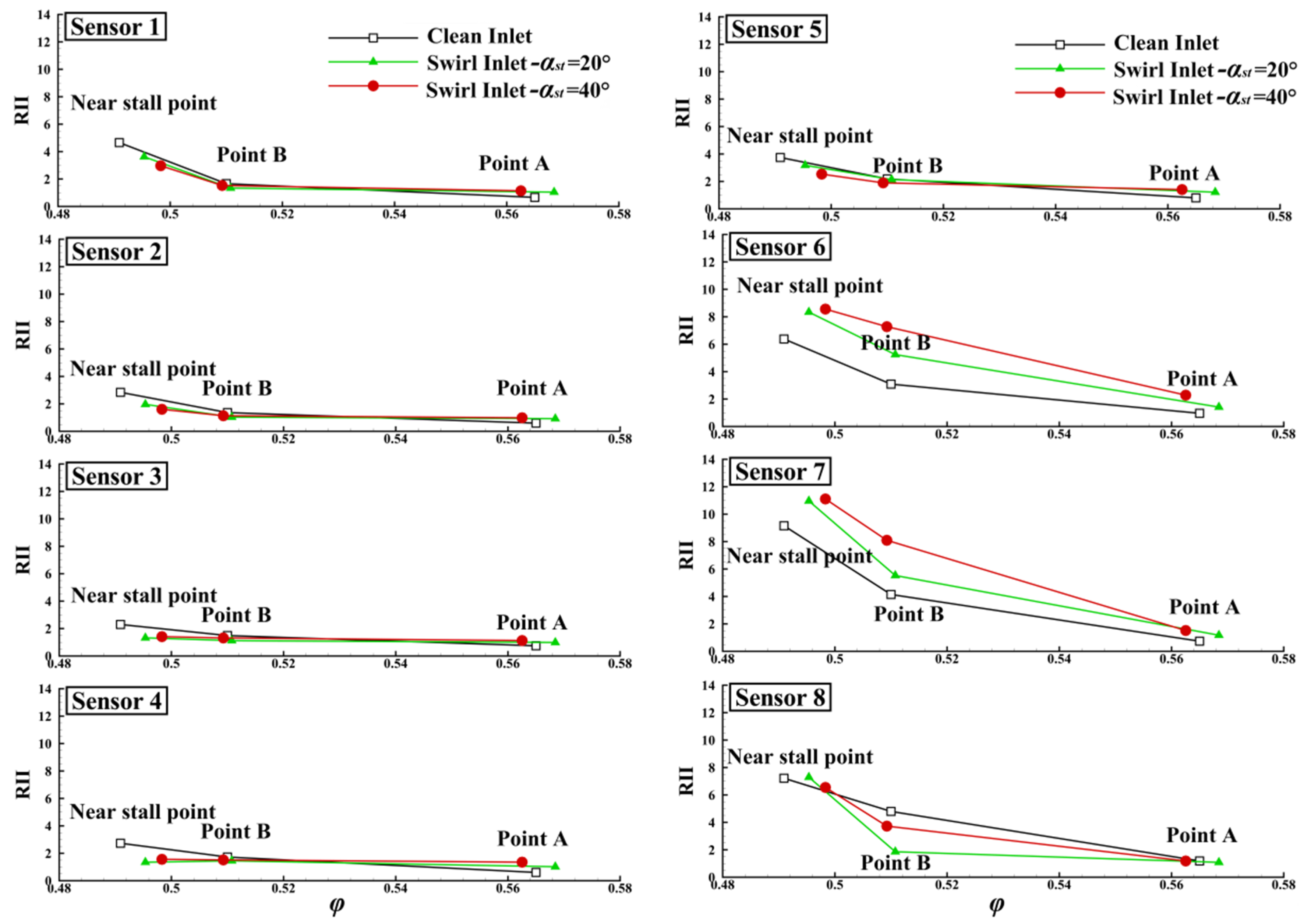
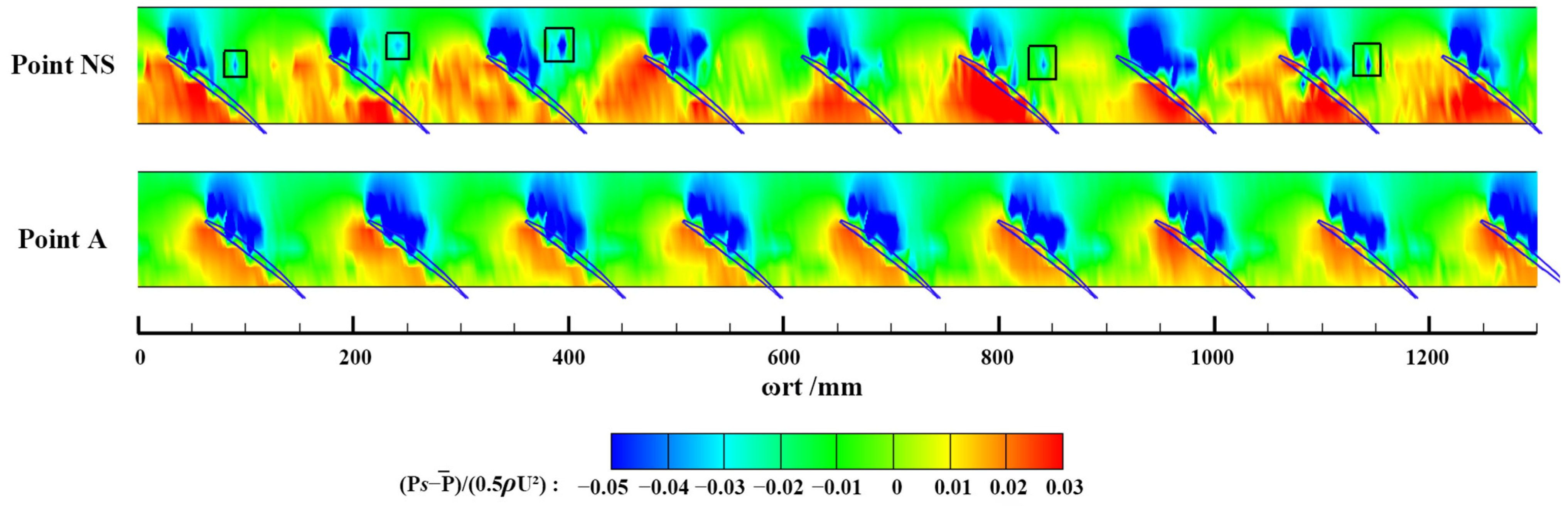
3.3. Effects on Stall Inception
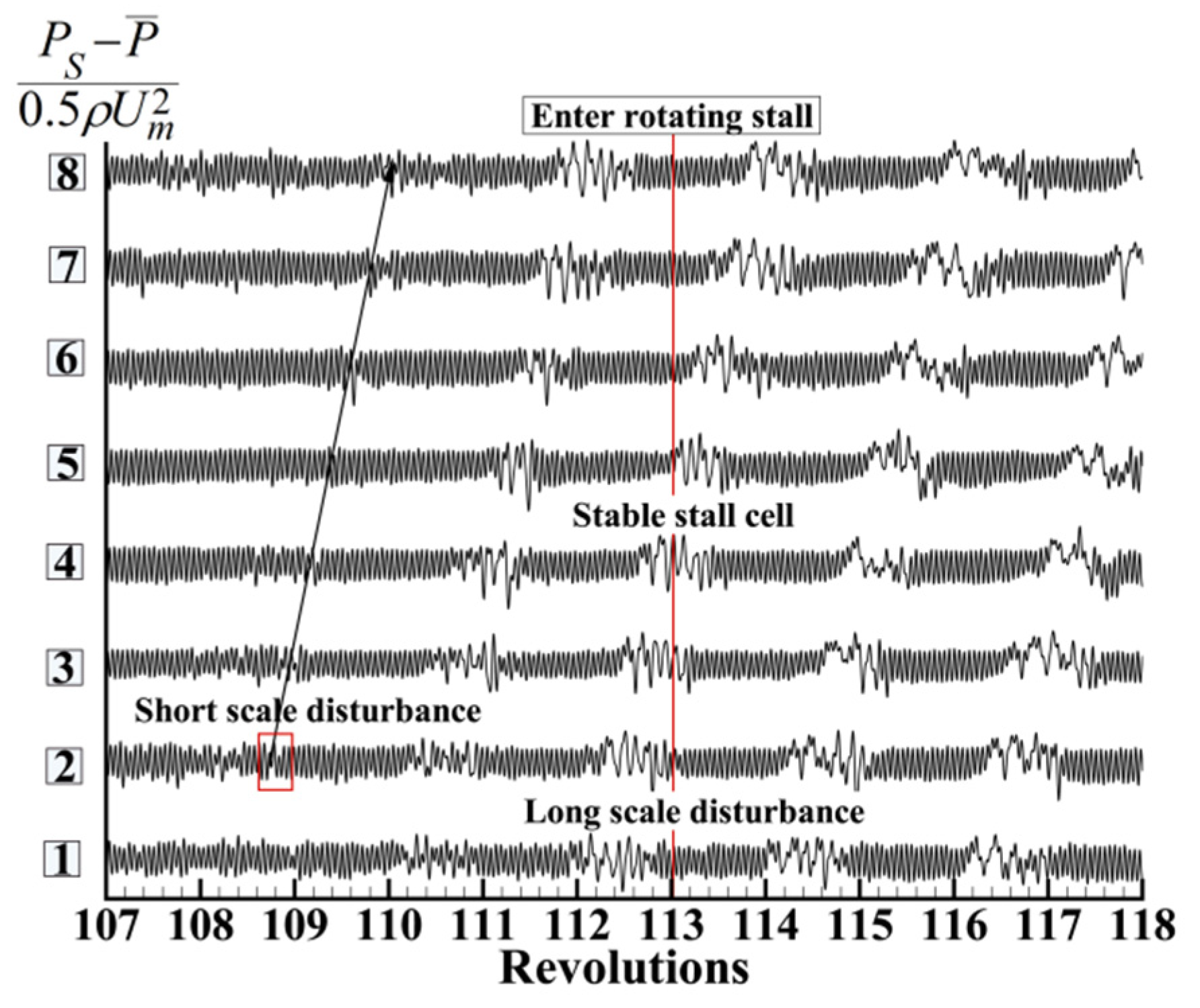
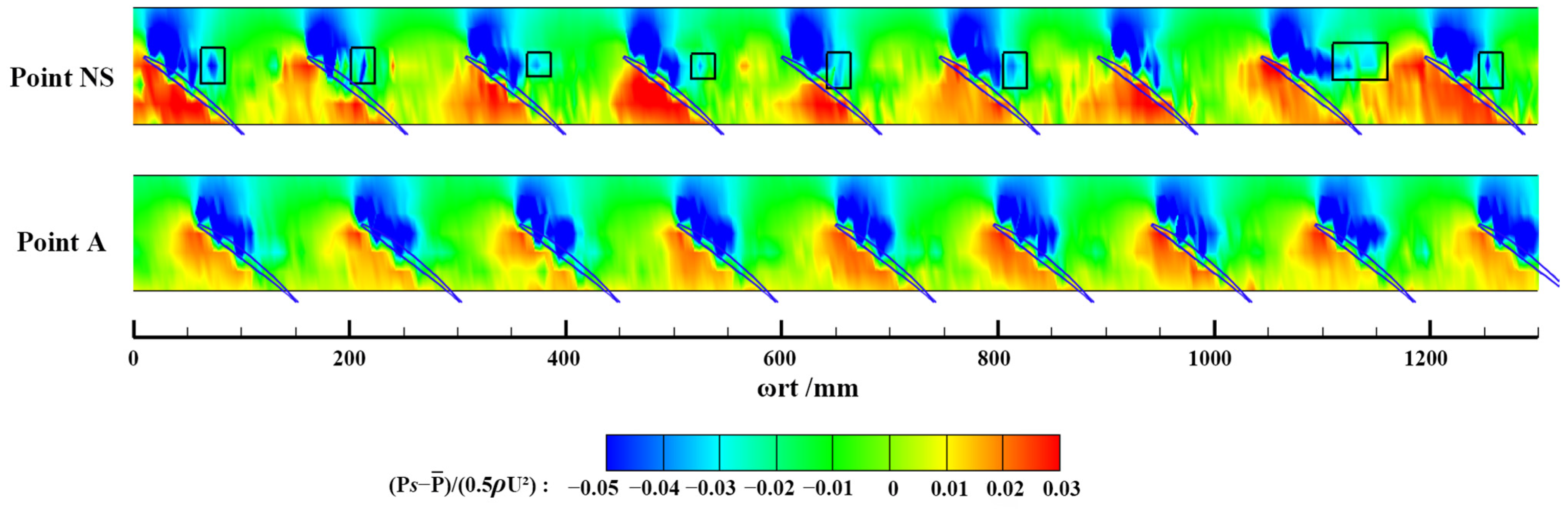
3.4. Rotating Instability with Paired Swirl Distortion Inlet
4. Conclusions
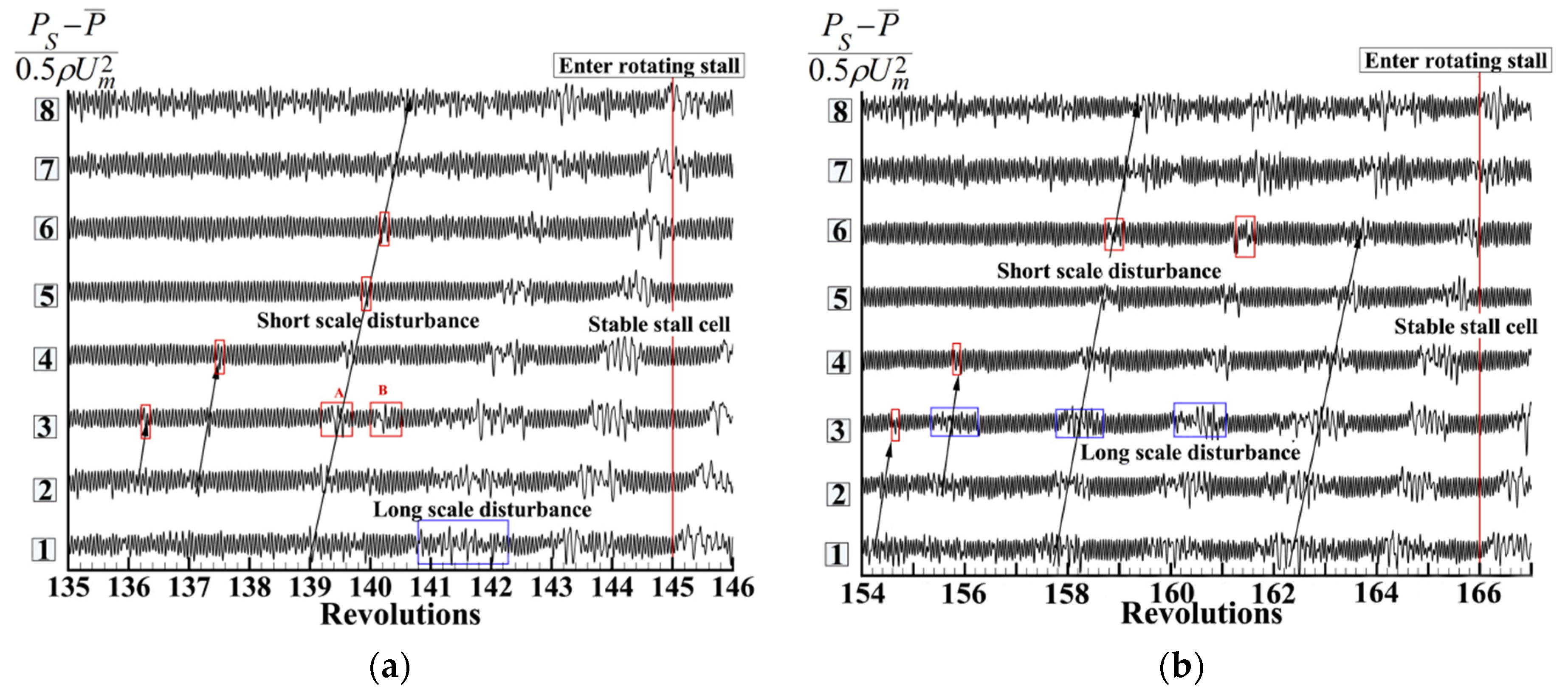
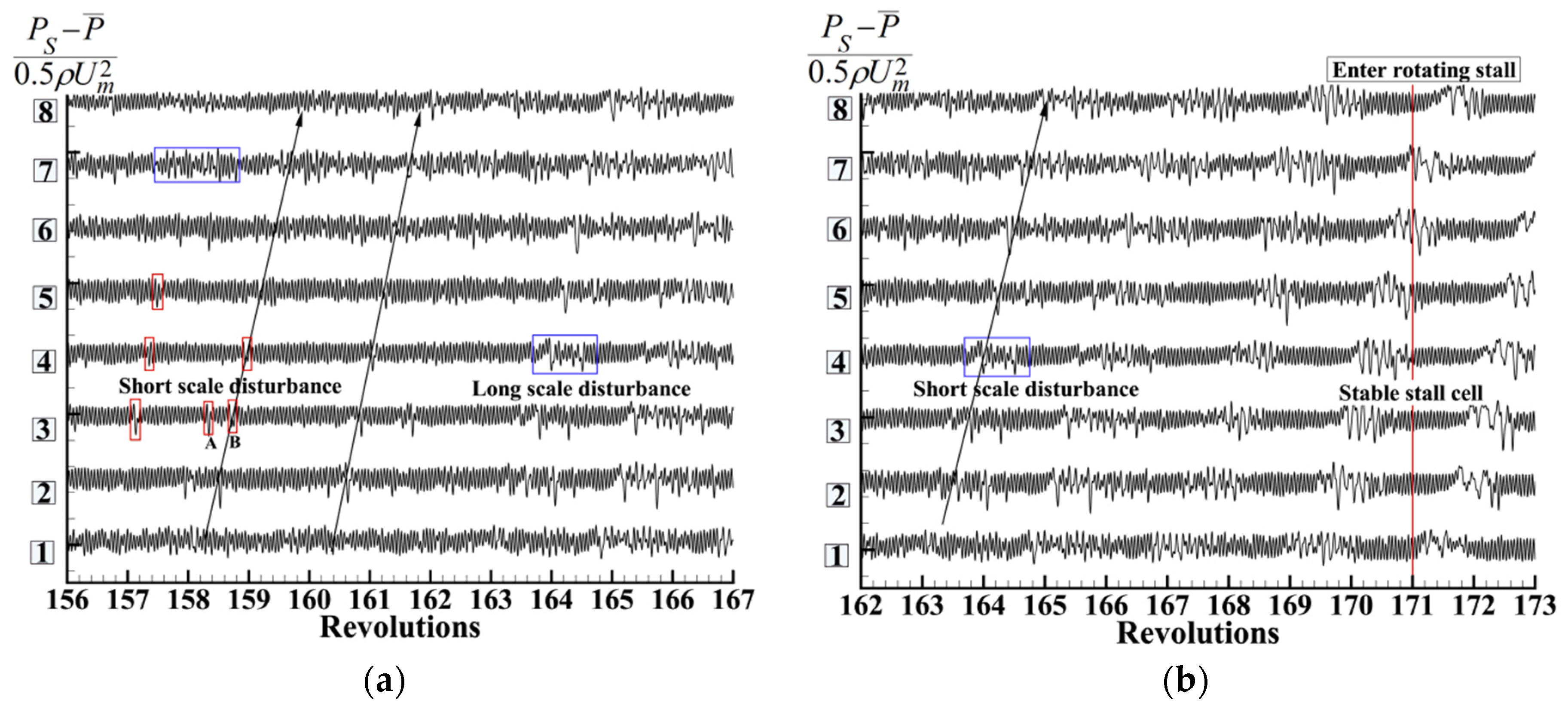
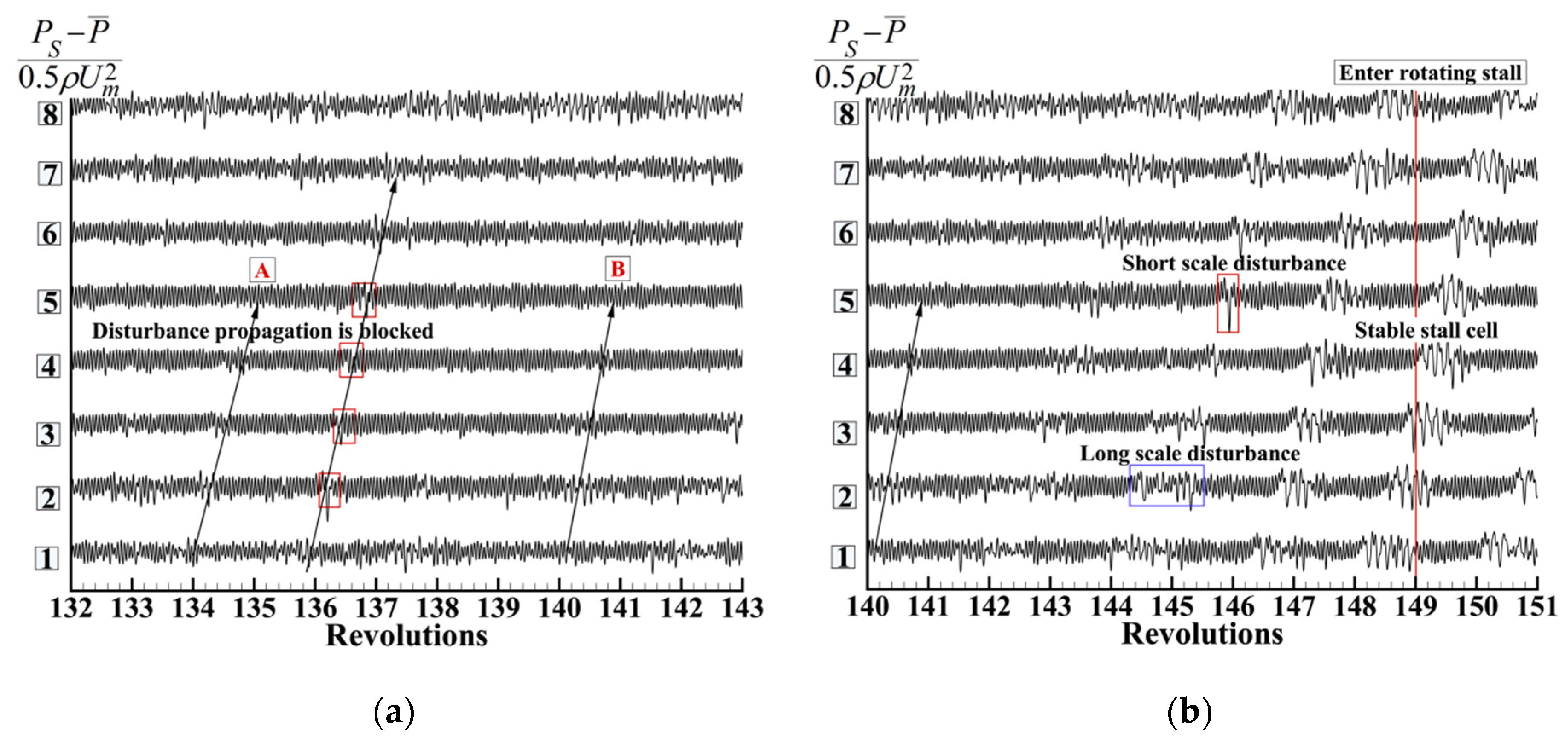
- Due to the existence of the paired swirl distortion, the initial development of the compressor stall involved the alternation of short-scale disturbance and long-scale disturbance. The long-scale disturbance in the counter-rotating swirl sector propagated along the direction of the rotor rotation and was suppressed in the non-swirl and co-rotating swirl sectors, turning into short-scale disturbance or even disappearing, until the counter-rotating swirl sector was reached in the next revolution, and the disturbance strengthened again. Once the co-rotating swirl no longer restrained the development of the disturbance, the compressor rapidly entered the stall.
- In the case of the paired swirl distortion inlet, the obvious RI mainly existed in the counter-rotating swirl sector.
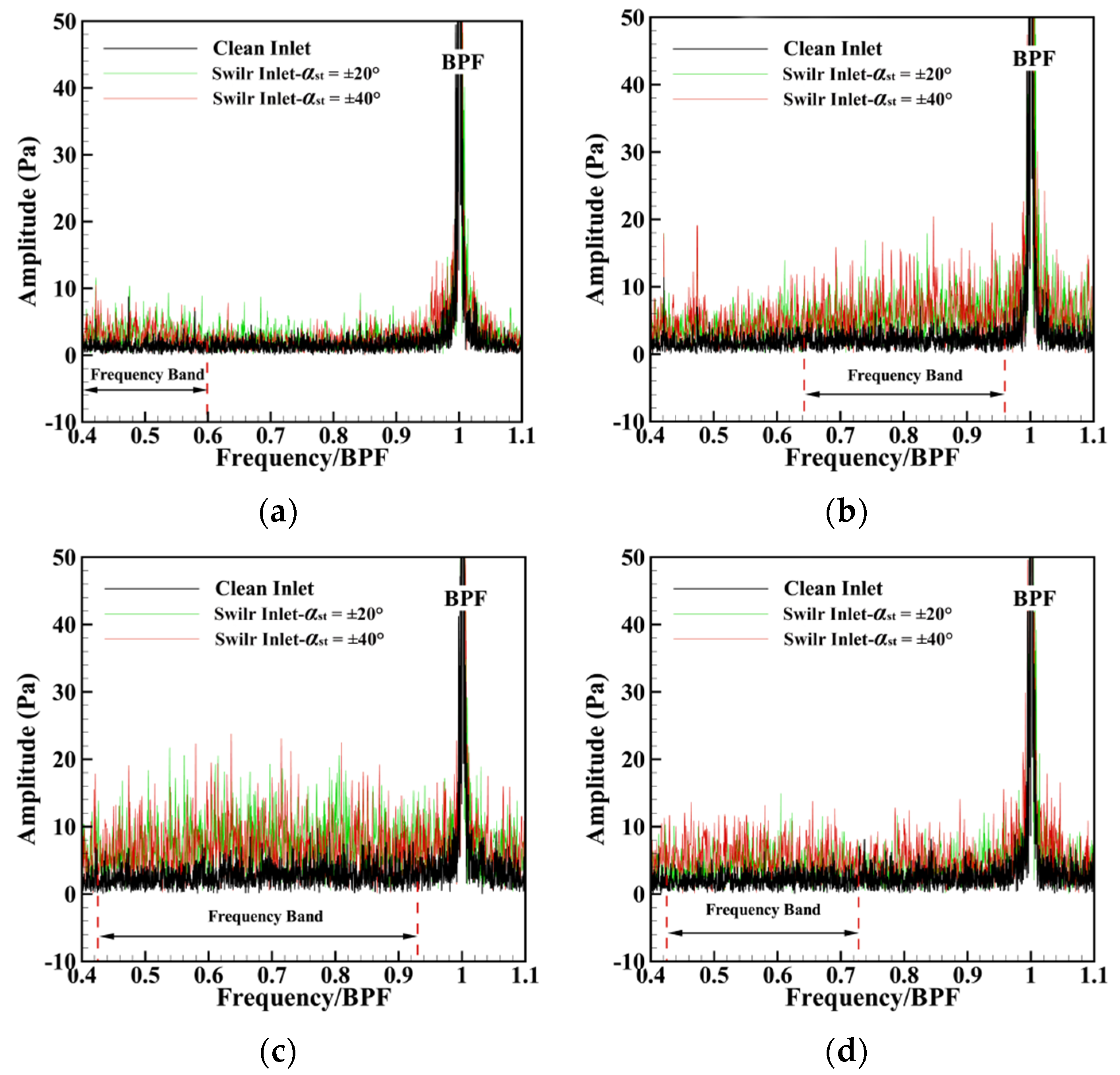
- For the compressor with a 2 mm rotor clearance, both paired swirl distortions with αst = ±20° and αst = ±40° induced RI. Compared with the RRI in the case of a clean inlet, when αst = ±20°, RRI increased by 69.8%, and when αst = ±40°, RRI increased by 135.8%.
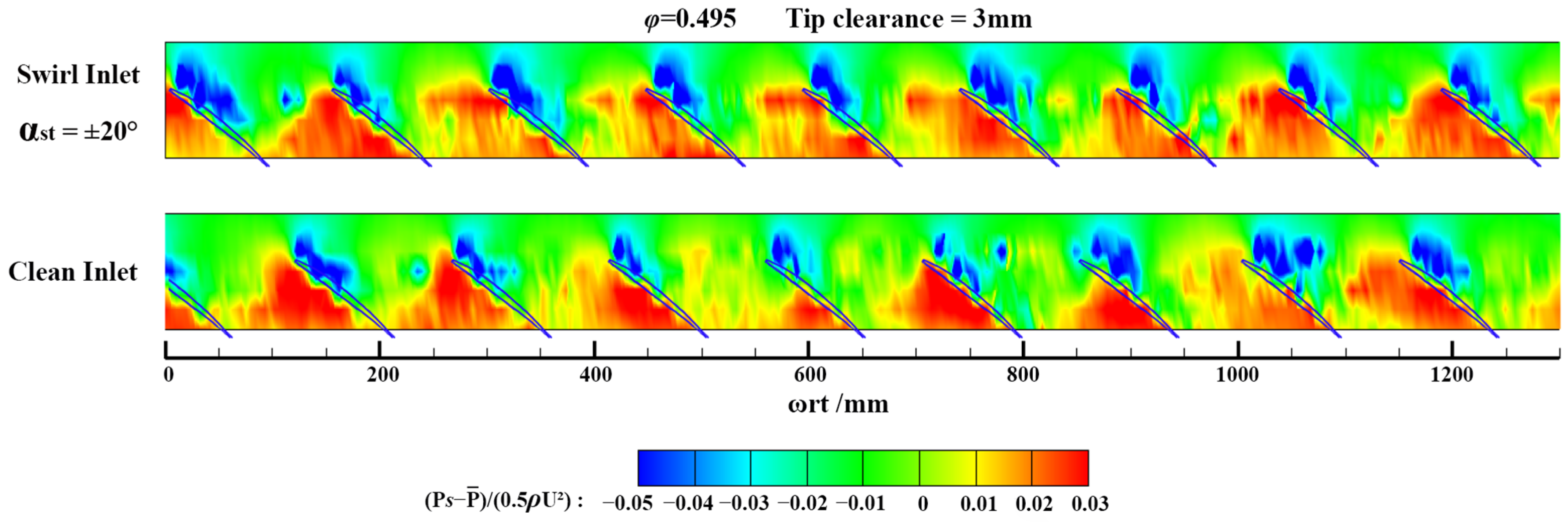
- As the rotor clearance increased to 3 mm, the paired swirl distortion with αst = ±20° had different effects on RI at different circumferential positions. The counter-rotating swirl part strengthened the RI, and the RRI increased significantly, with a maximum value of 7.79, while the co-rotating part suppressed the RI, and the RRI decreased, reaching the value of 4.45.
- The enhancement and weakening effect of the paired swirl distortion on RI were attributed to the generation and suppression of shedding vortices at the rotor blade tip. In the compressor with a 3 mm rotor clearance, the co-rotating swirl inhibited the formation of shedding vortices and ameliorated the flow field of the rotor tip, thus delaying the stall. However, in the compressor with a 2 mm rotor tip clearance, the counter-rotating swirl deteriorated the flow field at the rotor tip, and the generation of shedding vortices induced RI, which promoted the advancement of the stall.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| RI | Rotating instability |
| BPF | Blade passing frequency/Hz |
| Stagger angle of the swirl blades/° | |
| Flow coefficient | |
| Total to static pressure rise coefficient | |
| Rotor tip clearance/mm | |
| Static pressure/Pa | |
| Mean static pressure/Pa | |
| Density/kg·m−3 | |
| Circumferential speed of rotor/m·s−1 |
References
- Greitzer, E.M. Surge and Rotating Stall in Axial Flow Compressors—Part I: Theoretical Compression System Model. J. Eng. Power 1976, 98, 190. [Google Scholar] [CrossRef]
- Storer, J.A.; Cumpsty, N.A. Tip Leakage Flow in Axial Compressors. J. Turbomach. 1991, 113, 252–259. [Google Scholar] [CrossRef]
- Suder, K.L.; Celestina, M.L. Experimental and Computational Investigation of the Tip Clearance Flow in a Transonic Axial Compressor Rotor. J. Turbomach. 1996, 118, 218–229. [Google Scholar] [CrossRef] [Green Version]
- Lakshminarayana, B. Methods of Predicting the Tip Clearance Effects in Axial Flow Turbomachinery. J. Basic Eng. 1970, 92, 467–480. [Google Scholar] [CrossRef]
- You, D.; Wang, M.; Moin, P.; Mittal, R. Large-eddy simulation analysis of mechanisms for viscous losses in a turbomachinery tip-clearance flow. J. Fluid Mech. 2007, 586, 177–204. [Google Scholar] [CrossRef] [Green Version]
- You, D.; Wang, M.; Moin, P.; Mittal, R. Prediction and analysis of rotor tip-clearance flows using large-eddy simulation. In Proceedings of the 2004 Users Group Conference (DOD_UGC’04), Williamsburg, VA, USA, 7–11 June 2004; pp. 158–165. [Google Scholar]
- Day, I.J. Stall Inception in Axial Flow Compressors. J. Turbomach. 1991, 115I, 1–9. [Google Scholar]
- TR Camp. A study of Spike and Modal Phenomena in a Low-Speed Axial Compressor. Trans. ASME J. Turbomach. 1998, 120, 393–401. [Google Scholar]
- Nishioka, T.; Kuroda, S.; Kozu, T. Spike and Modal Stall-inception Patterns in a Variable-pitch Axial-flow Fan. Trans. Jpn. Soc. Mech. Eng. 2004, 70, 1746–1753. [Google Scholar] [CrossRef] [Green Version]
- Vo, H.D.; Tan, C.S.; Greitzer, E.M. Criteria for Spike Initiated Rotating Stall. J. Turbomach. 2008, 130, 11023. [Google Scholar] [CrossRef]
- Mathioudakis, K.; Breugelmans, F. Development of Small Rotating Stall in a Single Stage Axial Compressor. In Proceedings of the ASME 1985 International Gas Turbine Conference and Exhibit, Houston, TX, USA, 18 March 1985. [Google Scholar]
- Mailach, R.; Sauer, H.; Vogeler, K. The Periodical Interaction of the Tip Clearance Flow in the Blade Rows of Axial Compressors. ASME Pap. 2001, 78507, 1–9. [Google Scholar]
- Mailach, R.; Lehmann, I.; Vogeler, K. Rotating Instabilities in an Axial Compressor Originating from the Fluctuating Blade Tip Vortex. J. Turbomach. 2001, 123I, 453–460. [Google Scholar] [CrossRef]
- Biela, C.; Müller, M.W.; Schiffer, H.-P.; Zscherp, C. Unsteady Pressure Measurement in a Single Stage Axial Transonic Compressor Near the Stability Limit. In Proceedings of the ASME Turbo Expo 2008, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Schreiber, J.; Paoletti, B.; Ottavy, X. Observations on rotating instabilities and spike type stall inception in a high-speed multistage compressor. Int. J. Rotating Mach. 2017, 2017, 7035870. [Google Scholar] [CrossRef] [Green Version]
- März, J.; Hah, C.; Neise, W. An Experimental and Numerical Investigation into the Mechanisms of Rotating Instability. J. Turbomach. 2002, 124, 367–374. [Google Scholar] [CrossRef]
- Hah, C.; Bergner, J.; Schiffer, H. Tip clearance vortex oscillation, vortex shedding and rotating instabilities in an axial transonic compressor rotor. ASME Pap. 2008, 43161, 57–65. [Google Scholar]
- Hah, C.; Voges, M.; Mueller, H. Schiffer, Characteristics of tip clearance flow instability in a transonic compressor. ASME Pap. 2010, 44021, 63–74. [Google Scholar]
- Wu, Y.; Wu, J.; Zhang, G.; Chu, W. Experimental and Numerical Investigation of Flow Characteristics Near Casing in an Axial Flow Compressor Rotor at Stable and Stall Inception Conditions. J. Fluids Eng. 2014, 136, 111106. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, Y.; An, G. Tip leakage flow, tip aerodynamic loading and rotating instability in a subsonic high-speed axial flow compressor rotor. Aerosp. Sci. Technol. 2021, 110, 106486. [Google Scholar] [CrossRef]
- Inoue, M.; Kuroumaru, M.; Tanino, T.; Yoshida, S.; Furukawa, M. Comparative Studies on Short and Long Length-Scale Stall Cell Propagating in an Axial Compressor Rotor. J. Turbomach. 2001, 123, 24–30. [Google Scholar] [CrossRef]
- Vo, H.D. Role of Tip Clearance Flow in Rotating Instabilities and Nonsynchronous Vibrations. J. Propuls. Power 2010, 26, 556–561. [Google Scholar] [CrossRef]
- Holzinger, F.; Wartzek, F.; Jüngst, M.; Schiffer, H.; Leichtfuss, S. Self-Excited Blade Vibration Experimentally Investigated in Transonic Compressors: Rotating Instabilities and Flutter. J. Turbomach. 2016, 138, 041006. [Google Scholar] [CrossRef]
- Li, T.; Wu, Y.; Ouyang, H. Numerical investigation of tip clearance effects on rotating instability of a low-speed compressor. Aerosp. Sci. Technol. 2021, 111, 106540. [Google Scholar] [CrossRef]
- Yue, S.; Wang, Y.; Zhang, Z.; Wei, L.; Wang, H. Experimental investigation of rotating instability in a contra-rotating axial flow compressor. Aeronaut. J. 2021, 125, 742–762. [Google Scholar] [CrossRef]
- Society of Automotive Engineers. A Methodology for Assessing Inlet Swirl Distortion. Aerospace Information Report No. AIR 5686, October 2010; Reaffirmed July 2017. Available online: https://www.sae.org/standards/content/air5686/ (accessed on 10 September 2021).
- Frohnapfel, D.J.; O’Brien, W.F.; Lowe, K.T. Fan Rotor Flow Measurements in a Turbofan Engine Operating with Inlet Swirl Distortion. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Sheoran, Y.; Bouldin, B.; Krishnan, P.M. Compressor Performance and Operability in Swirl Distortion. J. Turbomach. 2012, 134, 041008. [Google Scholar] [CrossRef]
- Naseri, A.; Boroomand, M.; Sammak, S. Numerical Investigation of Effect of Inlet Swirl and Total-pressure Distortion on Performance and Stability of an Axial Transonic Compressor. J. Therm. Sci. 2016, 25, 501–510. [Google Scholar] [CrossRef]
- Dong, X.; Sun, D.; Li, F.; Jin, D.; Gui, X.; Sun, X. Effects of Stall Precursor-Suppressed Casing Treatment on a Low-Speed Compressor with Swirl Distortion. J. Fluids Eng. 2018, 140, 091101. [Google Scholar] [CrossRef]




| Related Parameter | Value |
|---|---|
| Rotational speed/r·min−1 | 1500 |
| Rotor hub/tip ratio | 0.6 |
| Blade numbers | 19/22 |
| Aspect ratio at pitch diameter | 1.459/1.709 |
| Tip clearance (1)/mm | 2/2 |
| Tip clearance (2)/mm | 3/2 |
| Design Parameters | Value |
|---|---|
| Chord length, mm | 100 |
| Blade height, mm | 200 |
| Camber angle, ° | 20 |
| Profile | Naca65 series |
| Inlet Condition | Sensor 1 | Sensor 2 | Sensor 3 | Sensor 4 | Sensor 5 | Sensor 6 | Sensor 7 | Sensor 8 |
|---|---|---|---|---|---|---|---|---|
| Clean | 6.48 | 4.13 | 3.96 | 7.90 | 12.51 | 14.69 | 9.45 | 11.68 |
| αst = ±20° | 10.35 | 7.19 | 5.84 | 7.11 | 8.23 | 10.24 | 17.25 | 16.54 |
| Absolute increase | 3.86 | 3.06 | 1.88 | −0.79 | −4.28 | −4.45 | 7.79 | 4.86 |
| Relative increase | 59.6% | 74.1% | 47.5% | −10.0% | −34.2% | −30.3% | 82.4% | 41.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Hu, J.; Wang, X.; Jiang, C.; Ji, J. Experimental Investigation of Rotating Instability in an Axial Compressor with a Steady Swirl Distortion Inlet. Energies 2021, 14, 8057. https://doi.org/10.3390/en14238057
Xu R, Hu J, Wang X, Jiang C, Ji J. Experimental Investigation of Rotating Instability in an Axial Compressor with a Steady Swirl Distortion Inlet. Energies. 2021; 14(23):8057. https://doi.org/10.3390/en14238057
Chicago/Turabian StyleXu, Rong, Jun Hu, Xuegao Wang, Chao Jiang, and Jiajia Ji. 2021. "Experimental Investigation of Rotating Instability in an Axial Compressor with a Steady Swirl Distortion Inlet" Energies 14, no. 23: 8057. https://doi.org/10.3390/en14238057
APA StyleXu, R., Hu, J., Wang, X., Jiang, C., & Ji, J. (2021). Experimental Investigation of Rotating Instability in an Axial Compressor with a Steady Swirl Distortion Inlet. Energies, 14(23), 8057. https://doi.org/10.3390/en14238057





