Numerical Investigation of the Secondary Swirling in Supersonic Flows of Various Nature Gases
Abstract
:1. Introduction
2. Materials and Methods
2.1. Flow Equations
2.2. Power Costs and Losses Estimation Inside SVT
2.3. Problem Formulation
2.4. Numerical Approaches
2.5. Mesh Independence Study
3. Results and Discussions
3.1. Case of Inviscid Gases
3.2. SVT with the Same Geometry
3.3. SVT with the Same Reynolds Number
3.4. SVT with the Same Reynolds Number and without Inner Body
4. Conclusions
- Kinematic viscosity plays the primary role in the formation of swirl cascaded structures which lead to the energy separation;
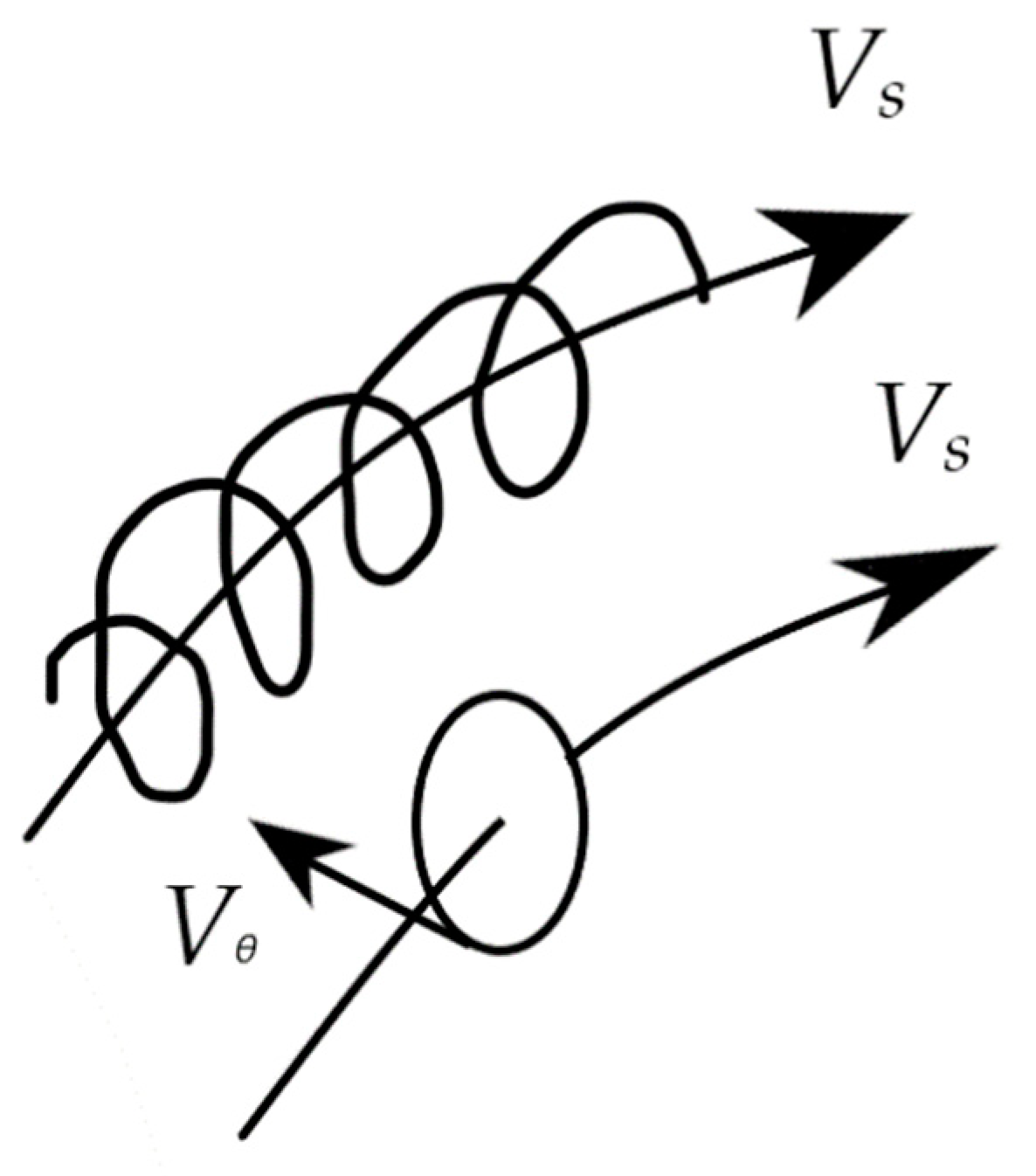
- It is shown that secondary swirls of the flow in SVT appeared for all considered gases of various nature;
- He and Ar have the most significant degree of swirl and, consequently, the highest separation effect;
- The presence of the inner body has led to a decrease of SVT cooling efficiency by 15%, 18%, 3%, and 6.5% for argon, helium, carbon dioxide, and air, respectively;
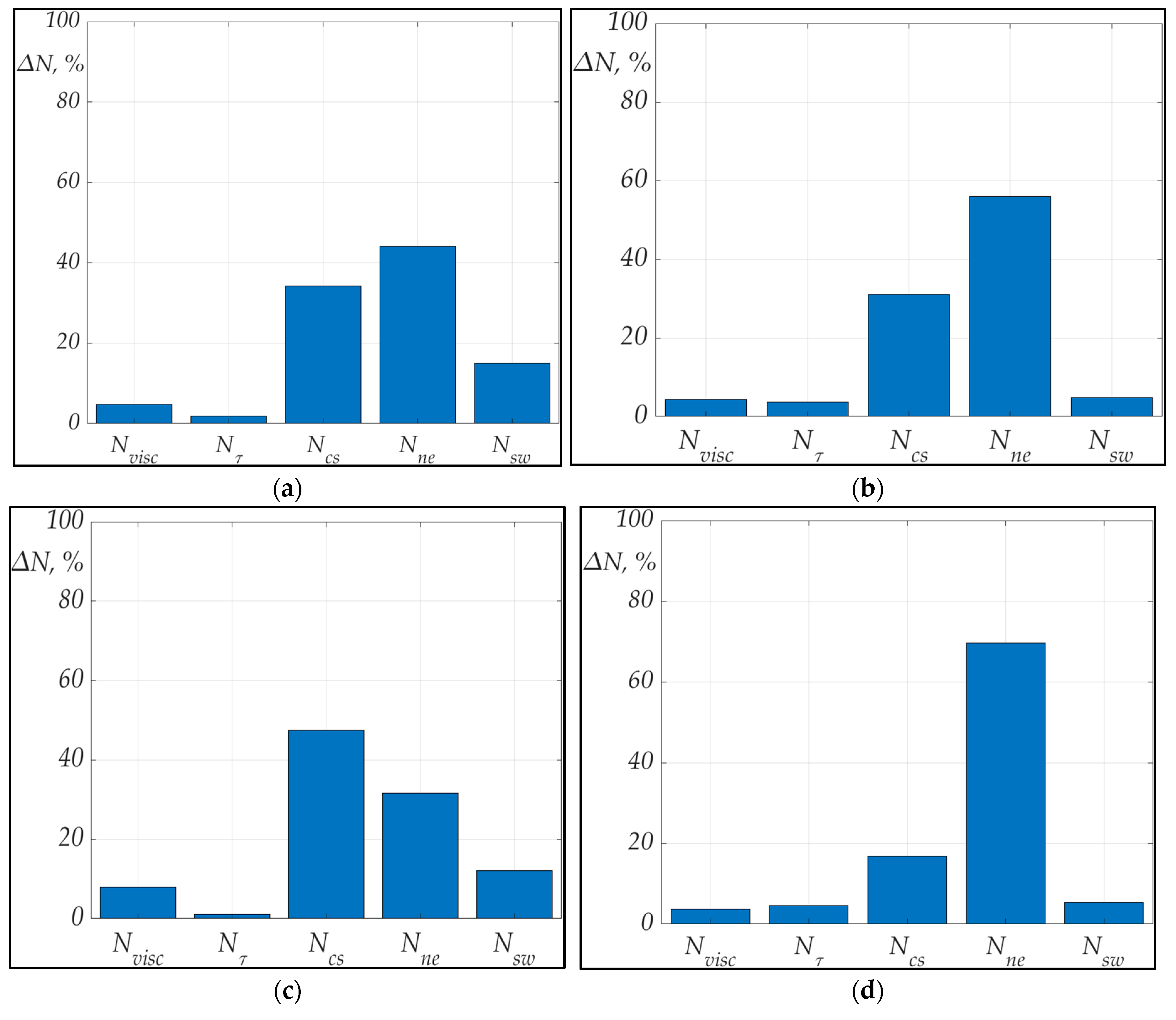
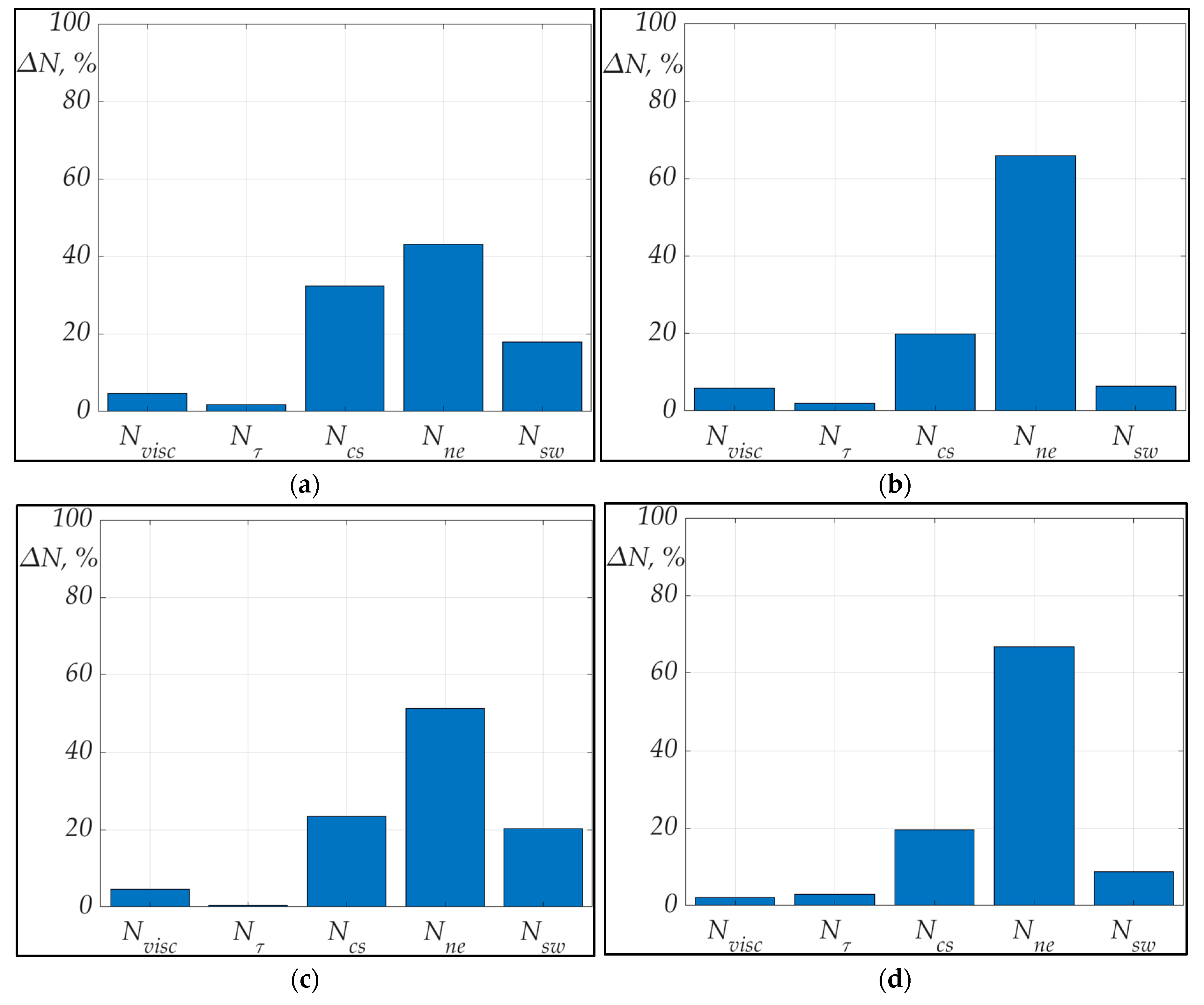
- Finally, a comparison of power losses obtained for argon, carbon dioxide, and air showed that the losses due to the formation of the swirl cascaded structures play the primary role in the efficiency of flow cooling.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ranque, G.J. Experiments on Expansions in a Vortex with Simultaneous Exhaust of Hot and Cold Air. Phys. Radium 1933, 4, 112–114. [Google Scholar]
- Hilsch, R. The Use of the Expansion of Gases in a Centrifugal Field as Cooling Process. Rev. Sci. Instrum. 1947, 18, 108–113. [Google Scholar] [CrossRef] [PubMed]
- Scheper, G.S. The vortex tube-internal flow data and a heat transfer theory. Refrig. Eng. 1951, 59, 985–989. [Google Scholar]
- Fulton, C.D. Ranque’s tube. ASHRAE J. 1950, 58, 473–479. [Google Scholar]
- Van Deemter, J.J. On the theory of the Ranque-Hilsch cooling effect. Appl. Sci. Res. 1952, 3, 174–196. [Google Scholar] [CrossRef]
- Deissler, R.G.; Perlmutter, M. Analysis of the flow and energy separation in a turbulent vortex. Int. J. Heat Mass Transf. 1960, 1, 173–191. [Google Scholar] [CrossRef]
- Reynolds, A.J. Energy flows in a vortex tube. Z. Angew. Math. Phys. 1961, 12, 343–357. [Google Scholar] [CrossRef]
- Holman, J.P.; Moore, G.D. An experimental study of vortex chamber flow. J. Basic. Eng. 1961, 83, 632–636. [Google Scholar] [CrossRef]
- Parulekar, B.B. Performance ofshort vortex tube. J. Refrig. 1961, 6, 74–80. [Google Scholar]
- Merkulov, A.P.; Kolyshev, N.D. The investigation of the temperature fields into vortex tube with the diffuser. Proc. Kuibyshev Aviat. Inst. 1965, 22, 81–89. (In Russian) [Google Scholar]
- Merkulov, A.P. The Vortex Effect and Its Application in Technology, 1st ed.; Mashinostroyenie: Moscow, Russia, 1969. (In Russian) [Google Scholar]
- Hinze, J.O. Turbulence, 2nd ed.; McGraw-Hill College: New York, NY, USA, 1975. [Google Scholar]
- Celik, A.; Yilaz, M.; Yildiz, O.F. Effects of vortex tube on exhaust emissions during cold start of diesel engines. Appl. Energy Combust. Sci. 2021, 6, 100027. [Google Scholar] [CrossRef]
- Celik, A.; Yilaz, M.; Yildiz, O.F. Improvement of diesel engine startability under low temperatures by vortex tubes. Energy Rep. 2019, 6, 17–27. [Google Scholar] [CrossRef]
- Chen, J.; Gao, X.; Shao, S.; Hu, H.; Xie, J.; Li, N.; Gao, N. Numerical investigation of the vortex tube performance in novel precooling methods in the hydrogen fueling station. Int. J. Hydrog. Energy 2021, 46, 5548–5555. [Google Scholar] [CrossRef]
- Maestre-Cambronel, D.; Barros, J.G.; Gonzalez-Quiroga, A.; Bula, A.; Duarte-Forero, J.; Sustain, J. Thermoeconomic analysis of improved exhaust waste heat recovery system for natural gas engine based on Vortex Tube heat booster and supercritical CO2 Brayton cycle. Energy Technol. Assess. 2021, 47, 101355. [Google Scholar] [CrossRef]
- Shmroukh, A.N.; Attalla, M.; Abd El-Naser Abd El-Hakim, A. Experimental investigation of a novel sea water desalination system using Ranque-Hilsch vortex tube. Appl. Therm. Eng. 2019, 149, 658–664. [Google Scholar] [CrossRef]
- Zhang, B.; Guo, X. Prospective applications of Ranque-Hilsch vortex tubes to sustainable energy utilization and energy efficiency improvement with energy and mass separation. Renew. Sustain. Energy Rev. 2018, 89, 135–150. [Google Scholar] [CrossRef]
- Nash, J.M. The Ranque-Hilsch vortex tube and its application to spacecraft environmental control systems. Dev. Theor. Appl. Mech. 1972, 6, 35–90. [Google Scholar]
- Matveev, K.I.; Leachman, J. Numerical investigation of vortex tubes with extended vortex chambers. Int. J. Refrig. 2019, 108, 145–153. [Google Scholar] [CrossRef]
- Qyyum, M.A.; Noon, A.A.; Wei, F.; Lee, M. Vortex tube shape optimization for hot control valves through computational fluid dynamics. Int. J. Refrig. 2019, 102, 151–158. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, B. Analysis of the unsteady heat and mass transfer processes in a Ranque-Hilsch vortex tube: Tube optimization criteria. Int. J. Heat Mass Transf. 2018, 127, 68–79. [Google Scholar] [CrossRef]
- Liang, F.; Tang, G.; Xu, C.; Wang, C.; Wang, Z.; Wang, J.; Li, N. Experimental investigation on improving the energy separation efficiency of vortex tube by optimizing the structure of vortex generator. Appl. Therm. Eng. 2021, 195, 117222. [Google Scholar] [CrossRef]
- Pourmahmoud, N.; Hassanzadeh, A.; Moutaby, O. Numerical analysis of the effect of helical nozzles gap on the cooling capacity of Ranque-Hilsch vortex tube. Int. J. Refrig. 2012, 35, 1473–1483. [Google Scholar] [CrossRef]
- Avci, M. The effects of nozzle aspect ratio and nozzle number on the performance of the Ranque-Hilsch vortex tube. Appl. Therm. Eng. 2013, 50, 302–308. [Google Scholar] [CrossRef]
- Rafiee, S.E.; Sadeghiazad, M.M. Experimental analysis on impact of navigator’s angle on velocimetry and thermal capability of RH-vortex tube. Appl. Therm. Eng. 2020, 169, 114907. [Google Scholar] [CrossRef]
- Guo, X.; Liu, B.; Lv, J.; Zhang, B.; Shan, Y. An optimization method on managing Ranque-Hilsch vortex tube with the synergy between flow structure and performance. Int. J. Refrig. 2021, 126, 123–132. [Google Scholar] [CrossRef]
- Xue, Y.; Arjomandi, M.; Kelso, R. Energy analysis within a vortex tube. Exp. Therm. Fluid Sci. 2014, 52, 139–145. [Google Scholar] [CrossRef]
- Liang, F.; Wang, H.; Tang, G. Temperature separation characteristics of CH4-CO2 binary gas mixture within a vortex tube. Int. J. Therm. Sci. 2021, 16, 106726. [Google Scholar] [CrossRef]
- Aghagoli, A.; Sorin, M. Thermodynamic performance of a CO2 vortex tube based on 3D CFD flow analysis. Int. J. Refrig. 2019, 108, 124–137. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, R.; Zhang, W.; Qiu, L.; Zhang, X. Numerical analysis of energy separation in Ranque-Hilsch vortex tube with gaseous hydrogen using real gas model. Appl. Therm. Eng. 2018, 140, 287–294. [Google Scholar] [CrossRef]
- Volov, V.; Lyaskin, A. Effect of secondary swirl in supersonic gas and plasma flows in the self-vacuuming vortex tube. In Proceedings of the MATEC of Web of Conferences, International Conference on Combustion Physics and Chemistry, Samara, Russia, 24–28 July 2018; Volume 208, p. 20. [Google Scholar]
- Volov, V.; Lyaskin, A. Investigation of the cascade mechanism of energy exchange in swirling gas flows based on the effect of secondary swirling. J. Phys. Conf. Ser. 2020, 1677, 012032. [Google Scholar] [CrossRef]
- Vitovsky, O.V. Experimental study of energy separation in a Ranque-Hilsch tube with a screw vortex generator. Int. J. Refrig. 2021, 126, 272–279. [Google Scholar] [CrossRef]
- Hamdan, M.O.; Al-Omari, S.-A.B.; Oweimer, A.S. Experimental study of vortex tube energy separation under different tube design. Exp. Therm. Fluid Sci. 2018, 91, 306–311. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, B.; Shan, Y. Analysis on the patterns of precessing frequency characteristics and energy separation processes in a Ranque-Hilsch vortex tube. Int. J. Therm. Sci. 2021, 168, 107067. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, B.; Shan, Y. LES study on the working mechanism of large-scale precessing vortices and energy separation process of Ranque-Hilsch vortex tube. Int. J. Therm. Sci. 2021, 163, 106818. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, B. Computational investigation of precessing vortex breakdown and energy separation in a Ranque-Hilsch vortex tube. Int. J. Refrig. 2018, 85, 42–57. [Google Scholar] [CrossRef]
- Kirmaci, V.; Kaya, H.; Celebi, I. An experimental and exergy analysis of a thermal performance of a counter flow Ranque-Hilsch vortex tube with different nozzle materials. Int. J. Refrig. 2018, 85, 240–254. [Google Scholar] [CrossRef]
- Kaya, H.; Gunver, F.; Kirmaci, V. Experimental investigation of thermal performance of parallel connected vortex tubes with various nozzle materials. Appl. Therm. Eng. 2018, 136, 287–292. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering application. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Andersson, B.; Andersson, R. Computational Fluid Dynamics for Engineers, 1st ed.; Cambridge University Press: Cambridge, UK, 2012; p. 97. [Google Scholar]
- Pettersson Rief, B.A.; Andersson, H.I. Prediction of turbulence-generated secondary mean flow in a square duct. Flow Turbul. Combust. 2002, 68, 41–61. [Google Scholar] [CrossRef]
- Volov, V.T. Limit energy theorem for gas flow systems. J. Eng. Thermophys. 2018, 27, 489–500. [Google Scholar] [CrossRef]
- Abramovich, G.N. Applied Gas Dynamics, 3rd ed.; Ft. Belvoir Defense Technical Information Center: Washington, CA, USA, 1973. [Google Scholar]
- Poling, B.E.; Thomson, G.H.; Friend, D.G.; Rowley, R.L.; Wilding, W.V. Perry’s Chemical Engineers. Handbook, 8th ed.; McGraw-Hill Companies: New York, NY, USA, 2008. [Google Scholar]
- Richardson, L.F. The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam. Philos. Trans. R. Soc. A 1911, 210, 307–357. [Google Scholar]
- Schwer, L.E. Is your mesh refined enough? Estimating discretization error using GCI. In Proceedings of the LS-DYNA Anwenderforum, Bamberg, Germany, 30 September–1 October 2008; Franz, U., Ed.; DYNAmore GmbH: Stuttgart, Germany, 2008; Volume 1, pp. 45–54. [Google Scholar]
- Volov, V.T.; Lamazhapov, K.D.; Margolin, A.D.; Mishchenko, A.V.; Shmelev, V.M. Vortex glow discharge theory and ways of creating a CO2 laser on its basis. The vortex effect and its application in technology. In Proceedings of the 5th All-Union Scientific and Technical Conference, Kuybyshev, Russia, 13–17 June 1988. [Google Scholar]








| Gas | Reynolds Number |
|---|---|
| He | 81,518 |
| Ar | 293,785 |
| CO2 | 188,425 |
| Air | 280,917 |
| Gas | Tube Diameter d, mm | Nozzle Length ln, mm | Nozzle Height hn, mm | Diffuser Diameter dd, mm | Diffuser Height hd, mm |
|---|---|---|---|---|---|
| Ar | 10 | 1.98 | 1.32 | 50 | 1 |
| He | 36 | 7.14 | 4.76 | 180 | 1.05 |
| CO2 | 15.6 | 2.95 | 1.96 | 78 | 1.56 |
| Air | 10.5 | 2.08 | 1.38 | 52.5 | 3.6 |
| Boundary Condition | Pressure p, atm | Temperature T, K |
|---|---|---|
| Inlet | 3 | 500 |
| Outlet | 1 | 300 |
| Gas | Elements Number for Case No. 1 | Elements Number for Case No. 2 | Elements Number for Case No. 3 |
|---|---|---|---|
| Ar | 2,825,328 | 3,932,631 | 6,028,786 |
| He | 5,291,541 | 7,078,257 | 9,568,966 |
| CO2 | 3,724,078 | 5,128,536 | 7,542,893 |
| Air | 2,969,191 | 4,206,553 | 6,572,770 |
| Gas | Elements Number for Case No. 1 | Elements Number for Case No. 2 | Elements Number for Case No. 3 |
|---|---|---|---|
| Ar | 2,6950,33 | 3,8203,92 | 5,957,826 |
| He | 5,259,305 | 6,891,704 | 9,360,088 |
| CO2 | 3,6697,40 | 5,068,259 | 6,899,789 |
| Air | 2,851,452 | 4,102,444 | 6,513,116 |
| Gas | Maximum Decreasing of Total Temperature T for Case No. 1 | Maximum Decreasing of Total Temperature T for Case No. 2 | Maximum Decreasing of Total Temperature T for Case No. 3 | Grid Convergence Index GCI21, % | Grid Convergence Index GCI32, % |
|---|---|---|---|---|---|
| Ar | 64.6 | 63.87 | 63.43 | 0.94 | 0.38 |
| He | 131.2 | 130.8 | 130.4 | 0.24 | 0.11 |
| CO2 | 56.1 | 56.3 | 55.8 | 0.39 | 0.67 |
| Air | 40.1 | 40.71 | 40.51 | 0.56 | 0.11 |
| Gas | Maximum Decreasing of Total Temperature T, K | Maximum Secondary Swirling Velocity M | Maximum Possible Power Loss and Costs ΔN, W |
|---|---|---|---|
| Ar | 64.6 | 0.94 | 194.5 |
| He | 67.2 | 0.95 | 593.8 |
| CO2 | 45.8 | 0.88 | 209.6 |
| Air | 40.1 | 0.86 | 243.4 |
| Gas | Maximum Decreasing of Total Temperature T for Case No. 1 | Maximum Decreasing of Total Temperature T for Case No. 2 | Maximum Decreasing of Total Temperature T for Case No. 3 | Grid Convergence Index GCI21, % | Grid Convergence Index GCI32, % |
|---|---|---|---|---|---|
| He | 131.2 | 131.08 | 130.7 | 0.06 | 0.17 |
| CO2 | 56.1 | 55.82 | 55.69 | 0.32 | 0.11 |
| Air | 40.7 | 40.64 | 40.51 | 0.32 | 0.50 |
| Gas | Maximum Decreasing of Total Temperature T, K | Maximum Secondary Swirling Velocity M | Maximum Possible Power Loss ΔN, W |
|---|---|---|---|
| Ar | 64.6 | 0.94 | 194.5 |
| He | 131.2 | 0.95 | 8106.1 |
| CO2 | 56.1 | 0.88 | 741.4 |
| Air | 40.7 | 0.86 | 247.9 |
| Gas | Maximum Decreasing of Total Temperature T for Case No. 1 | Maximum Decreasing of Total Temperature T for Case No. 2 | Maximum Decreasing of Total Temperature T for Case No. 3 | Grid Convergence Index GCI21, % | Grid Convergence Index GCI32, % |
|---|---|---|---|---|---|
| Ar | 76.3 | 76.7 | 76.9 | 0.32 | 0.10 |
| He | 159.9 | 160.0 | 159.7 | 0.05 | 0.11 |
| CO2 | 57.6 | 57.3 | 56.8 | 0.84 | 1.51 |
| Air | 43.5 | 43.4 | 43.3 | 1.47 | 1.70 |
| Gas | Maximum Decreasing of Total Temperature T, K | Maximum Secondary Swirling Velocity M | Maximum Possible Power Loss ΔN, W |
|---|---|---|---|
| Ar | 76.3 | 0.95 | 196.7 |
| He | 159.9 | 0.96 | 8263.6 |
| CO2 | 57.6 | 0.88 | 728.6 |
| Air | 43.5 | 0.87 | 271.2 |
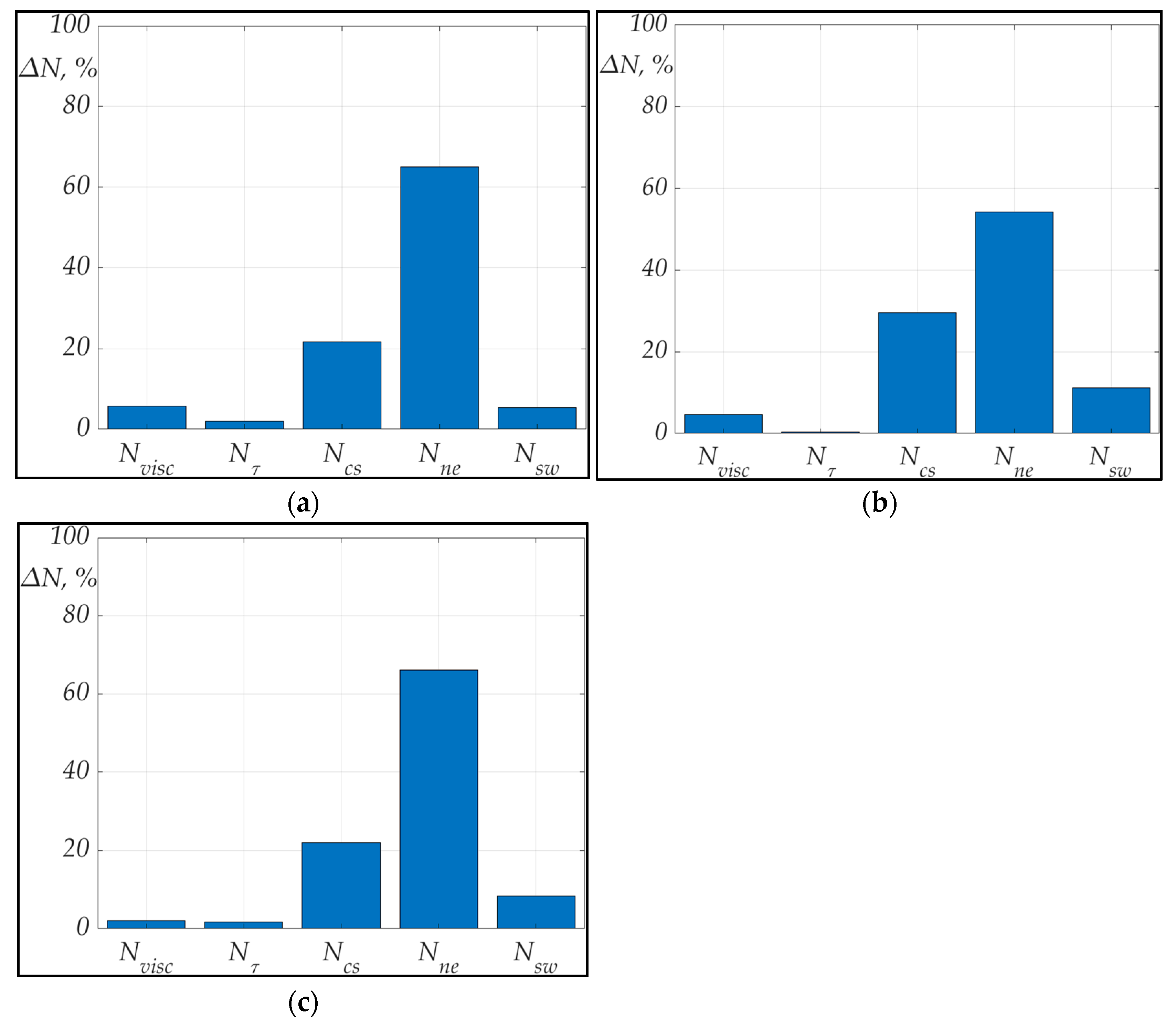
| Case Number | Power Losses on the Viscosity Nvisc, % | Power Losses on the Turbulence Nτ, % | Power Losses on the Expansion Ne, % | Power Losses on the Compression Shock Ncs, % | Power Losses on the Cascaded Swirl Structure Nsw, % |
|---|---|---|---|---|---|
| 1 | 4.83 | 1.85 | 44.1 | 34.2 | 15.1 |
| 2 | 4.72 | 1.83 | 43.1 | 32.4 | 17.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volov, V.; Elisov, N.; Lyaskin, A. Numerical Investigation of the Secondary Swirling in Supersonic Flows of Various Nature Gases. Energies 2021, 14, 8122. https://doi.org/10.3390/en14238122
Volov V, Elisov N, Lyaskin A. Numerical Investigation of the Secondary Swirling in Supersonic Flows of Various Nature Gases. Energies. 2021; 14(23):8122. https://doi.org/10.3390/en14238122
Chicago/Turabian StyleVolov, Vyacheslav, Nikolay Elisov, and Anton Lyaskin. 2021. "Numerical Investigation of the Secondary Swirling in Supersonic Flows of Various Nature Gases" Energies 14, no. 23: 8122. https://doi.org/10.3390/en14238122
APA StyleVolov, V., Elisov, N., & Lyaskin, A. (2021). Numerical Investigation of the Secondary Swirling in Supersonic Flows of Various Nature Gases. Energies, 14(23), 8122. https://doi.org/10.3390/en14238122






