Performance Analysis of a Floating Photovoltaic System and Estimation of the Evaporation Losses Reduction
Abstract
:1. Introduction
2. Materials and Methods
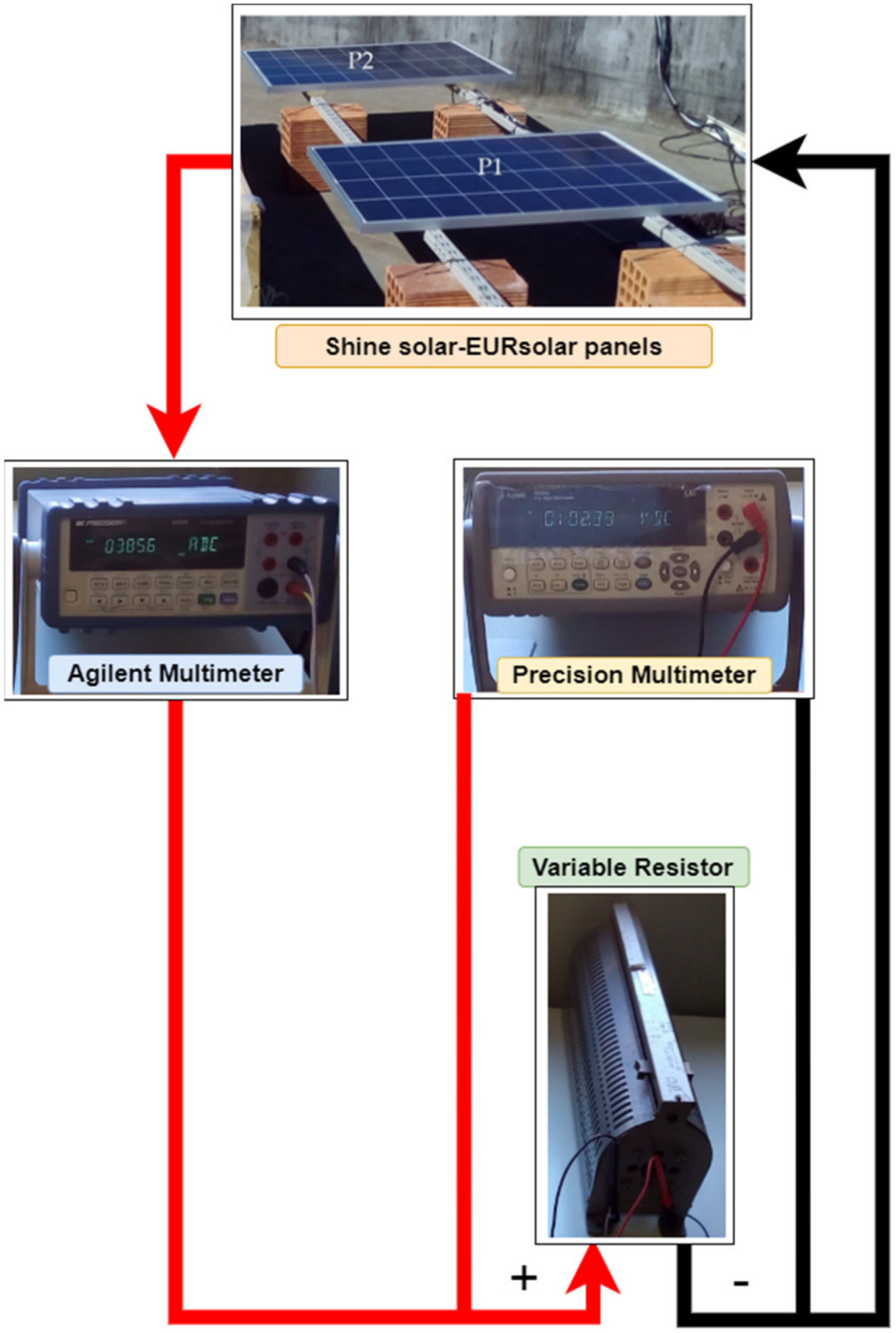
2.1. Instrumentation
2.2. Efficiency Evaluation
2.3. Evaporation Estimation
2.4. Efficiency Calculation and Choice of Load
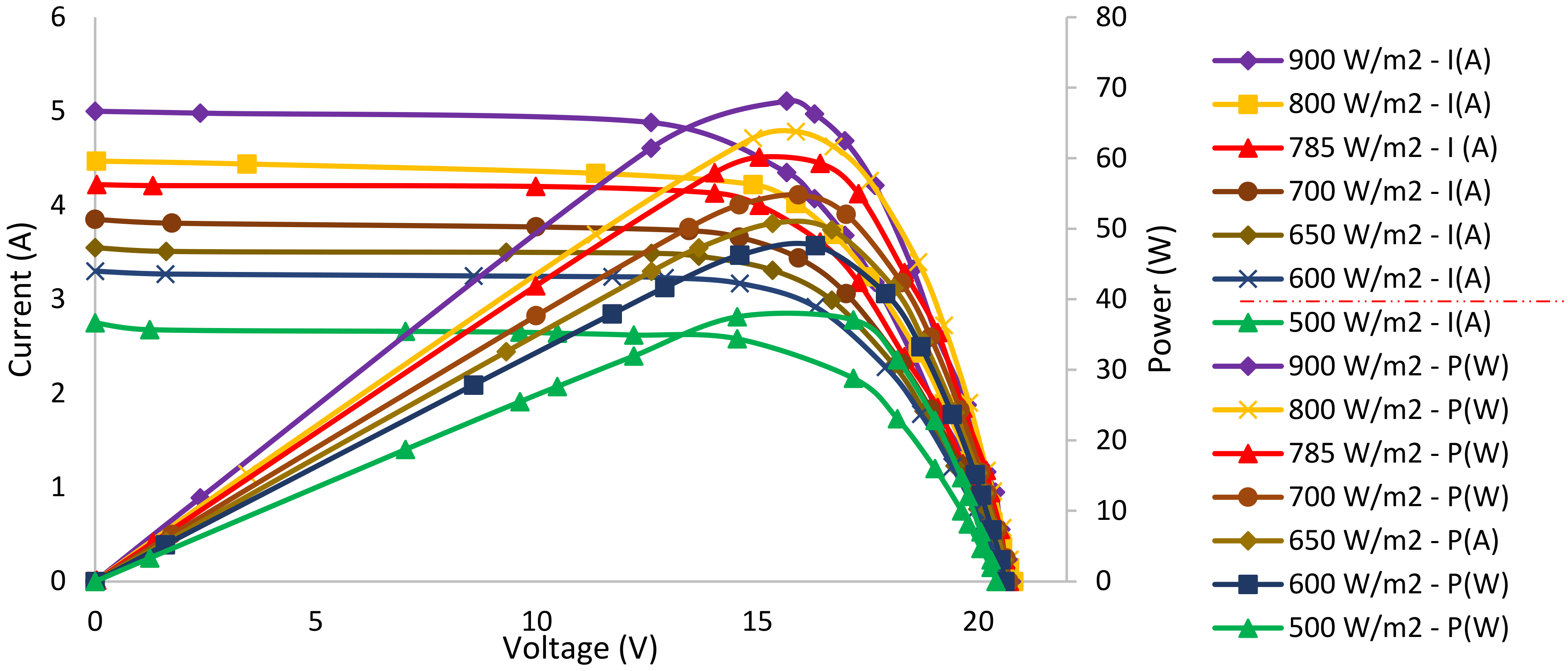
2.5. PV Panels Characteristic Curves
3. PV Panels—Performance Evaluation
3.1. Under Normal Outdoor Conditions
4. Situ Experimental Results, When P1 Placed on Water and P2 in Ambient Conditions
4.1. Temperature Reduction in the Panel (P1) Placed above the Water Surface
4.2. Efficiency Increment Calculation for P1 Panel
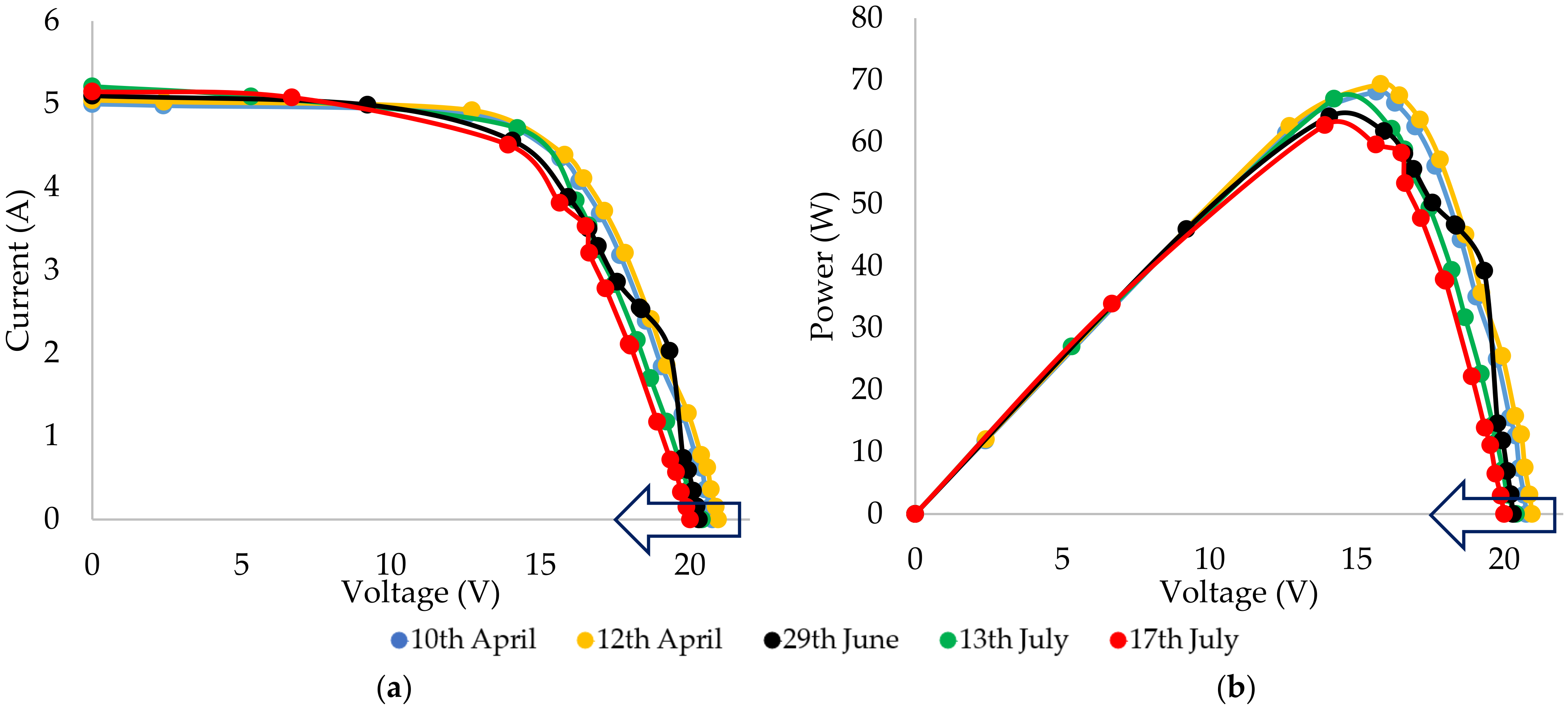
4.2.1. P1 and P2 Efficiencies during the Experiment Phase-I
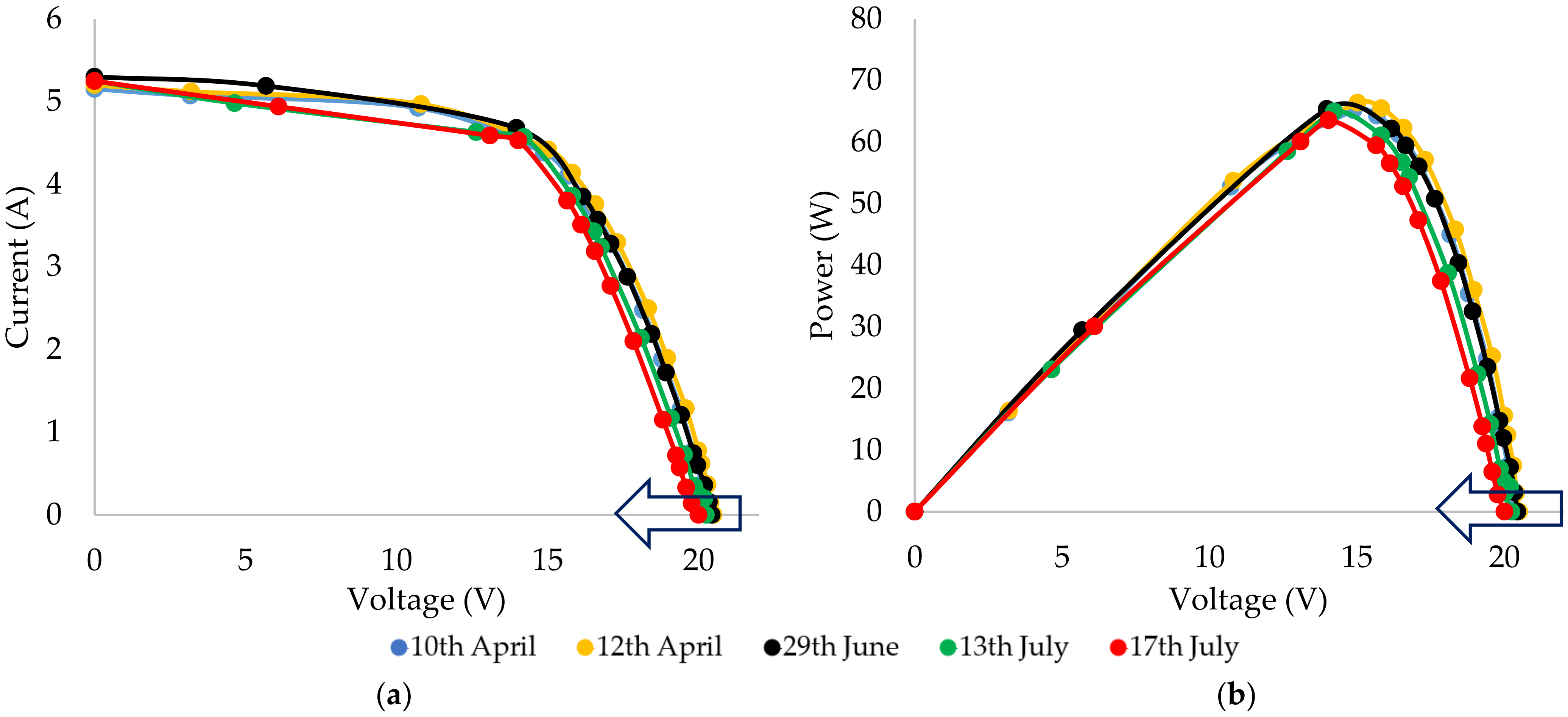
4.2.2. P1 and P2 Efficiencies during the Experiment Phase-II
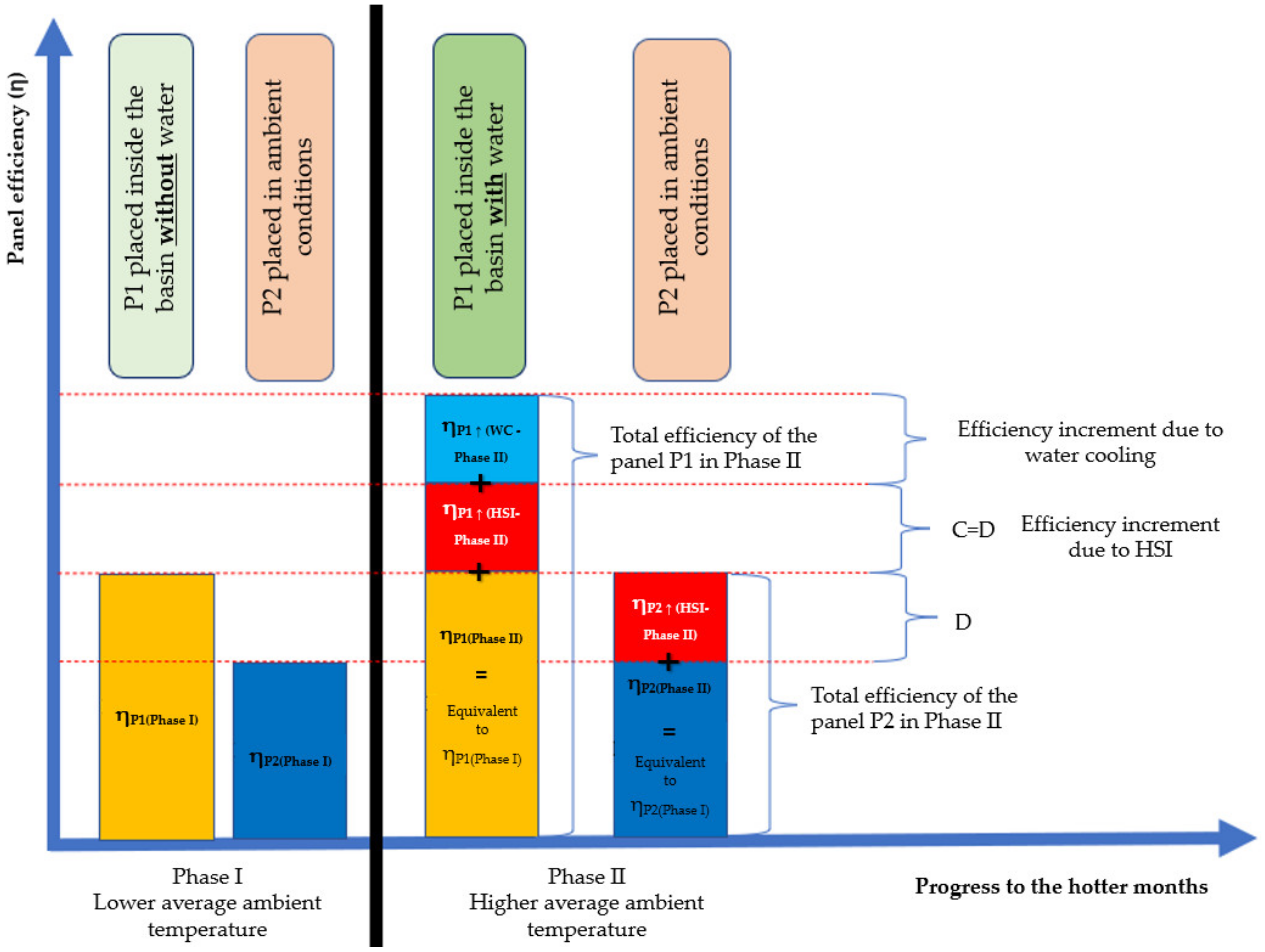
4.2.3. Total Efficiency Increment Due to Water Cooling of P1
5. Evaporation Reduction Estimation
6. Results and Discussion
6.1. Temperature Effect
6.2. Efficiency Increment
6.3. Water Evaporation Reduction
6.4. Efficiency and Evaporation-Integrated Approach
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Krumdieck, S. Transition Engineering- Building a Sustainable Future; CRC Press: Boca Raton, FL, USA, 19 September 2019. [Google Scholar] [CrossRef]
- Razak, A.; Irwan, Y.M.; Leow, W.Z.; Irwanto, M.; Safwati, I.; Zhafarina, M. Investigation of the effect temperature on photovoltaic (PV) panel output performance. Int. J. Adv. Sci. Eng. Inf. Technol. 2016, 6, 682–688. [Google Scholar] [CrossRef]
- Arpino, F.; Cortellessa, G.; Frattolillo, A. Experimental and numerical assessment of photovoltaic collectors performance dependence on frame size and installation technique. Sol. Energy 2015, 118, 7–19. [Google Scholar] [CrossRef]
- Dubey, S.; Sarvaiya, J.N.; Seshadri, B. Temperature dependent photovoltaic (PV) efficiency and its effect on PV production in the world—A review. Energy Procedia 2013, 33, 311–321. [Google Scholar] [CrossRef] [Green Version]
- Grubišić-Čabo, F.; Nižetić, S.; Giuseppe Marco, T. Photovoltaic panels: A review of the cooling techniques. Trans. FAMENA 2016, 40, 63–74. [Google Scholar]
- Bijjargi, Y.S.; Kale, S.S.; Shaikh, K.A. Cooling techniques for photovoltaic module for improving its conversion efficiency: A review. Int. J. Mech. Eng. Technol. (IJMET) 2016, 7, 22–38. [Google Scholar]
- Mazón-Hernández, R.; García-Cascales, J.R.; Vera-García, F.; Káiser, A.S.; Zamora, B. Improving the electrical parameters of a photovoltaic panel by means of an induced or forced air stream. Int. J. Photoenergy 2013, 2013, 830968. [Google Scholar] [CrossRef]
- Gang, P.; Huide, F.; Huijuan, Z.; Jie, J. Performance study and parametric analysis of a novel heat pipe PV/T system. Energy 2012, 37, 384–395. [Google Scholar] [CrossRef]
- Maiti, S.; Banerjee, S.; Vyas, K.; Patel, P.; Ghosh, P.K. Self regulation of photovoltaic module temperature in V-trough using a metal–wax composite phase change matrix. Sol. Energy 2011, 85, 1805–1816. [Google Scholar] [CrossRef]
- Arcuri, N.; Reda, F.; De Simone, M. Energy and thermo-fluid-dynamics evaluations of photovoltaic panels cooled by water and air. Sol. Energy 2014, 105, 147–156. [Google Scholar] [CrossRef]
- Ueda, Y.; Sakurai, T.; Tatebe, S.; Itoh, A.; Kurokawa, K. Performance analysis of PV systems on the water. In Proceedings of the 23rd European Photovoltaic Solar Energy Conference, Valencia, Spain, 1 September 2008; pp. 2670–2673. [Google Scholar]
- Dorobanţu, L.; Popescu, M.O. Increasing the efficiency of photovoltaic panels through cooling water film. UPB Sci. Bull. Ser. C 2013, 75, 223–232. [Google Scholar]
- Hachicha, A.A.; Ghenai, C.; Hamid, A.K. Enhancing the performance of a photovoltaic module using different cooling methods. World Acad. Sci. Eng. Technol. Int. J. Environ. Chem. Ecol. Geol. Geophys. Eng. 2015, 9, 1106–1109. [Google Scholar]
- Rosa-Clot, M.; Tina, G.M. Submerged and Floating Photovoltaic Systems: Modelling, Design and Case Studies; Academic Press: Cambridge, MA, USA, 2017; ISBN 9780128123232, Paperback ISBN 9780128121498. [Google Scholar]
- Abdulgafar, S.A.; Omar, O.S.; Yousif, K.M. Improving the efficiency of polycrystalline solar panel via water immersion method. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 96–101. [Google Scholar]
- Trapani, K. Flexible Floating Thin Film Photovoltaic (PV) Array Concept for Marine and Lacustrine Environments. Ph.D. Thesis, Laurentian University of Sudbury, Sudbury, ON, Canada, 2014. [Google Scholar]
- Redón-Santafé, M.; Ferrer-Gisbert, P.S.; Sánchez-Romero, F.J.; Torregrosa Soler, J.B.; Gozalvez, F.; Javier, J.; Ferrer Gisbert, C.M. Implementation of a photovoltaic floating cover for irrigation reservoirs. J. Clean. Prod. 2014, 66, 568–570. [Google Scholar] [CrossRef] [Green Version]
- Sahu, A.; Yadav, N.; Sudhakar, K. Floating photovoltaic power plant: A review. Renew. Sustain. Energy Rev. 2016, 66, 815–824. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Q.; Lin, H.; Li, H.; Sun, Q. Power generation efficiency and prospects of floating photovoltaic systems. Energy Procedia 2017, 105, 1136–1142. [Google Scholar] [CrossRef]
- Choi, Y.K. A study on power generation analysis of floating PV system considering environmental impact. Int. J. Softw. Eng. Its Appl. 2014, 8, 75–84. [Google Scholar] [CrossRef]
- Floating Photovoltaic. Available online: http://www.nrg-energia.it/fotovoltaico-galleggiante.html (accessed on 7 December 2021).
- Thi, N.D. The Evolution of Floating Solar Photovoltaics; Research Gate: Berlin, Germany, 16 July 2017. [Google Scholar]
- Rosa-Clot, M.; Tina, G.M.; Nizetic, S. Floating photovoltaic plants and wastewater basins: An Australian project. Energy Procedia 2017, 134, 664–674. [Google Scholar] [CrossRef]
- Sukhatme, S.P. Meeting India’s future needs of electricity through renewable energy sources. Curr. Sci. 2011, 101, 624–630. [Google Scholar]
- Piano, S.L.; Mayumi, K. Toward an integrated assessment of the performance of photovoltaic power stations for electricity generation. Appl. Energy 2017, 186, 167–174. [Google Scholar] [CrossRef] [Green Version]
- Martín-Chivelet, N. Photovoltaic potential and land-use estimation methodology. Energy 2016, 94, 233–242. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mekonnen, M.M.; Hoekstra, A.Y. Four billion people facing severe water scarcity. Sci. Adv. 2016, 12, e1500323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taboada, M.E.; Cáceres, L.; Graber, T.A.; Galleguillos, H.R.; Cabeza, L.F.; Rojas, R. Solar water heating system and photovoltaic floating cover to reduce evaporation: Experimental results and modeling. Renew. Energy 2017, 105, 601–615. [Google Scholar] [CrossRef] [Green Version]
- ISO-9060. Solar Energy—Specification and Classification of Instruments for Measuring Hemispherical Solar and Direct Solar Radiation; International Organization for Standardization: Geneva, Switzerland, 2018. [Google Scholar]
- Pandya, R. To Study and Used of Thermocouple for Temperature Measurement in Experiment Work. Vol-1 Issue-4 2015. JARIIE-ISSN(O)-2395-4396. Available online: http://ijariie.com/AdminUploadPdf/TO_STUDY_AND_USED_OF_THERMOCOUPLE_FOR_TEMPERATURE_MEASURMENT_IN_EXPERIMENT_WORK_ijariie1293_volume_1_14_page_181_190.pdf (accessed on 7 December 2021).
- Abdelhady, S.; Abd-Elhady, M.S.; Fouad, M.M. An understanding of the operation of silicon photovoltaic panels. Energy Procedia 2017, 113, 466–475. [Google Scholar] [CrossRef]
- Tobnaghi, D.M.; Madatov, R.; Naderi, D. The effect of temperature on electrical parameters of solar cells. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2013, 2, 6404–6407. [Google Scholar]
- Abd-Elhady, M.S.; Serag, Z.; Kandil, H.A. An innovative solution to the overheating problem of PV panels. Energy Convers. Manag. 2018, 157, 452–459. [Google Scholar] [CrossRef]
- Nelson, J. The Physics of Solar Cells; Imperial College Press: London, UK, 2003; ISBN 978-1-86094-340-9. [Google Scholar]
- Brooks, K.N.; Ffolliott, P.F.; Magner, J.A. Hydrology and the Management of Watersheds; John Wiley & Sons: Hoboken, NJ, USA, October 2012. [Google Scholar] [CrossRef]
- Wang, H.; Fu, B. The temperature effect of water body. Meteorol. Sci. 1991, 11, 233–243. [Google Scholar]






| Ambient Conditions | Panels Temperature | Panels Performance | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tabulated Values Considered Here Are the Average of the Measured Data, Only in the Time Frame When the Available Global Irradiance Was 900 W/m2 | |||||||||||||
| P1 | P2 | P1 | P2 | ||||||||||
| Test Date | Ta | RH | V | TP1 | TP2 | Measured Volt @ PMAX | Measured Current @ PMAX | PMAX | η | Measured Volt @ PMAX | Measured Current @ PMAX | PMAX | η |
| °C | % | m/s | °C | °C | V | A | W | V | A | W | |||
| 10 April | 21.4 | 30 | 1.8 | 46.10 | 46.15 | 15.66 | 4.35 | 68.12 | 11.95% | 14.88 | 4.38 | 65.19 | 11.57% |
| 12 April | 22.8 | 29 | 3.1 | 54.38 | 54.33 | 15.80 | 4.39 | 69.38 | 12.17% | 15.02 | 4.42 | 66.39 | 11.65% |
| 29 June | 27.9 | 61 | 3.3 | 56.57 | 56.29 | 14.22 | 4.71 | 66.98 | 11.75% | 13.97 | 4.68 | 65.38 | 11.47% |
| 13 July | 34.6 | 17 | 5.7 | 57.61 | 57.48 | 14.06 | 4.56 | 64.11 | 11.25% | 14.22 | 4.57 | 64.99 | 11.40% |
| 17 July | 30.0 | 38 | 3.7 | 56.63 | 56.50 | 13.91 | 4.51 | 62.73 | 11.01% | 14.03 | 4.53 | 63.56 | 11.15% |
| Global Radiation Ranges [W/m2] | Experiment—Phase I | Experiment—Phase II | The Total Reduction of Temp. [°C] for the Panel (P1) | ||||
|---|---|---|---|---|---|---|---|
| P1 Placed Inside the Wooden Basin WITHOUT Water | P2 Placed at Ambient Conditions | P1 Placed Inside the Wooden Basin WITH Water | P2 Placed at Ambient Conditions | ||||
| T P1 [°C] | T P2 [°C] | T P1 (pr.1) ↓ | T P1 [°C] | T P2 [°C] | T P1 (pr.2) ↓ | T P1 (Tot.temp) ↓ | |
| When temp. of P1 > P2 | When temp. of P1 < P2 | ||||||
| D | E | F = (D − E) | I | J | K = (I − J) | (−F) + (−K) | |
| 400 < G < 500 | 34.91 | 33.50 | 1.40 | 39.72 | 40.02 | −0.31 | −1.71 |
| 500 < G < 600 | 38.45 | 36.20 | 2.26 | 42.26 | 42.28 | −0.02 | −2.28 |
| 600 < G < 700 | 40.94 | 38.18 | 2.82 | 44.90 | 45.24 | −0.34 | −3.1 |
| 700 < G < 800 | 43.84 | 41.03 | 2.76 | 47.60 | 48.44 | −0.84 | −3.65 |
| 800 < G < 900 | 46.80 | 44.23 | 2.56 | 50.05 | 50.92 | −0.87 | −3.44 |
| 900 < G < 1000 | 48.99 | 47.07 | 1.93 | 52.21 | 53.10 | −0.88 | −2.81 |
| 1000 < G < 1100 | 45.87 | 44.40 | 1.47 | 49.96 | 50.71 | −0.75 | −2.22 |
| 1100 < G < 1200 | 45.78 | 44.23 | 1.55 | 52.64 | 54.02 | −1.38 | −2.93 |
| Average | Reduction | −2.7 | |||||
| ηP1 [%] of the Panel under Observation (P1) | ηP2 [%] of the Panel under Observation (P2) | ||||||
|---|---|---|---|---|---|---|---|
| Global Radiation Ranges | Experiment—Phase-I Wooden Basin WITHOUT Water | Experiment—Phase-II Wooden Basin WITH Water | Efficiency Increment Due to Water Cooling Effect +Efficiency Increment Due to Change in the Ambient Conditions | Experiment—Phase-I Ambient Conditions | Experiment—Phase-II Ambient Conditions | Efficiency Increment Due to the Change in the Ambient Conditions | ηP1↑ TOTAL Increase in Efficiency [%] |
| M | N | O = N − M | P | Q | R = Q − R | S = O − R | |
| 400 < G < 500 | 7.50% | 9.70% | 2.20% | 6.70% | 7.00% | 0.30% | 1.90% |
| 500 < G < 600 | 8.70% | 11.50% | 2.80% | 7.70% | 8.40% | 0.70% | 2.10% |
| 600 < G < 700 | 9.90% | 13.30% | 3.40% | 8.90% | 10.20% | 1.30% | 2.10% |
| 700 < G < 800 | 10.70% | 14.20% | 3.50% | 10.10% | 11.60% | 1.50% | 2.00% |
| 800 < G < 900 | 11.30% | 14.20% | 2.90% | 10.90% | 11.90% | 1.00% | 1.90% |
| 900 < G < 1000 | 11.50% | 13.60% | 2.10% | 11.00% | 11.50% | 0.50% | 1.60% |
| 1000 < G < 1100 | 11.20% | 13.20% | 2.00% | 10.60% | 11.30% | 0.70% | 1.30% |
| 1100 < G < 1200 | 10.50% | 12.30% | 1.80% | 9.90% | 10.60% | 0.70% | 1.10% |
| Avg. | 10.16% | 12.75% | 2.59% | 9.48% | 10.31% | 0.84% | 1.75% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majumder, A.; Innamorati, R.; Frattolillo, A.; Kumar, A.; Gatto, G. Performance Analysis of a Floating Photovoltaic System and Estimation of the Evaporation Losses Reduction. Energies 2021, 14, 8336. https://doi.org/10.3390/en14248336
Majumder A, Innamorati R, Frattolillo A, Kumar A, Gatto G. Performance Analysis of a Floating Photovoltaic System and Estimation of the Evaporation Losses Reduction. Energies. 2021; 14(24):8336. https://doi.org/10.3390/en14248336
Chicago/Turabian StyleMajumder, Arnas, Roberto Innamorati, Andrea Frattolillo, Amit Kumar, and Gianluca Gatto. 2021. "Performance Analysis of a Floating Photovoltaic System and Estimation of the Evaporation Losses Reduction" Energies 14, no. 24: 8336. https://doi.org/10.3390/en14248336
APA StyleMajumder, A., Innamorati, R., Frattolillo, A., Kumar, A., & Gatto, G. (2021). Performance Analysis of a Floating Photovoltaic System and Estimation of the Evaporation Losses Reduction. Energies, 14(24), 8336. https://doi.org/10.3390/en14248336







