Selected Problems of Power MOSFETs Thermal Parameters Measurements

Abstract

In the paper, selected problems that are related to the measurements of thermal parameters of power MOSFETs that are placed on a common heat sink are analysed. The application of the indirect electrical method, the contact method, and the optical method in measuring self and mutual transient thermal impedances of these transistors is presented. The circuits that are required to perform measurements are presented and described. The errors of measurements are assessed for each of the considered methods. In the case of the indirect electrical method, an additional influence of the selection of a thermo-sensitive parameter and the function approximating thermometric characteristics on the measurement error are taken into consideration. The measurement results of the thermal parameters of the investigated transistors that were obtained using the considered measurement methods in various supply conditions are presented and discussed.

1. Introduction

Power MOSFETs are semiconductor devices that are commonly used in electronic circuits. As a result of the current flowing through semiconductor devices and power losses, the temperature of the die of these devices increases over the ambient temperature [1,2]. This phenomenon is called self-heating [3]. The temperature of the die of the semiconductor device may also increase as a result of heat dissipation in the other device and the conduction of this heat, e.g., due to placing both devices on the same heat sink, namely thermal coupling [4,5].

The parameters that are used to characterize the thermal phenomena in electronic devices is transient thermal impedance Z_th(t), and, in the case of simplification of an analysis to the steady state, thermal resistance R_th [6,7].

The knowledge of transient thermal impedance allows computations of a waveform of the chip temperature at a known waveform of the power p(t) that is dissipated in this device [1,8,9,10]. According to the classical theory [1,7,11] the device internal temperature of a discrete semiconductor device can be computed using the following formula.

$$T_j(t)=T_a+{\displaystyle \underset{0}{\overset{t}{\int }}{Z}_{th}^{’}}\left(t-x\right)\cdot p\left(x\right)dx$$

(1)

where T_a denotes the ambient temperature, p(t) is the waveform of the power that is dissipated in this device, whereas Z’_th(t) is a time derivative of its transient thermal impedance. It is worth underlining that for semiconductor devices that are operating in power electronic networks, the waveforms p(t) and T_j(t) are periodical functions at the steady state [12,13]. Of course, the shape of the waveform p(t) does not influence the value of temperature T_j at the steady state, which mostly depends on the mean value of the dissipated power [14].

In the case of a discrete device, transient thermal impedance is defined with the formula [15,16].

$$Z_{th}(t)=\frac{T_j(t)-T_a}{P}$$

(2)

where T_j(t) denotes the waveform of the chip temperature, T_a—the ambient temperature and P is the amplitude of the step of the power that is dissipated in this device. The value of transient thermal impedance Z_th(t) at t → ∞ is equal to thermal resistance R_th.

In turn, in the case of thermal coupling between the devices “i” and “k”, mutual transient impedance is defined with the formula [10].

$$Z_{thi-k}(t)=\frac{T_{ji}(t)-T_a}{P_k},$$

(3)

where T_ji denotes the temperature of the device “i” and P_k the amplitude of the step of the power that is dissipated in the device “k”.

Both transient thermal impedance and thermal resistance may be determined by measurements or computations using the finite element method (FEM) in the determined device working conditions [11,17,18].

The measurements of the values of thermal parameters may be performed using contact methods, optical methods, or electrical methods [15,19].

The contact methods most often use the dependence of resistance (resistance temperature detectors—RTDs), or thermoelectric potential (thermocouples—TCs) of a temperature sensor. Such sensors must stay in touch with the surface, the temperature of which is measured.

In turn, the optical methods are based on a variation of an optical parameter with the temperature. The most frequently used optical parameter, due to common availability of dedicated commercial measurement instrumentation (thermal cameras, pyrometers), is the intensity of infrared radiation [15,19].

In a typical case, when the chips are encapsulated in packages, the disadvantage of the contact and the optical methods is that only the temperature of the package surface T_c can be measured. This temperature may be much lower than the chip temperature T_j and as a result, the values of the thermal parameters that are obtained with these methods may be underestimated [20].

The method that is recommended by the standardisation institutions [15,16] for the measurement of thermal parameters of semiconductor devices is, so called, the indirect electrical method. This method is based on the use of an electrical thermo-sensitive parameter (TSP), the value of which varies with changes of the chip temperature.

For power MOSFETs, the following TSPs are used [21,22]:

(a)

v_GS voltage at a selected value of drain current i_D for the transistor that is operating in the saturation range,

(b)

v_F voltage on the forward-biased body diode at a selected value of this forward current,

(c)

v_DS voltage between the drain and the source of the transistor that are operating in a linear range at a selected value of the drain current.

Carrying out the measurements of thermal parameters with the electrical method requires, among other things, the measurements of the thermometric characteristic, i.e., the dependence binding the selected TSP with the chip temperature—TSP(T_j) and next finding a function approximating this dependence. In the literature, for the approximation (modelling) of the TSP(T_j) dependence, the linear function is commonly applied [2,15,16].

The paper [21] shows the advantages of using selected TSPs of the power MOS transistor, whereas the paper [14] shows the influence of the selection of the TSP of the IGBT on the accuracy of determining its internal temperature. On the other hand, in [22] it is shown that the non-uniformity of the temperature distribution in the semiconductor die of the power MOS transistor may exceed even 50 K and the justifiability of using a compact thermal model of this device is discussed.

In the known literature, the lack of a systematic analysis of the typically used measurement methods of thermal parameters of semiconductor devices is observed. Typically used simplifications can strongly limit the accuracy of these methods.

In this paper, the selected problems that are related to the measurements of thermal parameters of power MOSFETs placed on a common heat sink are analysed. The application of the indirect electrical method, the contact method, and the optical method in measuring self and transfer transient thermal impedances of these transistors is presented. The measurement errors of each of the considered methods are formulated. For the indirect electrical methods, the influence of the selection of TSPs and the function approximating thermometric characteristics on the measurement error are taken into consideration. Some results that illustrate the influence of the used measurement method on the obtained waveforms of transient thermal impedances are presented and discussed.

The investigated MOSFETs that were coupled thermally via a common heat sink are described in Section 2. The methods and the setups for measuring the thermal parameters of the investigated transistors with the electrical method are described in Section 3. In Section 4, the problem of credible measurements and approximation of thermometric characteristics of the investigated transistors is analysed. In Section 5 the measurement error of thermal resistance in each of the considered measurement methods is analysed. The exemplary results of the measurements of self and mutual transient thermal impedances of the investigated MOSFETs are presented and discussed in Section 6.

2. Tested Devices

The devices that were being tested are shown in Figure 1. The set contained two IRF 840 [23] power MOSFETs that were situated in TO-220 packages that were mounted on a heat-sink made of extruded aluminum and produced by Stonecold [24]. The heat-sink had the dimensions: 50 × 74 × 30 mm and mass equal to 96 g.

Transistor M₁ is the device where the power was dissipated and M₂ is the device that was thermally coupled with M₁ via a common heat-sink. Both transistors were mounted to the heat sink with M3 bolts using a dynamometric wrench and the torque equal to 1 N∙m. The distance between the axes of the symmetry of the packages was 10 mm and 5 mm between the inner edges of the packages. As the thermal interface between the package of the M₁ transistor and the heat-sink, the thermal compound Electrolube HTC was used [25]. Due to different polarization and different drain potentials of the transistors M₁ and M₂ during the measurements, M₂ was electrically insulated from the heat-sink with the Teflon insert and the thermal pad Fisher Elektronik KAP 220 G [26]. The thermal resistance of the pad was lower than 0.15 K/W [26].

3. Measurement Methods

In this section, the applied measurement methods are characterised. In Section 3.1 the details of the contact method are given; in Section 3.2, the details of the optical method are given; and in Section 3.3, the details of the electrical method are given. In all the three methods, the Formulas (1) and (2) are used. Power P is a product of the measured drain current I_H and the drain-source voltage V_H of transistor M₁. The chip temperature was determined with the methods that are described in Section 3.1, Section 3.2, and Section 3.3.

3.1. Contact Method

The measurements with the contact method were carried out using the resistance temperature detectors (RTD) Proffuse PT1000-550 [27] that were placed in the middle of each transistor package. The thermo-conducting epoxy, Amepox Microelectronics Thermopox 85CT of thermal conductivity 1.4–2.2 W/m∙K [28], was used to attach them to the transistors package surface. The sensors had the dimensions 2.3 × 2.1 × 0.9 mm.

During the measurements, both of the sensors were fed with the current I_M = 1 mA from the measurement source Keithley 2651A working in the current source mode.

The temperature of the surface of each transistor was calculated from the formula

$$T_c(t)=T_0+\frac{v_{RTD}(t)/I_M-R_{T_0}}{R_{T_0}\cdot \alpha },$$

(4)

where R_T0 denotes the resistance of the sensor in the reference temperature T₀ = 273.15 K and v_RTD is a voltage drop on the sensor resistance at current I_M. The temperature coefficient of resistance α = 3850 ppm/K. It was assumed that the sensors had the linear characteristic R(T).

The measurement error of the employed sensors is equal to ΔT = ± (0.3 + 0.005 |T|), where T is the measured value of the temperature expressed in °C [27]. The thermal resistance of the sensors is equal to 400 K/W. In the case when I_M = 1 mA, an increase of the sensor temperature resulting from its the self-heating does not exceed 0.63 °C in the temperature range below 150 °C.

3.2. Optical Method

The optical method allows contactless measurements of the temperature of the device package thanks to detection of the infrared radiation that is emitted by this surface. The measurements with the optical method were carried out with the Optex PT-3S pyrometer and two flakes of the calibration tape Optex HB250 of emissivity ε = 0.95 and the dimensions 5 × 5 mm that were stuck to the surface of the heat sink on the opposite side to the baseplate of the transistors’ packages.

The diameter of the measurement field of the selected pyrometer lays in a range 2.5 to 4 mm. According to the producer’s data [29] the absolute measurement error of the temperature is equal to ±3 °C, at the measured surface emissivity ε = 0.95 and the ambient temperature 25 °C.

3.3. Electrical Method

To carry out the measurements using the indirect electrical method, the measurement setups that are shown in Figure 2, Figure 3 and Figure 4 were designed and constructed. Each of the setups allows the measurements of the die temperature of the transistor M₁ using different TSPs.

These parameters are: voltage v_DS that is proportional to the resistance R_DS(on) of the channel of the turned-on M₁ transistor that is operating in the linear range (Figure 2), voltage v_GS of the transistor that is operating in the saturation range (Figure 3), and the voltage v_F on the forward biased body diode (Figure 4). The measurements of the chip temperature of transistor M₂ in all the cases were carried out only using voltage v_F on the forward biased body diode.

Both the values of the TSPs and a voltage drop v_RTD on both the RTDs were logged with the Measurement Computing USB-2404-60 module [30].

In all the three cases, the measurement is performed in 5 stages:

• Measurement of thermometric characteristics describing dependences of the selected TSP on the temperature. Performing the measurement requires enclosing the transistors in the thermostatic chamber, where the temperature is set up for each measurement point. At this stage, switch S₁ in the setups from Figure 2 and Figure 3 and switches S₁ and S₂ from Figure 4 are set to the position 2.
• Selection of the function approximating the thermometric characteristic T_j(TSP) and calculation of its coefficients.
• Heating the transistors up to the thermally steady state by dissipation of power P that is equal to the product of voltage V_DS1 and current I₁ in transistor M₁. At this measurement stage, the switch S₁ in the setups from Figure 2 and Figure 3 and switches S₁ and S₂ in the setup from Figure 4 are set to the position 1. The temperature of the die of the transistor M₁ increases as a result of self-heating and the temperature of M₂ increases as a result of mutual thermal coupling with transistor M₁. This stage of measurement ends after the thermally steady state in both transistors is reached.
• Recording the TSP waveforms after a change of the positions of switch S₁ in the setups from Figure 2 and Figure 3, as well as switches S₁ and S₂ in the setups from Figure 4, from the position 1 to 2. The measurement ends when the transistors M₁ and M₂ cool down to the ambient temperature.
• Computation of Z_th(t) and Z_th12(t) from the formulas

$$Z_{th}(t)=\frac{a_2(TS{P}_1^2\left(t\right)-TS{P}_1^2\left(t=0\right))+b_2(TS{P}_1\left(t\right)-TS{P}_1\left(t=0\right))}{I_1\cdot V_{DS1}},$$

(5)

$$Z_{th12}(t)=\frac{a_2(TS{P}_2^2\left(t\right)-TS{P}_2^2\left(t=0\right))+b_2(TS{P}_2\left(t\right)-TS{P}_2\left(t=0\right))}{I_1\cdot V_{DS1}},$$

(6)

where a₂ and b₂ are the coefficients of the function approximating the thermometric characteristics T_j(TSP₁) of transistor M₁ or T_j(TSP₂) of transistor M₂.

Each of the measurement setups is composed of 3 main circuits: the circuit of the polarization of M₁ transistor, the circuit of the polarization of the M₂ transistor, and the measurement module with the PC. Current I_M1 of transistor M₁ in the setup form Figure 2 is determined by the measurement source Keithley 2651A working in the current source mode and in the setups from Figure 3 and Figure 4—the voltage source V_M and resistor R_M. The investigated transistors M₁ and M₂ are thermally coupled by the common heat-sink.

This module is composed of four independent measurement channels containing 24-bit Delta-Sigma DACs and it allows achieving the sampling rate in a range from 1.613 kS/s to 50 kS/s. The measurement range of the module embraces voltages from −60 V to 60 V. The measurements were performed at the sampling rate f_S = 10 kS/s. The results were logged in with the use of the dedicated software MCScan and the PC [31,32].

4. Measurement and Approximation of Thermometric Characteristics

Using the measurement setups that are shown in Figure 2, Figure 3 and Figure 4, the thermometric characteristics of transistor M₁ operating at various values of current I_M were measured. The results of the measurements are shown in the Figure 5, Figure 6 and Figure 7. The measurement points are marked with dots and the approximating functions with lines. The solid and dashed lines were applied for the quadratic and the linear approximating functions, respectively.

Figure 5 illustrates the thermometric characteristics v_F(T_j) of transistor M₁ that were measured at selected values of the forward current of the body diode I_F = I_M.

As it is seen, the measured characteristics are slightly nonlinear in the temperature range from 20 to 140 °C for all the considered I_M current values ranging from 1 mA to 20 mA. Quadratic and linear approximation lines are almost indistinguishable. The slope of the linear approximating function varies from −2.2 mV/°C for I_M = 20 mA to −2.5 mV/°C at I_M = 1 mA.

In turn, Figure 6 shows the thermometric characteristics v_DS(T_j) that were measured in the setup shown in Figure 2 at selected values of the drain current i_D = I_M and v_GS = 15 V.

As it is seen, the measured dependences v_DS(T_j) are nonlinearly increasing functions. The slope of the considered characteristics strongly depends on the drain current value I_M. The slope of the linear approximating function increases from about 0.4 mV/°C for I_M = 50 mA to about 2.45 mV/°C for I_M = 0.3 A. It is worth noticing that the measured v_DS voltage values at the considered I_M current values are low and therefore may be susceptible to interference. Obtaining the value of v_DS ranging in several hundred millivolts requires the measurement current of at least 0.2 A. The value of this current should be selected depending on the resistance R_DS(on), which for the transistor under consideration is 0.85 Ω at T_a = 25 °C and increases with the temperature to 1.95 Ω at T_a = 150 °C [23].

R_DS(on) of many contemporary power MOS transistors is even several hundred times lower, which means that the desired v_DS voltage value can be obtained only with I_M current of even several dozen amperes. This can be a significant technical problem when a voltage drop on the resistance of the channel of the turned on transistor v_DS is used to measure the thermal resistance of MOSFETs.

Figure 7 shows the thermometric characteristics v_GS(T_j) that were measured at selected values of the drain current i_D = I_M and the fixed value of the drain-source voltage v_DS = 7 V (Figure 7a) and v_DS = 20 V (Figure 7b), respectively.

As can be seen in Figure 7a, at a low value of voltage v_DS, the thermometric characteristics at the same drain current correspond to a higher v_GS value. It is related to the intuitively obvious situation when an increase in the drain current requires an increase in voltage v_GS. The slope of the linear approximation of v_GS(T_j) characteristics is a decreasing function of current i_D and varies from −6.6 mV/°C, at I_M = 1 mA to −4.9 mV/°C, at I_M = 0.1 A.

In turn, in Figure 7b, the results at a higher value of voltage v_DS = 20 V are shown. The influence of current i_D on voltage v_GS at the fixed temperature is described by a function having the maximum at I_M = 10 mA. The measured dependences v_GS(T_j) are monotonically decreasing functions and the slope of their linear approximation decreases from −6.6 mV/°C at I_M = 1 mA to −2.4 mV/°C at I_M = 50 mA. The observed influence of the drain current on the considered thermometric characteristics for currents I_M > 10 mA may be caused by a self-heating phenomenon. For the low values of current i_D (i_D ≤ 10 mA), the investigated transistor operates in the sub-threshold range, whereas for higher values of this current—in the saturation range. As it is clear from, e.g., the papers [33,34] for a transistor operating in the sub-threshold range, that the dependence i_D(v_GS) resulting from self-heating is an ambiguous relation.

In the paper [35], it is shown that an important influence on the characteristics v_GS(T_j)@I_M = const has the value of voltage v_DS. For example, for the IRF 840 transistor the values of voltage v_GS at a selected value, the drain current and the temperature differ between each other even by 1 V at voltage v_DS changes by 5 V. These differences are particularly visible at higher values of the drain current (exceeding several dozen mA). At low values of this current (up to 10 mA), the voltage v_DS has practically no influence on the characteristics under consideration.

From amongst the characteristics that are shown in Figure 5, Figure 6 and Figure 7, one was selected for each TSP. In the case of v_F for further consideration, the characteristic that was measured at current I_M = 1 mA was selected. In the case of v_DS, the characteristic that was measured at I_M = 0.3 A and v_GS = 15 V was chosen. In the case of v_GS, the characteristic that was measured at I_M = 5 mA was selected, which is identical at the changes of v_DS in a wide range. The independence of v_GS on v_DS changes is important because, in the setup shown in Figure 3, after the switchover of transistor M₁ from the heating stage to the measurement stage, its v_DS voltage shifts by several volts. In the case when the characteristics for various v_DS were not the same, the additional error that is related to a change of the slope of the thermometric characteristic would appear.

From the literature it appears that thermometric characteristics are typically approximated with linear functions [2,16]. Due to the nonlinearity of the measured dependences, TSP(T_j), such approximation may be a source of error.

As it is seen in Figure 5, Figure 6 and Figure 7, the measured dependences can be approximated with good accuracy with a polynomial of the second order. In Figure 8, the dependences of the difference of the transistor M₁ die temperature were computed with the linear T_jl and the quadratic approximation of selected characteristics for further measurements, referring to the same chip temperature T_j for all the three considered TSPs, are presented.

The temperature T_jl was computed from the formula

$$T_{jl}=a_1\cdot TSP+b_1,$$

(7)

and T_jq from the formula

$$T_{jq}=a_2\cdot TS{P}^2+b_2\cdot TSP+c_2.$$

(8)

In both of the formulas, the TSP denotes the value of a thermal parameter, hence a₁, b₁, a₂, b₂, and c₂ are the coefficients of the functions approximating the dependences T_j(TSP).

To illustrate the dependence of the difference, T_jl–T_jq form all the TSPs that are being considered on the transistor M₁ die temperature in a single figure, a variable of the x-axis was swapped from the TSP to T_j. To obtain that, it was assumed that as a result of dissipation of the power equal to 25 W in transistor M₁ in the ambient temperature 20 °C, the transistor temperature increased to 145 °C. The value of R_th that was calculated at such assumptions is equal to 5 K/W.

As is seen in Figure 8, the biggest differences between the chip temperature that were calculated using the linear and the quadratic approximations occurred in the middle and at the extremes of the considered temperature range and are directly related to the nonlinearity of the dependence TSP(T_j). In the case of v_F the difference is below 1 °C, but in the case of v_DS, it reaches 6.5 °C at the chip temperature 145 °C.

In turn, in the case of the measurements of transient thermal impedance and thermal resistance, the value of an increase of the die temperature over the ambient temperature ΔT_j has an important influence. In Figure 9 the difference of an increase of the chip temperature over the ambient temperature that is calculated at the linear ΔT_jl and the quadratic ΔT_jq approximations of the thermometric characteristics for the same conditions as for the case in Figure 7 is shown.

The value of an increase of the chip temperature over the ambient temperature in the case of the linear approximation was computed from the formula

$$\Delta T_{jl}=a_1\cdot \left(TSP-TS{P}_a\right),$$

(9)

and in the case of the quadratic approximation form the formula

$$\Delta T_{jq}=a_2\cdot \left(TS{P}^2-TS{P}_a^2\right)+b_2\cdot \left(TSP-TS{P}_a\right).$$

(10)

where TSP_a denotes the TSP value at temperature T_a.

As it is seen, the value of the difference of the temperature ΔT_jl − ΔT_jq that is being considered is the biggest at T_j = 90 °C. In the case of selection of v_F as a TSP, this difference does not exceed 1 °C, for v_GS it is equal to 5 °C and for v_DS it reaches 8.5 °C. The conclusion from the presented analysis is that the selection of the approximating function may have an important influence on the measured value of the MOSFET transistor chip temperature whilst the indirect electrical method is applied. The use of the linear approximation for the nonlinear dependence of v_DS(T_j)@I_M = const may cause an underestimation of the measured increase of the temperature T_j over the ambient temperature T_a even by 8.5 °C and as a result the underestimation of the value of Z_th(t) and R_th. The differences between the obtained results of estimation values of the devices internal temperature using the linear and quadratic approximation of thermometric characteristics result from the nonlinearity of these characteristics that are visible in Figure 5, Figure 6 and Figure 7.

5. Analysis of the Measurement Error

One of the features of the measurement method in deciding about its applicability is the measurement error. In this section the influence of selected factors on the measurement error of the power MOSFETs thermal resistance carried out using the methods that are described in the Section 3 is analysed.

The measurement error of thermal resistance can be calculated using the complete differential method [20] in relation to the Formula (2). In such a case, the dependence describing the absolute measurement error of R_th is obtained

$$\Delta R_{th}=\pm \left\{\frac{\Delta T_j+\Delta T_a}{P}+\frac{T_j-T_a}{P^2}\cdot \Delta P\right\}=\pm \left\{\frac{\Delta T_j+\Delta T_a}{P}+\frac{R_{th}}{P}\cdot \Delta P\right\}$$

(11)

and the relative error of the measurement is given by the formula

$$\frac{\Delta R_{th}}{R_{th}}=\pm \left\{\frac{\Delta T_j+\Delta T_a}{T_j-T_a}+\frac{\Delta P}{P}\right\}.$$

(12)

As it results from the Formula (10), the absolute value of the thermal resistance measurement is reversely proportional to the value of an increase in the die temperature over the ambient temperature and to the power that is dissipated in the transistor, causing this temperature increase.

The measurement error ΔP of the power is identical for each of the considered measurement methods and with the appropriate selection of measuring instruments, it does not exceed 0.1% of the measured value of the power P [20]. In turn, the error in the measurements of the internal temperature ΔT_j is different for each of the considered measurement methods. For the contact and optical methods, apart from the error in measuring the temperature of the surface, to which the thermo-resistor is attached, or for which the infrared radiation intensity is measured, there is an error that is related to the temperature difference between the semiconductor die and the housing of the investigated transistor. The value of this error is equal to the product of the power that is lost in the measured transistor and thermal resistance between its die and the case R_thj-c [20]. The value of this parameter is declared by the manufacturer of the transistor. For IRF840 transistor R_thj-c = 0.5 K/W [23].

To illustrate the influence of selection of the thermo-sensitive parameter and the method of approximation of the thermometric characteristic on the results of the measurements of thermal parameters of power MOSFETs by electrical methods, an error analysis of the internal temperature measurement using these methods was carried out.

Using the least squares method, the coefficients of the functions approximating the dependences T_j(v_DS), T_j(v_GS) and T_j(v_F) were determined. The values of the standard error of the internal temperature estimate T_j were also determined from the following dependence [36,37,38,39].

$$s=\sqrt{\frac{{{\displaystyle \sum _{i=1}^n\left(T_{ji}-\stackrel{}{T_{jie}}\right)}}^2}{n-k-1}},$$

(13)

where T_ji is the value of the internal temperature at the i-th measurement point, T_jie is the temperature value at this point determined from the approximating function, n is the number of measurement points, and k is the degree of the approximating polynomial. The calculated standard error values for each TSP are shown in

Table 1. Standard error of the approximation of thermometric characteristics for different TSPs and the linear and square approximating function.

Regression	TSP	vF	vDS	vGS
Linear	s [°C]	0.45	3.77	2.02
Quadratic	s [°C]	0.10	0.76	0.12

.

As can be seen from the comparison of the values of the errors that are collected in Table 1, the use of the square approximation of the dependence T_j(TSP) results in a significant reduction of the standard error of determining temperature T_j compared to the linear approximation. In the case of the linear approximation, the error in determining temperature T_j is the smallest when using voltage v_F as a thermo-sensitive parameter and the greatest when using voltage v_DS as a TSP; this error increases from 0.12 to 3.77 °C. With the quadratic approximation, this error decreases and has the values ranging from 0.1 °C using v_F as a TSP to 0.76 °C using v_DS as a TSP.

The temperature measurement error T_j resulting from the measurement inaccuracy of a TSP is equal to the product of the voltage measurement error by the measuring module and the characteristic slope T_j(TSP). For the measuring module that is used, the absolute error of the voltage measurement is about 5 mV [30]. In turn, the slope of the characteristic T_j(TSP) varies from about 0.5 K/mV using voltage v_F as a TSP to 0.16 K/mV using voltage v_GS as a TSP.

Figure 10 shows the dependence of the relative error of measurement of thermal resistance on the power that is dissipated in the transistor M₁, as determined from the Formula (10). It is assumed in the calculations that the values of the absolute error of measurements of the internal and ambient temperature are equal to each other. In this figure, the dashed lines correspond to the linear approximation of the thermometric characteristics and the solid lines correspond to the square approximation. The colors correspond to the particular thermo-sensitive parameters: red lines—voltage v_DS, blue lines—voltage v_GS, and green lines—voltage v_F.

As can be seen, the dependence of the relative measurement error of thermal resistance R_th of the transistor M₁ on the power that is dissipated in this transistor is a decreasing function of power. This shape of the considered dependences shows that the main component of the measurement error depends on the error of determining an increase in the device’s internal temperature value. The absolute value of this error is constant, but the relative error decreases with an increase in the internal temperature value and consequently in the dissipated power value. The value of thermal resistance is most accurately determined using the quadratic approximation of the thermometric characteristics and the use of v_F1 and v_GS as a thermo-sensitive parameter. In such a case, the measurement error does not exceed 1% in the entire considered range of power values. The use of the linear approximation of the dependence T_j(v_F) causes an increase in the measurement error to 3.7% at the power equal to 5 W and 0.8% at the power equal to 25 W. Using the quadratic approximation and v_DS voltage causes the measurement error to increase to 6% at 5 W and 1.3% at the power of 25 W. The measurement of R_th using v_GS and v_DS as a TSP and the linear approximation is burdened with a much bigger error, reaching as much as 30% at 5 W and decreasing to 6% at 25 W. It should be noted that the values that are shown in Figure 10 are the maximum values of the measurement error.

6. Results

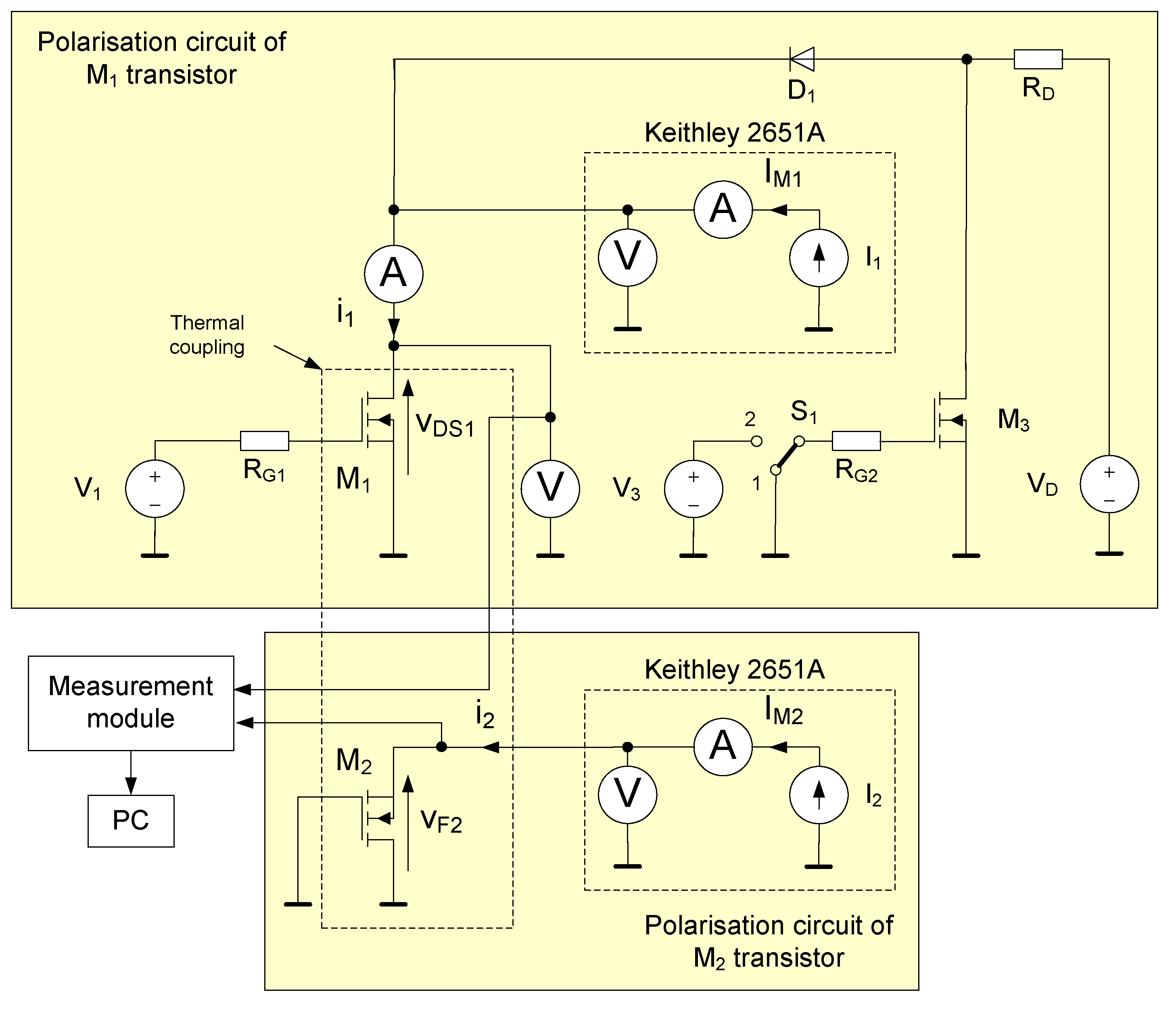
To verify the practical usefulness of the presented methods, the measurements of self and mutual thermal transient impedances for two power MOSFETs that were mounted on a heat-sink were carried out in the manner as shown in Figure 1. The measurements were made using the methods and the measurement systems that are described in Section 3 at different values of the power that was dissipated in transistor M₁. In the case of the electrical method, three thermo-sensitive parameters as well as the linear and quadratic approximations of thermometric characteristics were used. Some of the measurements that were made with the electrical method were repeated with the use of the contact and optical methods.

Figure 11a shows the dependence of thermal resistance of the transistor M₁ on the power that was measured with the use of different thermo-sensitive parameters as well as the linear and the quadratic approximations of thermometric characteristics. Figure 11b shows the dependence of mutual thermal resistance between transistors M₁ and M₂ on the power that was dissipated in transistor M₁. The measurements were performed using the electrical, optical, and contact methods. The solid lines mark the results that were obtained using the square approximation of the thermometric characteristic and the dashed lines mark the results that were obtained using the linear approximation of this characteristic.

As shown in Figure 11a, the measured dependences R_th(p) are non-linear and the differences in the results that were obtained using the square and linear approximations of thermometric characteristics and different thermo-sensitive parameters decrease with the increasing power. The measured values of thermal resistance of the investigated device also decreased with an increase of the power that was dissipated in the transistor, with the exception of the characteristic that was obtained using voltage v_DS as a TSP and the linear approximation of the thermometric characteristic. In this case, the dependence R_th(p) had a local minimum, which had no physical justification. The differences in the thermal resistance that were obtained with the use of the linear and non-linear approximations of thermometric characteristics for this thermo-sensitive parameter were the biggest and reached 24% at the power p = 5 W.

At the same value of power, smaller differences in the value R_th were obtained by using voltage v_GS as a thermo-sensitive parameter. In this case, the thermal resistance values that were determined on the basis of the linear and quadratic approximations of thermometric characteristics did not differ from each other by more than 10%. In the case of voltage v_F, the maximum difference in the value R_th was less than 2%.

The thermal resistance values that were obtained using v_GS and v_F voltages and the square approximation of thermometric characteristics differed by less than 5% over the entire power range under consideration. It should be noted that for p > 20 W, the results that were obtained using v_F, v_GS, and the linear and quadratic approximations, as well as the results that were obtained using v_DS and the linear approximation differed by about 4% at 20 W and by 3.3% at the power of 24 W. Despite the use of the quadratic approximation of the thermometric characteristic, in the case of voltage v_DS the result was higher by the approximation of high values of the power p, e.g., at 24 W, and may be associated with the difficulty in providing constant cooling conditions in a situation where the main mechanism of the device cooling is natural convection. In such a situation, even a slight movement of the air around the heat sink can significantly affect the internal temperature of the investigated transistors [40]. The use of the linear approximation of thermometric characteristics caused a decrease in the thermal resistance value by up to 20%.

The measured values of mutual thermal resistance R_th21 were lower than the corresponding values of thermal resistance R_th. For all of the measurement methods, a monotonically decreasing dependence of R_th21(p) was obtained. The values of R_th21 and R_th that were obtained with the optical and contact methods were, in all the cases, less than the corresponding values of these parameters that were measured with the electrical method. The differences between these values were up to 50% in the case of R_th and 35% in the case of R_th21.

An important problem is not only the reliable measurement of the thermal resistance value, but also the measurements of the transient thermal impedance waveforms. This problem is important because the values of thermal time constants are determined using the transient thermal impedance waveforms [11] and are used as parameters of thermal models that allow, e.g., for determination of the internal temperature waveforms of the tested devices.

Figure 12 compares the waveforms of transient thermal impedance of transistor M₁ that was measured in the setup shown in Figure 3, using the linear (Figure 12a) and the quadratic (Figure 12b) approximations of its thermometric characteristics T_j(v_GS). The presented results were obtained for different values of power that were dissipated in this transistor.

As can be seen, the waveforms of transient thermal impedance of transistor M₁ that were obtained using the linear and quadratic approximation of thermometric characteristics and voltage v_GS as a thermo-sensitive parameter differed significantly from each other. For the time t = 10 s, the differences reached as much as 15%. The linear approximation of the non-linear thermometric characteristic caused a distortion of the transient thermal impedance waveforms, including the overestimation or underestimation of the thermal resistance value. Figure 12a shows the non-physical observation that the thermal resistance that was obtained at p = 20 W was lower than that obtained at p = 24 W, and from Figure 12b it can be seen that the opposite relation is true.

The use of the cooling curve in the measurements of Z_th(t) caused a reversal of the trend resulting from Figure 8 and Figure 9, consisting in lowering the value of the internal temperature and the difference T_j − T_a using the linear approximation of the dependence T_j(TSP). In the case of measuring the waveform Z_th(t), the value of this parameter was underestimated at the extremes of the temperature interval that was considered in Figure 8 and overestimated in the central part of this interval.

In turn, Figure 13 shows the transient thermal impedance waveforms that were obtained using voltage v_DS and the approximation of the thermometric characteristic by a square function.

As can be seen, Z_th(t) waveforms that were obtained for different power values in the interval t < 200 s overlap. This transient thermal impedance pattern is associated with the removal of heat from the die of transistor M₁ by the heat conductivity mechanism. The Z_th(t) waveforms in the time interval t > 200 s for different values of the power that was dissipated in the transistor M₁ are related to an increase in the efficiency of natural convection with an increase of the temperature of the heat-sink, on which both the transistors are mounted [40]. With an increase in the power in the range from 5 to 24.6 W, the value of thermal resistance decreased by over 20%.

Figure 14 shows the waveforms of mutual thermal impedance Z_th21(t) between the transistors at selected values of the power that was dissipated in transistor M₁.

The recording of Z_th21(t) waveforms allows for the analysis of delays in the heat flow in the tested system. As it is visible, the waveform starts after about 1 s from switching on the power dissipated in transistor M₁. This is the time that is necessary for thermal energy to travel from the die of transistor M₁ to the die of transistor M₂. An increase in the power that is dissipated in transistor M₁ in the range from 5 to 24 W causes a decrease in the value of the parameter under consideration at the steady state even by 35%.

Figure 15 compares the waveforms of the internal temperature and the case temperature of the transistors M₁ and M₂ that were measured during the power dissipation with a step shape of 24 W in transistor M₁. The internal temperature was measured by the electrical method and the case temperature was measured by the contact method.

As expected, the internal temperature of transistor M₁ increased the fastest and reached its highest value in the steady state. There is a visible delay in the course of other temperatures by a few seconds in relation to the course of T_j1(t). It is worth noting that the heat transfer between the semiconductor dies of both the transistors through the common heat-sink is more effective than the heat transfer between the semiconductor die and the case of transistor M₁. In the steady state, the differences between the temperatures under consideration exceeded even 50 °C.

Figure 16 compares the excess over the ambient temperature in:

(a)

the internal temperature T_j of the transistors M₁ and M₂ in the steady state that were obtained using the electrical method,

(b)

the case temperature T_c that was obtained by the contact method,

(c)

the temperature of the heat-sink T_ra that was obtained by the optical method.

The measurements were made with the power dissipated in the transistor that was equal to 20 W. Index 1 is the symbols of particular temperatures that relate to transistor M₁, and index 2 relates to transistor M₂.

The values of temperatures T_j2, T_c1, T_c2, T_ra1, and T_ra2 that are presented in the Figure 16 are the result of averaging from three results of the measurements that were performed with the use of each thermo-sensitive parameter.

As can be seen, the dissipation of the power of 20 W in transistor M₁ caused its internal temperature to rise above the ambient temperature by about 100 °C. The results that were obtained with the electrical method using voltages v_GS and v_F as a TSP differ from each other by only 2 °C. The temperature obtained by using voltage v_DS as a TSP is 13 °C higher. Both the temperature of the heat-sink and the temperature of the case of transistor M₁ were lower than the internal temperature that was measured by the electrical method. The temperature of the heat-sink was lower by 20 °C and the case temperature of transistor M₁ by 27.5 °C. As can be seen, the use of the case temperature or the heat-sink temperature to determine the thermal resistance can lead to the values R_th lowered by 20% or 27.5%, respectively.

In turn, the internal temperature of transistor M₂ increased above the ambient temperature only due to thermal coupling with transistor M₁ by as much as 81.5 °C. As can be seen, thermal coupling can cause a significant increase in the internal temperature of the coupled device solely due to the flow of heat from the device in which the power is dissipated. This increase in temperature, due to thermal coupling, should be taken into account in the design process as it may be important in the case of, e.g., the cyclical operation of one of the components. The described phenomenon is also important from the point of view of stabilising the internal temperature of semiconductor devices. Mounting the devices to a common heat-sink and their thermal coupling can reduce temperature variations during thermal cycling and consequently improve the system reliability. Thermal cycles consist of rapid heating of the semi-conductive structure to high temperatures as a result of a cyclic release of the significant power in the device and rapid cooling of this structure after the power is turned off. On the other hand, the omission of thermal couplings between the elements when designing the cooling system may result in a failure of one of the elements as a result of exceeding the allowable internal temperature.

Mutual thermal resistance R_th21 that was determined using the electrical method is 4 K/W. The heat-sink temperature T_ra2 that was obtained from the measurement with the optical method was lower by 3 °C than T_j2. Taking into account the heat flow in the tested system, such a result has no physical justification and is probably related to the measurement errors. In turn, the temperature of transistor M₂ case was lower than its internal temperature by 16 °C.

In the case when the measured temperature value T_c2 is used to determine the thermal resistance R_th21, the result will be lower by 20%, and in the case when temperature T_ra2 is used–only by 3.5%.

Thermal parameters of the investigated transistors depend not only on the dissipated power, but also on the cooling conditions. In Figure 17 the dependences of thermal resistance and transfer thermal impedance on air flow speed v are presented. The measurements were performed at the power that was dissipated in transistor M₁ equal to 20 W.

As it is visible, the transfer thermal resistance was smaller by about 1 K/W than thermal resistance of transistor M₁. Both the dependences R_th(v) and R_th12(v) are monotonically decreasing functions. In the considered range of the change in the air flow speed, the values of thermal parameters decreased even by 70%. This decrease results from an increase in the efficiency of heat convection on the surface of the heat-sink.

7. Conclusions

The paper presents the results of investigations of selected methods of measuring thermal parameters of power MOSFETs. The manner of implementation of the contact, optical, and electrical methods of measuring these parameters is presented. The measurement error of the considered methods was analyzed and the selected results of the measurements that were carried out with the use of these methods are presented.

The performed investigations show that the electrical methods ensure obtaining higher values of the internal temperature of the power MOSFETs during its operation than the contact and optical methods. The difference in the measured values of the transistor internal temperature increase above the ambient temperature with the use of the considered methods may exceed 20%.

While determining waveforms Z_th(t), the use of the contact methods result in obtaining the waveforms that are lowered and delayed in relation to the results that were obtained with the electrical method. It was shown that, in the case of the electrical methods, the accuracy of the approximation of the thermometric characteristic has a large influence on the measurement error. If the voltage across a body diode is used as a thermo-sensitive parameter, the linear approximation of this characteristic gives satisfactory results. On the other hand, when voltages v_DS or v_GS are used as a TSP, satisfactory accuracy is ensured by the approximation of the thermometric characteristic by a quadratic function. For each of the considered measurement methods, the measurement error of thermal resistance is a decreasing function of the power that is dissipated in the transistor. The best accuracy of the measurements is obtained for voltage v_GS used as a TSP and the quadratic function approximating the thermometric characteristic.

The obtained Z_th(t) waveforms prove that the selection of the function approximating the thermometric characteristic may have an impact on the credibility of the results that were obtained with the use of electrical methods. For example, it is possible to obtain a false measurement result, indicating an influence of the power dissipated in the transistor on Z_th(t) waveform in a range of low values of time, where only heat conduction is responsible for the heat transfer.

The performed analysis of the accuracy of the considered measurement methods makes it possible to select the most accurate method. With this method, the accurate value of the device’s internal temperature can be estimated. This temperature determines the lifetime of the network containing this device.

When measuring thermal parameters of power MOSFETs that are situated on a common heat-sink, it was shown that the heat transfer between these transistors occurs mainly due to heat conduction through the heat-sink. This transfer is more effective than between the semiconductor die of the transistor and its case. Therefore, the use of the contact and optical methods causes a significant underestimation of the measured values of thermal parameters. This is an obvious theorem when measuring the transistor’s self thermal parameters. However, the presented investigation results also showed that the mutual thermal parameters that were measured using these methods are also underestimated. A very important consideration for the designer of power electronics networks is presented in Figure 16, which shows that the use of the contact methods to measure the device internal temperature can cause a big error that exceeded even 50 °C; much better accuracy can be obtained using the electrical methods.

The results of the investigation present only one type of power MOSFETs with the case TO-220. The conclusions of the performed measurements have global applicability. The presented discussion about the measurement methods is universal for all power MOSFETs. The analysis of the measurement error gives the same results for different types of considered devices. On the other hand, the results of the measurements will be similar for different semiconductor devices (MOSFETs, BJTs, IGBTs, diodes) that are mounted in TO-220 cases. The differences between the results that were obtained with the use of the electrical, optical, and contact methods will be similar for different semiconductor devices that are mounted in such cases.

The results of the investigation that are presented in this paper may be useful for designers of power semiconductor devices and networks with these devices, and for designers of setups for measuring the thermal parameters of these devices. They can be also applied in many communications systems that are used in the internet of things or autonomous vehicles that are considered in [41,42].

The investigations that are presented in this article can be continued to examine an influence of the different shape and thickness of heat-sinks on the thermal parameters of semiconductor devices. An influence of temperature and forced cooling conditions on these parameters can be also investigated.