Rotating Instabilities in a Low-Speed Single Compressor Rotor Row with Varying Blade Tip Clearance
Abstract
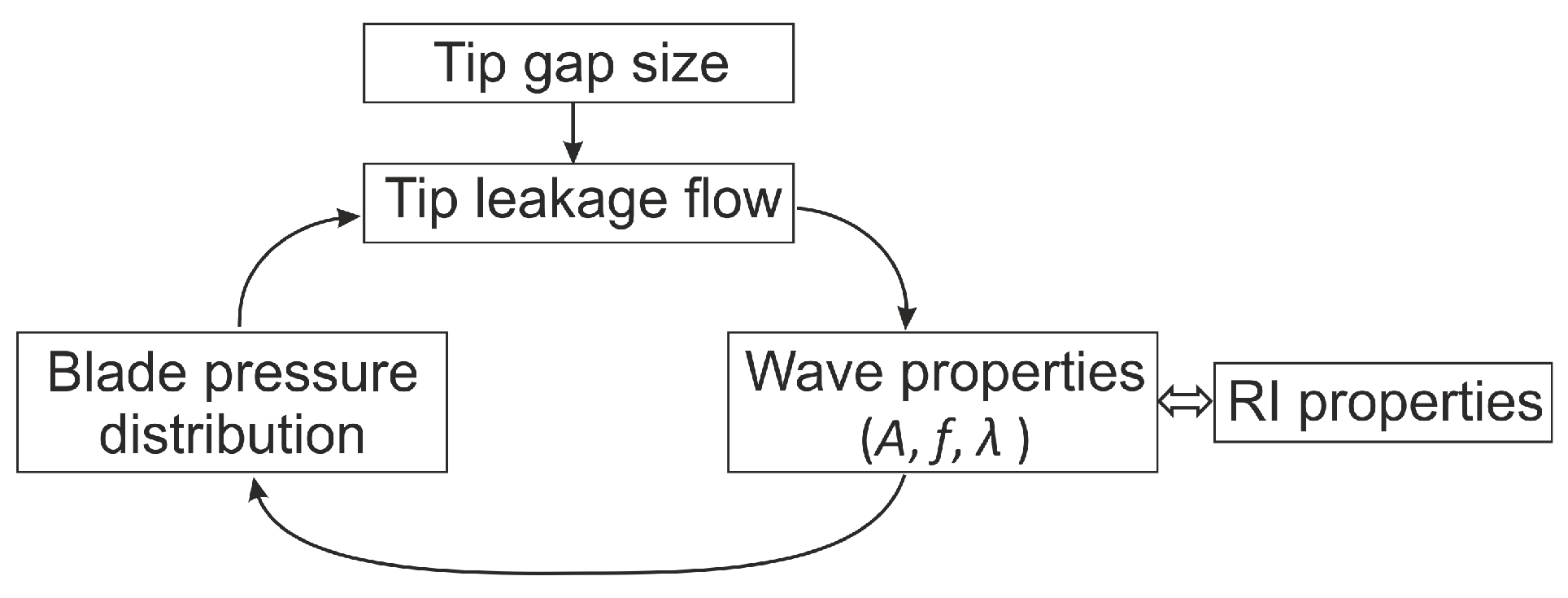
1. Introduction
2. Experimental Setup
3. Numerical and Mathematical Approaches
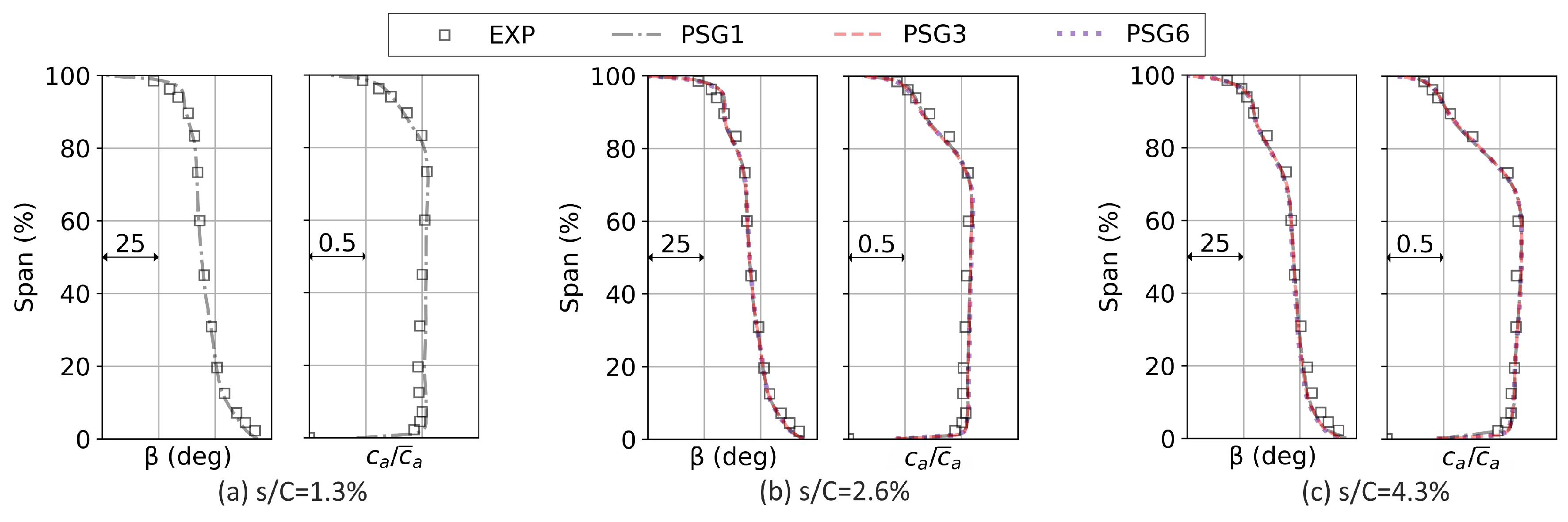
3.1. Mesh Setup
3.2. Numerical Setup
3.3. DMD Method
4. Results and Discussion
4.1. Overall Performance
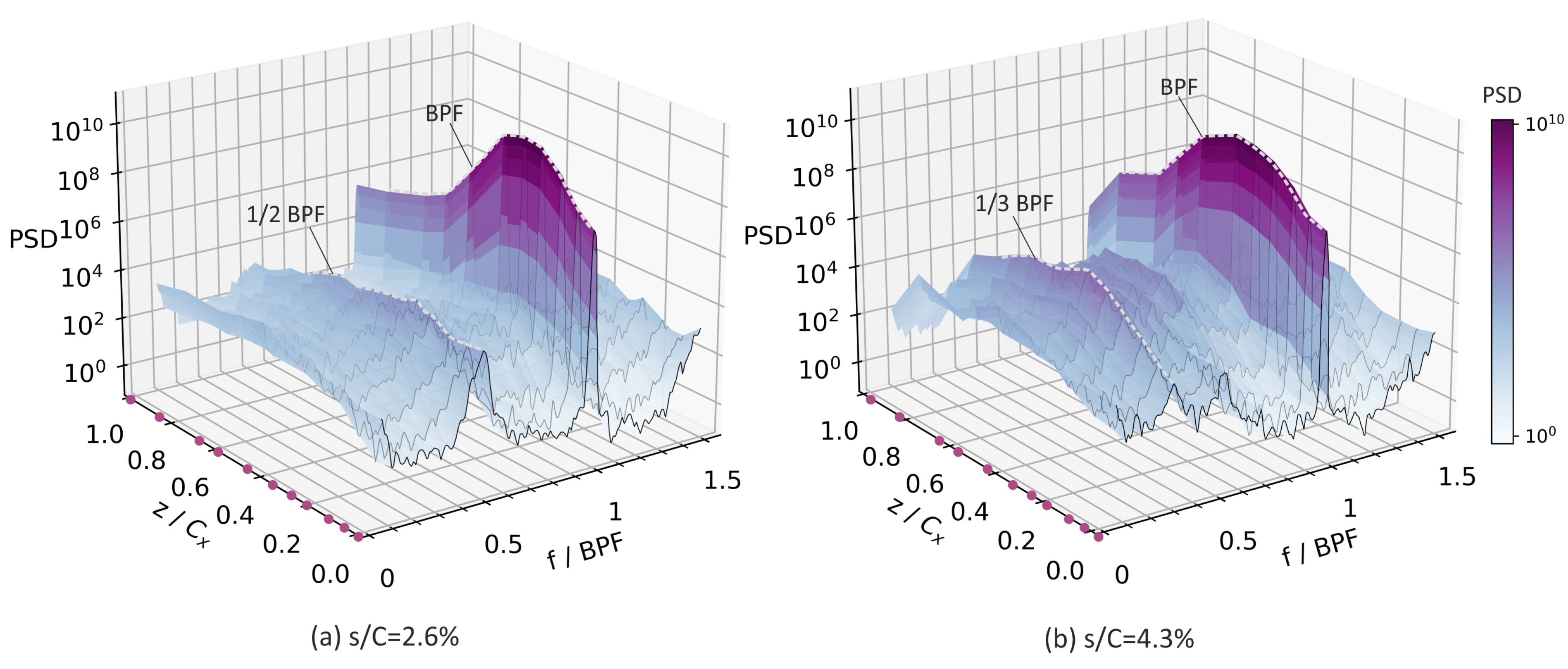
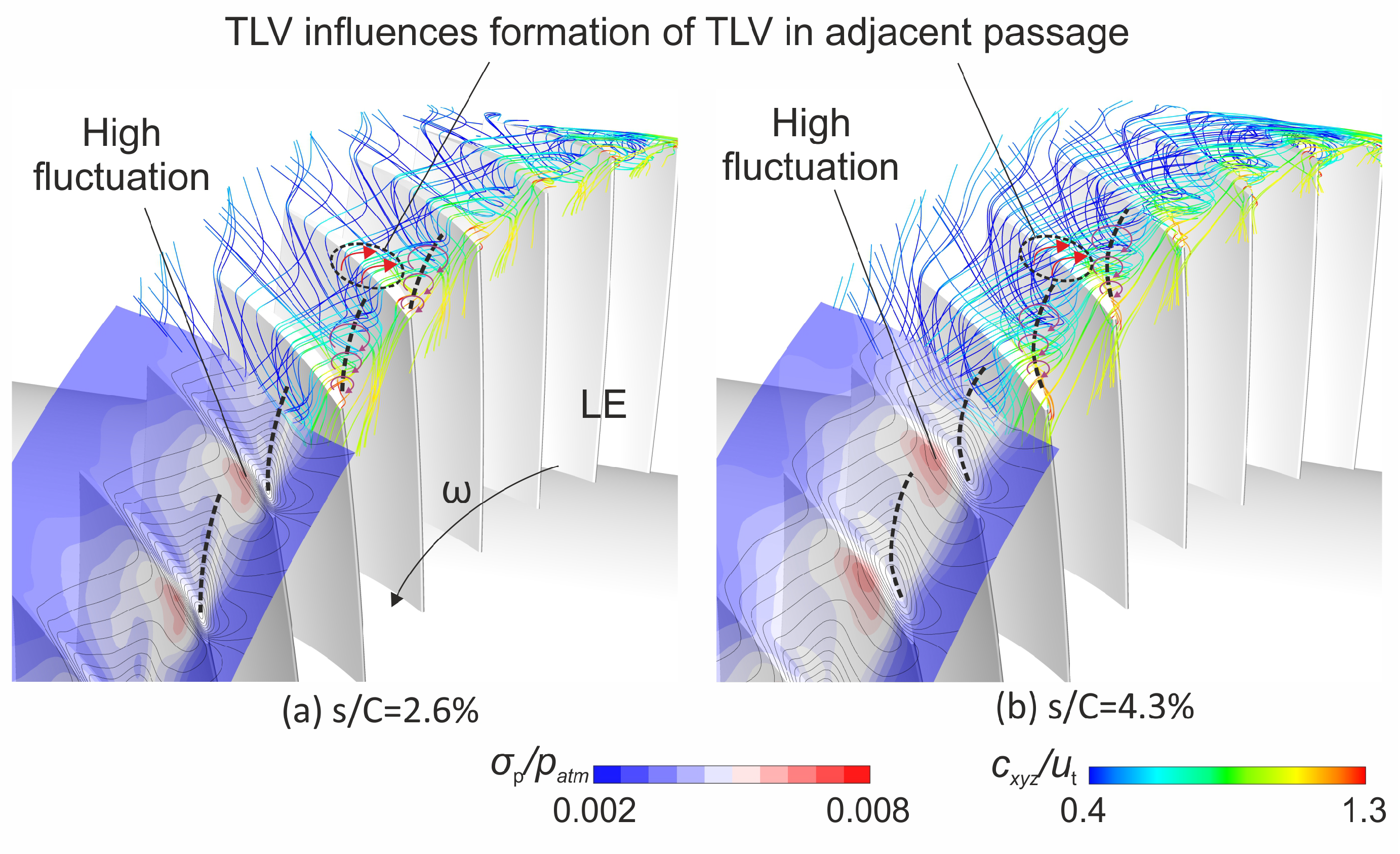
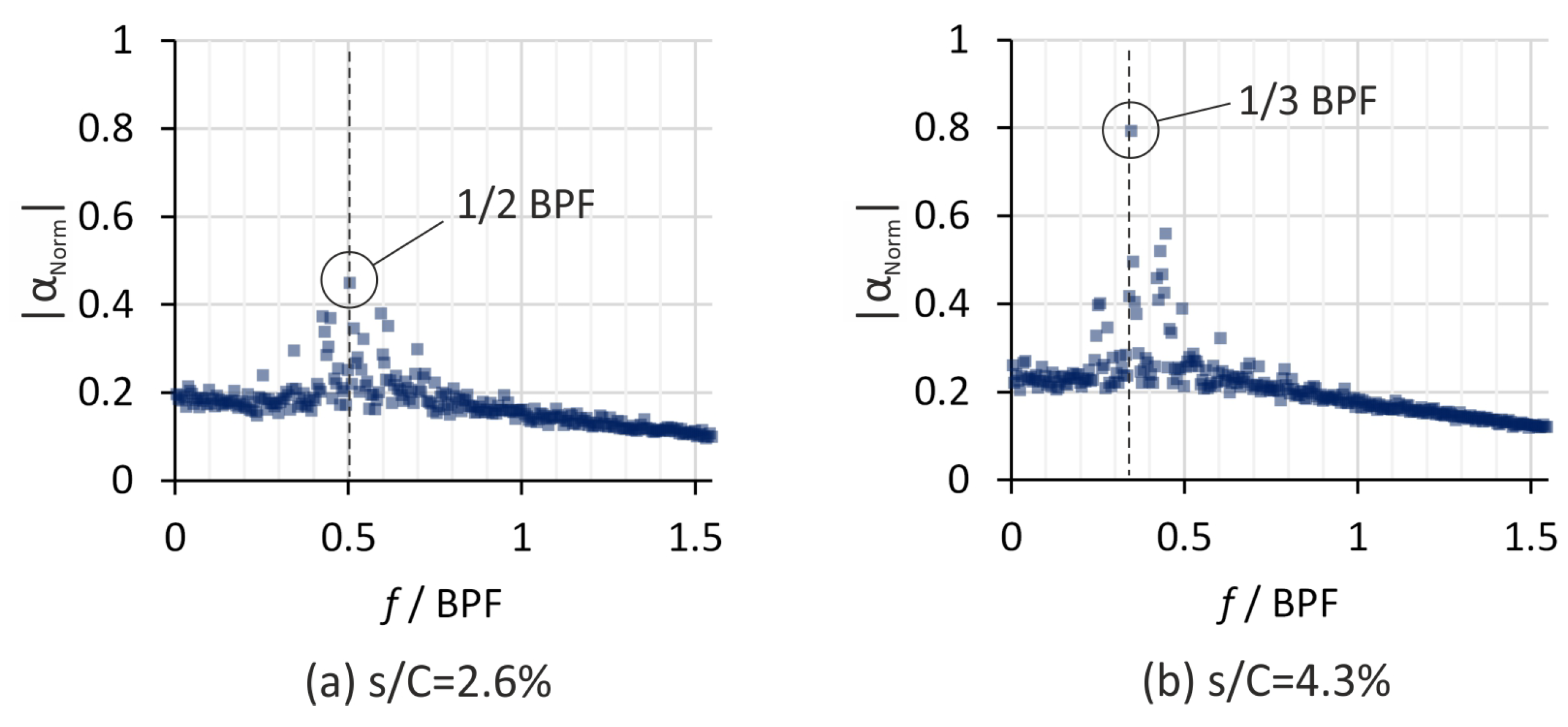
4.2. Dynamic Characteristics
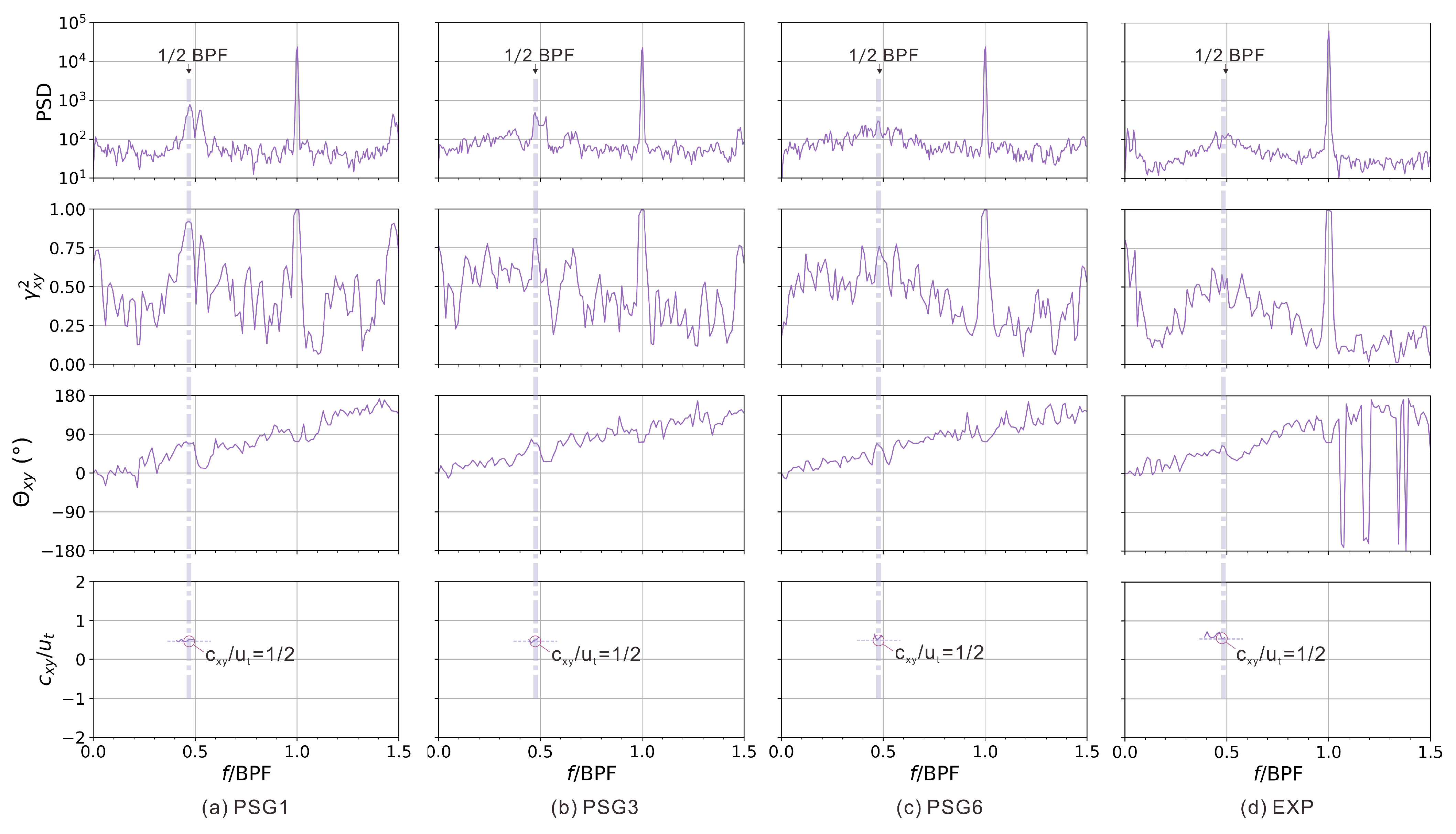
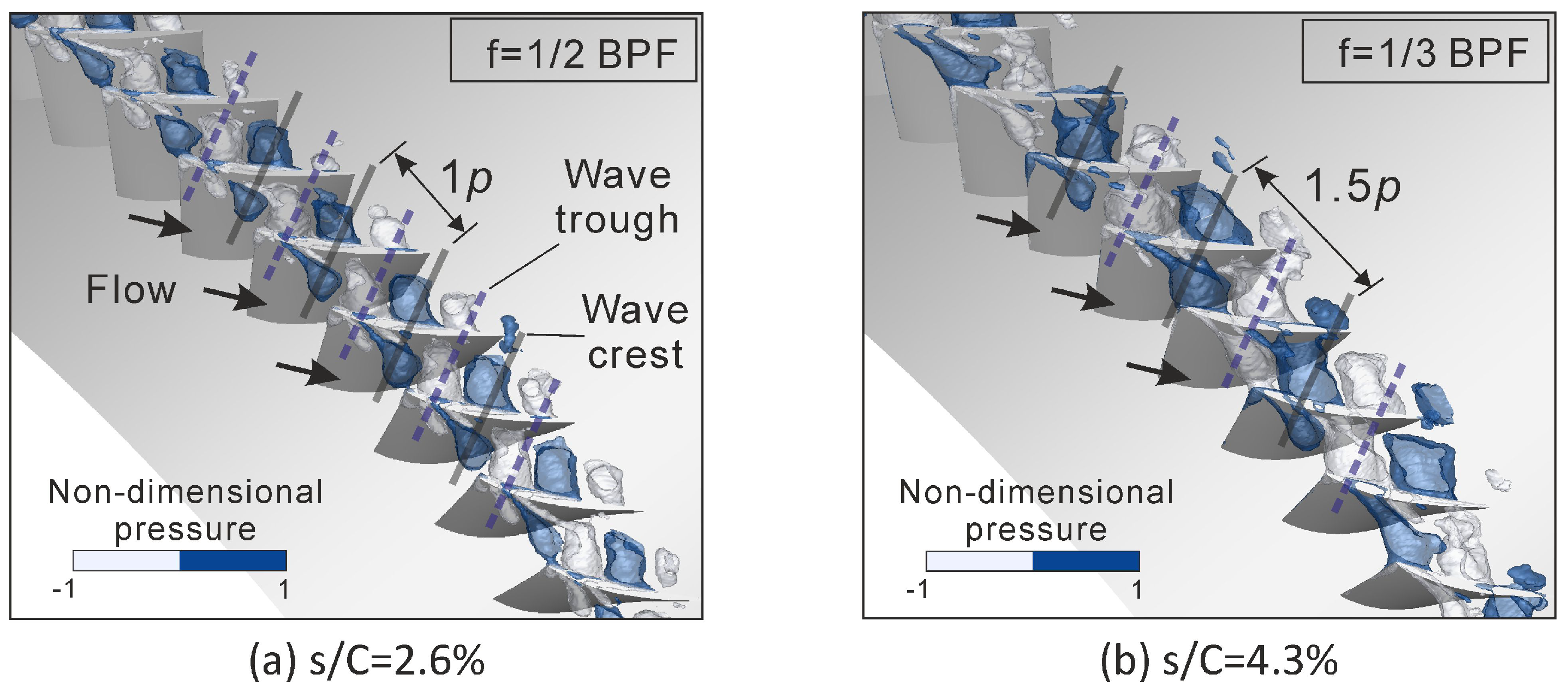
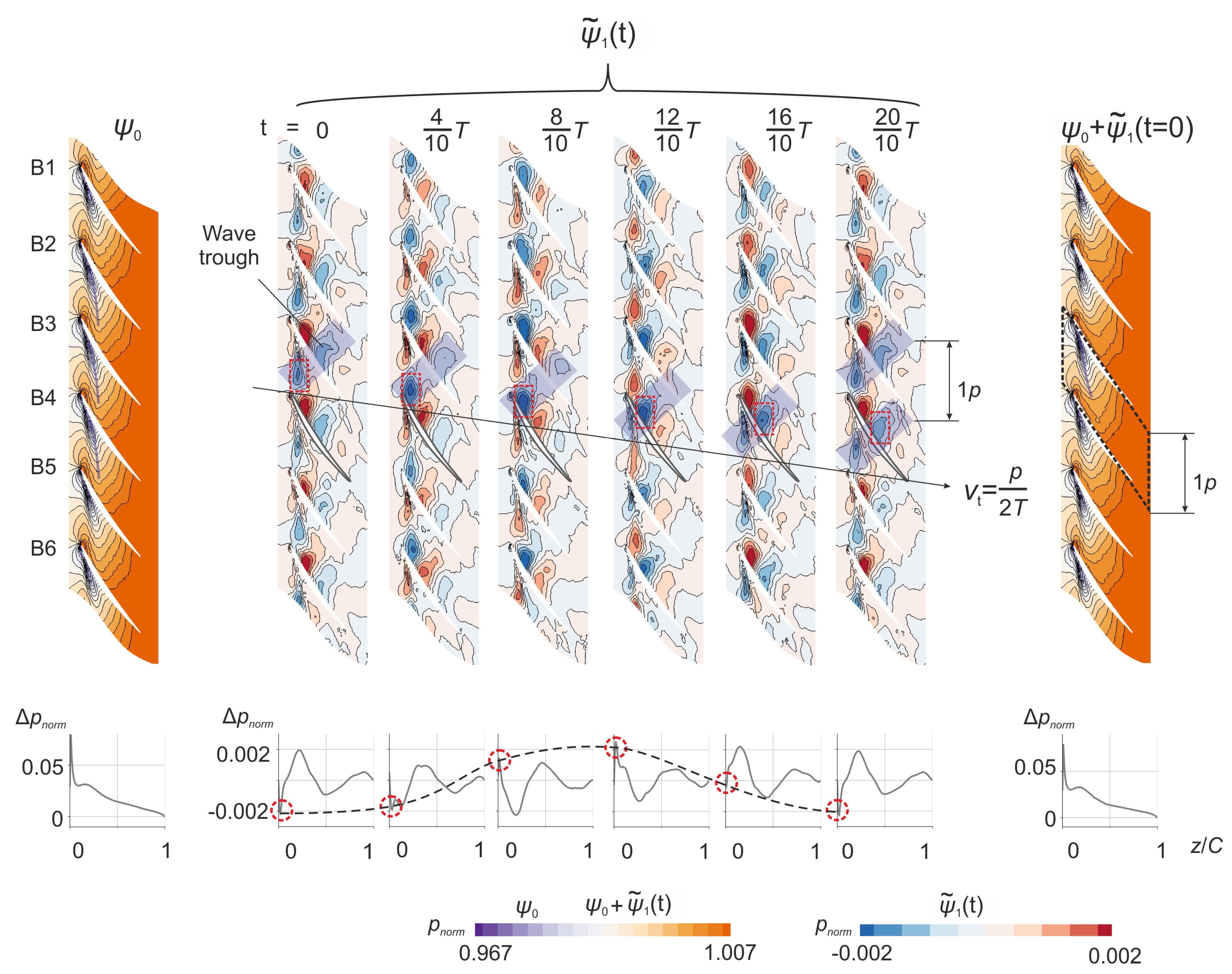
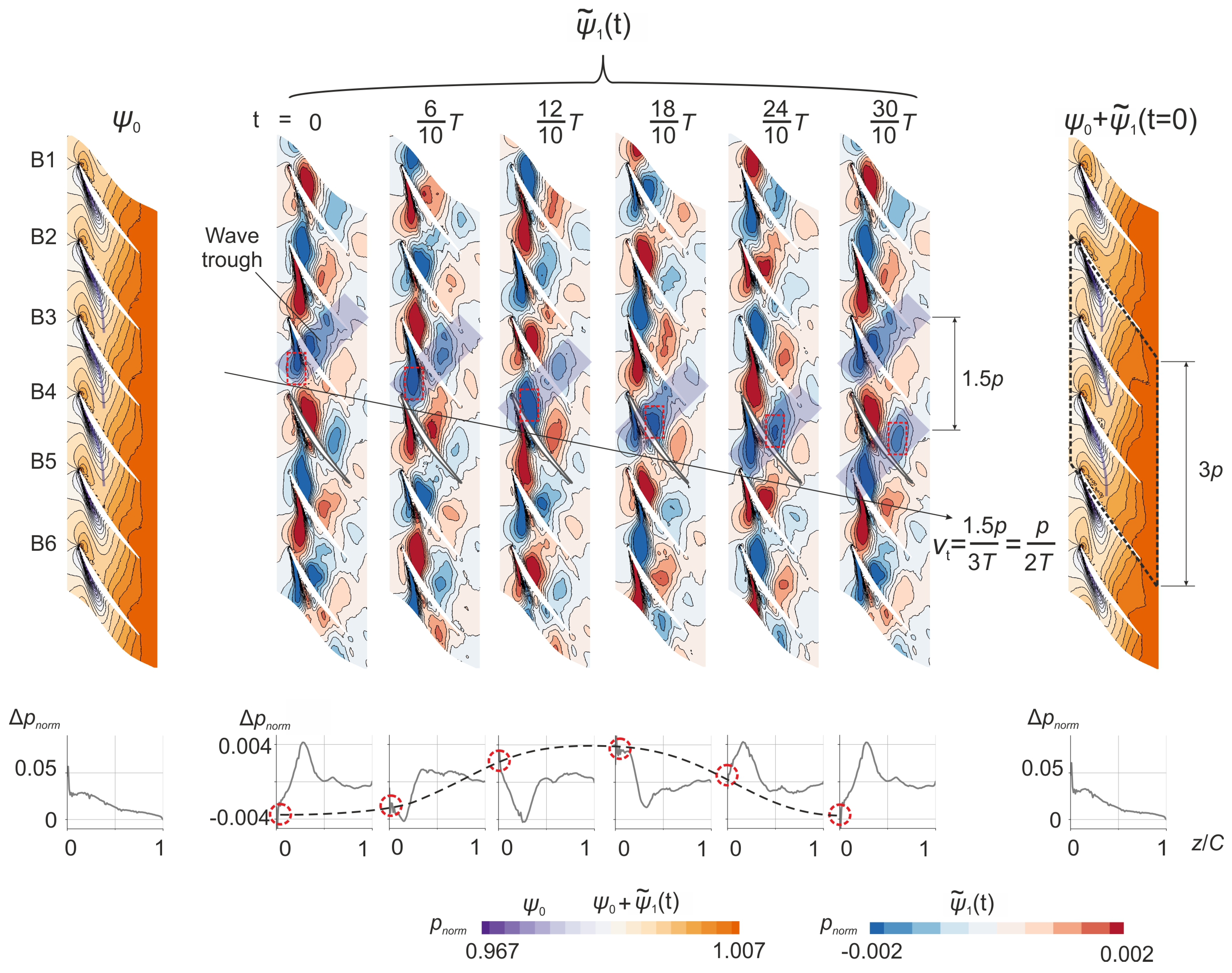
4.3. DMD-Based Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BPF | Blade passing frequency |
| CFD | Computational fluid dynamics |
| DMD | Dynamic mode decomposition |
| FFT | Fast Fourier transform |
| LE | Leading edge |
| LSRC | Low speed research compressor |
| NSV | Non-synchronous vibration |
| PSD | Power spectral density |
| RANS | Reynolds-averaged Navier–Stokes |
| RI | Rotating instability |
| SST | Shear stress transport |
| STD | Standard deviation |
| TE | Trailing edge |
| TLV | Tip leakage vortex |
| ZLES | Zonal large eddy simulation |
References
- Day, I.J. Stall, Surge, and 75 Years of Research. J. Turbomach. 2015, 138, 011001. [Google Scholar] [CrossRef]
- Mailach, R.; Lehmann, I.; Vogeler, K. Rotating Instabilities in an Axial Compressor Originating from the Fluctuating Blade Tip Vortex. J. Turbomach. 2000, 123, 453–460. [Google Scholar] [CrossRef]
- Mathioudakis, K.; Breugelmans, F.A.E. Development of Small Rotating Stall in a Single Stage Axial Compressor. In Volume 1: Aircraft Engine; Marine; Turbomachinery; Microturbines and Small Turbomachinery; V001T03A064; Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 1985. [Google Scholar] [CrossRef]
- Liu, J.; Holste, F.; Neise, W. On the azimuthal mode structure of rotating blade flow instabilities in axial turbomachines. In Proceedings of the Aeroacoustics Conference, State College, PA, USA, 6–8 May 1996; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1996. [Google Scholar] [CrossRef]
- Kameier, F.; Neise, W. Experimental Study of Tip Clearance Losses and Noise in Axial Turbomachines and Their Reduction. J. Turbomach. 1997, 119, 460–471. [Google Scholar] [CrossRef]
- Mailach, R.; Sauer, H.; Vogeler, K. The Periodical Interaction of the Tip Clearance Flow in the Blade Rows of Axial Compressors. In Volume 1: Aircraft Engine; Marine; Turbomachinery; Microturbines and Small Turbomachinery; American Society of Mechanical Engineers: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Rolfes, M.; Lange, M.; Mailach, R. Investigation of Performance and Rotor Tip Flow Field in a Low Speed Research Compressor with Circumferential Groove Casing Treatment at Varying Tip Clearance. Int. J. Rotating Mach. 2017, 2017, 4631751. [Google Scholar] [CrossRef]
- Beselt, C.; van Rennings, R.; Sorge, R.; Peitsch, D.; Thiele, F.; Ehrenfried, K.; Thamsen, P.U.; Pardowitz, B.; Enghardt, L. Influence of the clearance size on rotating instability in an axial compressor stator. In Proceedings of the 10th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, Lappeenranta, Finland, 15–19 April 2013; European Turbomachinery Society: Florence, Italy, 2013. [Google Scholar]
- Wu, Y.; Wu, J.; Zhang, G.; Chu, W. Experimental and Numerical Investigation of Flow Characteristics Near Casing in an Axial Flow Compressor Rotor at Stable and Stall Inception Conditions. J. Fluids Eng. 2014, 136, 111106. [Google Scholar] [CrossRef]
- Yang, W.; Wang, Y.; Han, L.; Zhang, X.; Li, Z. Effect of Rotating Instabilities on Aerodynamic Damping of Axial Flow Fan Blades. In Volume 7A: Structures and Dynamics; American Society of Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Biela, C.; Müller, M.W.; Schiffer, H.P.; Zscherp, C. Unsteady Pressure Measurement in a Single Stage Axial Transonic Compressor near the Stability Limit. In Volume 6: Turbomachinery, Parts A, B, and C; American Society of Mechanical Engineers: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Hah, C.; Bergner, J.; Schiffer, H.P. Tip Clearance Vortex Oscillation, Vortex Shedding and Rotating Instabilities in an Axial Transonic Compressor Rotor. In Volume 6: Turbomachinery, Parts A, B, and C; American Society of Mechanical Engineers: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Sun, Z.; Zou, W.; Zheng, X. Instability detection of centrifugal compressors by means of acoustic measurements. Aerosp. Sci. Technol. 2018, 82–83, 628–635. [Google Scholar] [CrossRef]
- He, X.; Zheng, X. Roles and mechanisms of casing treatment on different scales of flow instability in high pressure ratio centrifugal compressors. Aerosp. Sci. Technol. 2019, 84, 734–746. [Google Scholar] [CrossRef]
- Zhang, L.Y.; He, L.; Stüer, H. A Numerical Investigation of Rotating Instability in Steam Turbine Last Stage. J. Turbomach. 2012, 135, 011009. [Google Scholar] [CrossRef]
- Gerschütz, W.; Casey, M.; Truckenmüller, F. Experimental investigations of rotating flow instabilities in the last stage of a low-pressure model steam turbine during windage. Proc. Inst. Mech. Eng. Part A J. Power Energy 2005, 219, 499–510. [Google Scholar] [CrossRef]
- Hoying, D.A.; Tan, C.S.; Vo, H.D.; Greitzer, E.M. Role of Blade Passage Flow Structurs in Axial Compressor Rotating Stall Inception. J. Turbomach. 1999, 121, 735–742. [Google Scholar] [CrossRef]
- Vo, H.D. Role of Tip Clearance Flow in Rotating Instabilities and Nonsynchronous Vibrations. J. Propuls. Power 2010, 26, 556–561. [Google Scholar] [CrossRef]
- März, J.; Hah, C.; Neise, W. An Experimental and Numerical Investigation into the Mechanisms of Rotating Instability. J. Turbomach. 2002, 124, 367–374. [Google Scholar] [CrossRef]
- Kielb, R.E.; Barter, J.W.; Thomas, J.P.; Hall, K.C. Blade Excitation by Aerodynamic Instabilities: A Compressor Blade Study. In Proceedings of the Turbo Expo 2003, Atlanta, GA, USA, 16–19 June 2003; American Society of Mechanical Engineers: New York, NY, USA, 2003; Volume 4. [Google Scholar] [CrossRef]
- Pardowitz, B.; Tapken, U.; Enghardt, L. Time-resolved Rotating Instability Waves in an annular Cascade. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 June 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar] [CrossRef]
- Pardowitz, B.; Tapken, U.; Sorge, R.; Thamsen, P.U.; Enghardt, L. Rotating Instability in an Annular Cascade: Detailed Analysis of the Instationary Flow Phenomena. J. Turbomach. 2013, 136, 061017. [Google Scholar] [CrossRef]
- Pardowitz, B.; Moreau, A.; Tapken, U.; Enghardt, L. Experimental identification of rotating instability of an axial fan with shrouded rotor. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 520–528. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, Z.; An, G.; Liu, J.; Yang, G. Origins and Structure of Rotating Instability: Part 1—Experimental and Numerical Observations in a Subsonic Axial Compressor Rotor. In Volume 2D: Turbomachinery; American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Geng, S.; Lin, F.; Chen, J.; Nie, C. Evolution of unsteady flow near rotor tip during stall inception. J. Therm. Sci. 2011, 20, 294–303. [Google Scholar] [CrossRef]
- Cravero, C.; Marsano, D. Criteria for the Stability Limit Prediction of High Speed Centrifugal Compressors with Vaneless Diffuser: Part I—Flow Structure Analysis. In Volume 2E: Turbomachinery; V02ET39A013; Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Eck, M.; Geist, S.; Peitsch, D. Physics of Prestall Propagating Disturbances in Axial Compressors and Their Potential as a Stall Warning Indicator. Appl. Sci. 2017, 7, 285. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Y.; Wang, Y.; Deng, S. Evolution of the flow instabilities in an axial compressor rotor with large tip clearance: An experimental and URANS study. Aerosp. Sci. Technol. 2020, 96, 105557. [Google Scholar] [CrossRef]
- Chen, X.; Koppe, B.; Lange, M.; Chu, W.; Mailach, R. Comparison of Turbulence Modeling for a Compressor Rotor at Different Tip Clearances. AIAA J. 2021. [Google Scholar] [CrossRef]
- Boos, P.; Möckel, H.; Henne, J.M.; Selmeier, R. Flow Measurement in a Multistage Large Scale Low Speed Axial Flow Research Compressor. In Volume 1: Turbomachinery; American Society of Mechanical Engineers: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- ANSYS CFX. ANSYS CFX-Solver Theory Guide; ANSYS CFX Release 2020; ANSYS: Canonsburg, PA, USA, 2020. [Google Scholar]
- Menter, F.R. Best Practice: Scale-Resolving Simulations in ANSYS CFD; ANSYS Germany GmbH: Otterfing, Germany, 2012; Volume 1. [Google Scholar]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014, 1, 391–421. [Google Scholar] [CrossRef]
- Yamada, K.; Kikuta, H.; Iwakiri, K.I.; Furukawa, M.; Gunjishima, S. An Explanation for Flow Features of Spike-Type Stall Inception in an Axial Compressor Rotor. J. Turbomach. 2012, 135, 021023. [Google Scholar] [CrossRef]
- Pullan, G.; Young, A.M.; Day, I.J.; Greitzer, E.M.; Spakovszky, Z.S. Origins and Structure of Spike-Type Rotating Stall. J. Turbomach. 2015, 137, 051007. [Google Scholar] [CrossRef]
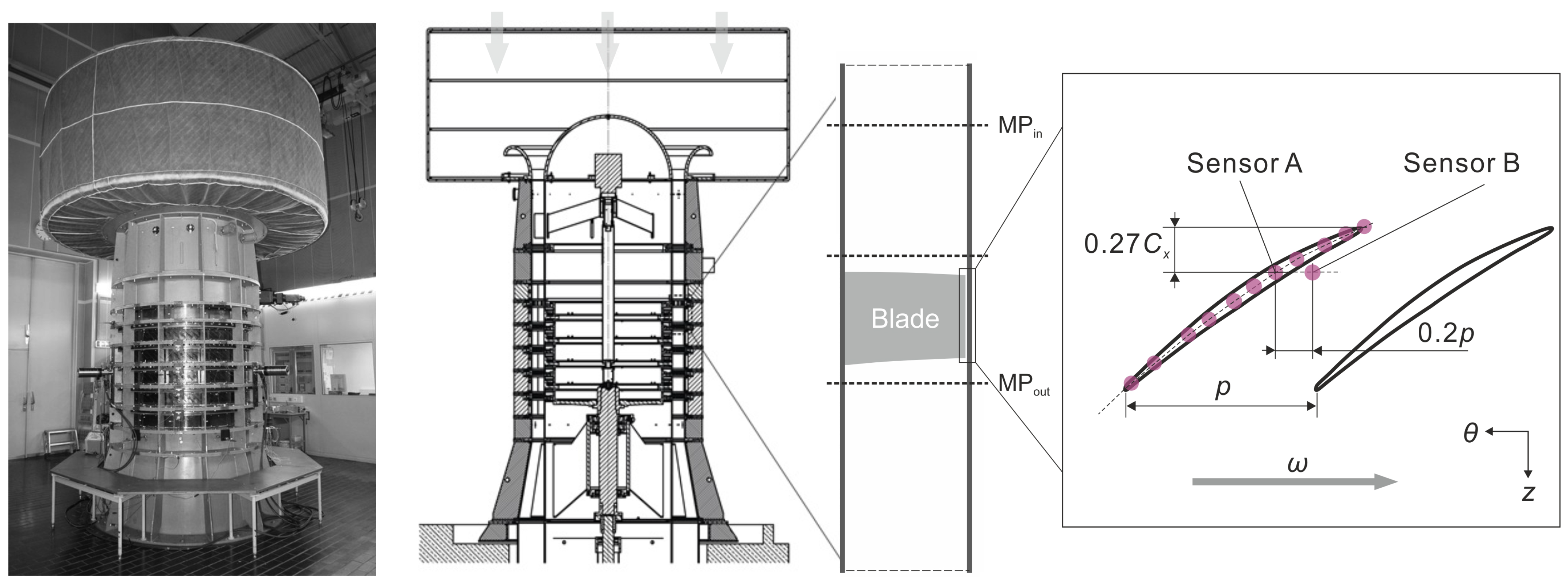
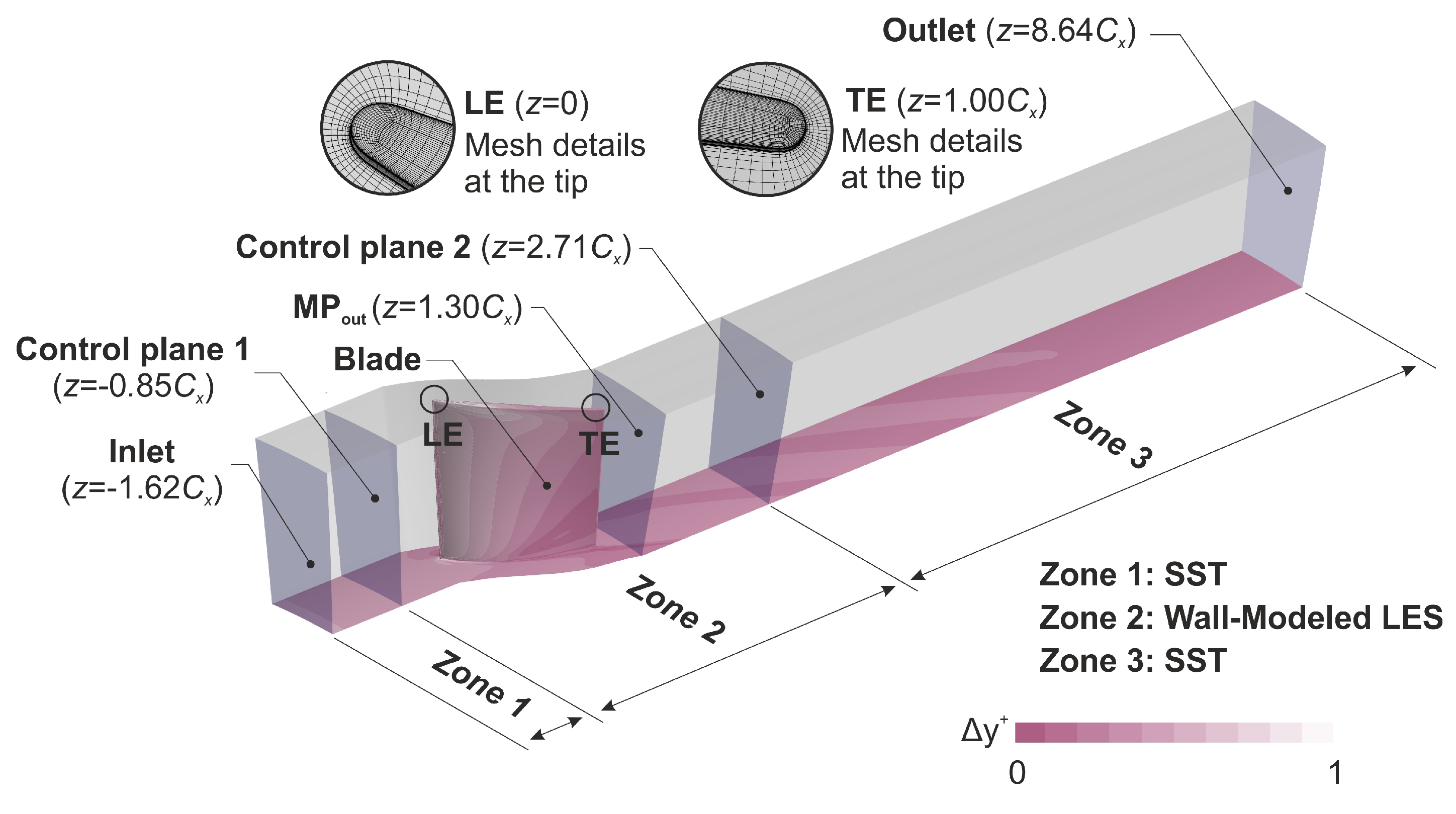
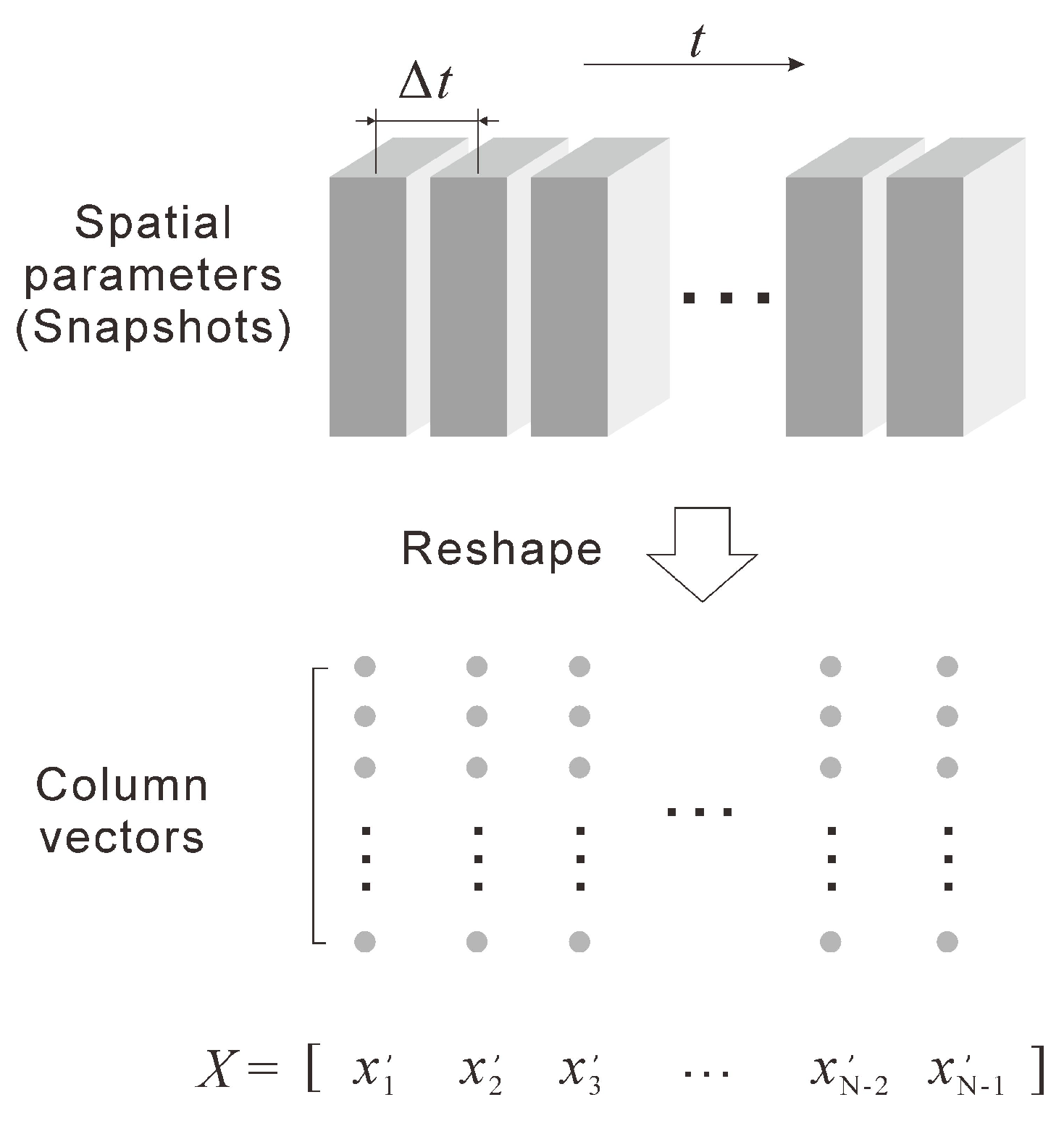
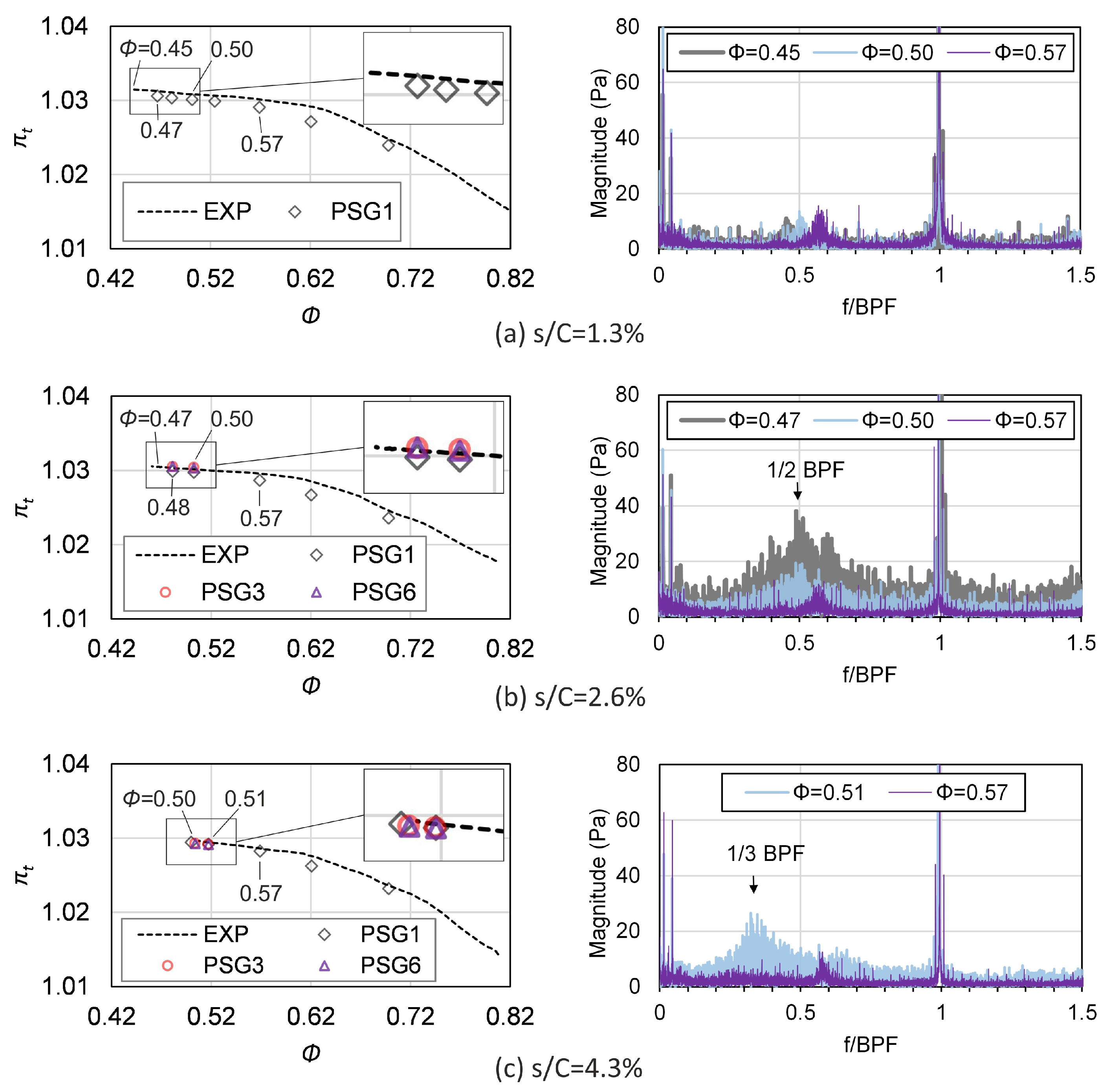

| Characteristic | Value |
|---|---|
| Rotating speed | 1000 rpm |
| Casing diameter | 1500 mm |
| Hub-to-tip ratio | 0.84 |
| Rotor blade count | 63 |
| Rotor blade chord length (Tip) | 116 mm |
| Solidity of rotor blades (Tip) | 1.55 |
| Mass flow at design point | 27.89 kg/s |
| Reynolds number at rotor inlet (Mid-span, design point) | |
| Mach number at rotor inlet (Mid-span) | 0.24 |
| Configuration | s (mm) | (%) |
|---|---|---|
| Small | 1.5 | 1.3 |
| Middle | 3.0 | 2.6 |
| Large | 5.0 | 4.3 |
| Case | Number of Meshed Passages | Total Grid Number (Million) |
|---|---|---|
| PSG1 | 1 | 2.39 |
| PSG3 | 3 | 7.17 |
| PSG6 | 6 | 14.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Koppe, B.; Lange, M.; Chu, W.; Mailach, R. Rotating Instabilities in a Low-Speed Single Compressor Rotor Row with Varying Blade Tip Clearance. Energies 2021, 14, 8369. https://doi.org/10.3390/en14248369
Chen X, Koppe B, Lange M, Chu W, Mailach R. Rotating Instabilities in a Low-Speed Single Compressor Rotor Row with Varying Blade Tip Clearance. Energies. 2021; 14(24):8369. https://doi.org/10.3390/en14248369
Chicago/Turabian StyleChen, Xiangyi, Björn Koppe, Martin Lange, Wuli Chu, and Ronald Mailach. 2021. "Rotating Instabilities in a Low-Speed Single Compressor Rotor Row with Varying Blade Tip Clearance" Energies 14, no. 24: 8369. https://doi.org/10.3390/en14248369
APA StyleChen, X., Koppe, B., Lange, M., Chu, W., & Mailach, R. (2021). Rotating Instabilities in a Low-Speed Single Compressor Rotor Row with Varying Blade Tip Clearance. Energies, 14(24), 8369. https://doi.org/10.3390/en14248369





