Solar Radiation Prediction Based on Convolution Neural Network and Long Short-Term Memory
Abstract
:1. Introduction
2. Data Collection and Preprocessing
2.1. Data Collection
2.2. Data Preprocessing
2.2.1. DNI Clear-Sky Index
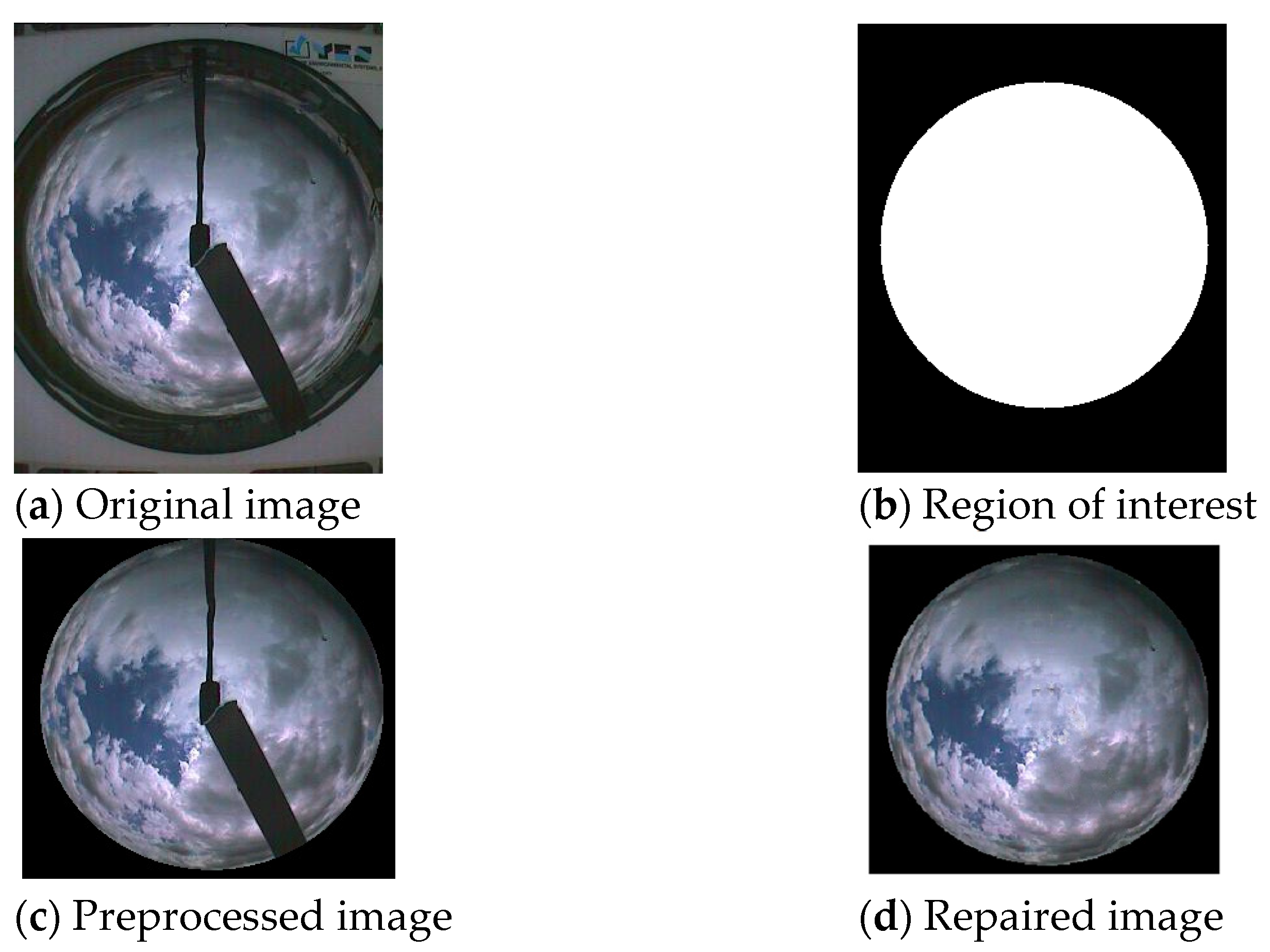
2.2.2. Image Preprocessing
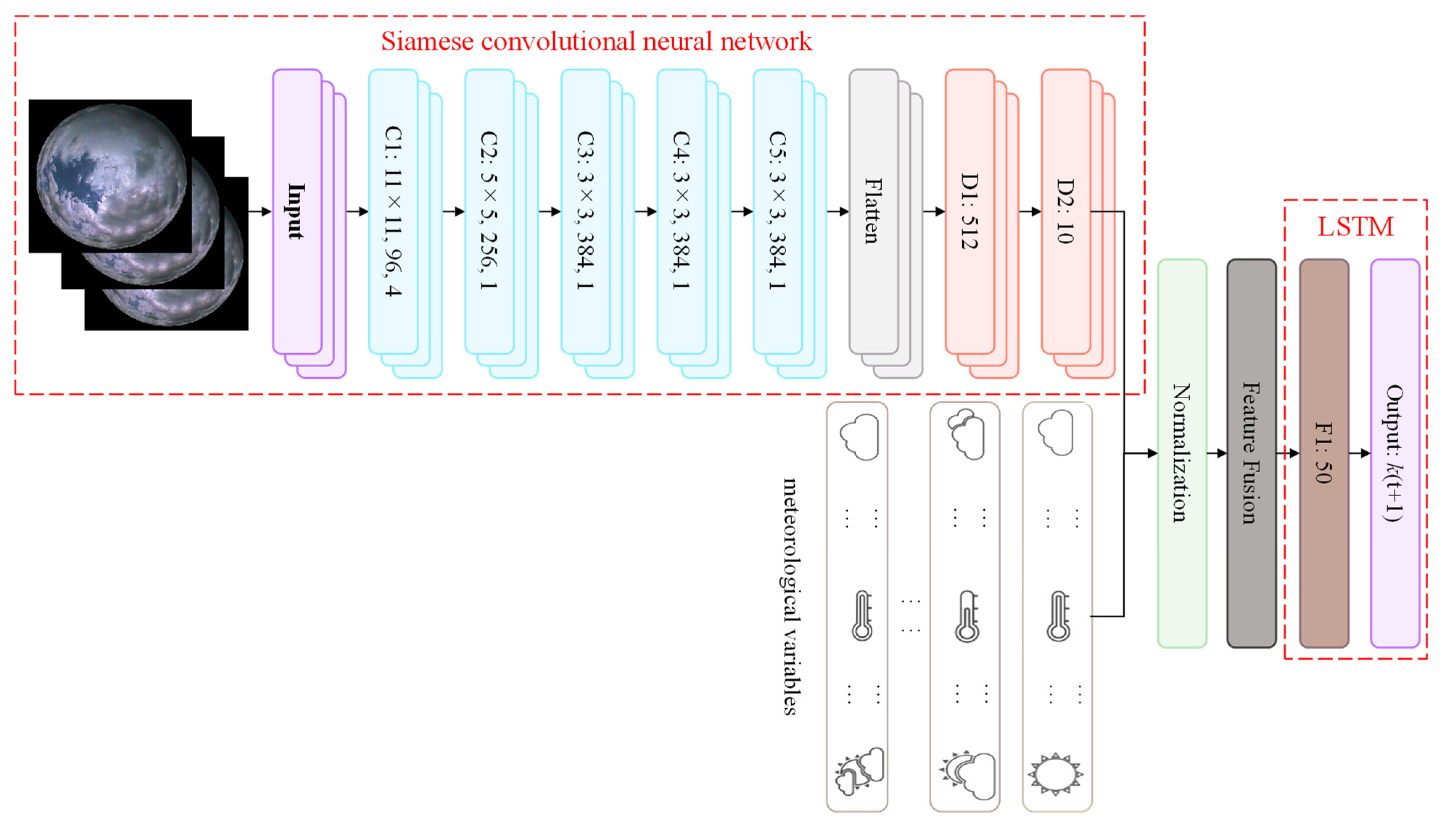
3. SCNN-LSTM Prediction Model
3.1. Input Dimension
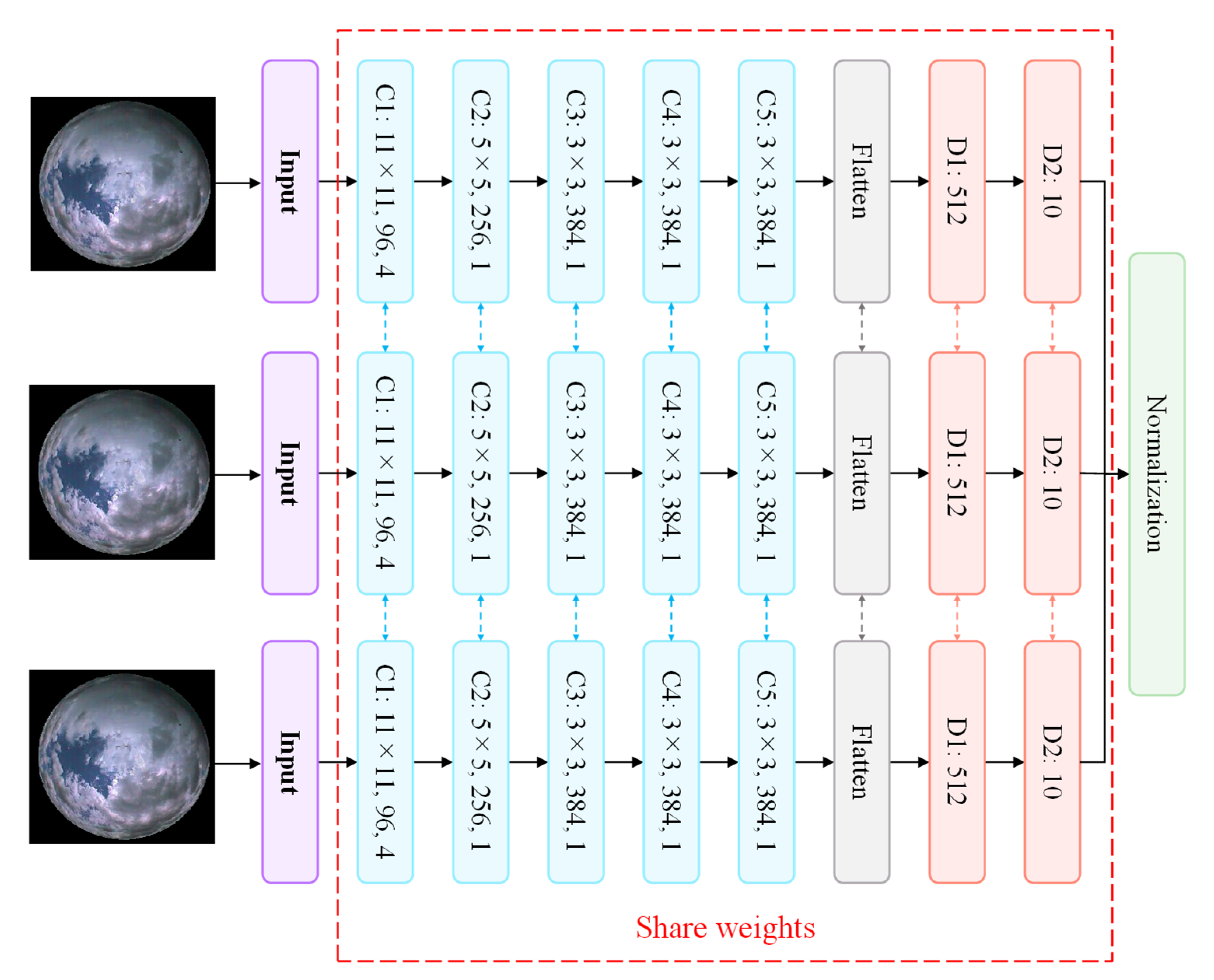
3.2. Siamese Convolutional Neural Network
3.3. Long Short-Term Memory
3.4. Loss Function
4. Results and Discussion
4.1. Evaluation Index
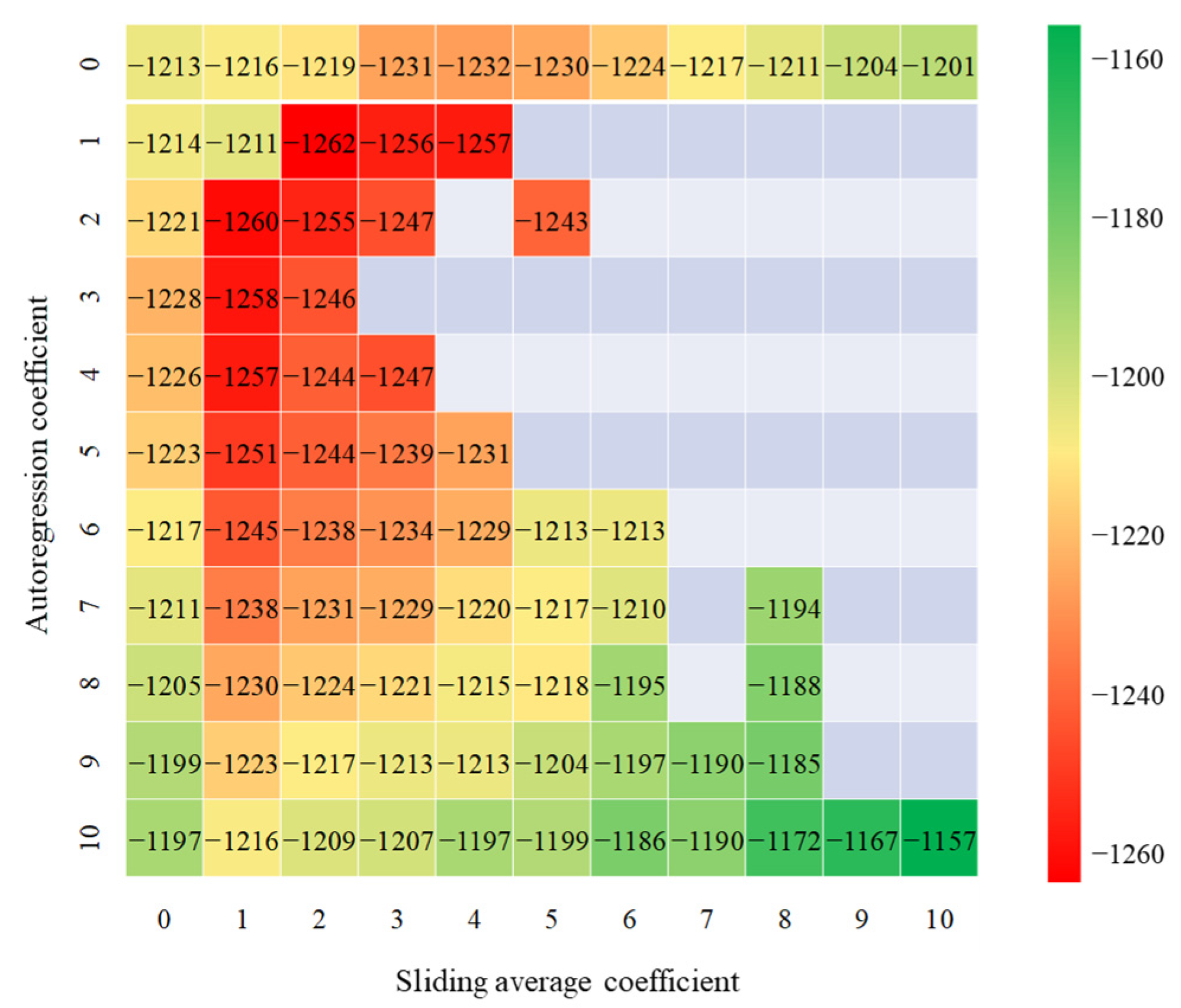
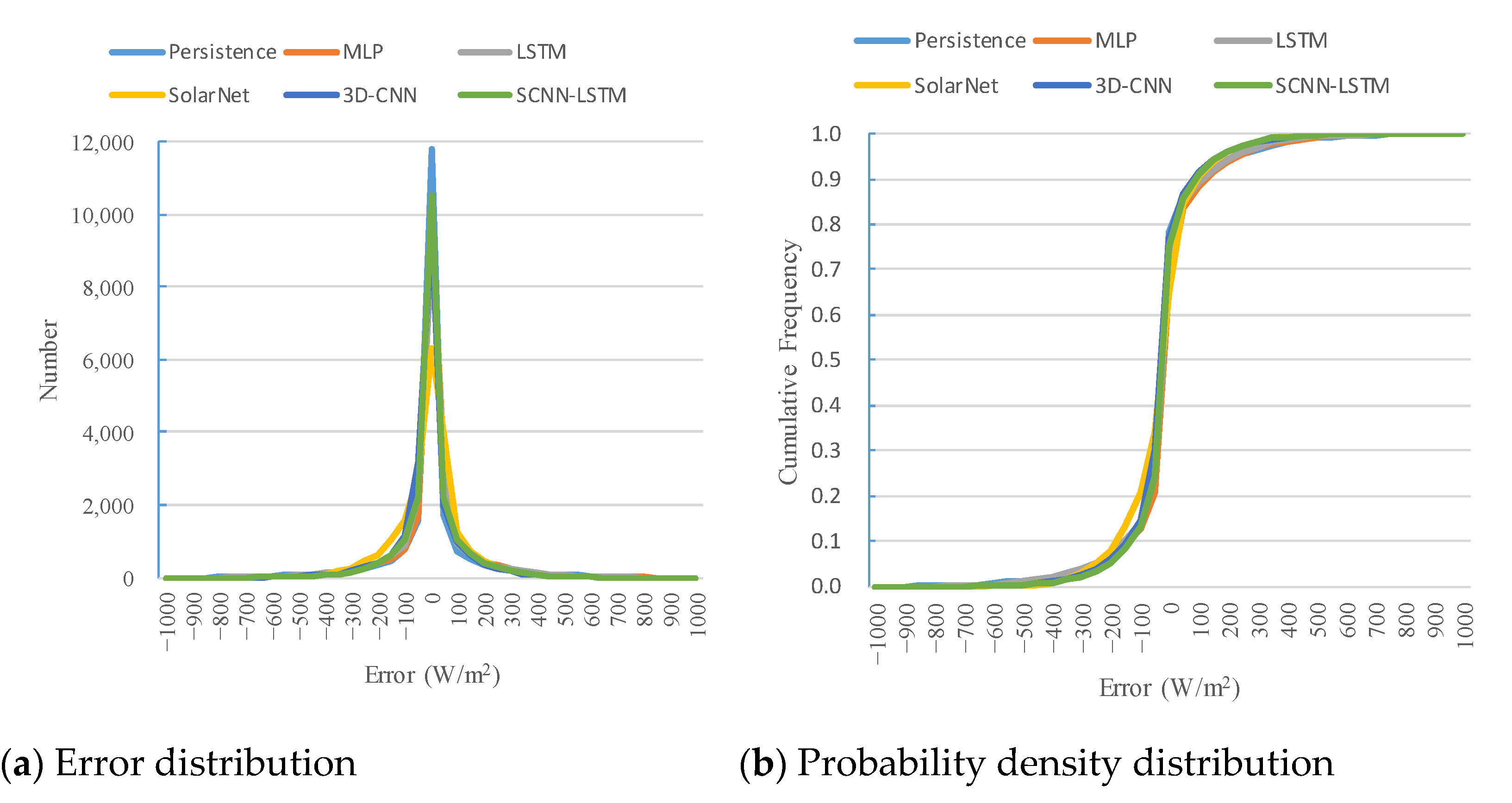
4.2. Performance of the SCNN-LSTM
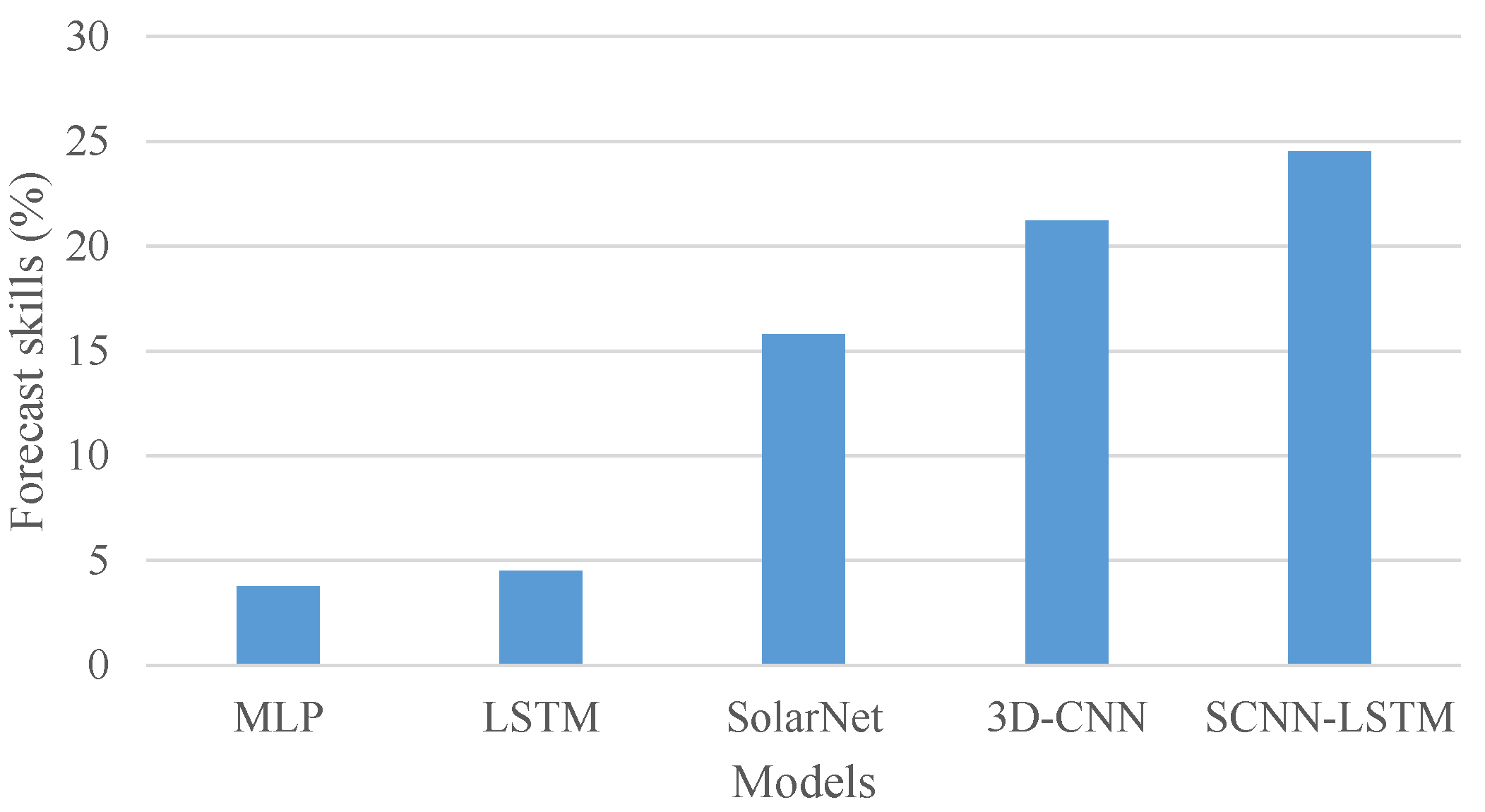
4.3. Performance of Different Forecast Models for the Inter-Hour DNI Forecast
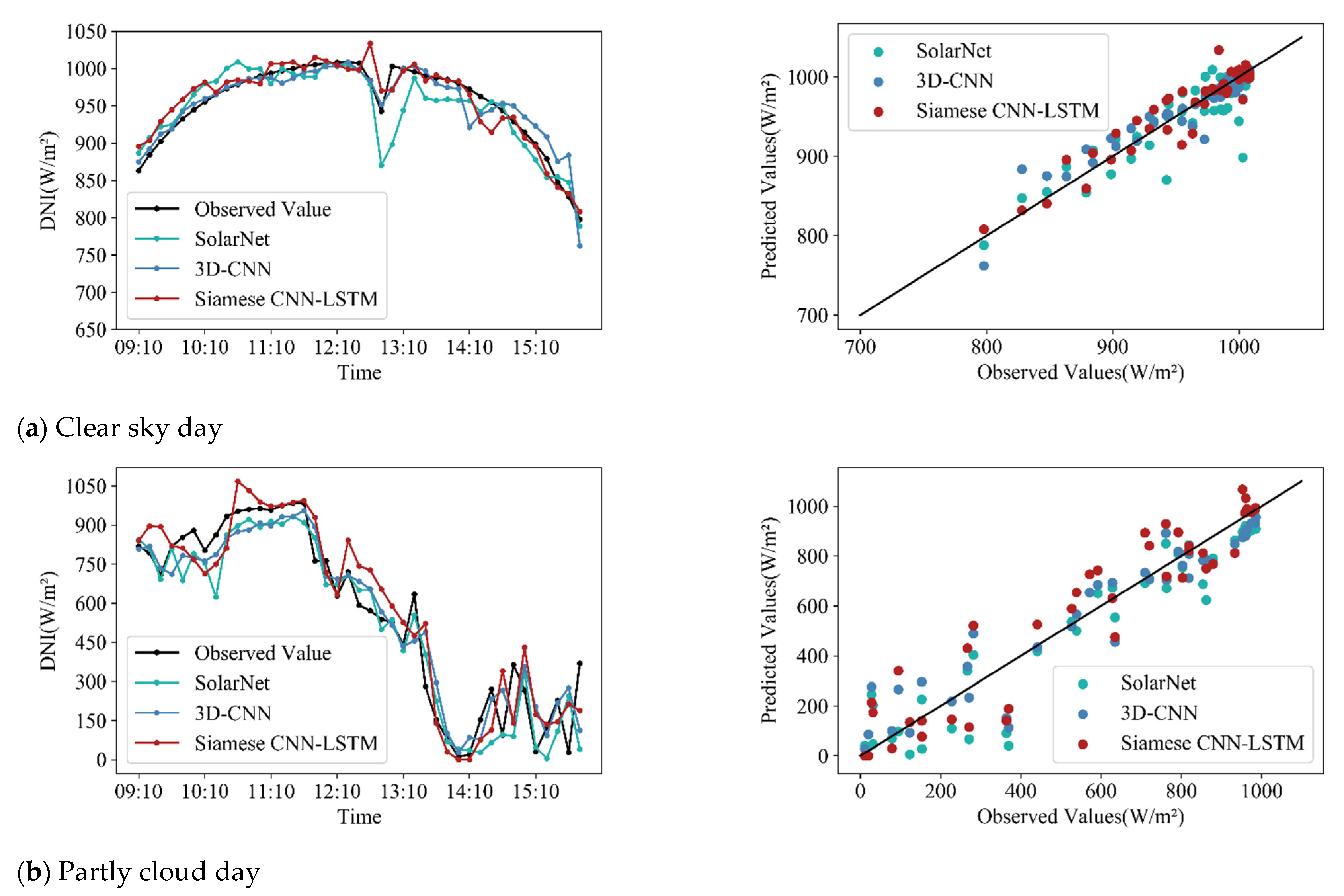
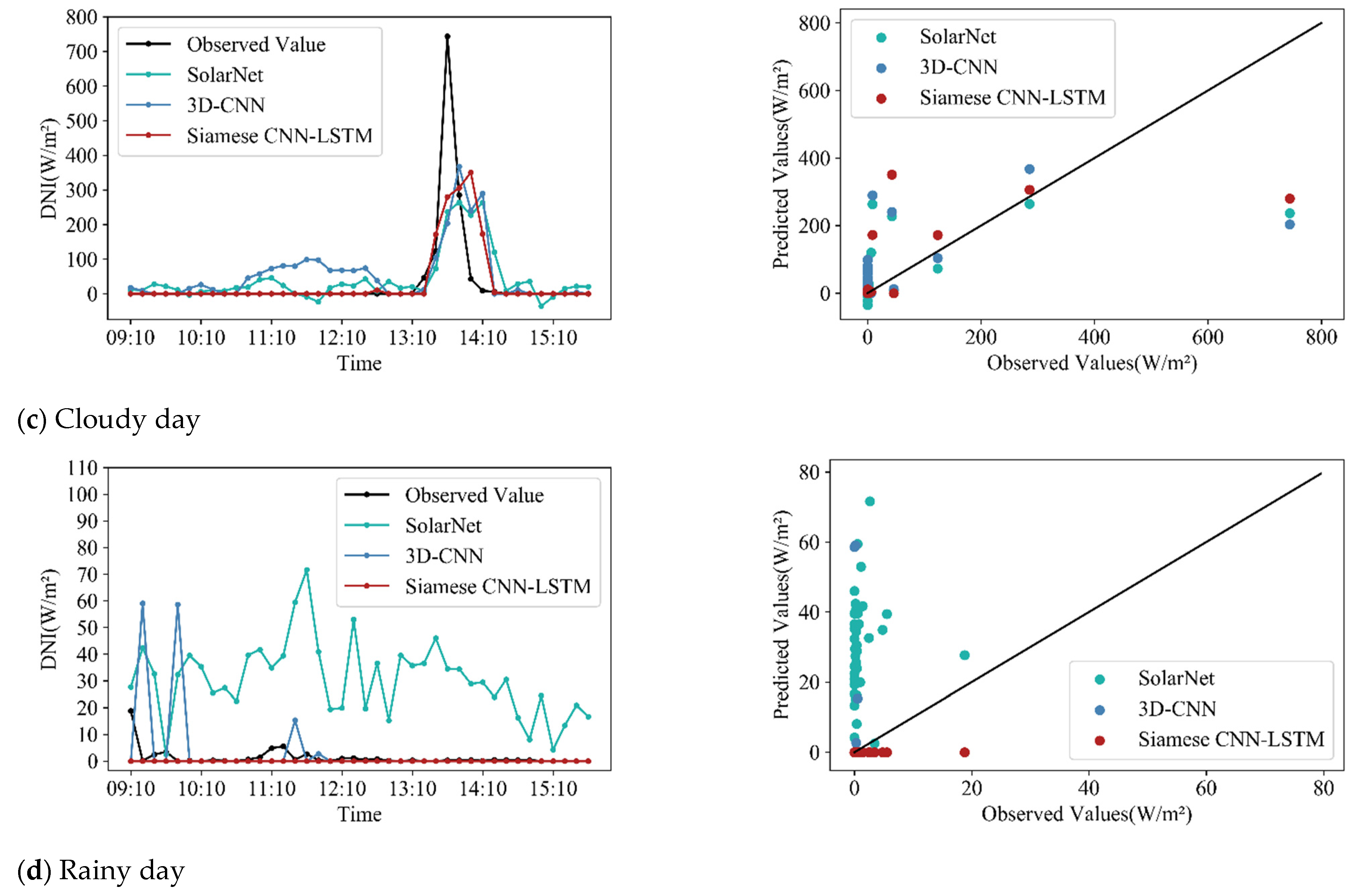
4.4. Performance of Different Forecast Models under Different Weather Conditions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Yang, Y.; Campana, P.E.; Stridh, B.; Yan, J. Potential analysis of roof-mounted solar photovoltaics in Sweden. Appl. Energy 2020, 279, 115786. [Google Scholar] [CrossRef]
- Qiao, Y.H.; Han, S.; Xu, Y.P.; Liu, Y.Q.; Ma, T.D.; Cai, Q. Analysis Method for Complementarity between Wind and Photovoltaic Power Output Based on Weather Classification. Autom. Elect. Power Syst. 2021, 45, 82–88. [Google Scholar]
- Moreira, M.; Balestrassi, P.; Paiva, A.; Ribeiro, P.; Bonatto, B. Design of experiments using artificial neural network ensemble for photovoltaic generation forecasting. Renew. Sustain. Energy Rev. 2020, 135, 110450. [Google Scholar] [CrossRef]
- Murty, V.V.V.S.N.; Kumar, A. Optimal Energy Management and Techno-economic Analysis in Microgrid with Hybrid Renewable Energy Sources. J. Mod. Power Syst. Clean Energy 2020, 8, 929–940. [Google Scholar] [CrossRef]
- Rodríguez, F.; Fleetwood, A.; Galarza, A.; Fontán, L. Predicting solar energy generation through artificial neural networks using weather forecasts for microgrid control. Renew. Energy 2018, 126, 855–864. [Google Scholar] [CrossRef]
- Ge, L.; Xian, Y.; Yan, J.; Wang, B.; Wang, Z. A Hybrid Model for Short-term PV Output Forecasting Based on PCA-GWO-GRNN. J. Mod. Power Syst. Clean Energy 2020, 8, 1268–1275. [Google Scholar] [CrossRef]
- Ji, W.; Chee, K.C. Prediction of hourly solar radiation using a novel hybrid model of ARMA and TDNN. Sol. Energy 2011, 85, 808–817. [Google Scholar] [CrossRef]
- Sun, H.; Yan, D.; Zhao, N.; Zhou, J. Empirical investigation on modeling solar radiation series with ARMA–GARCH models. Energy Convers. Manag. 2015, 92, 385–395. [Google Scholar] [CrossRef]
- Alfadda, A.; Rahman, S.; Pipattanasomporn, M. Solar irradiance forecast using aerosols measurements: A data driven approach. Sol. Energy 2018, 170, 924–939. [Google Scholar] [CrossRef]
- Lin, J.; Li, H. A Short-Term PV Power Forecasting Method Using a Hybrid Kmeans-GRA-SVR Model under Ideal Weather Condition. J. Comput. Commun. 2020, 8, 102–119. [Google Scholar] [CrossRef]
- Wu, X.; Lai, C.S.; Bai, C.; Lai, L.L.; Zhang, Q.; Liu, B. Optimal Kernel ELM and Variational Mode Decomposition for Probabilistic PV Power Prediction. Energies 2020, 13, 3592. [Google Scholar]
- Zhu, T.; Zhou, H.; Wei, H.; Zhao, X.; Zhang, K.; Zhang, J. Inter-hour direct normal irradiance forecast with multiple data types and time-series. J. Mod. Power Syst. Clean Energy 2019, 7, 1319–1327. [Google Scholar] [CrossRef] [Green Version]
- Fonseca, J.G.D.S.; Uno, F.; Ohtake, H.; Oozeki, T.; Ogimoto, K. Enhancements in Day-Ahead Forecasts of Solar Irradiation with Machine Learning: A Novel Analysis with the Japanese Mesoscale Model. J. Appl. Meteorol. Clim. 2020, 59, 1011–1028. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Global solar radiation prediction by ANN integrated with European Centre for medium range weather forecast fields in solar rich cities of Queensland Australia. J. Clean. Prod. 2019, 216, 288–310. [Google Scholar] [CrossRef]
- Pereira, S.; Canhoto, P.; Salgado, R.; Costa, M.J. Development of an ANN based corrective algorithm of the operational ECMWF global horizontal irradiation forecasts. Sol. Energy 2019, 185, 387–405. [Google Scholar] [CrossRef]
- Awan, S.M.; Khan, Z.A.; Aslam, M. Solar Generation Forecasting by Recurrent Neural Networks Optimized by Levenberg-Marquardt Algorithm. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 20–23 October 2018. [Google Scholar]
- Yeom, J.-M.; Park, S.; Chae, T.; Kim, J.-Y.; Lee, C.S. Spatial Assessment of Solar Radiation by Machine Learning and Deep Neural Network Models Using Data Provided by the COMS MI Geostationary Satellite: A Case Study in South Korea. Sensors 2019, 19, 2082. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moncada, A.; Richardson, W., Jr.; Vega-Avila, R. Deep learning to forecast solar irradiance using a six-month UTSA SkyImager dataset. Energies 2018, 11, 1988. [Google Scholar] [CrossRef] [Green Version]
- Chu, Y.; Pedro, H.; Li, M.; Coimbra, C.F. Real-time forecasting of solar irradiance ramps with smart image processing. Sol. Energy 2015, 114, 91–104. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, J. SolarNet: A sky image-based deep convolutional neural network for intra-hour solar forecasting. Sol. Energy 2020, 204, 71–78. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, H.; Wang, H.; Zhu, T.; Zhang, K. 3D-CNN-based feature extraction of total cloud images for direct normal irradiance prediction. Sol. Energy 2019, 181, 510–518. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Ge, Y.; Nan, Y.; Bai, L. A Hybrid Prediction Model for Solar Radiation Based on Long Short-Term Memory, Empirical Mode Decomposition, and Solar Profiles for Energy Harvesting Wireless Sensor Networks. Energies 2019, 12, 4762. [Google Scholar]
- Huynh, A.N.-L.; Deo, R.C.; An-Vo, D.-A.; Ali, M.; Raj, N.; Abdulla, S. Near Real-Time Global Solar Radiation Forecasting at Multiple Time-Step Horizons Using the Long Short-Term Memory Network. Energies 2020, 13, 3517. [Google Scholar]
- Law, E.W.; Prasad, A.A.; Kay, M.; Taylor, R.A. Direct normal irradiance forecasting and its application to concentrated solar thermal output forecasting—A review. Sol. Energy 2014, 108, 287–307. [Google Scholar] [CrossRef]
- Andreas, A.; Stoffel, T. NREL Solar Radiation Research Laboratory (SRRL): Baseline Measurement System (BMS); Golden, Colorado (Data). NREL Report No. DA-5500-56488. 1981. Available online: http://dx.doi.org/10.5439/1052221 (accessed on 15 July 2021).
- Feng, C.; Yang, D.; Hodge, B.-M.; Zhang, J. OpenSolar: Promoting the openness and accessibility of diverse public solar datasets. Sol. Energy 2019, 188, 1369–1379. [Google Scholar] [CrossRef]
- Eduardo, W.F.; Ramos, M.R.; Santos, C.E.; Pereira, E.B. Comparison of methodologies for cloud cover estimation in Brazil—A case study. Energy Sust. Dev. 2018, 43, 15–22. [Google Scholar]
- Zhu, T.; Wei, H.; Zhao, X.; Zhang, C.; Zhang, K. Clear-sky model for wavelet forecast of direct normal irradiance. Renew. Energy 2017, 104, 1–8. [Google Scholar] [CrossRef]
- Zhu, X.; Zhou, H.; Zhu, T.T.; Jin, S.; Wei, H. Pre-processing of Ground-based Cloud Images in Photovoltaic System. Autom. Electr. Power Syst. 2018, 42, 140–145. [Google Scholar]
- Pfister, G.; Mckenzie, R.L.; Liley, J.B.; Thomas, A.; Forgan, B.W.; Long, C.N. Cloud Coverage Based on All-Sky Imaging and Its Impact on Surface Solar Irradiance. J. Appl. Meteorol. 2003, 42, 1421–1434. [Google Scholar] [CrossRef]
- Rodríguez-Benítez, F.J.; López-Cuesta, M.; Arbizu-Barrena, C.; Fernández-León, M.M.; Pamos-Ureña, M.; Tovar-Pescador, J.; Santos-Alamillos, F.J.; Pozo-Vázquez, D. Assessment of new solar radiation nowcasting methods based on sky-camera and satellite imagery. Appl. Energy 2021, 292, 116838. [Google Scholar] [CrossRef]
- Wealliem, D.L. A Critique of the Bayesian Information Criterion for Model Selection. Sociol. Methods Res. 1999, 27, 359–397. [Google Scholar] [CrossRef]
- Ni, C.; Wang, D.; Vinson, R.; Holmes, M.; Tao, Y. Automatic inspection machine for maize kernels based on deep convolutional neural networks. Biosyst. Eng. 2019, 178, 131–144. [Google Scholar] [CrossRef]
- Chopra, S.; Hadsell, R.; Lecun, Y. Learning a similarity metric discriminatively, with application to face verification. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR′05), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Xiaoyu, L.; Zhang, L.; Wang, Z.; Dong, P. Remaining useful life prediction for lithiumion batteries based on a hybrid model combining the long short-term memory and Elman neural networks. J. Energy Storage 2019, 21, 510–518. [Google Scholar]


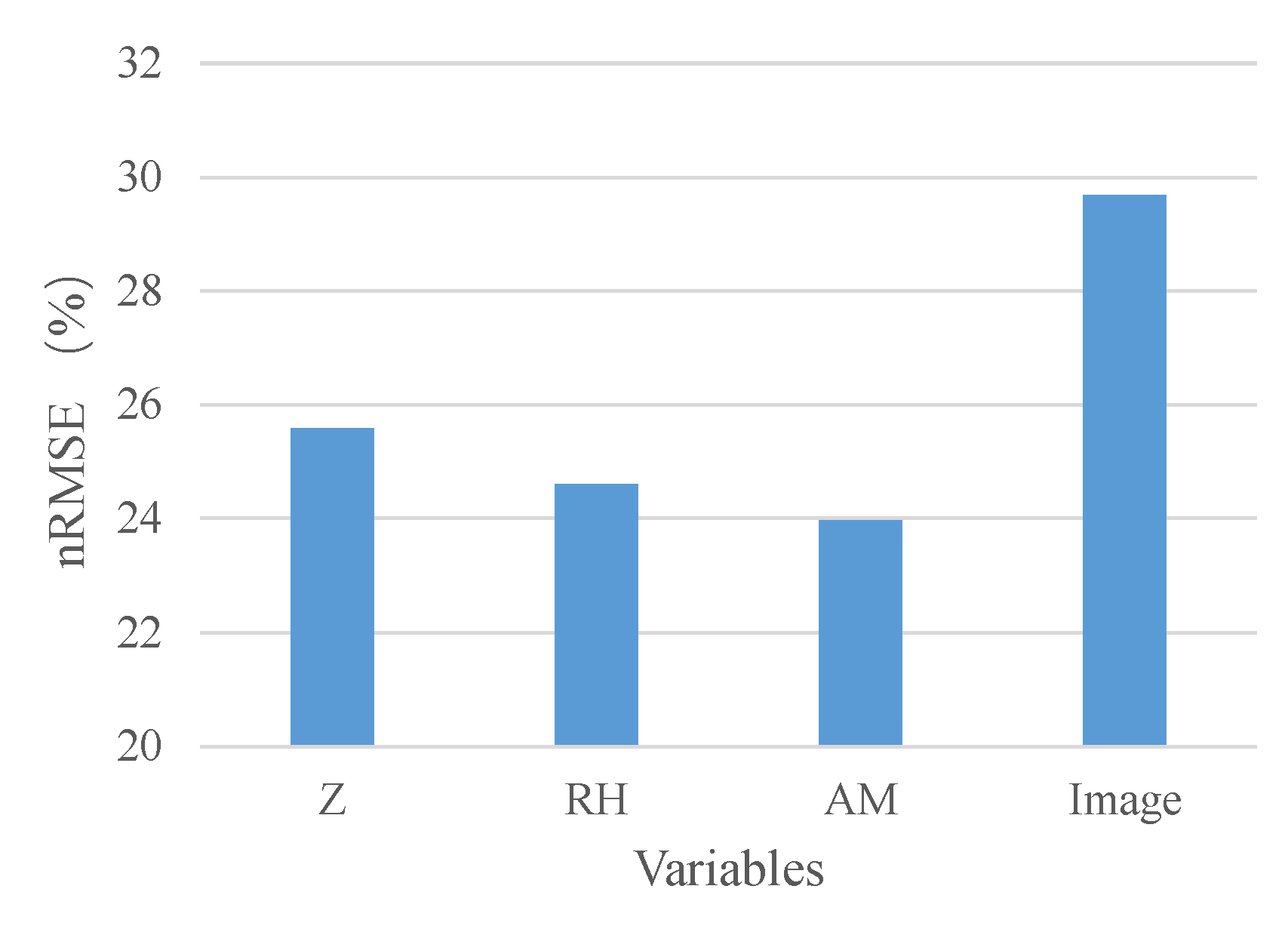
| Variables | Names in Database | Units | Instruments |
|---|---|---|---|
| DNI | Direct CH1 | Wm−2 | Kipp and Zonen pyrheliometer |
| Solar zenith angle | Zenith angle | Degrees | - |
| Relative humidity | Relative humidity (Tower) | - | Vaisala probe |
| Air mass | Airmass | % | - |
| Dateset | Time | Number of Data Groups |
|---|---|---|
| Training set | February, March, April, May, June, August, Spetember, October, November and December in 2013 | 16,843 |
| Validation set | January 2013, July 2013 | 3678 |
| Testing set | 2014 | 20,618 |
| Models | Number of Neurons | r | nMBE (%) | nMAE (%) | nRMSE (%) | Fs (%) |
|---|---|---|---|---|---|---|
| 1 | 10 | 0.9560 | −0.22 | 13.94 | 24.84 | 20.84 |
| 2 | 512, 10 | 0.9596 | 0.14 | 13.75 | 23.47 | 24.51 |
| 3 | 512, 256, 10 | 0.9590 | 0.07 | 13.37 | 23.95 | 22.97 |
| Models | Number of Neurons | r | nMBE (%) | nMAE (%) | nRMSE (%) | Fs (%) |
|---|---|---|---|---|---|---|
| A | 30 | 0.9585 | −0.52 | 13.41 | 23.89 | 23.16 |
| B | 50 | 0.9596 | 0.14 | 13.75 | 23.47 | 24.51 |
| C | 50, 30 | 0.9544 | −2.44 | 14.65 | 25.13 | 19.17 |
| Models | r | nMBE (%) | nMAE (%) | nRMSE (%) |
|---|---|---|---|---|
| Persistent model | 0.9311 | 0.50 | 15.54 | 31.09 |
| MLP 1 | 0.9348 | 2.73 | 16.89 | 29.92 |
| LSTM 2 | 0.9351 | 0.65 | 16.78 | 29.69 |
| SolarNet [20] | 0.9505 | −1.07 | 17.28 | 26.18 |
| 3D-CNN [21] | 0.9564 | 1.13 | 13.92 | 24.49 |
| SCNN-LSTM | 0.9596 | 0.14 | 13.75 | 23.47 |
| Weather Conditions | Models | r | nMBE (%) | nMAE (%) | nRMSE (%) | Fs (%) |
|---|---|---|---|---|---|---|
| Clear sky | Persistent model | 0.9684 | 0.24 | 2.33 | 6.32 | 0 |
| MLP | 0.9731 | 0.37 | 2.30 | 5.83 | 7.82 | |
| LSTM | 0.9719 | −1.16 | 2.60 | 6.05 | 4.28 | |
| SolarNet [20] | 0.9650 | −0.92 | 3.74 | 6.69 | −5.86 | |
| 3D-CNN [21] | 0.9789 | −1.10 | 3.16 | 5.27 | 16.66 | |
| SCNN-LSTM | 0.9838 | 0.16 | 2.50 | 4.53 | 28.25 | |
| Partly cloud | Persistent model | 0.8895 | 0.98 | 17.06 | 29.21 | 0 |
| MLP | 0.8949 | 1.92 | 17.41 | 27.96 | 4.28 | |
| LSTM | 0.8940 | −0.31 | 17.48 | 27.98 | 4.22 | |
| SolarNet | 0.9080 | −6.71 | 21.40 | 27.66 | 5.29 | |
| 3D-CNN | 0.9249 | −0.48 | 15.39 | 23.69 | 18.88 | |
| SCNN-LSTM | 0.9323 | 1.33 | 15.19 | 22.62 | 22.56 | |
| Cloudy | Persistent model | 0.8888 | 0.90 | 30.90 | 51.35 | 0 |
| MLP | 0.8918 | 7.34 | 33.44 | 49.88 | 2.87 | |
| LSTM | 0.8938 | 5.66 | 33.07 | 49.12 | 4.36 | |
| SolarNet | 0.9226 | −4.79 | 30.66 | 42.28 | 17.66 | |
| 3D-CNN | 0.9356 | 3.78 | 25.44 | 38.59 | 24.85 | |
| SCNN-LSTM | 0.9274 | 4.65 | 27.09 | 41.05 | 20.07 | |
| Rainy | Persistent model | 0.8912 | 0.52 | 32.33 | 65.62 | 0 |
| MLP | 0.8957 | 7.20 | 36.81 | 63.27 | 3.58 | |
| LSTM | 0.8949 | 3.87 | 36.42 | 63.08 | 3.88 | |
| SolarNet | 0.9320 | 0.13 | 37.40 | 52.92 | 19.35 | |
| 3D-CNN | 0.9291 | 2.91 | 28.43 | 52.44 | 20.09 | |
| SCNN-LSTM | 0.9405 | −0.79 | 26.33 | 47.84 | 27.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, T.; Guo, Y.; Li, Z.; Wang, C. Solar Radiation Prediction Based on Convolution Neural Network and Long Short-Term Memory. Energies 2021, 14, 8498. https://doi.org/10.3390/en14248498
Zhu T, Guo Y, Li Z, Wang C. Solar Radiation Prediction Based on Convolution Neural Network and Long Short-Term Memory. Energies. 2021; 14(24):8498. https://doi.org/10.3390/en14248498
Chicago/Turabian StyleZhu, Tingting, Yiren Guo, Zhenye Li, and Cong Wang. 2021. "Solar Radiation Prediction Based on Convolution Neural Network and Long Short-Term Memory" Energies 14, no. 24: 8498. https://doi.org/10.3390/en14248498
APA StyleZhu, T., Guo, Y., Li, Z., & Wang, C. (2021). Solar Radiation Prediction Based on Convolution Neural Network and Long Short-Term Memory. Energies, 14(24), 8498. https://doi.org/10.3390/en14248498







