Suppression Method of Partial Discharge Interferences Based on Singular Value Decomposition and Improved Empirical Mode Decomposition
Abstract
:1. Introduction
2. PD and Interference Signals for Simulation Analysis
2.1. PD Signal Simulation
2.2. Simulation of PD Signal with Noise
3. Simulation Analysis of SVD Suppression Effect on Interference Signal
3.1. SVD of Signal
3.2. Signal Reconstruction Based on SVD Results
3.3. Singular Value Distribution Characteristics of Periodic Narrowband Interference Signals
3.4. Analysis on the Suppression of SVD on Periodic Narrowband Interference
3.5. Singular Value Distribution Characteristics of White Noise Interference Signals
3.6. SVD Suppression Effect in the Presence of White Noise and Periodic Narrowband Interference
4. Simulation Analysis of Suppression Effect of EMD on Interference Signal
4.1. EMD
- (1)
- In the entire data sequence interval, the number of extreme points is equal to or differs by at most one unit from the number of zero crossings.
- (2)
- The upper envelope and the lower envelope are symmetric about the time axis, that is, the mean value m(t) = 0.
- (1)
- Find all maximum and minimum points of signal x(t).
- (2)
- The upper envelope emax(t) and the lower envelope emin(t) are obtained by the cubic spline interpolation method to interpolate the maximum and minimum points, respectively.
- (3)
- Calculate the average value of the upper envelope emax(t) and the lower envelope emin(t) as follows:
- (4)
- Remove m(t) from x(t) and separate h(t) as follows:
- (5)
- Determine whether h(t) satisfies the two constraints of the IMF. If so, h1(t) = h(t) is the first-order IMF component, and step (6) is executed. Otherwise, let x(t)= h(t) and repeat steps (1)–(5) until the condition is satisfied.
- (6)
- Let r1(t) = x(t) − h1(t) to determine whether r1(t) is a monotone function or the absolute value is small enough. If so, EMD ends. Otherwise, let x(t) = r1(t) and return to step (1).
4.2. Endpoint Effect
4.3. Suppression Effect of EMD on Periodic Narrowband Interference
4.4. Suppression Effect of EMD on White Noise
5. IEMD Method for Interference Suppression of PD Signal
5.1. IMF Component Processing Method Based on Improved 3σ Criterion
- (1)
- Estimate the absolute value of each sequence of IMF component hi(t) to obtain the absolute value sequence f(t). The standard deviation of f(t) is obtained as σ, and the threshold th = 3σ.
- (2)
- According to the threshold, identify the “gross error” outside the threshold range in the hi(t) component.
- (3)
- A new sequence f′(t) is obtained by removing the “gross error” from the f(t) sequence. The standard deviation of f′(t) is σ′, and th′= 3σ′.
- (4)
- Assess whether a “gross error” exists in hi(t). If so, go back to Step (3). If not, end the statistical processing.
- (1)
- The PD signal with periodic narrowband interference and white noise interference is decomposed by SVD.
- (2)
- According to the singular value distribution characteristics of the periodic narrowband interference signals, the singular value corresponding to periodic narrowband interference is determined and set to zero. Signal reconstruction is completed by an inverse SVD operation, and periodic narrowband interference suppression is realized.
- (3)
- The IMF component is obtained by EMD of the signal after SVD interference suppression.
- (4)
- Based on the improved 3σ criterion, the IMF components are statistically processed.
- (5)
- The IMF component after processing is reconstructed to achieve the suppression of white noise interference to obtain the PD signal.
5.2. Comparison of Interference Suppression Effects
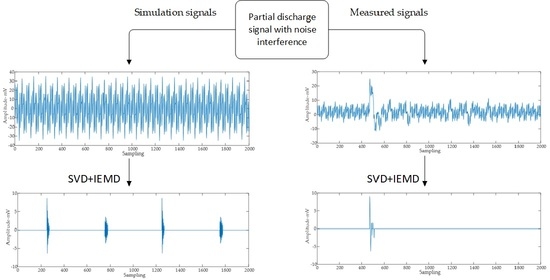
6. Actual Measurement of PD Interference Suppression
7. Conclusions
- (1)
- The singular value distribution characteristics of periodic narrowband interference are obvious. SVD can effectively suppress the periodic narrowband interference in PD signals, but it has poor suppression effects on white noise interference.
- (2)
- EMD is better than SVD in suppressing white noise interference, but SVD has obvious advantages in suppressing periodic narrowband interference.
- (3)
- Based on the improved 3σ criterion, statistical processing of the IMF derived from EMD can effectively solve the problem of mode mixing of EMD and can more effectively suppress the interference of white noise.
- (4)
- Compared with SVD and SVD + EMD interference suppression methods, the proposed method yields larger SNR values, waveform similarity coefficients closer to unity, smaller MSE values, and larger noise suppression ratios. For the simulated and measured signals, the PD pulse waveform can be restored more effectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baug, A.; Choudhury, N.R.; Ghosh, R.; Dalai, S.; Chatterjee, B. Identification of single and multiple partial discharge sources by optical method using mathematical morphology aided sparse representation classifier. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3703–3712. [Google Scholar] [CrossRef]
- Li, J.; Han, X.; Liu, Z.; Yao, X. A Novel GIS Partial Discharge Detection Sensor with Integrated Optical and UHF Methods. IEEE Trans. Power Deliv. 2018, 33, 2047–2049. [Google Scholar] [CrossRef]
- Santos, M.G.; Braulio, G.A.; Bernardes, J.V.; De Salles, C.; Milanez, J.R.C.; Bortoni, E.C.; Bastos, G.S. Continuous Partial Discharges Analysis During Automated Thermal Cycle Aging Experiment. IEEE Trans. Energy Convers. 2020, 35, 1989–1992. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, G.; Bi, J.; Li, J.; Peng, X.; Liu, T. Interference Rejection of High Voltage Cables Partial Discharge Detection Based on Combina-tion Features Analysis. In Proceedings of the 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, China, 1–4 December 2019; pp. 1–5. [Google Scholar]
- Abdel-Galil, T.K.; El-Hag, A.; Gaouda, A.M.; Salama, M.M.; Bartnikas, R. De-noising of partial discharge signal using eigen-decomposition technique. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1657–1662. [Google Scholar] [CrossRef]
- Tang, J.; Dong, Y.; Fan, L.; Li, L. Feature information extraction of partial discharge signal with complex wavelet trans-form and singular value decomposition based on Hankel matrix. Proc. CSEE 2015, 35, 1808–1817. (In Chinese) [Google Scholar]
- Rajendran, A.; Meena, K.P.; Buijupati, N.R. Simulation of partial discharges and implementation of noise elimination techniques. In Proceedings of the 2017 3rd International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Rupnagar, India, 16–18 November 2017; pp. 412–417. [Google Scholar]
- Zhao, Y.; Liu, X. Extracting Partial Discharge Signals of Generator Based on Elevated Minimum Description Length Cri-terion and Fast Fourier Transform. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 11–12 April 2009; pp. 222–225. [Google Scholar]
- Luo, X.; Niu, H.; Wu, J. A modified method of suppressing narrow-band interference using FFT power spectrum. In Proceedings of the 2013 IEEE International Conference on Solid Dielectrics (ICSD), Bologna, Italy, 30 June–4 July 2013; pp. 83–87. [Google Scholar]
- Shim, I.; Soraghan, J.; Siew, W.H. Detection of PD utilizing digital signal processing methods. Part 3: Open-loop noise reduction. IEEE Electr. Insul. Mag. 2001, 17, 6–13. [Google Scholar] [CrossRef]
- Shams, M.A.; Anis, H.I.; El-Shahat, M. Denoising of Heavily Contaminated Partial Discharge Signals in High-Voltage Cables Using Maximal Overlap Discrete Wavelet Transform. Energies 2021, 14, 6540. [Google Scholar] [CrossRef]
- Soltani, A.A.; El-Hag, A. Denoising of Radio Frequency Partial Discharge Signals Using Artificial Neural Network. Energies 2019, 12, 3485. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; He, B.; Wang, X.; Cui, L.; Li, Y. Extraction of Partial Discharge Signal Feature Based on Dual-tree Complex Wave-let Transform and Singular-value Decomposition. In Proceedings of the 2018 Condition Monitoring and Diagnosis (CMD), Perth, WA, Australia, 23–26 September 2018; pp. 1–5. [Google Scholar]
- Ashtiani, M.B.; Shahrtash, S.M. Partial discharge de-noising employing improved singular value decomposition. In Proceedings of the 2012 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Montreal, QC, Canada, 14–17 October 2012; pp. 137–140. [Google Scholar]
- Ran, H.; Xu, Y.; Jiang, J.; Tang, K.; He, Z.; Zhang, T.; Tang, X. Application of Singular Value Reconstruction in Suppressing Narrowband Interference of Partial Discharge. In Proceedings of the 2019 4th International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 21–23 September 2019; pp. 239–243. [Google Scholar]
- Ashtiani, M.B.; Shahrtash, S.M. Partial discharge de-noising employing adaptive singular value decomposition. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 775–782. [Google Scholar] [CrossRef]
- Zhou, K.; Li, M.; Li, Y.; Xie, M.; Huang, Y. An Improved Denoising Method for Partial Discharge Signals Contaminated by White Noise Based on Adaptive Short-Time Singular Value Decomposition. Energies 2019, 12, 3465. [Google Scholar] [CrossRef] [Green Version]
- Wei, L.; Liu, Y.; Cheng, D.; Li, P.; Shi, Z.; Huang, N.; Ai, H.; Zhu, T. A Novel Partial Discharge Ultra-High Frequency Signal De-Noising Method Based on a Single-Channel Blind Source Separation Algorithm. Energies 2018, 11, 509. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Herold, C.; Wenig, S.; Leibfried, T. Advanced de-noising of power cable Partial Discharge signals by Empirical Mode De-composition. In Proceedings of the 2010 20th Australasian Universities Power Engineering Conference, Christchurch, New Zealand, 5–8 December 2010; pp. 1–5. [Google Scholar]
- Chan, J.C.; Ma, H.; Saha, T.K.; Ekanayake, C. Self-adaptive partial discharge signal de-noising based on ensemble empirical mode decomposition and automatic morphological thresholding. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 294–303. [Google Scholar] [CrossRef]
- Zhong, J.; Bi, X.; Shu, Q.; Chen, M.; Zhou, D.; Zhang, D. Partial Discharge Signal Denoising Based on Singular Value Decomposition and Empirical Wavelet Transform. IEEE Trans. Instrum. Meas. 2020, 69, 8866–8873. [Google Scholar] [CrossRef]
- Yan, Z. A New Adaptive Threshold Algorithm for Narrow-band Interference Suppression in Partial Discharge Based on Improved Empirical Mode Decomposition and MDL Criterion. In Proceedings of the 2010 International Conference on Intelligent Computation Technology and Automation, Changsha, China, 11–12 May 2010; Volume 1, pp. 203–206. [Google Scholar]
- Ren, W.; Song, J.; Tian, S.; Zhang, X. Estimation of the Equivalent Number of Looks in SAR Images Based on Singular Value Decomposition. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2208–2212. [Google Scholar] [CrossRef]
- Beard, J.K. Singular Value Decomposition of a Matrix Representation of the Costas Condition for Costas Array Selection. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1139–1161. [Google Scholar] [CrossRef]
- Govindarajan, S.; Subbaiah, J.; Cavallini, A.; Krithivasan, K.; Jayakumar, J. Partial Discharge Random Noise Removal Using Hankel Matrix-Based Fast Singular Value Decomposition. IEEE Trans. Instrum. Meas. 2019, 69, 4093–4102. [Google Scholar] [CrossRef]
- Li, Q.; Bu, B.; Zhao, J. A Novel Hierarchical Situation Awareness Model for CBTC Using SVD Entropy and GRU With PRD Algorithms. IEEE Access 2021, 9, 132290–132300. [Google Scholar] [CrossRef]
- Yang, X.; Huang, H.; Shu, Q.; Zhang, D.; Chen, B. Partial Discharge Signal Extraction Method Based on EDSSV and Low Rank RBF Neural Network. IEEE Access 2021, 9, 9744–9752. [Google Scholar] [CrossRef]
- Karaaslan, O.F.; Bilgin, G. Comparison of Variational Mode Decomposition and Empirical Mode Decomposition Features for Cell Segmentation in Histopathological Images. In Proceedings of the 2020 Medical Technologies Congress (TIPTEKNO), Antalya, Turkey, 19–20 November 2020; pp. 1–4. [Google Scholar]
- Gan, G.; Zhou, X.; Li, H. Predicting Trend of High Frequency CSI 300 Index: Based on Empirical Mode Decomposition and BP Neural Network. In Proceedings of the 2021 4th International Conference on Artificial Intelligence and Big Data (ICAIBD), Chengdu, China, 28–31 May 2021; pp. 315–319. [Google Scholar]
- Huang, S.; Zhang, Y.; Liu, Z. Image feature extraction and analysis based on Empirical mode decomposition. In Proceedings of the 2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 3–5 October 2016; pp. 615–619. [Google Scholar]
- Ahmed, M.S.; Indira, B. Detection of exudates from RGB fundus images using 3σ control method. In Proceedings of the 2017 International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 22–24 March 2017; pp. 767–770. [Google Scholar]
- Yücetaş, M.; Pulkkine, M.; Gronicz, J.; Halonen, K. A temperature sensor with 3σ inaccuracy of +0.5/−0.75 °C and energy per conversion of 0.65 μJ using a 0.18 μm CMOS technology. In Proceedings of the 2013 NORCHIP, Vilnius, Lithuania, 11–12 November 2013; pp. 1–4. [Google Scholar]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. A 2004, 460, 1597–1611. [Google Scholar] [CrossRef]






















| Partial Discharge (PD) Pulse | A | B | C | D |
|---|---|---|---|---|
| Signal amplitude (A/mV) | 10 | 20 | 10 | 20 |
| Oscillation frequency (fc/MHz) | 20 | 40 | 20 | 40 |
| Attenuation coefficient (τ/μs) | 0.1 | 0.15 | 0.1 | 0.15 |
| Narrowband Interference | C1 | C2 | C3 |
|---|---|---|---|
| signal amplitude (Ai/mV) | 10 | 15 | 10 |
| Frequency (fi/MHz) | 2 | 10 | 15 |
| Noise Reduction Method | Signal-to-Noise Ratio (SNR) | Normalized Correlation Coefficient (NCC) | Mean-Squared Error (MSE) |
|---|---|---|---|
| Method used in this paper | 14.86 | 98.35% | 0.01 |
| SVD | 0.52 | 65.05% | 0.33 |
| SVD + EMD | 0.70 | 65.89% | 0.29 |
| Noise Reduction Method | Method Used in This Paper | SVD | SVD + EMD |
|---|---|---|---|
| ρ | 14.17 | 11.09 | 12.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Wei, X. Suppression Method of Partial Discharge Interferences Based on Singular Value Decomposition and Improved Empirical Mode Decomposition. Energies 2021, 14, 8579. https://doi.org/10.3390/en14248579
Li L, Wei X. Suppression Method of Partial Discharge Interferences Based on Singular Value Decomposition and Improved Empirical Mode Decomposition. Energies. 2021; 14(24):8579. https://doi.org/10.3390/en14248579
Chicago/Turabian StyleLi, Linao, and Xinlao Wei. 2021. "Suppression Method of Partial Discharge Interferences Based on Singular Value Decomposition and Improved Empirical Mode Decomposition" Energies 14, no. 24: 8579. https://doi.org/10.3390/en14248579
APA StyleLi, L., & Wei, X. (2021). Suppression Method of Partial Discharge Interferences Based on Singular Value Decomposition and Improved Empirical Mode Decomposition. Energies, 14(24), 8579. https://doi.org/10.3390/en14248579