An eDrive-Based Estimation Method of the Laundry Unbalance and Laundry Inertia for Washing Machine Applications
Abstract
:1. Introduction
- (1)
- Tumbling—The laundry is washed with water and detergent, while the drum speed is kept constant, typically around 50 rpm, and called tumbling speed.
- (2)
- Rinsing—The dirty water is drained out so that the laundry can be rinsed with clean water, while the drum speed is kept at the same level as the tumbling process.
- (3)
- Spinning—Starting from a standstill, the drum speed is increased to the maximum spinning value (typically in the range of 800–1600 rpm), extracting the water from the clean laundry.
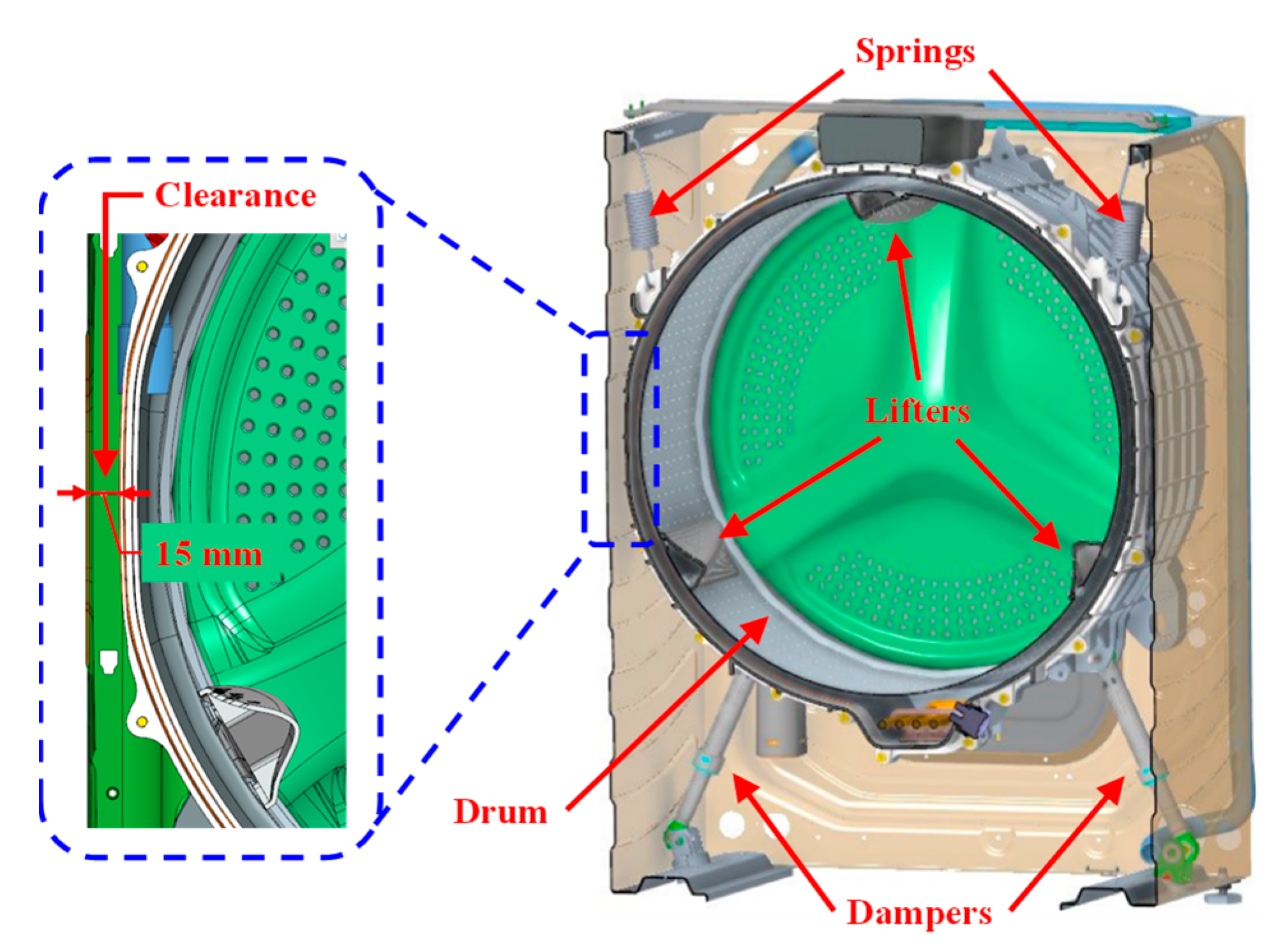
- If the washing machine has standard lifters (Figure 1), the drum is stopped and then started again to redistribute the laundry inside the drum.
- If the washing machine has balancing lifters, these can be filled with the right amount of water to compensate for the laundry unbalance, getting the same results of a redistribution action but without stopping the drum.
- (1)
- The laundry inertia is evaluated at a constant average drum speed, avoiding the risks of washer damaging caused by performing an acceleration ramp.
- (2)
- The proposed approach does not use any lookup table (LUT), avoiding demanding off-line tuning procedures by the washer manufacturer.
- (3)
- The laundry inertia estimation method does not require evaluating the friction losses and the load torque generated by the laundry unbalance.
- (4)
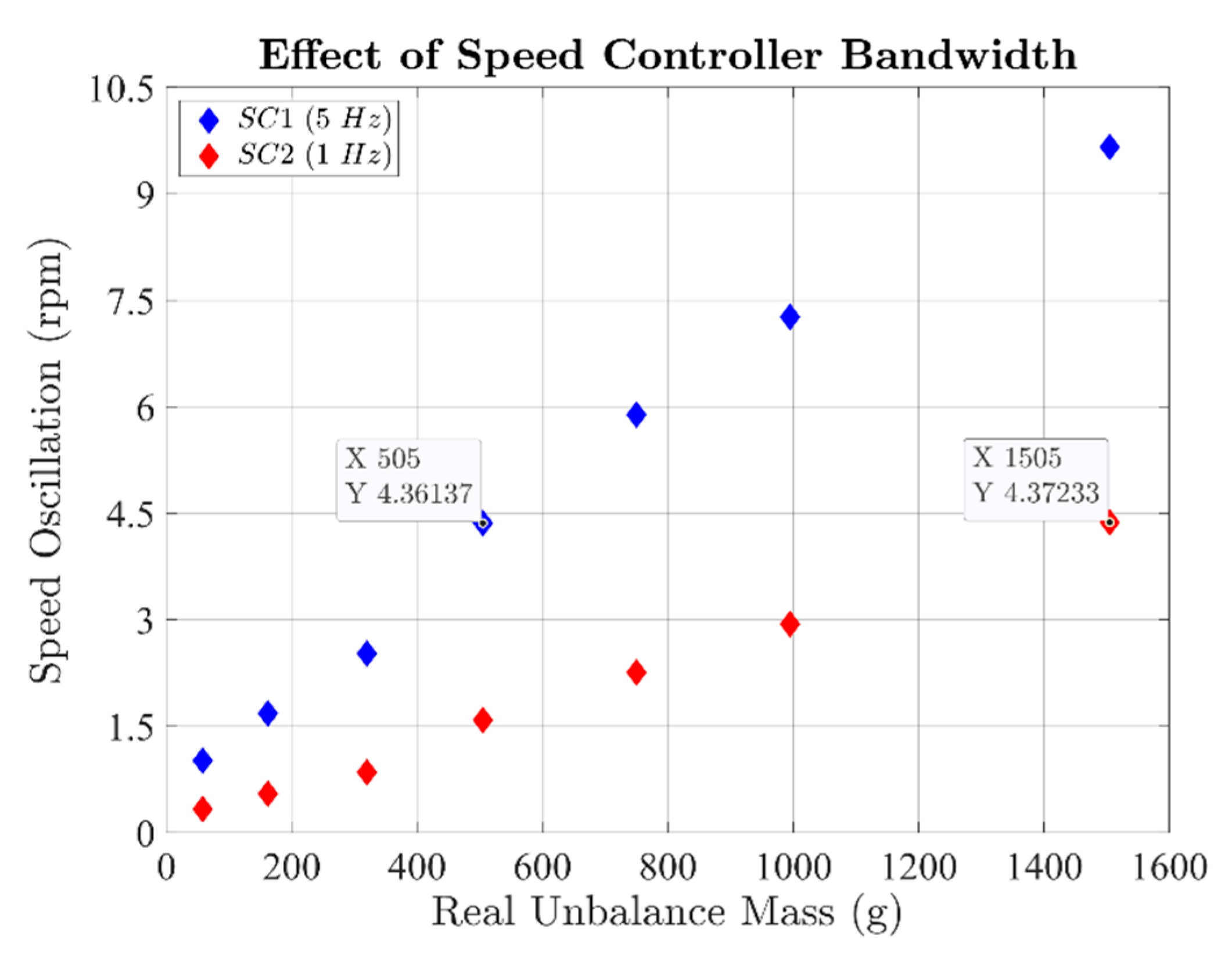
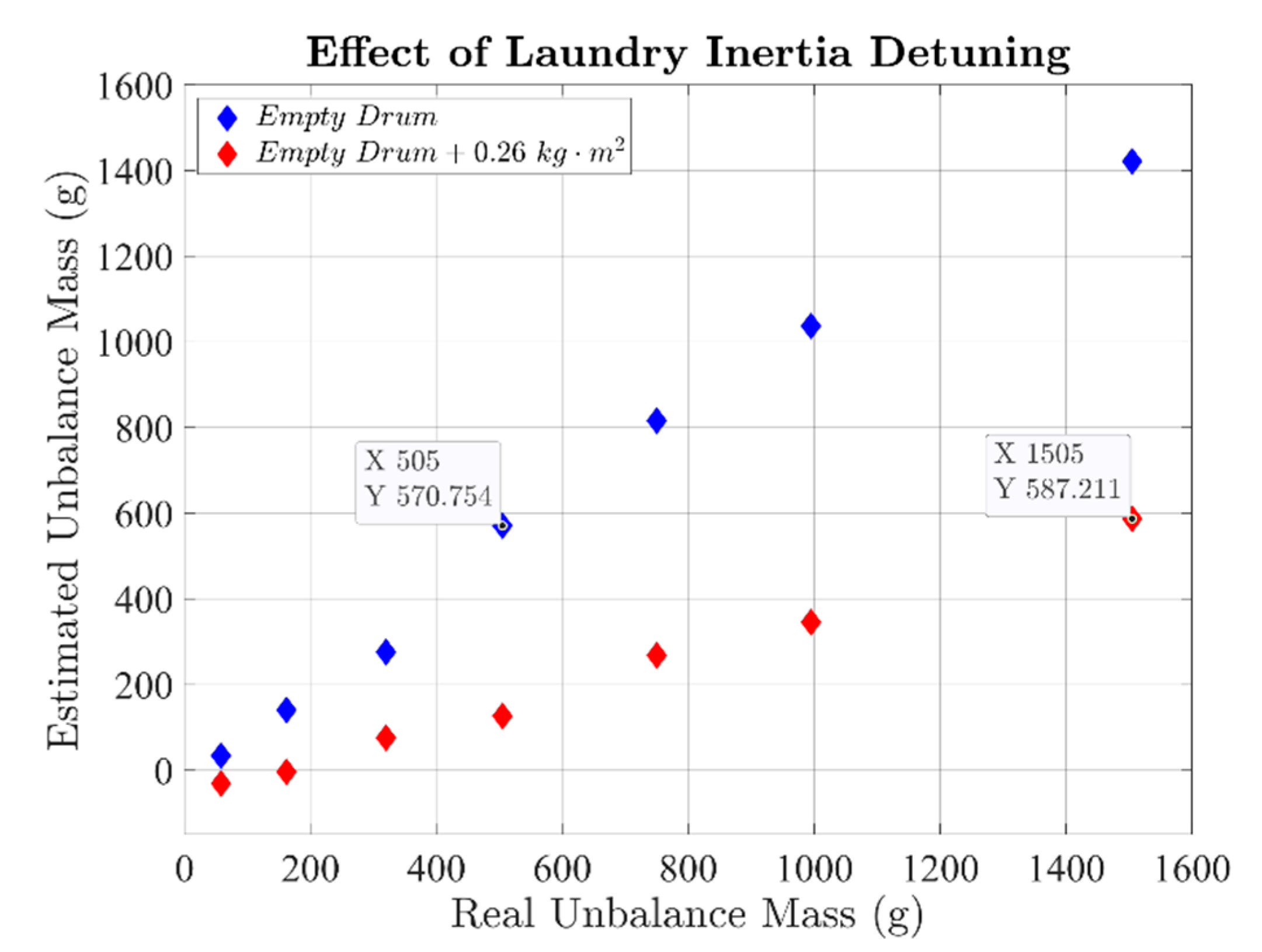
- Neither the speed controller bandwidth nor the laundry inertia affect the accuracy of the laundry unbalance estimation.
- (5)
- The proposed methodology can be easily embedded in the already implemented eDrive control algorithm, using the microcontrollers that are usually employed for such applications.
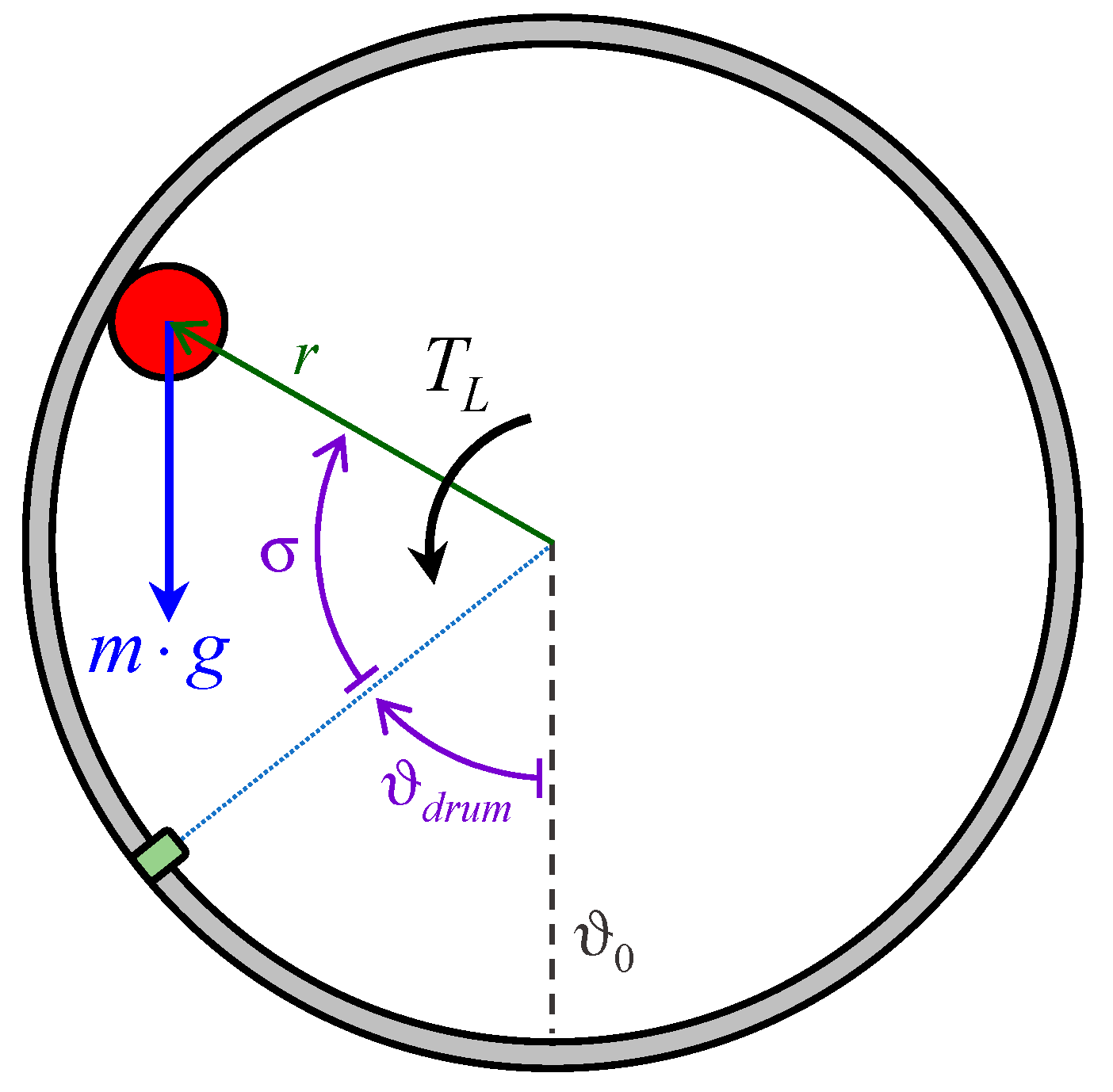
2. Model of the Laundry Unbalance
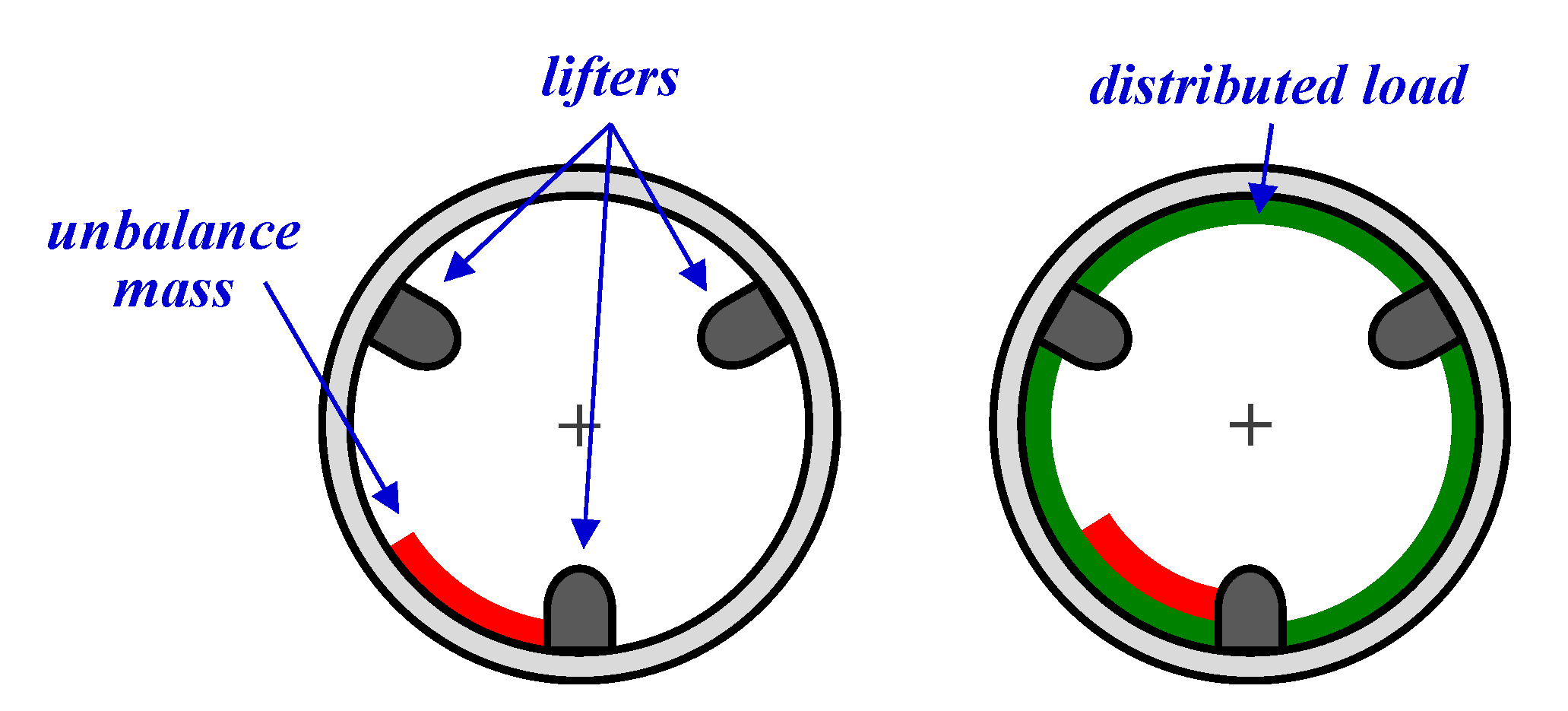
- (1)
- Distributed load—Consisting of the laundry portion that is uniformly distributed inside the drum.
- (2)
- Unbalance mass—Consisting of the laundry portion that, on the contrary, is not uniformly distributed inside the drum.
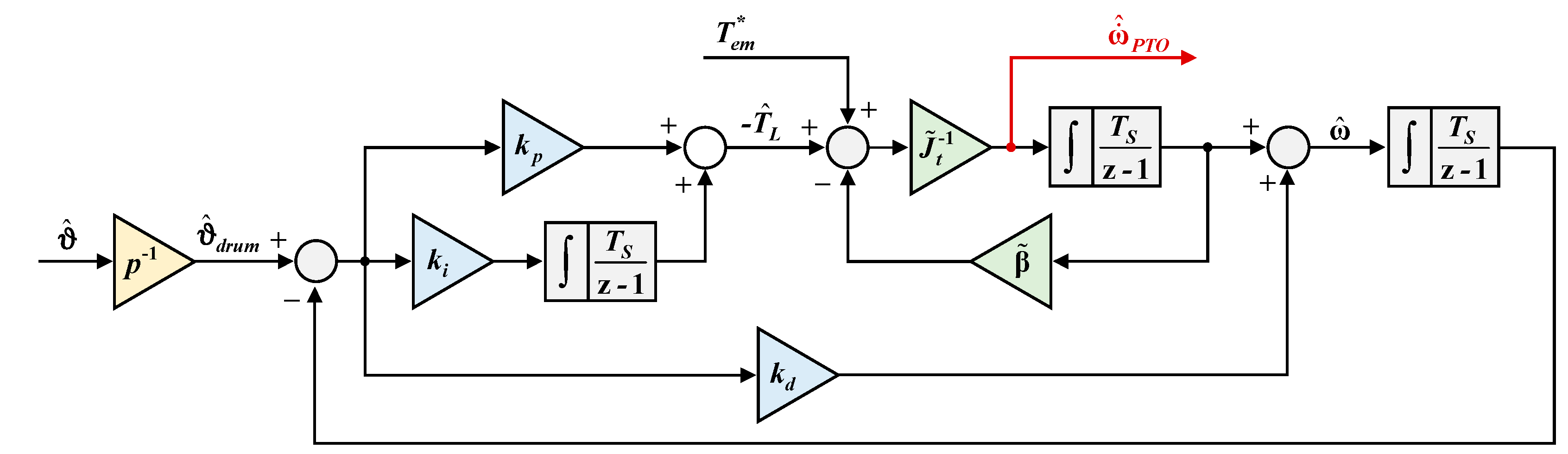
3. Conventional Method for Estimating the Laundry Unbalance and Laundry Inertia
3.1. Conventional Method Speed Profile
- (I)
- Distribution ramp—The speed drum is set to the satelization value, allowing for the laundry’s distribution inside the drum.
- (II)
- Acceleration ramp—The drum is accelerated with a constant average torque using the motor control scheme, allowing for the estimation of laundry inertia.
- (III)
- Unbalance estimation—According to the speed controller settings, the oscillations of the drum speed are used to estimate the unbalance mass.
- (IV)
- Decision making—Based on the estimated unbalance mass, two options are possible. If this value is below the maximum limit, (a) the spinning process is started, completing the washing cycle. Conversely, if the estimated unbalance mass overcomes the safety limit, (b) the drum is stopped, and a new distribution ramp is started, thus repeating the whole sequence.
3.2. Conventional Method’s Critical Points
- (1)
- The estimation of unbalance mass requires experimental LUTs, forcing the washer manufacturer to perform demanding identification procedures that must be performed off-line using dedicated test rigs.
- (2)
- The laundry inertia evaluation needs to estimate friction (2), thus requiring in-depth modeling of the mechanical transmission system (motor to the drum).
- (3)
- The acceleration ramp may excite the drum’s mechanical resonance, running the risk of the washing unit’s oscillations exceeding the clearance (see Figure 1), touching the cabinet, and damaging the washer.
- ⚬
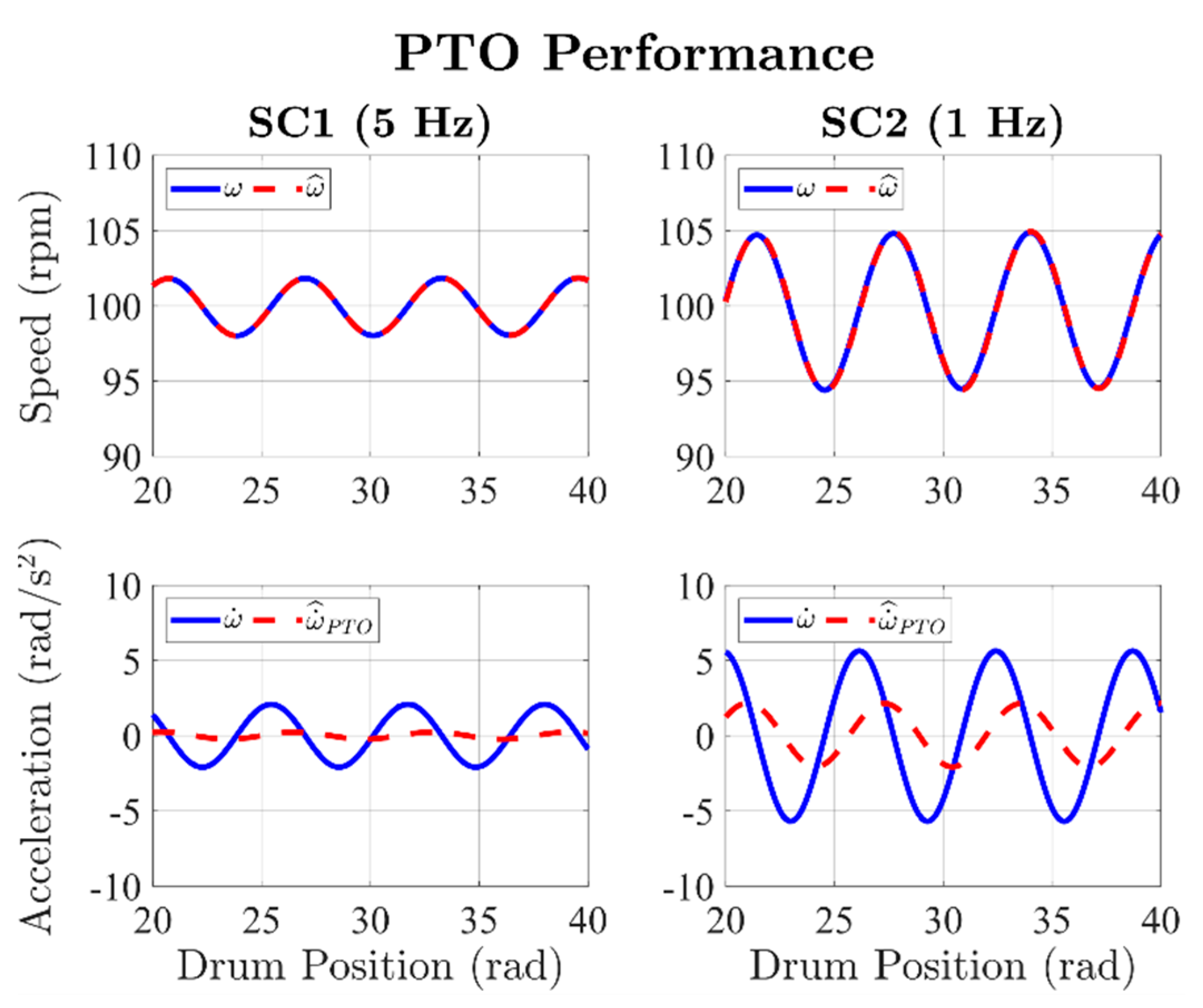
- Speed controller bandwidth of 5 Hz; such a setting is from now onwards denoted as SC1.
- ⚬
- Speed controller bandwidth of 1 Hz; by analogy, this setting is denoted as SC2.
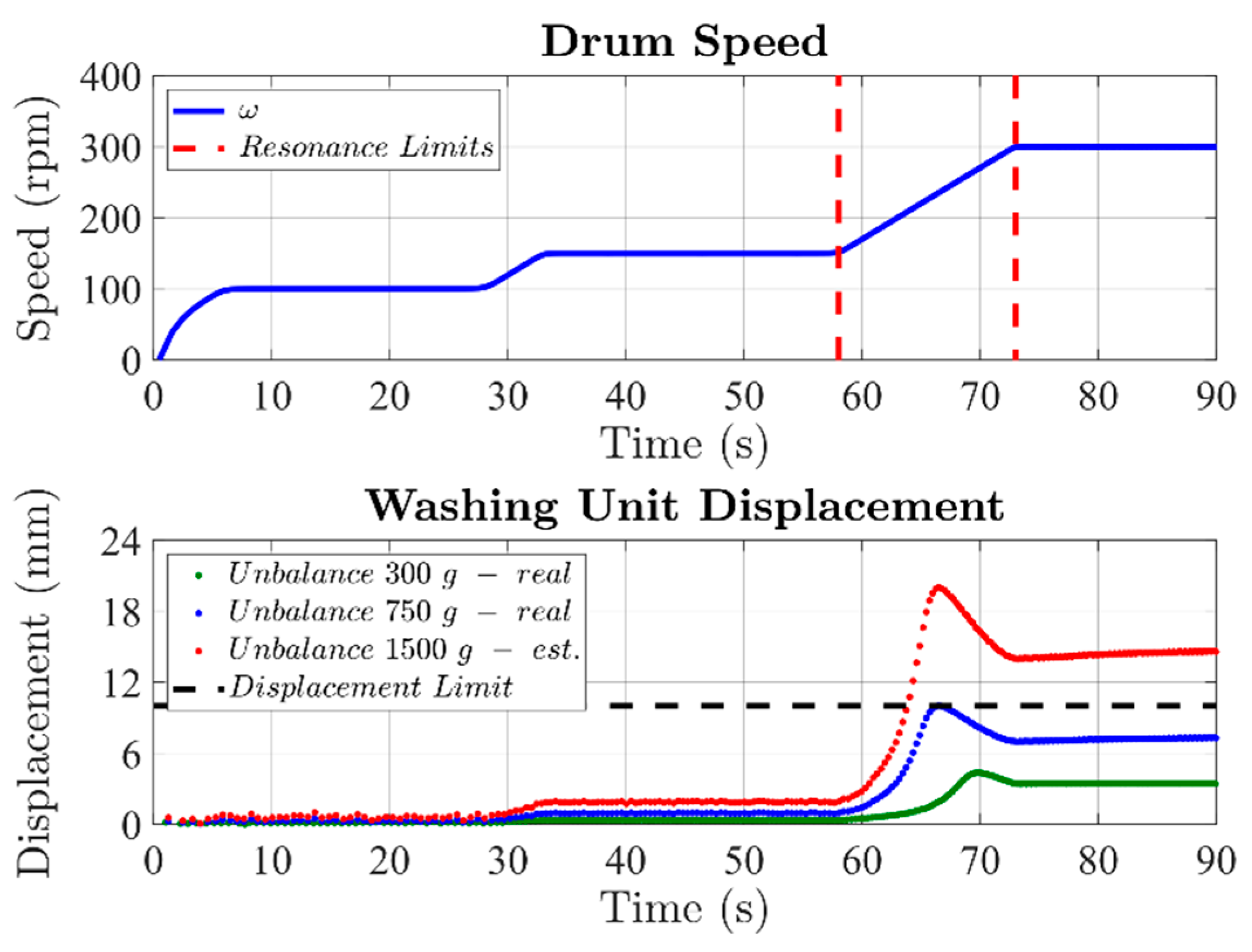
- (1)
- The unbalance mass has a small value; therefore, the washer resonances excitation does not lead to dangerous oscillations of the washing unit, allowing the execution of the acceleration ramp without running any risk.
- (2)
- The unknown unbalance mass has a high value; the washer resonances excitation leads to the washing unit oscillations whose amplitude exceeds the clearance and may damage the washer (see Figure 3).
3.3. Conventional Method Literature
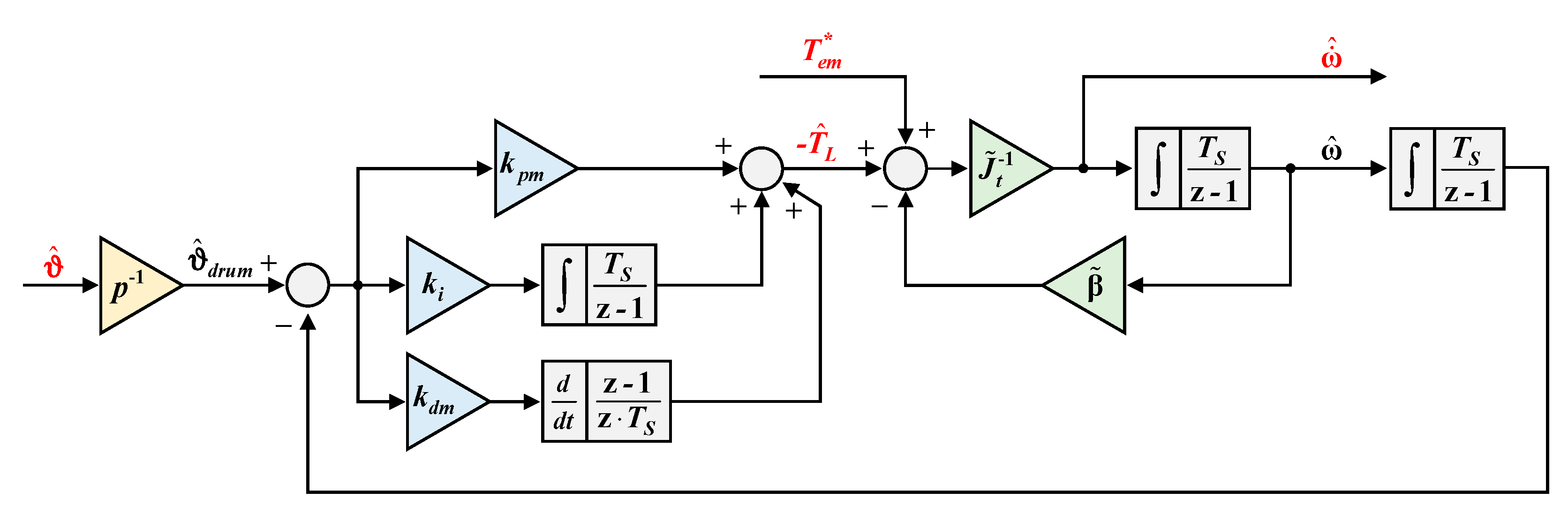
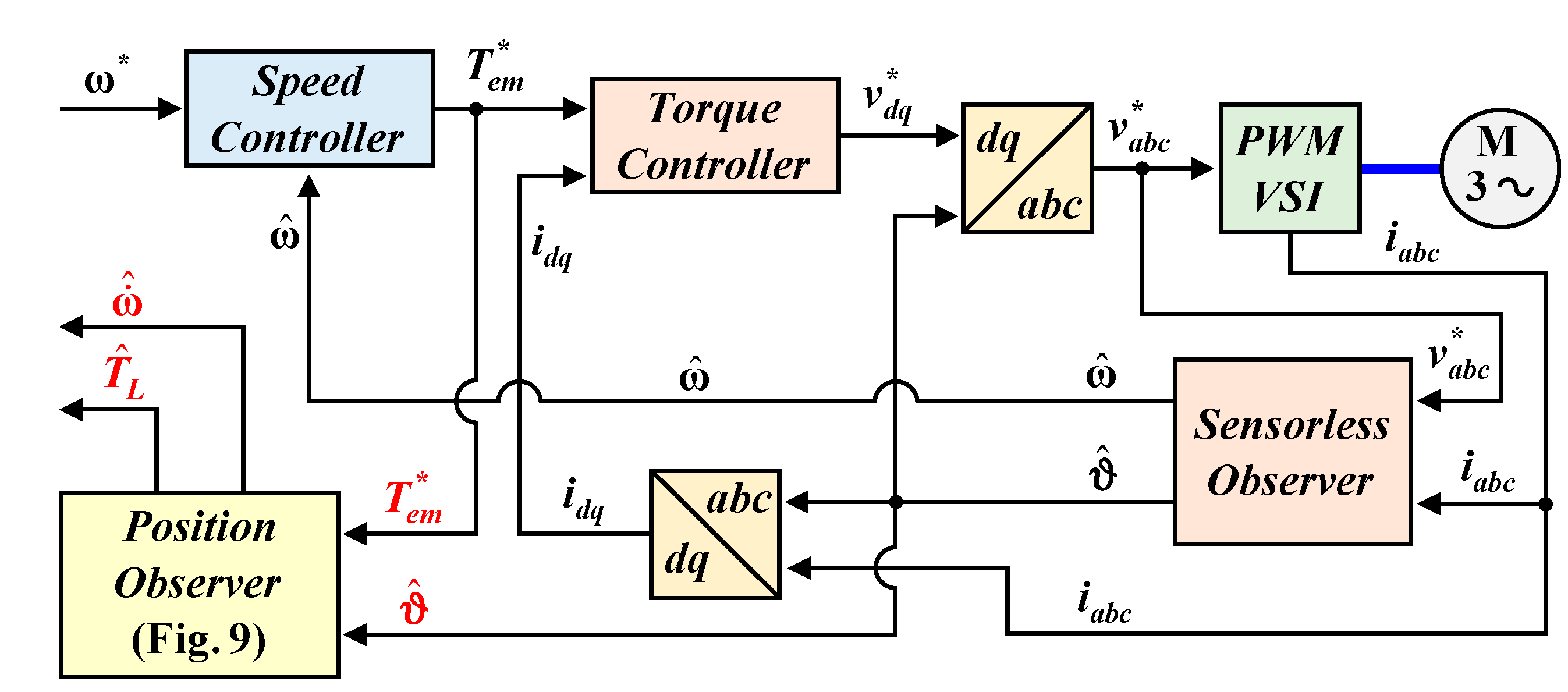
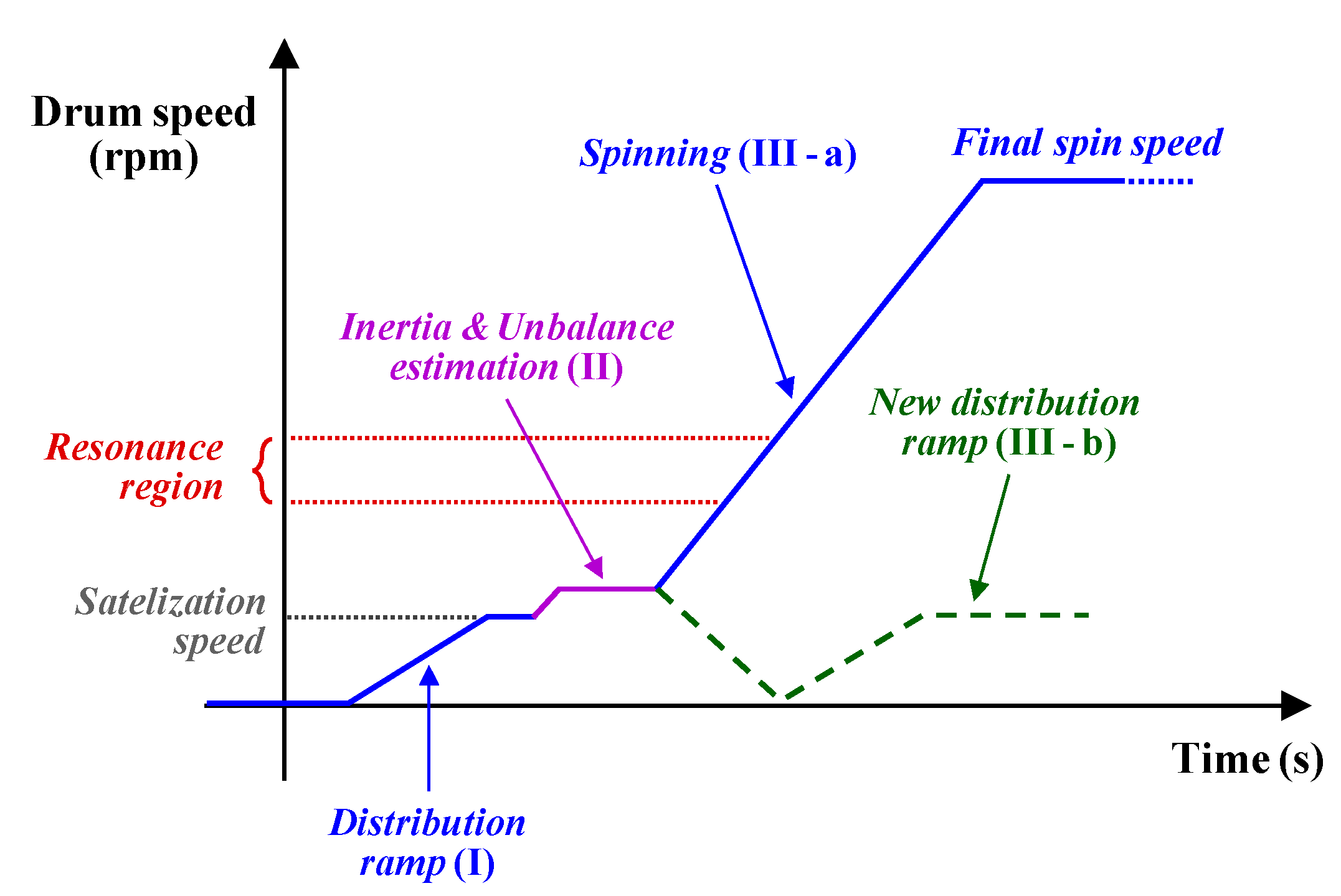
4. Proposed Method for Estimating the Laundry Unbalance and Laundry Inertia
- The drum speed must be higher or at least equal to the satelization threshold, avoiding any movement of the laundry inside the drum.
- The drum speed must be significantly lower than the resonance speed, avoiding any mechanical interference.
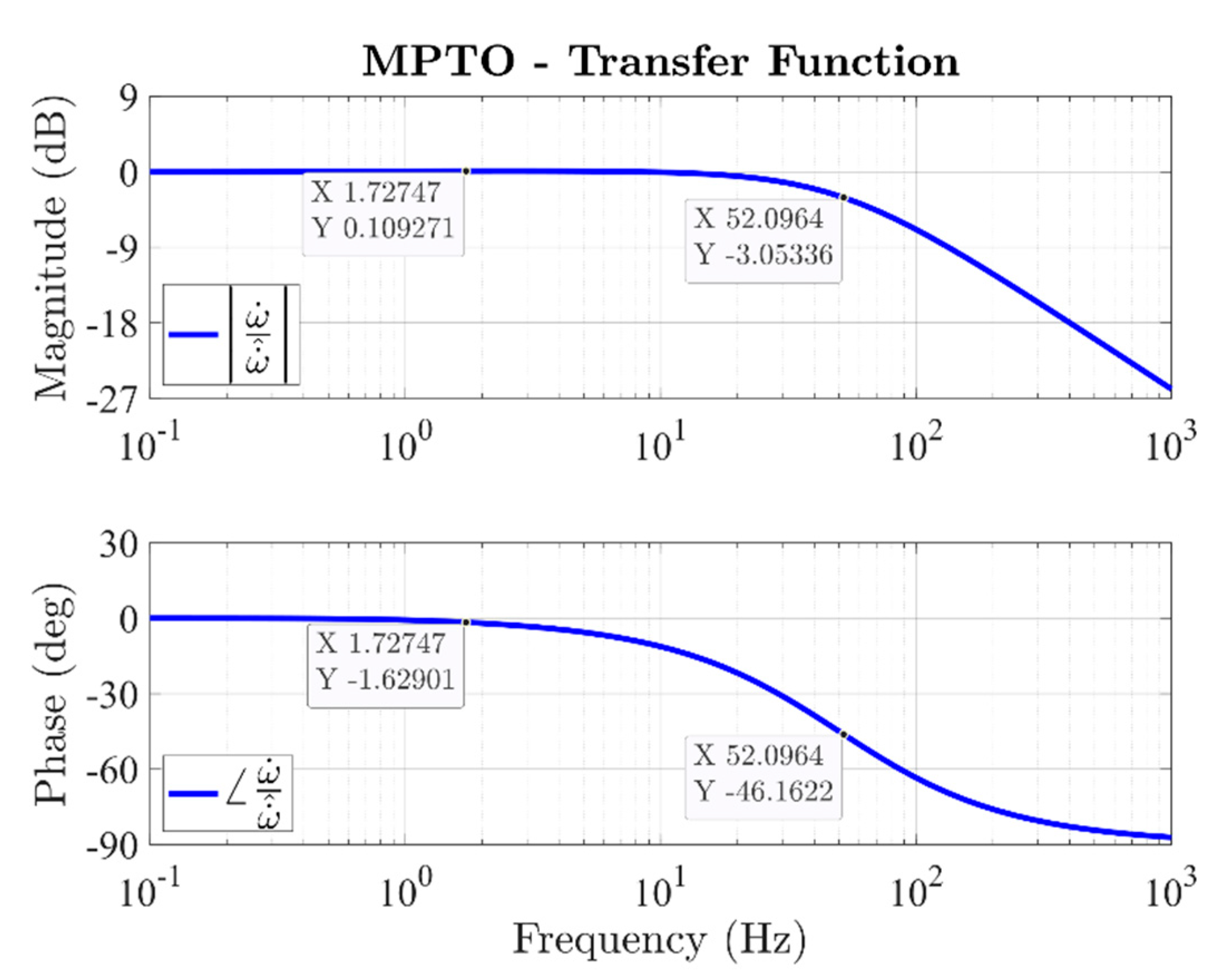
- Accurate estimation of the drum acceleration due to the speed oscillations
- Accurate estimation of the load torque that is oscillating for the considered application (washers)
- is set to the value related to the empty drum condition Jdrum
- is set to the value related to the bearings βbearings
5. Validation
5.1. Simulation Results
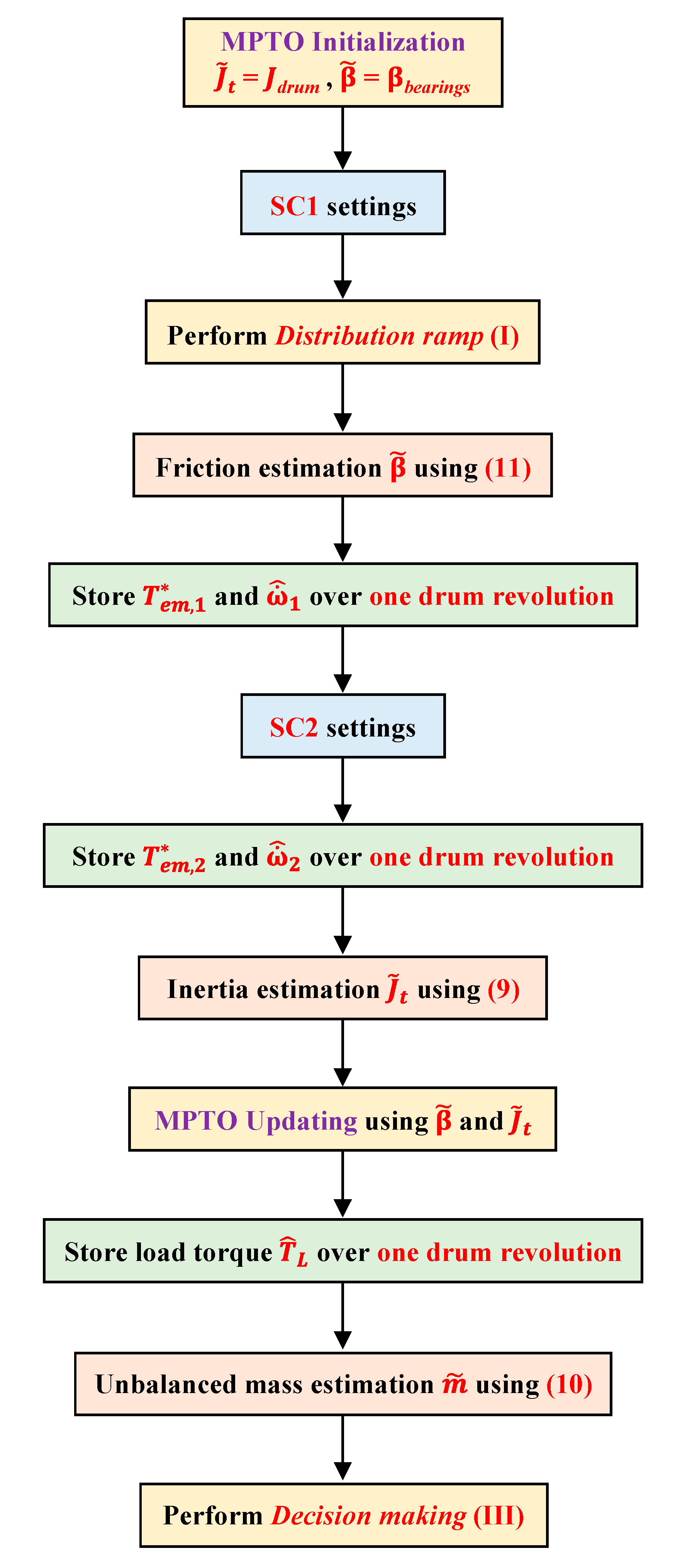
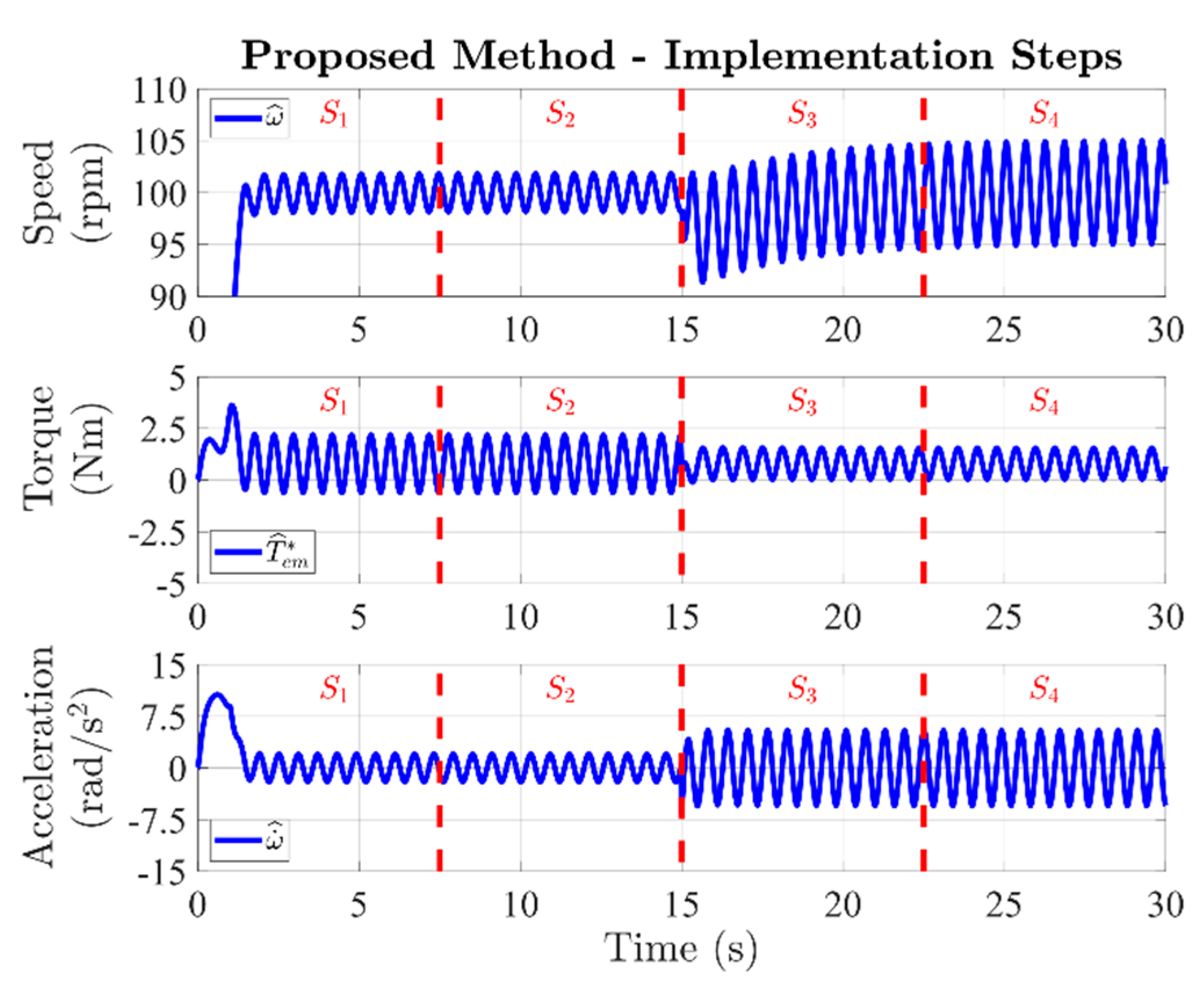
- S1—
- S2—
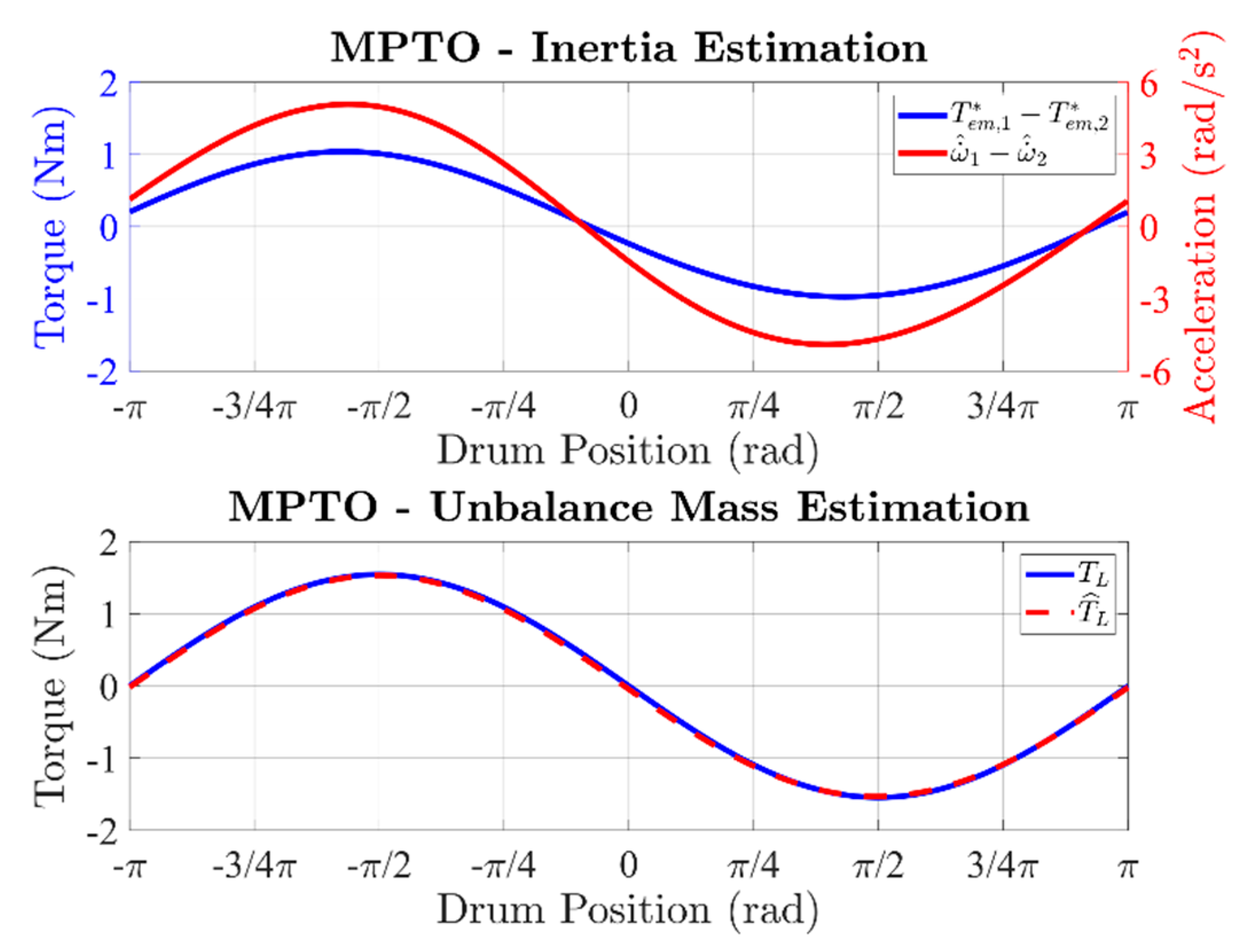
- The viscous friction coefficient β using (11) is estimated, allowing the calibration of the MPTO. Finally, the profiles of the electromagnetic torque and observed drum acceleration , over one drum revolution, are stored.
- S3—
- The speed controller is set as SC2, and a reasonable waiting time is used to reach steady-state operation.
- S4—
- The new profiles of the electromagnetic torque and observed drum acceleration , over one drum revolution, are stored. The overall inertia Jt is evaluated using (9), allowing for the full calibration of the MPTO. Finally, the observed load torque profile L over one drum revolution is stored, leading to the estimation of the unbalance mass m using (10).
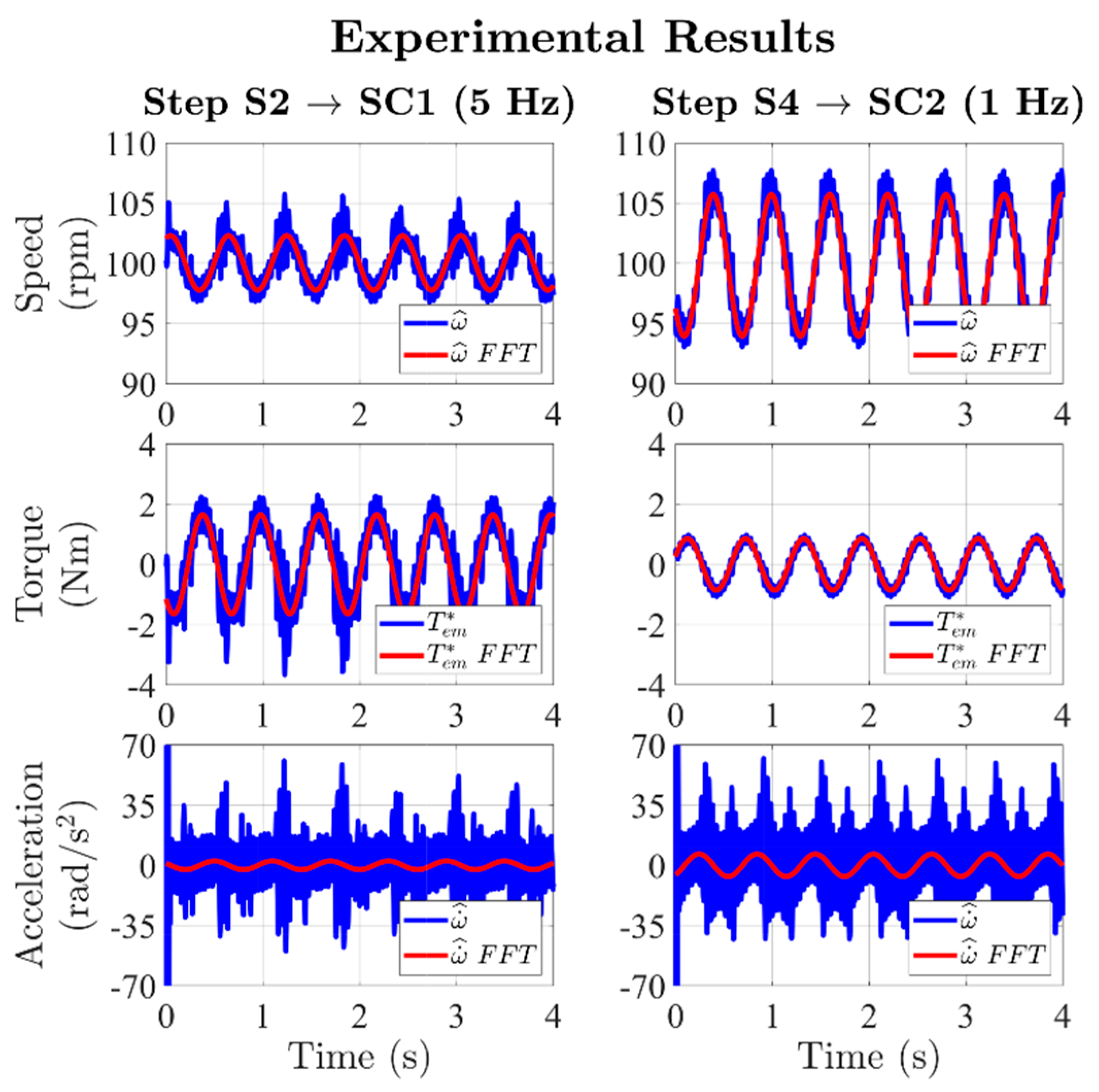
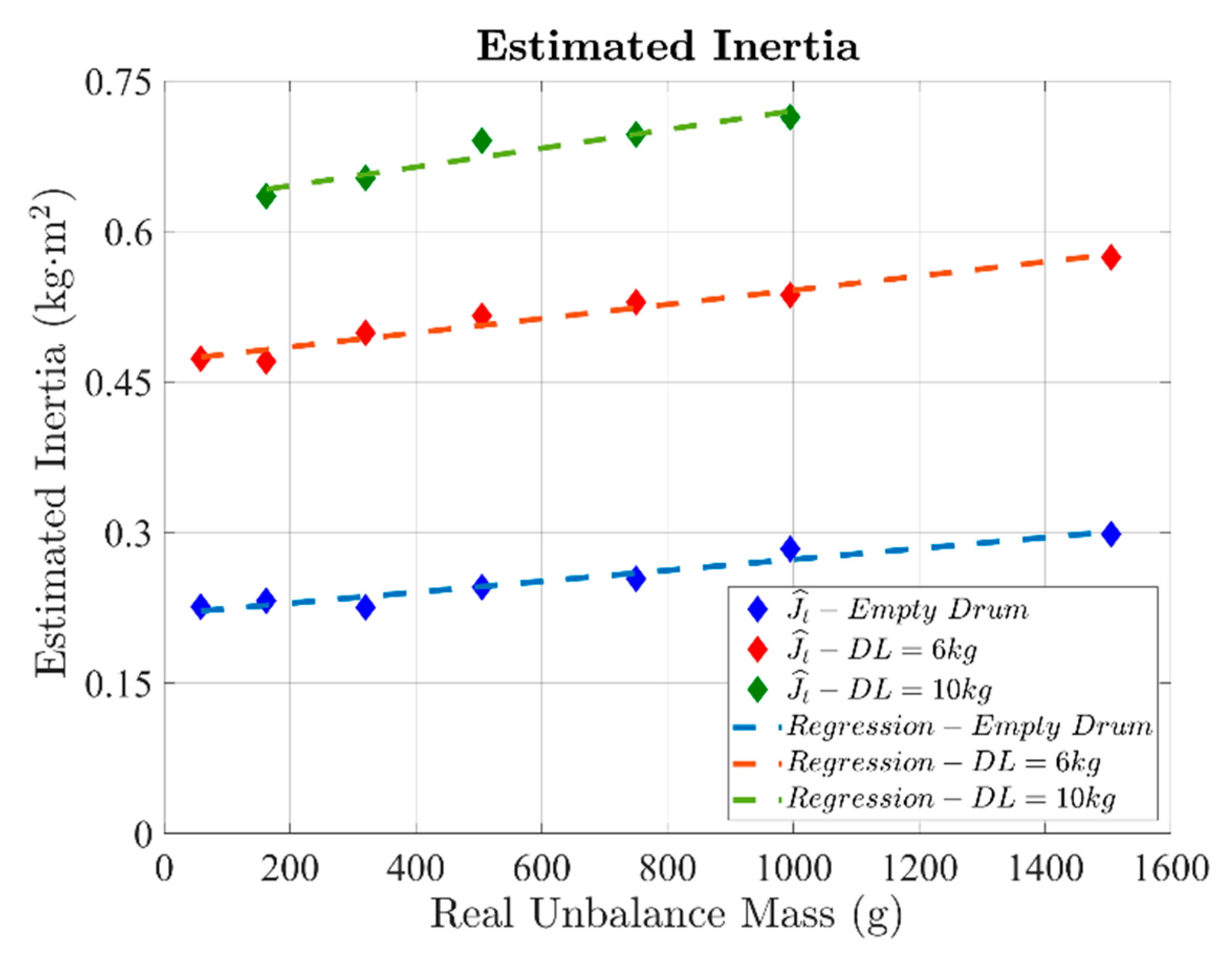
5.2. Experimental Results
- (1)
- 0 kg DL, corresponding to the empty drum condition (Jdrum = 0.22 kg∙m2).
- (2)
- 6 kg DL, emulating a laundry inertia of Jl = 0.26 kg∙m2.
- (3)
- 10 kg DL, emulating a laundry inertia of Jl = 0.46 kg∙m2.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Commission Delegated Regulation (EU) 2019/2014 of 11 March 2019 Supplementing Regulation (EU) 2017/1369 of the European Parliament and of the Council with Regard to Energy Labelling of Household Washing Machines and Household Washer-Dryers and Repealing Commission Delegated Regulation (EU) No 1061/2010 and Commission Directive 96/60/EC (Text with EEA Relevance), Vol. 315. 2019. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?qid=1575536811417&uri=CELEX:32019R2014 (accessed on 15 September 2020).
- Commission Regulation (EU) 2019/2023 of 1 October 2019 Laying down Ecodesign Requirements for Household Washing Machines and Household Washer-Dryers Pursuant to Directive 2009/125/EC of the European Parliament and of the Council, Amending Commission Regulation (EC) No 1275/2008 and Repealing Commission Regulation (EU) No 1015/2010 (Text with EEA Relevance), Vol. 315. 2019. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?toc=OJ%3AL%3A2019%3A315%3ATOC&uri=uriserv%3AOJ.L_.2019.315.01.0285.01.ENG (accessed on 15 September 2020).
- Liu, T.-H.; Lin, C.-K.; Lo, C.-H. Implementation of a novel high-performance sensorless IPMSM drive for washing machines. In Proceedings of the 2010 IEEE International Conference on Industrial Technology, Vina del Mar, Chile, 14–17 March 2010; pp. 367–372. [Google Scholar] [CrossRef]
- Cho, K.Y.; Yang, S.B.; Hong, C.H. Sensorless control of a PM synchronous motor for direct drive washer without rotor position sensors. IEE Proc. Electr. Power Appl. 2014, 151, 61–69. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, H.; Xu, L.; Heilman, L.E. Sensorless direct field-oriented control of three-phase induction motors based on “Sliding Mode” for washing-machine drive applications. IEEE Trans. Ind. Appl. 2006, 42, 694–701. [Google Scholar] [CrossRef]
- Bojoi, R.; He, B.; Rosa, F.; Pegoraro, F. Sensorless Direct Flux and Torque Control for Direct Drive washing machine applications. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 347–354. [Google Scholar] [CrossRef]
- Balazovic, P.; Filka, R. Sensorless PMSM control for H-axis washing machine drive. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 4237–4242. [Google Scholar] [CrossRef]
- Dianov, A.; Kim, N.S.; Lim, S.M. Sensorless starting of horizontal axis washing machines with direct drive. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Korea, 26–29 October 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Chi, S.; Zhang, Z.; Xu, L. Sliding-Mode Sensorless Control of Direct-Drive PM Synchronous Motors for Washing Machine Applications. IEEE Trans. Ind. Appl. 2009, 45, 582–590. [Google Scholar] [CrossRef]
- Washing Machine. Wikipedia. 13 September 2020. Available online: https://en.wikipedia.org/w/index.php?title=Washing_machine&oldid=978198687 (accessed on 15 September 2020).
- Kim, H. On-line mechanical unbalance estimation for permanent magnet synchronous machine drives. IET Electr. Power Appl. 2009, 3, 178–186. [Google Scholar] [CrossRef]
- Suel, I.R.D. Washing Machine Appliance and Method for Calculating a Load Size of Articles. U.S. Patent 9206538B2, 8 December 2015. [Google Scholar]
- Lee, J.-H.; Hwang, C.-H.; Kim, K.-M.; Lee, W.; Won, W.-C.; Won, C.-Y.; Kim, Y.-R. Optimal washing time control algorithm for the drum washing machine using an inertia estimator. In Proceedings of the 2008 IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 1–3 December 2008; pp. 1393–1398. [Google Scholar] [CrossRef]
- Lee, J.-H.; Kong, T.-W.; Lee, W.-C.; Yu, J.-S.; Won, C.-Y. Load modeling for the drum washing machine system simulation. In Proceedings of the 2007 7th Internatonal Conference on Power Electronics, Daegu, Korea, 22–26 October 2007; pp. 861–865. [Google Scholar] [CrossRef]
- Broker, J.F.; Ochsner, D.A. Unbalance Detection System for a Washing Machine. U.S. Patent 6594841B2, 22 July 2003. [Google Scholar]
- Hwang, U.K. Method for Determining Imbalance in Drum Washing Machine. U.S. Patent 2692928A2, 5 February 2014. [Google Scholar]
- Joo, K.-H. Unbalance Detecting Device and Method of Washing Machine. U.S. Patent 6240586B1, 5 June 2001. [Google Scholar]
- Murray, P.; Marcetic, D.; Henderson, M.L.; Marcinkiewicz, J.G.; Sadasivam, V.; Rajarathnam, A.V.C. Method and System for Determining a Washing Machine Load Unbalance. WO2004097099A1, 11 November 2004. [Google Scholar]
- Yoldaş, K.; Tekin, A.; Boztepe, M. An Improved Speed Controller for PMSM Drive with Unbalanced Load Using Load Torque Observer. In Proceedings of the 2019 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 7–8 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Yorukoglu, A.; Altug, E. Determining the mass and angular position of the unbalanced load in horizontal washing machines. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 118–123. [Google Scholar] [CrossRef]
- Yörükoğlu, A.; Altuğ, E. Estimation of Unbalanced Loads in Washing Machines Using Fuzzy Neural Networks. IEEEASME Trans. Mechatron. 2013, 18, 1182–1190. [Google Scholar] [CrossRef]
- Yuan, Y.; Buendia, A.; Martin, R.; Ashrafzadeh, F. Unbalanced Load Estimation Algorithm Using Multiple Mechanical Measurements for Horizontal Washing Machines. In Proceedings of the 2007 IEEE SENSORS, Atlanta, GA, USA, 28–31 October 2007; pp. 1303–1306. [Google Scholar] [CrossRef]
- Bedetti, N.; Bellinetto, E.; Maroni, M.; Paganini, R. Method for determining total inertia and unbalanced load in a laundry drum of a washing machine. European Patent 1113102A1, 4 July 2001. [Google Scholar]
- Lorenz, R.D.; van Patten, K.W. High-resolution velocity estimation for all-digital, AC servo drives. IEEE Trans. Ind. Appl. 1991, 27, 701–705. [Google Scholar] [CrossRef]
- Harke, M.C.; de Donato, G.; Capponi, F.G.; Tesch, T.R.; Lorenz, R.D. Implementation Issues and Performance Evaluation of Sinusoidal, Surface-Mounted PM Machine Drives with Hall-Effect Position Sensors and a Vector-Tracking Observer. IEEE Trans. Ind. Appl. 2008, 44, 161–173. [Google Scholar] [CrossRef]
- Ahn, H.-J.; Lee, D.-M. A New Bumpless Rotor-Flux Position Estimation Scheme for Vector-Controlled Washing Machine. IEEE Trans. Ind. Inform. 2016, 12, 466–473. [Google Scholar] [CrossRef]
- Yoo, A.; Sul, S.-K.; Lee, D.-C.; Jun, C.-S. Novel Speed and Rotor Position Estimation Strategy Using a Dual Observer for Low-Resolution Position Sensors. IEEE Trans. Power Electron. 2009, 24, 2897–2906. [Google Scholar] [CrossRef]
- Sul, S.-K. Control. of Electric Machine Drive Systems; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]




| Symbol | Quantity | Unit | Value |
|---|---|---|---|
| m | Unbalance mass | kg | 0.75 |
| r | Drum radius | m | 0.2 |
| Jt | Overall inertia | kg∙m2 | 0.2 |
| β | Viscous friction coefficient | N∙m∙s/rad | 0.075 |
| TL,peak | Peak load torque | N∙m | 1.47 |
| ωavg | Drum speed | rpm | 100 |
| kpm | MPTO proportional gain | N∙m/rad | 342 |
| kp | PTO proportional gain | N∙m/rad | 320 |
| ki | MPTO/PTO integral gain | N∙m/rad/s | 120 |
| kdm | MPTO derivative gain | N∙m∙s/rad | 64 |
| kd | PTO derivative gain | 1/s | 320 |
| DL | Coefficient | Unit | Value |
|---|---|---|---|
| 0 kg | k0 | kg∙m2 | 0.22 |
| k1 | g∙m2/g | 0.1 | |
| 6 kg | k0 | kg∙m2 | 0.47 |
| k1 | g∙m2/g | 0.1 | |
| 10 kg | k0 | kg∙m2 | 0.63 |
| k1 | g∙m2/g | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinello, D.; Rubino, S.; Bojoi, R. An eDrive-Based Estimation Method of the Laundry Unbalance and Laundry Inertia for Washing Machine Applications. Energies 2021, 14, 637. https://doi.org/10.3390/en14030637
Martinello D, Rubino S, Bojoi R. An eDrive-Based Estimation Method of the Laundry Unbalance and Laundry Inertia for Washing Machine Applications. Energies. 2021; 14(3):637. https://doi.org/10.3390/en14030637
Chicago/Turabian StyleMartinello, Daniele, Sandro Rubino, and Radu Bojoi. 2021. "An eDrive-Based Estimation Method of the Laundry Unbalance and Laundry Inertia for Washing Machine Applications" Energies 14, no. 3: 637. https://doi.org/10.3390/en14030637
APA StyleMartinello, D., Rubino, S., & Bojoi, R. (2021). An eDrive-Based Estimation Method of the Laundry Unbalance and Laundry Inertia for Washing Machine Applications. Energies, 14(3), 637. https://doi.org/10.3390/en14030637







