Study on Thermo-Hydro-Mechanical Coupling and the Stability of a Geothermal Wellbore Structure

Abstract

For processes such as water injection in deep geothermal production, heat transfer and fluid flow are coupled and affect one another, which leads to numerous challenges in wellbore structure safety. Due to complicated wellbore structures, consisting of casing, cement sheaths, and formations under high temperature, pressure, and in situ stress, the effects of thermo-hydro-mechanical (THM) coupling are crucial for the instability control of geothermal wellbores. A THM-coupled model was developed to describe the thermal, fluid, and mechanical behavior of the casing, cement sheath, and geological environment around the geothermal wellbore. The results show that a significant disturbance of effective stress occurred mainly due to the excess pore pressure and temperature changes during cold water injection. The effective stress gradually propagated to the far-field and disrupted the integrity of the wellbore structure. A serious thermal stress concentration occurred at the junction of the cased-hole and open-hole section. When the temperature difference between the injected water and the formation was up to 160 °C, the maximum hoop tensile stress in the granite formation reached up to 43.7 MPa, as high as twice the tensile strength, which may increase the risk of collapse or rupture of the wellbore structure. The tensile radial stress, with a maximum of 31.9 MPa concentrated at the interface between the casing and cement sheath, can cause the debonding of the cementing sheath. This study provides a reference for both the prediction of THM responses and the design of drilling fluid density in geothermal development.

1. Introduction

With changes in the fossil energy demand around the world, the development of safe and efficient renewable geothermal resources has received increasing attention [1,2,3]. At present, geothermal energy has been used for electricity generation, heating, and cooling in several countries, such as Indonesia, Iceland, New Zealand, and the United States [4]. Geothermal resources are mainly stored in high-temperature and low-permeability granite rock at underground depths of 2–10 km [5], which can be extracted by injecting cold water into the wellbore and then exchanging heat from the high-temperature formation [6,7]. Owing to the complexity of the thermal mechanical properties in geological formations under high temperature and pressure, the drilling and production processes often result in collapses of the wellbore and stuck drilling, which greatly decreases the drilling and production efficiency as well as increases the cost of production [8]. Therefore, the deformation, instability, and failure of the wellbore caused by the thermal effects of a high-temperature difference have become an urgent technical and scientific issue in deep geothermal production.

Wellbore deformation and its stability control in deep geothermal production has become an interdisciplinary task due to the complex thermo-hydro-mechanical coupling mechanism involved. The evaluation of multi-field coupling effects in geothermal engineering mainly includes numerical simulations and experimental methods [9,10]. Liu et al. [11] studied the response of strain and cohesion corresponding to temperature and time for Three Gorges granite. They proposed a model for uniaxial stress-strain constitutive equations for thermo-mechanical damage.

The rheological properties of polycrystalline granite under high temperature and high pressure are crucial for hot dry rock (HDR) engineering. Xi et al. [12,13] further studied the parameters of steady creep state rates of the surrounding rock within 600 °C and hydrostatic stress at 600 m. This is of great significance for the stability of the HDR borehole wall. The thermal-hydraulic-mechanical (THM) coupling mechanism and related numerical analysis methods have been a long-term concern in geo-mechanical engineering fields.

Large-scale fracturing, fire floods, or hot/cool water injection can alter the principal stress magnitudes and directions, which will affect both the failure mode and potential of the rock reservoir [14,15]. The thermal and pressure regimes of the well during drilling and mud circulation consist of alternate cooling and reheating, with simultaneous variations of pressure. Maury and Idelovici [16] numerically evaluated the borehole stress and fracture gradients near wellbores.

Tao and Ghassemi [17] studied the poro-thermoelastic effects on borehole failure, in particular, the heating and cooling effects from injection fluid for the accurate assessment of the shear failure of wellbores. When drilling through high-pressure and high-temperature rocks, THM coupling processes result in a time-dependent stress redistribution and microfracture around the borehole. Ge and Ghassemi [18] developed a hydraulically-driven and water-flood model for injection-induced fractures in jointed rock. Their model provides the stresses around an injection-induced fracture, including those induced by thermo- and poro-elasticity as well as fracture compression.

In wellbore stability control technology of HDR drilling, Xi et al. [19] recognized that the degradation of the formation properties and thermal cracks induced by cooling drilling fluid were the main cause of wellbore collapse. Rutqvist and Jeanne [20,21] proposed that wellbore instability was the coupling of hydraulic and thermal effects, and the injection of cold water into the wellbore increased the shear failure risk of the wellbore. As for the positive effects of thermal stress, Zhu et al. [22] found that the thermal effects caused a lower collapse pressure at the bottom section of the vertical wellbore, which is conducive to the stability of the wellbore wall.

Considering the dynamic change of the stress field of geothermal energy production, Huang et al. [23] found that the hydraulic performance was improved due to the permeability enhancement by the cooling effect of injection, since the influence of thermal stress overwhelms that of the pore pressure. The temperature difference between the injected fluid and surrounding rock can play an important role in the initiation and propagation of fractures in completion and simulation operations. Li et al. [24] investigated the microscopic behavior of rocks under a THM coupling mechanism, and the results showed that thermal stresses could greatly affect the initiation and propagation of fractures and assist the communication between the injection pressure and pore pressure in the rock formation.

Simone et al. [25] realized that rock instability is likely to result from the superposition of hydraulic and thermal effects. They showed that thermal effects induce a significant perturbation on the stress in the intact rock during the cold water injection. Salimzadeh et al. [26] studied the thermal-induced pore pressure partial dissipation in very low-permeability rocks. The thermos-hydro (TH) model is coupled to a separate mechanical contact model (M) and solves for the fracture contact stresses due to thermoporoelastic compression.

For fractured geothermal reservoirs, Salimzadeh et al. [27] investigated the influence of fracture deformation on the water injection process through numerical simulation. The results showed that the injection of cold water forms a cooling zone near the borehole wall. The decrease of the thermal stress leads to the instability of a crack located near the cooling zone, which could easily trigger the propagation of an unstable crack. Pandey et al. [10] summarized several modeling tools regarding geothermal reservoirs from the last four decades. These tools were found to be effective for numerical modeling of various processes, such as thermo (T), hydro (H), mechanical (M), and chemical (C) processes.

Based on a discrete fracture numerical model, Zhang et al. [28] established a temperature–percolation–stress coupling model for geothermal resource development and proposed a fuzzy evaluation method containing multiple evaluation indexes of geothermal resource development. Through comparative experiments and numerical simulations, Meng et al. [29] found that the mechanical properties of rock under geothermal conditions varied significantly when compared with those under conventional environments. The conventional failure criteria, therefore, present differences in evaluating the stability of deep geothermal borehole walls.

Ding et al. [30] proposed a three-dimensional large-scale THM finite element model and analyzed the seepage and heat transfer process of the enhanced geothermal system. Zhao et al. [31] simplified the wellbore into a one-dimensional line element and proposed a THM coupling simulation method that was applicable to the far-field scale of deep geothermal engineering. The results were effective in revealing the long-term evolution behaviors of the temperature field, seepage field, and deformation field in a deep geothermal reservoir.

The focus of most current studies is the intrinsic properties, failure criteria, and failure mechanisms of rocks under temperature variation, and the hydraulic fracturing of the formation induced by the effects of thermal and water injection [32]. The research on the critical issue of wellbore integrity was also primarily around the collapse and necking of wellbores and stuck drills in conventional oil/gas drilling. However, little research has been conducted on the coupled THM response of a wellbore structure in the process of water injection (cold) in geothermal production.

In this study, an integrated THM coupled model consisting of casings, a cement sheath, and formation under high temperature, pressure, and in situ stress was established to predict the THM behaviors of geothermal wells. Subsequently, the established model was used to investigate the stability of geothermal wellbores in northern Shandong in China. We conducted a numerical analysis of the THM coupling effects to study the effective stress accumulation induced by cool water injection and the failure process of geothermal wellbore structures. The damage features and failure position of the wellbore structure were evaluated using the collapse and fracture coefficient. This can provide a mechanical basis for the structural failure control and safety evaluation of a geothermal wellbore.

2. THM Coupling Models of the Wellbore in the Process of Water Injection

Numerical modeling of a geothermal reservoir can help understand the interaction mechanisms of the injected water and the deformation of the formation. The injection of cold water into the formations will change the transport properties, including the porosity and permeability, and finally, lead to thermal and mechanical disequilibrium in the reservoir. Based on the granite formation’s porosity, permeability, thermal diffusivity, and other physical and mechanical characteristic parameters, a three-dimensional THM coupling model of a wellbore structure was established, in which the mechanical equilibrium equation, fluid flow or seepage equation, heat transfer equation of the formations’ rock matrix, and the THM stress governing equation are involved.

The mechanical equilibrium equation can be expressed as follows

$${\sigma }_{ji,j}+f_i=0$$

(1)

where ${\sigma }_{ji}$ is the total stress tensor (N/m²), and $f_i$ is the body force (N/m³).

The fluid flow through the porous rock mass follows Darcy’s law

$$v=\frac{k}{\mu }\left[-\nabla p+{\rho }_{w}g\nabla z\right],$$

(2)

where $v$ is the Darcy velocity of the fluid (m/s), $k$ is the permeability of the pore fluid in porous media (md), $\mu$ is the pore fluid dynamic viscosity (Pa·s), $p$ is the pore fluid pressure (MPa), and ${\rho }_w$ is the density of the pore fluid (kg/m³).

According to the incompressibility of the fluid, the equation of continuity of the fluid flow in rock follows

$$\frac{\partial {\rho }_w}{\partial t}+\frac{\partial ({\rho }_{w}r{v}_r)}{r\partial r}+\frac{\partial ({\rho }_w{v}_{\theta })}{r\partial \theta }+\frac{\partial ({\rho }_{w}w)}{\partial z}=0,$$

(3)

where $v_r$, $v_{\theta }$, and $w$ are the Darcy velocities along the radial, hoop, and well-depth directions in the porous rock, respectively. Both fracture and seepages flow appear near the region of the geothermal wellbore, which can be described by Equation (3) and the corresponding numerical model boundary conditions.

The constitutive relation between the porosity/permeability change of the porous rock and stress gives [33]

$$\left\{\begin{array}{l}\varphi ={\varphi }_{\mathrm{r}}+({\varphi }_0-{\varphi }_r)\exp (\alpha \cdot {\sigma }_M)\\ k=k_0\exp (c\cdot (\varphi /{\varphi }_0-1))\end{array}\right.,$$

(4)

where ${\sigma }_M$ is the mean effective stress, ${\varphi }_0$ and $k_0$ are the porosity and permeability at zero stress, respectively; ${\varphi }_r$ is the residual porosity at high stress; and the exponents α and c are determined experimentally.

Considering the heat transfer process, the total energy conservation equation of the fluid-rock system can be written as follows [34]

$${\left(\rho c\right)}_t\frac{\partial T}{\partial t}-\frac{1}{r}\frac{\partial }{\partial r}(k_{t}r\frac{\partial T}{\partial r})-\frac{1}{r^2}\frac{\partial }{\partial \theta }(k_t\frac{\partial T}{\partial \theta })-\frac{\partial }{\partial z}(k_t\frac{\partial T}{\partial z})-q_{t}r=0,$$

(5)

where ${\left(\rho c\right)}_t=(1-\varphi )c_s{\rho }_s+\varphi c_f{\rho }_f$ is the total heat capacity of the solid and fluid phase (J/(m³·°C)); $k_t=\varphi k_f+(1-\varphi )k_s$ is the total thermal conductivity (J/(m·s·°C)), $q_t$ is the internal heat source intensity (J/(m³·s)); $c_s$ and $c_f$ are the specific heat capacities of the formation and fluid, respectively; ${\rho }_s$ and ${\rho }_f$ are the density of the formation and fluid, respectively; and $k_s$ and $k_f$ are the heat conductivity of the formation and fluid, respectively.

The stress governing equation for the THM model of rock mass is expressed as follows [35]

$$2\alpha \frac{(1-2\nu )}{(1+\nu )}{\nabla }^{2}p+6\beta B \frac{(1-2\nu )}{(1+\nu )}{\nabla }^{2}T-\nabla \cdot f-3 \frac{(1-\nu )}{(1+\nu )}{\nabla }^2{\sigma }_m=0,$$

(6)

where ${\sigma }_m$ is the mean total stress (MPa), $\nu$ is the Poisson’s ratio of the rock mass, $\alpha$ is the Biot coefficient, $\beta$ is the linear thermal expansion coefficient (1/°C), and B is the bulk modulus of the rock (MPa). The three terms on the right side of Equation (6) describe the effects of the poroelastic stress, thermoelastic stress, and body force, respectively.

3. Numerical Analysis of the Geothermal Wellbore Structure during Water Injection

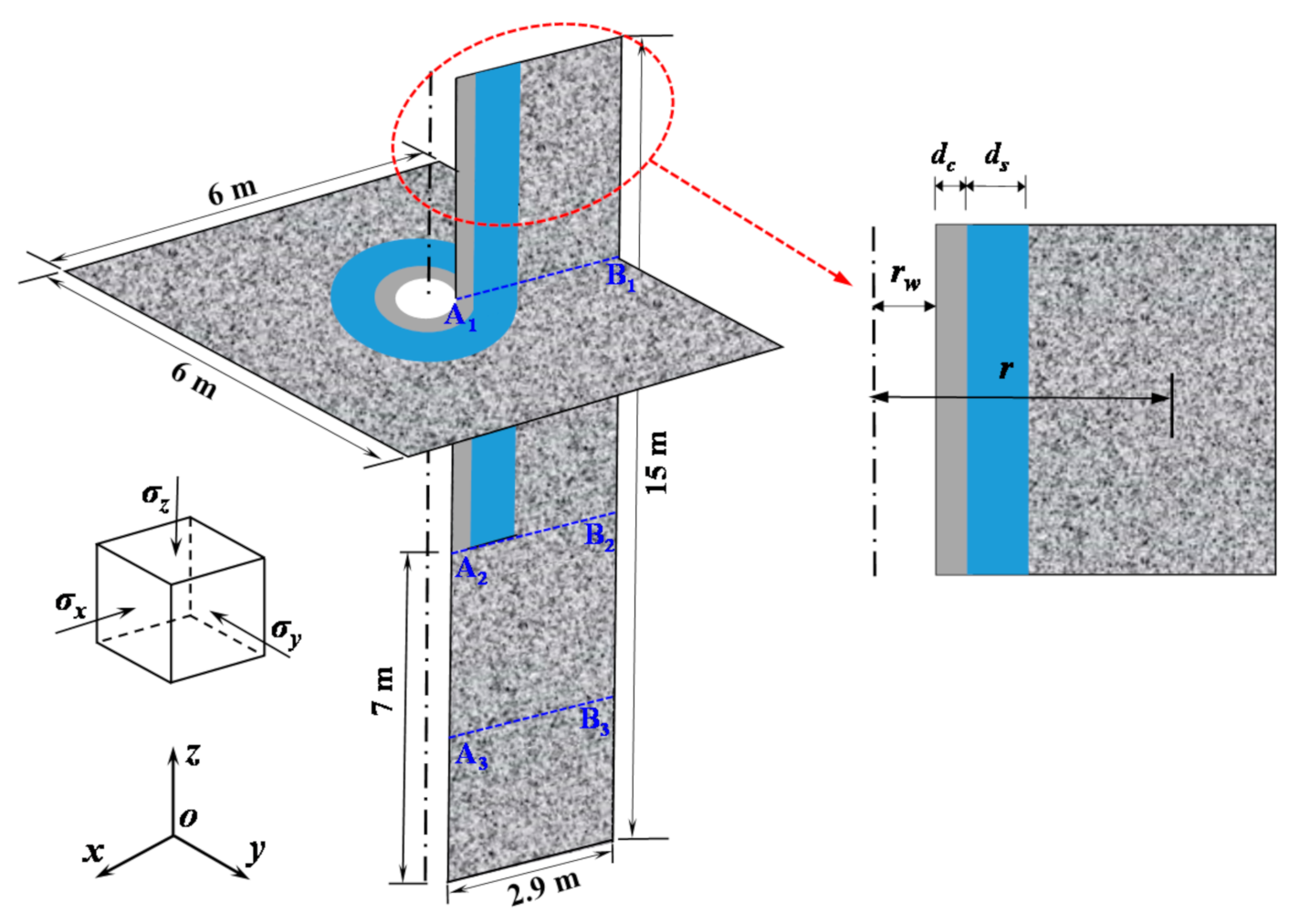
3.1. Wellbore Geometry Model

According to the measured data of the geothermal wells in northern Shandong province, a conceptual mechanical model of the wellbore structure was established [36]. The wellbore is located in a thermal reservoir zone at a depth of 2160 m. The formation structure is mainly composed of continuous granite. The wellbore and formation structure can be divided into overburden and producing zones [37], as shown in Figure 1.

To directly reflect the wellbore structure, wellbore stress, deformation, and failure, the geothermal wellbore structure was simplified and is shown in Figure 2. The dimensions of the numerical model were 15 × 6 × 6 m, in which the borehole radius r_w = 0.1 m, the casing thickness d_c = 10 mm, and the cement sheath thickness d_s = 35 mm. The section of the well model was segmented into two parts, and the thicknesses of the cased-hole and open-hole were 8 m and 7 m, respectively. The minimum horizontal principal stress σ_h = 22 MPa was along the x-direction, the maximum horizontal principal stress σ_H = 25 MPa was along the y-direction, and the overburden pressure was 30 MPa. The initial pore pressure and temperature of the thermal reservoir were 10 MPa and 182 °C, respectively. The initial temperature of heat exchange water was 20 °C, and the injection flow velocity was $7.2\times {10}^{-3}$ m³/min. The maximum injection pressure in the section analyzed was over 18 MPa.

It is well known that it is very difficult and time-consuming to obtain the precise numerical simulation of the geothermal wellbore using the three-dimensional space element directly. In this work, a simple and effective simplified method is proposed to numerically simulate the problem of a geothermal wellbore. In this simplified method, the space problem of a geothermal wellbore was equivalently described as the combination of a two-dimensional axisymmetric problem and a plane strain problem, which are schematicly diagrammed in Figure 2. The longitudinal section of the model was parallel to the direction of the maximum horizontal principal stress. The casing, cement sheath, and formations were assumed to be well bonded. In the numerical simulation, the thermoelastic four-node quadratic elements were adopted for the non-permeable casing and cement sheath, while a permeable formation in the production zone was simulated with a thermoporoelastic four-node quadratic element. The discrete longitudinal section of the model was identified using the axisymmetric quadrilateral elements, whose total number was 68 × 300. However, the discrete transversal section of the model was identified by the plane strain elements, whose total number was 160 × 160. In order to obtain more precise numerical results, the heterogeneous mesh is used for both axisymmetric and strain problems. The smaller the distance is from the wellhead, the greater the mesh density is. For both kinds of elements, the minimum and maximum sizes were 2.5 mm and 200.0 mm, respectively.

The mechanical and thermophysical properties of the casing, cement sheath, and formation are listed in

Table 1. Material properties of the casing and cement sheath.

Parameters	Casing	Cement Sheath
Density (kg/m3)	7800	3100
Young’s modulus (GPa)	230	13.5
Poisson’s ratio (-)	0.3	0.286
Thermal expansion coefficient (1/°C)	1.3 × 10−5	1.1 × 10−5
Specific heat (J/kg·°C)	461	837
Thermal conductivity (W/m·°C)	45	0.98

and

Table 2. The mechanical, thermal, and hydraulic properties of the formation.

Parameters	Value
Rock mass density (kg/m3)	2600
Young’s modulus (GPa)	30
Poisson’s ratio (-)	0.25
Cohesion (MPa)	39
Internal friction angle (°)	52
Tensile strength (MPa)	21
Rock mass permeability coefficient (m/s)	1.2 × 10−13
Porosity	0.01
Rock mass thermal conductivity (W/m·°C)	3.5
Rock mass specific heat (J/kg·°C)	900
Rock mass thermal expansion coefficient (1/°C)	5 × 10−6
Density of water (kg/m3)	1000
Bulk modulus of water (GPa)	2.5
Thermal conductivity of water (W/m·°C)	11.9
Specific heat of water (J/kg·°C)	40
Thermal expansion coefficient of water (1/°C)	2.08 × 10−4

, which can be obtained from any general material parameter manual.

3.2. Procedures of Numerical Simulation

The main steps are presented as follows:

(1)

Stress equilibrium at the initial deformation state

There were three principle stresses around the wellbore of geothermal formations, i.e., the vertical (overburden) stress (σ_ν), minimum horizontal stress (σ_hmin), and maximum horizontal stress (σ_Hmax). The normal displacements were restricted at the wellbore casing and the outer boundary of formations. A geostatic analysis step was adopted to build the initial equilibrium of the three principal stresses.

(2)

Thermal and fluid loading during cold water injection

The hydraulic and thermal parameters of the cold water injection, including the fluid and heat flux, pressure, and temperature, were applied to the inner wall of the wellbore. Combined with the displacement constraints, a complete THM model of the geothermal wellbore is completely developed.

(3)

THM coupling simulation of water injection

• Steady and static thermal analysis was carried out to determine the temperature fields around the wellbore. As the main driving mechanism, it is of great importance to capture the thermal load correctly.
• The thermal loads achieved from temperature fields were applied to the hydro-mechanical model.
• THM coupling analysis was conducted to study the thermal stress accumulation and failure process of the geothermal wellbore structure.

4. Results and Discussion

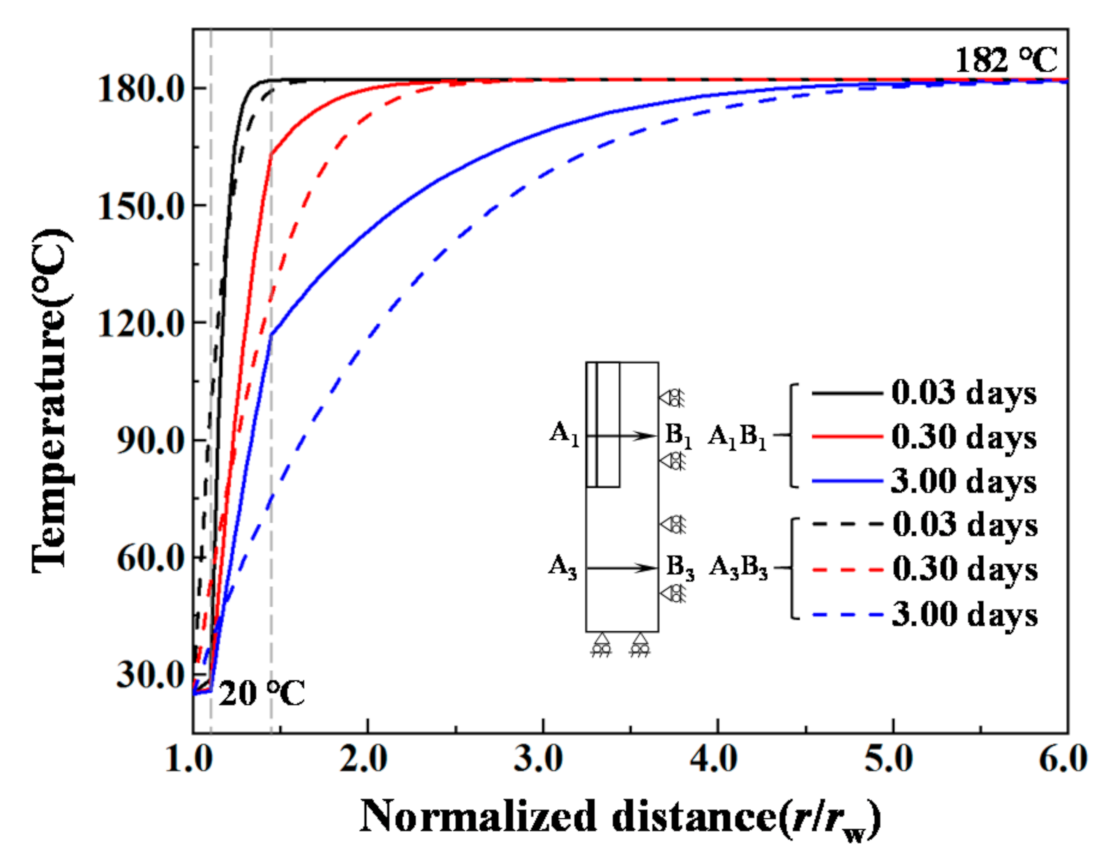
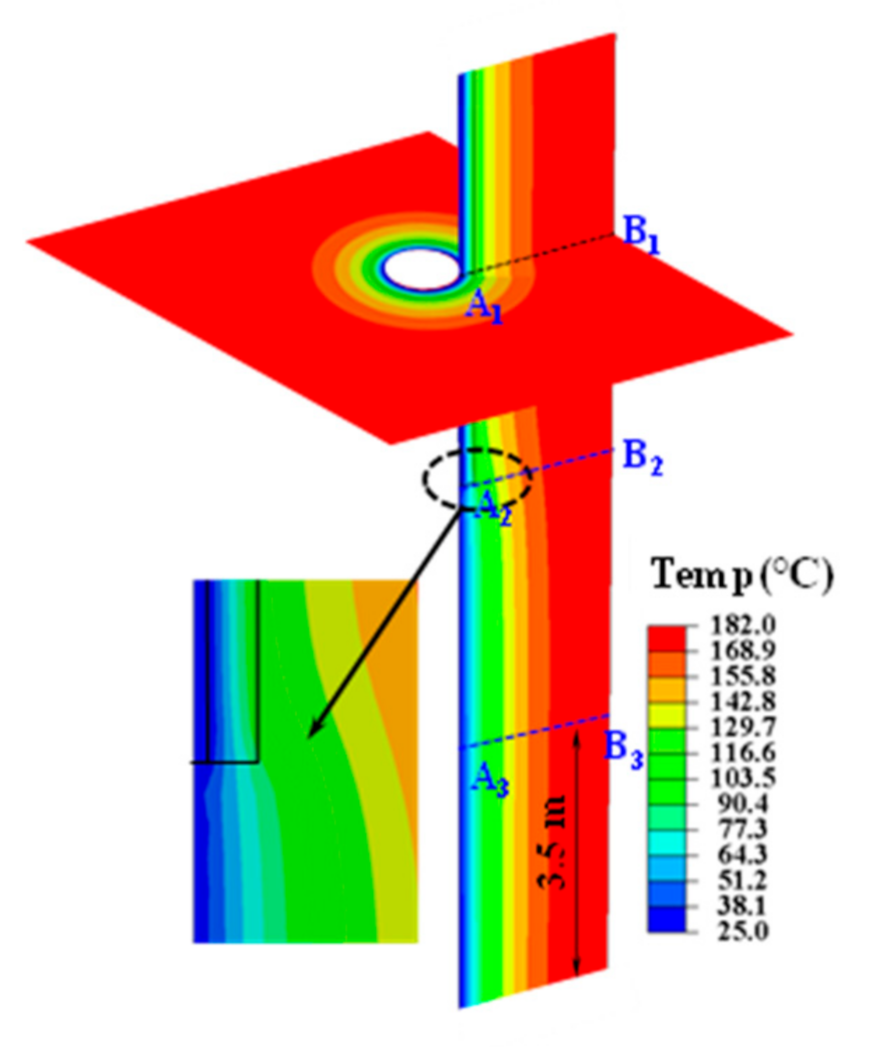
4.1. Temperature Distribution of the Geothermal Wellbore during the Water Injection

To demonstrate the temperature distribution in the wellbore clearly, two cross-sections, i.e., the A₁B₁ (casing-cement sheath-formation) and A₃B₃ (formations), were selected. Figure 3 shows the temperature evolutions in A₁B₁ and A₃B₃ sections. At the initial stage of water injection, the casing temperature at the section A₁B₁ quickly dropped to 25 °C (temperature of injected water) due to the high thermal conductivity of the casing in the vicinity of the wellbore ($1\le r/r_w<1.1$). In the range of $1.1\le r/r_w<1.45$, the heat conduction at section A₃B₃ was faster than that at section A₁B₁ due to the low thermal conductivity of the cement sheath.

The temperature gap between section A₃B₃ and A₁B₁ gradually increased over time. In the range of $r/r_w\ge 1.45$, the heat conduction in sections A₁B₁ and A₃B₃ gradually became stable when it went into the matrix rock mass. After 3.0 days of water injection, the temperature disturbance diffused to $r/r_w=5.5$. For low-permeability granite thermal reservoirs, a high-temperature gradient in local scale will serve as the thermal driving load to reform the deformation and flow pattern near the wellbore.

Figure 4 shows the temperature distribution near the wellbore after 3.0 days of water injection. The temperature at the junction of the casing, cement sheath, and formation changed significantly, and the heat conduction region of the section A₃B₃ became slightly larger than that of the section A₁B₁.

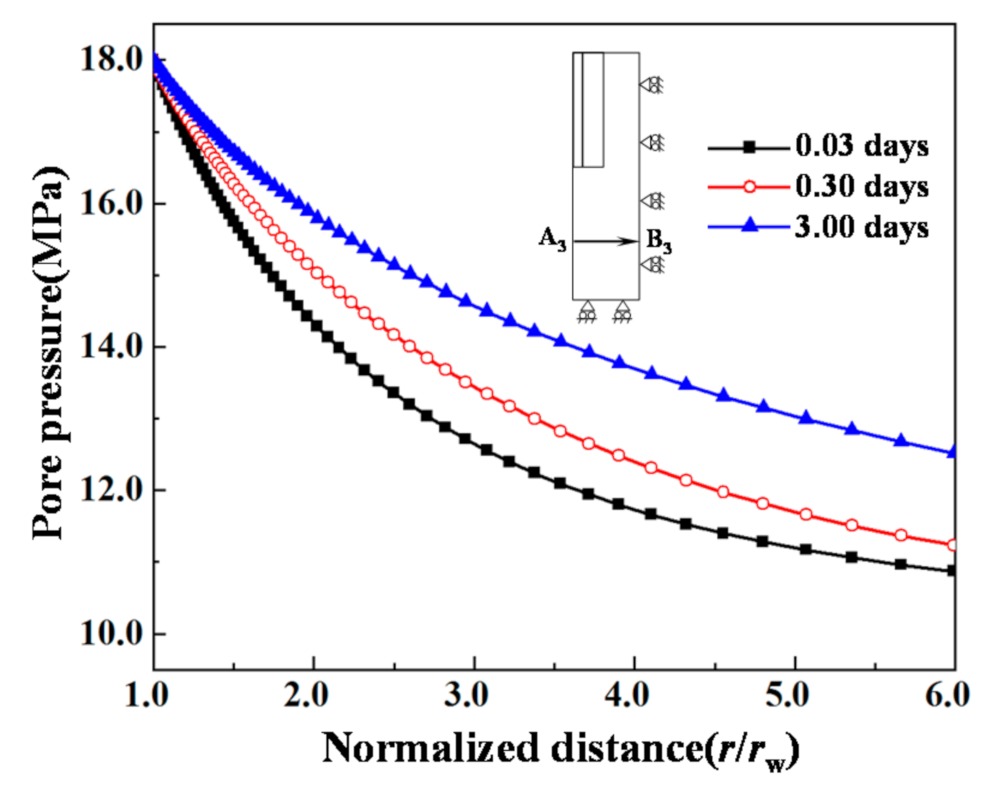
4.2. Pore Pressure of Near-Wellbore Formations during Water Injection

During the water injection cycle, the heat exchange fluid was in direct contact with the rock of the thermal reservoir.

The injection of cool water can cause shrinkage of the rock matrix, a decrease of thermal stress, and an increase in permeability. The water injection and production changed the pore pressure and permeability. We found that both the pore pressure and permeability increased near the injection well but decreased near the production well. The effective stress, which is defined as the difference between the stress of the solid matrix and the pore pressure, was enhanced by the variation of the thermal stress and pore pressure in the injection well. However, the effective stress was decreased by the variation of the thermal stress and pore pressure in the production well.

Due to its low permeability and high flow resistance in granite formations, an ultra-high pore pressure, also known as excess pore pressure [38], appeared near the wellbore during water injection. The evolution of excess pore pressure with time near the wellbore along A₃B₃ is shown in Figure 5. When low-temperature water was injected with a rate of $7.2\times {10}^{-3}$ m³/min, the maximum value of injecting pressure in the wellbore was over 18.0 MPa. The maximum pore pressure (18.0 MPa) near the wellbore may lead to the emergence of high tensile stress and, hence, the fracture of the cement sheath structure or the debonding of the interface between the cement sheath and formations.

4.3. THM Coupling Stress Near the Wellbore during the Water Injection

The structural stability of the geothermal wellbore was evaluated quantitatively based on the stress variation near the wellbore. According to the particularity of the model, the THM coupling stress variations, including the radial stress and hoop stress in the different regions of the geothermal wellbore were analyzed.

Figure 6 shows the variations of the radial stress and hoop stress of the A₁B₁ section with time, respectively. With the increase of time, the radial stress of the casing changed slightly. The radial stresses of the cement sheath and formations gradually increased under temperature load. The radial stress of the cement sheath-formations interface was as high as 22.0 MPa, which reaches the failure strength and may lead to detachment.

The hoop stress variation exhibited a snap-through behavior due to the different properties between the metal casing and formations, which may affect the bonding strength of the casing–cement sheath–formation interface. The discontinuity of the hoop stress distribution increased with time. After 3.0 days of water injection, the casing, cement sheath, and near-wellbore formations experienced continuous deformation and shrinkage, which resulted in a circumferential tensile stress state and increased the risk of tensile failure of the cement sheath.

The local radial stress distribution of the model is shown in Figure 7a. An obvious radial tensile stress concentration appeared at the junction of the casing, cement sheath, and formations. This tensile stress concentration resulted in inferior cementation performance of the cemented surface and even debonding and channeling. Figure 7b shows the formations of a large hoop tensile stress concentration in the contact area between the casing and borehole wall. The maximum stress was 43.7 MPa, which was about 2.08 times the tensile strength.

The section A₂B₂ was located at the junction of the open-hole completion and the casing completion and, thus, was a key region for the wellbore instability. Figure 8a shows the local stress variations of the casing–cement sheath on section A₂B₂. The maximum radial tensile stress (31.9 MPa) appeared at the casing–cement sheath’s cementing surface. The maximum hoop stress was about 1.24 times larger than that at section A₁B₁. At this interface, the casing–cement sheath–formation was in a stress state of radial contraction and hoop tensile, which increases the complexity of the stress distribution. The radial stress and hoop stress at section A₂B₂ were greatly affected by the local casing–cement sheath, and the variation trend was significant in the range of $1\le r/r_w\le 1.45$ as shown in Figure 8b.

Figure 9 shows the stress evolutions in the formations of the A₃B₃ section. The formation in the near-wellbore region was compressed in the radial direction and stretched in the hoop direction. The radial and hoop stresses reached their maximum values, namely, 18.0 and 33.4 MPa, respectively, at the borehole wall. During the water injection, the THM coupling effect was significantly controlled by the stress distribution near the wellbore. The effective radial stress of the formations gradually decreased with the water injection time, from 9.53 MPa in 0.03 days to 3.14 MPa in 3.0 days. The effective hoop stress of the formations gradually changed from compression to tension. After 3.0 days of water injection, tensile hoop stress and compressive hoop stress were generated on both sides at the position of $r/r_w=1.90$.

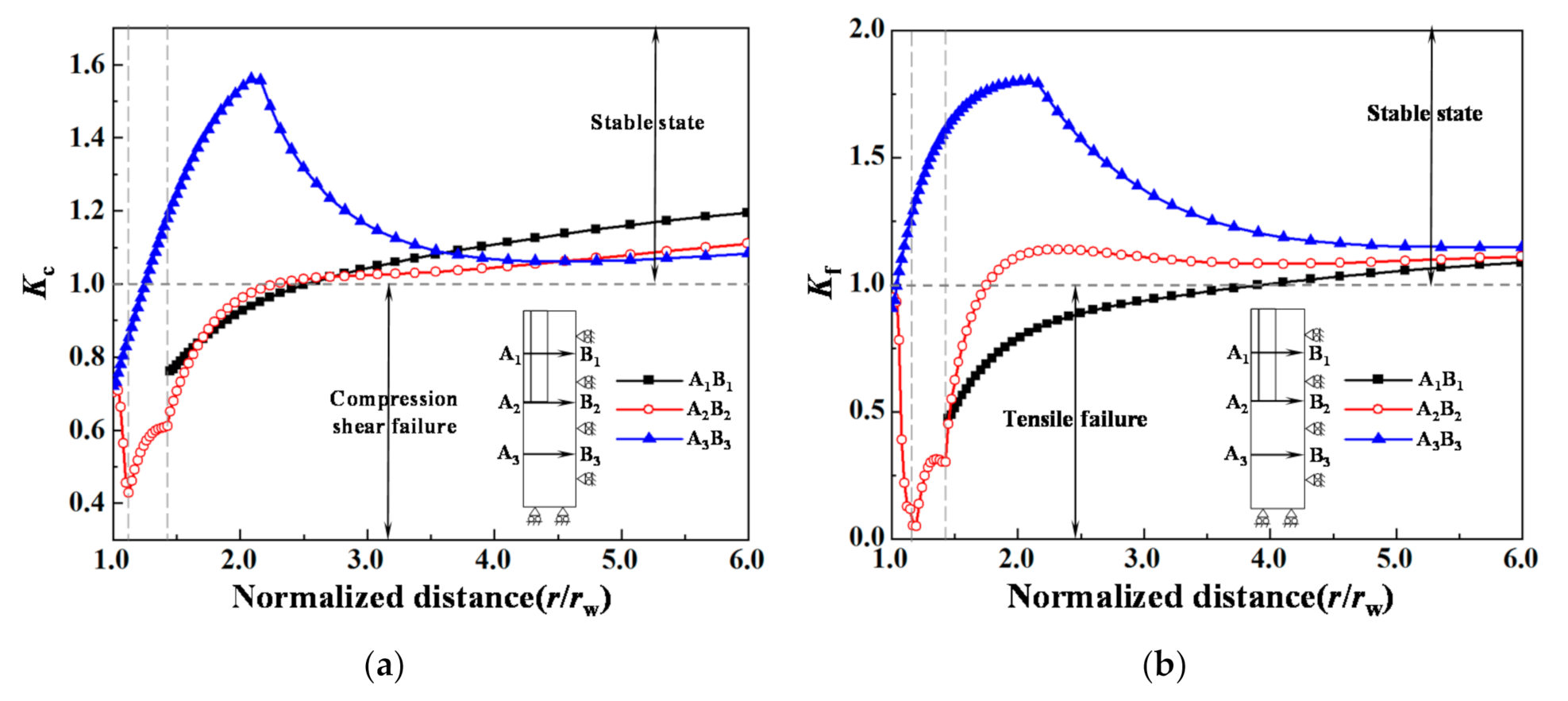
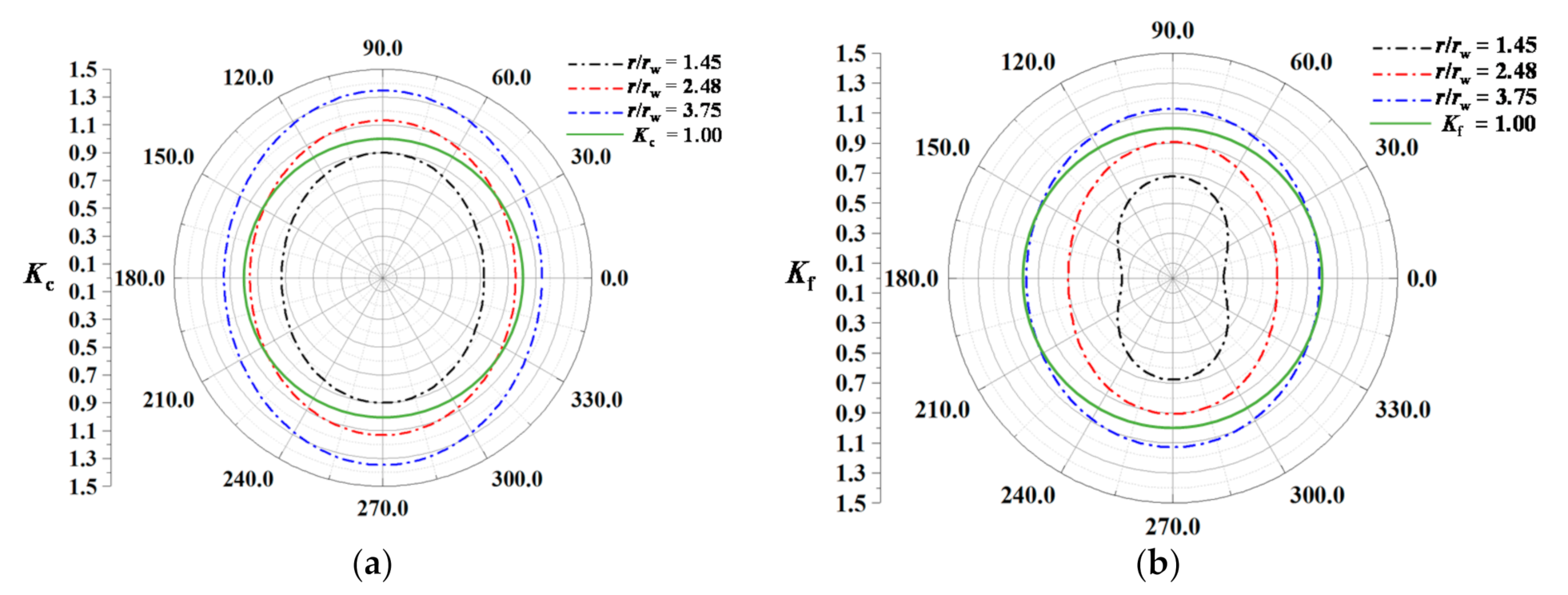
4.4. Instability Coefficient of the Wellbore Structure

The wellbore instability mainly includes compressive shear failure and tensile failure, which can be evaluated using the Mohr–Coulomb strength criterion and maximum tensile stress strength criterion, respectively. The wellbore collapse coefficient K_c and wellbore rupture coefficient K_f are defined, and the corresponding evaluation criteria of the wellbore stability are listed as follows [39]:

$$K_{\mathrm{c}}=\frac{(2C\cos \varphi )/(1-\sin \varphi )}{({\sigma }_1-p_p)-({\sigma }_3-p_p)(1+\sin \varphi )/(1-\sin \varphi )}$$

(7)

$$K_f=2+({\sigma }_3-p_p)/{\sigma }_t$$

(8)

where ${\sigma }_{{}_1}$ and ${\sigma }_3$ are the maximum and minimum principal ground stresses, respectively (MPa); C is the cohesion of the rock formations (MPa); $\varphi$ is the internal friction angle of the rock formations (°); P_p is the pore pressure of the formations (MPa), and ${\sigma }_t$ is the tensile strength of the rock formations (MPa).

Here K_c < 1 indicates the collapse or damage of the wellbore, and K_f < 1 means the rupture of the surrounding rock of the wellbore. The wellbore is in a critical stable state when K_c = 1 and K_f = 1, and the surrounding rock of the wellbore is stable if K_c > 1 and K_f > 1.

4.5. Stability Coefficient Evaluation of Wellbore

The wellbore stability coefficient has a great reference value for predicting the collapse and fracture range as well as the depth of the wellbore. When the near-wellbore formation is subjected to tensile/compressive stress, it is prone to cause the collapse/rupture of the wellbore formation. In this study, the wellbore collapse and rupture coefficient were adopted as the benchmark to characterize the damage degree and depth of the wellbore. The critical value of the wellbore collapse and rupture coefficient were set to 1.0.

Figure 10a shows the evolution of the wellbore collapse coefficient in sections A₁B₁, A₂B₂, and A₃B₃. For section A₁B₁, within the range of $r/r_w\le 2.48$, the wellbore collapse coefficient K_c was less than 1.0, and this section was prone to failure. The minimum value of the wellbore collapse coefficient was located at the cement sheath–formations interface, where the damage would be the most severe. The section A₂B₂ is the junction between the casing and open-hole segments; the stress distribution there changed relatively complexly.

The collapse coefficient fluctuated significantly and dropped to the lowest value of K_c = 0.427 at the junction of the casing, cement sheath, and formations, which indicated a severe collapse and had a dominant impact on the integrity of the geothermal wellbore structure. The risk was relatively high. The collapsed damage region in the A₃B₃ section was relatively small. This is attributed to the fact that the heat exchange fluid reduces the temperature of the casing, cement sheath, and formations during the water injection process.

Figure 10b shows the variation of the wellbore rupture coefficient in three sections. At section A₁B₁ of the wellbore, the main load was the internal pressure of the wellbore casing. Affected by the coordination of different deformations of the casing, cement, sheath, and formations, the collapse, and fracture range expanded, reaching the range of $r/r_w\le 3.75$. In the partial completion section A₂B₂, affected by the pore pressure and temperature changes of the injected water, the near-wellbore formations underwent tensile failure. At the interface between the casing, cement sheath, and formations, the rupture coefficient of the wellbore reached the minimum value K_f = 0.1. At section A₃B₃, the deformation of formation was relatively uniform and less affected by the tensile failure.

The transverse plane strain model corresponding to the A₁B₁ section was examined to analyze the collapse and rupture of the borehole wall. When subjected to non-uniform ground stress, correspondingly, the radial and hoop stress distribution on the wellbore were centralized and asymmetric. Figure 11 shows the collapse coefficient distribution at the borehole wall, where the positions $r/r_w=1.45$, $r/r_w=2.48$, and $r/r_w=3.75$ correspond to the starting position of the formation, the critical point of formations collapse, and the critical point of formations fracture of the A₁B₁ section, respectively.

The wellbore collapse coefficient K_c reached 1 at $r/r_w=2.48$ along the minimum horizontal principal stress direction. The wellbore rupture coefficient K_f was equal to 1 at $r/r_w=3.75$, along the minimum horizontal principal stress direction. These results indicate that the collapse and fracture of the wellbore formations mainly occurred in the direction of the minimum horizontal principal stress, and the damage range and extent were higher than along the direction of the maximum horizontal principal stress.

5. Conclusions

A case study was conducted to investigate the water injection cycle production process of geothermal wells in northern Shandong. According to the finite element numerical analysis of the THM coupled model, the following conclusions were obtained:

(1)

The injected fluid diffused from the open-hole wall to the distal end along the radial and axial directions of the well, simultaneously. The stress caused by the excess pore pressure led to debonding of the interface between the cement sheath and the formations, which greatly shortened the service life of the geothermal well.

(2)

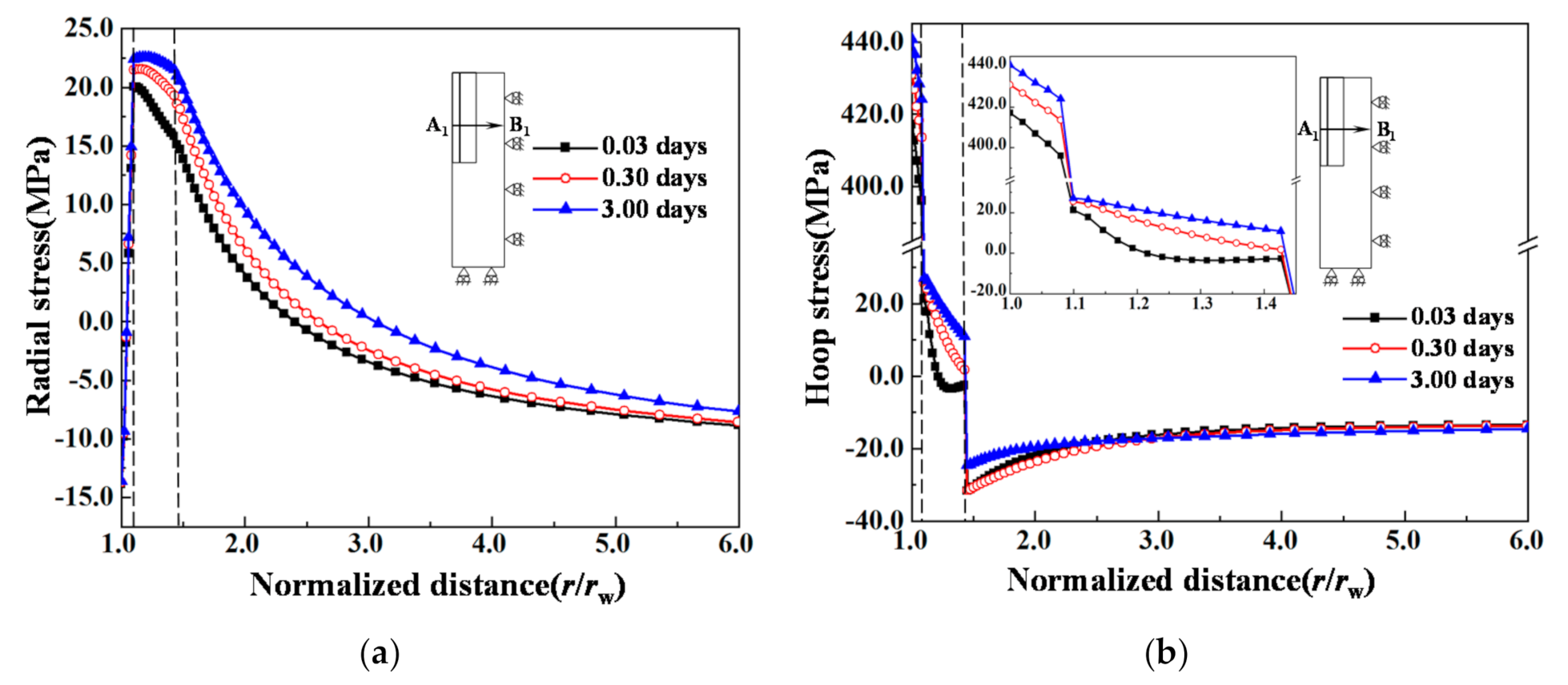
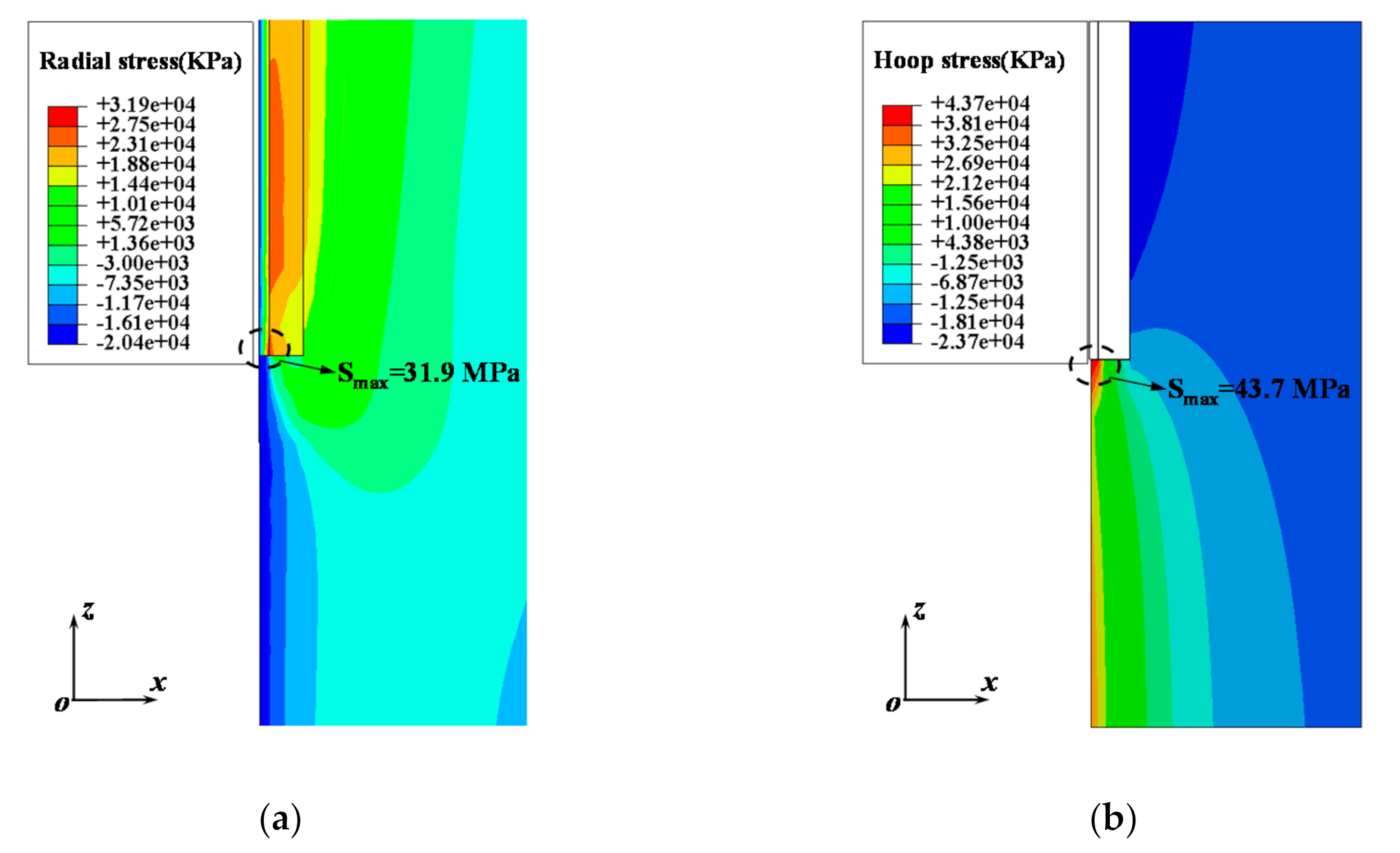
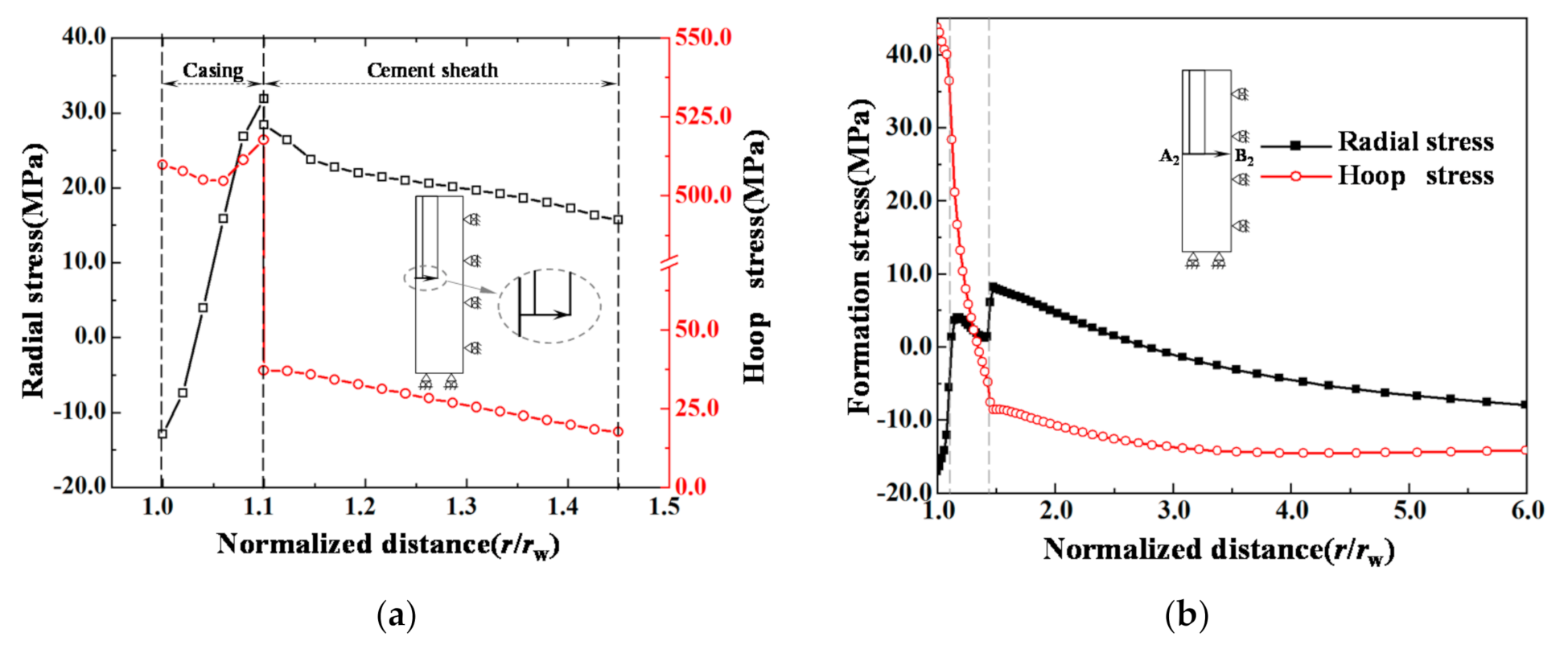
During the cold water injection, the thermal stress concentration appeared at two interfaces of the geothermal wellbore structure, i.e., section A₁B₁ of the casing–cement sheath cementation surface and section A₂B₂ of the local open-hole completion segment. The radial tensile stress concentration mainly occurred at section A₁B₁. The radial tensile stress was up to 31.9 MPa, which was likely to cause debonding at the casing–cement sheath interface. While at section A₂B₂ the stress concentration was dominated by the hoop tensile stress, which was up to 43.7 MPa, about 2.08 times the tensile strength of the cement sheath.

(3)

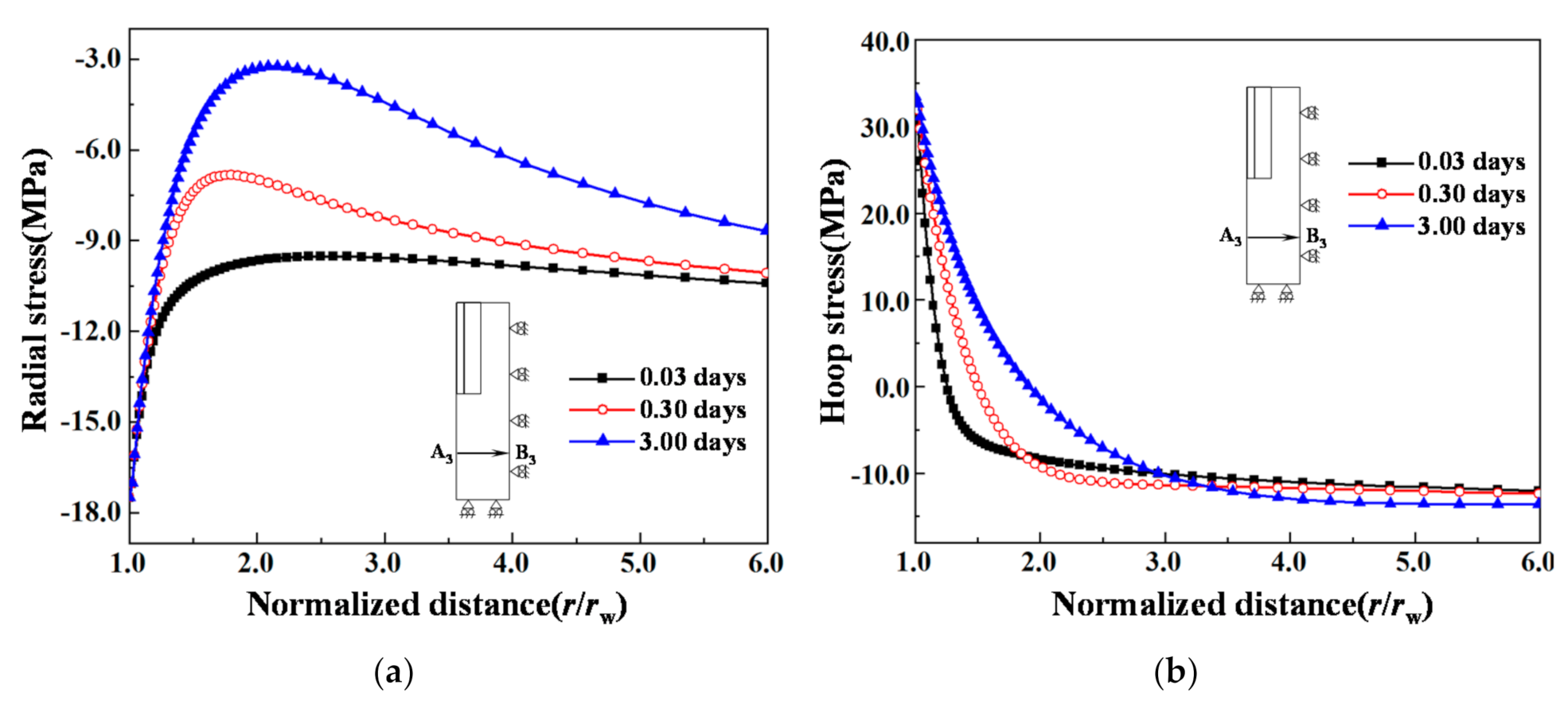
Due to the partial casing completion, the collapses and fractures of the wellbore were severe in the formations at section A₂B₂. The wellbore collapse and the rupture in section A₁B₁ were relatively small; however, the damaged region was wider. The wellbore structure at the open-hole completion A₃B₃ section was less affected by the variations of temperature and pore pressure. Therefore, both the collapse damage degree and damage region were much smaller than at sections A₁B₁ and A₂B₂.

(4)

The method presented in this study was effective for the THM coupling analysis of the wellbore structure. This method can provide a mechanical basis for wellbore structural failure control and the safety evaluation of a geothermal wellbore.