Does Rheology of Bingham Fluid Influence Upscaling of Flow through Tight Porous Media?
Abstract
1. Introduction
2. Materials and Methods
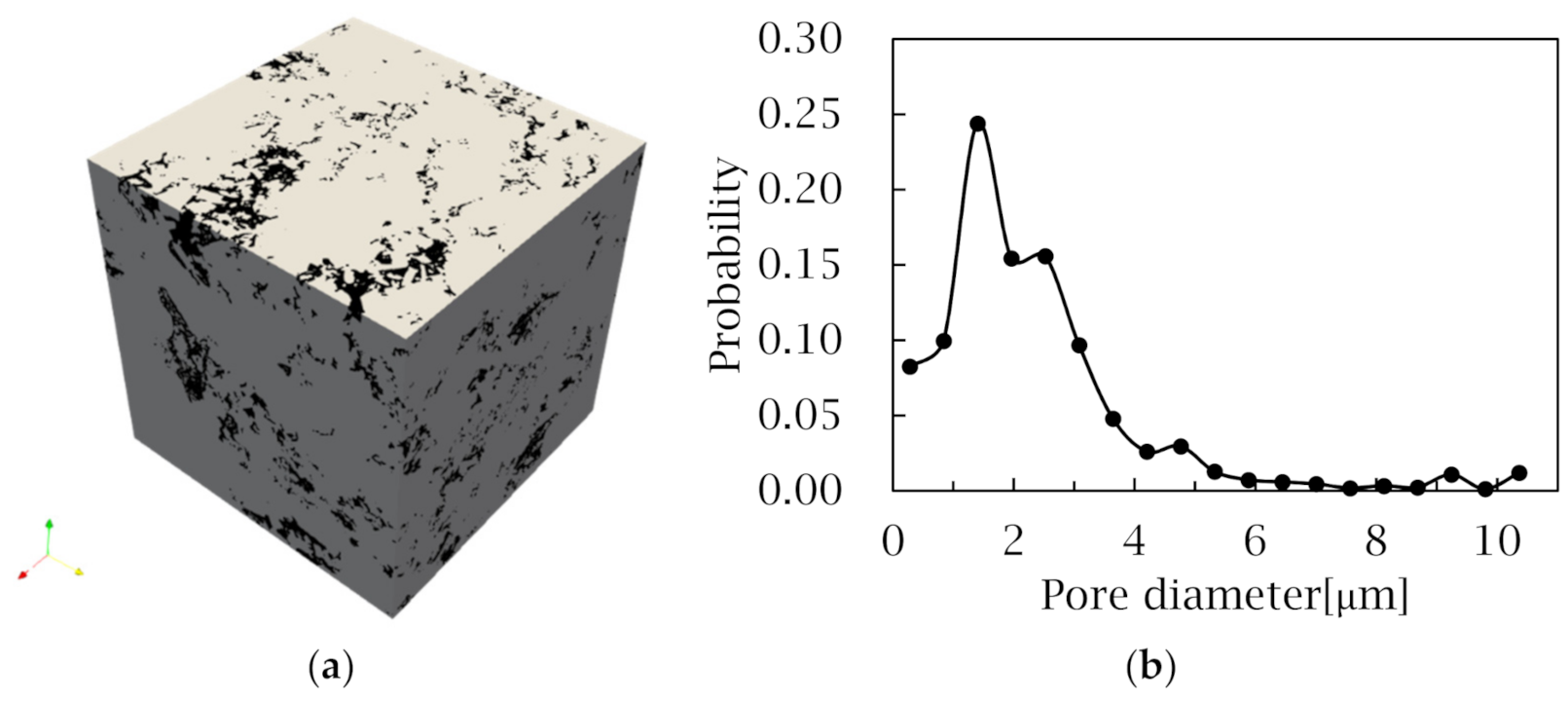
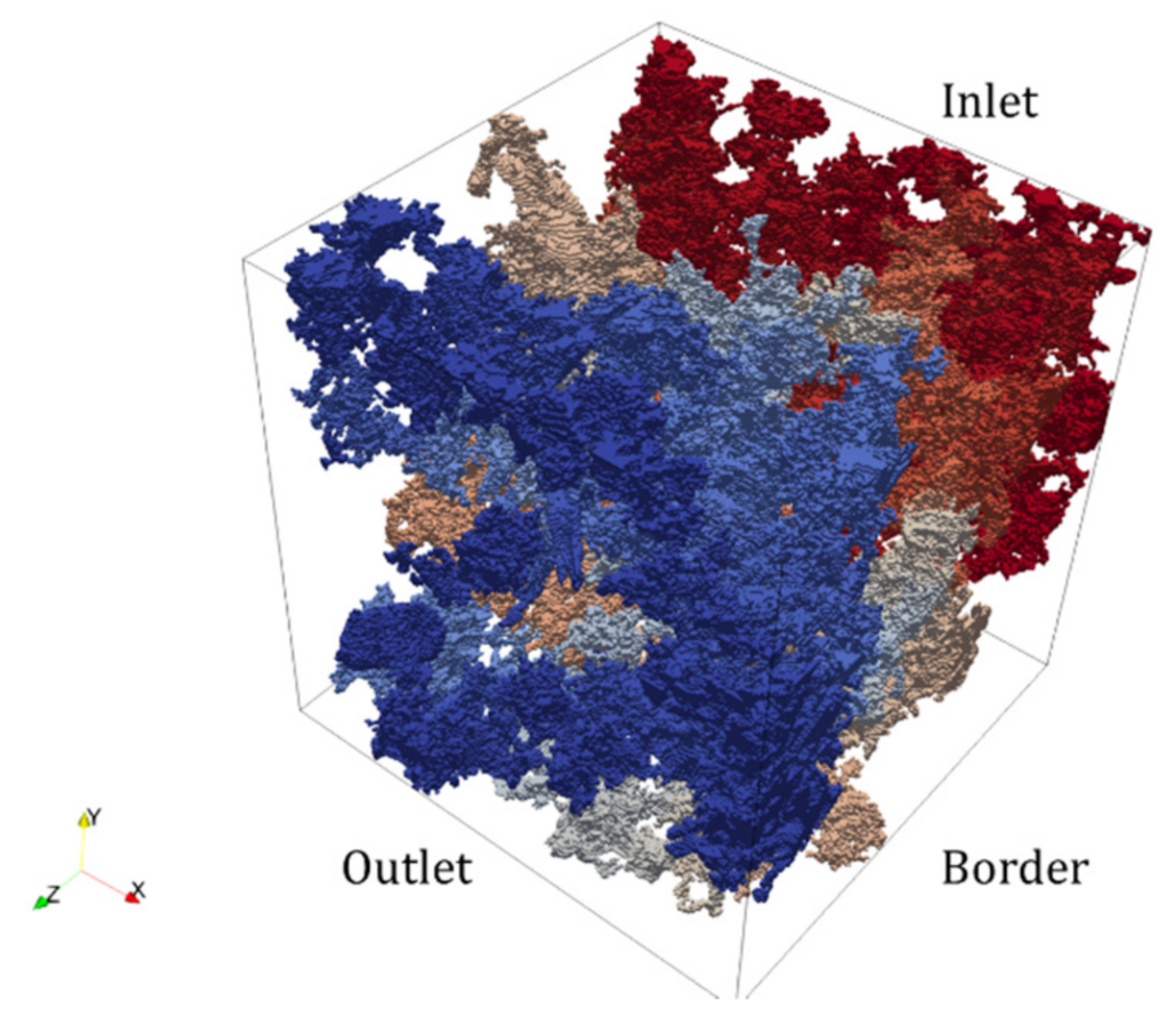
2.1. Structure & Oil Properties
2.2. Pore-Scale Modeling of Bingham Fluid Flow
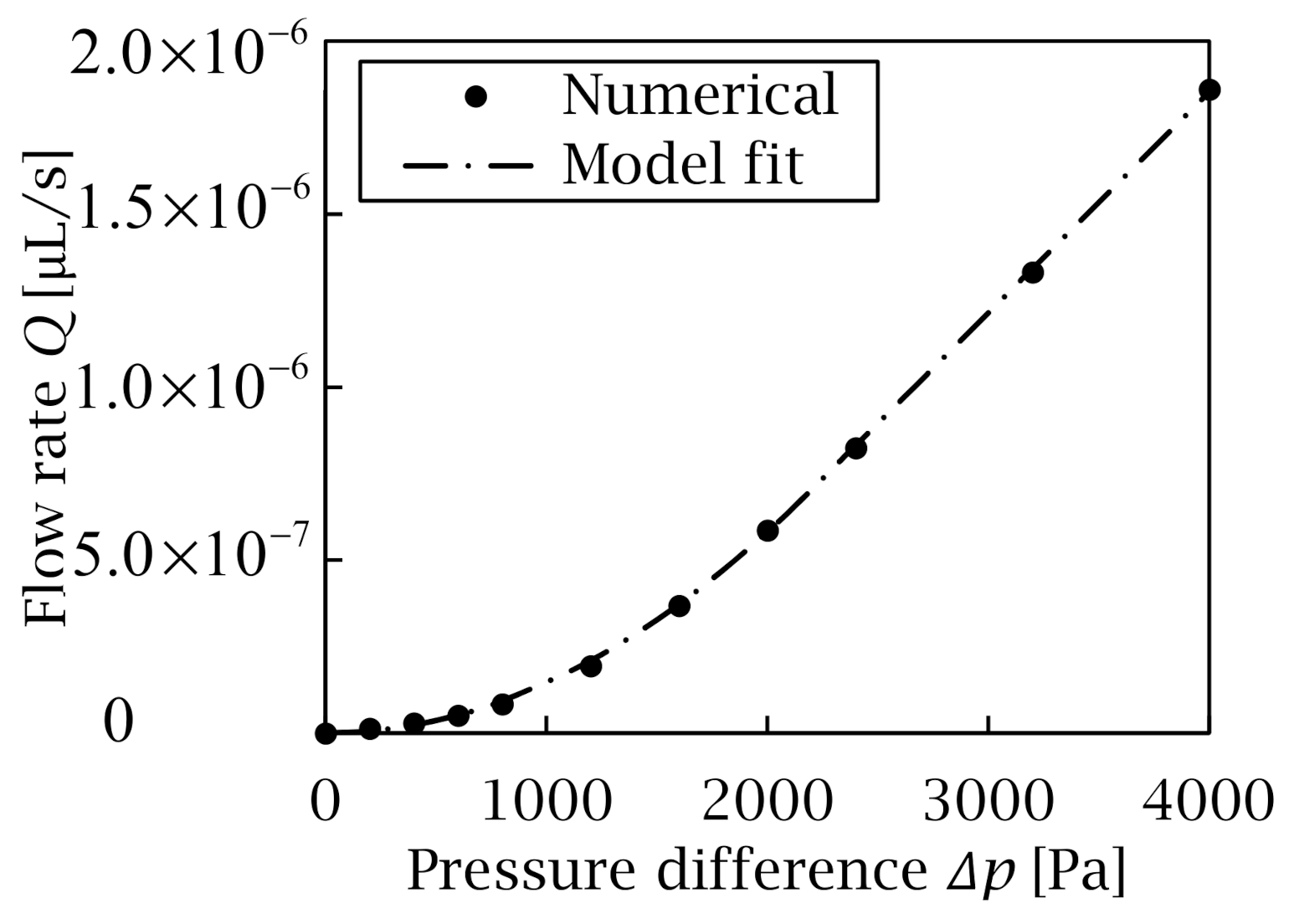
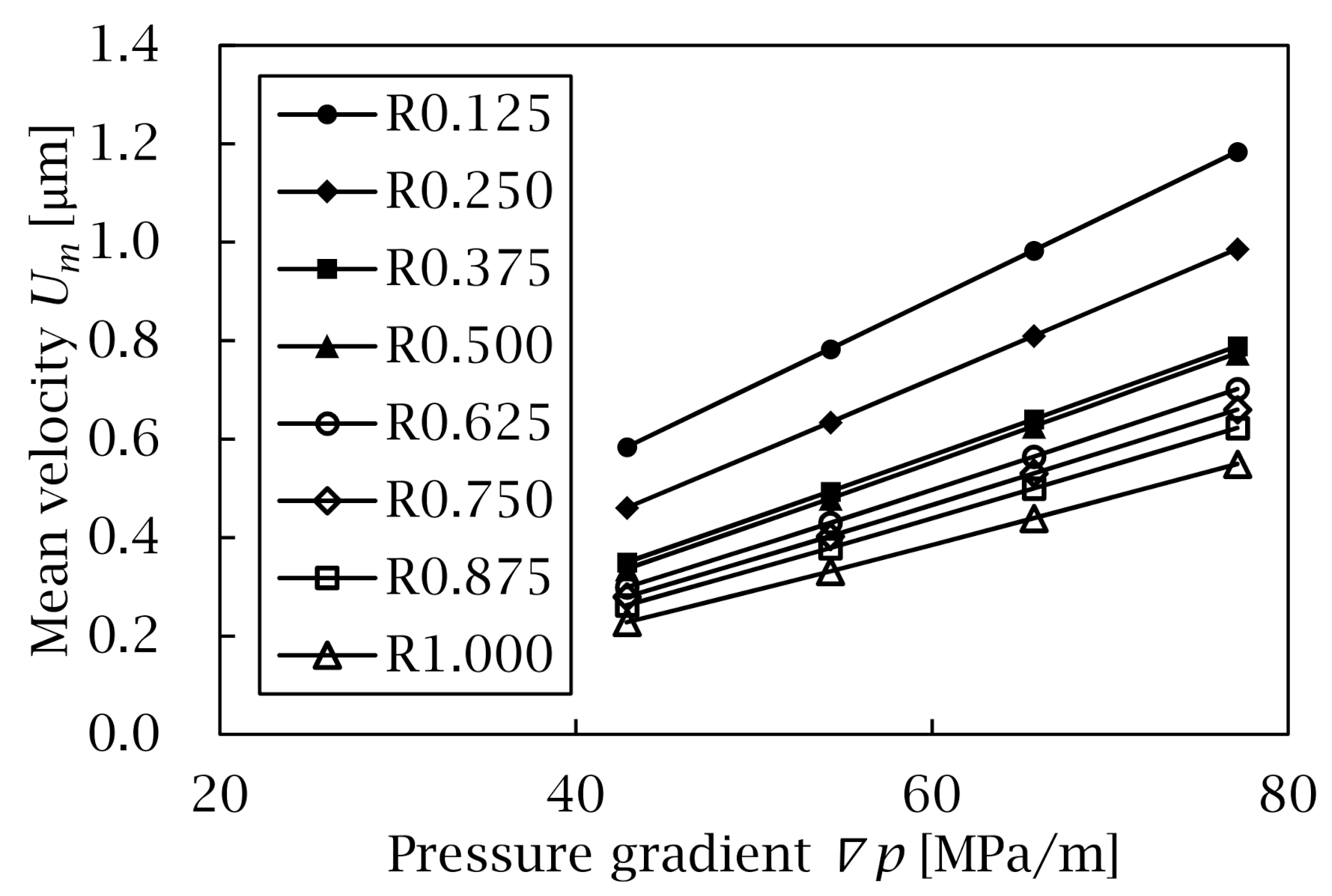
2.3. Upscaling of Bingham Fluid Flow
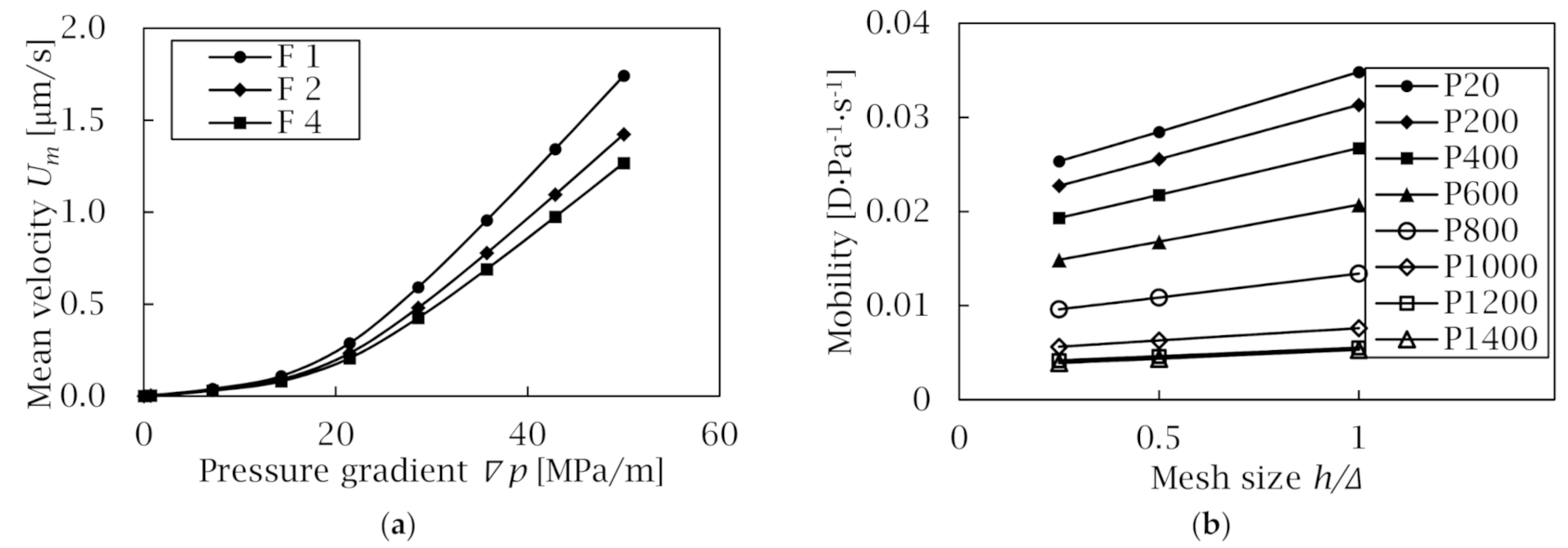
3. Results
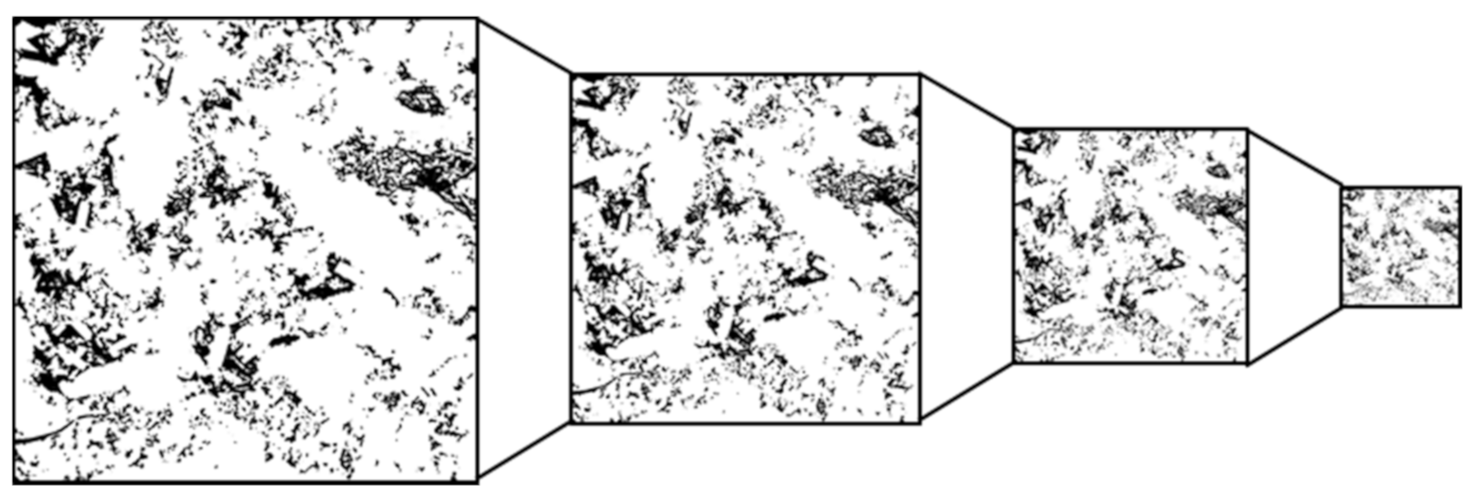
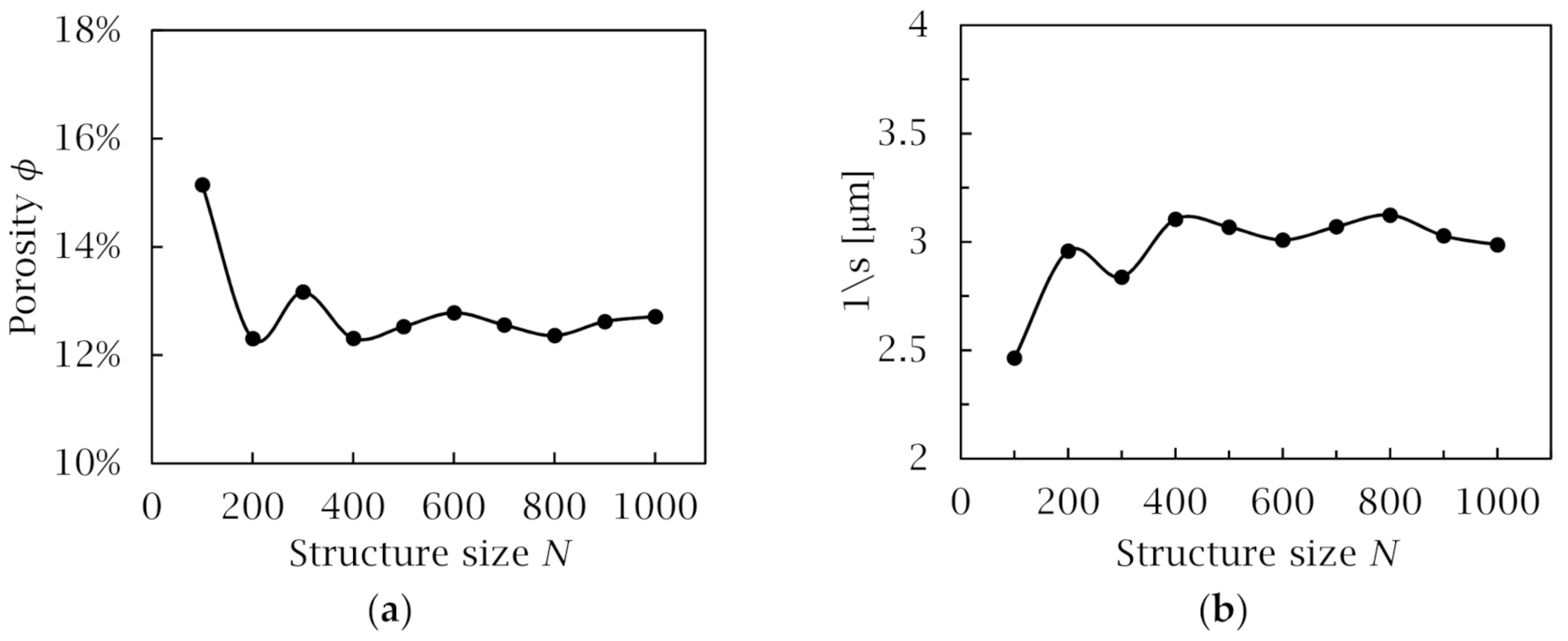
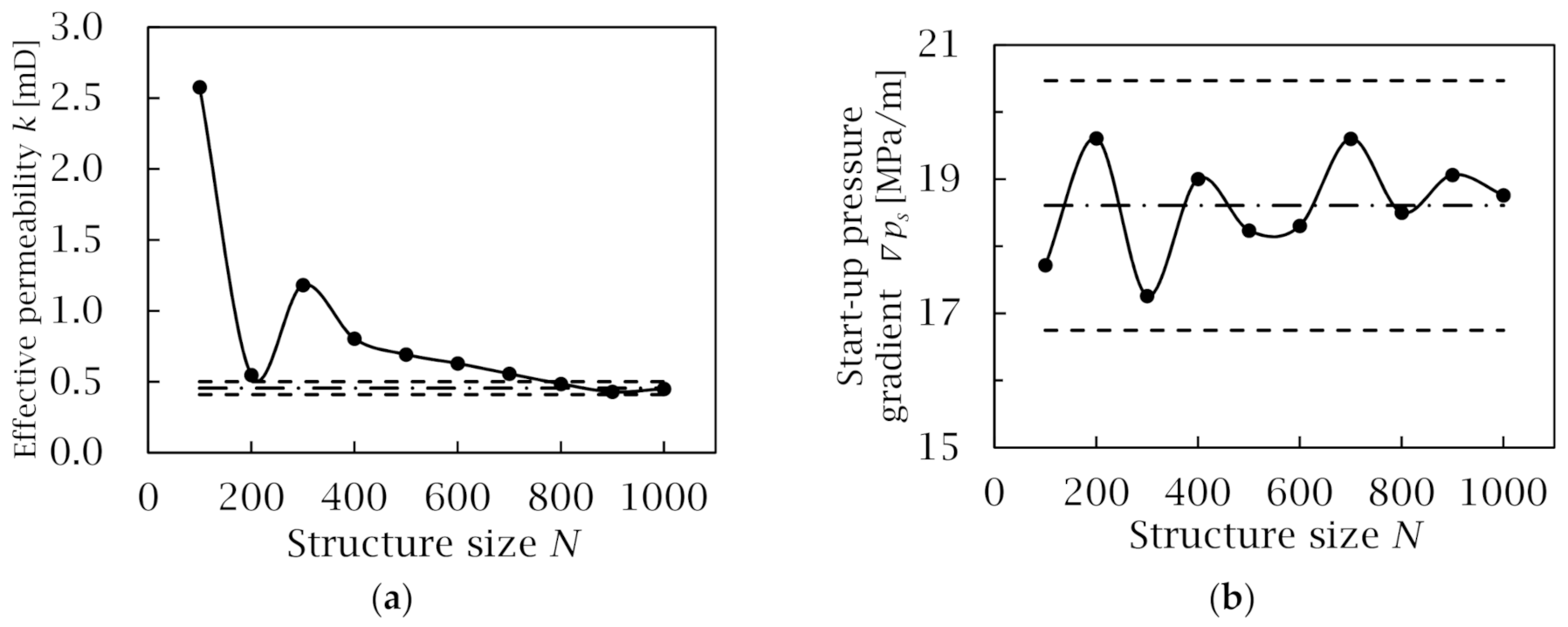
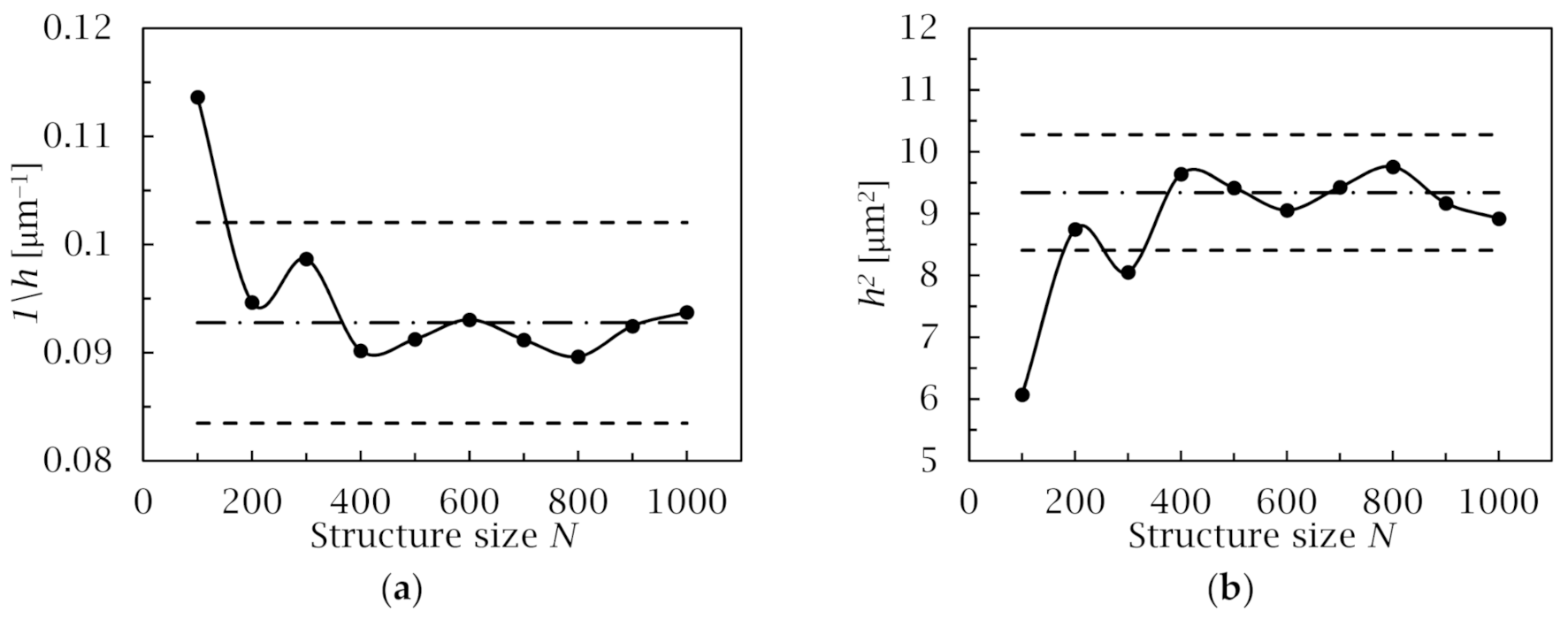
3.1. REV Size
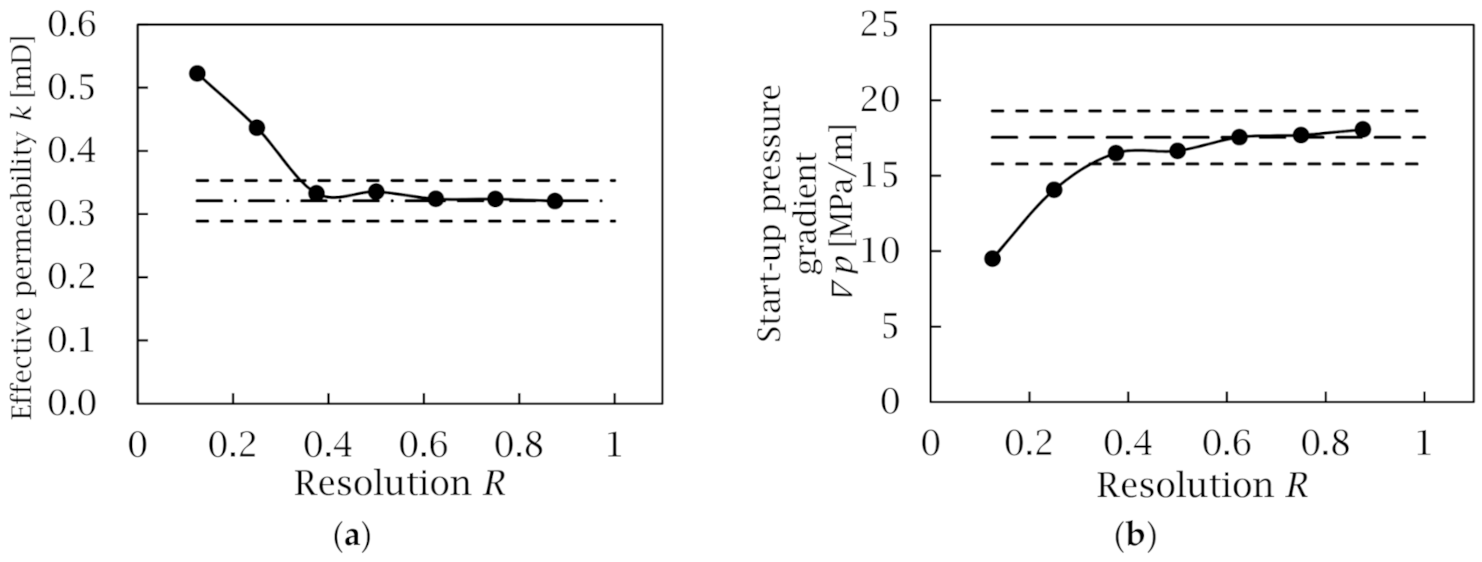
3.2. Cut-Off Resolution (COR)
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Bingham Flow in 2D Parallel Plate
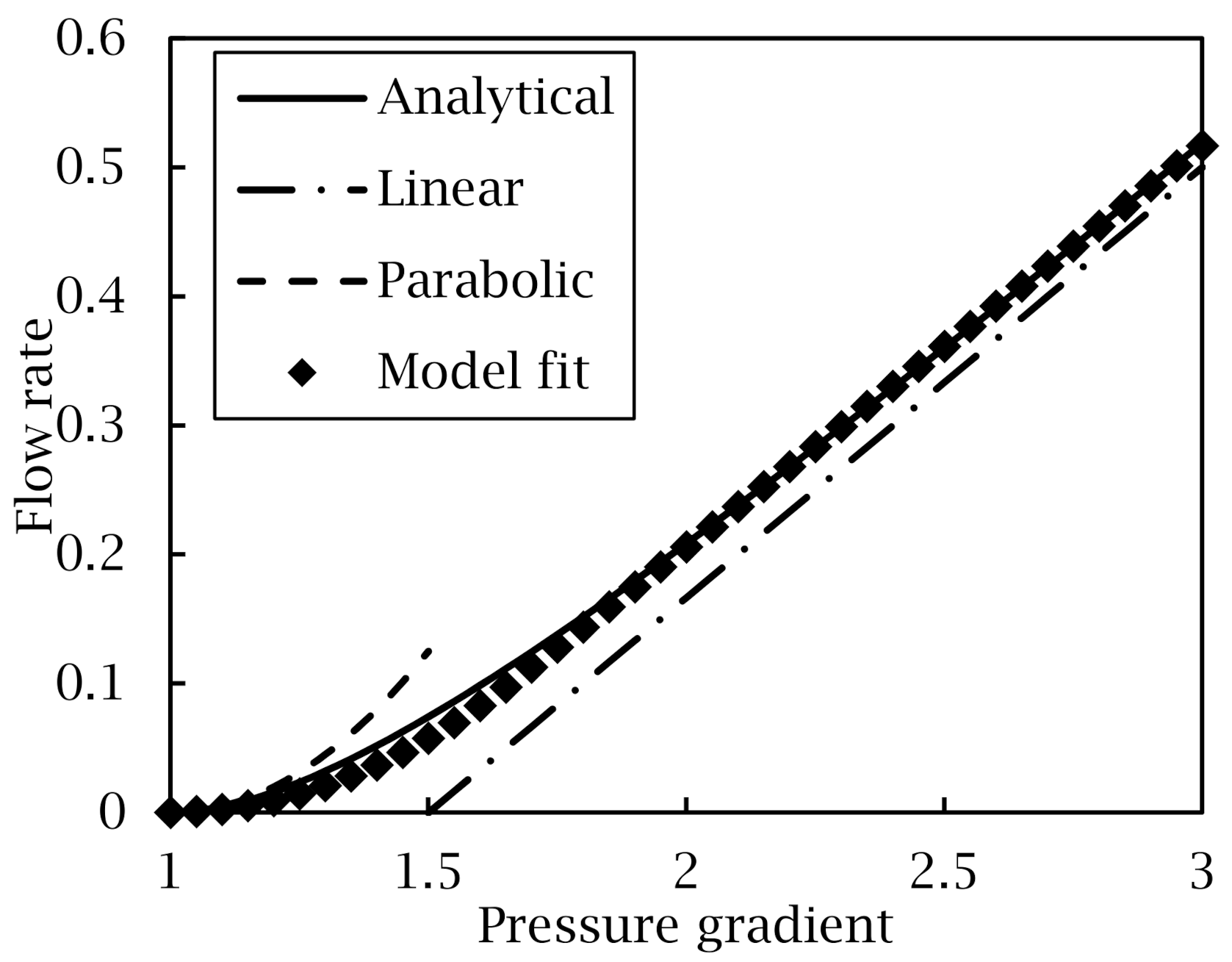
Appendix A.2. Bingham Flow in 3D Cylinder
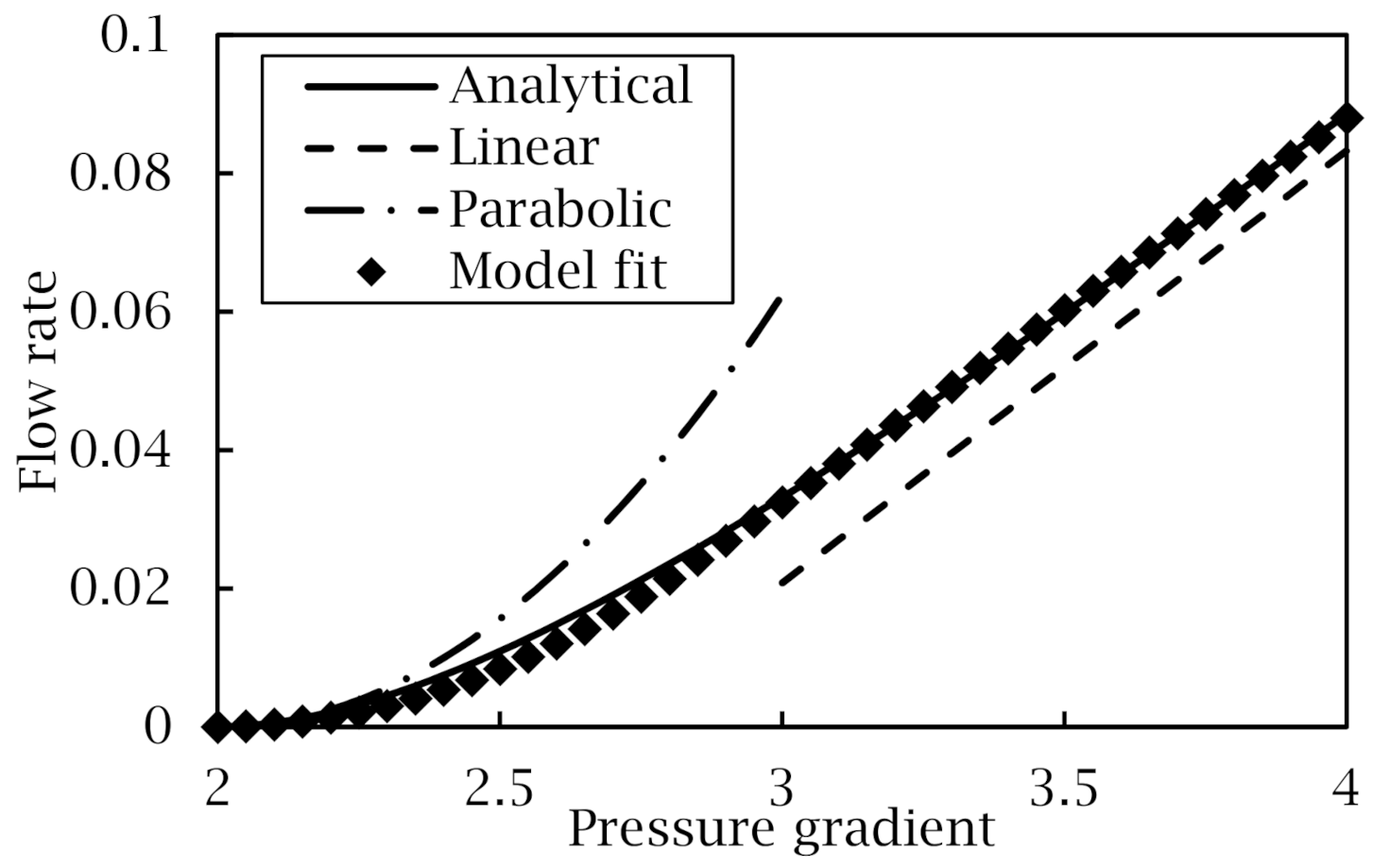
References
- Bear, J. Dynamics of Fluids in Porous Media; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Blunt, M.J. Multiphase Flow in Permeable Media: A Pore-Scale Perspective; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Sochi, T. Flow of non-Newtonian fluids in porous media. J. Polym. Sci. Part B Polym. Phys. 2010, 48, 2437–2767. [Google Scholar] [CrossRef]
- Neuman, S.P. Theoretical derivation of Darcy’s law. Acta Mech. 1977, 25, 153–170. [Google Scholar] [CrossRef]
- Whitaker, S. Flow in porous media I: A theoretical derivation of Darcy’s law. Transp. Porous Media 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Sangani, A.S.; Acrivos, A. Slow flow through a periodic array of spheres. Int. J. Multiph. Flow 1982, 8, 343–360. [Google Scholar] [CrossRef]
- Torquato, S.; Haslach, H., Jr. Random Heterogeneous Materials: Microstructure and Macroscopic Properties; Springer: Berlin/Heidelberg, Germany, 2002; Volume 55. [Google Scholar]
- Teng, H.; Zhao, T. An extension of Darcy’s law to non-Stokes flow in porous media. Chem. Eng. Sci. 2000, 55, 2727–2735. [Google Scholar] [CrossRef]
- Zeng, Z.; Grigg, R. A criterion for non-Darcy flow in porous media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
- Roustaei, A.; Chevalier, T.; Talon, L.; Frigaard, I. Non-Darcy effects in fracture flows of a yield stress fluid. J. Fluid Mech. 2016, 805, 222–261. [Google Scholar]
- Chen, Y.-F.; Zhou, J.-Q.; Hu, S.-H.; Hu, R.; Zhou, C.-B. Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures. J. Hydrol. 2015, 529, 993–1006. [Google Scholar] [CrossRef]
- Yao, Y.; Ge, J. Characteristics of non-Darcy flow in low-permeability reservoirs. Pet. Sci. 2011, 8, 55–62. [Google Scholar] [CrossRef]
- Metzner, A.; Otto, R. Agitation of non-Newtonian fluids. AIChE J. 1957, 3, 3–10. [Google Scholar] [CrossRef]
- Chhabra, R.P. Bubbles, Drops, and Particles in Non-Newtonian Fluids; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Yu, Y. Study on Rheological Properties of Waxy Crude Oil; Daqing Petroleum Institute: Heilongjiang, China, 2008. [Google Scholar]
- Hemmingsen, P.V.; Silset, A.; Hannisdal, A.; Sjöblom, J. Emulsions of heavy crude oils. I: Influence of viscosity, temperature, and dilution. J. Dispers. Sci. 2005, 26, 615–627. [Google Scholar] [CrossRef]
- Chang, C.; Nguyen, Q.D.; Rønningsen, H.P. Isothermal start-up of pipeline transporting waxy crude oil. J. Non Newton. Fluid Mech. 1999, 87, 127–154. [Google Scholar] [CrossRef]
- Xiao, G.; Yong, W. Influence of start-up pressure gradient and stress sensitivity on productivity of low-permeability gas reservoirs. Oil Gas Geol. 2007, 4, 539–543. [Google Scholar]
- Yizhong, Z.; Yuanfang, C.; Yuchuan, L.; Efficiency, R. Study on influence of start-up pressure gradient to microseepage in low permeability reservoirs and development trends. Pet. Geol. 2013, 20, 67–73. [Google Scholar]
- Bauer, D.; Talon, L.; Peysson, Y.; Ly, H.; Batôt, G.; Chevalier, T.; Fleury, M. Experimental and numerical determination of Darcy’s law for yield stress fluids in porous media. Phys. Rev. Fluids 2019, 4, 063301. [Google Scholar] [CrossRef]
- Chase, G.G.; Dachavijit, P. A correlation for yield stress fluid flow through packed beds. Rheol. Acta 2005, 44, 495–501. [Google Scholar]
- Talon, L.; Bauer, D. On the determination of a generalized Darcy equation for yield-stress fluid in porous media using a Lattice-Boltzmann TRT scheme. Eur. Phys. J. E 2013, 36, 139. [Google Scholar] [CrossRef]
- Chevalier, T.; Talon, L. Generalization of Darcy’s law for Bingham fluids in porous media: From flow-field statistics to the flow-rate regimes. Phys. Rev. E 2015, 91, 023011. [Google Scholar] [CrossRef]
- Arns, C.H.; Knackstedt, M.A.; Pinczewski, M.V.; Lindquist, W. Accurate estimation of transport properties from microtomographic images. Geophys. Res. Lett. 2001, 28, 3361–3364. [Google Scholar] [CrossRef]
- Keehm, Y.; Mukerji, T.; Nur, A. Permeability prediction from thin sections: 3D reconstruction and Lattice-Boltzmann flow simulation. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Grader, A.; Kalam, M.; Toelke, J.; Mu, Y.; Derzhi, N.; Baldwin, C.; Stenger, B. A comparative study of digital rock physics and laboratory SCAL evaluations of carbonate cores. In Proceedings of the International Symposium of the Society-of-Core-Analysts, Halifax, NS, Canada, 4–7 October 2010. [Google Scholar]
- Miller, K.; Vanorio, T.; Keehm, Y. Evolution of permeability and microstructure of tight carbonates due to numerical simulation of calcite dissolution. J. Geophys. Res. Solid Earth 2017, 122, 4460–4474. [Google Scholar] [CrossRef]
- Berg, S.; van Wunnik, J. Shear rate determination from pore-scale flow fields. Transp. Porous Media 2017, 117, 229–246. [Google Scholar] [CrossRef]
- Bultreys, T.; De Boever, W.; Cnudde, V. Imaging and image-based fluid transport modeling at the pore scale in geological materials: A practical introduction to the current state-of-the-art. Earth Sci. Rev. 2016, 155, 93–128. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, P.; Wu, J.; Mezzatesta, A.; Jin, G.; Satti, R.; Koliha, N.; Bautista, J.; Crouse, B.; Freed, D. Using Digital Rock Modeling to Estimate Permeability and Capillary Pressure from NMR and Geochemical Logs. In Proceedings of the SPE Middle East Oil & Gas Show and Conference, Manama, Bahrain, 6–9 March 2017. [Google Scholar]
- Li, G.G.; Diaz, E.; Nur, A.M. Rock Physical Properties Computed from Digital Core and Cuttings with Applications to Deep Gas Exploration and Development. In Proceedings of the SPE Deep Gas Conference and Exhibition, Manama, Bahrain, 24–26 January 2010. [Google Scholar]
- Nordahl, K.; Ringrose, P.S. Identifying the Representative Elementary Volume for permeability in heterolithic deposits using numerical rock models. Math Geosci. 2008, 40, 753–771. [Google Scholar] [CrossRef]
- Borujeni, A.T.; Lane, N.; Thompson, K.; Tyagi, M. Effects of image resolution and numerical resolution on computed permeability of consolidated packing using LB and FEM pore-scale simulations. Comput. Fluids 2013, 88, 753–763. [Google Scholar] [CrossRef]
- Mostaghimi, P.; Blunt, M.J.; Bijeljic, B. Computations of absolute permeability on micro-CT images. Math Geosci. 2013, 45, 103–125. [Google Scholar] [CrossRef]
- Alyafei, N.; Raeini, A.Q.; Paluszny, A.; Blunt, M.J. A sensitivity study of the effect of image resolution on predicted petrophysical properties. Transp. Porous Media 2015, 110, 157–169. [Google Scholar] [CrossRef]
- Shah, S.; Gray, F.; Crawshaw, J.; Boek, E. Micro-computed tomography pore-scale study of flow in porous media: Effect of voxel resolution. Adv. Water Resour. 2016, 95, 276–287. [Google Scholar] [CrossRef]
- Cui, D.; Sun, W.; Wang, Q.N.; Gu, C.P. Use of tomography to estimate the representative elementary volume in mortars stained with potassium iodide. Mater. Des. 2018, 147, 80–91. [Google Scholar] [CrossRef]
- Ledesma-Alonso, R.; Barbosa, R.; Ortegon, J. Effect of the image resolution on the statistical descriptors of heterogeneous media. Phys. Rev. E 2018, 97, 14. [Google Scholar]
- Liu, T.; Jin, X.; Wang, M. Critical resolution and sample size of digital rock analysis for unconventional reservoirs. Energies 2018, 11, 1798. [Google Scholar] [CrossRef]
- Sheppard, A.P.; Sok, R.M.; Averdunk, H. Techniques for image enhancement and segmentation of tomographic images of porous materials. Phys. A Stat. Mech. Appl. 2004, 339, 145–151. [Google Scholar] [CrossRef]
- Schlüter, S.; Sheppard, A.; Brown, K.; Wildenschild, D. Image processing of multiphase images obtained via X-ray microtomography: A review. Water Resour. Res. 2014, 50, 3615–3639. [Google Scholar] [CrossRef]
- Huang, L.-K.; Wang, M.-J.J. Image thresholding by minimizing the measures of fuzziness. Pattern Recognit. 1995, 28, 41–51. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. In Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics, Dubrovnik, Croatia, 19–21 September 2007. [Google Scholar]
- Hassanizadeh, S.M.; Gray, W.G. High velocity flow in porous media. Transp. Porous Media 1987, 2, 521–531. [Google Scholar] [CrossRef]





| 4.6 | 0.048 | 0.527 | 9.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Zhang, S.; Wang, M. Does Rheology of Bingham Fluid Influence Upscaling of Flow through Tight Porous Media? Energies 2021, 14, 680. https://doi.org/10.3390/en14030680
Liu T, Zhang S, Wang M. Does Rheology of Bingham Fluid Influence Upscaling of Flow through Tight Porous Media? Energies. 2021; 14(3):680. https://doi.org/10.3390/en14030680
Chicago/Turabian StyleLiu, Tong, Shiming Zhang, and Moran Wang. 2021. "Does Rheology of Bingham Fluid Influence Upscaling of Flow through Tight Porous Media?" Energies 14, no. 3: 680. https://doi.org/10.3390/en14030680
APA StyleLiu, T., Zhang, S., & Wang, M. (2021). Does Rheology of Bingham Fluid Influence Upscaling of Flow through Tight Porous Media? Energies, 14(3), 680. https://doi.org/10.3390/en14030680







