Torque Ripple Suppression of PMSM Based on Robust Two Degrees-of-Freedom Resonant Controller
Abstract
:1. Introduction
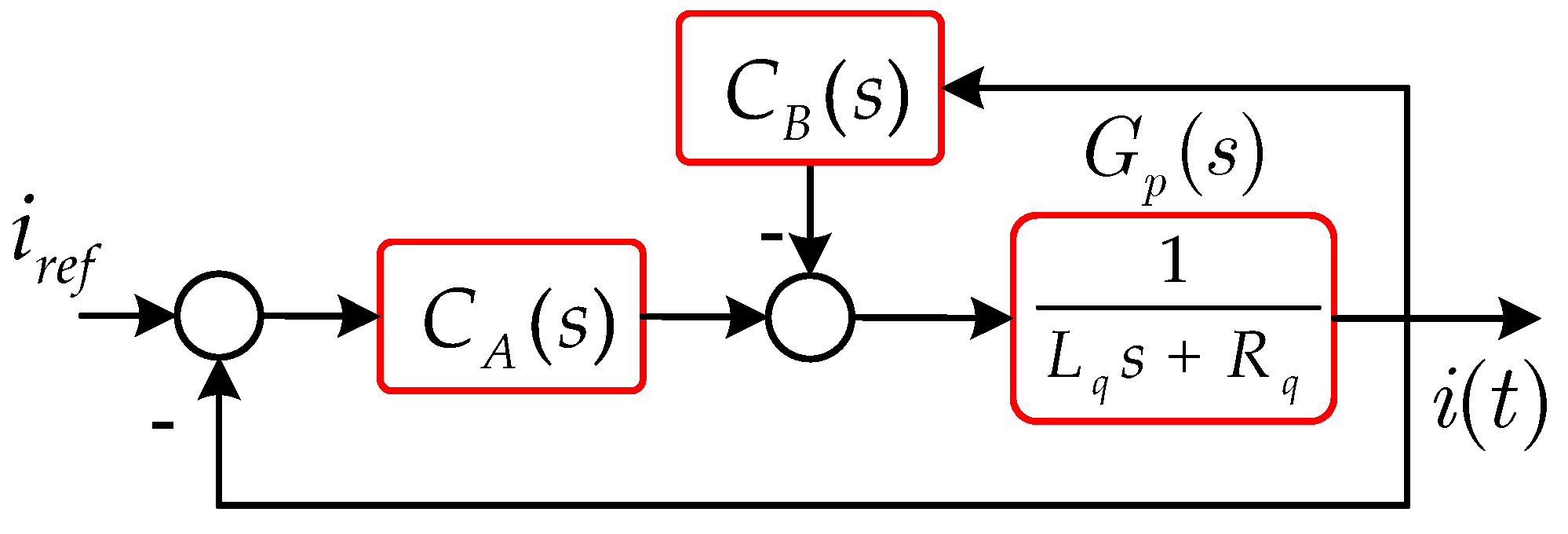
2. Dynamic Model of a PMSM
3. Design of Robust-TDOFR Controller
3.1. Preliminaries of Robust-TDOF Controller
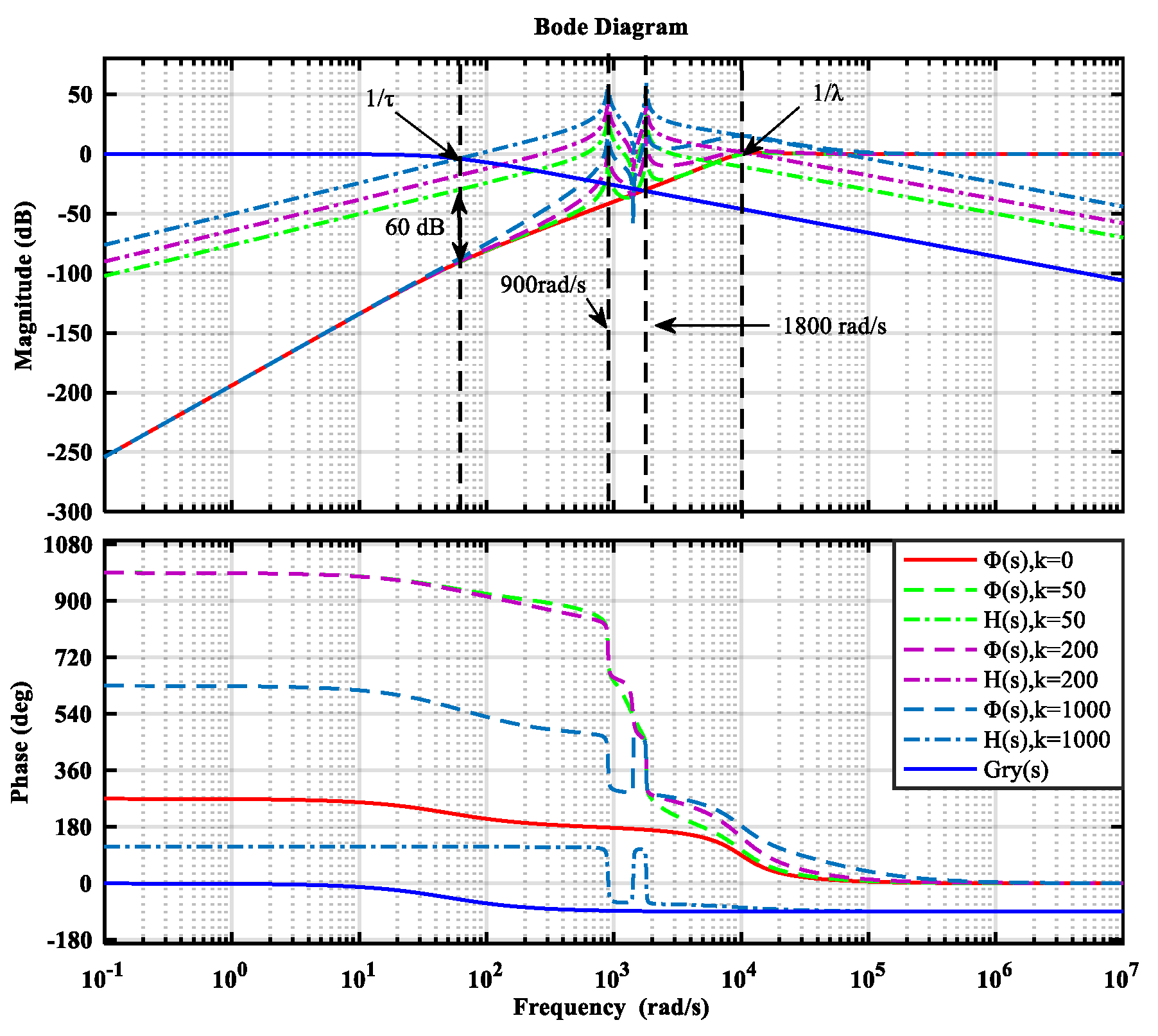
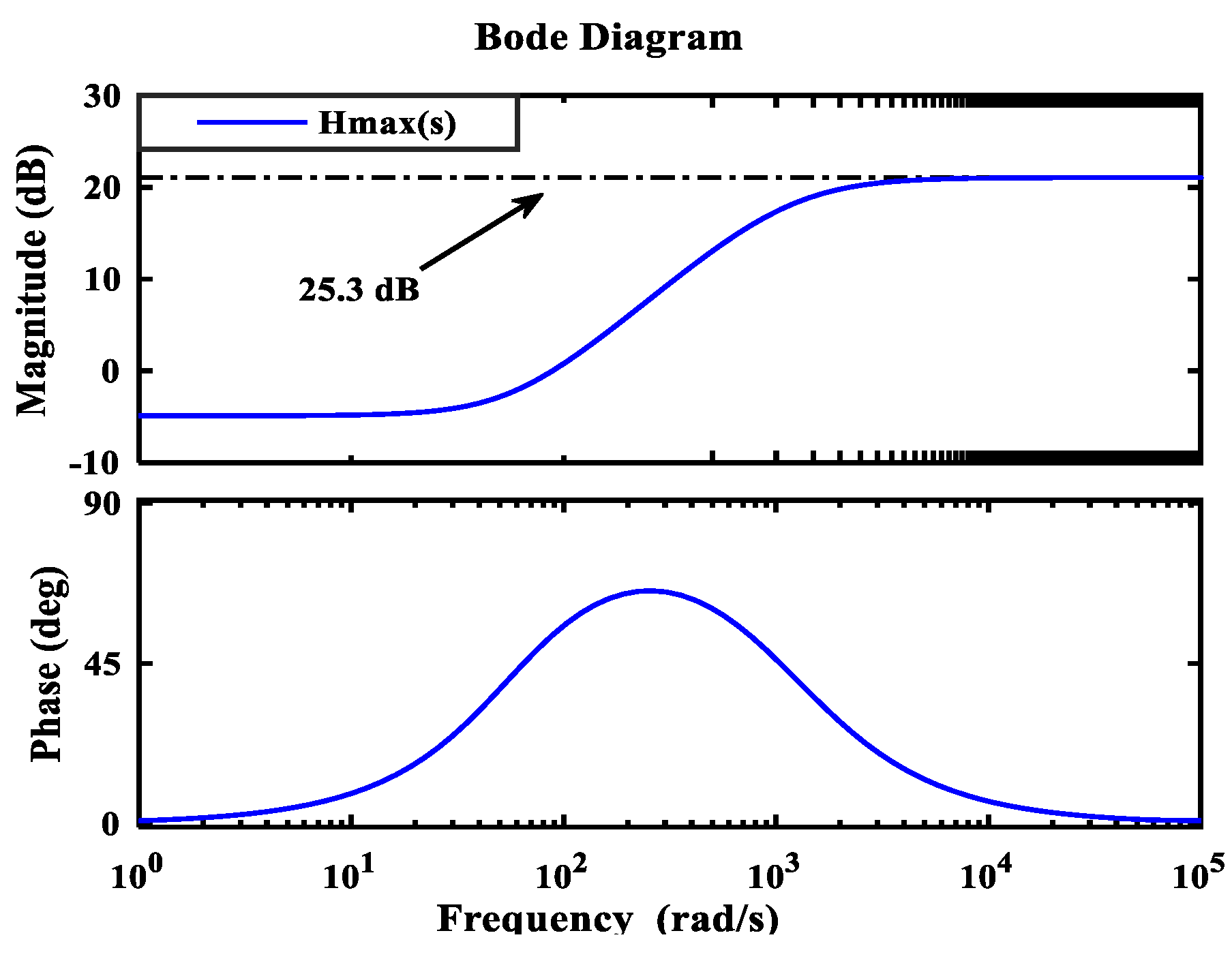
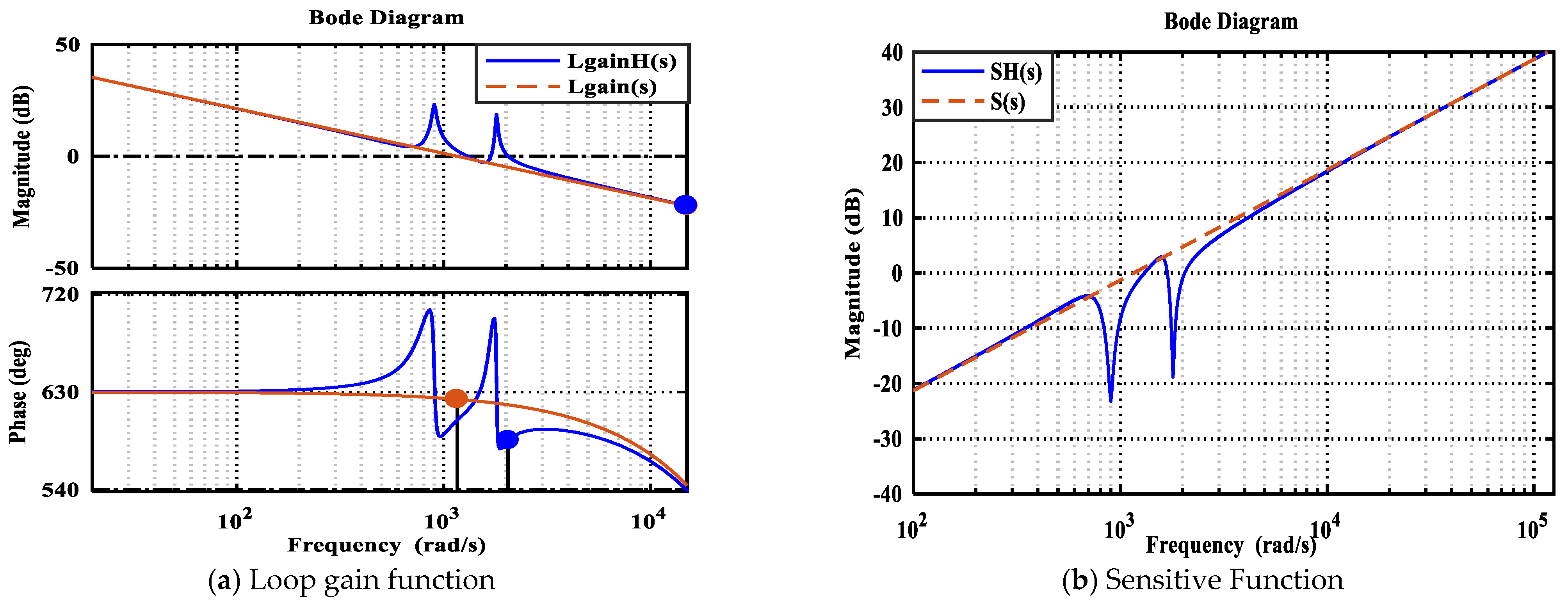
3.2. Robust Performance Analysis of Robust-TDOF
3.3. Disturbance Suppression with Resonant Controller
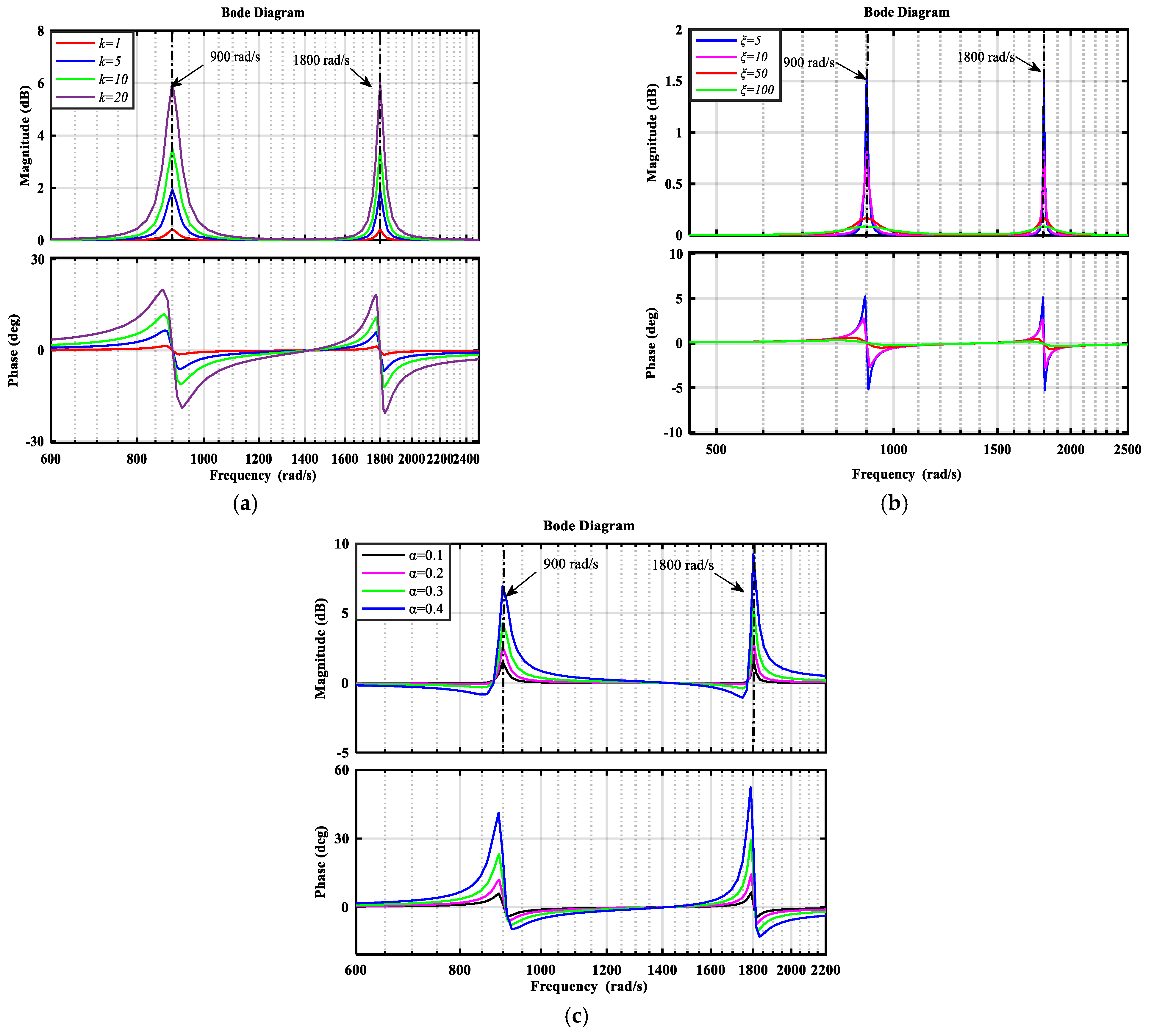
3.4. Parameters Analysis of the Resonant Controller
3.5. Robust-TDOF with Resonant Controller (Robust-TDOFR) Analysis
3.6. Design of Robust-TDOFR Controller
4. Simulation and Experimental Verification
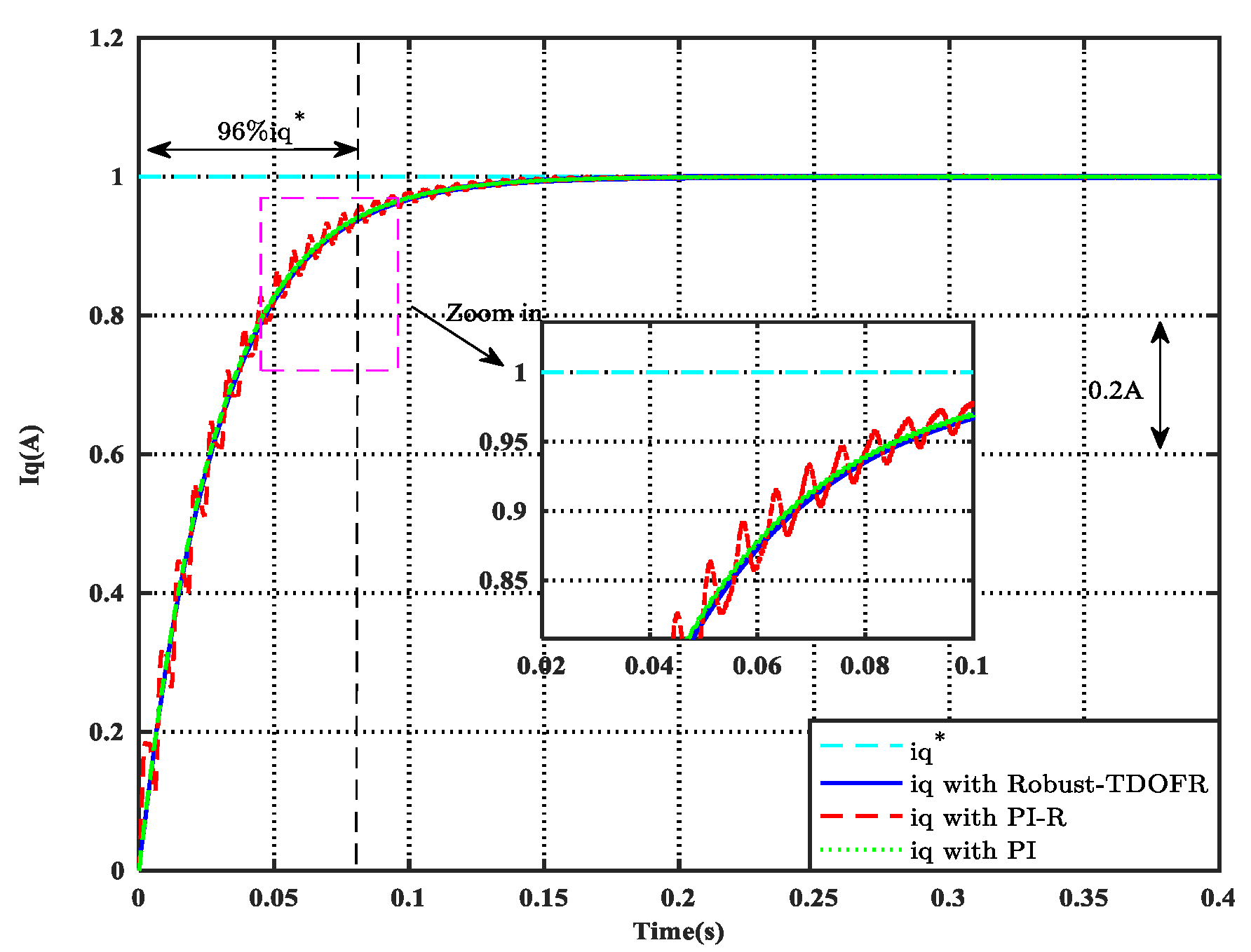
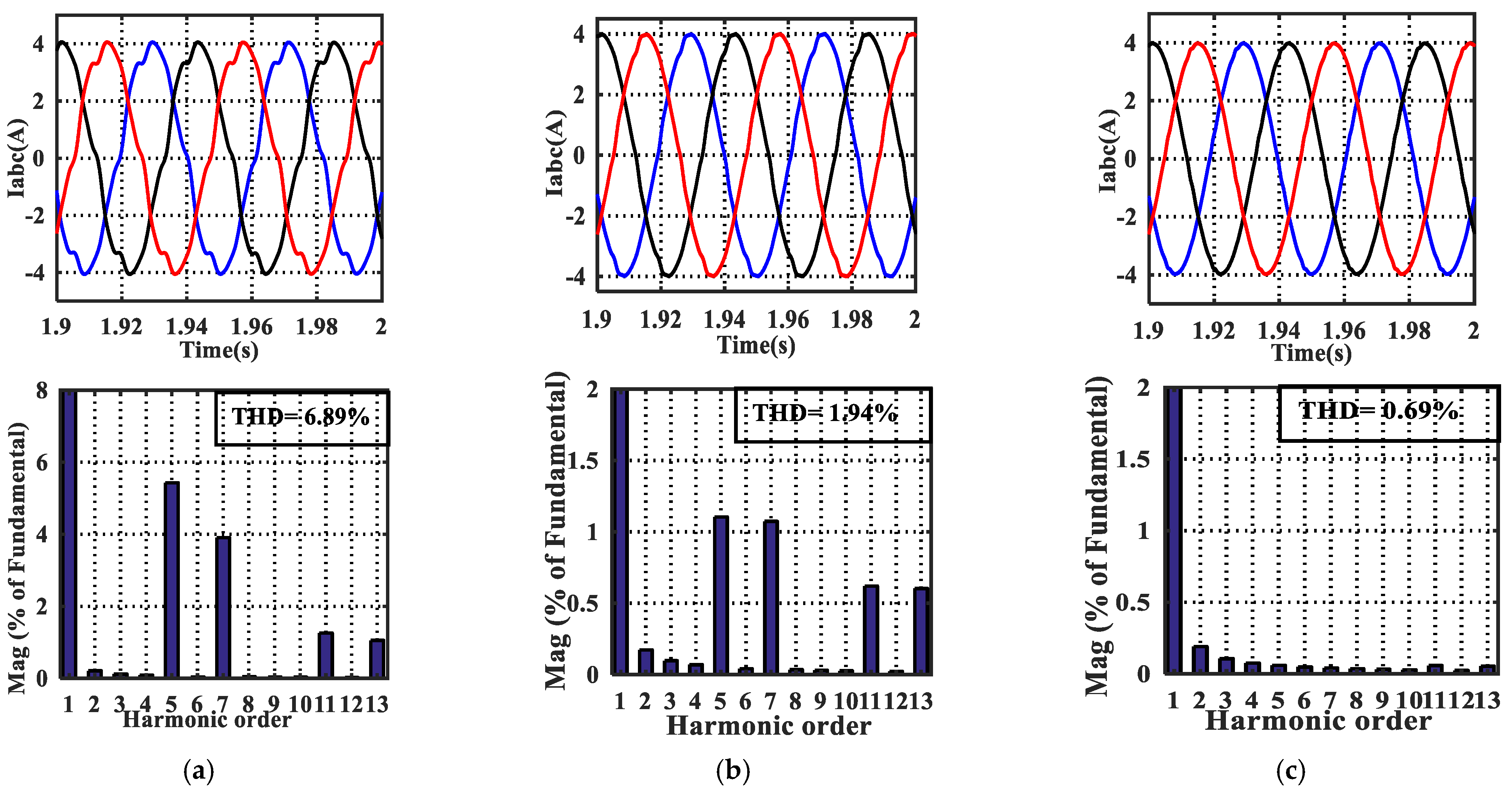
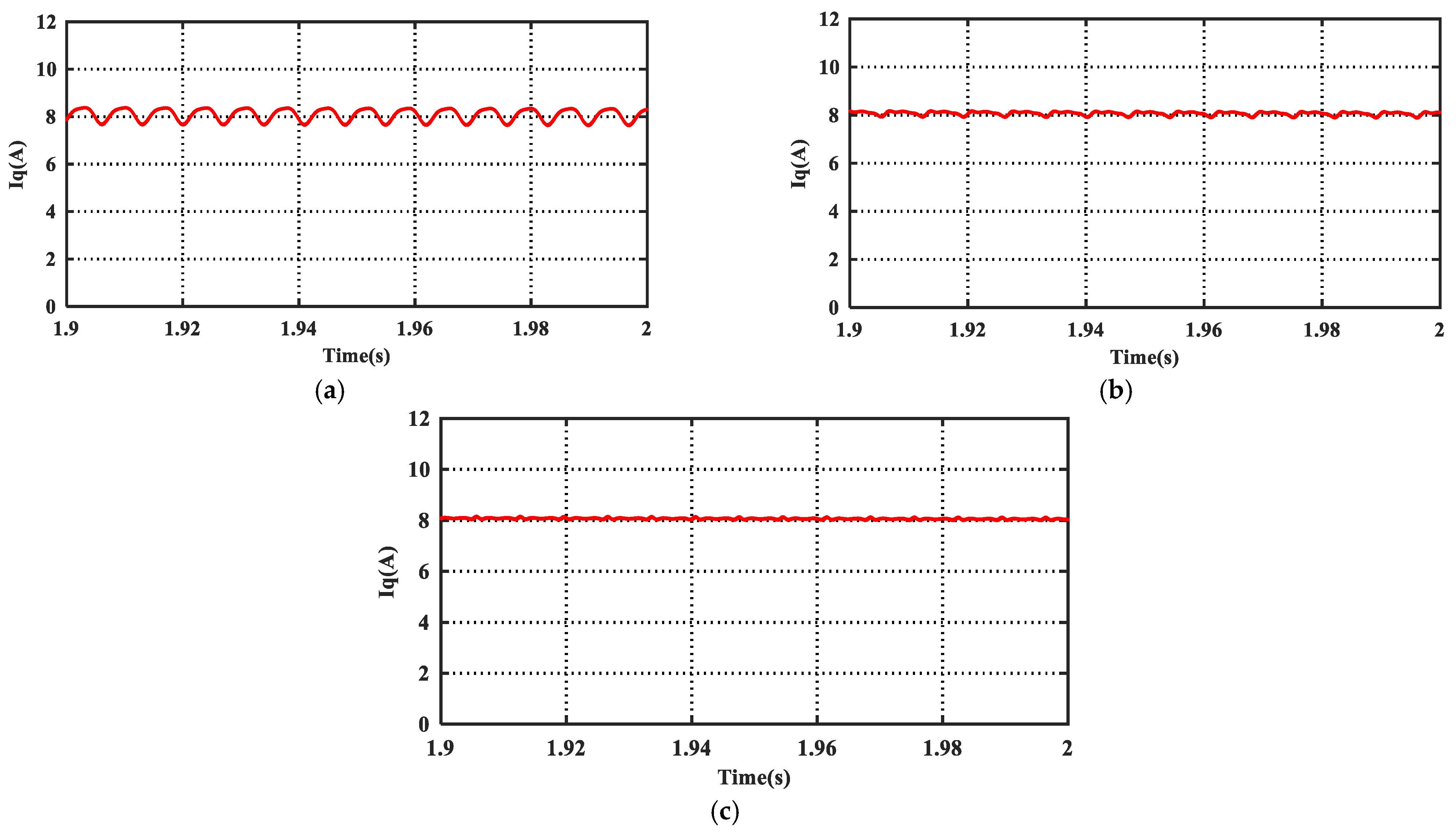
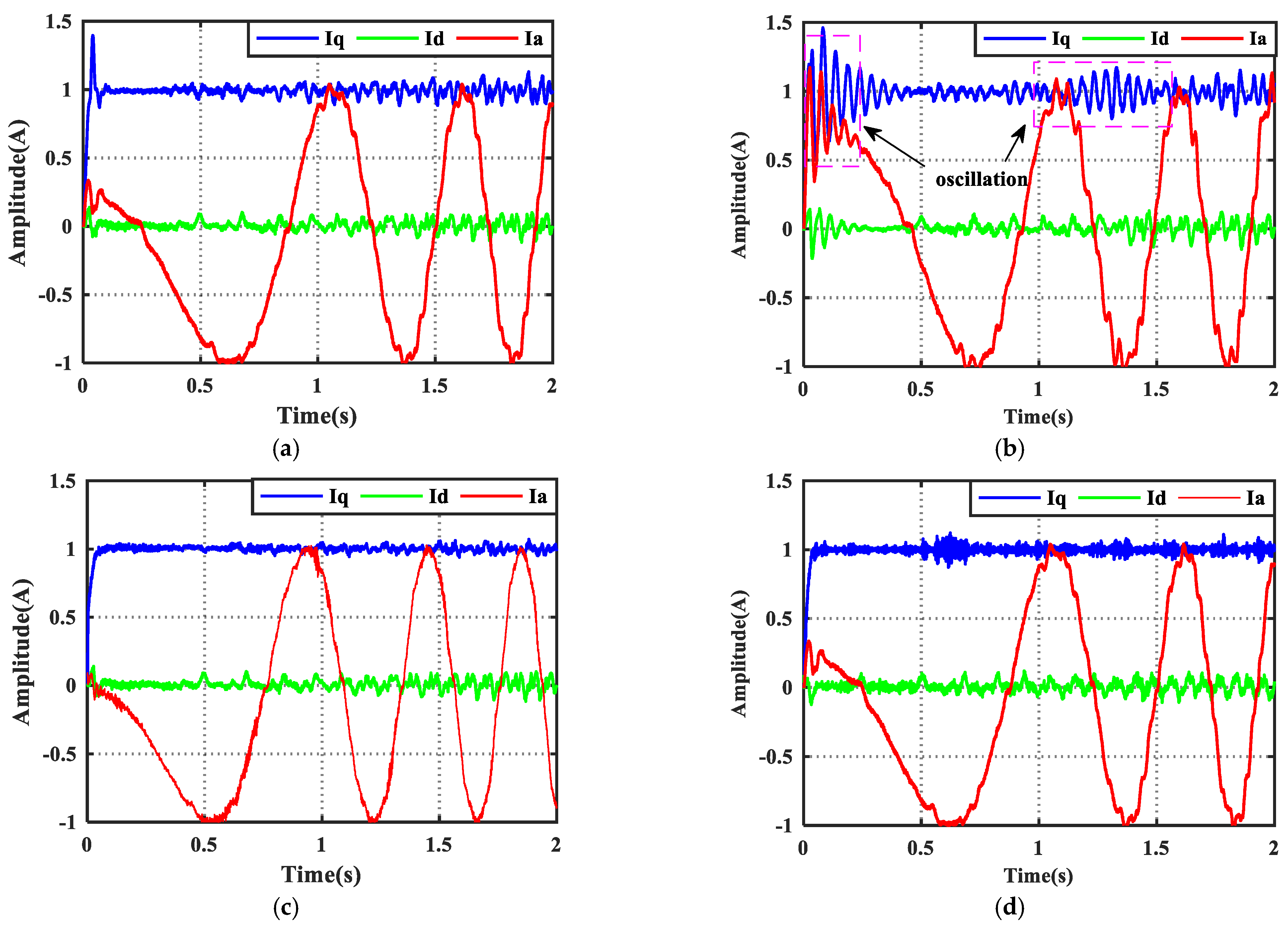
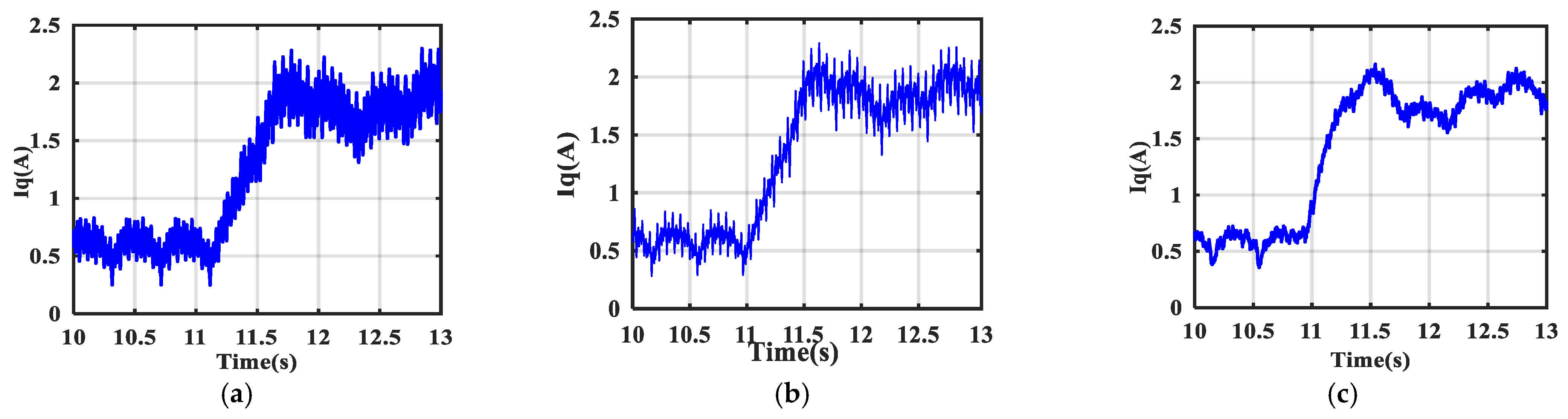
4.1. Simulation Results
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, X.; Sun, J.; Li, H.; Song, X. High performance three-phase PMSM open-phase fault-tolerant method based on reference frame transformation. IEEE Trans. Ind. Electron. 2019, 66, 7571–7580. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.; Xia, M.; Ding, S.; Hua, W. Interturn fault diagnosis for model-predictive-controlled-PMSM based on cost function and wavelet transform. IEEE Trans. Power Electron. 2020, 35, 6405–6418. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, S.; Zhang, C. Enhanced robust deadbeat predictive current control for PMSM drives. IEEE Access. 2019, 7, 148218–148230. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, L.; Zhao, K.; Sun, L. Nonlinear Speed Control for PMSM System Using Sliding-Mode Control and Disturbance Compensation Techniques. IEEE Trans. Power Electron. 2013, 28, 1358–1365. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, J.; Li, H.; Liu, J.; Tian, D. Adaptive sliding mode current control with sliding mode disturbance observer for PMSM drives. ISA Trans. 2019, 88, 113–126. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z. Sliding-mode observer-based mechanical parameter estimation for permanent magnet synchronous motor. IEEE Trans. Power Electron. 2016, 31, 5732–5745. [Google Scholar] [CrossRef]
- Liu, M.; Chan, K.W.; Hu, J.; Xu, W.; Rodriguez, J. Model predictive direct speed control with torque oscillation reduction for PMSM drives. IEEE Trans. Ind. Informat. 2019, 15, 4944–4956. [Google Scholar] [CrossRef]
- Li, J.; Ren, H.; Zhong, Y. Robust Speed Control of Induction Motor Drives Using First-Order Auto-Disturbance Rejection Controllers. IEEE Trans. Ind. Appl. 2015, 51, 712–720. [Google Scholar] [CrossRef]
- Guo, T.; Sun, Z.; Wang, X.; Li, S.; Zhang, K. A simple current-constrained controller for permanent-magnet synchronous motor. IEEE Trans. Ind. Informat. 2019, 15, 1486–1495. [Google Scholar] [CrossRef]
- Dai, C.; Guo, T.; Yang, J.; Li, S. A disturbance observer-based current-constrained controller for speed regulation of PMSM systems subject to unmatched disturbances. IEEE Trans. Ind. Electron. 2021, 68, 767–775. [Google Scholar] [CrossRef]
- Umeno, T.; Hori, Y. Robust DC servosystem design based on the parametrization of two degrees-of-freedom control systems. In Proceedings of the 15th Annual Conference of IEEE Industrial Electronics Society, Philadelphia, PA, USA, 6–10 November 1989; Volume 2, pp. 313–318. [Google Scholar]
- Umeno, T.; Hori, Y. Robust speed control of dc servomotor using modern two degrees-of-freedom controller design. IEEE Trans. Ind. Electron. 1991, 38, 363–368. [Google Scholar] [CrossRef]
- Harnefors, L.; Saarakkala, S.E.; Hinkkanen, M. Speed control of electrical drives using classical control methods. IEEE Trans. Ind Appl. 2013, 49, 889–898. [Google Scholar] [CrossRef]
- Chuen-Gan, W.; Qiu, L. Robust two degree of freedom regulators for velocity ripple elimination of AC permanent magnet motors. In Proceedings of the 2000 IEEE International Conference on Control Applications, Anchorage, AK, USA, 25–27 September 2000; pp. 156–161. [Google Scholar]
- Son, Y.I.; Kim, I.H.; Choi, D.S.; Shim, H. Robust cascade control of electric motor drives using dual reduced-order PI observer. IEEE Trans. Ind. Electron. 2015, 62, 3672–3682. [Google Scholar] [CrossRef]
- Xia, C.; Ji, B.; Shi, T.; Yan, Y. Two-degree-of-freedom proportional integral speed control of electrical drives with Kalman-filter-based speed estimation. IET Electr. Power Appl. 2016, 10, 18–24. [Google Scholar] [CrossRef]
- Mendoza-Mondragón, F.; Hernández-Guzmán, V.M.; Rodríguez-Reséndiz, J. Robust Speed Control of Permanent Magnet Synchronous Motors Using Two-Degrees-of-Freedom Control. IEEE Trans. Ind. Electron. 2018, 65, 6099–6108. [Google Scholar] [CrossRef]
- Fei, Q.; Deng, Y.; Li, H.; Liu, J.; Shao, M. Speed ripple minimization of permanent magnet synchronous motor based on model predictive and iterative learning controls. IEEE Access. 2019, 7, 31791–31800. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Deng, Y. Torque ripple minimization of PMSM based on robust ILC via adaptive sliding mode control. IEEE Trans. Power Electron. 2018, 33, 3655–3671. [Google Scholar] [CrossRef]
- Zhu, Q.; Song, F.; Xu, J.; Liu, Y. An Internal Model Based Iterative Learning Control for Wafer Scanner Systems. IEEE/ASME Trans. Mechatron. 2019, 24, 2073–2084. [Google Scholar] [CrossRef]
- Wang, L.; Freeman, C.T.; Chai, S.; Rogers, E. Predictive-repetitive control with constraints: From design to implementation. J. Process Control. 2013, 23, 956–967. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Kar, N.C. Speed harmonic based decoupled torque ripple minimization control for permanent magnet synchronous machine with minimized loss. IEEE Trans. Energy Convers. 2020, 35, 1796–1805. [Google Scholar] [CrossRef]
- Seifi, K.; Moallem, M. An adaptive PR Controller for synchronizing grid-connected inverters. IEEE Trans. Ind. Electron. 2019, 66, 2034–2043. [Google Scholar] [CrossRef]
- Pang, B.; Nian, H.; Wu, C.; Cheng, P. Stator harmonic current suppression for DFIG system considering integer harmonics and inter harmonics. IEEE Trans. Ind. Electron. 2019, 66, 7001–7011. [Google Scholar] [CrossRef]
- Xia, C.; Ji, B.; Yan, Y. Smooth speed control for low-speed high-torque permanent-magnet synchronous motor using proportional–integral–resonant controller. IEEE Trans. Ind. Electron. 2015, 62, 2123–2134. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, J.; Wang, L.; Li, M.; Hu, Y. Combined vector resonant and active disturbance rejection control for PMSLM current harmonic suppression. IEEE Trans. Ind. Informat. 2020, 16, 5691–5702. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Petras, I.; Xue, D. Fractional order control—A tutorial. In Proceedings of the 2009 American Control Conference (ACC), St. Louis, MO, USA, 10–12 July 2009; pp. 1397–1411. [Google Scholar]
- Malti, R.; Moreau, X.; Khemane, F.; Oustaloup, A. Stability and resonance conditions of elementary fractional transfer functions. Automatica 2011, 47, 2462–2467. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Basit, A.; Ullah, N.; Ro, J.-S. Integral super twisting sliding mode based sensorless predictive torque control of induction motor. IEEE Access. 2020, 8, 186740–186755. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Ullah, N.; Ro, J.-S. Sensorless fractional order composite sliding mode control design for wind generation system. ISA Trans. 2020. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Ali, Z.; Ullah, N.; Ro, J.-S. A super twisting fractional order terminal sliding mode control for DFIG-Based wind energy conversion system. Energies 2020, 13, 2158. [Google Scholar] [CrossRef]
- Araki, M.; Taguchi, H. Two-degree-of-freedom PID controllers. Int. J. Control Autom. Syst. 2003, 1, 401–411. [Google Scholar]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional resonant controllers and filters for grid-connected voltage-source converters. IEEE Proc. Electric Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.; Zhuo, F.; Wang, F. Analysis about overshoot peaks appearing in the current loop with resonant controller. IEEE J. Emerg. Sel. Topics Power Electron. 2016, 4, 26–36. [Google Scholar]
- Li, D.; Iwaji, Y.; Notohara, Y.; Kishita, K. Harmonic Current Cancellation Method for PMSM Drive System using Resonant Controllers. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018—ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 1301–1307. [Google Scholar]
- Li, C.-X.; Gu, G.-Y.; Yang, M.-J.; Zhu, L.-M. High-speed tracking of a nanopositioning stage using modified repetitive control. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1467–1477. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A.; McGrath, B.P.; Kong, W.Y. Optimized design of stationary frame three phase AC current regulators. IEEE Trans. Power Electron. 2009, 24, 2417–2426. [Google Scholar] [CrossRef]
- Elkayam, M.; Kolesnik, S.; Kuperman, A. Guidelines to classical frequency-domain disturbance observer redesign for enhanced rejection of periodic uncertainties and disturbances. IEEE Trans. Power Electron. 2019, 34, 3986–3995. [Google Scholar] [CrossRef]







| Symbol | Quantity | Value |
|---|---|---|
| L | d–q frame inductance | 0.0085 H |
| R | Armature resistance | 0.569 Ω |
| P | Number of pole pairs | 3 |
| F | Flux linkage | 0.00175 Wb |
| J | Inertia | 0.0012 kg·m2 |
| Robust-TDOFR | |||||||
| 0.0006 | 0.028 | 0.0085 | 0.569 | 20 | 15 | 0.3 | |
| PI-R | |||||||
| 0.3 | 20 | 20 | 20 | 15 | |||
| Harmonic Order | Fifth | Seventh | Eleventh | Thirteenth | THD (%) | |
|---|---|---|---|---|---|---|
| PI | Amplitude (A) | 0.22 | 0.002 | 0.049 | 0.042 | 6.89 |
| PIR | 0.044 | 0.042 | 0.0244 | 0.0238 | 1.94 | |
| Robust-TDOFR | 0.0023 | 0.0016 | 0.0022 | 0.0021 | 0.69 | |
| Harmonic Order | Fifth | Seventh | Eleventh | Thirteenth | THD (%) | |
|---|---|---|---|---|---|---|
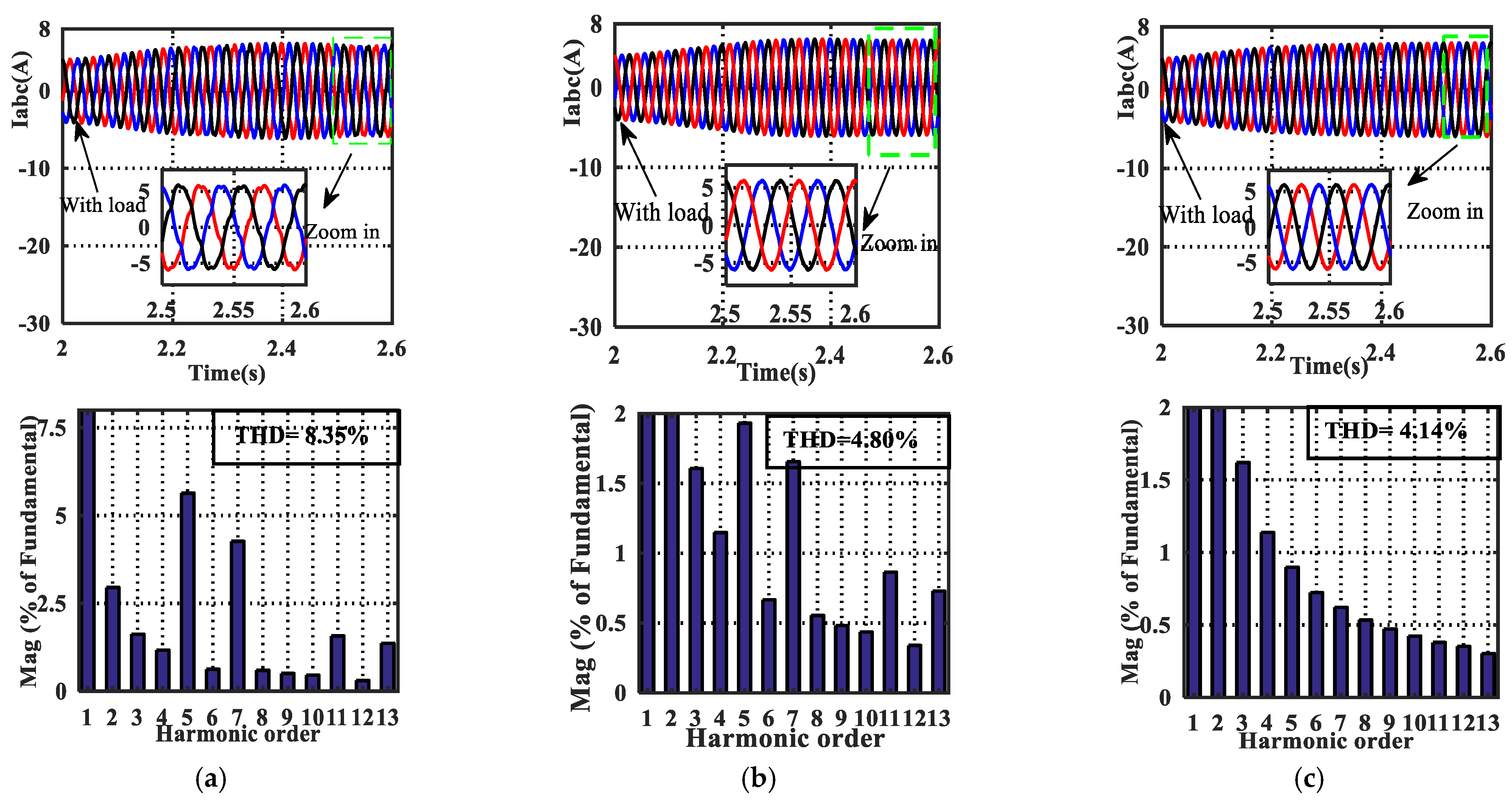
| PI | Amplitude (A) | 0.33 | 0.25 | 0.092 | 0.079 | 8.35 |
| PIR | 0.115 | 0.098 | 0.051 | 0.0238 | 4.80 | |
| Robust-TDOFR | 0.053 | 0.037 | 0.022 | 0.017 | 4.14 | |
| Harmonic Order | Fifth | Seventh | Eleventh | Thirteenth | THD (%) | |
|---|---|---|---|---|---|---|
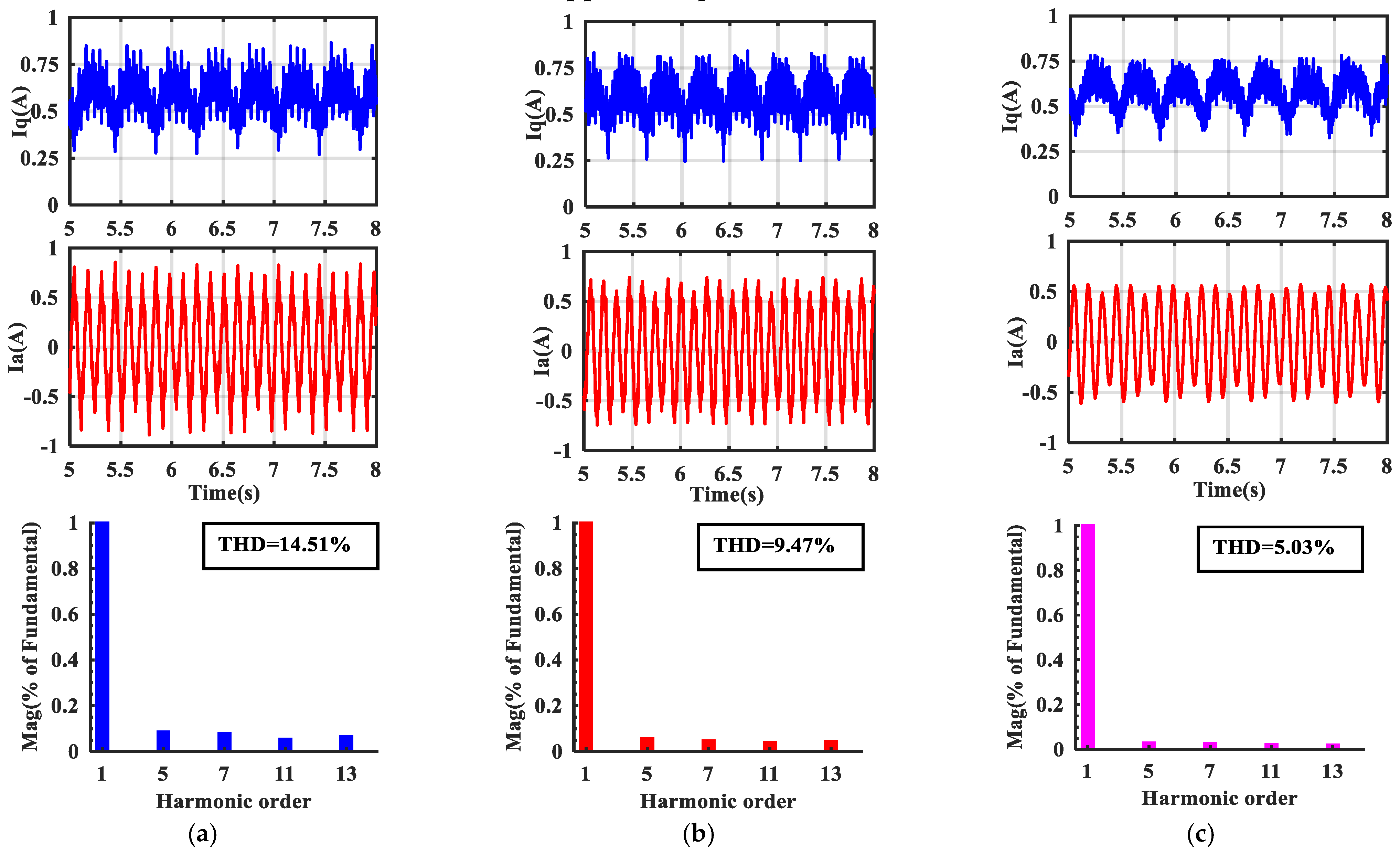
| PI | Amplitude (A) | 0.037 | 0.033 | 0.023 | 0.028 | 14. 51 |
| PIR | 0.018 | 0.0148 | 0.012 | 0.014 | 9.47 | |
| Robust-TDOFR | 0.0075 | 0.0072 | 0.006 | 0.0052 | 5.03 | |
| Harmonic Order | Fifth | Seventh | Eleventh | Thirteenth | THD (%) | |
|---|---|---|---|---|---|---|
| PI | Amplitude (A) | 0.048 | 0.042 | 0.033 | 0.031 | 18. 67 |
| PIR | 0.020 | 0.0152 | 0.0125 | 0.0155 | 10.16 | |
| Robust-TDOFR | 0.0086 | 0.00817 | 0.0069 | 0.00618 | 5.79 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Deng, Y.; Li, H.; Liu, J.; Shao, M.; Fei, Q. Torque Ripple Suppression of PMSM Based on Robust Two Degrees-of-Freedom Resonant Controller. Energies 2021, 14, 1015. https://doi.org/10.3390/en14041015
Huang M, Deng Y, Li H, Liu J, Shao M, Fei Q. Torque Ripple Suppression of PMSM Based on Robust Two Degrees-of-Freedom Resonant Controller. Energies. 2021; 14(4):1015. https://doi.org/10.3390/en14041015
Chicago/Turabian StyleHuang, Mingfei, Yongting Deng, Hongwen Li, Jing Liu, Meng Shao, and Qiang Fei. 2021. "Torque Ripple Suppression of PMSM Based on Robust Two Degrees-of-Freedom Resonant Controller" Energies 14, no. 4: 1015. https://doi.org/10.3390/en14041015







