Development of a Two-Stage DQFM to Improve Efficiency of Single- and Multi-Hazard Risk Quantification for Nuclear Facilities
Abstract
:1. Introduction
2. Direct Quantification of Fault Tree Using MCS (DQFM)
2.1. Basic Ideas of DQFM
2.2. Computational Cost of the Conventional DQFM
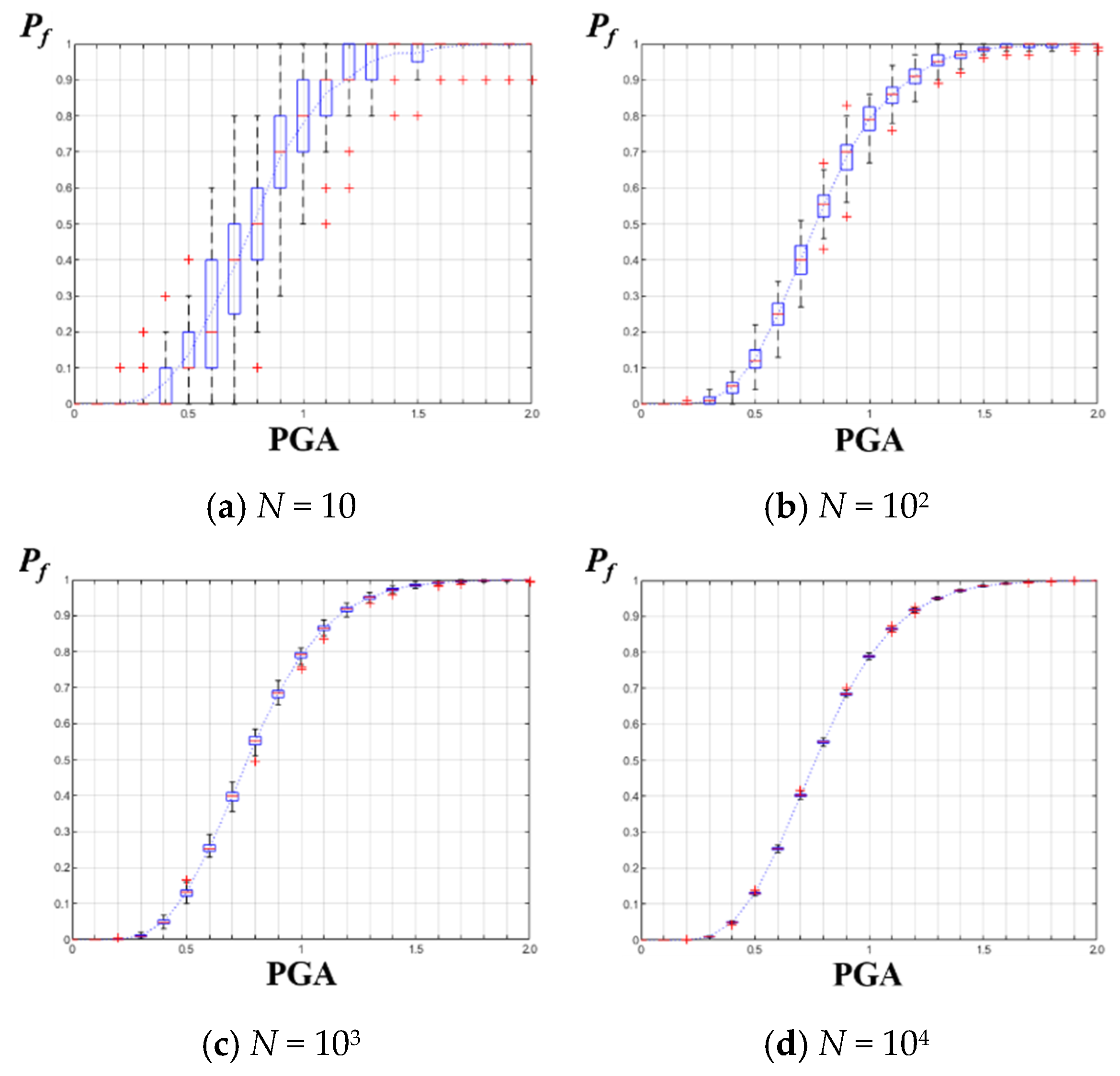
2.3. Performance of the Conventional DQFM
3. Development of Two-Stage DQFM for Single- and Multi-Hazard Risk Quantification
3.1. Sorting Hazard Points
3.2. Evaluating Cumulative Rates
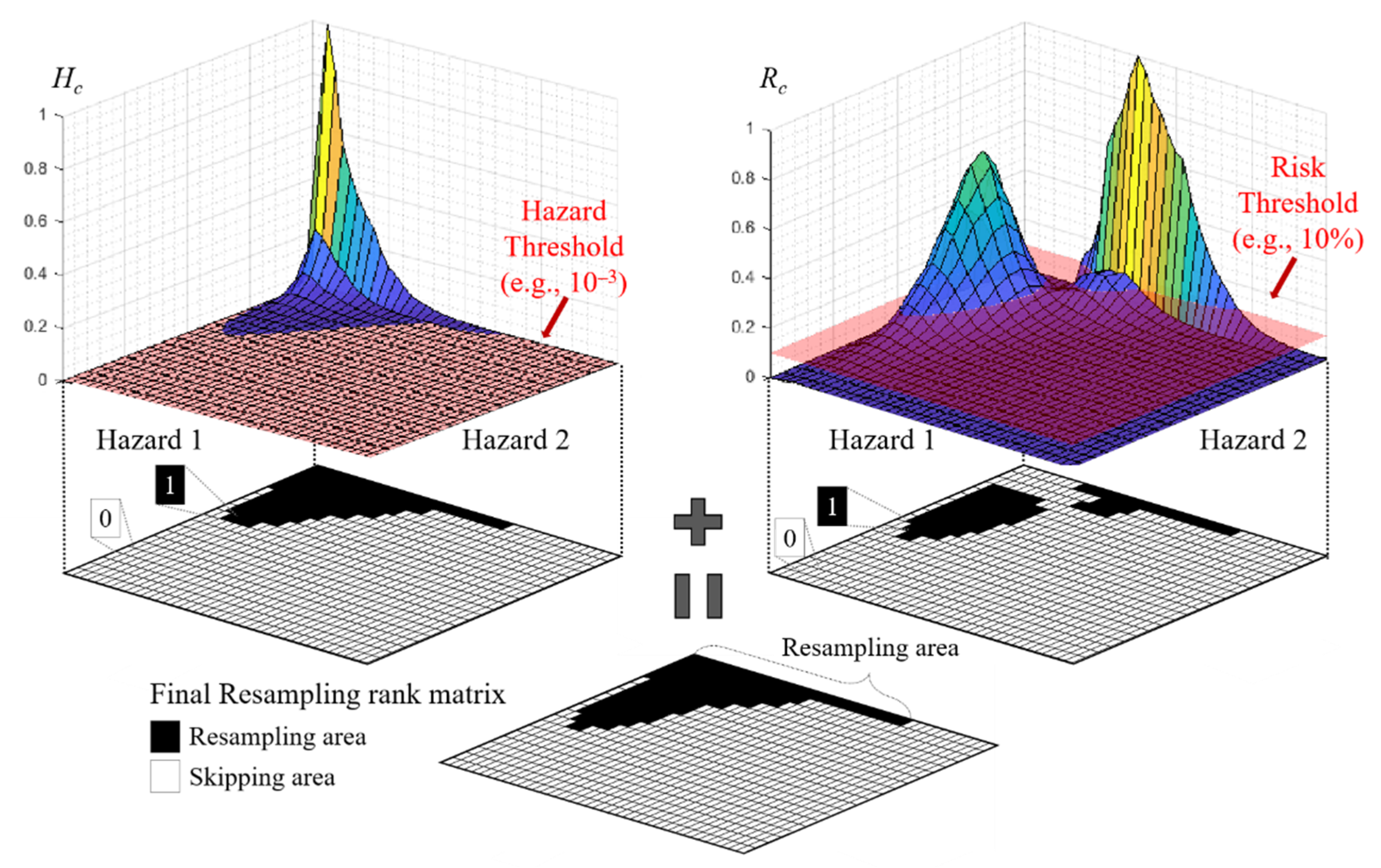
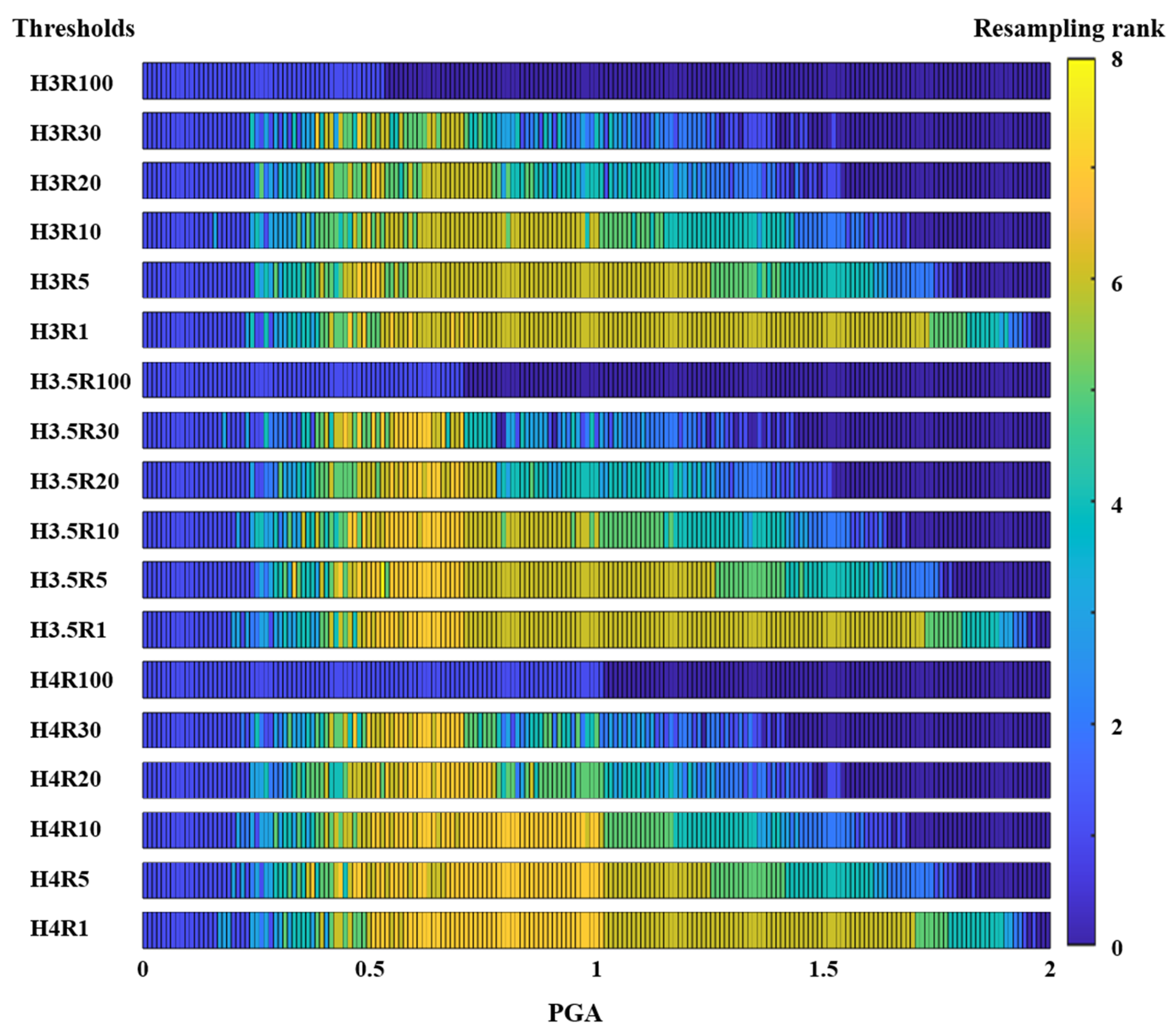
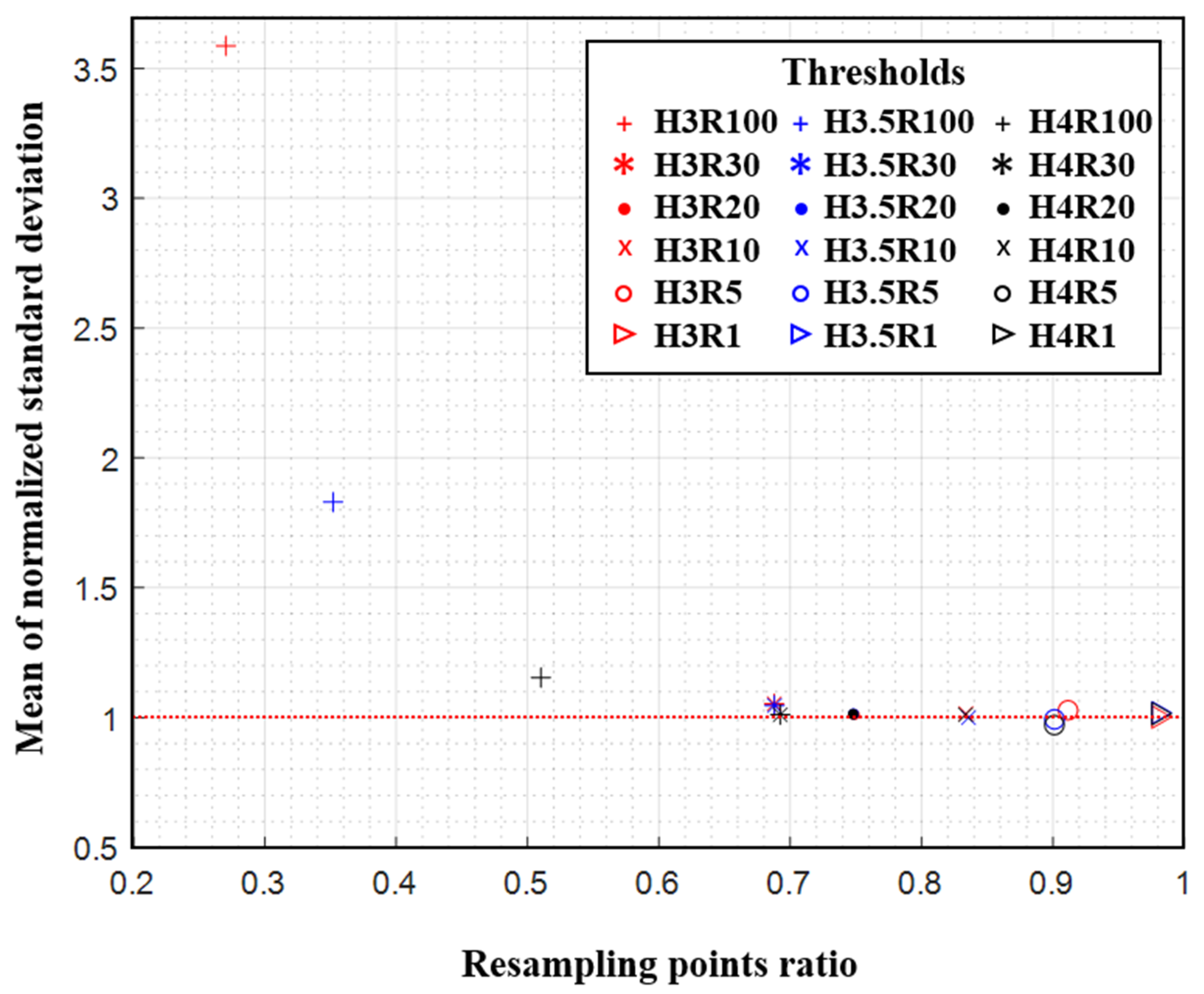
3.3. Selecting Threshold Values and Assigning the Resampling Rank
4. Single Hazard Example: Seismic Hazard
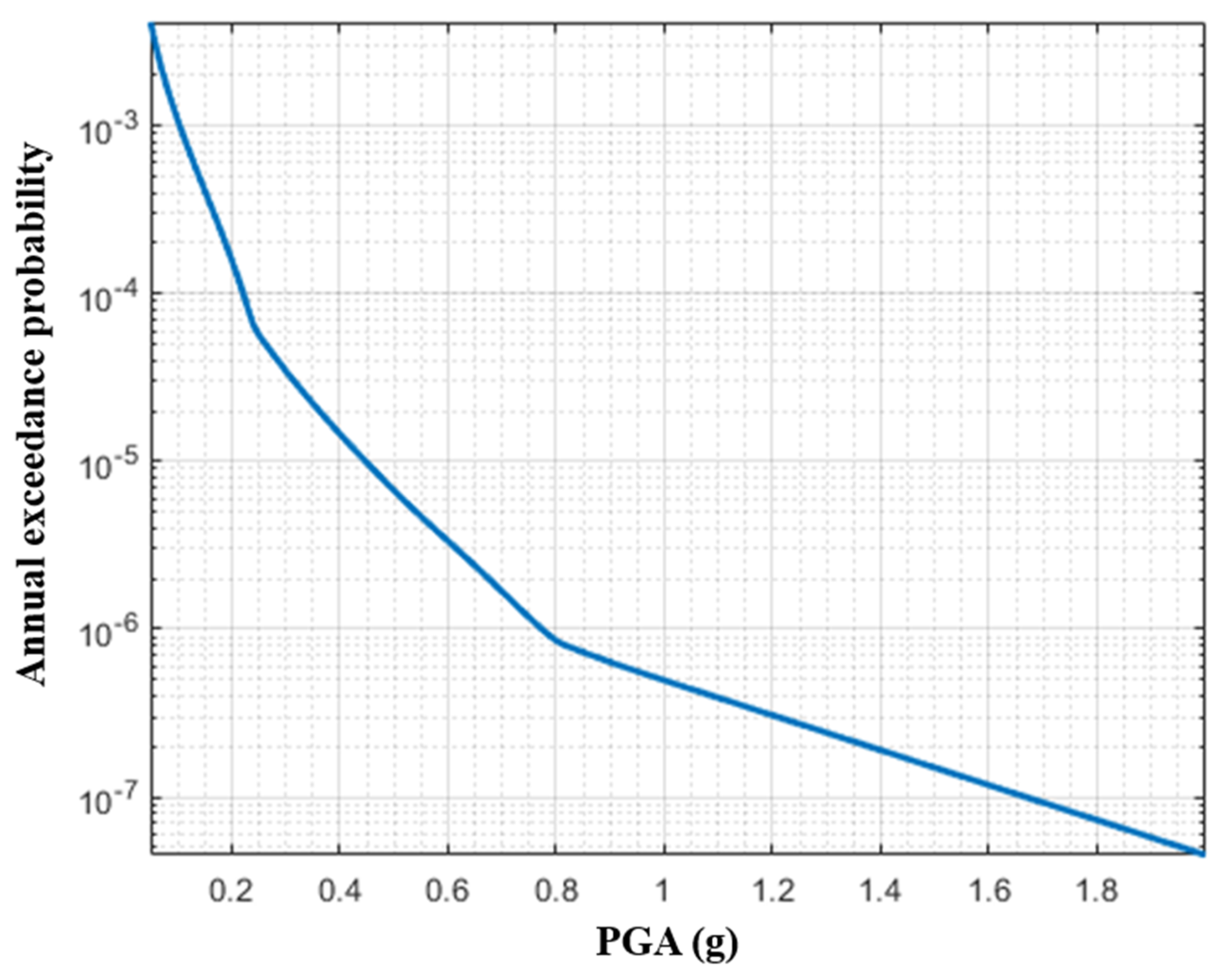
4.1. Setting the Problem
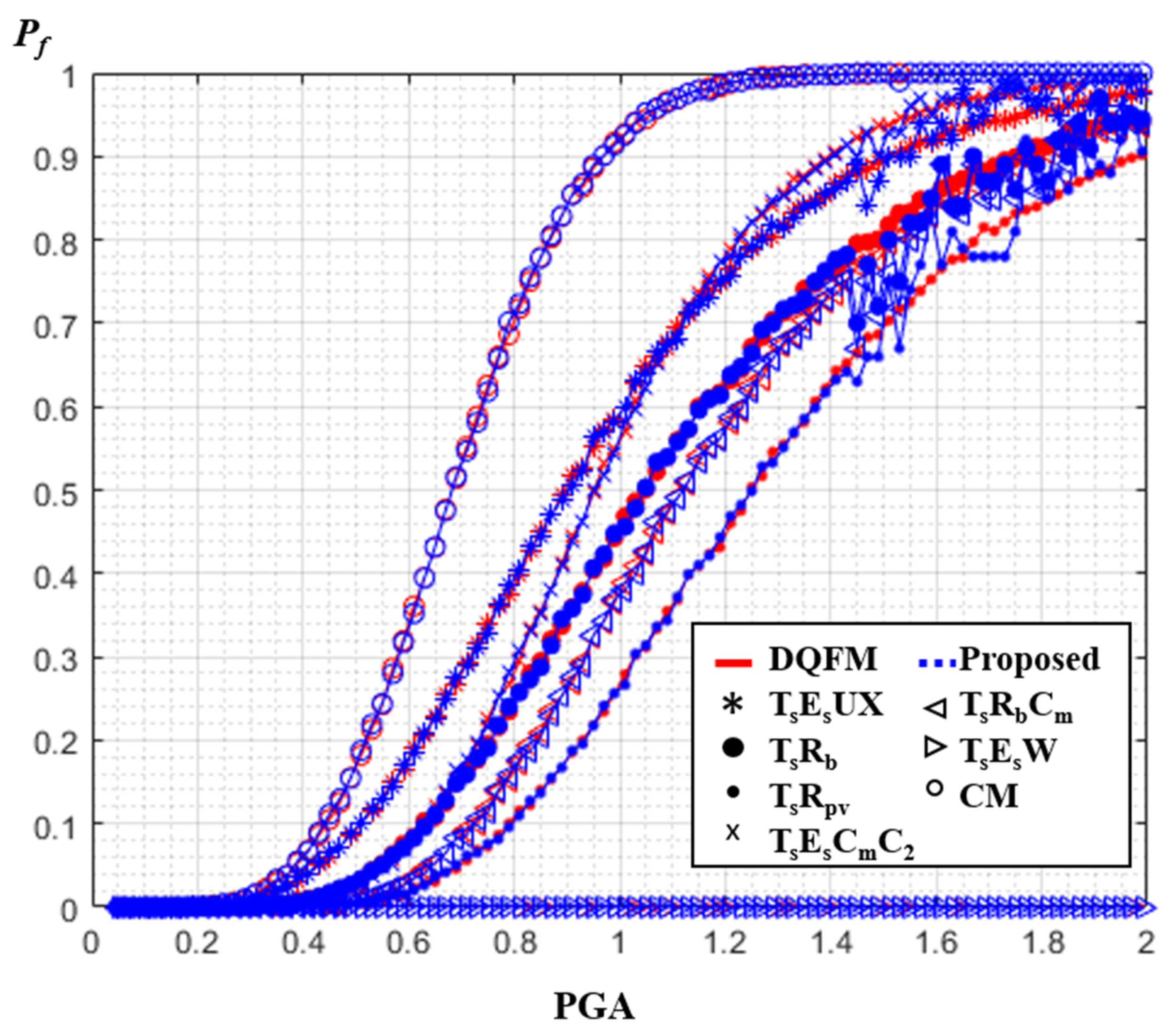
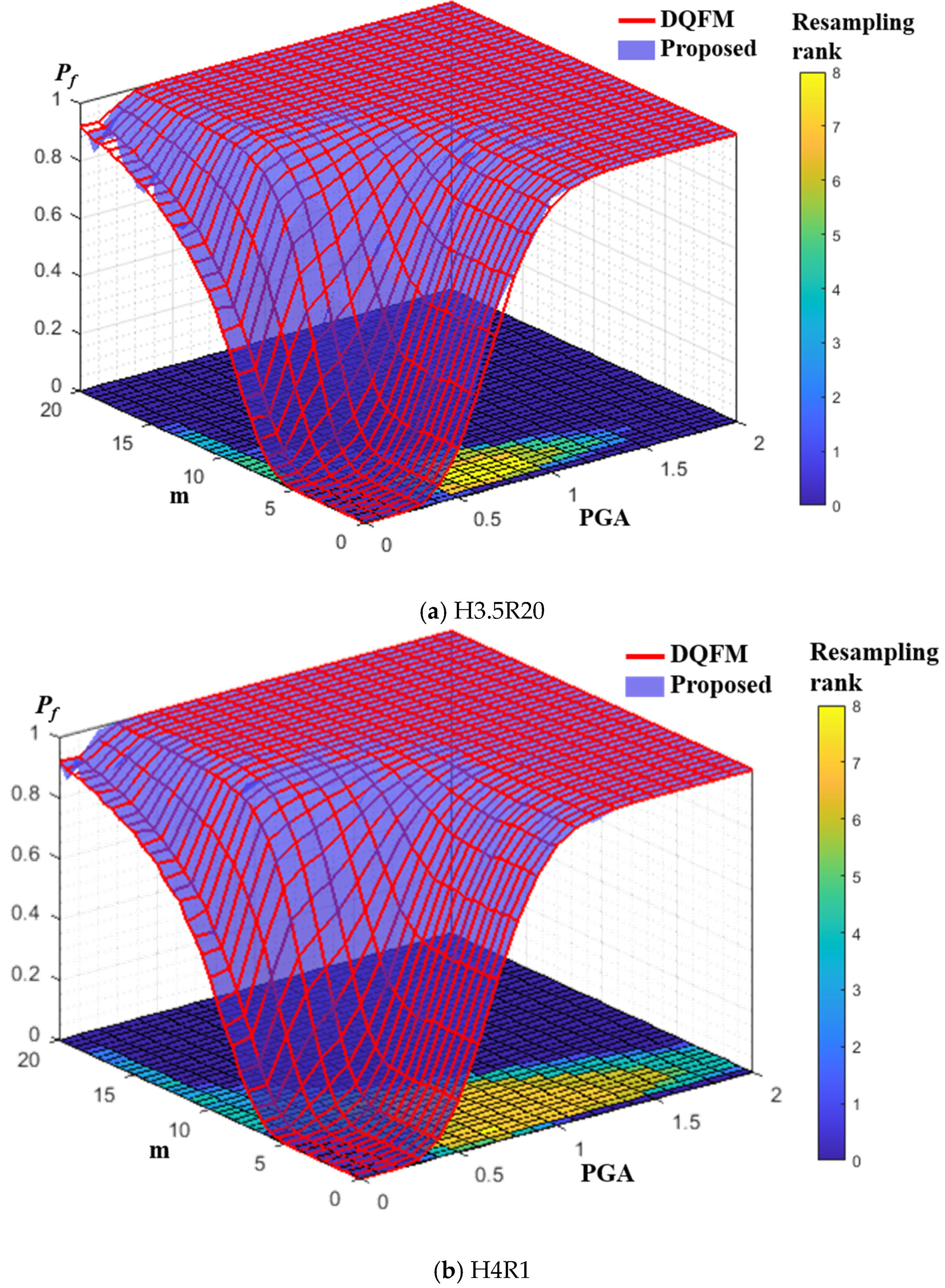
4.2. Results and Discussion
5. Multi-Hazard Example: Earthquake and Tsunami
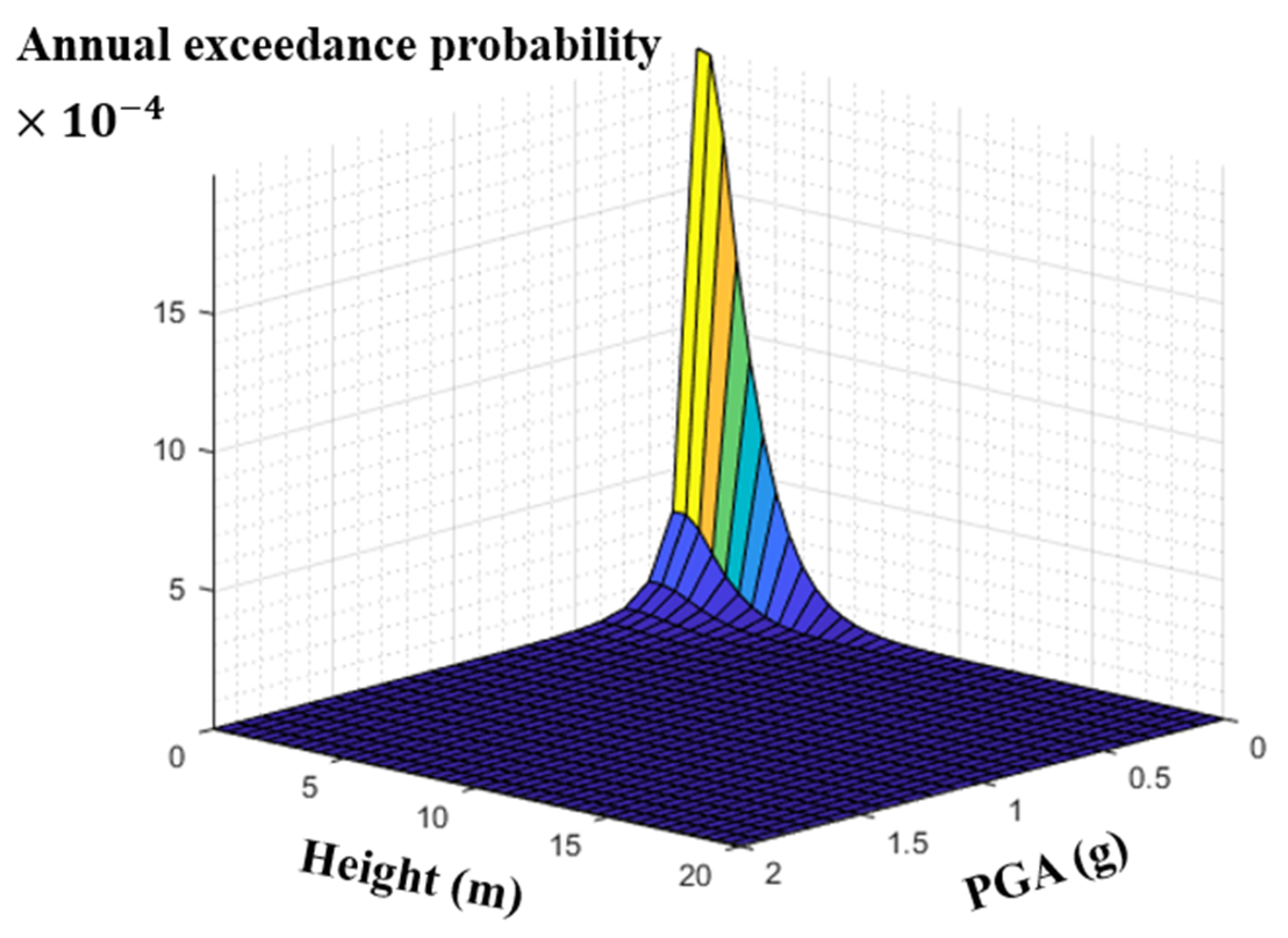
5.1. Setting the Problem
5.2. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, J.E. Fukushima Dai-Ichi accident: Lessons learned and future actions from the risk perspectives. Nucl. Eng. Technol. 2014, 46, 27–38. [Google Scholar] [CrossRef] [Green Version]
- Tsuboi, S.; Mine, T.; Kanke, S.; Ohira, T. Who needs care? The long-term trends and geographical distribution of deaths due to acute myocardial infarction in Fukushima Prefecture following the Great East Japan Earthquake. Int. J. Disaster Risk Reduct. 2019, 41, 101318. [Google Scholar] [CrossRef]
- Choi, E.; Ha, J.; Hahm, D.; Kim, M. A Review of Multihazard Risk Assessment: Progress, Potential, and Challenges in the Application to Nuclear Power Plants. Int. J. Disaster Risk Reduct. 2020, 101933. [Google Scholar] [CrossRef]
- Ebisawa, K.; Fujita, M.; Iwabuchi, Y.; Sugino, H. Current issues on PRA regarding seismic and tsunami events at multi units and sites based on lessons learned from Tohoku earthquake/tsunami. Nucl. Eng. Technol. 2012, 44, 437–452. [Google Scholar] [CrossRef]
- Reed, J.W.; Kennedy, R.P. Methodology for Developing Seismic Fragilities; EPRI TR-103959; Electric Power Research Institute: Palo Alto, CA, USA, 1994. [Google Scholar]
- Hur, J.; Shafieezadeh, A. Multi-hazard probabilistic risk analysis of off-site overhead transmission systems. In Proceedings of the 25th Conference on Structural Mechanics in Reactor Technology, SMiRT25, Charlotte, NC, USA, 4–9 August 2019. [Google Scholar]
- Mun, C.U. Bayesian Network for Structures Subjected to Sequence of Main and Aftershocks. Master’s Thesis, Seoul National University, Seoul, Korea, 2019. [Google Scholar]
- Ryu, H.; Luco, N.; Uma, S.R.; Liel, A.B. Developing fragilities for mainshock-damaged structures through incremental dynamic analysis. In Proceedings of the Ninth Pacific Conference on Earthquake Engineering, Auckland, New Zealand, 14–16 April 2011. [Google Scholar]
- Salman, A.M.; Li, Y. A probabilistic framework for multi-hazard risk mitigation for electric power transmission systems subjected to seismic and hurricane hazards. Struct. Infrastruct. Eng. 2018, 14, 1499–1519. [Google Scholar] [CrossRef]
- Prabhu, S.; Javanbarg, M.; Lehmann, M.; Atamturktur, S. Multi-peril risk assessment for business downtime of industrial facilities. Nat. Hazards 2019, 97, 1327–1356. [Google Scholar] [CrossRef]
- Prabhu, S.; Ehrett, C.; Javanbarg, M.; Brown, D.A.; Lehmann, M.; Atamturktur, S. Uncertainty Quantification in Fault Tree Analysis: Estimating Business Interruption due to Seismic Hazard. Nat. Hazards Rev. 2020, 21, 04020015. [Google Scholar] [CrossRef]
- Leverenz, F.L.; Kirch, H. User’s Guide for the WAM-BAM Computer Code; No. PB--249624; Science Applications. Inc.: Palo Alto, CA, USA, 1976. [Google Scholar]
- Bohn, M.P.; Shieh, L.C.; Wells, J.E. Application of the SSMRP Methodology to the Seismic Risk at the Zion Nuclear Power Plant; No. NUREG/CR—3428; Lawrence Livermore National Lab.: Fermore, CA, USA, 1983. [Google Scholar]
- Watanabe, Y.; Oikawa, T.; Muramatsu, K. Development of the DQFM method to consider the effect of correlation of component failures in seismic PSA of nuclear power plant. Reliab. Eng. Syst. Saf. 2003, 79, 265–279. [Google Scholar] [CrossRef]
- Li, J. Fault-Event Trees Based Probabilistic Safety Analysis of a Boiling Water Nuclear Reactor’s Core Meltdown and Minor Damage Frequencies. Safety 2020, 6, 28. [Google Scholar] [CrossRef]
- EPRI. Seismic Fragility Application Guide; TR-1002988; Electric Power Research Institute: Palo Alto, CA., USA, 2002. [Google Scholar]
- Kim, J.H.; Choi, I.-K.; Park, J.-H. Uncertainty analysis of system fragility for seismic safety evaluation of NPP. Nucl. Eng. Design 2011, 241, 2570–2579. [Google Scholar] [CrossRef]
- Kwag, S.; Oh, J.; Lee, J.M.; Ryu, J.S. Bayesian based seismic margin assessment approach: Application to research reactor system. Earthq. Struct. 2017, 12, 653–663. [Google Scholar]
- Zhou, T.; Modarres, M.; Droguett, E.L. Issues in dependency modeling in multi-unit seismic PRA. In Proceedings of the International Topical Meeting on Probabilistic Safety Assessment (PSA 2017), American Nuclear Society, Pittsburgh, PA, USA, 24–28 September 2017. [Google Scholar]
- Budnitz, R.J.; Hardy, G.S.; Moore, D.L.; Ravindra, M.K. Correlation of Seismic Performance in Similar SSCs (Structures, Systems, and Components); No. NUREG/CR-7237; US Nuclear Regulatory Commission: Rockville, MD, USA, 2017. [Google Scholar]
- Kaplan, S. A Method for handling dependency and partial dependency of fragility curve in seismic risk quantification. In Transactions SMiRT 8 Int. Conf.; IASMiRT: Brussels, Belgium, 1985; Volume M, pp. 595–600. [Google Scholar]
- Kim, J.H.; Kim, S.Y.; Choi, I.K. Combination Procedure for Seismic Correlation Coefficient in Fragility Curves of Multiple Components. J. Earthq. Eng. Soc. Korea 2020, 24, 141–148. [Google Scholar] [CrossRef]
- Kwag, S.; Ha, J.G.; Kim, M.K.; Kim, J.H. Development of Efficient External Multi-Hazard Risk Quantification Methodology for Nuclear Facilities. Energies 2019, 12, 3925. [Google Scholar] [CrossRef] [Green Version]
- Kwag, S.; Eemb, S.; Choi, E.; Ha, J.G.; Hahm, D. Toward Improvement of Sampling-based Seismic Probabilistic Safety Assessment Method for Nuclear Facilities. Reliab. Eng. Syst. Saf. Under review.
- Aksoy, A.; Martelli, M. Mixed partial derivatives and Fubini’s theorem. Coll. Math. J. 2002, 33, 126–130. [Google Scholar] [CrossRef]
- Ellingwood, B. Validation studies of seismic PRAs. Nucl. Eng. Des. 1990, 123, 189–196. [Google Scholar] [CrossRef]
- Choi, E.; Song, J. Cost-effective retrofits of power grids based on critical cascading failure scenarios identified by multi-group non-dominated sorting genetic algorithm. Int. J. Disaster Risk Reduct. 2020, 49, 101640. [Google Scholar] [CrossRef]
- Kwag, S.; Hahm, D. Multi-objective-based seismic fragility relocation for a Korean nuclear power plant. Nat. Hazards 2020, 103, 3633–3659. [Google Scholar] [CrossRef]
- KAERI. Development of Site Risk Assessment & Management Technology including Extreme External Events; KAERI/RR-4225/2016; Korea Atomic Energy Research Institute: Daejeon, Korea, 2017. [Google Scholar]







| Component | Rms (Ams) | βRcs | ΒCcs | Mean Failure Rate (Per year) | |
|---|---|---|---|---|---|
| S1 | Offsite power | 0.20 g | 0.226 | 0.226 | - |
| S2 | Condensate storage tank | 0.24 g | 0.273 | 0.273 | - |
| S3 | Reactor internals | 0.67 g | 0.300 | 0.300 | - |
| S4 | Reactor enclosure structure | 1.05 g | 0.282 | 0.282 | - |
| S6 | Reactor pressure vessel | 1.25 g | 0.252 | 0.252 | - |
| S10 | Standby liquid control system tank | 1.33 g | 0.233 | 0.233 | - |
| S11 | 440 V bus/steam generator breakers | 1.46 g | 0.411 | 0.411 | - |
| S12 | 440 V bus transformer breaker | 1.49 g | 0.397 | 0.397 | - |
| S13 | 125/250-V DC bus | 1.49 g | 0.397 | 0.397 | - |
| S14 | 4 kV bus/steam generator | 1.49 g | 0.397 | 0.397 | - |
| S15 | Diesel generator circuit | 1.56 g | 0.368 | 0.368 | - |
| S16 | Diesel generator heat and vent | 1.55 g | 0.363 | 0.363 | - |
| S17 | Residual heat removal system heat exchangers | 1.09 g | 0.330 | 0.330 | - |
| DGR | DGR—diesel generator common mode | - | - | - | 0.00125 |
| WR | WR—containment heat removal | - | - | - | 0.00026 |
| CR | CR—scram system mechanical failure | - | - | - | 1.00 × 105 |
| SLCR | SLCR—standby liquid control | - | - | - | 0.01 |
| System Failure Scenario | DQFM | Two-stage DQFM * | ||
|---|---|---|---|---|
| μ | σ | μ | σ | |
| TsEsUX | 2.57 × 106 | 2.16 × 108 | 2.57 × 106 | 1.95 × 108 |
| TsRb | 1.14 × 106 | 6.31 × 109 | 1.14 × 106 | 6.33 × 109 |
| TsRpv | 4.96 × 107 | 2.01 × 109 | 4.94 × 107 | 2.22 × 109 |
| TsEsCmC2 | 1.17 × 106 | 7.29 × 109 | 1.17 × 106 | 7.32 × 109 |
| TsRbCm | 6.65 × 107 | 2.46 × 109 | 6.64 × 107 | 2.52 × 109 |
| TsEsWm | 1.13 × 107 | 3.79 × 108 | 1.15 × 107 | 3.80 × 108 |
| CM | 4.32 × 106 | 4.34 × 108 | 4.32 × 106 | 4.41 × 108 |
| Average Ns ** | 196 × 2 × 104 | First stage Second stage Total | 196.00 × 2 × 102 135.71 × 2 × 104 137.67 × 2 × 104 | |
| Total computation time | 529.0 s | 424.5 s | ||
| Component | Rmt (Amt) | βRct | ΒCct | |
|---|---|---|---|---|
| S1 | Offsite power | 10 m | 0.354 | 0.354 |
| S2 | Condensate storage tank | 10 m | 0.212 | 0.212 |
| S11 | 440 V bus/SG * breakers | 11 m | 0.212 | 0.212 |
| S12 | 440 V bus transformer breaker | 11 m | 0.212 | 0.212 |
| S13 | 125/250 V DC ** bus | 11 m | 0.212 | 0.212 |
| S14 | 4 kV bus/SG | 11 m | 0.212 | 0.212 |
| S15 | Diesel generator circuit | 11 m | 0.212 | 0.212 |
| S17 | RHR *** heat exchangers | 10 m | 0.212 | 0.212 |
| System Failure Scenario | DQFM | Two-Stage DQFM * | ||
|---|---|---|---|---|
| μ | σ | μ | σ | |
| TsEsUX | 5.53 × 106 | 3.62 × 108 | 5.53 × 106 | 3.67 × 108 |
| TsRb | 1.04 × 106 | 5.84 × 109 | 1.04 × 106 | 5.65 × 109 |
| TsRpv | 4.10 × 107 | 2.24 × 109 | 4.10 × 107 | 2.41 × 109 |
| TsEsCmC2 | 1.10 × 106 | 6.71 × 109 | 1.10 × 106 | 6.92 × 109 |
| TsRbCm | 5.83 × 107 | 2.73 × 109 | 5.83 × 107 | 2.82 × 109 |
| TsEsWm | 8.51 × 107 | 2.84 × 108 | 8.50 × 107 | 2.83 × 108 |
| CM | 8.20 × 106 | 4.63 × 108 | 8.21 × 106 | 4.72 × 108 |
| Average Ns ** | 861 × 4 × 1× 104 | First stage Second stage Total | 861.00 × 4 × 102 175.47 × 4 × 104 184.08 × 4 × 104 | |
| Total computation time | 3128.5 s | 862.9 s | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, E.; Kwag, S.; Ha, J.-G.; Hahm, D. Development of a Two-Stage DQFM to Improve Efficiency of Single- and Multi-Hazard Risk Quantification for Nuclear Facilities. Energies 2021, 14, 1017. https://doi.org/10.3390/en14041017
Choi E, Kwag S, Ha J-G, Hahm D. Development of a Two-Stage DQFM to Improve Efficiency of Single- and Multi-Hazard Risk Quantification for Nuclear Facilities. Energies. 2021; 14(4):1017. https://doi.org/10.3390/en14041017
Chicago/Turabian StyleChoi, Eujeong, Shinyoung Kwag, Jeong-Gon Ha, and Daegi Hahm. 2021. "Development of a Two-Stage DQFM to Improve Efficiency of Single- and Multi-Hazard Risk Quantification for Nuclear Facilities" Energies 14, no. 4: 1017. https://doi.org/10.3390/en14041017






