A Novel Iron Chloride Red-Ox Concentration Flow Cell Battery (ICFB) Concept; Power and Electrode Optimization
Abstract
1. Introduction
1.1. Redox Cells vs. Concentration Cells
1.2. Problem Formulation
2. Theory
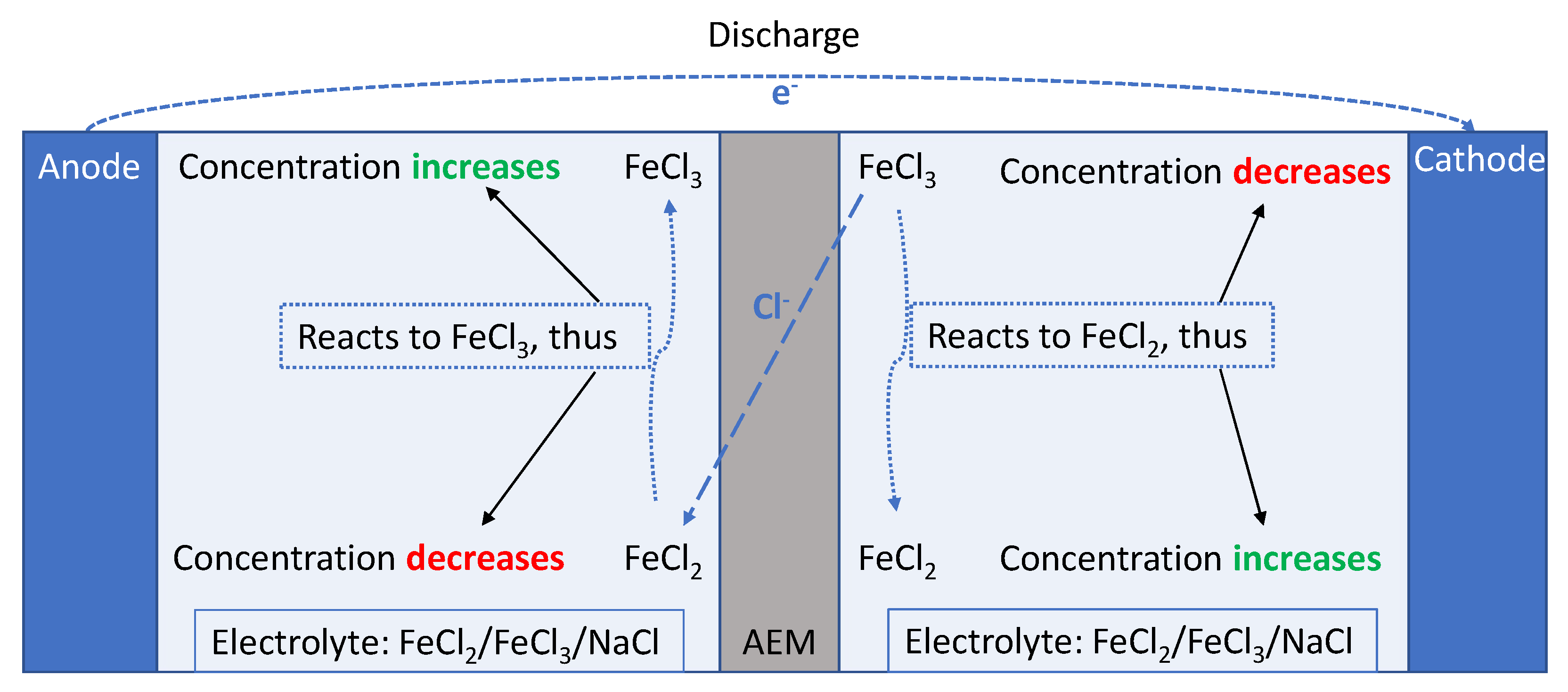
2.1. Cell Description, at Discharge
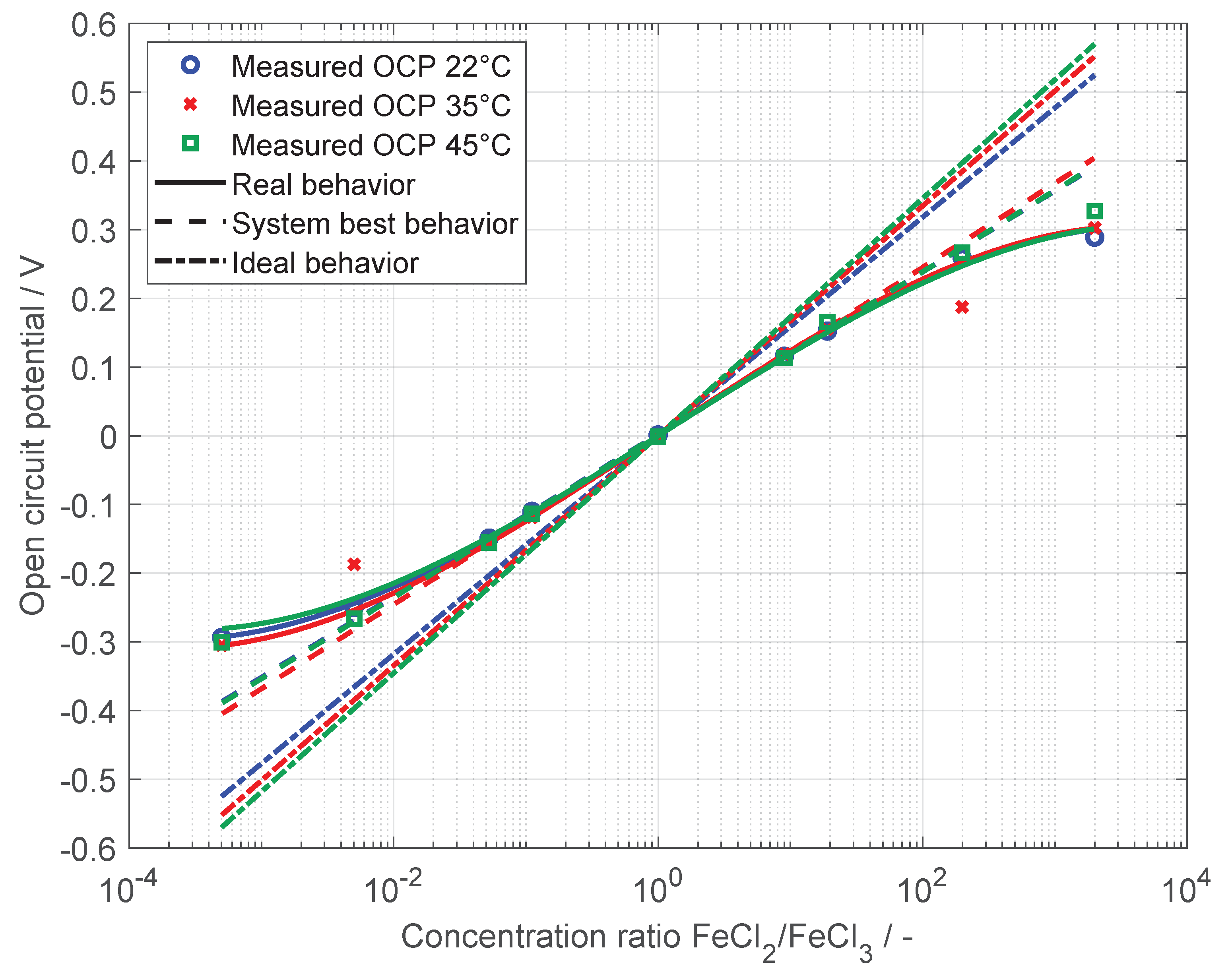
Reversible Reduction Potential
2.2. Membrane Potential
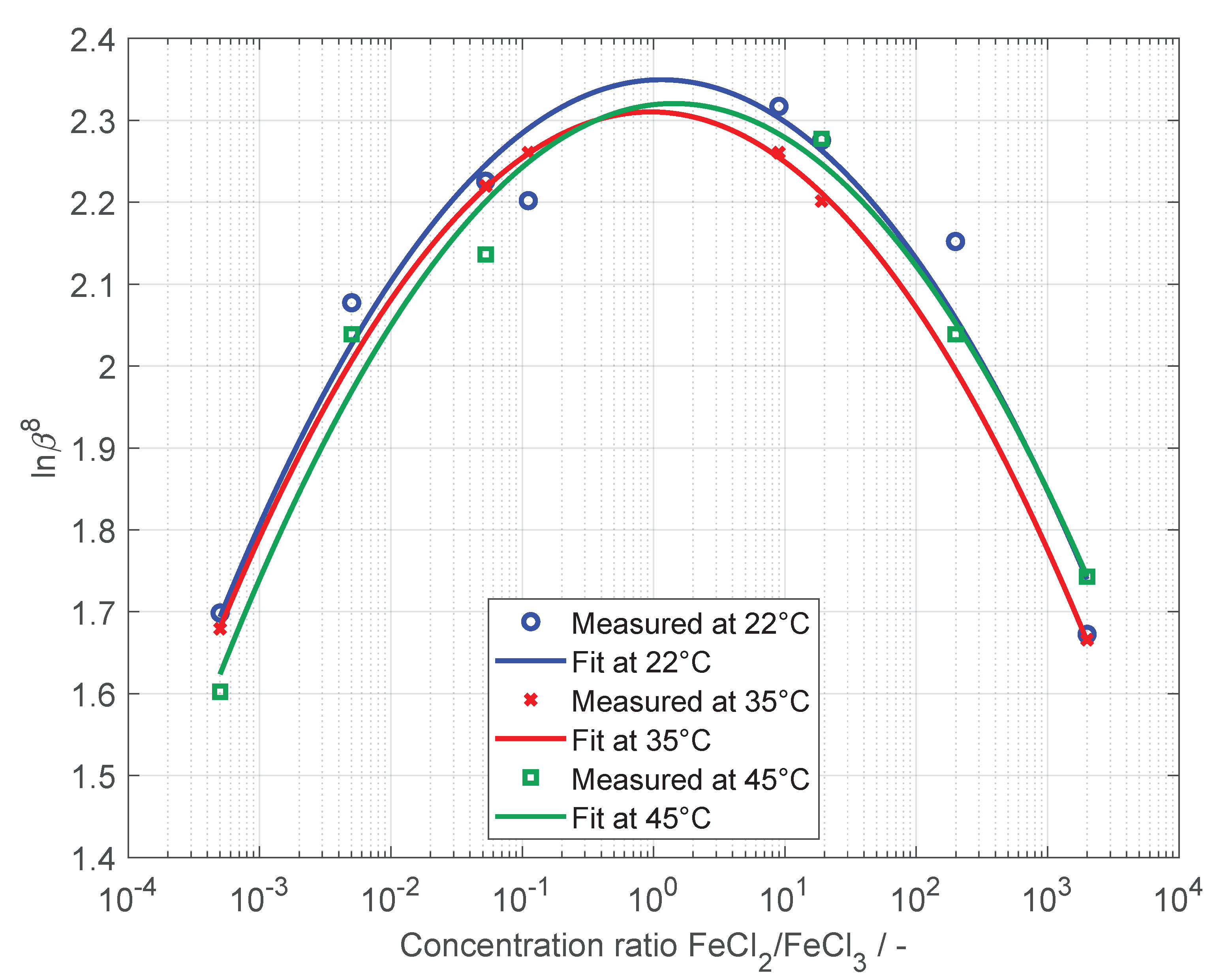
2.3. Power of the Battery
3. Experimental
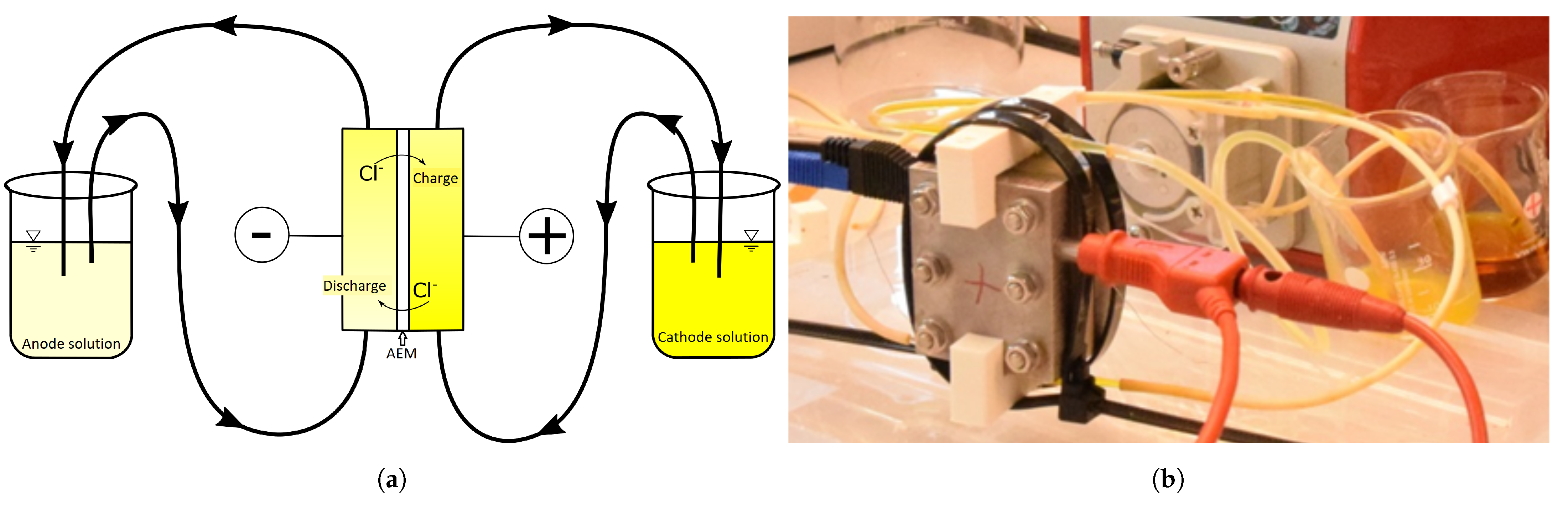
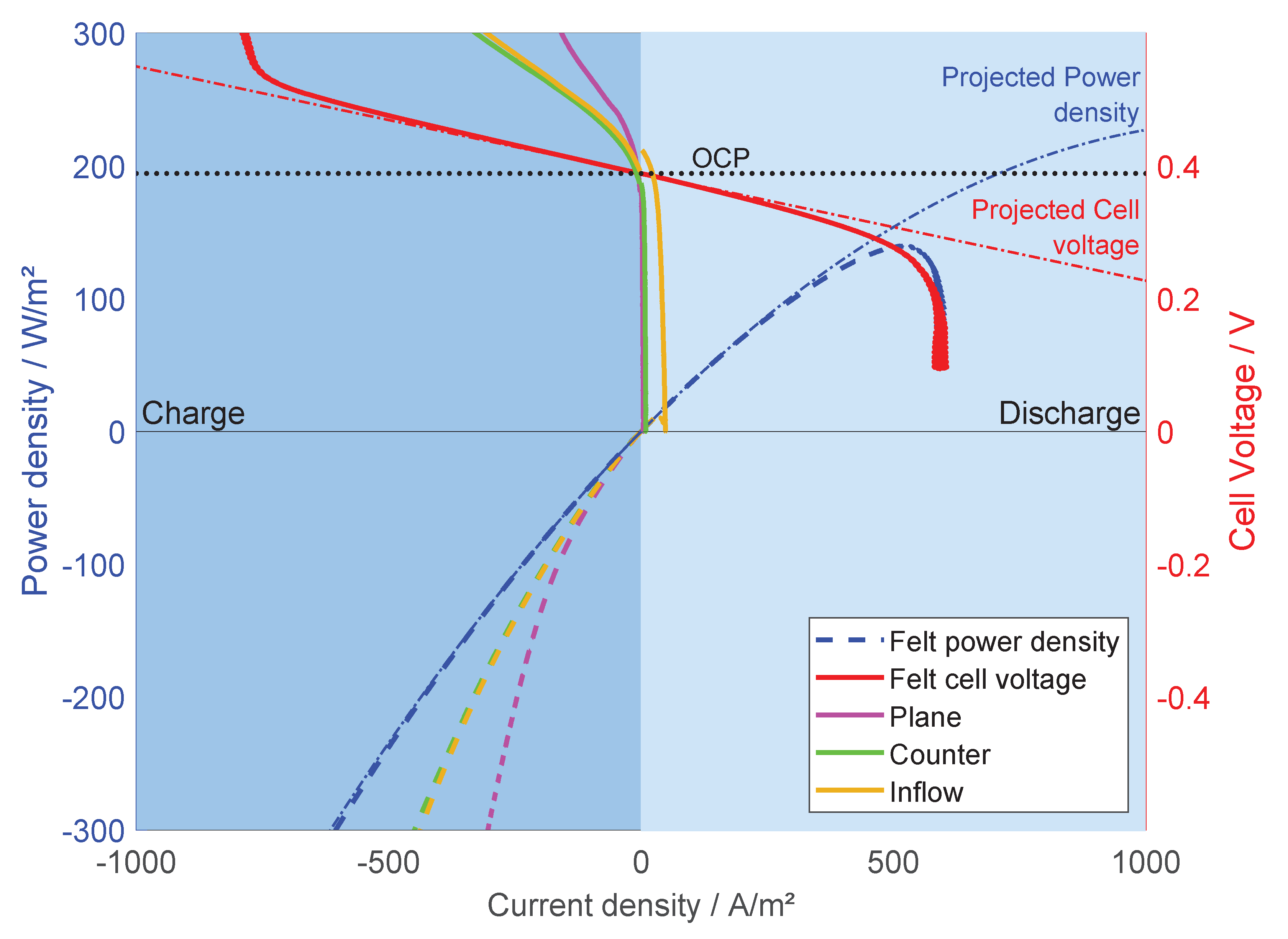
3.1. Measurement Setup
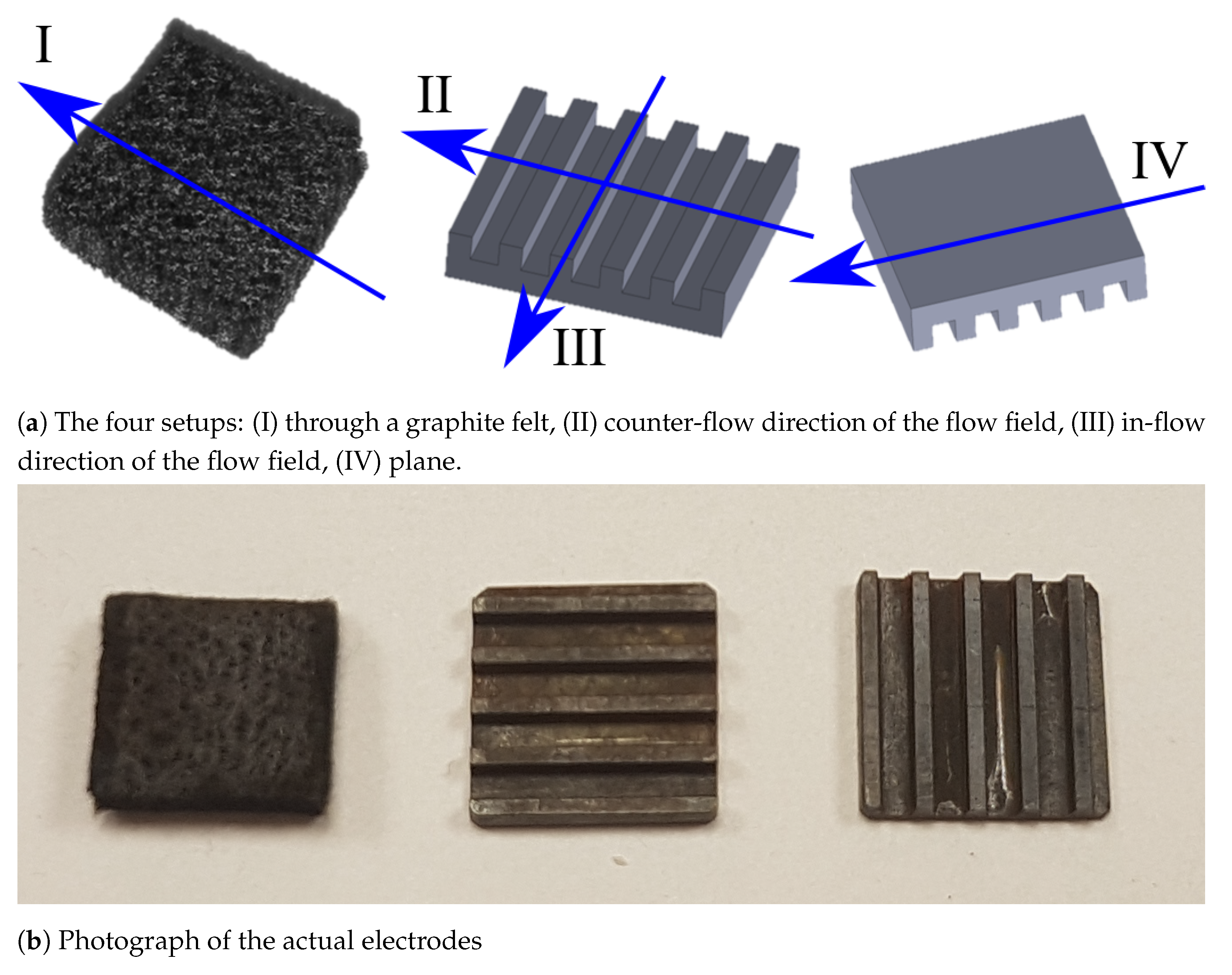
3.2. Electrodes
3.3. Ion Exchange Membrane
3.4. Measurement Technique
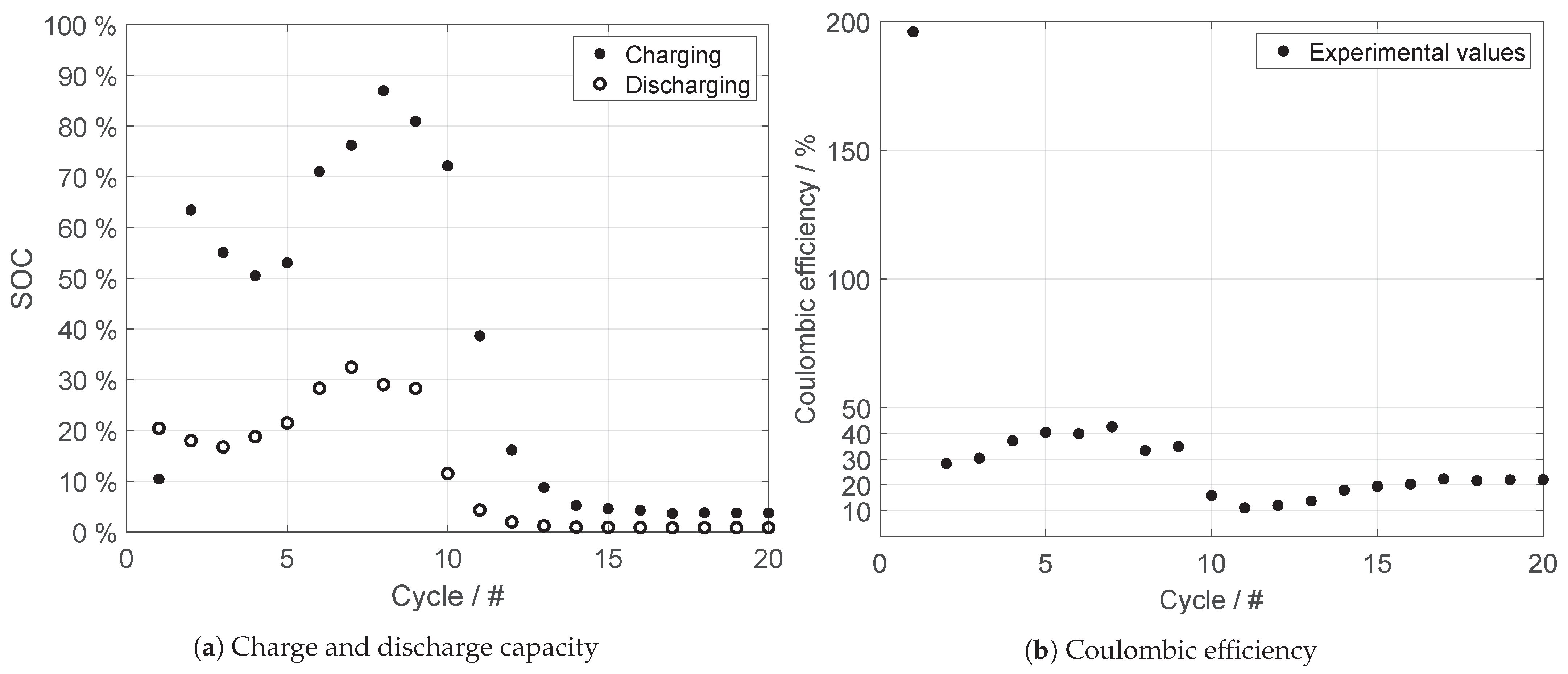
4. Results and Discussion
Outlook and Research Needs
- Increase the surface area of the carbon felt electrode and tailor them to the needs of this system to increase power output;
- Investigate different inhibitors and other electrolyte stabilizing measures to increase cyclability;
- Investigate and understand the scalability of the system, both in terms of cell cross sectional area, flow rates and stacking;
- Investigate different membranes in terms of permselectivity of ions and water transport.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weber, A.Z.; Mench, M.M.; Meyers, J.P.; Ross, P.N.; Gostick, J.T.; Liu, Q. Redox flow batteries: A review. J. Appl. Electrochem. 2011, 41, 1137–1164. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M.; Cao, L.; Kazacos, M.; Kausar, N.; Mousa, A. Vanadium Electrolyte Studies for the Vanadium Redox Batter—A Review. ChemSusChem 2016, 9, 1521–1543. [Google Scholar] [CrossRef]
- Burheim, O.S. Engineering Energy Storage, 1st ed.; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Hoberecht, M.; Thaller, L. Design Flexibility of Redox Flow Systems; Technical Report No. NASA-TM-82854; NASA Lewis Research Center: Cleveland, OH, USA, 1982.
- Pletcher, D.; Wills, R. A novel flow battery—A lead acid battery based on an electrolyte with soluble lead (II): III. The influence of conditions on battery performance. J. Power Sources 2005, 149, 96–102. [Google Scholar] [CrossRef]
- De Leon, C.P.; Frías-Ferrer, A.; González-García, J.; Szánto, D.; Walsh, F.C. Redox flow cells for energy conversion. J. Power Sources 2006, 160, 716–732. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, L.; Yang, Y.S.; Wen, Y.H.; Cao, G.P.; Wang, X.D. Preliminary study of single flow zinc–nickel battery. Electrochem. Commun. 2007, 9, 2639–2642. [Google Scholar] [CrossRef]
- Lai, Q.; Zhang, H.; Li, X.; Zhang, L.; Cheng, Y. A novel single flow zinc–bromine battery with improved energy density. J. Power Sources 2013, 235, 1–4. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M. New All-Vanadium Redox Flow Cell. J. Electrochem. Soc. 1986, 133, 1057. [Google Scholar] [CrossRef]
- Rychcik, M.; Skyllas-Kazacos, M. Characteristics of a new all-vanadium redox flow battery. J. Power Sources 1988, 22, 59–67. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M. Efficient Vanadium Redox Flow Cell. J. Electrochem. Soc. 1987, 134, 2950. [Google Scholar] [CrossRef]
- Shi, Y.; Eze, C.; Xiong, B.; He, W.; Zhang, H.; Lim, T.; Ukil, A.; Zhao, J. Recent development of membrane for vanadium redox flow battery applications: A review. Appl. Energy 2019, 238, 202–224. [Google Scholar] [CrossRef]
- Schwenzer, B.; Zhang, J.; Kim, S.; Li, L.; Liu, J.; Yang, Z. Membrane Development for Vanadium Redox Flow Batteries. ChemSusChem 2011, 4, 1388–1406. [Google Scholar] [CrossRef]
- Kim, K.J.; Park, M.S.; Kim, Y.J.; Kim, J.H.; Dou, S.X.; Skyllas-Kazacos, M. A technology review of electrodes and reaction mechanisms in vanadium redox flow batteries. J. Mater. Chem. A 2015, 3, 16913–16933. [Google Scholar] [CrossRef]
- Shaheen, S.M.; Alessi, D.S.; Tack, F.M.; Ok, Y.S.; Kim, K.H.; Gustafsson, J.P.; Sparks, D.L.; Rinklebe, J. Redox chemistry of vanadium in soils and sediments: Interactions with colloidal materials, mobilization, speciation, and relevant environmental implications—A review. Adv. Colloid Interface Sci. 2019, 265, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Post, J.W.; Veerman, J.; Hamelers, H.V.; Euverink, G.J.; Metz, S.J.; Nymeijer, K.; Buisman, C.J. Salinity-gradient power: Evaluation of pressure-retarded osmosis and reverse electrodialysis. J. Membr. Sci. 2007, 288, 218–230. [Google Scholar] [CrossRef]
- Ramon, G.Z.; Feinberg, B.J.; Hoek, E.M. Membrane-based production of salinity-gradient power. Energy Environ. Sci. 2011, 4, 4423–4434. [Google Scholar] [CrossRef]
- Kingsbury, R.S.; Chu, K.; Coronell, O. Energy storage by reversible electrodialysis: The concentration battery. J. Membr. Sci. 2015, 495, 502–516. [Google Scholar] [CrossRef]
- Krakhella, K.W.; Bock, R.; Burheim, O.S.; Seland, F.; Einarsrud, K.E. Heat to H2: Using Waste Heat for Hydrogen Production through Reverse Electrodialysis. Energies 2019, 12, 3428. [Google Scholar] [CrossRef]
- Krakhella, K.W.; Morales, M.; Bock, R.; Seland, F.; Burheim, O.S.; Einarsrud, K.E. Electrodialytic Energy Storage System: Permselectivity, Stack Measurements and Life-Cycle Analysis. Energies 2020, 13, 1247. [Google Scholar] [CrossRef]
- Manohar, A.K.; Kim, K.M.; Plichta, E.; Hendrickson, M.; Rawlings, S.; Narayanan, S.R. A High Efficiency Iron-Chloride Redox Flow Battery for Large-Scale Energy Storage. J. Electrochem. Soc. 2015, 163, A5118–A5125. [Google Scholar] [CrossRef]
- Yensen, N.; Allen, P.B. Open source all-iron battery for renewable energy storage. HardwareX 2019, 6, e00072. [Google Scholar] [CrossRef]
- Silverman, J.; Dodson, R.W. The Exchange Reaction between the Two Oxidation States of Iron in Acid Solution. J. Phys. Chem. 1952, 56, 846–852. [Google Scholar] [CrossRef]
- Zlotorowicz, A.; Strand, R.V.; Burheim, O.S.; Wilhelmsen, Ø.; Kjelstrup, S. The permselectivity and water transference number of ion exchange membranes in reverse electrodialysis. J. Membr. Sci. 2017, 523, 402–408. [Google Scholar] [CrossRef]
- Melin, T.; Rautenbach, R. Membranverfahren: Grundlagen der Modul-und Anlagenauslegung; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Nagarale, R.; Gohil, G.; Shahi, V.K. Recent developments on ion-exchange membranes and electro-membrane processes. Adv. Colloid Interface Sci. 2006, 119, 97–130. [Google Scholar] [CrossRef] [PubMed]
- Aaron, D.; Liu, Q.; Tang, Z.; Grim, G.; Papandrew, A.; Turhan, A.; Zawodzinski, T.; Mench, M. Dramatic performance gains in vanadium redox flow batteries through modified cell architecture. J. Power Sources 2012, 206, 450–453. [Google Scholar] [CrossRef]
| FeCl | FeCl | NaCl | SOC |
|---|---|---|---|
| mol/L | mol/L | mol/L | % |
| 0.9995 | 0.0005 | 1 | 99.95 |
| 0.995 | 0.005 | 1 | 99.50 |
| 0.95 | 0.05 | 1 | 94.74 |
| 0.9 | 0.1 | 1 | 88.89 |
| 0.5 | 0.5 | 1 | 0 |
| 0.1 | 0.9 | 1 | 88.89 |
| 0.05 | 0.95 | 1 | 94.74 |
| 0.005 | 0.995 | 1 | 99.50 |
| 0.0005 | 0.9995 | 1 | 99.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bock, R.; Kleinsteinberg, B.; Selnes-Volseth, B.; Stokke Burheim, O. A Novel Iron Chloride Red-Ox Concentration Flow Cell Battery (ICFB) Concept; Power and Electrode Optimization. Energies 2021, 14, 1109. https://doi.org/10.3390/en14041109
Bock R, Kleinsteinberg B, Selnes-Volseth B, Stokke Burheim O. A Novel Iron Chloride Red-Ox Concentration Flow Cell Battery (ICFB) Concept; Power and Electrode Optimization. Energies. 2021; 14(4):1109. https://doi.org/10.3390/en14041109
Chicago/Turabian StyleBock, Robert, Björn Kleinsteinberg, Bjørn Selnes-Volseth, and Odne Stokke Burheim. 2021. "A Novel Iron Chloride Red-Ox Concentration Flow Cell Battery (ICFB) Concept; Power and Electrode Optimization" Energies 14, no. 4: 1109. https://doi.org/10.3390/en14041109
APA StyleBock, R., Kleinsteinberg, B., Selnes-Volseth, B., & Stokke Burheim, O. (2021). A Novel Iron Chloride Red-Ox Concentration Flow Cell Battery (ICFB) Concept; Power and Electrode Optimization. Energies, 14(4), 1109. https://doi.org/10.3390/en14041109







