Numerical Study of Spray-Induced Turbulence Using Industrial Fire-Mitigation Nozzles
Abstract
:1. Introduction
2. Numerical Modeling
2.1. Modeling Assumptions
2.2. Governing Equations
3. Study of a Single Spray Nozzle
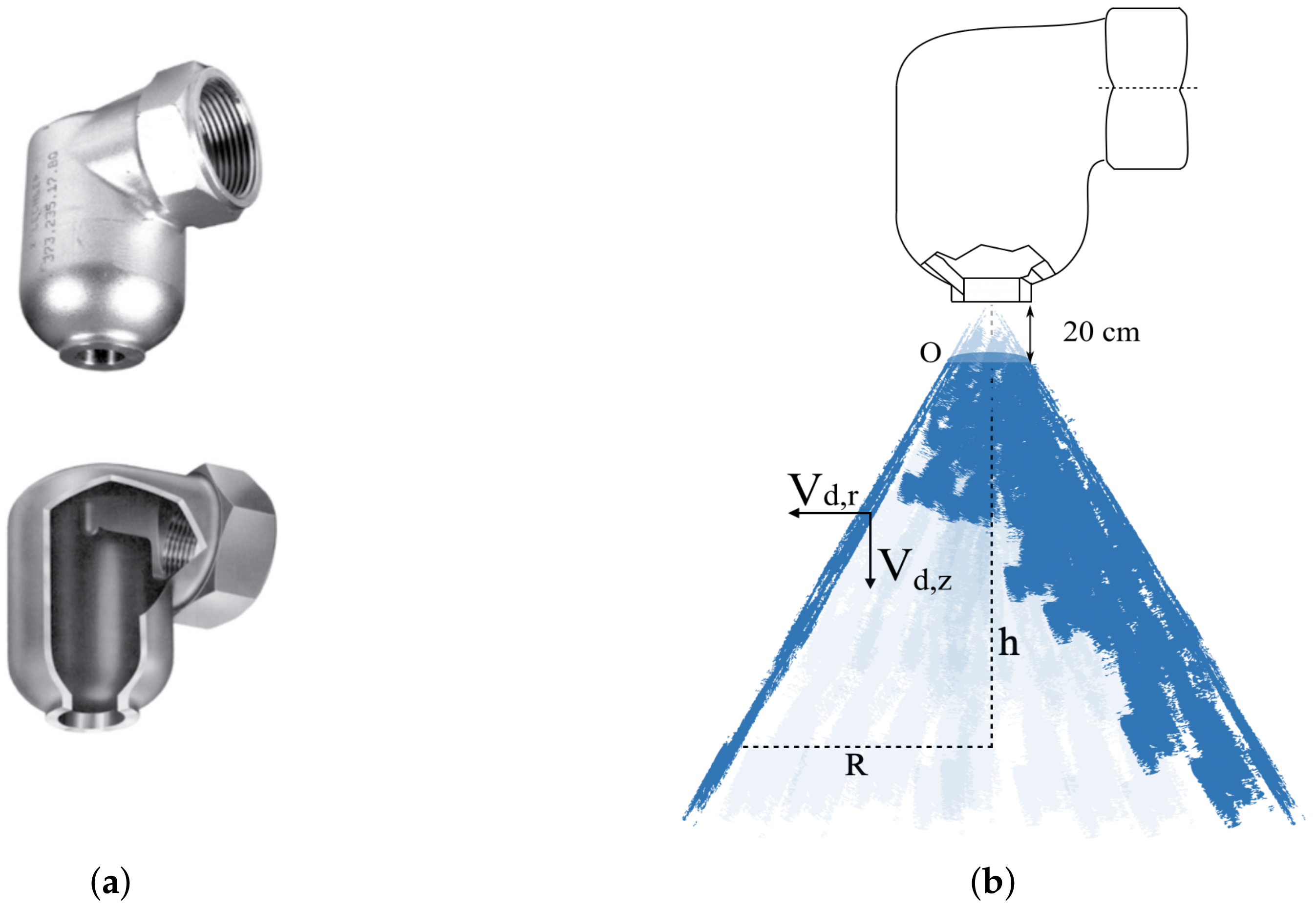
3.1. Spray Nozzle
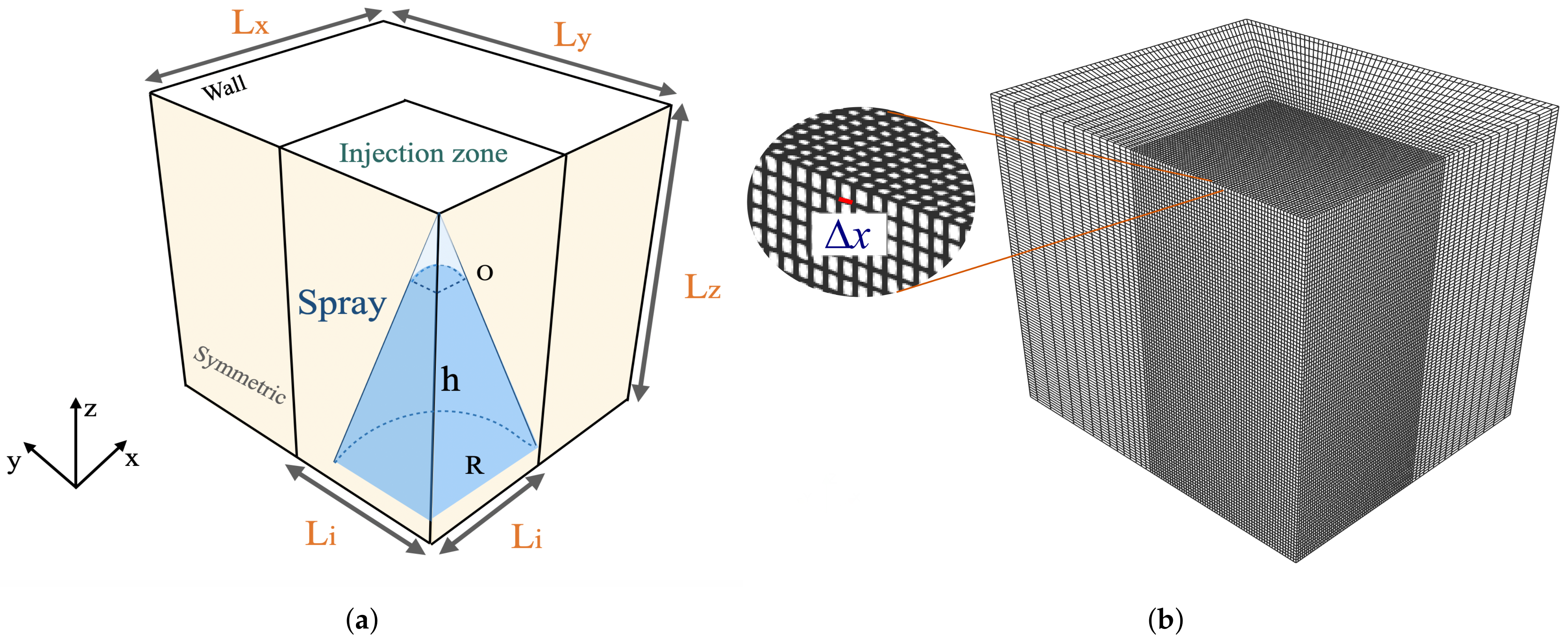
3.2. Geometry, Mesh, and Spray Characteristics
3.3. Simulation Convergence
3.3.1. Mesh Size Effects
3.3.2. Time Convergence
3.4. Code Validation
3.4.1. Monodisperse Spray
3.4.2. Polydisperse Spray
3.5. Turbulent Properties of the Monodisperse Spray
3.6. Turbulent Properties of the Polydisperse Spray
3.6.1. Droplet Volume Fraction
3.6.2. Droplet Size Distribution
3.6.3. Surface-Averaged Volume Fraction
4. Study of Two Interacting Nozzles
5. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Droplet diameter | |
| Gravity acceleration | |
| h | Vertical distance from the spray nozzle |
| Phase-averaged specific enthalpy for phase | |
| Maximal turbulent kinetic energy | |
| , , | Geometry sizes |
| Turbulence integral length scale | |
| M | Interphase momentum transfer term |
| Number of droplets of diameter | |
| p | Gas pressure |
| Droplet momentum number | |
| q | Heat transfer flux |
| R | Radius from spray cone center |
| Reynolds stress | |
| Gas velocity | |
| Particle velocity | |
| Total volume fraction of droplets | |
| Surface-averaged droplet volume fraction | |
| Mass density | |
| Turbulent dissipation rate | |
| Interphase mass transfer rate | |
| Time step | |
| Grid size | |
| DNS | Direct Numerical Simulation |
| RANS | Reynolds-Averaged Navier–Stokes |
| LES | Large Eddy Simulation |
| TKE | Turbulent Kinetic Energy |
References
- Landahl, H.; Herrmann, R. Sampling of liquid aerosols by wires, cylinders, and slides, and the efficiency of impaction of the droplets. J. Colloid Sci. 1949, 4, 103–136. [Google Scholar] [CrossRef]
- Thomas, G. On the conditions required for explosion mitigation by water sprays. Process. Saf. Environ. 2000, 78, 339–354. [Google Scholar] [CrossRef] [Green Version]
- Gai, G.; Kudriakov, S.; Hadjadj, A.; Studer, E.; Thomine, O. Modeling pressure loads during a premixed hydrogen combustion in the presence of water spray. Int. J. Hydrogen Energy 2019, 44, 4592–4607. [Google Scholar] [CrossRef] [Green Version]
- Kudriakov, S.; Dabbene, F.; Studer, E.; Beccantini, A.; Magnaud, J.; Paillère, H.; Bentaib, A.; Bleyer, A.; Malet, J.; Porcheron, E.; et al. The TONUS CFD code for hydrogen risk analysis: Physical models, numerical schemes and validation matrix. Nucl. Eng. Des. 2008, 238, 551–565. [Google Scholar] [CrossRef] [Green Version]
- Wingerden, K.; Wilkins, B. The influence of water sprays on gas explosions. Part 2: Mitigation. J. Loss Prevent. Proc. 1995, 8, 61–70. [Google Scholar] [CrossRef]
- Gai, G.; Kudriakov, S.; Rogg, B.; Hadjadj, A.; Studer, E.; Thomine, O. Numerical study on laminar flame velocity of hydrogen-air combustion under water spray effects. Int. J. Hydrogen Energy 2019, 44, 17015–17029. [Google Scholar] [CrossRef]
- Wingerden, K.; Wilkins, B. The influence of water sprays on gas explosions. Part 1: Water-spray-generated turbulence. J. Loss Prevent. Proc. 1995, 8, 53–59. [Google Scholar] [CrossRef]
- Hetsroni, G.; Sokolov, M. Distribution of mass velocity and intensity of turbulence in a two-phase turbulent jet. ASME J. Appl. Mech. 1971, 38, 315–327. [Google Scholar] [CrossRef]
- Hetsroni, G. Particles-turbulence interaction. Int. J. Multiph. Flow 1989, 15, 735–746. [Google Scholar] [CrossRef]
- Elghobashi, S. On predicting particle-laden turbulent flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Sadiki, A.; Chrigui, M.; Janicka, J.; Maneshkarimi, M.R. Modeling and simulation of effects of turbulence on vaporization, mixing and combustion of liquid-fuel sprays. Flow Turbul. Combust. 2005, 75, 105–130. [Google Scholar] [CrossRef]
- Mallouppas, G.; George, W.; van Wachem, B. Dissipation and inter-scale transfer in fully coupled particle and fluid motions in homogeneous isotropic forced turbulence. Int. J. Heat. Fluid Flow 2017, 67, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Gadalla, M.; Kannan, J.; Tekgül, B.; Karimkashi, S.; Kaario, O.; Vuorinen, V. Large-eddy simulation of ECN spray A: Sensitivity study on modeling assumptions. Energies 2020, 13, 3360. [Google Scholar] [CrossRef]
- Crowe, C.; Schwarzkopf, J.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles; CRC, Taylor and Francis: Boca Raton, FL, USA, 2012; ISBN 9781439840504. [Google Scholar]
- Gai, G.; Hadjadj, A.; Kudriakov, S.; Thomine, O. Particles-induced turbulence: A critical review of physical concepts, numerical modelings and experimental investigations. Theor. App. Mech. Lett. 2020, 10, 1–7. [Google Scholar] [CrossRef]
- Gore, R.; Crowe, C. Modulation of turbulence by a dispersed phase. ASME J. Fluids Eng. 1991, 113, 304–307. [Google Scholar] [CrossRef]
- Gore, R.; Crowe, C. Effect of particle size on modulating turbulent intensity. Int. J. Multiph. Flow 1989, 15, 279–285. [Google Scholar] [CrossRef]
- Tanaka, T.; Eaton, J. Sub-Kolmogorov resolution particle image velocimetry measurements of particle-laden forced turbulence. J. Fluid Mech. 2010, 643, 177–206. [Google Scholar] [CrossRef]
- Lefebvre, A.; McDonell, V.G. Atomization and Sprays; CRC, Taylor and Francis: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kim, K.; Lim, O. Investigation of the spray development process of gasoline-biodiesel blended fuel sprays in a constant volume chamber. Energies 2020, 13, 4819. [Google Scholar] [CrossRef]
- Foissac, A. Modélisation des Interactions Entre Gouttes en Environnement Hostile. Ph.D. Thesis, Université Pierre & Marie Curie, Paris, France, 2011. [Google Scholar]
- Keser, R.; Ceschin, A.; Battistoni, M.; Im, H.; Jasak, H. Development of a eulerian multi-fluid solver for dense spray applications in OpenFOAM. Energies 2020, 13, 4740. [Google Scholar] [CrossRef]
- Mimouni, S.; Lamy, J.S.; Lavieville, J.; Guieu, S.; Martin, M. Modeling of sprays in containment applications with A CMFD code. Nucl. Eng. Des. 2010, 240, 2260–2270. [Google Scholar] [CrossRef] [Green Version]
- Elghobashi, S.; Balachandar, S.; Prosperetti, A. An updated classification map of particle-Laden turbulent flows. IUTAM Symp. Comput. Approaches Multiph. Flow 2006, 81, 3–10. [Google Scholar]
- Yuan, Z.; Michaelides, E. Turbulence modulation in particulate flows. A theoretical approach. Int. J. Multiph. Flow 1992, 18, 779–785. [Google Scholar] [CrossRef]
- Yarin, L.; Hetsroni, G. Turbulence intensity in dilute two-phase flows -3 The particles-turbulence interaction in dilute two-phase flow. Int. J. Multiph. Flow 1994, 20, 27–44. [Google Scholar] [CrossRef]
- Wacks, D.H.; Chakraborty, N. Flame structure and propagation in turbulent flame-droplet interaction: A direct numerical simulation analysis. Flow Turbul. Combust. 2016, 96, 1053–1081. [Google Scholar] [CrossRef] [Green Version]
- Crowe, C. On models for turbulence modulation in fluid-particle flows. Int. J. Multiph. Flow 2000, 26, 719–727. [Google Scholar] [CrossRef]
- Mandø, M. Turbulence Modulation by Non-Spherical Particles. Ph.D. Thesis, Aalborg Universitet, Aalborg, Denmark, 2009. [Google Scholar]
- Mandø, M.; Lightstone, M.; Rosendahl, L.; Yin, C.; Sørensen, H. Turbulence Modulation in Dilute Particle-Laden Flow. Int. J. Heat. Fluid Flow 2009, 30, 331–338. [Google Scholar] [CrossRef]
- Elghobashi, S. Direct numerical simulation of turbulent flows laden with droplets or bubbles. Annu. Rev. Fluid Mech. 2019, 51, 217–244. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, S.; Rutland, C. Study of spray induced turbulence using large eddy simulations. At. Sprays 2015, 25, 285–316. [Google Scholar] [CrossRef] [Green Version]
- Gexcon, A.S. FLACS Code User Manual. 2020. Available online: http://www3.gexcon.com/files/manual/flacs/html/index.html (accessed on 12 November 2020).
- Khan, M.; Zou, R.; Yu, A. Computational simulation of air-side heat transfer and pressure drop performance in staggered mannered twisted oval tube bundle operating in crossflow. Int. J. Therm. Sci. 2021, 161, 106748. [Google Scholar] [CrossRef]
- Thomine, O. Development of Multi-Scale Methods for the Numerical Simulation of Biphasic Reactive Flows. Ph.D. Thesis, University of Rouen, Mont-Saint-Aignan, France, 2011. [Google Scholar]
- Mimouni, S.; Boucker, M.; Laviéville, J.; Guelfi, A.; Bestion, D. Modeling and computation of cavitation and boiling bubbly flows with the NEPTUNE_CFD code. Nucl. Eng. Des. 2008, 238, 680–692. [Google Scholar] [CrossRef]
- Neptune_CFD Version 4.3.1 Theory Guide; EDF: Paris, France, 2019.
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow; Springer: Berlin, Germany, 2006. [Google Scholar]
- Pironneau, O.; Mohammadi, B. Analysis of the k-Epsilon Turbulence Model; Mason: Paris, France, 1994. [Google Scholar]
- Mimouni, S. Modeling and cavitation flows: A two-phase flow approach. La Houille Blanche 2006, 6, 121–128. [Google Scholar] [CrossRef]
- Lechler. Precision Spray Nozzles and Engineered Solutions for the Chemical Industry; Technical Report; Lechler: Metzingen, Germany, 1996. [Google Scholar]
- Foissac, A.; Malet, J.; Vetrano, R.; Buchlin, J.; Mimouni, S.; Feuillebois, F.; Simonin, O. Experimental measurements of droplet size and velocity distributions at the outlet of a pressurized water reactor containment swirling spray nozzle. In Proceedings of the XCFD4NRS-3, Bethesda, MD, USA, 14–16 September 2010. [Google Scholar]
- Foissac, A.; Sestier-Carlin, R.; Malet, J. Dimensionnement du Banc CALIST; Rapport IRSN/DSU/SERAC/LEMAC/10-28; IRSN: Paris, France, 2010. [Google Scholar]
- Risso, F. Agitation, mixing, and transfers induced by bubbles. Annu. Rev. Fluid Mech. 2018, 50, 25–48. [Google Scholar] [CrossRef] [Green Version]
 ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ), and cm (
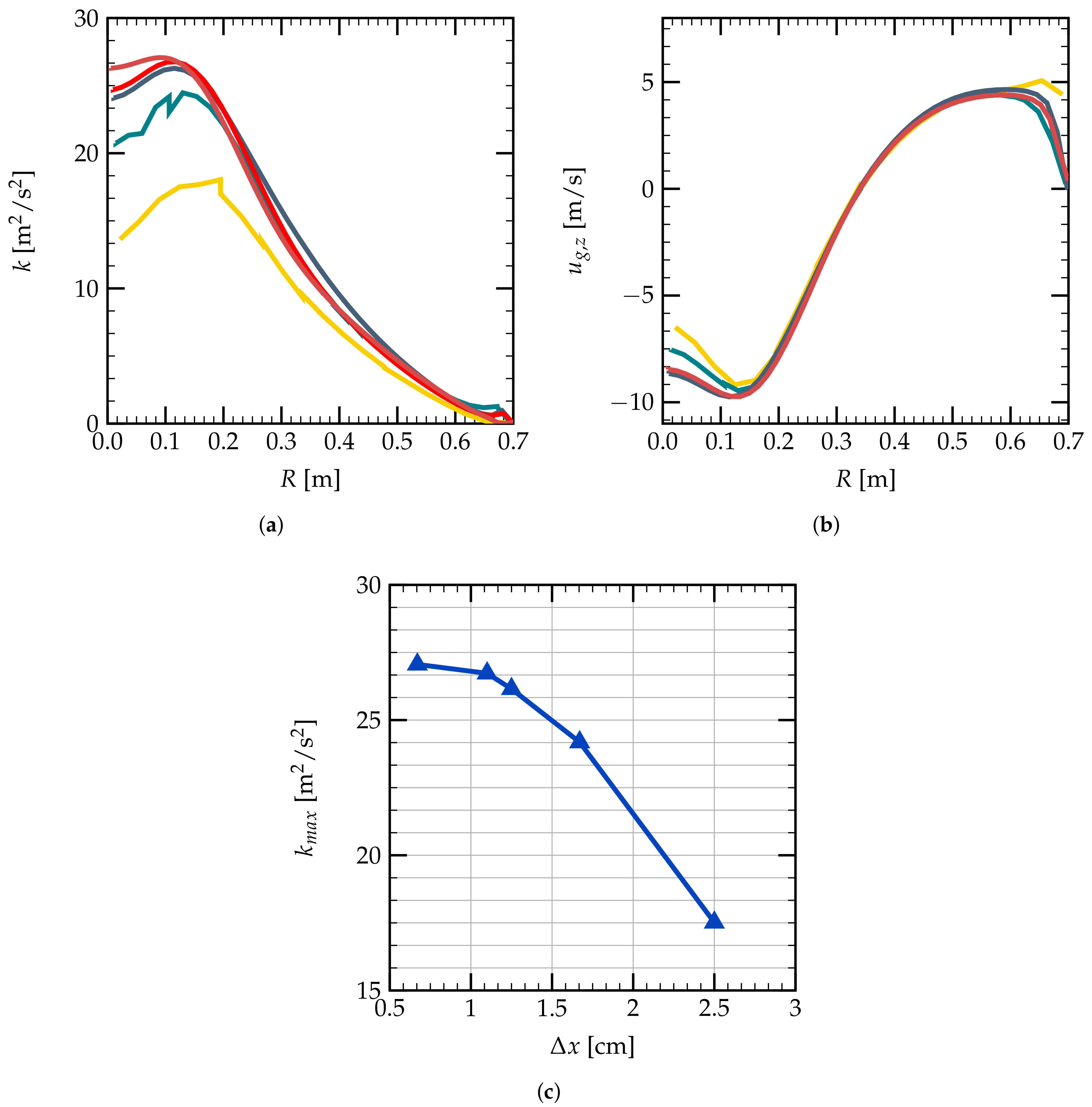
), and cm (  ); (a) turbulence kinetic energy k, (b) axial gas velocity , and (c) the mesh convergence tendency for as a function of mean mesh size at plane cm (
); (a) turbulence kinetic energy k, (b) axial gas velocity , and (c) the mesh convergence tendency for as a function of mean mesh size at plane cm (  ).
).
 ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ), and cm (
), and cm (  ); (a) turbulence kinetic energy k, (b) axial gas velocity , and (c) the mesh convergence tendency for as a function of mean mesh size at plane cm (
); (a) turbulence kinetic energy k, (b) axial gas velocity , and (c) the mesh convergence tendency for as a function of mean mesh size at plane cm (  ).
).
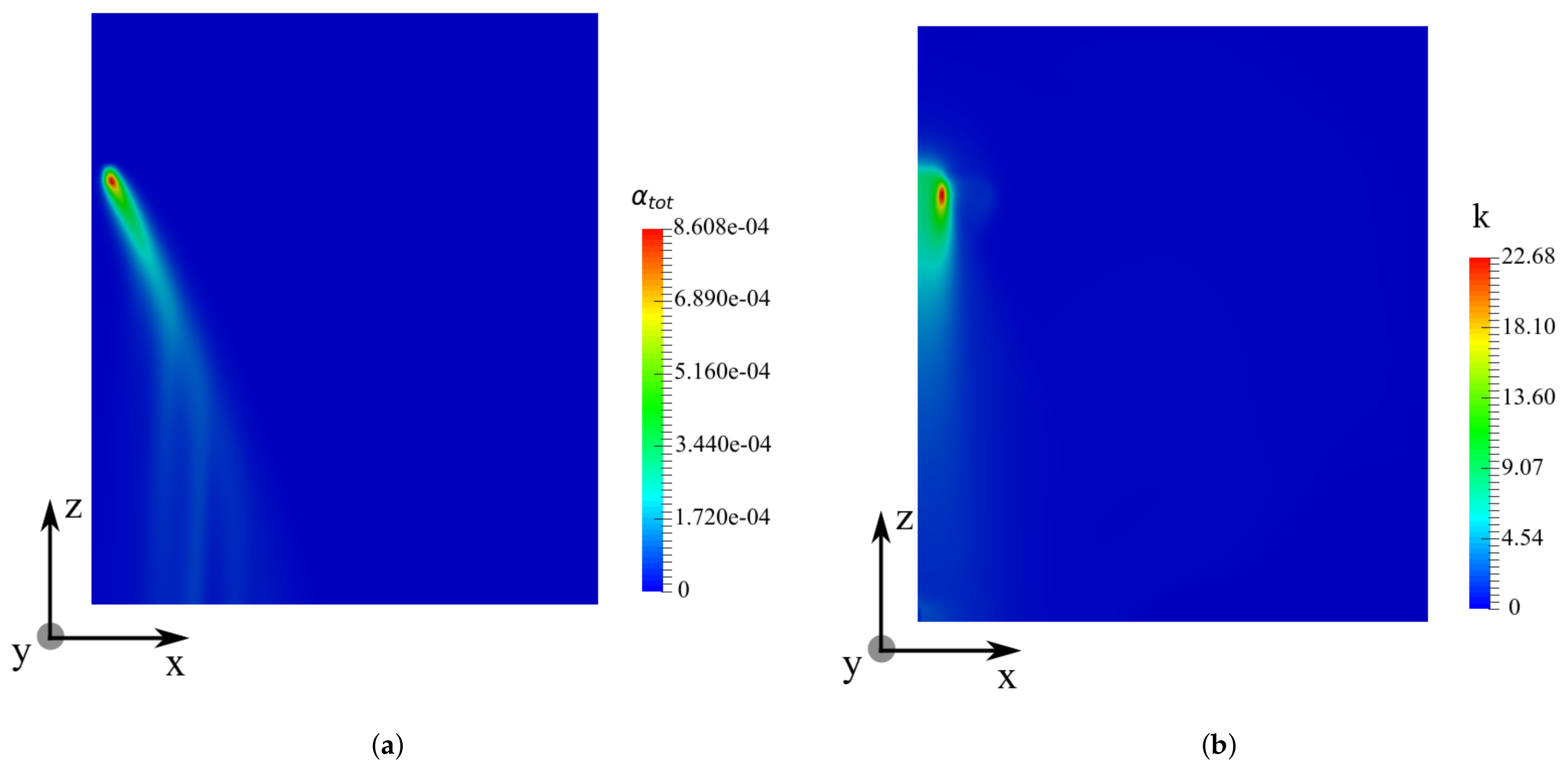
 ), Position 2 ( m) (
), Position 2 ( m) (  ), and Position 3 ( m) (
), and Position 3 ( m) (  ); (a) vertical gas velocity and (b) turbulent kinetic energy as a function of time.
); (a) vertical gas velocity and (b) turbulent kinetic energy as a function of time.
 ), Position 2 ( m) (
), Position 2 ( m) (  ), and Position 3 ( m) (
), and Position 3 ( m) (  ); (a) vertical gas velocity and (b) turbulent kinetic energy as a function of time.
); (a) vertical gas velocity and (b) turbulent kinetic energy as a function of time.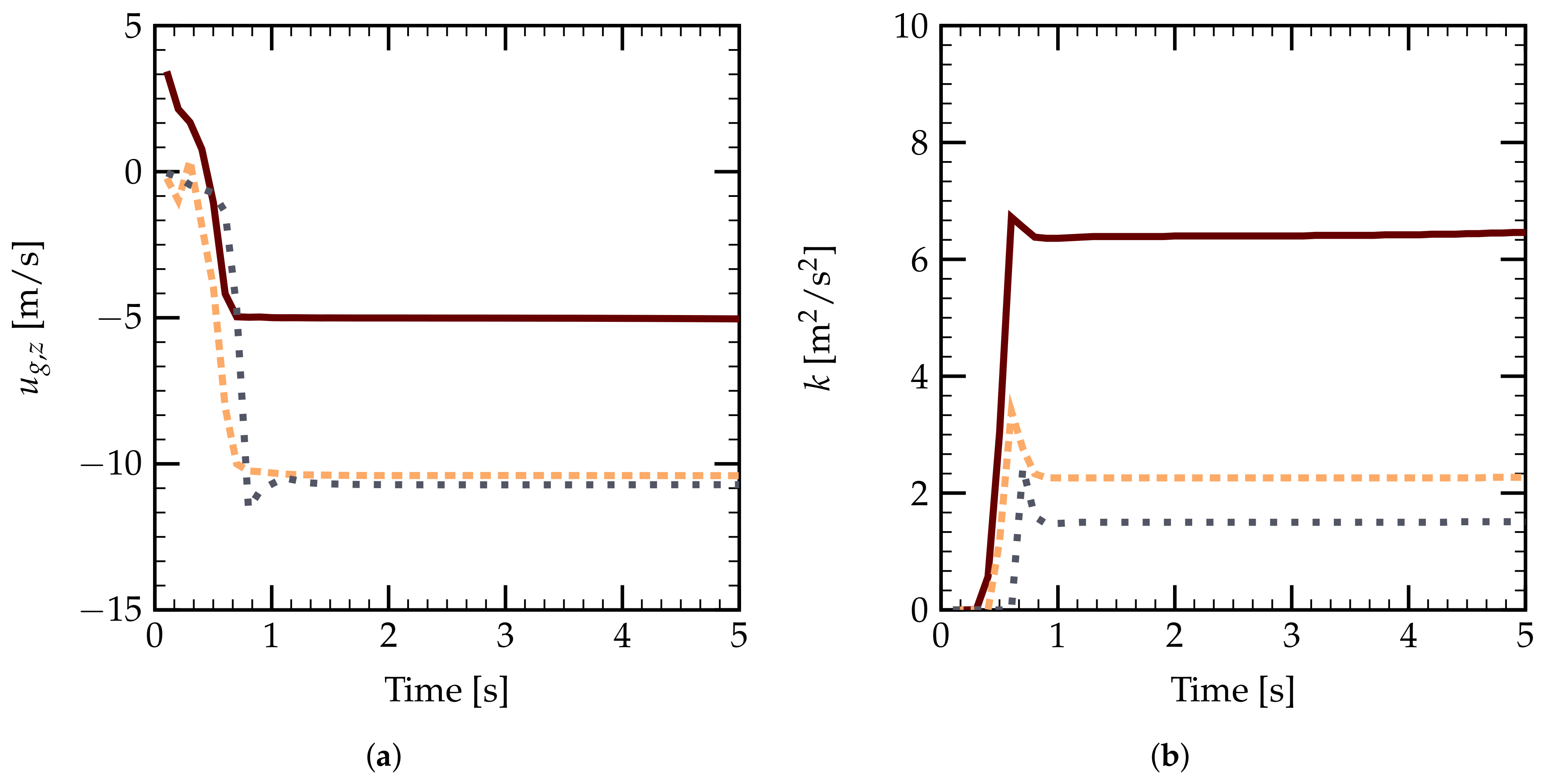
 ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ); numerical simulation of [21] at cm (
); numerical simulation of [21] at cm (  ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ); current simulation at cm (
); current simulation at cm (  ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ).
).
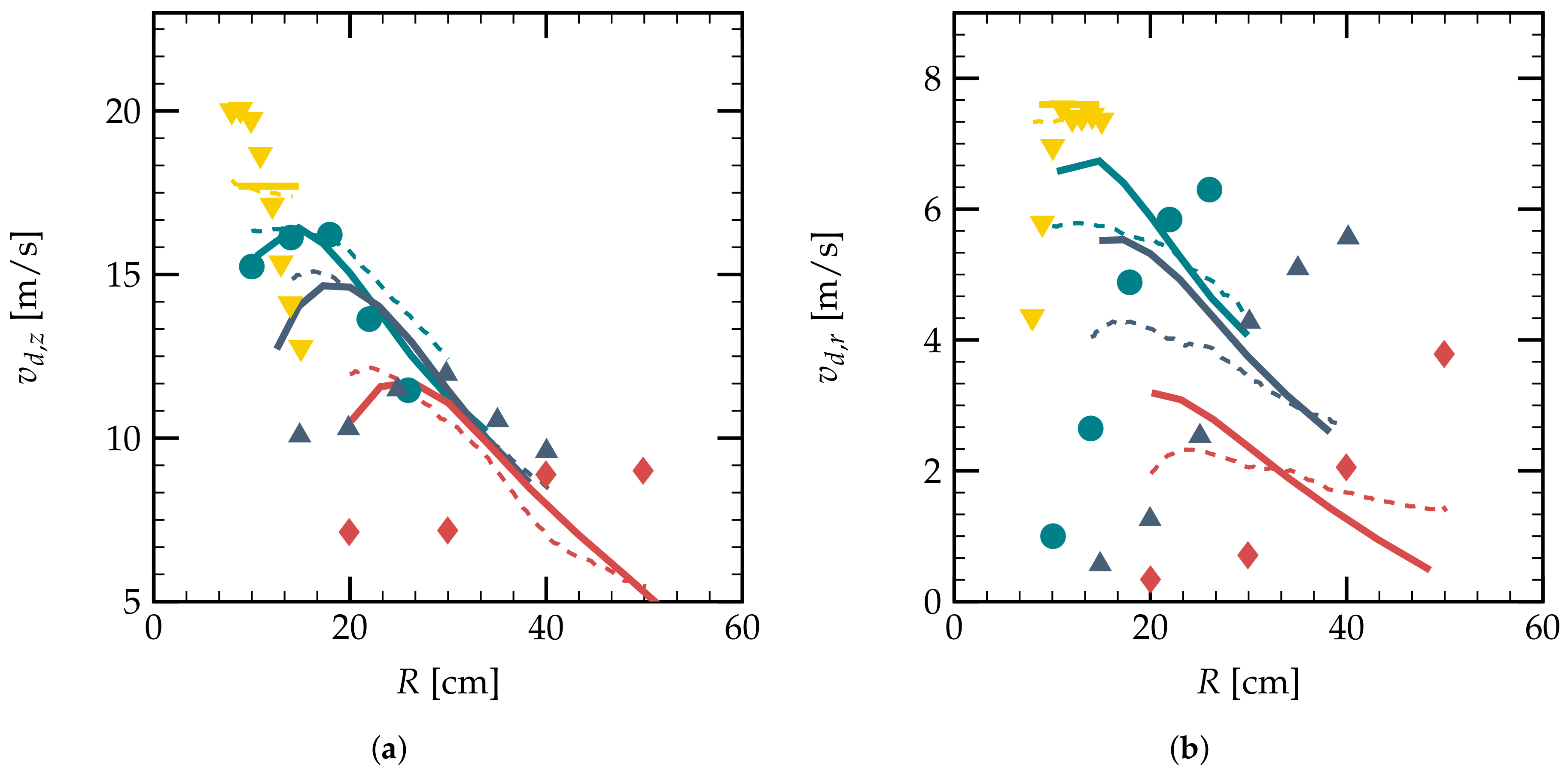
 ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ); numerical simulation of [21] at cm (
); numerical simulation of [21] at cm (  ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ); current simulation at cm (
); current simulation at cm (  ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ).
).
 ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ); Numerical simulation of [21] at cm (
); Numerical simulation of [21] at cm (  ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ); current simulation at cm (
); current simulation at cm (  ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ).
).
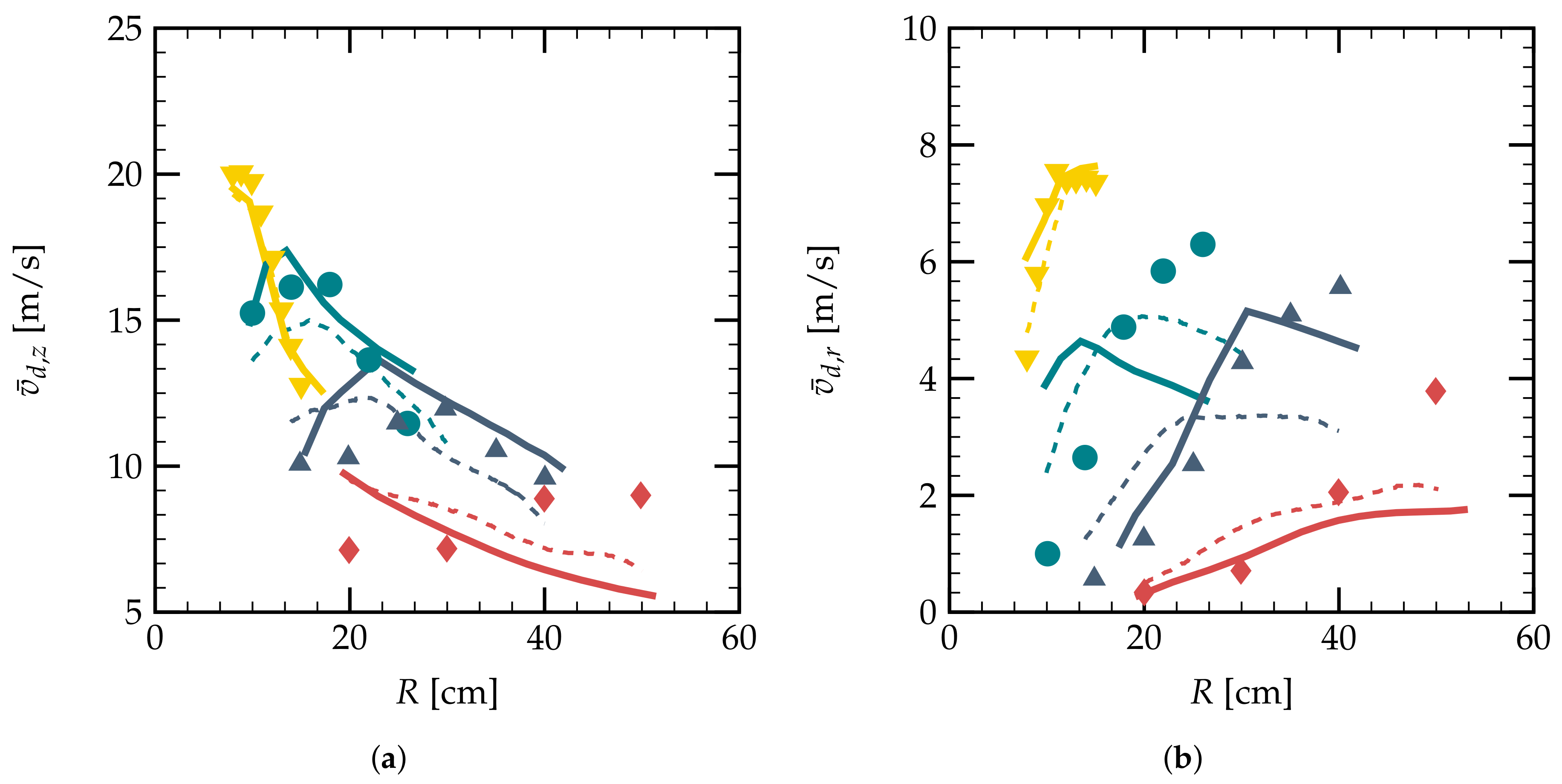
 ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ); Numerical simulation of [21] at cm (
); Numerical simulation of [21] at cm (  ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ); current simulation at cm (
); current simulation at cm (  ), cm (
), cm (  ), cm (
), cm (  ), cm (
), cm (  ).
).
 ), μm (
), μm (  ), μm (
), μm (  ), μm (
), μm (  ), μm (
), μm (  ), μm (
), μm (  ), μm (
), μm (  ), μm (
), μm (  ); (a) cm and (b) cm.
); (a) cm and (b) cm.
 ), μm (
), μm (  ), μm (
), μm (  ), μm (
), μm (  ), μm (
), μm (  ), μm (
), μm (  ), μm (
), μm (  ), μm (
), μm (  ); (a) cm and (b) cm.
); (a) cm and (b) cm.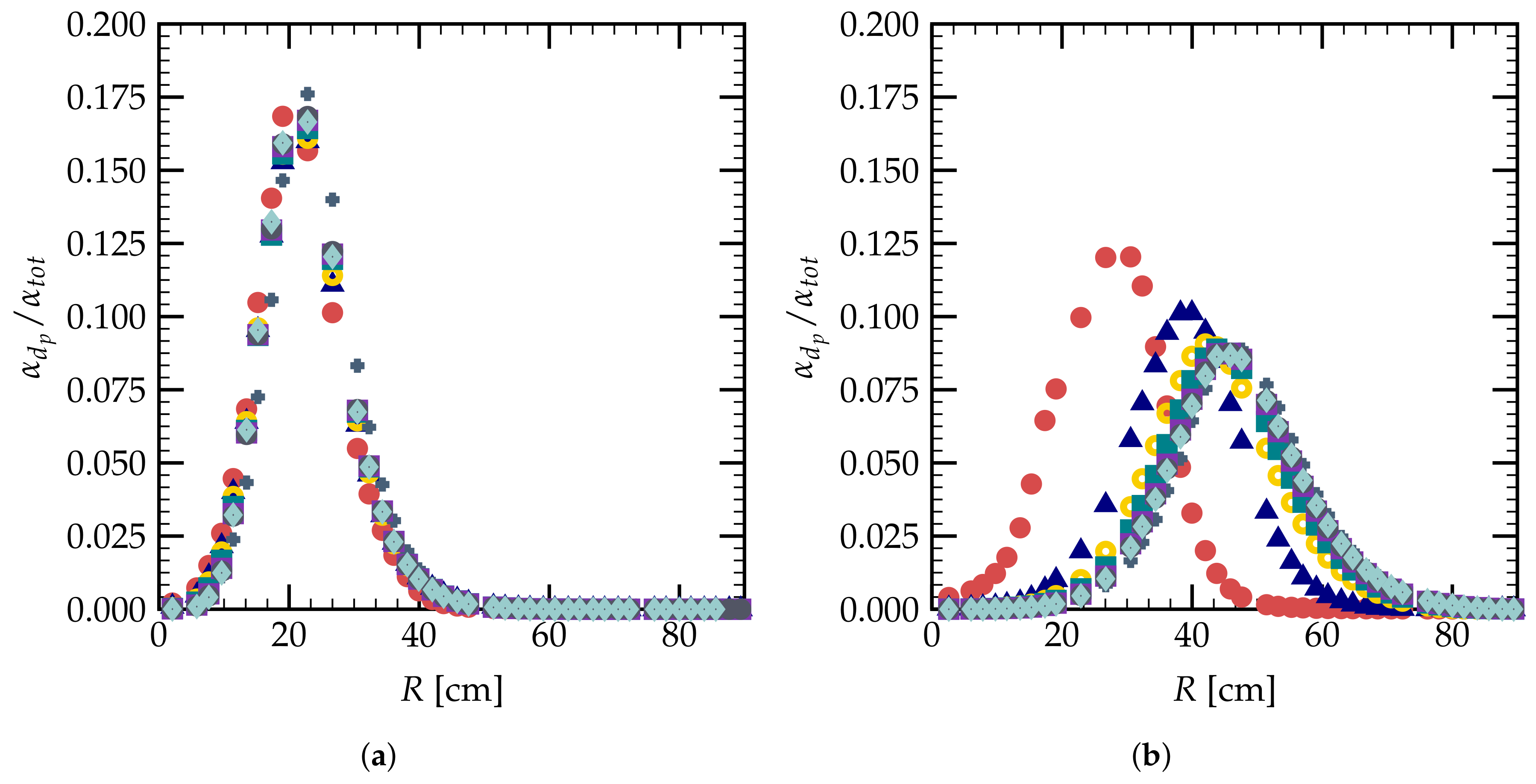

 ), polydisperse spray (
), polydisperse spray (  ); (b) Evolution of at different vertical surfaces as a function of the vertical distance; monodisperse spray (
); (b) Evolution of at different vertical surfaces as a function of the vertical distance; monodisperse spray (  ), polydisperse spray (
), polydisperse spray (  ).
).
 ), polydisperse spray (
), polydisperse spray (  ); (b) Evolution of at different vertical surfaces as a function of the vertical distance; monodisperse spray (
); (b) Evolution of at different vertical surfaces as a function of the vertical distance; monodisperse spray (  ), polydisperse spray (
), polydisperse spray (  ).
).

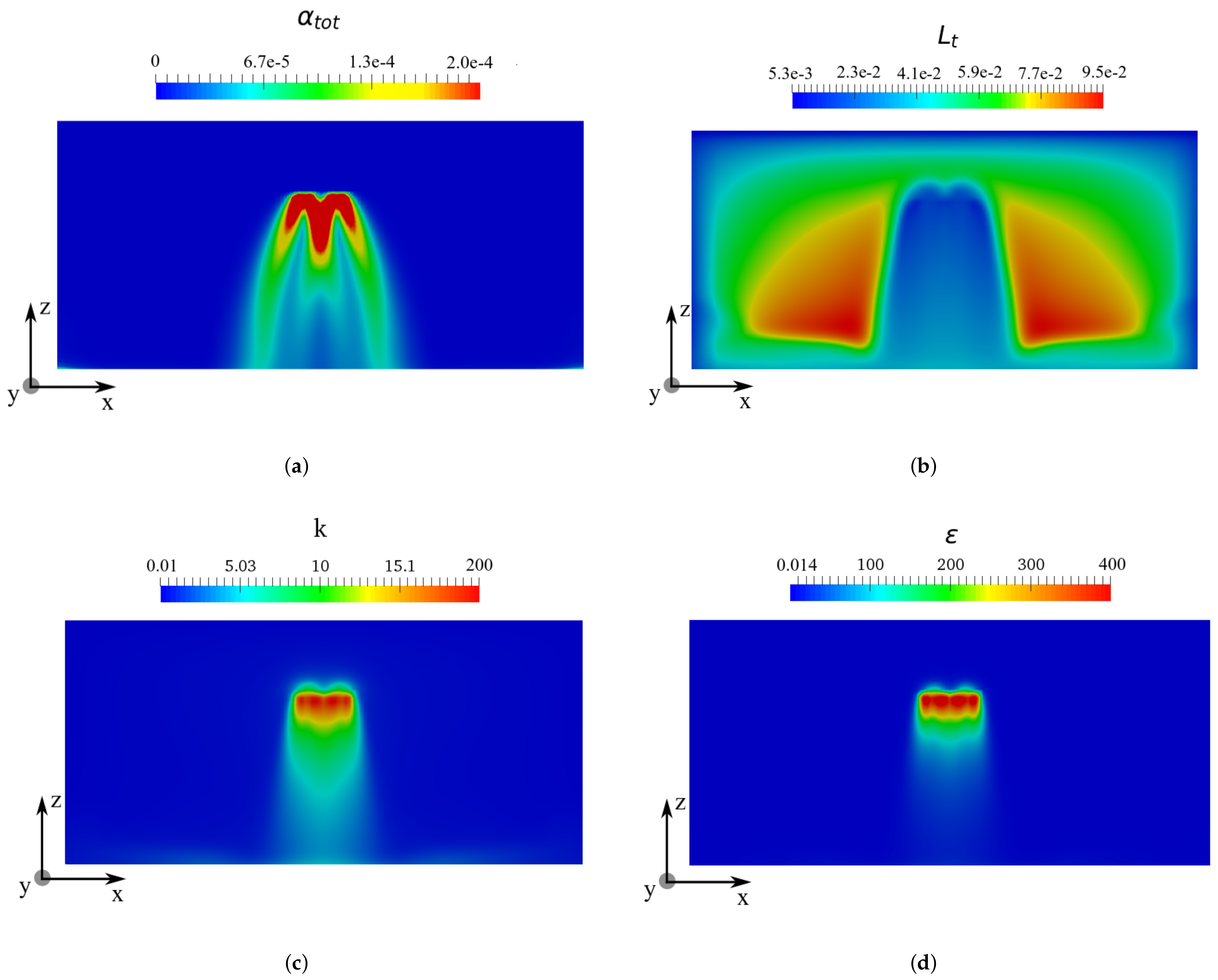
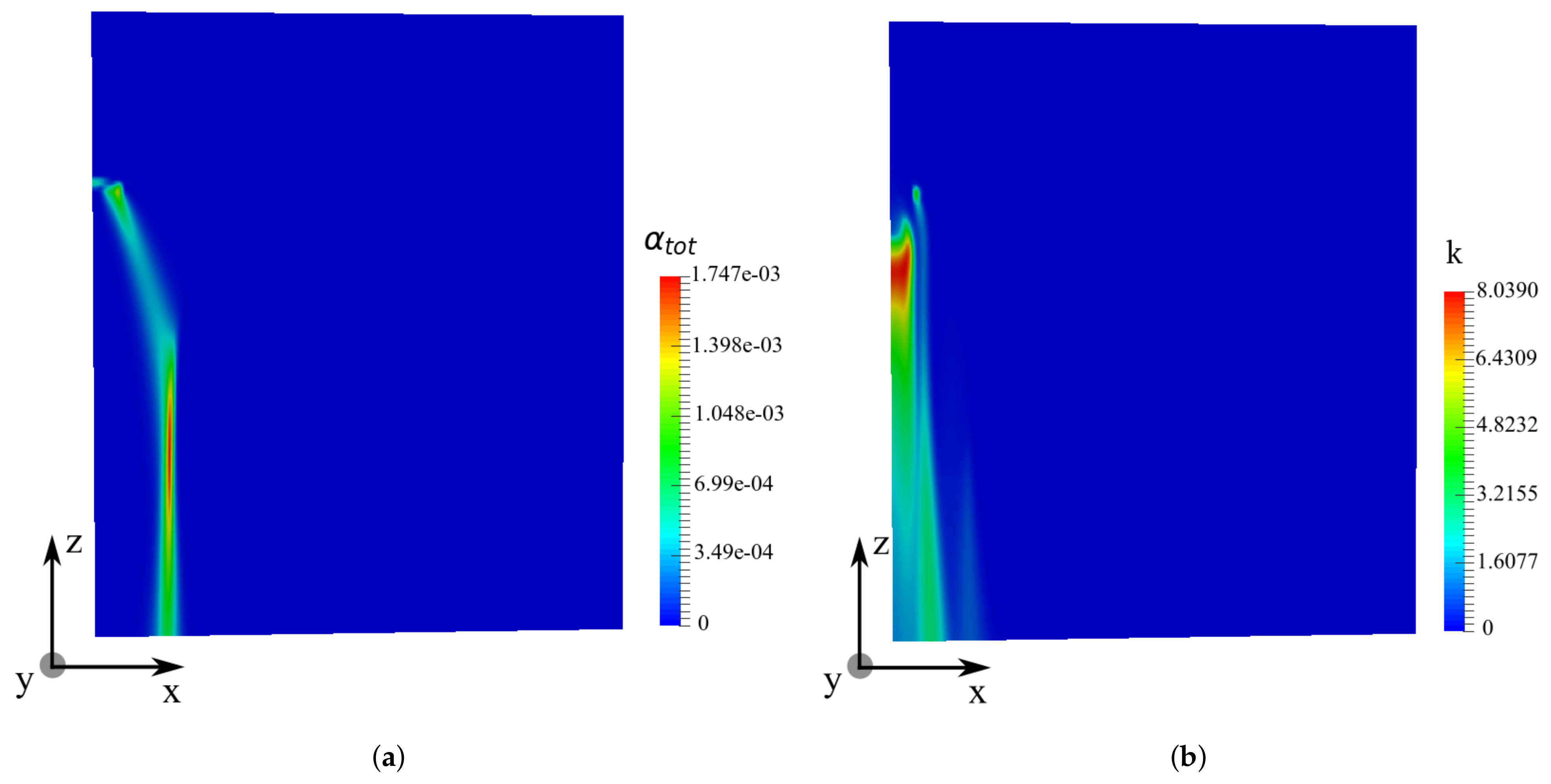
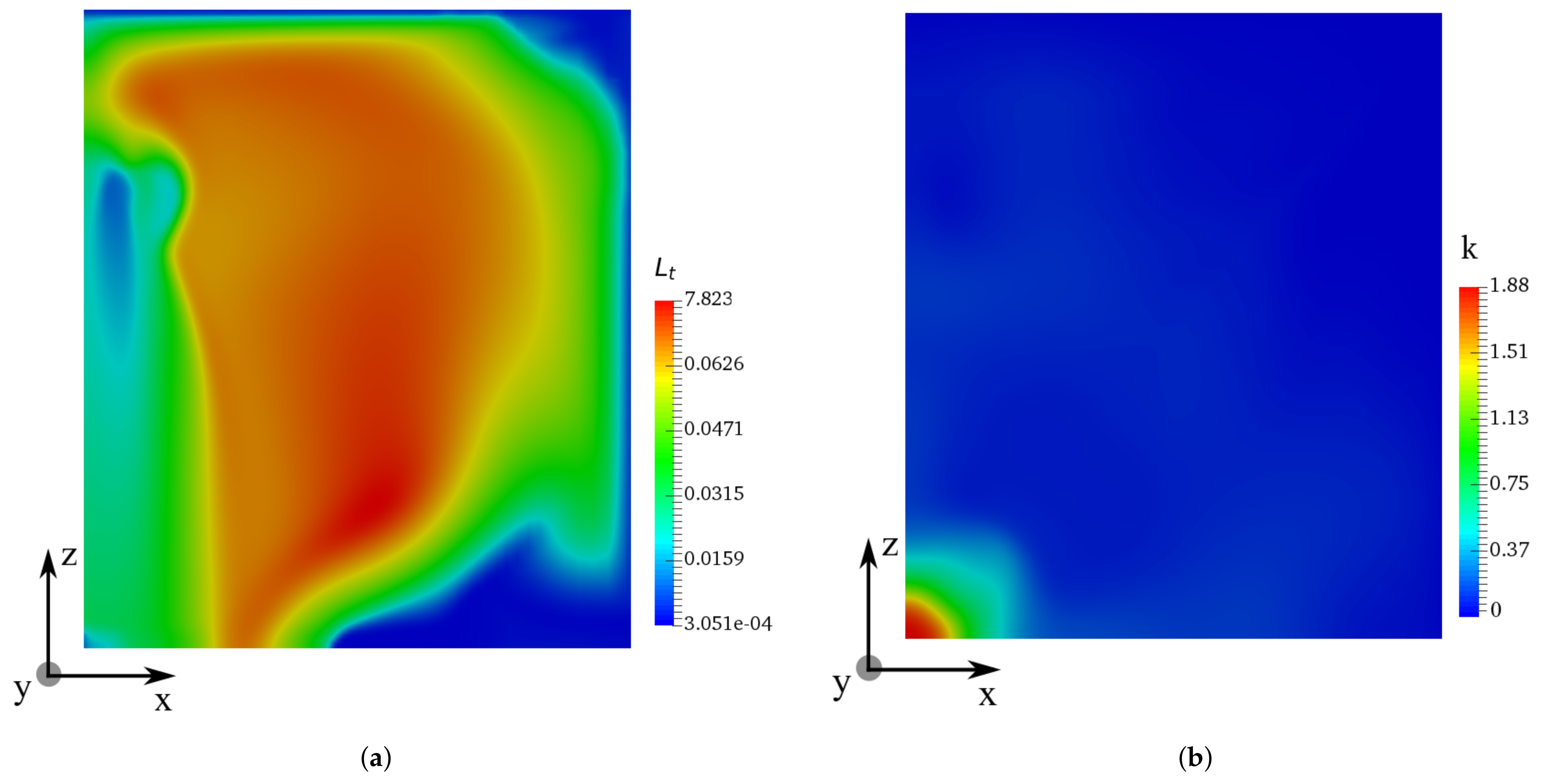
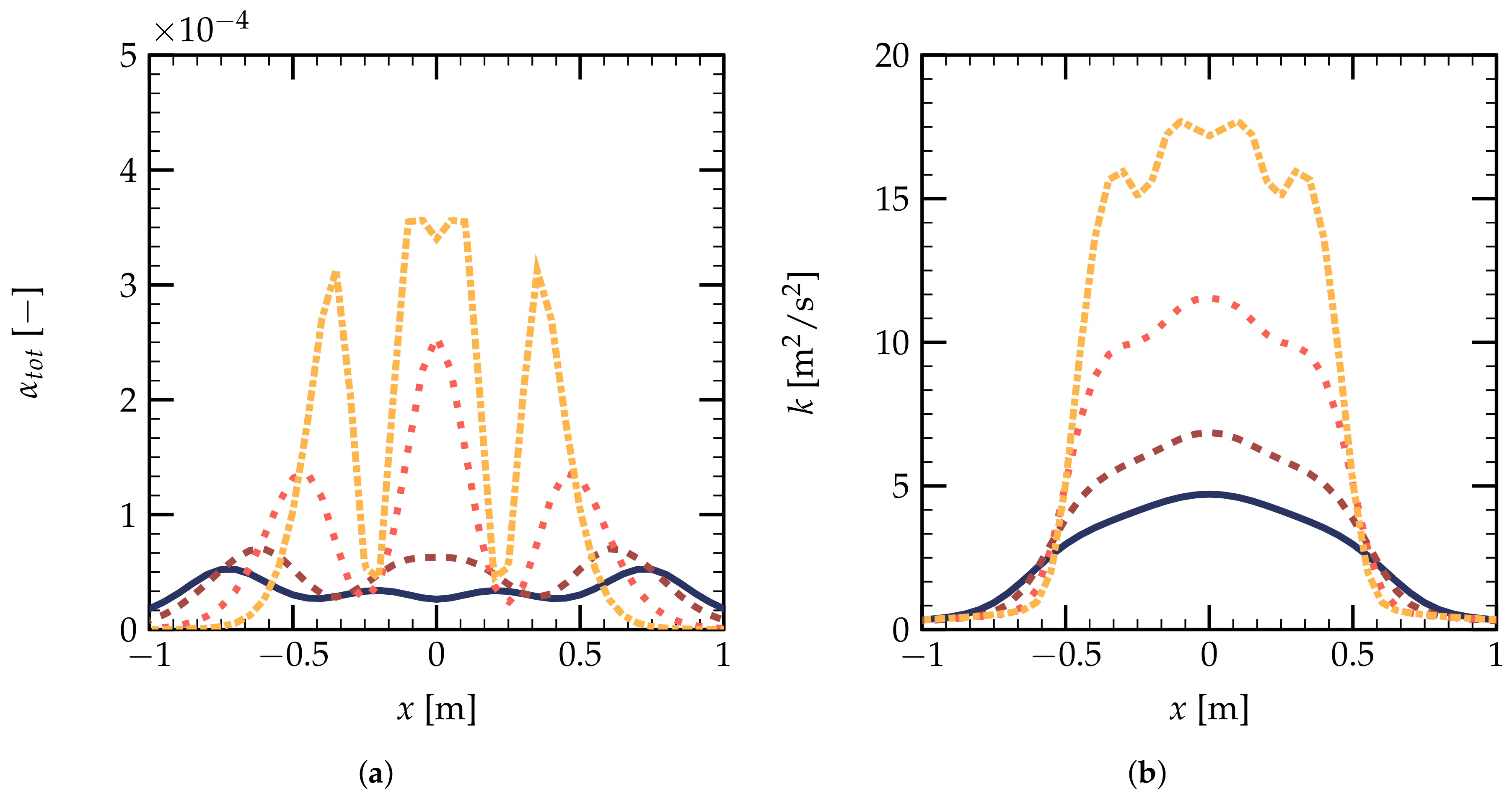
 ), m (
), m (  ), m (
), m (  ), and m (
), and m (  ).
).
 ), m (
), m (  ), m (
), m (  ), and m (
), and m (  ).
).
 ) and single nozzle (
) and single nozzle (  ); (b) evolution of as a function of the vertical distance h: two nozzles (
); (b) evolution of as a function of the vertical distance h: two nozzles (  ) and single nozzle (
) and single nozzle (  ).
).
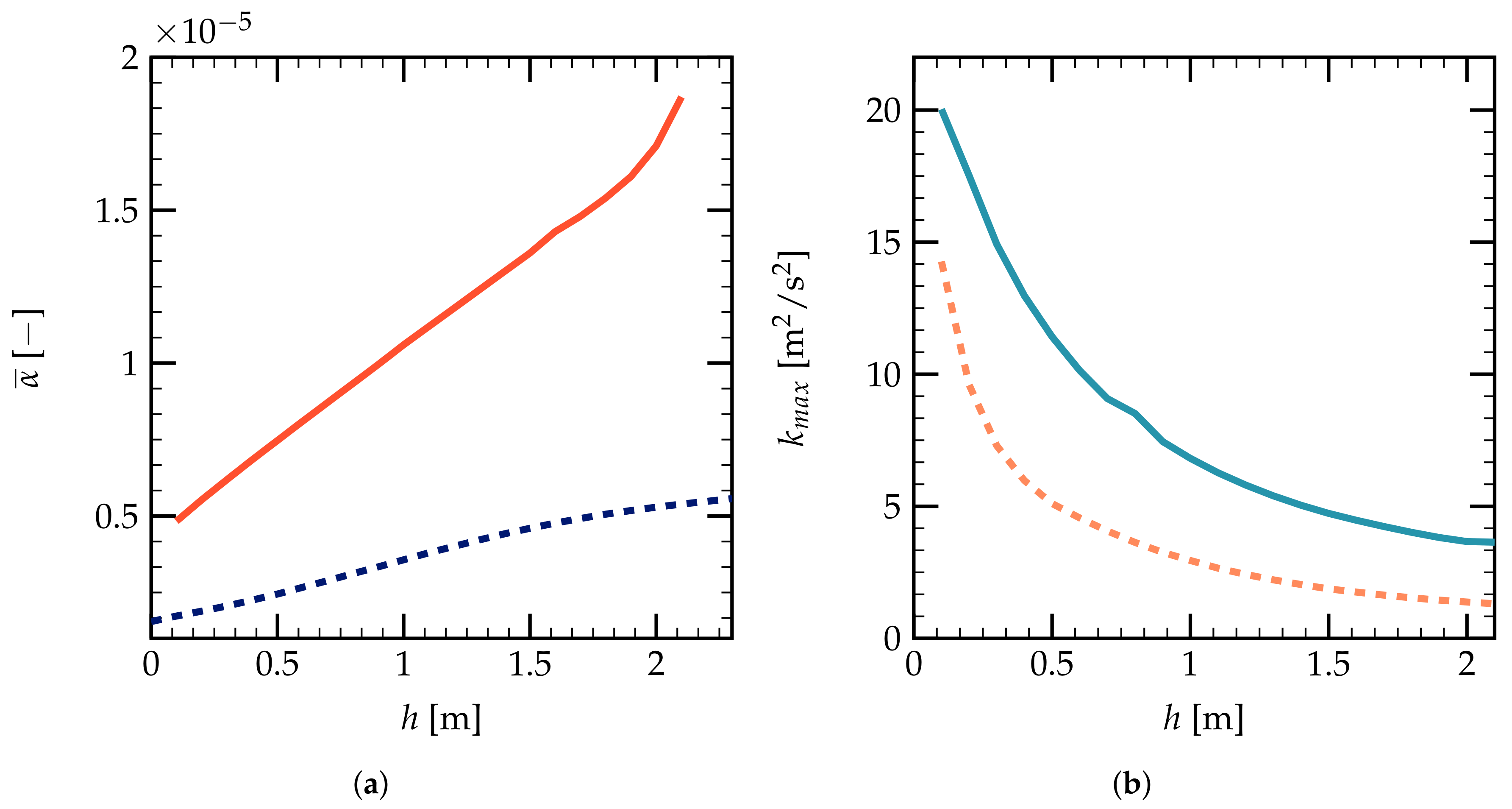
 ) and single nozzle (
) and single nozzle (  ); (b) evolution of as a function of the vertical distance h: two nozzles (
); (b) evolution of as a function of the vertical distance h: two nozzles (  ) and single nozzle (
) and single nozzle (  ).
).
| Particle Class | Diameter (m) |
|---|---|
| 1 | 55 |
| 2 | 166 |
| 3 | 277 |
| 4 | 388 |
| 5 | 500 |
| 6 | 611 |
| 7 | 722 |
| 8 | 833 |
| 9 | 944 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gai, G.; Hadjadj, A.; Kudriakov, S.; Mimouni, S.; Thomine, O. Numerical Study of Spray-Induced Turbulence Using Industrial Fire-Mitigation Nozzles. Energies 2021, 14, 1135. https://doi.org/10.3390/en14041135
Gai G, Hadjadj A, Kudriakov S, Mimouni S, Thomine O. Numerical Study of Spray-Induced Turbulence Using Industrial Fire-Mitigation Nozzles. Energies. 2021; 14(4):1135. https://doi.org/10.3390/en14041135
Chicago/Turabian StyleGai, Guodong, Abdellah Hadjadj, Sergey Kudriakov, Stephane Mimouni, and Olivier Thomine. 2021. "Numerical Study of Spray-Induced Turbulence Using Industrial Fire-Mitigation Nozzles" Energies 14, no. 4: 1135. https://doi.org/10.3390/en14041135
APA StyleGai, G., Hadjadj, A., Kudriakov, S., Mimouni, S., & Thomine, O. (2021). Numerical Study of Spray-Induced Turbulence Using Industrial Fire-Mitigation Nozzles. Energies, 14(4), 1135. https://doi.org/10.3390/en14041135








